Selective spectral displacement projection for multifrequency MRE

Abstract

We introduce a new motion encoding concept for the displacement vector in multifrequency Magnetic Resonance Elastography (MRE). Selective spectral displacement projection (SDP)-MRE can be applied to a vibration spectrum composed of three frequencies and exploits the filter condition of MRE for selecting one frequency each per spatial motion encoding direction. The selected components are simultaneously encoded in the phase of the MR signal. Therefore, the total MR phase is represented by a sum of phase portions, each corresponding to a distinct spatial projection and vibration frequency. The individual components can be decomposed by applying a Fourier-transform to the temporally-resolved phase images. SDP-MRE reduces the number of temporally-resolved MRE experiments for data acquisition by a factor of 3, while providing similar wave images as found using conventional monofrequency MRE.

1 Introduction

Pathological changes involve an alteration of tissue mechanical properties. For example, the increase of connective tissue within the liver during the progression of hepatic fibrosis leads to a stiffening of the organ [1]. On the other hand, the mechanical response of the brain is decreased in neurodegenerative diseases such as Multiple Sclerosis and Alzheimer’s disease [2, 3]. The correlation of the mechanical behavior of tissue and its integrity or disease state provides the basis for manual palpation which has been applied by medical doctors for centuries in order to detect stiffened tissue close to the body surface. The sensitivity of manual palpation was motivation for the development of Magnetic Resonance Elastography (MRE) as a non-invasive “remote palpation” technique [4, 5]. In MRE, external vibrations are introduced into the body and snapshots of the resulting mechanical wave are visualized using phase contrast-based MRI techniques. Subsequently, the phase images are analyzed for determining the mechanical properties of tissue deep under the surface in its in vivo environment [6]. Recently, MRE has matured to an accurate technique for grading the stage of hepatic fibrosis [7–9], and, to date, MRE represents the only noninvasive method that is capable of determining the in vivo mechanical properties of the brain without surgical intervention [2, 10, 11]. In addition, clinical MRE protocols have been engineered to assess developing pathologies in the breast [12], heart [13] and skeletal muscle [14, 15]. In addition, preclinical MRE studies at 9.4 T have found changes in brain tissue stiffness in multiple sclerosis and in hepatic fibrosis in animal models; therefore, pre-clinical MRE analysis should be useful for monitoring the therapeutic success of new treatments [16–18].

In conventional MRE the frequency of the motion encoding gradient (MEG) is matched to the frequency of the harmonic (monofrequency) vibration; therefore, the minimum echo time TE is increased by the duration of the MEG. This approach can suffer from low phase-to-noise ratio (PNR), particularly when low vibration frequencies are applied in tissues with relatively fast MR signal relaxation (short T2) such as the liver. Further, due to the long duration of the MEG, conventional MRE is not suitable for the examination of non-static structures such as the beating heart. To overcome this drawback, fractional encoding of harmonic motions, also referred to as fractional MRE, was introduced [19]. This method utilizes MEGs with durations shorter than the vibration period enabling fast data acquisition at the cost of a decreased motion encoding efficiency. Fractional encoding schemes were applied in order to examine the mechanical behavior of liver [20] and to reduce acquisition time in cardiac MRE [13].

Soon after, fractional MRE was refined for the simultaneous acquisition of multifrequency vibrations along one spatial dimension within one temporally-resolved MRE experiment [21]. This approach is commonly referred to as multifrequency MRE. In multifrequency MRE, the frequency-independent material parameters of the tissue are calculated either by fitting the measured dispersion curves of the complex shear modulus to rheological models [21] or by solving the inverse problem of viscoelasticity reconstruction employing an algebraic least-square solution [22]. So far, studies employing the simultaneous acquisition of multifrequency vibrations have been performed solely in 2D; only displacements perpendicular to the image plane were measured. In spite of this limitation, the new insights gained by multifrequency 2D MRE are significant, as a correlation of brain mechanics with the aging brain [23] as well as with Multiple Sclerosis [3] and Normal Pressure Hydrocephalus (NPH) [24] has been revealed.

Recently, MRE studies were conducted in which the full 3D displacement vector field was acquired [25–27]. 3D vector field MRE exhibits several advantages when compared with 2D MRE. For example, in shear modulus-based approaches, the shear wave can be separated from the compression wave by applying the curl-operator to the displacement vector field [27]. In addition, more realistic tissue models incorporating porosity can be considered [26] and tissue pressure changes can be identified by analyzing the divergence of the 3D displacement vector field [25].

However, the benefits of 3D vector field MRE are offset by a longer measurement time, which increases by a factor of three (the number of motion encoding directions) for each slice. Ultimately, for the derivation of frequency-independent material parameters beyond the shear modulus, multifrequency 3D displacement vector MRE data sets will have to be acquired. This further prolongs the measurement time of conventional MRE, in which individual experiments are performed consecutively with various monofrequency vibrations. An alternative would be to simultaneously excite and encode multifrequency vibrations for each of the three motion encoding directions in successive steps, reducing the number of individual experiments to three temporally-resolved MRE experiments per image slice. However, this approach implies reduced motion sensitivity at vibration frequencies that do not match the MEG frequency [19]. Further, increasing the number of MEG cycles does not increase the motion sensitivity, when the MEG and the spectral components of the vibration have different frequencies. This issue is less of a problem using low mechanical vibration frequency MRE (< 100 Hz) as typically performed in human scanners, where sufficient motion sensitivity can be provided using the fractional technique.

In high mechanical vibration frequency MRE (as is typically performed in pre-clinical or phantom studies using small scale, high field MR scanners), a larger number of MEG cycles needs to be applied in order to enhance motion sensitivity; here, the use of lower sensitivity fractional encoding schemes is not reasonable [28, 29]. For this reason, previous MRE studies examining the mechanical behavior of biological tissue at multiple frequencies in the higher dynamic range were performed by applying consecutive monofrequency MRE measurements with varying mechanical frequencies [30–32]. These limitations were motivation for the present work to develop a fast algorithm for the encoding of a multifrequency signal composed of three superposed sinusoidal vibrations along three sensitization directions. The proposed method reduces the measurement time without degrading motion sensitivity compared with conventional monofrequency MRE. In the proposed approach, three MEGs are applied simultaneously in the Read, Phase and Slice directions. The sequence parameters are carefully chosen for exploiting the filter condition of MRE, which has previously been applied to observe higher harmonics of a nonlinear shear wave [33]. We describe our new approach as selective spectral displacement projection (SDP)-MRE, since the filter condition is exploited for selecting one frequency in each spatial direction. The selected components are simultaneously encoded into the phase of the MR signal and the acquisition of temporally resolved phase images enables the decomposition of the individual components.

2 Theory

The basic equation in MRE is represented by an integral, which describes the encoding of the displacement u(t) of an isochromat into the phase φ(s) of the MR signal by applying a time-harmonic magnetic field gradient G [4]:

$$\phi (s)=\gamma {\int }_s^{s+T}\mathit{G}(t)·\mathit{u}(t)dt.$$ (1)

Here, the gyromagnetic ratio of the proton, the duration and the start time of the MEG are represented by γ, T and s, respectively. The phase φ of the MR signal can be expressed as the sum of three integrals featuring the projections of G and u onto the axes of a Cartesian system:

$$\phi (s)={\sum }_{j=1}^3{\phi }_j(s)=\gamma {\sum }_{j=1}^3{\int }_s^{s+T}{G}_j(t)·u_j(t)dt.$$ (2)

This formulation implies that all MEG-projections exhibit the same start time s and duration T. Further, we assume sinusoidal time-harmonic functions for the MEG-projections with frequencies (1/τ_j) and that the vibration is represented by a superposition of Q sinusoidal waveforms with frequencies f_q, q=1, 2, …, Q. With these assumptions, the solution of the integral equation is represented by,

$$\phi (s)={\sum }_{j=1}^3{\phi }_j(s)={\sum }_{j=1}^3{\sum }_{q=1}^Q{\xi }_{jq}{u}_{jq}^{0}sin\left(2\pi f_{q}s+{\theta }_{jq}\right),$$ (3)

with

$${\xi }_{jq}=\{\begin{array}{ll}\frac{1}{2}\gamma g_j{N}_j{\tau }_j,\hfill & f_q=\frac{1}{{\tau }_j}\hfill \\ \frac{\gamma g_j{\tau }_{j}sin(\pi N_j{\tau }_j{f}_q)}{\pi ({\tau }_j^2{f}_q^2-1)},\hfill & f_q\ne \frac{1}{{\tau }_j}.\hfill \end{array}$$ (4a) (4b)

In (3), the amplitude $u_{jq}^0$ of the harmonic displacement projection, the encoding efficiency ξ_jq and a phase shift θ_jq are specified for each frequency component and projection.

The parameters of the MEG projections on the Cartesian axes, specifically the amplitude g_j, the number of MEG-cycles N_j and the duration τ_j of one harmonic cycle of the respective MEG projection are identified in (4). Of special note, SDP-MRE imposes that the MEG duration T is equal to T = N_jτ_j for all j and that the vibration spectrum represents a superposition of three sinusoidal waveforms with the frequencies f_q, q=1,2,3, that are equal to the frequencies of the MEG-projections (1/τ_j), j=1,2,3.

We can derive the filter condition [33], which sets the basis of SDP-MRE, directly from (4b). No harmonic motion is encoded, if the argument of the sinusoidal function in (4b) is equal to multiples of π. Therefore, it follows:

Filter condition

$$f_q=\frac{n}{N_j{\tau }_j}=\frac{n}{T},n\in \mathbb{N}\backslash \{N_j\}\Rightarrow {\xi }_{jq}=0$$ (5)

Eq. (5) essentially reveals that the base frequency f_b, defined as the reciprocal of the MEG duration T, does not contribute to the phase accumulation. Further, all multiples of f_b are filtered out with the exception of the vibration frequency that is equal to the frequency (1/τ_j) of the respective MEG projection. Therefore, the total MR phase φ (3) is represented by a sum of phase portions φ_j, each corresponding to a distinct spatial projection and vibration frequency. Thus, the individual components can be decomposed by applying a Fourier-transform to φ along the MEG-start time s.

3 Methods

In this article, we show the feasibility of the new motion encoding concept in an SDP-MRE experiment with a mechanical excitation signal, which represents a superposition of 5 kHz, 6 kHz and 7 kHz harmonic vibrations. The results are compared to three conventional MRE measurements using monofrequency motion encoding as described below.

3.1 Experimental Setup

The experimental apparatus used in this study has been previously described [29] and is illustrated in figure 1. Briefly, experiments were performed in an 11.74 Tesla Bruker vertical bore magnet (φ = 56 mm). A clear bore 10 mm internal diameter saddle RF coil was used inside a 19 mm internal diameter gradient coil with a maximum magnetic field gradient of 300 Gauss/cm per direction. The test tube attached to a piezoelectric stack (6.5 mm × 6.5 mm × 18 mm, Thor Labs Inc.), which was fixed to a counter mass, was centered in the RF saddle coil.

Figure 1.

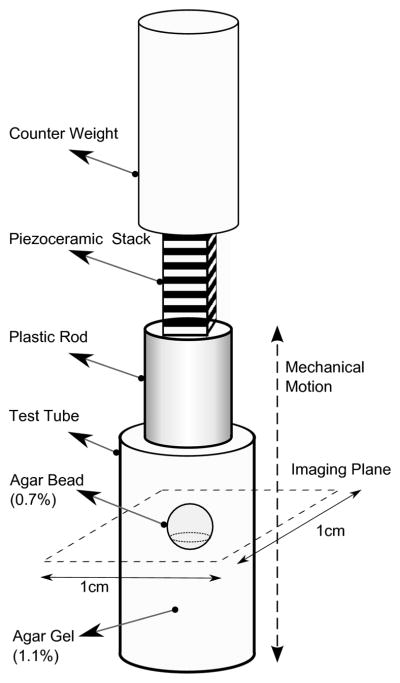
The axisymmetric experimental setup used in this study. The dashed line indicates the position of the image plane.

For mechanical excitation, in all experiments the piezoelectric stack was excited with a signal of 5 ms duration that was a superposition of sinusoidal wave forms of 5 kHz, 6 kHz and 7 kHz with equal amplitudes. A direct current bias was added to the harmonic signal in order to prevent negative voltages which are harmful to the integrity of the piezoelectric stack. The axisymmetric experimental setup causes a geometric focusing of mechanical shear waves within the sample, and this configuration compensates for the strong damping of soft tissue in the kHz-range [34]. We used an inhomogeneous sample composed of an agarose bead embedded in agarose gel of a different concentration in all experiments. In this way, we generated displacements in all three spatial dimensions within the image slice caused by reflection and refraction of the mechanical shear wave at the spherical surface of the bead.

3.2 Sample Preparation

A cylindrical plastic container (height = 40 mm; inner diameter = 9 mm) was used as the test tube. The sample was composed of an agarose bead (0.7% by water) with diameter 4 mm embedded in agarose gel (1.1% by water). The sample was freshly prepared 1 day before the experiment.

3.3 Image Acquisition

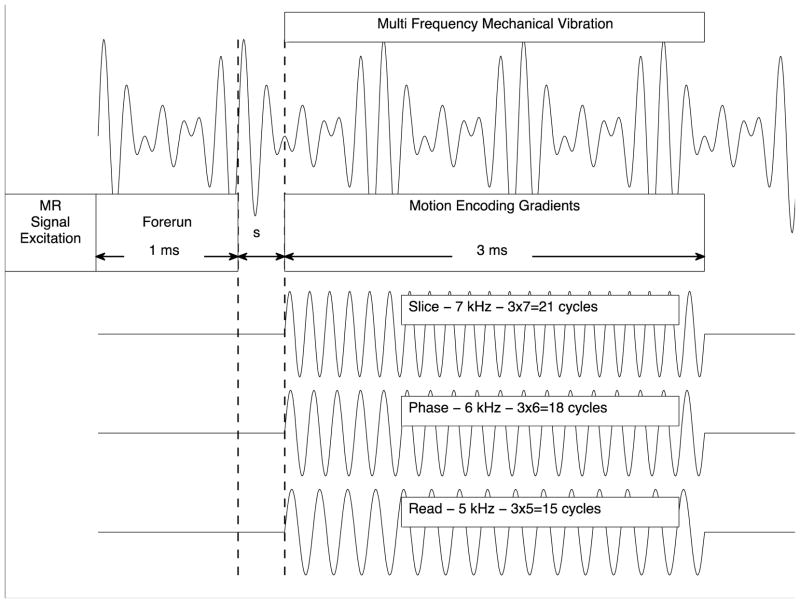
We used a gradient-echo based MR pulse sequence for data acquisition in one axial slice with the following sequence parameters: repetition time TR=500 ms; echo time TE=2.94 ms; flip angle 30°; Field of View (FOV)=10 mm × 10 mm; slice thickness = 0.25 mm; matrix size = 128 × 128. The MR sequence was upgraded with MEGs with a strength of 80 Gauss/cm in each spatial direction for motion sensitization. As illustrated in figure 2, we exploited the filter condition (5) by choosing an MEG gradient cycle number of 15, 18 and 21, and an MEG frequency of 5, kHz, 6 kHz and 7 kHz for the MEG component in Read-, Phase- and Slice-direction, respectively. This resulted in an MEG duration of T = 3 ms. Depending on the respective time step, the start of the MEG was delayed between 1 ms and 2 ms relative to the start of the multifrequency mechanical excitation signal. A forerun of 1 ms is to ensure penetration of the shear wave into the sample center before application of the MEG. Thus the motion encoding upgrade of the standard gradient-echo based MR pulse sequence involves an increase of TE from 2.94 ms to 7.94 ms. With the chosen MEG parameters, the base frequency f_b, as defined in the theory section, is equal to 0.3̄ kHz and all vibration frequencies used were multiples of f_b. Consequently, with regard to one motion component, only the vibration corresponding to the frequency of the respective MEG-component contributed to the accumulated MR phase φ, while the other two frequencies were filtered out for this projection. Thus, out of the applied three frequencies, the 5 kHz-vibration in Read-, the 6 kHz-vibration in Phase- and the 7 kHz-vibration in Slice-direction were encoded simultaneously into φ. Finally, the temporal resolution of φ(s) was achieved by shifting the trigger 16 times over 1 ms period. At each time step, two acquisitions were performed with inverse polarity MEG for calculating phase difference images, which are cleared of biases due to constant field inhomogeneities.

Figure 2.

A sketch of the motion encoding scheme in SDP-MRE relative to the multifrequency mechanical excitation signal is shown during one TR. The trigger is shifted 16 times over a 1 ms interval in order to vary the starting time s of the MEG relative to the mechanical vibration for temporal resolution. The start of the MEG was delayed 1 ms – 2 ms (depending on the respective time step) relative to the start of the mechanical excitation signal to ensure penetration of the shear wave into the sample center before motion encoding.

3.4 Choice of image plane

The position of the image slice was determined in MRE-pretests of reduced spatial and temporal resolution in 10 axial slices covering the beads. The image slice was chosen by the decision criterion that displacement in phase, read and slice directions were maximal. An axial slice in between the equator and the south pole of the bead fulfilled this criterion (see figure 1).

3.5 Data Processing

The accumulated, temporally-resolved MR phase φ(s) represents a multifrequency function of the starting time s of the MEG. The discrete Fourier transformation of φ(s) was calculated for obtaining complex phase images Φ(f) at the frequency f and Φ(f) was scaled to complex wave images using the scaling factor given in (4a). This decomposition procedure is similar to that applied to MR phase data that originated from multifrequency vibrations along one dimension and that were acquired by exploiting the broad-band motion sensitization nature of the MEG [21]. This is different from SDP-MRE. Here we exploit the filter condition of MRE by encoding one of the three vibration components along each of the three spatial directions and combine these three portions of data content into the MR phase (see (3)).

3.6 Comparative Experiment

In order to check the performance of the new approach, we also performed a comparative experiment utilizing a conventional motion encoding scheme. For this purpose, we acquired the wave images using the same sequence parameters as that used in SDP-MRE with the exception that the wave images were acquired in three consecutive steps. In each individual step, only one of the three gradients, which are illustrated in figure 2, was active. Due to the consecutive acquisition of the individual motion components, the total measurement time of the comparative experiment was three times longer than of SDP-MRE. For comparison, a 2D local frequency estimation algorithm (LFE) [35] was applied to the wave images and the resulting images of the wavelength were spatially averaged over the agarose bead.

4 Results

The complex wave images acquired with SDP-MRE and with conventional MRE are illustrated in figure 3. The wave length varies from column to column, as both the vibration frequency and the displacement projection are different. For the same reason we can also observe different wave amplitudes in different projections determined with the same method. The amplitude difference between both methods for same frequencies is small. More importantly, we observe similar wave structures for same projections in figure 3. Consequently, the LFE-derived wave lengths are identical within the error margins. The spatial average of the wave length over the agarose bead results in (0.7±0.1) mm, (0.5±0.1) mm and (0.4±0.1) mm for the 5 kHz-, 6 kHz- and 7 kHz-vibration, respectively, independent of the used MRE approach.

Figure 3.

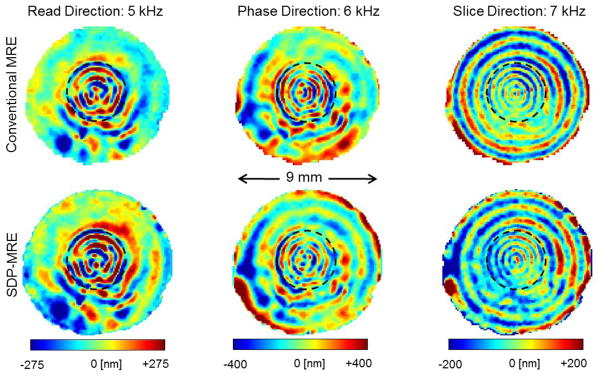
Complex wave images (real part) are shown for the axial image slice of a test tube filled with the agarose bead embedded in agarose gel of a higher concentration. The bead is visible within the image slice and is demarcated with dashed lines. The three images in the top row correspond to MRE experiments using conventional motion encoding conducted in individual, consecutive steps for each displacement projection. Images in the bottom row were acquired simultaneously with SDP-MRE. The motion encoding direction for the 5 kHz-, 6 kHz- and 7 kHz-vibrations, respectively were Read, Phase and Slice.

Discussion

The presented work describes a new motion encoding concept (SDP-MRE) for the displacement vector in multifrequency MRE. SDP-MRE enables the simultaneous acquisition of three mutually orthogonal displacement components of different frequencies by exploiting the MRE filter condition (5). In the present proof-of-concept study, we successfully applied SDP-MRE to a multifrequency vibration and selected the 5 kHz-, 6 kHz- and 7 kHz-frequency for the Read-, Phase- and Slice-projection of the displacement, respectively. For the acquisition of all displacement components of the three frequency vibration spectrum, these relations have to be permuted, resulting in a total of three SDP-MRE experiments. A feature of the arrangement of the MEGs in SDP-MRE is that it is not bound to a specific sequence type, but can be integrated into most pulse sequences typically used in MRE, such as the gradient-echo, spin-echo and EPI sequences. Further, the new approach is not bound to a specific dynamic range. It is applicable all the way from the low frequency range of human MRE to the high frequency range of micro-MRE, as long as the three used frequencies used exhibit a common divisor and the filter condition (5) is satisfied.

SDP-MRE is faster than conventional MRE, where all three displacement projections are acquired individually for each frequency component in consecutive steps. The time saving factor, however, cannot be quantified exactly. In the presented study, the available hardware setup limited us to the applied frequency range. Thus 16 time steps had to be acquired for frequency decomposition. The minimum number of time steps can be reduced by choosing a spectrum that consists of the first three harmonics; in the range of human MRE, for example 25 Hz, 50 Hz and 75 Hz. For the decomposition of such a signal, a minimum of only eight time steps are necessary. In conventional, monofrequency MRE typically four [2, 18] to eight [11, 29, 36] time steps are acquired. With these values we can deduce that SDP-MRE is 1.5 – 3 times faster than conventional MRE. However, beyond the pure measurement time, other factors play a role concerning the duration of a multifrequency experiment. The measurement interruption due to the manual adjustment of the waveform generator, which has to be performed in between consecutive conventional MRE experiments, is not applicable by SDP-MRE and saves additional time in between experiments.

In addition to speeding up the acquisition of a three frequency vibration spectrum along three encoding directions, SDP-MRE also helps, we believe, to increase the measurement accuracy. In conventional MRE, nine individual experiments have to be conducted, each during a different physical vibration state. This represents a possible source of error, as misalignment of the image slices can occur between the individual acquisitions, especially when performing in vivo MRE. Data acquisition using SDP-MRE necessitates the generation of only three physical vibration states, which is an improvement compared to the conventional approach.

One limitation of the proposed approach is that it can only be applied to a vibration spectrum composed of three frequencies maximum. Also, we expected the wave images to be noisier with SDP-MRE when compared with the conventional approach, as the additional MEGs reinforce dephasing due to diffusion. However, we found that the quality of the wave images were similar in both approaches. Diffusion effects will even be lower, when performing SDP-MRE exams on real organs, which typically exhibit a lower diffusion coefficient than agarose [37–39].

The time saved by SDP-MRE, as outlined above, can also be achieved by applying multifrequency MRE based on fractional motion encoding [21]. Using this approach, the three mechanical frequencies are recorded simultaneously for each of the three directions reducing by a factor of three the number temporally resolved experiments needed for the acquisition of the three frequency spectrum along three encoding directions. However, it is inherent to fractional motion encoding concepts that the encoding efficiency cannot be increased by increasing the number of MEG cycles, whereas this is the case in SPD-MRE (see eq. 4). We therefore expect SDP to be adopted by the community for multifrequency MRE studies in the high dynamic range, where typically multiple MEG cycles are used to compensate for the strong mechanical damping necessitating increased motion sensitivity. Here, the number of temporally-resolved MRE experiments can be reduced without any downside. For example, for in vivo human MRE studies, mechanical excitation frequencies as low as ~ 25 Hz – 100 Hz are often used. The duration of the MEG in this case is restricted by tissue relaxation, because the MEG duration has to be added to the minimum echo time. The MR signal decay due to T2-relaxation is stronger in liver than in brain [40]. Therefore, using the same spin-echo EPI-MRE sequence, MEGs with longer durations can be used in brain (~ 66 ms) as compared to liver (~ 20 ms) [21]. In SDP-MRE, the three frequencies have to be chosen carefully to be multiples of the reciprocal value of the MEG duration (see theory section). In the dynamic range of human MRE, for example combinations for the three frequencies such as 25 Hz, 50 Hz and 75 Hz with a 40 ms MEG duration, or also 40 Hz, 60 Hz and 80 Hz with a 50 ms MEG duration can be used. In the context of these considerations, SDP-MRE can potentially be adapted for the multifrequency examination of in vivo human brain rather than liver.

5 Conclusion

We introduced a new motion encoding concept (SDP-MRE) that exploits the filter condition of MRE for reducing the acquisition time for a displacement vector of a vibration spectrum comprised of three frequencies. In SDP-MRE, one vibration frequency each is selected per spatial direction, and the respective displacement projections are simultaneously encoded into the MR phase with the same encoding efficiency as in conventional monofrequency MRE. A comparison of SDP-MRE with conventional MRE yielded the same LFE-derived wave lengths.