Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Sep 7.
Published in final edited form as: Phys Med Biol. 2013 Aug 6;58(17):5821–5831. doi: 10.1088/0031-9155/58/17/5821

Measurement of characteristic prompt gamma rays emitted from oxygen and carbon in tissue-equivalent samples during proton beam irradiation

Jerimy C Polf 1, Rajesh Panthi 1, Dennis S Mackin 2, Matt McCleskey 3, Antti Saastamoinen 3, Brian T Roeder 3, Sam Beddar 2
PMCID: PMC3799908  NIHMSID: NIHMS515093  PMID: 23920051

Abstract

The purpose of this work was to characterize how prompt gamma (PG) emission from tissue changes as a function of carbon and oxygen concentration, and to assess the feasibility of determining elemental concentration in tissues irradiated with proton beams. For this study, four tissue-equivalent water-sucrose samples with differing densities and concentrations of carbon, hydrogen, and oxygen were irradiated with a 48 MeV proton pencil beam. The PG spectrum emitted from each sample was measured using a high-purity germanium detector, and the absolute detection efficiency of the detector, average beam current, and delivered dose distribution were also measured. Changes to the total PG emission from 12C (4.44 MeV) and 16O (6.13 MeV) per incident proton and per Gray of absorbed dose were characterized as a function of carbon and oxygen concentration in the sample. The intensity of the 4.44 MeV PG emission per incident proton was found to be nearly constant for all samples regardless of their carbon concentration. However, we found that the 6.13 MeV PG emission increased linearly with the total amount (in grams) of oxygen irradiated in the sample. From the measured PG data, we determined that 1.64 × 107 oxygen PGs were emitted per gram of oxygen irradiated per Gray of absorbed dose delivered with a 48 MeV proton beam. These results indicate that the 6.13 MeV PG emission from 16O is proportional to the concentration of oxygen in tissue irradiated with proton beams, showing that it is possible to determine the concentration of oxygen within tissues irradiated with proton beams by measuring 16O PG emission.

Keywords: Proton therapy, prompt gamma, tissue elemental concentration

1. Introduction

In external beam radiation therapy, uncertainties in dose delivery arising from variations in patient anatomy can lead to under dosage of the tumor volume, as well as, over dosage of healthy tissue, leading to reduced tumor control and an increased rate of normal tissue complications. To address these problems, researchers have put forth a large effort to improve both treatment accuracy (i.e., IMRT, IGRT, proton radiation therapy) and understanding of the responses of both cancerous and healthy tissues to radiation (Kuban et al. 2003; Beddar et al. 2007; Zhang et al. 2007; Butterworth et al. 2012; Paganetti 2012b). Despite these advances, the accuracy of dose delivery remains limited because of organ motion, daily variation in patient anatomy, and insufficient knowledge of the day-to-day responses of cancerous and normal tissues to irradiation. These limitations continue to present a major barrier to improving the efficacy of both photon and proton beam radiation therapy.

Fortunately, inherent to proton therapy is the emission of elemental “prompt” gammas (PG) resulting from nonelastic (Paganetti 2012a) proton-nucleus interactions in tissues during irradiation. Because PG emission occurs only where the proton beam interacts with the patient, PG emission is strongly correlated to delivered dose (Moteabbed et al. 2011), making PG emission a prime signal for beam range verification (Min et al. 2006; Polf et al. 2009; Testa et al. 2010; Smeets et al. 2012). Additionally, each element in tissue emits a unique spectrum of PG energies, providing a signal that is proportional to the elemental composition and density of the tissues irradiated (Polf et al. 2009; Richard et al. 2009; Moteabbed et al. 2011; Polf et al. 2011).

In vivo measurement of the PG spectrum during proton beam irradiation would provide information about the true interactions of the proton beam during treatment delivery. This fact has led several researchers to study methods for PG measurement and PG imaging for range verification (Kim et al. 2009; Roellinghoff et al. 2011; Bom et al. 2012; Mackin et al. 2012; Min et al. 2012). Additionally, other researchers have studied the application of PG measurement to determine the composition and density of tumors and healthy tissues irradiated over the course of proton radiation therapy (Polf et al. 2009; Polf et al. 2011).

The ability to monitor and image changes to the composition of tumor and healthy tissues over a full course of treatment could provide a direct method for evaluating the response of these tissues to proton therapy. For instance, measurement of a tissue’s elemental composition could be used to determine tissue oxygen concentration, providing a method to track changes in the oxygenation levels and blood flow of tumors. Additionally, changes in the elemental composition or density of irradiated healthy tissues over the course of treatment could be correlated to the onset of adverse treatment related side effects. If such a relationship could be quantified, then measurement of elemental PG emission during each daily treatment fraction could be used to predict a patient’s probability of developing post treatment side effects. This information on the response of the tumor and healthy tissues to irradiation could then be used by the oncologist to adjust the patient’s treatment plan to ensure proper dose delivery to the tumor while minimizing irradiation of healthy tissues to help reduce post treatment side effects.

However, to fully deploy a PG measurement system clinically, much effort is still needed to 1) develop efficient and accurate PG detection or imaging systems capable of working in a proton treatment vault, 2) obtain a full understanding of the spatial characteristics of PG emission around the patient, and 3) understand the relationship between PG emission and the density and elemental concentration of the irradiated tissues. The purpose of this work was to characterize how PG emission from tissue changes as a function of carbon and oxygen concentration, and to assess the feasibility of determining elemental concentration in tissues irradiated with proton beams. First we produced samples of a water-sucrose mixture with differing amounts of sucrose and determined the density and elemental composition of each sample mixture. Then, we measured the PG spectra emitted from these mixtures as they were irradiated with a 48 MeV proton pencil beam, and we determined the intensity of the 6.13 MeV PGs from 16O and the 4.44 MeV PGs from 12C. Next, we characterized the changes in these two elemental emission lines as a function of the concentration of oxygen and carbon in the mixtures. Finally, we were able to use the data to determine the total amount of oxygen irradiated in the samples as a function of 16O PGs emitted from the samples.

2. Methods and Materials

2.1. Sample preparations

For this study, we irradiated four sample solutions of differing densities and containing differing concentrations of oxygen, carbon, and hydrogen in a small container (130 cm3 volume). The first sample consisted of 130 grams of water, the second sample consisted of a solution of 130 grams of water and 25 grams of sucrose (C12H22O11, 1.59 g/cm3), the third sample consisted of a solution of 130 grams of water and 75 grams of sucrose, and the fourth sample consisted of a solution of 130 grams of water and 130 grams of sucrose. Each solution was stirred to fully dissolve the sucrose in the water. For the spectral measurements, the sample container (130 cm3) was completely filled with one of the four sample solutions. The sample container was weighed first while empty and then again after being filled with a solution; with the difference in weights considered the weight of the sample. The density of the solution was then calculated as ρ (g/cm3) = sample weight/container volume. The chemical composition, density, and grams of oxygen, carbon, and hydrogen in each irradiated sample are given in Table 1, along with the composition and density (ICRU 1992) of several types of tissue. Because the elemental composition and density of the samples used in our study are similar to the composition and density of human tissues, the PG signal produced during proton beam irradiation of these samples is an analog to the signal produced during proton therapy.

Table 1.

Composition and density of the water-sucrose samples used in our study and of several human tissues with similar composition and density (ICRU 1992).

sample water (g) sucrose (g) density (g/cm3) composition (% by mass)
oxygen carbon hydrogen
1 130 0 1 88.9 0 11.1
2 114.7 22 1.05 82.7 6.9 10.4
3 89.7 52.3 1.1 75.2 15.4 9.4
4 78.6 78.6 1.21 70.2 21.1 8.7
Brain 1.04 71.2 14.5 10.7
Heart 1.05 71.8 13.9 10.4
Liver 1.06 71.6 13.9 10.2
Muscle 1.05 71 14.3 10.2
Open in a new tab

2.2. PG spectra measurement

For the PG spectra measurements, the front face of the sample container was placed 20 cm from the end of the beam transport pipe, with the beam incident on the center of the front face of the sample container, as shown in Figure 1. The sample container consisted of a 5 × 5 × 5.2 cm3 Lucite phantom, with a volume of 130 cm3. The side, back, and bottom walls of the container were 3 mm thick, and the front face was 1.5 mm thick. We irradiated our samples with a 48 MeV proton pencil beam. Each sample was irradiated for ~20 minutes, with average beam currents at the sample container of 7.5 picoAmps for samples 1, 2, and 3 and 15 picoAmps for sample 4. We used the measurements of the average beam current and irradiation time to determine the total number of protons delivered to each sample during each irradiation.

Figure 1.

Figure 1

Open in a new tab

The sample container was placed 20 cm from the end of the beam pipe, with the clover detector located perpendicular to the container. (a) Gafchromic film was placed along the beam direction and attached to the front face of the container, and (b) an optically stimulated luminescence dosimeter holder used for dose calibration was placed perpendicular to the beam direction at a depth of 1.4 cm.

The spectrum of PGs emitted during sample irradiation was measured using a high-purity germanium (HPGe) clover detector identical to that described by Lesher et al. (2010). This detector setup consisted of 4 n-type germanium crystals, 50 mm in diameter and 80 mm in length, arranged in a four-leaf clover pattern inside of a single cryostat located 30 cm from the central axis of the proton beam. For each irradiation, the PG spectrum was measured from 0 to 6.5 MeV by each of the 4 HPGe detectors in the clover and summed together to produce the total measured PG spectrum for the clover, which was considered the total PG spectrum for each sample.

To compare the total spectra, we first divided the spectrum measured for each sample by the number of protons delivered during irradiation. This allowed us to directly compare the PG intensity per incident proton emitted from each sample. To determine the true intensity of the 12C and 16O emission lines at 4.44 MeV and 6.13 MeV, respectively, we subtracted the background signal from the emission peaks by fitting a straight line through the high and low energy values of the emission peak. Then, using the background fit equation, we determined the background value for each energy bin contained in the emission peak and subtracted this value from the measured value in each energy bin. We then summed the background subtracted values for each energy bin in the emission peak to get the true number of 12C and 16O PGs measured during irradiation.

2.3. Detector efficiency

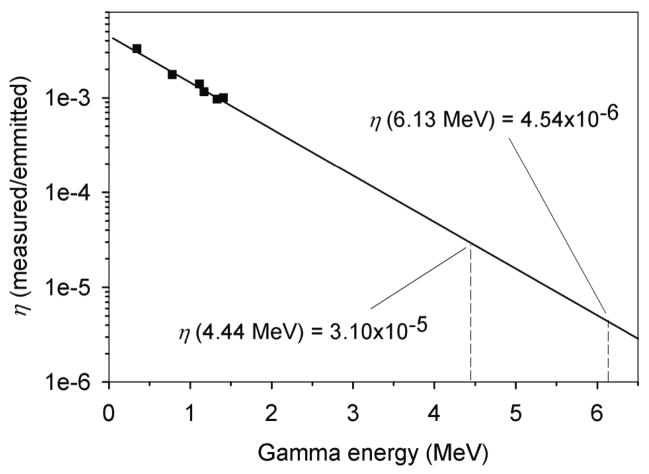
To determine the total detection efficiency of the clover detector, we used 60Co and 152Eu check sources of known activity. We first individually placed each check source in the center of the empty sample container, which was located in the same position as it was during the sample irradiations. Next, we measured the emission spectra from these check sources for a known time. Then, on the basis of the activity of the check source, the time of the measurement, and the known branching ratios for each gamma emission line, we determined the total number of emitted gammas of a given energy (E). We then determined the clover detectors absolute detection efficiency η (E) as a function of energy, as given by the equation η(E)=(numberofmeasuregammas(E))/(totalnumberofemittedgammas(E)). Finally, as shown in Figure 2, we fit the η values at gamma energies of 1.17 MeV and 1.33 MeV (from 60Co) and 0.334 MeV, 0.779 MeV, 1.112 MeV, and 1.408 MeV (from 152Eu) to an exponential function. Using this function, we determined the detection efficiency of the clover detector for 16O PG emission to be η(6.13 MeV) = 4.54 × 10−6 and for 12C PG emission to be η(4.44 MeV) = 3.10 × 10−5.

Figure 2.

Figure 2

Open in a new tab

Absolute detection efficiency (η) measured using 60Co and 152Eu check sources (squares) and the exponential fit of η (solid line) as a function of gamma energy. The η values at the energy of 12C (4.44 MeV) and 16O (6.13 MeV) prompt gammas are shown.

2.4. Beam characterization and dose measurements

We first determined the spatial profile of the proton beam using gafchromic EBT2 film (International Specialty Products, Wayne, NJ). We placed the EBT2 film on the outer surface of the front face of the sample container to determine the lateral fluence distribution and along the beam central axis within the (water filled) container to determine the depth dose distribution. Because gafchromic film has been shown to be accurate in measuring the lateral profiles and distal range of low-energy proton beams (Daftari et al. 1999; Kirby et al. 2010), and because we were not interested in measuring the absolute dose delivered with the films, we concluded that film measurements were adequate for determining the size and range of the proton beam.

After irradiation, the films were scanned at a resolution of 150 dpi using an Epson Perfection 330 Photo LED scanner, as shown in Figure 3, and analyzed using the ImageJ processing software (Rasband 2013). Prior to exposure, calibration marks were made along the edges of the films at 1 cm intervals with a ballpoint pen. Because these marks were visible along the bottom edge of the image (Figure 3b), we analyzed the spacing of the marks using ImageJ to determine a pixels-per-centimeter (pixels/cm) calibration for the image so that the Bragg peak range and lateral extent of the beam could be determined. Next, 1D profiles were extracted from the film images along the central axis of the Bragg peak and along the center of the fluence profile in both lateral directions. Using these profiles and our pixels/cm calibration for the images, we determined that the shape of the beam was highly rectangular, with lateral full-width-half-maximum (FWHM) dimensions of 1.1 cm wide by 0.6 cm high, and that the depth of the distal 50% of the Bragg peak was 1.50 cm, 1.44 cm, 1.36 cm, and 1.26 cm for samples 1, 2, 3, and 4, respectively.

Figure 3.

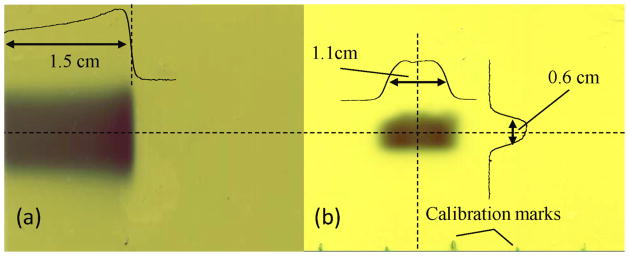
Figure 3

Open in a new tab

EBT2 film measurements of (a) the proton Bragg peak in water and (b) the beam lateral fluence profile at the entrance of the sample container. Dashed lines indicate location of 1D depth dose and lateral profiles overlaid on the films. The distance to the 50% distal falloff of the Bragg peak in water was 1.5 cm and the FWHM of the lateral profiles were 1.1 cm and 0.6 cm, as indicated.

Next, we determined the dose delivered per proton at the depth of the Bragg peak in water by the proton beam. To do this, we first determined the total dose delivered by irradiating 5 optically stimulated luminescence dosimeters (OSLD). Each OSLD measured 1 mm in diameter and ~0.3 mm thick, and all 5 were placed in a thin (0.9 mm) light-tight package (Yukihara et al. 2005). The package (containing all 5 OSLDs) was placed at a depth of 1.4 mm (corresponding to the position of the Bragg peak) in the sample container filled with water. The samples were irradiated for 76 seconds with the proton beam, with an average beam current of 15 picoAmps at the sample container. Therefore, we determined that the number of protons (p) delivered to the water sample for the dose measurement was ~7.1 × 109.

Following irradiation, the OSLDs were sent to the Oklahoma Center for Radiation Research (OCRP 2013), where they were processed and read out. The final OSL signal was determined as the average of the signal measured from each of the 5 individual OSLDs. The dose delivered to the OSLDs was then determined according to the procedures outlined by Yukihara et al. (2005; 2008). From the OSLD measurements, we determined that a dose (Dw) of 14 Gy was delivered to the water sample at a depth of 1.4 cm during the irradiation. Dividing the delivered dose by p gave us the dose per proton in water at a depth of 1.4 cm of Dw/p = 1.96 × 10−9 Gy/proton for our experimental setup. We used Dw/p as our standard dose calibration value. For the irradiation of a given sample solution (s), we determined the “dose to water” delivered according to the equation D(s)=(Dw/p)·p(s), where p(s) is the total number of protons delivered during the irradiation of sample s.

3. Results and Discussion

3.1. PG spectra

The measured PG spectra are plotted in Figure 4. The plotted spectrum for each sample is divided by the total number of protons delivered during irradiation, given in Table 2. Present in the measured spectra are PG emission lines for 16O: 6.13 MeV, 5.62 MeV (single escape peak), 5.11 MeV (double escape peak), 2.74 MeV, and 2.23 MeV (single escape peak), for 15O: 5.21 MeV, 4.70 MeV (single escape peak), and 4.19 MeV (double escape peak), and for 12C: 4.44 MeV, 3.93 MeV (single escape peak), and 3.42 MeV (double escape peak). We found that the PG emission per incident proton was almost identical for all 4 irradiated samples. However, as shown in the inset in Figure 4, the intensity of the PG emission from 16O and 15O decreased as the amount of sucrose in the sample increased, yet the 4.44 MeV PG emission intensity from 12C was constant for all irradiated samples.

Figure 4.

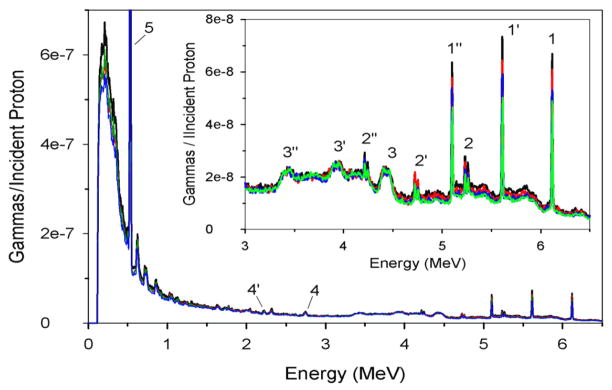
Figure 4

Open in a new tab

Measured prompt gamma spectra per incident proton emitted from the irradiated water (black line), and the 25 g (red line), 75 g (blue line), and 130 g (green line) sucrose solutions. The spectra show the prompt gamma, single escape, and double escape emission peaks for 16O (1, 1′, 1″, 4, 4′), 15O (2, 2′, 2″), and 12C (3, 3′, 3″), as well as the positron annihilation gamma peak (5).

Table 2.

Calculation of 16O and 12C Prompt Gammas emitted from each sample.

sample # incident protons irradiated volume (cm3) PG/proton
PG/Gy
6.13 MeV 4.44 meV 6.13 MeV 4.44 MeV
1 6×1010 1.01 2.79×10−2 3.44×10−3 1.42×107 1.76×107
2 6×1010 0.98 2.55×10−2 3.38×10−3 1.30×107 1.73×107
3 6×1010 0.92 2.20×10−2 3.29×10−3 1.12×107 1.68×107
4 1×1011 0.85 2.09×10−2 3.33×10−3 1.07×107 1.70×107
Open in a new tab

3.2. Oxygen and carbon PG emission

Table 2 lists the total number of 6.13 MeV and 4.44 MeV gammas emitted by each sample per incident proton (PGs/proton) and per delivered dose (PGs/Gy). To determine these numbers, we divided the true number of PGs measured (see Section 2.2) by η(E) for the detector at the desired gamma energy to get the total number of gammas emitted. Next, we divided the total number of gammas emitted from each sample by: p(s) to get PGs/proton, or D(s) to get PGs/Gy, where p(s) and D(s) are defined in section 2.4.

From Table 2, we see that approximately 0.0314 PGs (oxygen + carbon) were emitted from water per proton incident. Because the nonelastic scattering probability for a proton with a hydrogen nucleus is reported to be zero for a 48 MeV proton beam (Janni 1982), we interpret our measured carbon + oxygen PG production rate to mean that the total probability of the incident 48 MeV proton beam producing a PG through a nonelastic nuclear interaction in water is approximately 3.14%. This value agrees very well with the nonelastic nuclear interaction probability of approximately 3.2% reported by Janni (1982) for a 48 MeV proton beam irradiating water. The high level of agreement between our PG production probability and other published results provides an initial validation of our process for determining total PG production from our measured data.

As seen from the data in Table 2 and Figure 4, the total 16O PG emission decreased as the amount of sucrose in the sample increased. This is because the 6.13 MeV PGs are emitted only during interactions involving a proton and an oxygen nucleus (16O(p,pγ)16O). As the concentration of oxygen in the samples decreased (Table 1), the number of proton-oxygen nuclei interactions that produce 6.13 MeV PGs also decreased. For the samples used in our study, we found that the 16O PG emission decreased linearly with the percentage of oxygen in the sample. In contrast, the total 12C emission was nearly constant, decreasing by only 3% over the range of carbon concentrations in the sample solutions. This is because the 4.44 MeV PG was produced by proton interactions with both carbon (12C(p,pγ)12C) and oxygen (16O(p,χ)12C(γ)) nuclei, where χ represents the spallation products (e.g., alpha, triton, deuteron, neutrons, etc). As shown in Table 1, for our samples the percentage of oxygen decreased as the amount of sucrose increased, whereas the percentage carbon increased as the amount of sucrose increased. Therefore, the oxygen + carbon percentage remained nearly constant for all of the samples. Because the maximum and energy dependence of the cross-section for the (16O(p,χ)12C(γ)) and (12C(p,pγ)12C) interaction processes for proton irradiation are very similar (Kozlovsky et al. 2002) for the proton energies (48 - 0 MeV) present in our samples, we believe that the reduction of 4.44 MeV PGs created by proton-oxygen nuclei interactions was offset by the increase in PGs created by the proton-carbon nuclei interactions.

3.3. Determining oxygen concentration from PG emission

For each sample, we determined, the total amount of oxygen irradiated using the equation,

irradiatedoxygen(grams)=V·ρ·FO, (1)

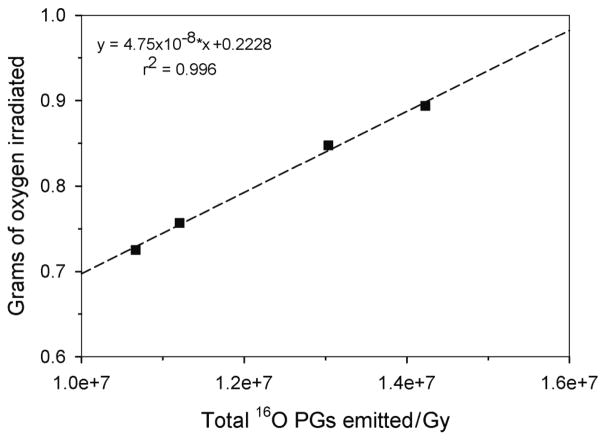
where ρ is the sample density in g/cm3, FO is the fraction of oxygen by mass (Table 1), and V is the “irradiated volume” for each sample. On the basis of the measured beam profiles, we assumed that V was rectangular. Thus, we defined the width (W) and height (H) of the irradiated volume as the FWHM of the measured lateral profiles and the length (L) as the measured 50% distal range of the beam. V for each sample, shown in Table 2, was then simply calculated using the relationship, V = L x W x H. Figure 5 shows a plot of the amount of irradiated oxygen as a function of the measured total 16O PG emission. This shows that a linear relationship exists between the number of 16O PGs emitted from an irradiated sample and the amount of oxygen contained within the sample. Using the linear fit for our experimental setup, given in Figure 5, it would then be possible to measure the 16O PG emission from a sample, calculate the total 16O PG emission (see sections 2.2 and 2.3), and determine the amount of oxygen (in grams) contained within the volume of the sample irradiated by the proton beam.

Figure 5.

Figure 5

Open in a new tab

Amount of oxygen within the irradiated volume (squares) as a function of measured emission of 6.13 MeV prompt gammas. A linear fit (dashed line) using the inset equation provides a method to determine oxygen concentration in an irradiated sample volume from the measurement of prompt gamma emission with the experimental setup used in our study.

4. Conclusions

In this study, we measured the PG emission spectra from several tissue-equivalent solutions composed of hydrogen, carbon, and oxygen. Our results showed that as the concentration of oxygen decreased, so too did the 6.13 MeV PG emission from oxygen, indicating that it is directly proportional to the amount of oxygen in the volume of irradiated tissues. However, the 4.44 MeV PG intensity was found to depend on both the carbon concentration and the oxygen concentration. This means that measurement of the 4.44 MeV PG emission alone is not enough to determine carbon concentration. Instead, knowledge of the oxygen concentration (6.13 MeV PGs) and the 12C emission would be needed to determine carbon concentration within an irradiated volume of tissue.

From the measured beam profile and known density values of our samples, we were able to determine the relationship between 16O PG emission and the amount of oxygen within an irradiated volume. This proves that it is possible to determine oxygen concentration within irradiated tissues by measuring 16O PG emission, provided that the detection efficiency of the PG measurement system and the lateral and depth profiles of the proton beam are well established. In fact, for our measurement setup using a 48 MeV proton beam, we calculated that 1.64 × 107 oxygen PGs will be emitted per Gy of dose per gram of oxygen in the irradiated volume.

On the basis of these studies, we believe that if a PG measurement system with adequate detection efficiency existed, it would make the determination of the oxygen concentration feasible in tissues irradiated during proton radiation therapy. Such a system could then be used, for instance, to measure and track changes to the oxygen levels in treated tumors on a daily basis over the course of treatment. If changing oxygen concentrations could be tied to post-treatment tumor control rates or toxicity in critical structures, the oncologist could track the response of each individual patient to their treatment and adapt the treatment plan accordingly.

Acknowledgments

This work was supported by Award Number R21CA137362 from the National Institutes of Health through the National Cancer Institute. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute or the National Institutes of Health. All measurements in this work were performed at the Texas A&M University Cyclotron Institute. We would like to thank the director of the Cyclotron Institute, Dr Robert Tribble, for allowing beam time for our experiments, and we would like to thank all of the staff who helped us prepare and carry out the irradiations.

References

  1. Beddar AS, Kainz K, Briere TM, Tsunashima Y, Pan T, Prado K, Mohan R, Gillin M, Krishnan S. Correlation between internal fiducial tumor motion and external marker motion for liver tumors imaged with 4D-CT. Int J Radiat Oncol Biol Phys. 2007;67(2):630–638. doi: 10.1016/j.ijrobp.2006.10.007. [DOI] [PubMed] [Google Scholar]
  2. Bom V, Joulaeisadeh F, Beekman F. Real-time prompt gamma monitoring in spot-scanning proton therapy using imaging through a knife-edge-shaped slit. Phys Med Biol. 2012;57:297–308. doi: 10.1088/0031-9155/57/2/297. [DOI] [PubMed] [Google Scholar]
  3. Butterworth KT, McGarry CK, Clasie B, Carabe-Fernandez A, Schuemann J, Depauw N, Tang S, McMahon SJ, Schettino G, O’Sullivan JM, Lu HM, Kooy H, Paganetti H, Hounsell AR, Held KD, Prise KM. Relative biological effectiveness (RBE) and out-of-field cell survival responses to passive scattering and pencil beam scanning proton beam deliveries. Physics in medicine and biology. 2012;57(20):6671–6680. doi: 10.1088/0031-9155/57/20/6671. [DOI] [PubMed] [Google Scholar]
  4. Daftari I, Castenadas C, Petti PL, Singh RP, Verhey LJ. An application of GafChromic MD-55 film for 67.5 MeV clinical proton beam dosimetry. Physics in medicine and biology. 1999;44(11):2735–2745. doi: 10.1088/0031-9155/44/11/304. [DOI] [PubMed] [Google Scholar]
  5. ICRU. Report Number 46. International Commission on Radiation Units and Measurements; Bethesda, MD: 1992. Photon, electron, proton, and neutron interaction data for body tissues. [Google Scholar]
  6. Janni JF. Proton Range Energy Tables, 1 KeV - 1 GeV. At Data Nucl Data Tables. 1982;27 :147–339. 341–527. [Google Scholar]
  7. Kim D, Yim H, Kim JW. Pinhole camera measurements of prompt gamma rays for detection of beam range in proton therapy. J Kor Physi Soc. 2009;55(4):1673–1676. [Google Scholar]
  8. Kirby D, Green S, Palmans H, Hugtenburg R, Wojnecki C, Parker D. LET dependence of GafChromic films and an ion chamber in low-energy proton dosimetry. Physics in medicine and biology. 2010;55(2):417–433. doi: 10.1088/0031-9155/55/2/006. [DOI] [PubMed] [Google Scholar]
  9. Kozlovsky B, Murphy RJ, Ramaty R. Nuclear de-excitation gamma ray lines from accelerated particle interactions. Astro J Suppl Series. 2002;141:523–541. [Google Scholar]
  10. Kuban D, Pollack A, Huang EH, Levy L, Dong L, Starckschall G, Rosen I. Hazards of dose escalation in prostate cancer radiotherapy. Int J Radiat Oncol Biol Phys. 2003;57(5):1260–1268. doi: 10.1016/s0360-3016(03)00772-7. [DOI] [PubMed] [Google Scholar]
  11. Lesher SR, Phair C, Berstein LA, Bleuel DL, Burke JT, Church JA, Fallon P, Gibelin J, Scielzo ND, Weideking M. STARS/LiBerACE: segmented silicon and high-purity germanium detector arrays for low-energy nuclear reaction and structure studies. Nucl Intstr Met Phys Res A. 2010;621:286–291. [Google Scholar]
  12. Mackin D, Peterson S, Beddar S, Polf J. Evaluation of a stochastic reconstruction algorithm for use in Compton camera imaging and beam range verification from secondary gamma emission during proton therapy. Phys Med Biol. 2012;57:3537–3553. doi: 10.1088/0031-9155/57/11/3537. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Min CH, Kim CH, Youn M, Kim J. Prompt Gamma Measurements for Locating Dose falloff Region in Proton Therapy. App Phys Lett. 2006;89:183517, 183511–183513. [Google Scholar]
  14. Min CH, Lee HR, Kim CH, Lee SB. Development of array-type prompt gamma measurement system for in vivo range verification in proton therapy. Med Phys. 2012;39 (4):2100–2107. doi: 10.1118/1.3694098. [DOI] [PubMed] [Google Scholar]
  15. Moteabbed M, Espana S, Paganetti H. Monte Carlo patient study on the comparison of prompt gamma and PET imaging for range verification in proton therapy. Phys Med Biol. 2011;59:1063–1082. doi: 10.1088/0031-9155/56/4/012. [DOI] [PubMed] [Google Scholar]
  16. OCRP. Oklahoma Center for Radiation Physics. 2013 from: http://physics.okstate.edu/yukihara/dosimetry/
  17. Paganetti H. Proton Therapy Physics. 1. Boca Raton, FL: CRC Press; 2012a. [Google Scholar]
  18. Paganetti H. Range uncertainties in proton therapy and the role of Monte Carlo simulations. Physics in medicine and biology. 2012b;57(11):R99–117. doi: 10.1088/0031-9155/57/11/R99. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Polf J, Peterson S, Ciangaru G, Gillin M, Beddar S. Prompt gamma-ray emission from biological tissues during proton irradiation: a preliminary study. Phys Med Biol. 2009;54(3):731–743. doi: 10.1088/0031-9155/54/3/017. [DOI] [PubMed] [Google Scholar]
  20. Polf J, Peterson S, Roberts DA, Beddar S. Measuring prompt gamma ray emission during proton radiotherapy for assessment of treatment delivery and patient response. AIP Conf Proc. 2011;1336:364–367. [Google Scholar]
  21. Rasband W. ImageJ image processing program. 2013;1.45s from: http://imagej.nih.gov/ij/ [Google Scholar]
  22. Richard MH, Chevillier M, Dauvergne D, Freud N, Henriquet P, Le Foulher F, Letang JM, Montarou G, Ray C, Roellinghoff E, Testa E, Testa M, Walenta AH. Design study of a Compton camera for prompt gamma imaging during ion beam therapy. IEEE Nucl. Sci. Sympos. Conf. Record, IEEE.2009. [Google Scholar]
  23. Roellinghoff F, Richard MH, Chevillier M, Constanzo M, Dauvergne D, Freud N, Henriquet P, Foulher F, Letang JM, Montarou G, Ray C, Testa E, Testa M, Walenta AH. Design of a Compton camera for 3D prompt gamma imaging during ion beam therapy. Nucl Intstr Met Phys Res A. 2011;648:s20–s23. [Google Scholar]
  24. Smeets J, Roellinghoff F, Prieels D, Stichelbaut F, Benilov A, Busca P, Fiorini C, Peloso R, Basilavecchia M, Frizzi T, Dehaes JC, Dubus A. Prompt gamma imaging with a slit camera for real-time range control in proton therapy. Physics in medicine and biology. 2012;57(11):3371–3405. doi: 10.1088/0031-9155/57/11/3371. [DOI] [PubMed] [Google Scholar]
  25. Testa M, Bajard M, Chevallier M, Dauvergne D, Freud N, Henriquet P, Karkar S, Le Foulher F, Letang JM, Plescak R, Ray C, Richard MH, Schardt D, Testa E. Real-time monitoring of the Bragg-peak position in ion therapy by means of single photon detection. Radiat Environ Biophys. 2010;49(3):337–343. doi: 10.1007/s00411-010-0276-2. [DOI] [PubMed] [Google Scholar]
  26. Yukihara EG, Mardirossian G, Mirzasadeghi M, Guduru S, Ahmad S. Evaluation of Al2O3:C optically stimulated luminescence (OSL) dosimeters for passive dosimetry of high-energy photon and electron beams in radiotherapy. Med Phys. 2008;35(1):260–269. doi: 10.1118/1.2816106. [DOI] [PubMed] [Google Scholar]
  27. Yukihara EG, Yoshimura EM, Lindstrom TD, Ahmad S, Taylor KK, Mardirossian G. High-precision dosimetry for radiotherapy using the optically stimulated luminescence technique and thin Al2)3:C dosimeters. Phys Med Biol. 2005;50:5619–5628. doi: 10.1088/0031-9155/50/23/014. [DOI] [PubMed] [Google Scholar]
  28. Zhang X, Dong L, Lee AK, Cox JD, Kuban DA, Zhu RX, Wang X, Li Y, Newhauser WD, Gillin M, Mohan R. Effect of anatomic motion on proton therapy dose distributions in prostate cancer treatment. Int J Radiat Oncol Biol Phys. 2007;2007:620–629. doi: 10.1016/j.ijrobp.2006.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES