Development of Surrogate Spinal Cords for the Evaluation of Electrode Arrays Used in Intraspinal Implants

Abstract

We report the development of a surrogate spinal cord for evaluating the mechanical suitability of electrode arrays for intraspinal implants. The mechanical and interfacial properties of candidate materials (including silicone elastomers and gelatin hydrogels) for the surrogate cord were tested. The elastic modulus was characterized using dynamic mechanical analysis, and compared with values of actual human spinal cords from the literature. Forces required to indent the surrogate cords to specified depths were measured to obtain values under static conditions. Importantly, to quantify surface properties in addition to mechanical properties normally considered, interfacial frictional forces were measured by pulling a needle out of each cord at a controlled rate. The measured forces were then compared to those obtained from rat spinal cords. Formaldehyde-crosslinked gelatin, 12 wt% in water, was identified as the most suitable material for the construction of surrogate spinal cords. To demonstrate the utility of surrogate spinal cords in evaluating the behavior of various electrode arrays, cords were implanted with two types of intraspinal electrode arrays (one made of individual microwires and another of microwires anchored with a solid base), and cord deformation under elongation was evaluated. The results demonstrate that the surrogate model simulates the mechanical and interfacial properties of the spinal cord, and enables in vitro screening of intraspinal implants.

I. Introduction

INTRASPINAL microstimulation (ISMS) is a promising technique for restoring function (such as standing and walking) in people with spinal cord injury [1]–[4]. In this technique, microwires are inserted into the spinal cord below the point of injury, where they can be used to transmit signals to functioning neural networks which are no longer connected to the brain. Ideally, an array of electrodes could be implanted into the spinal cord to achieve electrical connections with a number of different sets of motor neuronal pools and locomotor neural networks.

There are currently a number of electrode arrays available for implantation in the brain, including the Huntington Medical Research Center [5] and the University of Utah [6], [7] multi-electrode arrays. While these devices are known to be effective within the brain [5], [6], [8], their mechanical and electrical stability while implanted in the spinal cord remains unknown. The spinal cord is a soft, hydrated material, which moves independently from the surrounding vertebrae. It undergoes a relatively large range of deformations (as compared with brain) during typical daily activities, including extension, compression, and torsion. Electrode arrays implanted in the spinal cord must therefore be mechanically compatible with the cord itself, and must neither impede the natural motion of the spinal cord nor damage it during deformation. A physical model of the spinal cord is vital for the development and testing of new electrode arrays designed for ISMS. A surrogate spinal cord would allow accurate in vitro testing of proposed intraspinal implants and allow the device/spinal cord mechanics to be determined for a variety of implants and test conformations. This approach is preferable to working with spinal cords from animals for initial screening tests, both to minimize the number of animals used in testing, and to facilitate high throughput, bench, mechanical testing experiments.

To create a physical model of the spinal cord, the properties of the material from which the model is made must closely match those of an actual spinal cord. A number of surrogate spinal cord models, constructed from either silicone elastomers [9]–[12] or uncrosslinked gelatin [13], have been described in the literature. These models have focused mainly on mimicking the elastic properties of the spinal cord for investigating spinal cord injury mechanics. However, none of the existing surrogate systems have considered the interfacial or surface properties of the materials, and their interaction with devices implanted within the cord. When tissue (i.e., spinal cord tissue, brain tissue, etc.) which has been embedded with an array is subjected to a mechanical deformation, the interactions that occur at the interface between the array and the tissue play a key role in determining the mechanical response of the system. For example, if high frictional forces exist at the interface, the array will be firmly anchored to the tissue, causing high levels of stress to develop. If lower levels of friction are present, the electrodes and tissue may move more independently. The interfacial properties between the surrogate material and the implant must therefore be carefully considered, particularly for spinal cord implants, as this tissue undergoes large deformations.

In this study, we evaluated a number of materials (including silicone elastomers and uncrosslinked and crosslinked gelatin) for use in surrogate spinal cords for the preliminary testing of the mechanical stability of spinal implants. Three methods were used to evaluate the suitability of the materials for use in surrogate spinal cords. First, the tensile module of rectangular samples were measured using dynamic mechanical analysis (DMA), with the goal of finding materials with tensile moduli matching a value for spinal cord tissue without pia mater obtained from the literature (89 kPa) [14]. Indentation testing on samples with geometry representative of actual spinal cords was then performed to characterize the elastic modulus of these materials under static conditions and large strains. The properties of ex vivo rat spinal cords were also measured using this technique, and compared to known values from the literature (8.1 ± 1.1 kPa, [15]). To characterize the interfacial properties of promising candidate materials, frictional forces between the cords and implants were quantified by measuring the amount of force required to withdraw a needle at a controlled speed from a surrogate cord. Values were again compared with those obtained from excised rat spinal cords. Once a suitable candidate was identified, surrogate cords were fabricated and used to evaluate the interactions that take place between surrogate cords and different implanted electrode arrays. Two arrays were selected for investigation: the first consisted of independent microwires, and the second consisted of microwires connected by a stiff solid base (the design commonly employed for recording and stimulation in the central nervous system [6], [7], [16]–[18]). These arrays represent opposite ends of the spectrum in terms of de-formability, and establish expected bounds for the development of future electrode arrays.

II. Materials and Methods

A. Candidate Materials

Three types of silicone elastomers were evaluated as candidate materials from which to construct surrogate spinal cords: Sylgard 184, and QM Skin 30, which have been utilized previously in surrogate spinal cords [11], [12], and TCB5101, an ultra-soft silicone elastomer. Gelatin, a hydrogel derived from collagen, was also examined due to its low modulus of elasticity in the hydrated state. Because the mechanical properties of gelatin are highly tunable through variations in hydration and crosslinking, we evaluated a wide range of formulations.

Dow Corning Sylgard 184 was obtained as a two component system (elastomer and crosslinker), and was prepared by mixing in elastomer:crosslinker ratios of 10:1, 20:1, 30:1, and 40:1, by weight. Samples were crosslinked by baking at 60 °C for 3 h. QM Skin30 was obtained from Quantum Silicones LLC (Richmond, VA, USA), and was prepared by mixing the two components 10:1 (as directed) and curing for 24 h at room temperature. TCB 5101 was obtained from BJB Enterprises, Inc. (Tustin, CA, USA), and samples were prepared by mixing the two components in a 1:1 ratio (as directed) and curing for 24 h at room temperature.

Gelatin powder was obtained from Sigma Aldrich (G1890, gelatin from porcine skin, Oakville, ON, Canada), and was used as received. To prepare the uncrosslinked gelatin, a suitable mass of powder was dissolved in distilled water. Solutions were heated to 55 °C and stirred at a rate of 60 rev/min for 20 min. The solutions were then poured into a mold, and allowed to set overnight in the refrigerator. Crosslinked gelatin samples were prepared by dissolving gelatin in water (as above), followed by addition of formaldehyde (19.4 mmol/100 mL) and an additional 15 min of stirring at 45 °C [19]. This solution was then set in the refrigerator overnight in a suitable mold. Flat samples for measurements of modulus of elasticity were polymerized in 90 mm × 90 mm polystyrene weighing boats, and surrogate cords with elliptical cross sections were prepared using an aluminum mold, as described in Section II-C.

B. Uniaxial Tension Testing by DMA

A starting point for our work was to utilize DMA (Perkin Elmer DMA 8000, Waltham, MA, USA) to compare the elastic moduli of candidate materials with the elastic modulus measured for ex vivo human spinal cords without pia mater reported in the literature (89 kPa) [14]. Our target did not include the pia mater because the majority of the surface of the electrodes (which can be 3–4 mm long) will be in contact with the spinal tissue itself rather than with the much stiffer pia mater (which itself is less than 300 µm thick [20]).

In DMA, rectangular samples are typically characterized as the measurement of nonrectangular samples can be highly inconsistent due to effects associated with clamping. Flat, hydrated gelatin samples were therefore prepared and were cut into rectangles approximately 11 mm × 7.5 mm × 3.5 mm (length × width × thickness), and silicone samples were cut with dimensions of approximately 13 mm × 7 mm × 2 mm. Samples were loaded into the DMA using the clamps for tensile measurements. To ensure repeatable results and minimize clamping effects, care was taken to tighten the fixtures as much as possible without visibly compressing the sample. After clamping, a typical sample length was ~ 6 mm. All tests were taken at room temperature (between 21.7 and 25.5 °C). During characterization, the displacement and frequency of the strain were controlled to 0.01 mm and 1 Hz, respectively. This displacement was selected both to minimize nonlinear viscoelastic effects observed at larger displacements and to enable accurate measurements of elastic modulus. For each material, a minimum of three different samples were measured, and each sample was characterized three times.

C. Construction of Surrogate Cord

Surrogate cords with elliptical cross sections (6 mm × 8 mm) were prepared by curing silicones or gelatin in a custom-made aluminum mold. The length of each as-molded cord was 7 cm, although the cords could be cut to desired lengths. Samples were typically cured overnight in the mold (wrapped in plastic to minimize drying), and characterized the following day. When preparing silicone cords, the mold was precoated with vacuum grease (Dow Corning, High Vacuum Grease, Midland, MI, USA) to prevent the silicones from bonding to the surface of the mold.

D. Extraction of Rat Spinal Cords

The spinal cords from five adult female Sprague Dawley rats (350 g) were extracted for use in indentation and interfacial frictional force testing (see Sections II-E and II-F below). The procedures were approved by the University of Alberta Animal Care and Use Committee. Anesthesia was induced through inhalation of isoflurane (5%) in a carbogen mixture (95% oxygen, 5% carbon dioxide), and maintained with 2–3% isoflurane. The back was shaved and a midline incision was made from the upper thoracic (T1) to the lower sacral (S4) levels of the spinal column. The muscles overlying the vertebral spinous processes were removed and a laminectomy was performed to expose spinal cord segments T1–S4. The dura mater was opened with fine iridectomy scissors and the dorsal and ventral roots were cut bilaterally. The spinal segments were then removed, immediately placed on a cold plate, and prepared for mechanical testing. The rats were euthanized with an overdose of Euthanyl (30 mg/kg) administered through the heart.

E. Indentation Testing of Surrogate and Rat Cords

Due to the viscoelastic nature of the candidate materials, characterization by DMA will be dependent on the rate of oscillation. To characterize these materials in a static state, indentation testing was utilized. For comparison, excised rat spinal cords were also examined. Measurements were obtained from rat cords with pia mater intact. Surrogate cords with elliptical cross sections were prepared for characterization using the aluminum mold described in Section II-C.

To measure the force required to achieve similar indentations of the surrogate and ex vivo rat spinal cords, a custom indenting arm was used to displace a cylindrical tip with a 1.7-mm diameter into the sample. The vertical position of the indenter was varied in the direction perpendicular to the length of the cord using a micrometer (#1922, Narishige, Tokyo, Japan), and the force resulting at the tip during this displacement was recorded using an in-house built force transducer. For each measurement, the position was adjusted, and the resulting displacement was allowed to reach equilibrium before the measurement was read, ensuring that steady-state (i.e., time independent) values were recorded. At least two cords of each material and three rat spinal cords were tested. The testing was repeated at three different spots for each cord (one near each end, and in the middle). Gelatin cords were sealed in plastic during testing to reduce drying, although a small hole was cut through which the indenter tip could access the cord. Prior to each test, the indenter was positioned just in contact with the top surface of the cord, and the force transducer was set to 0 N. For each indentation, the force was recorded as the tip was displaced at increments of 0.05 mm for the first 0.5 mm, and then at increments of 0.1 mm until the indenting depth reached 1 mm.

F. Interfacial Frictional Force Tests of Surrogate and Rat Cords

The interfacial properties for implantation are an important parameter in the design of penetrating electrodes. Therefore, the interfacial properties of the surrogate cords had to be carefully chosen to mimic those of the physiological spinal cord, both to facilitate realistic behavior during the insertion of the electrodes, and to ensure realistic mechanical interactions between the cord and the electrodes during deformation.

An Instron 5943 single column testing system with 10-N load cell (Grove City, PA, USA) was used to measure the peak static interfacial frictional force between a 30 gauge stainless steel hypodermic needle and the surface of a variety of surrogate spinal cords. The peak static interfacial frictional force between the needle and two rat spinal cords was also tested. For each surrogate material, at least three different samples were tested, and each sample was tested at three different locations (one in the middle and one near each end). Three spots were also tested for each of the two rat spinal cord samples.

To obtain these measurements, a 3-mL syringe fitted with a 30 gauge needle was securely mounted to the moving head of the Instron tester. During testing, samples were glued to the stage to prevent movement. In addition, the rat cords and the gelatin cords were covered with plastic to minimize drying. Rat spinal cords were characterized immediately after harvesting to minimize degradation, and characterization of these samples was completed within 80 min of extraction. At the start of each test, the needle tip was positioned at the surface of the cord, and the force was set to 0 N. The needle was then pushed downward until it was inserted to a depth of 2 mm (as determined by a marker on the surface of the needle) and pulled upward for 2 mm at a rate of 0.3 mm/min. The force required to maintain this rate was recorded, and the peak static frictional force was measured. Typically, some displacement of the needle occurred before the peak force was achieved due to deformation of the material that occurred before sufficient force was achieved to overcome the surface friction.

G. Mechanical Interactions Between Implanted Electrode Arrays and the Surrogate Spinal Cord

During daily motion, the spinal cord is subjected to a range of motion, including torsion, flexion, and elongation. The extent to which the spinal cord deforms has been studied by motion-tracking experiments conducted by several groups. Yuan et al. [21] studied the deformation of the cervical spinal cord during different increments of flexion using MRI, and found that the maximal strain varied between 6.8% and 13.6% on the posterior surface and between 3.7% and 8.7% on the anterior side. Margulies et al. [22] used motion-tracking MRI to evaluate the deformation of the cervical spinal cord during neck flexion and extension, and found that the maximal strain during natural motion was 12%. To demonstrate the utility of the surrogate cords, the mechanical stability of electrode arrays implanted in the surrogate spinal cords was therefore tested by observing local cord deformation at a 12% total elongation of the cord.

Cords were implanted with one of two different electrode arrays and then elongated in a Teflon stand (see Fig. 1). As a reference, the same tests were also performed on a surrogate cord without implanted electrodes. To facilitate the clamping of the cord within the stand, the ends of the cords were coated with a thick layer of epoxy (MG Chemicals Fast Set Epoxy 8332, Surrey, BC, Canada), which was allowed to set overnight at 4 °C. The cords were then soaked in water at 4 °C for 24 h to ensure thorough hydration, and to provide a buffer against the drying that would occur during the setup of the experiment. The surrogate cords were implanted with the appropriate electrodes, a procedure that took up to 45 min for the case of individual electrodes. To visualize the distribution of strain within the cord under elongation, four pairs of reference marks were drawn on the surface of the cord using India ink. The cord was loaded in the Teflon stand (see Fig. 1) and was elongated by 12% of its initial length (corresponding to the maximum elongation that occurs during daily motion, as discussed in Section 2-G). At least three photographs of each configuration were taken using a Canon EOS 1000D camera with Canon 18–55 mm DS lens (Rockville, MD, USA) as the cords were relaxed and stretched. The distance between the reference markings was measured before and after the deformation using both Adobe Illustrator (Adobe, San Jose, CA, USA) and AxioVision software (Carl Zeiss Microscopy, Göttingen, Germany), and the results were used to determine the strain in different parts of the cord. To calculate the distance between markings in absolute units (millimeter), the dimensions of the stand itself were used to calibrate the measurements. Each set of measurements was repeated with at least two surrogate cords for each array type.

Fig. 1.

Teflon stand used for deformation experiments. The stand is comprised of a fixed central platform, which can be raised or lowered to support the middle section of the surrogate cord, and two adjustable rods that can be moved laterally to apply tension to the cord.

H. Statistical Analysis

To compare the modulus values measured by DMA with the target value for spinal cord tissue obtained from the literature, the discrepancy between the average measured value and the target value was compared using the unpaired t-test for a two-tailed distribution (α = 0.05). To apply this test, the standard error of the mean (21 kPa) and the sample size (n = 6) of the target value of 89 kPa were taken from the literature [14]. The unpaired two-tailed t-test (α = 0.05) was also utilized to compare the results of the DMA testing with the indentation testing.

Analysis of variance (ANOVA) and Tukey honest significant difference (HSD) post hoc analyses were used to compare the peak interfacial frictional forces of the candidate materials and the rat spinal cords, and to determine whether the deformation behaviors of cords implanted with different types of arrays were significantly different from each other. The properties of a fresh formaldehyde-crosslinked 12 wt% gelatin sample and a 12 wt% gelatin sample soaked in water overnight were compared using paired, two-tailed Student’s t-test, while the properties of crosslinked and uncrosslinked gelatin of the same water content were compared using unpaired, two-tailed Student’s t-test. For all analyses, p values < 0.05 were considered significant.

III. Results and Discussion

A. Mechanical Properties of Surrogate Spinal Cord Materials

1) Uniaxial Tension Testing by DMA

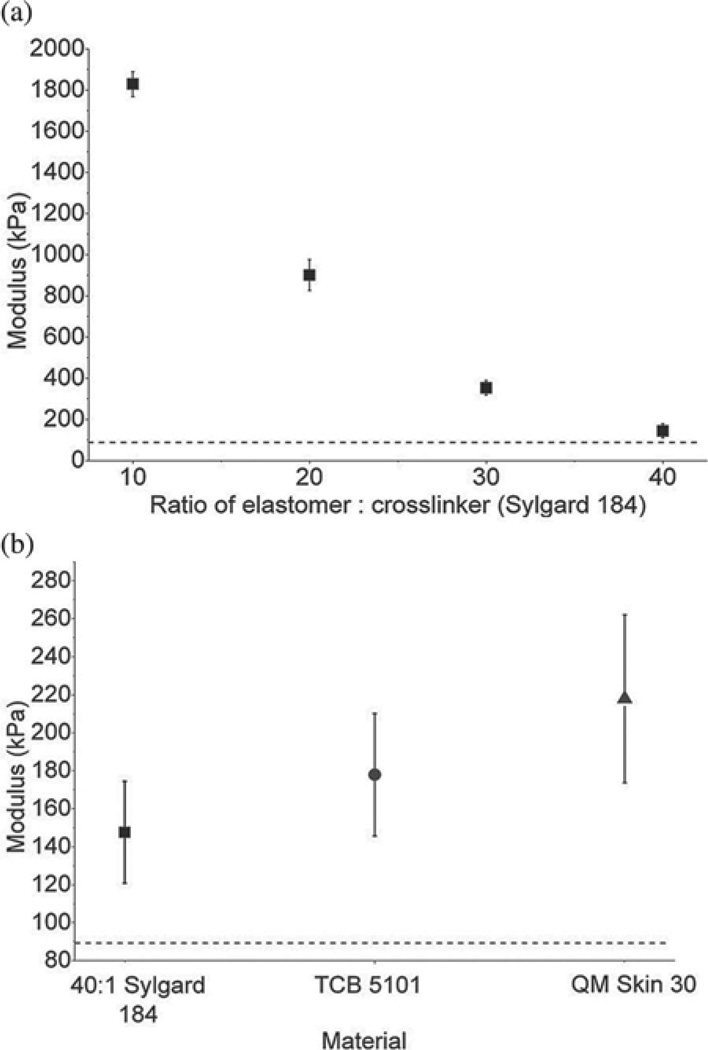
The modulus of each candidate material was measured using DMA in tension mode, and the results for various crosslinker:elastomer ratios of the Sylgard 184 silicone elastomer are shown in Fig. 2(a). The results for the three different types of silicones tested (Sylgard 184 mixed in a 40:1 ratio, TCB 5101, and QM Skin 30) are shown in Fig. 2(b). The modulus of elasticity of each of these materials (which have all been utilized in previous surrogate spinal cord models) was significantly different from the target modulus of 89 kPa (p < 0.043).

Fig. 2.

Tensile moduli of elasticity of silicone elastomers. (a) Tensile modulus of elasticity of Sylgard 184 at mixing ratios (base:crosslinking agent) of 10:1, 20:1, 30:1, and 40:1. (b) Tensile moduli of Sylgard 184 mixed in a 40:1 ratio (square), TCB 5101 (circle), and QM Skin 30 (triangle). The horizontal dashed line indicates the target modulus of 89 kPa. Average values (± standard deviation) are shown. All silicones have a much higher modulus than the target.

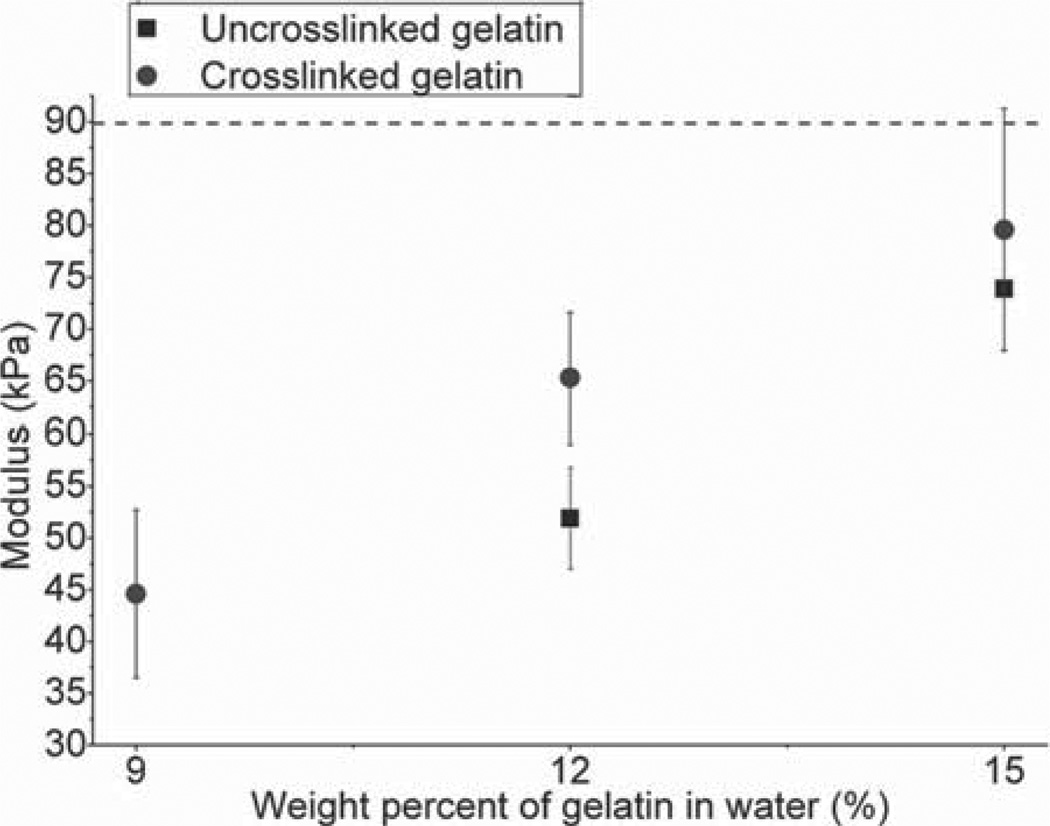
The moduli of elasticity of uncrosslinked and formaldehyde-crosslinked gelatin samples composed of various concentrations of gelatin in water are shown in Fig. 3. The modulus of the uncrosslinked 9 wt% gelatin was less than the minimal value that could be reliably measured in tension mode by DMA (<40 kPa), and is therefore not included in the results. As expected, the uncrosslinked gelatin samples had consistently (and statistically significant) lower moduli than the crosslinked gelatin at the same weight percent in water.

Fig. 3.

Tensile moduli of elasticity of uncrosslinked and crosslinked hydrated gelatins. The tensile moduli of uncrosslinked (square) and crosslinked (circle) gelatin for 9%, 12%, and 15% gelatin weight in water are shown. The modulus of the uncrosslinked 9% gelatin weight in water was lower than the measurement capacity of the DMA system. The horizontal line indicates the target modulus of 89 kPa. Average values (± standard deviation) are shown. The formaldehyde crosslinked 15 wt% gelatin in water is closest to the target value.

The crosslinked 15 wt% gelatin had the closest modulus to that of the target modulus (79.6 kPa ± 11.7 kPa), and was not statistically different from the target modulus (p > 0.67). The modulus of the crosslinked 12 wt% gelatin was less than the target modulus (65 kPa ± 6 kPa) and the difference was also not statistically significant (p > 0.30).

Both spinal cord tissue and the candidate materials are viscoelastic materials, whose properties can vary as a function of both strain and strain rate. To obtain accurate measurements of elastic modulus by DMA, a relatively low strain (~0.00167) and a set frequency (1 s⁻¹) were utilized to minimize the viscoelastic effects. To enable measurements over a larger strain in a time-independent manner, indentation testing was also utilized, as described in the following section.

2) Indentation of Surrogate and Rat Cords:

Indentation testing was utilized to measure the elastic modulus of the surrogate materials under static loading conditions at strains of 0.1. Two to three cords of each material were tested, and the value required to achieve a specific displacement was measured three times per cord. Excised rat spinal cords were also characterized for comparison.

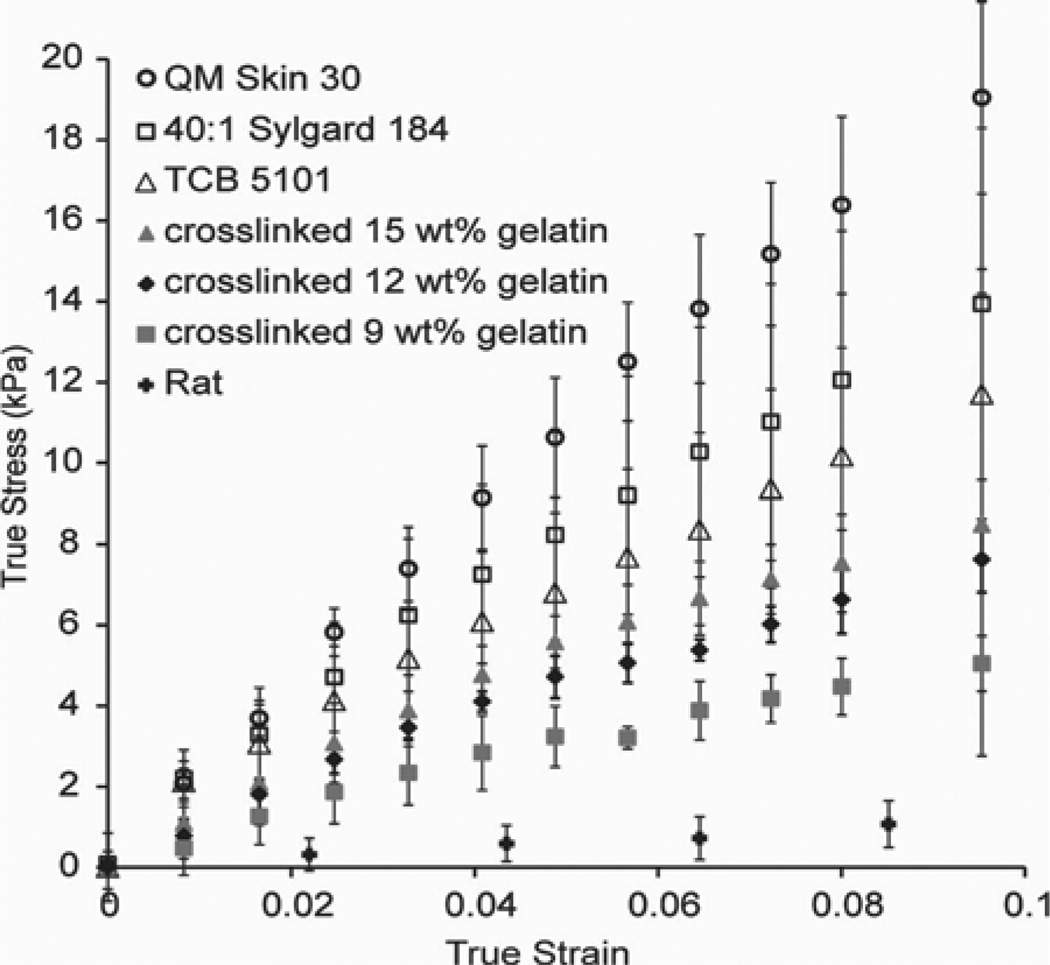
The modulus of each material was calculated as follows: for each sample, the force required to achieve the desired indentation depth d at each of the three locations on the sample was averaged. The area of contact at each depth was calculated using the equation A = πr² + d2πr, where r is the radius of the tip (0.85 mm). The engineering stress σ_E and engineering strain ε_E were then obtained from the following relations: σ_E= F/A, and ε_E= d/h, where h is the initial height of the cord (6 mm for surrogate cords, and 2.25 mm for rat cords). As the dimensions of the cord are expected to change during the indentation, the instantaneous (i.e., true) strain and stress provide a better description of the properties of the material. On the assumption that the cords are incompressible, the true stress σ_T and true strain ε_T were obtained from the following equations: ε_T= ln(1 + ε_E), and σ_T= σ_E(1 + ε_E) [23]. The true stress was then plotted against the true strain. The resulting curve was approximately linear with a near-zero intercept, as shown in Fig. 4. The elastic modulus for each material was obtained by using linear regression to determine the slope of the portion of the curve corresponding to an engineering strain of 0–0.1. For each material, the average and standard deviation between the different samples of the same material were then calculated.

Fig. 4.

True stress–true strain curves for silicone elastomer and gelatin surrogate spinal cords, and actual rat spinal cords. Each cord was indented three times. Average values (± standard deviation) of the two to three cords of each material characterized are shown.

The elastic modulus of each material was calculated from the slope of the curves, and summarized in Table I.

TABLE I.

E‘ Measured by Indentation Testing and by DMA

	Elastic Modulus (kPa)
Sample	Indentation	DMA
9% Gelatin, Crosslinked	52.5 ± 9.6	44.6 ± 8.1
12% Gelatin, Crosslinked	77.3 ± 7.5	65.3 ± 6.3
15% Gelatin, Crosslinked	89.8 ± 6.4	79.6 ± 11.7
Rat	9.5 ± 4.5
40:1 Sylgard 184	141.1 ± 43.7	147.6 ± 26.8
TCB5101	118.4 ± 32.1	177.9 ± 32.2
QM Skin 30	188.7 ± 22.5	217.9 ± 44.2

There was reasonably good agreement between the DMA and indentation results, with significant differences between the methods observed only for the formaldehyde-crosslinked15 wt% gelatin and the TCB 5101. The value obtained for the rat cords (9.5 ± 4.5 kPa) agreed very well with a value from the literature, 8.1 ± 1.1 kPa [15].

The formaldehyde-crosslinked 15 wt% gelatin in water had the closest modulus to the target value of 89 kPa. However, the value measured for the formaldehyde-crosslinked 12 wt% gelatin was also not significantly different from the target. The target modulus itself was measured in tension for human spinal cords (without pia mater), over relatively large strains of 1.5. As spinal cord tissue typically exhibits a “J” shaped stress–strain curve (with larger forces being required to deform the sample at larger strains), the large strain utilized in the literature study may have resulted in a larger elastic modulus than is relevant to our scale of deformation. Therefore, both the formaldehyde-crosslinked 12 wt% gelatin in water and the formaldehyde-crosslinked 15 wt% gelatin in water were considered suitable candidates for use in the surrogate spinal cord.

B. Interfacial Frictional Force Tests of Silicone and Gelatin Cords

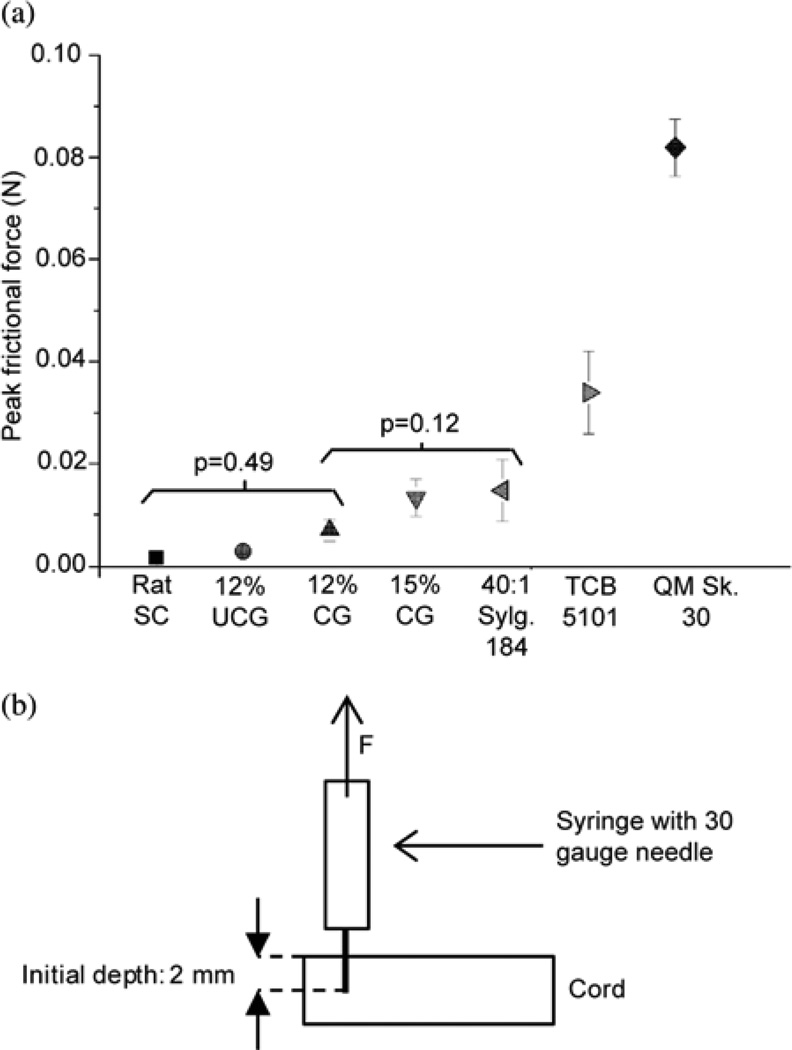
To test the interfacial properties of the candidate materials deemed suitable based on their tensile modulus, the force required to initiate the withdrawal of a stainless steel needle from various types of cords was tested. This force corresponds to the force required to overcome the static frictional forces at the interface between the needle and the cord. The peak frictional forces for all materials tested are summarized in Fig. 5. Very low forces (1.7 ± 0.5 mN) were required to withdraw the needle from the rat cords. Of the surrogate materials, the lowest forces were required to withdraw the needle from the uncrosslinked 12 wt% gelatin samples (3.0 ± 0.7 mN), followed by the formaldehyde-crosslinked 12 wt% gelatin samples (7.0 ± 2.1 mN). The peak force required to withdraw the needle from the formaldehyde crosslinked 15 wt% gelatin was considerably higher: 13.3 ± 3.7 mN). For all types of silicone elastomers, comparatively high forces (14.8 ± 6.0 mN, 33.9 ± 8.1 mN, and 81.9 ± 5.6 mN for the 40:1 Sylgard 184, TCB 5101, and QM Skin 30, respectively) were required to withdraw the needle. ANOVA and Tukey HSD post hoc analyses showed that the differences between the peak interfacial frictional forces exhibited by the 12 wt% gelatin in water cords (both formaldehyde-crosslinked and un-crosslinked) and the rat cords were not significant (p = 0.49), while the peak forces observed for the formaldehyde crosslinked 15 wt% gelatin and for all silicone cords were significantly different from those observed for the rat cords (p < 0.05). These results are consistent with observations made in the lab, as we found that it was difficult to insert microwires a few millimeters in length into even the softest silicone surrogate cords due to the high frictional forces at the interface of the wires and the cords. In these systems, dimpling of the cord would occur preferentially over insertion as the force was increased. These results could also have significance for the development of a surrogate for use in contusion injury studies in which the cord is penetrated by a blunt object [24]. Overall, these experiments showed that the formaldehyde-crosslinked 12 wt% gelatin in water exhibited behavior statistically similar to that of the physiological spinal cord. While work has been done previously to characterize the insertion behavior of deep brain stimulation implants (such as the force required to penetrate brain tissue in vivo) [25], to the best of our knowledge, this is the first investigation of the influence of interfacial frictional stress of the electrodes on the spinal cord or other tissue of the central nervous system.

Fig. 5.

(a) Average peak interfacial frictional forces of the candidate surrogate spinal cord materials. Average ± standard deviation of peak interfacial frictional forces required to withdraw a 30 gauge needle from candidate silicone, crosslinked gelatin (CG), and uncrosslinked gelatin (UCG) surrogate spinal cords, as well as rat spinal cords. For each test, the needle was inserted to 2 mm and withdrawn for 2 mm. The results of the ANOVA and Tukey HSD post hoc analyses are shown along with the p-values. The brackets denote the groups within which differences were not statistically significant. The forces required to withdraw the needle from the 12 wt% gelatin cords were not significantly different from those required to withdraw the needle from the rat cords. (b) Diagram of the setup utilized to characterize the peak frictional force required to withdraw the needle.

C. Mechanical Interaction of Surrogate Cords With Implanted Electrode Arrays

Formaldehyde-crosslinked 12% gelatin surrogate cords were used to evaluate the mechanical interaction of electrode arrays implanted in a spinal cord. Surrogate spinal cords were fabricated by using a mold with dimensions based on MR images of the lumbosacral region of the cat spinal cord. This shape was chosen as cat is the primary model for ISMS, enabling comparison with histological and electrophysiological results [26], [27].

Samples were soaked in water overnight to guard against drying during electrode insertion and characterization. To validate this approach, the modulus and indentation behavior of cords soaked overnight in water were also tested on three different samples, and were compared to those of the fresh gelatin. Small changes were seen: the modulus decreased from 65 ± 6 to 58 ± 3 kPa (paired t-test, p = 0.05), and the force of indentation required to achieve a 0.5-mm displacement increased slightly from 0.028 ± 0.002 to 0.031 ± 0.003 N (paired t-test, p = 0.2). As the samples dried gradually during characterization, it is expected that the final properties of the surrogate cords were between those of fresh crosslinked 12 wt% gelatin and crosslinked 12 wt% gelatin samples which had been soaked in water.

Two different types of electrode arrays with very different mechanical properties were tested: an array consisting of eight individual 30-µm stainless steel microwires, arranged in two rows and implanted in pairs at 2–3 mm intervals along the length of the cord, and an array consisting of a solid base embedded with eight 75-µm electrodes in two rows at 3 mm intervals along the length of the cord. Cords implanted with these arrays are shown in Fig. 6(a) and (b), respectively. A surrogate cord without implanted electrodes (denoted as the reference cord) is shown in Fig. 6(c). The schematic diagram in Fig. 6(d) indicates the numbering of the reference markers used to calculate the overall strain in different parts of the cord. Tension was applied to elongate the cords by 12% with respect to their original length.

Fig. 6.

Effect of the electrode array architecture on spinal cord deformation. Shown are examples of (a) surrogate cord implanted with individual microwires, (b) surrogate spinal cord implanted with electrodes held with solid base, and (c) surrogate spinal cord with no implant. (d) Schematic diagram indicating the regions between ink reference markers used to measure the deformation in the cord when strain was applied. Images of the cord were taken before and during deformation, from which the change in distance between the markers was calculated. Care was taken to measure between the same features on the ink markings each time.

The deformation in surrogate cords without implanted electrodes was relatively uniform throughout the cord, ranging from 10±1%to13±1%. The 1% uncertainty in all measurements was due to the distortion caused by the lens of the camera, the difficulty of achieving perfect focus for all relevant planes on the curved surface of the cord, and measuring lengths from a digital photograph. Furthermore, the applied deformation may have been nonuniformly distributed throughout the sample due to the method by which the sample was clamped, causing larger deformations to occur near the ends and smaller deformations toward the center of the sample. Collectively, this accounts for the inhomogeneous strain measured for each set of reference markers on the reference cord.

For surrogate cords implanted with the individual microwires, measured strains ranged from 9±1%to13±1% (see Table II). The following p-values were obtained when comparing the average values measured for these cords with reference cords that had no implants: L1 (p = 0.3), L2 (p = 0.4), L3 (p = 0.06), L4 (p = 0.4), L5 (p = 0.08), indicating that cords implanted with individual electrodes and no connecting base underwent deformations similar to those exhibited by the reference cords (see Table II). This behavior shows that the presence of the individual electrodes does not significantly modify the mechanical behavior of the surrogate spinal cord during elongation. Individual microwire arrays move with the cord, and cause minimal damage to spinal tissue. The findings provide, for the first time, mechanical evidence in support of the physiological and histological findings reported previously by our group, which showed that individual microwires chronically implanted in cat and rat spinal cords cause minimal tissue damage upon insertion and electrical stimulation [26]–[28].

TABLE II.

Observed Strain Between Reference Markers Under 12% Total Applied Strain

		Reference Marker
Array Type	Cord#	L1		L2		L3		L4		L5
		Upper (%)	Lower (%)	Upper (%)	Lower (%)	Upper (%)	Lower (%)	Upper (%)	Lower (%)	Upper (%)	Lower (%)
Individual microwires	1	13±1	11±1	9±1	9±1	10±1	11±1	11±1	11±1	12±1	10±1
Individual microwires	2	10±1	13±1	10±1	11 ± 1	10±1	9±1	10±1	9±1	12±1	11±1
Solid base array	1	3±1	4±1	6±1	9±1	6±1	6±1	10±1	10±1	15±1	14±1
solid base array	2	3±1	5±1	5±1	7±1	7±1	7±1	8±1	8±1	16±1	14±1
No array (reference)	1	11±1	11±1	12±1	11±1	12±1	13±1	12±1	12±1	13±1	13±1
No array (reference)	2	10±1	10±1	11±1	10±1	11±1	10±1	11±1	10±1	12±1	13±1

The deformations in the cords implanted with the solid base arrays were significantly different from those seen in both the reference cords, and cords implanted with arrays of individual microwires. The deformations in L1, L2, and L3, corresponding to the reference markers directly beneath the solid base, were the smallest, ranging from 3 ± 1% to 7 ± 1%. The deformation between the upper markers in this region was consistently smaller than that between the lower set of markers. Because the deformation of the cord was impeded beneath the base, a larger deformation was observed in the region outside of the array, particularly in L5, which underwent a strain of 14 ± 1% to 16 ± 1% (for upper and lower reference markers on the two different samples). ANOVA and Tukey HSD post hoc analyses returned the following p-values for the reference cords and the cords embedded with the solid base: [Upper: L1 (p < 0.0001), L2 (p < 0.001), L3 (p < 0.0001), L4 (p = 0.2), and L5 (p < 0.001); Lower: L1 (p < 0.001), L2 (p < 0.001), L3 (p < 0.001), L4 (p = 0.3), and L5 (p < 0.001)]. The only set of markers which underwent a deformation that was not significantly different from the reference cord was L4. These were the longest set of markers, and took into account both the area under the array (which underwent smaller strain) and the area flanking the array (which underwent larger strain) to accommodate the overall strain of 12%.

Solid base arrays similar to those employed in this study were developed for both stimulation and recording in a variety of neural applications. These have been implanted in cat ventral cochlear cells for the restoration of hearing [17], in various regions of the cerebral cortex [8], [18], [29], in cat spinal cords for short-term restoration of bladder control (less than 150 days) [16], and in peripheral nerves [30], [31]. There is an increasing interest in the functional electrical stimulation community in developing electrodes and electrode arrays that are mechanically compliant with the surrounding tissue, so as to minimize the tissue damage that can occur after implantation [32]–[34]. Models such as ours will be useful to screen the mechanical suitability of new implants, in spinal cord tissue as well as in brain tissue, which has an elastic modulus of ~20 kPa [23].

Histological and physiological evaluations have been conducted for solid base arrays implanted in the spinal cord for periods of 2 weeks to 3 months [35]; however, this study is the first to characterize the mechanical interactions between these arrays and the spinal cord. The fact that significantly lower deformations were seen for the reference markers directly beneath the base as compared with the sets of reference markers flanking either side of the array suggests that the electrode array prevented the region of the cord directly beneath it from elongating, due to interactions between the cord, the electrodes (which are not free to move independently of each other), and the stiff, glassy base. This finding is further supported by the fact that larger deformations were seen for the bottom sets of reference markers than the top ones. Larger deformations are seen in the region outside of the arrays to compensate for the lack of elongation nearer the array. In the long term, it is expected that this impediment could cause damage to the cord itself, due to the stress created at the interface between the electrodes and cord during elongation, particularly during repeated cycles of loading and unloading. Other typical deformation modes (including bending and twisting) could further contribute to this damage for electrode arrays in which the electrodes are not free to move independently. In the future, we intend to use surrogate cords as a testing tool in the development of new electrode arrays for ISMS which have flexible bases, in an effort to engineer arrays which exhibit mechanical behavior that is more similar to that of the independent array of wires than that of the array with a stiff and glassy base.

IV. Conclusion

The overall goal of this study was to develop a surrogate spinal cord that mimics the mechanical as well as interfacial properties of a real spinal cord to enable the in vitro testing of different designs of electrode arrays for ISMS. These properties are important determinants of the interactions that take place between spinal cords and implanted devices including electrode arrays, particularly as spinal cord tissue is regularly subjected to compression, elongation, and rotation, which will cause stress to develop at the tissue/implant interface. As an initial example of the utility of the surrogate cord developed in this study, two commonly used electrode array approaches (solid base, individual wires) were implanted into these cords to test the resulting mechanical interactions under deformation. In the future, the mechanical interactions of arrays in the surrogate spinal cords will be compared with histological reactions of spinal cord tissue to the implantation of different types of electrode arrays. In the meantime, the surrogate cord developed here presents a valuable tool to evaluate prospective ISMS electrodes as well as other spinal implants such as shunt catheters.

We found that silicone elastomers, previously proposed as materials for surrogate spinal cords, have high indentation forces and interfacial frictional forces relative to the physiological spinal cord. Instead, formaldehyde-crosslinked gelatin (12 wt% in water) has mechanical and interfacial properties that closely mimic those of the natural spinal cord. Surrogate cords made from this material can provide reliable in vitro media for realistic assessments of the mechanical compatibility of intraspinal implants. Using surrogate cords made of formaldehyde-crosslinked 12 wt% gelatin, we demonstrated that intraspinal electrode arrays made of individual microwires are more mechanically compatible with the cord than arrays of microwires connected with a stiff, solid base (characteristic of the types of arrays typically employed in the central nervous system). The latter impede the motion of the tissue during elongation and could cause tissue damage.

While actual spinal cord tissue is anisotropic (with the axons running primarily in the direction perpendicular to the length of the cord), our model exhibits isotropic mechanical properties. In subsequent work, our model could be refined by mimicking the anisotropic architecture of actual spinal cords. Nonetheless, our surrogate cords provide a valuable starting point for bench-top testing of cord–implant interactions, prior to deployment in animal studies. The formaldehyde-crosslinked 12 wt% gelatin could also be used to assess the mechanical compatibility of brain implants.

Biographies

Cheng Cheng received the exchange certificate in mechanical engineering from the Hong Kong Polytechnic University, Hong Kong, in 2008, the B.Sc. degree in materials engineering from Shandong University, Shandong, China, in 2009, and the M.Sc. degree in materials engineering from the University of Alberta, Edmonton, AB, Canada, in 2012.

Jonn Kmech received the B.Sc. degree in physiology from the University of Alberta, Edmonton, AB, Canada, in 2010.

Vivian K. Mushahwar (M’97) received the B.S. degree in electrical engineering from Brigham Young University, Provo, UT, USA, in 1991, and the Ph.D. degree in bioengineering from the University of Utah, Salt Lake City, UT, in 1996.

She was a Postdoctoral Researcher at Emory University, Atlanta, GA, USA, and the University of Alberta, Edmonton, AB, Canada. She is currently an Associate Professor in the Centre for Neuroscience, University of Alberta. Her research interests include identification of spinal cord systems involved in locomotion, development of spinal-cord-based neuroprostheses, incorporation of motor control concepts in functional electrical stimulation applications, and development of systems for alleviating secondary side effects of immobility such as pressure ulcers.

Dr. Mushahwar is a member of the International Functional Electrical Stimulation Society, the New York Academy of Sciences, the American Physiological Society, the International Society for Magnetic Resonance in Medicine, and the Society for Neuroscience. She is also an Alberta Heritage Foundation for Medical Research Senior Scholar.

Anastasia L. Elias received the B.Sc. degree in engineering physics and the Ph.D. degree from the University of Alberta, Edmonton, AB, Canada, in 2002 and 2007, respectively.

From 2003 to 2006, she was a Visiting Researcher at the Technische Universiteit Eindhoven, Eindhoven, The Netherlands. Since 2007, she has been a Visiting Worker at the National Research Council National Institute for Nanotechnology. She is currently an Assistant Professor in the Department of Chemical and Materials Engineering, University of Alberta. Her research interest include designing and fabricating biocompatible electrode arrays for implantation, developing new techniques for shaping materials on the micro- and nanoscale, and engineering smart materials.