An overview of wideband immittance measurements techniques and terminology: You say absorbance, I say reflectance

Abstract

This paper reviews the relationships among different acoustic measurements of the mobility of the tympanic membrane, including: impedance, admittance, reflectance and absorbance, which we group under the rubric of immittance measures. Each of these quantities is defined and related to the others. The relationship is most easily grasped in terms of a straight rigid ear canal of uniform area terminated by a uniform middle-ear immittance placed perpendicular to the long axis of the ear canal. Complications due to variations from this geometry are discussed. Different methods for measuring these quantities are described and the assumptions inherent within each method are made explicit. The benefits of wideband measurements of these quantities are described, as are the benefits and limitations of different components of immittance and reflectance/absorbance. While power reflectance (the square of the magnitude of pressure reflectance) is relatively invariant along the length of the ear canal, it has the disadvantage that it ignores phase information that may be useful in assessing the presence of acoustic leaks in ear-canal measurements and identifying other potential error sources. A combination of reflectance and impedance magnitude and angle give a more complete description of the middle ear from measurements in the ear canal.

The Definition of Acoustic Impedance and Admittance

Multiple acoustic techniques and devices have been used to measure the average motion of the tympanic membrane in response to sound, where the basic task is to figure out what is the relationship between sound pressure as a function of time, p(t), and the rate of alternating volume displacement, u(t), (usually called the volume velocity) of the tympanic membrane (Figure 1). If the stimulus is a sinusoid of frequency f, i.e. p(t)=P cos(2πft+θ_P), with an amplitude P and a phase argument θ_P (which specifies the value of the cosine function when time equals 0), and the sound intensity is within the range where the middle ear is linear (sound levels less than 120 dB SPL, (Guinan and Peake 1967; Goode et al. 1994; Dalhoff et al. 2007), then the volume velocity at the tympanic membrane (TM) is also a sinusoid at the stimulus frequency u(t)=U(f) cos(2πft +θ_U (f)), with a frequency-dependent magnitude U(f) and a phase θ_U (f)¹. From these relationships we can define a frequency dependent acoustic impedance Z(f), where Z is a complex number with a magnitude equal to the ratio of the magnitudes of the pressure and volume velocity at each stimulus frequency, |Z(f)| = P/U(f), and a phase angle ∠Z(f) that equals the difference between the phases of p(t) and u(t), i.e. ∠Z(f) = θ_P – θ_U (f). (Note that while the sound pressure and volume velocity vary with time, the magnitude and phase angle of the impedance do not.)

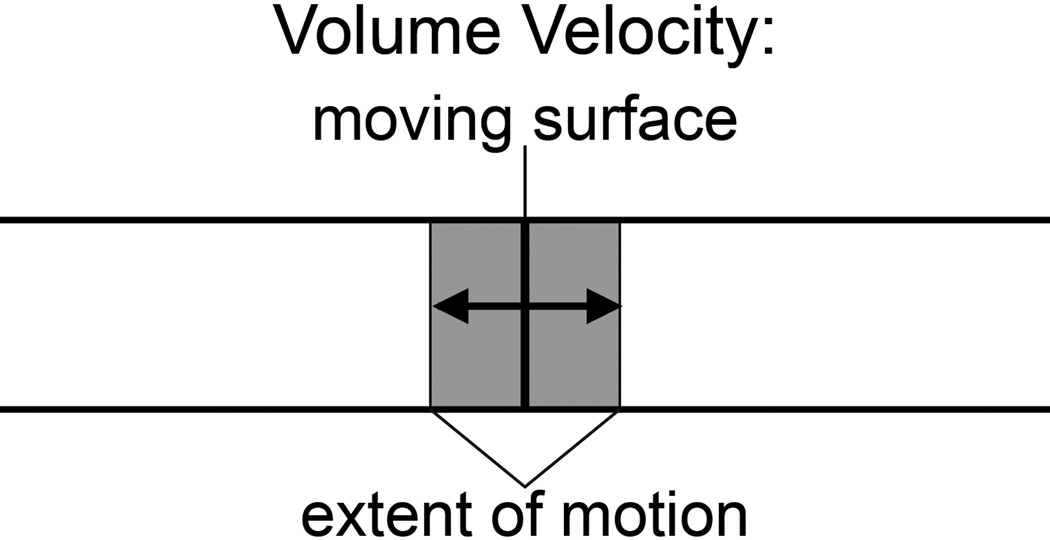
Figure 1.

Volume velocity is the rate-of-change of the volume displaced by the back and forth motion of a surface in a constrained space. Inside the tube is a hypothetical surface (the black vertical line) made up of acoustic particles moving with similar amplitude and phase. The sound induced back and forth motion of the surface sweeps out a volume. The volume velocity is the change in this volume with time.

Alternatively, we can use measurements of u(t) and p(t) to define an acoustic admittance Y(f), where the admittance magnitude |Y(f),| is the ratio of U(f)/P, and its phase angle is the phase of the volume velocity relative to the phase of the sound pressure, i.e. ∠Y(f) = θ_U(f) – θ_P. In terms of complex numbers² Z(f) = 1 / Y(f). The simple relationship between Z(f) and Y(f) makes them effectively interchangeable; a fact that leads to the use of the term immittance to describe Z(f) and Y(f) collectively. The two quantities have different but related units. The Système International (SI) unit of acoustic impedance is the acoustic ohm: 1 acoustic ohm = 1 Pa-s-m⁻³. The unit of acoustic admittance is the acoustic siemen: 1 acoustic siemen = 1 m³-s⁻¹-Pa⁻¹. The pascal (Pa) is the SI unit of pressure, where 1 Pa = 1 kg-m⁻¹-s⁻².

The techniques used to measure immittance in the ear canal are tabulated in Table 1, and include: (i) the combination of sound pressure measurements with the volume velocity output from a well characterized sound source (determination of the equivalent source characteristics - as described in the Appendix - is required because it is difficult to measure directly volume velocity), (ii) acoustic bridges that estimate Z(f) or Y(f) from direct comparisons of the sound pressures produced in unknown acoustic immittance and known acoustic immittances, (iii) wave-tubes that quantify the variation in sound pressure magnitude and phase angle along the length of a uniform tube coupled to a structure of unknown Z(f) or Y(f), and (iv) wave-tube methods that use sound pressure measurements along the length of the ear canal. Methods (i), and (ii) are direct measurements of acoustic immittance determined from the measurement of sound pressure produced by a volume velocity source. Methods (iii) and (iv) actually measure acoustic reflectance within tubes and ear canals from which the immittance at the termination of the tube can be calculated.

Table 1.

Methods Used to Estimate Immittance in the Ear Canal

Technique	Measured variables	References
(i) Use of determined equivalent sound source to estimate immittance	Determination of equivalent circuit of the sound source (Appendix 1). Unknown immittance determined from sound pressure measurements.	Sivian & White 1932; Møller 1960; Zwislocki 1957; Rabinowitz 1981; Allen 1986; Keefe et al. 1992; Lynch et al. 1994
(ii) The acoustic bridge balances known and unknown immittances	Direct comparison of sound pressures produced in loads of known and unknown immittance.	Metz 1946; Zwislocki 1961; Zwislocki & Feldman 1970
(iii) A wave tube characterizes standing waves allowing direct estimates of reflectance and immittance	Measurements of the sound pressure along the length of a long tube coupled to the ear canal	Tröger 1930; Shaw 1976
(iv) Standing waves and reflectance in the ear canal used to estimate immittance	Measurements of sound pressure at different locations within the ear canal	Mehrgardt & Mellert, 1977; Hudde 1983; Stinson et al. 1982; Farmer-Fedor & Rabbitt 2002

Waves in Tubes

A long narrow rigid-walled tube of constant cross-section S acts like a one-dimensional acoustic device. The sound pressure varies along the long axis of the tube (the x axis) in the form of forward (p⁺) and backward (p⁻) traveling waves:

$$p(t,x)=p^{+}(t,x)+p^{-}(t,x),\text{where}{p}^{+}(t,x)=P^{+}\text{cos}(\omega t-kx+{\theta }_P^{+}),\text{and}{p}^{-}(t,x)=P^{-}\text{cos}(\omega t+kx+{\theta }_P^{-})$$ (Eqn 1)

ω=2πf, and k=ω/c. Figure 2 schematizes the presence of a forward and a backward wave traveling in a rigid tube of uniform cross section. The tube is terminated on the right-hand side with an unknown acoustic immittance. The forward wave is initiated by a sound source on the left-hand side. The backward wave is initiated by reflection of the forward wave at the tube’s terminal end.

Figure 2.

Forward and backward traveling waves in a tube of length l and uniform cross-sectional area S. A sound source on the left (at x = −l) launches forward going waves in the tube, which are reflected at the termination on the right (at x = 0) to form backward traveling waves. Note that when the cross-sectional dimensions of the tube are small compared to the wavelength of the generated sound, the sound pressure and volume velocity is constant within any tubal cross-section (e.g. the red colored section in the middle of the tube), and we can describe the spatial variation in sound pressure and volume velocity within the tube in terms of a single spatial variable x, the position along the long axis of the tube (e.g. Eqn. 1).

Acoustic Reflectance and Absorbance

When discussing acoustic reflectance we need to distinguish between pressure reflectance and power or energy reflectance. Lets start with the more basic quantity. Acoustic pressure reflectance R(f, x) compares the complex sound pressure (magnitude and phase) in a sinusoidal wave that propagates toward a terminal boundary (the incident or forward wave) within the tube with the sound pressure of the reflected (backward traveling) wave that originates at the tubes terminal boundary. More specifically, R(f, x) is the ratio of the complex amplitude of the reflected and incident waves with a magnitude |R(f, x)| equal to the ratio of the magnitudes of the reflected and incident pressures wave and an angle ∠R(f, x) (which varies with distance from the source of the reflection) equal to the difference in phase angle between the reflected and incident waves at the measurement location. In terms of the description of the forward and backward waves of Eqn. 1, the magnitude of the pressure reflection coefficient is:

$$|\mathit{R}(f,x)|=\frac{P^{-}}{P^{+}},$$ (Eqn 2a)

and the phase of the pressure reflection coefficient is:

$$\angle \mathit{R}(f,x)=(kx+{\theta }_P^{-})-(-kx+{\theta }_P^{+})=2kx+({\theta }_P^{-}-{\theta }_P^{+}).$$ (Eqn 2b)

Reflectance is most easily understood and determined in a well-controlled system such as a wave tube (e.g. Figure 2). A wave tube is a long cylindrical tube of constant (uniform) cross-sectional area with rigid walls. A sound source is placed at one end of the long tube, and an object with unknown immittance is used to terminate the other end of the tube. The tube construction includes some mechanism enabling measurements of sound pressure at varied x-locations along the length of the tube, where the sound pressure at any x equals the sum of the forward going ‘incident’ pressure wave and the backward ‘reflected’ wave at the measurement location (Eqn. 1). The relative magnitude of the backward and forward going waves depends on the magnitude of the acoustic immittance that terminates the tube. The relative phase angle of the two waves at position x depends on the phase angle of the waves at the termination and the distance between the measurement location and the termination. If the measurement tube walls are rigid, the tube is of uniform or slowly (variations in cross-section that are much smaller than a wavelength) and regularly (the derivative of the area with x is continuous and of a single sign) varying cross-section, and effects of the viscosity of air are small (a reasonable assumption for many circumstances) then |R(f,x)| is constant throughout the tube, and the phase angle of the reflectance ∠R(f,x) varies regularly with position along the tube (Eqn. 2). Local maxima in sound pressure occur at positions in the tube where the phase angles of the incident and reflected waves are equal. Local minima occur at positions where the two waves are 180° out-of-phase. The ratio of the magnitude of the pressures at the local maxima and minima can be used to define the magnitude of the pressure reflectance |R(f,x)| within the tube produced by the termination, and the location of the minima together with the speed of sound and the frequency of the tonal signal defines the phase angle of the pressure reflectance ∠R(f,0) at the termination (Kinsler et al. 1982; Stinson, Shaw & Lawton 1982).

The pressure reflectance at the termination (at position x = 0 in Figure 2) can be quantified in terms of the acoustic impedance of the termination Z_T(f) = Z(f, 0) and the characteristic impedance of the air-filled measurement tube Z₀, where Z₀ depends on the density of air ρ₀, the speed of sound in air c, and the cross-sectional area of the tube S (Z₀ = ρ₀ c / S ), such that:

$$\mathit{R}(f,0)=\frac{{\mathit{Z}}_T(f)-Z_0}{{\mathit{Z}}_T(f)+Z_0}$$ (Eqn. 3)

You can also determine the pressure reflectance in the tube at any distance x away from the termination by comparing the impedance measured at that distance with Z₀ based on the cross-sectional area at location x.:

$$\mathit{R}(f,x)=\frac{\mathit{Z}(f,x)-\raisebox{1ex}{${\rho }_{0}c$}\!\left/ \!\raisebox{-1ex}{$S(x)$}\right.}{\mathit{Z}(f,x)+\raisebox{1ex}{${\rho }_{0}c$}\!\left/ \!\raisebox{-1ex}{$S(x)$}\right.}$$ (Eqn. 4)

At the terminal boundary, when the magnitude of Z_T(f) is much larger than Z₀ , R(f, 0) is approximately 1, i.e. the reflected pressure magnitude approximates the incident pressure magnitude, and the phase of the incident and reflected waves at the terminal boundary are nearly equal. When the magnitude of Z_T(f) is much smaller than Z₀, R(f, 0) is approximately −1 , and the reflected pressure magnitude also approximates the incident pressure magnitude, but the phases of the incident and reflected waves are opposite (i.e. they differ by 180°). When the magnitude of Z_T(f) equals Z₀ the magnitude of the reflected wave is zero and R(f, 0) =0. As noted in Equation 2a, for a rigid-walled air-filled tube of uniform or slowly and regularly-varying cross section, the magnitude of the pressure reflectance along the tube is constant and equals the magnitude of the pressure reflectance at the termination where x=0, i.e. |R(f, x)| = |R(f, 0)|. The angle of the pressure reflectance measured along the tube equals the angle of the reflectance at the termination plus a factor related to the round trip travel time of the pressure wave between the measurement point and the termination (Equation 2b), i.e. ∠R(f, x) =∠R(f,0) +4π x /λ, where λ is the wavelength of sound at the stimulus frequency f and is equal to c/f. We can also express the right hand term on the right side of the equation (4π x /λ) in terms of wave number (2kx) (e.g. Eqn. 2b).

The power reflectance ℜ describes the ratio of the power or energy in the reflected wave to the power or energy in the incident wave. Power reflectance (sometimes called energy reflectance) equals the square of the magnitude of the pressure reflectance: ℜ(f)=|R(f)|². Note that the power reflectance is a real number and contains no phase information. Again, within an air-filled rigid tube of uniform or regularly varying cross section, the terminating acoustic impedance and the tube’s cross-sectional area at the termination determine the power reflectance. This reflectance is constant along the tubes length, as long as losses are negligible.

While reflectance quantifies the amount of sound pressure or power reflected from the termination of the wave tube, absorbance defines the sound power that is absorbed by the termination. The absorbance is A(f)=1−ℜ(f). In some cases it is useful to quantify the absorbance as a dB value³ where the absorbance level in dB is 10 log10(A). This quantity has also been called transmittance (Allen, Jeng and Levitt, 2005).

Measurements in Ear Canals

Modern techniques of estimating impedance and reflectance use measurements of sound pressure at a point x in the ear canal along with a completely characterized sound source to compute the impedance at the point of measured pressure Z(f, x). If power reflectance at the tympanic membrane is the desired final measurement, Eqn. 4 is used along with an estimate of the cross-sectional area of the ear canal at the measurement point (necessary to define Z₀ at that point) to calculate the pressure reflectance R(f, x) at the measurement point and the power reflectance at the TM is assumed to equal the square of the magnitude of the pressure reflectance ℜ(f)=|R(f,x)|². The accuracy of the measured ℜ(f) therefore depends on the accuracy of the estimate of reflectance at the measurement point, and the approximations that (i) the viscosity of air is negligible, and (ii) that the ear canal is a rigid-walled tube of constant or slowly and regularly varying cross-section. Figure 3 illustrates some schematic representations of the human ear canal that demonstrate that the ear canal is only approximated by a uniform tube, and that the assumption of a slowly and regularly varying cross-section is not accurate everywhere within the canal: Near the eardrum termination the cross-section of the canal doubles within a significant fraction (> 10%) of the wavelength of a moderate to high frequency sound; and half-way down the length of the canal, there is a local minimum in the cross-sectional area (Farmer-Fedor and Rabbitt 2002).

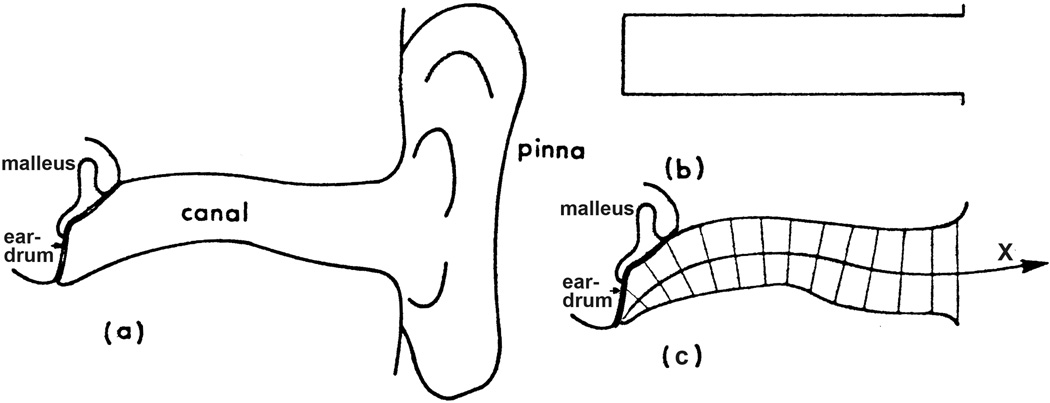
Figure 3.

Schematic representations of the human ear canal (modified from Stinson & Lawton 1989). (a) A schematic of an anatomically realistic ear canal with pinna, eardrum and malleus. (b) A uniform tube approximation of the ear canal. (c) An attempt to model the complex ear canal shape with a concatenation of uniform length sections in which the centers of each section are fit by the line labeled ‘X’. Note, the rapid expansion of the canal near the TM, the curvature, induce changes in the orientation of the different canal sections, and the local minimum in cross-section about half way down the tube length. (Reprinted with permission from Stinson, M.R., Lawton, B.W., Journal of the Acoustical Society of America, 85, 2493. Copyright (1989), Acoustical Society of America.)

One major advantage of using the reflectance is that as long as the approximations of slow, regular variations in cross-section and low-viscosity hold, the power reflectance at the point of measurement in the ear canal is a good approximation of the power reflectance at the TM. This is not the case with measurements of immittance in the ear canal, where the immittance magnitude and angle varies regularly with position in the canal. This variation occurs because the immittance measured at any point in the ear canal is influenced not only by the immittance at the TM (the middle-ear input immittance) but also by the immittance of the air space between the TM and the measurement point (Moller 1960; Zwislocki 1962; Rabinowitz 1981). At frequencies where the length of the remaining canal lEC is less than a tenth of the sound wavelength, the air space in the canal acts like an acoustic compliance in parallel with the immittance of the TM such that

$$\mathit{Y}(f,l_{EC})={\mathit{Y}}_{TM}+j2\pi f{C}_{EC};\text{with}{C}_{EC}=\frac{l_{EC}\times S}{1.4\times {10}^5}\left(\frac{m^3}{Pa}\right)$$ Eqn 5

where the average cross-sectional area of the ear canal is S, l_EC x S is the volume of the residual ear-canal space, and 1.4×10⁵ Pa is the compressibility of air at 1 atmosphere of static pressure and 20° C. The parallel arrangement of the compliance and the TM immittance makes it convenient to use admittances in the calculation of Equation 5. At frequencies where the length of the remaining canal is more than 0.1 λ, more complicated and less certain descriptions of the effect of the immittance of the intervening canal (Rabinowitz 1981; Lynch et al. 1994; Huang et al. 2000) can be used to estimate Z_TM from the impedance measured at a location in the ear canal Z(f, l_EC). Some of these techniques rely on measurements of the phase of the pressure reflectance to help determine the length of the canal between the measurement location and the TM (Keefe 2007; Voss, Merchant and Horton 2012).

Wideband Measurements

One of the benefits of modern signal generation and averaging techniques is the ability to quickly measure the acoustic response of tubes and ears over a wide frequency range. These techniques rely on the use of wideband stimuli that are the sum of many sinusoidal waves of varied frequencies. Averaging the sound pressures produced by such wideband stimuli allows a fairly rapid computation of the immittance or reflectance over a wide frequency range (e.g. 0.2 to 6 kHz) with a relatively fine frequency resolution (e.g. a point every 100 Hz). The combination of fine resolution and wide bandwidth produces a more detailed look at the immittance and reflectance. Later papers in this volume will demonstrate that (1) finer frequency resolution can help detect variations in reflectance due to ossicular interruption and superior canal dehiscence (Nakajima et al. this issue, pp. XXXX), and (2) that the reflectance in the higher-frequency range (1–4 kHz) can be a useful indicator of the presence of fluid-related conductive hearing loss in infants (Prieve et al. this issue, pp. XXXX).

Complications in the Measurement of Immittance/Reflectance

Variations in canal cross section

The wideband immittance and reflectance at the TM can be readily and accurately estimated from measurements made in a rigid ear canal of uniform cross-section. However the ear canal cross-section is not uniform along its length; the canal geometry (Figure 3) includes local constrictions and expansions as well as bends and curves, and significant tapering of the canal near the TM (Johansen 1975; DiMaio & Tonndorf 1978; Stinson & Lawton 1989). Local constrictions and expansions in area are particularly critical for the generation of non-uniformities in the sound field (Farmer-Fedor & Rabbitt 2002). The significance of these deviations from uniformity increases with stimulus frequency.

One reflectance measurement technique that is less affected by the variations in canal cross-section along its length is based on finely spaced measurements of sound pressure within the ear canal (Stinson, Shaw & Lawton 1982; Stinson 1990; Farmer-Fedor & Rabbitt 2002). Such reflectance estimates for the human TM can be readily calculated at frequencies as high as 20 kHz, and the fine spatial deviations in sound pressure observed in such studies are the best evidence for the significance of variations in canal cross-section.

Non-uniformities in the sound field within a given cross section

The impedance and reflectance techniques that depend on the measurement of the sound pressure at a single point in the ear canal also assume that the pressure measured at that point describes the sound pressure throughout the canal cross-section (Figure 2). This ‘uniform plane wave’ assumption is common in describing sound flow in tubes, but it can break down in the presence of spatial variations in tubal cross sections. Sudden or irregular variations in ear canal area actually generate non-uniformities in sound pressure across a canal cross-section (Farmer-Fedor & Rabbitt 2002). Such non-uniform pressure waves generally only propagate short distances in the ear canal before dying out (this is true in the adult human ear canal at sound frequencies less than about 20 kHz), but they can be large enough to affect measurements at a single point. It is the effect of such non-uniformities on single point sound pressure measurements within the ear canal that are the likely root of uncertainties in the reflectance and immittance at frequencies above 5–6 kHz in adult human ear canals (Farmer-Fedor & Rabbitt 2002).

Variation in the rigidity of the ear canal walls

The walls of the adult human ear canal are not perfectly rigid. This is especially true of the cartilage and other soft tissues that compose the walls of the outer half of the ear canal. However, for the most part, the deviations from rigidity are small compared to the compliance of the air in the canal, and can be ignored. The same cannot be said for newborn and infant ear canals in which the deviations from wall rigidity are even larger. Indeed, the increased compliance of the newborn and infant ear canal is known to play a significant role in tympanometric measurements where the compliance of the ear canal walls can add to the measured compliance in both the static and pressurized conditions. Tympanometry depends on the response to both acoustic and static pressures, and the utility of such measurements in the infant and newborn population has been questioned (Holte et al. 1991; Prieve et al. this issue, pp. XXXX; Hunter et al. this issue, pp. XXXX). While the tissues of the canal wall are less stiff in infants and newborns, as sound frequency increases, it is the density of these tissues that determines the degree of their rigidity, and the effect of density increases as sound frequency increases. Experimental results suggest that at 1000 Hz and higher, the walls of the infant and newborn ear canals are significantly more rigid than the air in the canal. Acoustic measurements made at these higher frequencies are less affected by the ear canal, and better reflect the acoustics and mechanics of the TM and middle ear (Prieve et al. . this issue, pp. XXXX; Hunter et al. . this issue, pp. XXXX).

The effect of viscosity

The viscosity of air is small and generally negligible; however, there are circumstances where it can play a small role in measurements of immittance and reflectance. An area where its effect is minor is in the estimation of reflectance magnitude at the tympanic membrane from measurements made in the ear canal. While viscous interactions between the air in the ear canal and the stationary walls of the canal will cause sound power to be absorbed as sound travels between the reflector and the measurement location, over dimensions relevant to measurements in humans, the losses involved are small (Huang et al. 2000; Voss et al. 2008; Keefe et al. 2010).

An area where the effect of viscosity is also small but more significant is in the calibration procedure used to describe the acoustic source in the first immittance measurement technique listed in Table 1. That method (Appendix) uses measurements of sound pressure at the entrance of well-defined acoustic loads to characterize the output pressure and impedance of the sound source. The loads used are tubes of varied length. The fitting procedure used in the calculation works better if viscous looses (which are most significant at the resonant and anti-resonant frequencies of the tube impedances) and ‘heat’ losses (which are most significant at frequencies below 100 Hz) are included in the description of the calibration loads (Lynch, Peake & Rosowski 1994).

Power reflectance ℜ(f) vs. pressure reflectance R (f,x)

Descriptions of the power reflectance at the TM based on ear canal measurements, by themselves, have advantages and disadvantages. The primary advantage of power reflectance (and the closely related absorbance A(f)) is that both are relatively independent of the measurement position within the ear canal, and they provide a simple frequency dependent measure of the power transfer at the tympanic membrane. A significant disadvantage is that power reflectance and absorbance depend only on the magnitude of the pressure reflectance and ignore significant information in the phase angle of the pressure reflectance and terminating immittance. Equations 2, 3 and 4 document that the terminating impedance of the ear canal Z_T(f) and the associated pressure reflectance R(f,x) can be calculated from each other if one knows the diameter and the length of the intervening ear canal. However, the loss of the pressure reflectance phase information in the transformation to power reflectance makes it impossible to derive Z_T(f) from ℜ(f) or A(f). This loss of information can be significant. For example, attempts to determine if a low power reflectance reading at low frequencies results from a leak of sound pressure out of the ear canal are greatly aided by inspection of the immittance phase (Voss et al. this issue, pp. XXXX; Voss et al. 2008; Huang et al. 2000; Keefe et al. 2010).

Summary

This paper details the close theoretical relationship between acoustic immittance (impedance or admittance) and pressure and power reflectance. The relationship is strongest in cases of pressure reflectance at the termination of a uniform rigid ear-canal tube; the pressure reflectance in the canal depends only on the immittance at the TM, the canal cross-sectional area and the distance between the TM and the measurements location within the canal. The power reflectance is simpler and only depends on the immittance at the TM and the cross-sectional area. This simplicity comes at a cost in that the power reflectance, by itself, does not completely describe the mechanics and acoustics at the TM.

A major advantage of power reflectance, or pressure reflectance magnitude, is that these measures are relatively independent of position within a canal with slowly and regularly varying cross-section. On the other hand, the pressure reflectance phase angle and the magnitude and angle of the immittance measured in the canal vary significantly at different locations within the ear canal. Indeed, measurements of immittance within the ear canal include effects of the canal space between the measurement location and the TM. The effect of this space on the measured immittance can be removed at frequencies where the space is small compared to a wavelength; such compensation is easiest and most accurate when the ear canal acts like a rigid uniform tube. Non-uniformities in the cross-section of the ear canal and other complications in ear canal geometry can generate non-uniform sound-pressure variations in the ear canal that complicate the measurement of reflectance and impedance with sound frequencies above 4 to 5 kHz when the single point techniques is used. Reflectance and impedance estimated from measurements at multiple locations in the ear canal are less affected by such non-uniformities.

List of Symbols

c

the speed of sound

f

frequency

k

the wave number

l

tube length

p

sound pressure as a function of time

p+

sound pressure in a forward wave

p−

sound pressure in a backward wave

u

volume velocity as a function of time

x

linear position

P

the sinusoidal amplitude of p(t)

U

the sinusoidal amplitude of u(t)

TM

the tympanic membrane

θ_P

the cosine phase of p(t)

θ_U

the cosine phase of u(t)

P

the complex amplitude of sound pressure

U

complex sound volume velocity

R

complex pressure reflectance

Y

Acoustic Admittance

Z

Acoustic Impedance

|P|

the magnitude of P

∠P

the phase angle of P

A

sound power absorbance

ℜ

sound power reflectance

Z₀

the characteristic impedance of an air-filled tube

λ

the wave length of sound at frequency f

ρ₀

the density of air

ω

the radian frequency

Appendix: Determination of the source characteristics

The ear canal sound pressure, by itself, is not a sufficient descriptor of the sound drive to the ear canal and middle ear. A more complete description includes a measurement of sound volume velocity, where knowledge of both volume velocity and sound pressure is needed to define the acoustic immittance and calculate reflectance. To estimate the immittance and reflectance of the middle ear, from a measurement at a single location in the ear canal, the sound delivery system needs to be completely defined. A common characterization is to describe the source by its Norton or Thévenin equivalent circuit (Rabinowitz 1981; Allen 1986; Keefe et al. 1992; Lynch, Peake & Rosowski 1994). The measurement of the sound pressure magnitude and angle (P_L) at the entrance to the acoustic load (Z_L) is illustrated in Figure A1 along with a Thévenin equivalent description of the sound source.

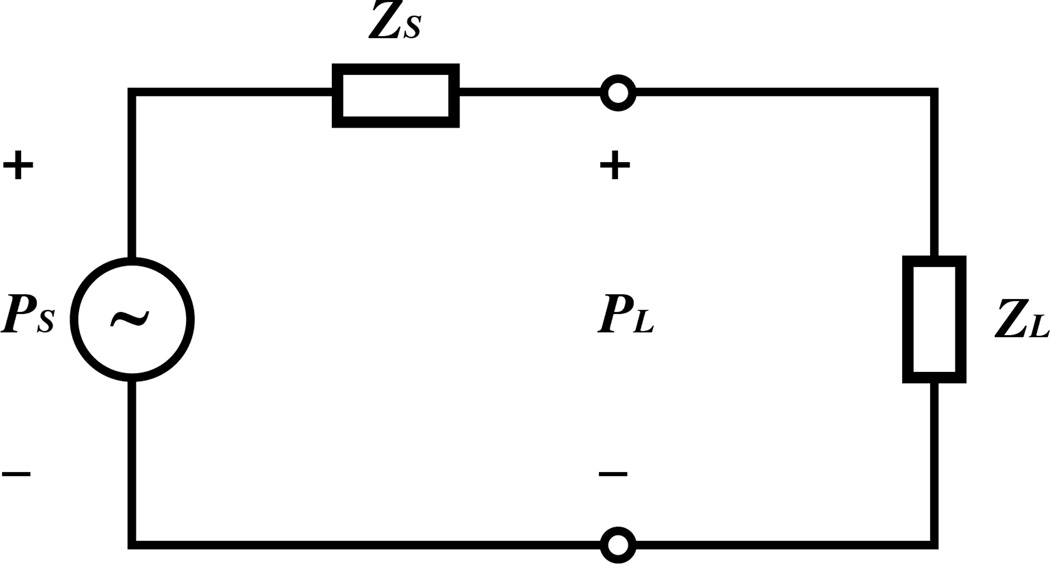
Figure A1.

The Thévenin equivalent circuit for the measurement of the tube or ear canal sound pressure. P_S and Z_S describe the equivalent pressure source and impedance of the source. Z_S and P_L describe the impedance of the load and the sound pressure measured at the entrance to the load.

The source is described by an ideal sound pressure generator (P_S) in series with a source impedance (Z_S), which is in series with Z_L. The impedances are complex and of the form Z = a + jb where j is the imaginary number $\sqrt{-1}$. The volume velocity output from the source is the ratio of the pressure difference and the source impedance: (P_S – P_L) / Z_S. The relation between P_S and P_L is also described by equation A1:

$${\mathit{P}}_S={\mathit{P}}_L(\frac{{\mathit{Z}}_S}{{\mathit{Z}}_L}+1).$$ (A1)

Measurements of P_L in two different loads (Z_A and Z_B) allow the calculation of the two equivalent circuit descriptors for the source (P_S and Z_S) (e.g. Rabinowitz 1981). Specifically, Z_S can be directly estimated from the pressures measured at the entrance of the two loads (A & B):

$${\mathit{Z}}_S=\frac{{\mathit{Z}}_A(\frac{{\mathit{P}}_A}{{\mathit{P}}_B}-\mathbf{1})}{1-\frac{{\mathit{Z}}_A}{{\mathit{Z}}_B}\frac{{\mathit{P}}_B}{{\mathit{P}}_A}},$$ (A2)

and P_S can then be determined from Equation A1 (Lynch, Peake & Rosowski 1994).

The most common method to determine the equivalent source pressure and source impedance is by measurements in closed tubes of different lengths. The impedance at the entrance of a lossless tube with a closed ending is given in equation A3.

$$\mathit{Z}=-j\frac{{\rho }_{0}c}{S}\text{cot}\left(\frac{2\pi f}{c}l\right).$$ (A3)

Again, ρ₀ is the density of the air, c is the speed of sound, S is the cross-section area, f the frequency, l is the length of the tube and j is the imaginary number $\sqrt{-1}$ (Stevens 1998). The tubes are of a hard and smooth material consistent with the lossless approximation, and the cross-sectional area is chosen to be similar to the ear-canal cross-section area. We show the lossless equation for simplicity, the lossy versions are well described in the literature (e.g. Egolf 1977). The inclusion of losses becomes important at very low frequencies (< 100 Hz) where heat losses can be significant and at the frequencies near the peaks and valleys in the cotangent function, where viscous losses dominate the impedance.

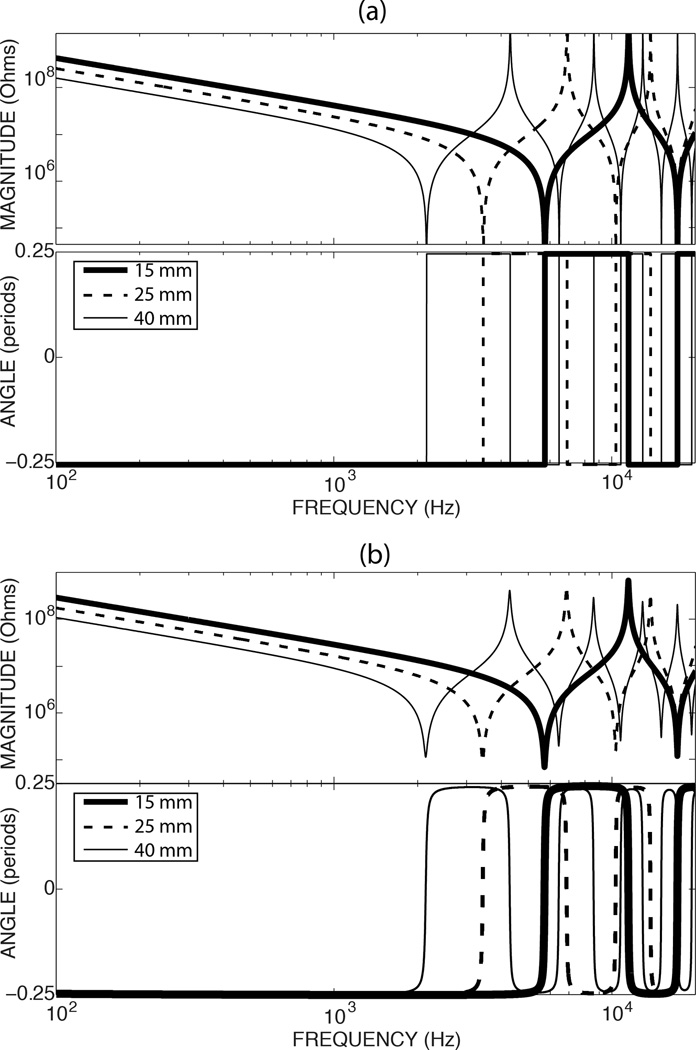
Examples of the calculated lossless impedance at the entrance of three tubes of different lengths (15, 25, and 40 mm) and a diameter of 8 mm are illustrated in Figure A2a; note the sudden and sharp phase transitions that occur at the frequencies with extremely sharp variations in magnitude. The calculated lossy impedances in the same three tubes are illustrated in Figure A2b; note the more rounded phase transitions and magnitude maxima and minima.

Figure A2.

Magnitude and phase of the impedance of three lossless closed tubes of 15, 25, and 40 mm. The diameter of the tubes is 8 mm. The top panels illustrate the magnitude of the impedance of the tubes; the lower panels illustrate the impedance phase angle. The frequency is coded on the x-axis on a log scale from 100 to 20000 Hz. In (a), which assumes the air and tubes are lossless, the impedances at the tube resonances go to 0 (which is difficult to plot on the log magnitude axis) and the impedance at the anti-resonance frequencies is infinite. In (b) the inclusion of viscous and heat losses introduces small deviations at frequencies less than 100 Hz, limits the infinitely sharp peaks and valleys, and smooths the sudden half-cycle phase changes at the tube resonance and anti-resonances (Lynch, Peake and Rosowski 1984).

The parameters P_S and Z_S are often determined by measurements in more than two tubes, resulting in an over-determined system. One way to estimate the source components in an over-determined equation system is by using a least-squares approach. If the number of tubes for the determination of the source generator and source impedance is n, there are n measurements of P_L. If equation A1 is written in matrix form, the equation for the n measurements is

$$\left[\begin{array}{c}\hfill {\mathit{P}}_{L1}{\mathit{Z}}_{L1}\hfill \\ \hfill {\mathit{P}}_{L2}{\mathit{Z}}_{\mathit{P}2}\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathit{P}}_{Ln}{\mathit{Z}}_{Ln}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\mathit{P}}_{L1},-{\mathit{Z}}_{L1}\hfill \\ \hfill {\mathit{P}}_{L2},-{\mathit{Z}}_{L2}\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathit{P}}_{Ln},\hspace{1em}-{\mathit{Z}}_{Ln}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\mathit{P}}_S\hfill \\ \hfill {\mathit{Z}}_S\hfill \end{array}\right]$$ (A4)

or

$$\mathbf{A}=\mathbf{B}\mathbf{C},$$ (A5)

where A is the column array containing n rows of the product of the measured pressure in each load and the load impedance, B is the two column array of n rows of the load impedance and −1 times the measured pressure, and C is a two-element column array with the elements P_S and Z_S. The estimated least-square values for the source, P̂_S and Ẑ_S is then

$$\left[\begin{array}{c}\hfill {\widehat{\mathit{P}}}_S\hfill \\ \hfill {\widehat{\mathit{Z}}}_S\hfill \end{array}\right]={\left({\mathit{B}}^T\mathit{B}\right)}^{-1}{\mathit{B}}^T\mathit{A}$$ (A6)

where B⁻¹ is the inverse of B and BT is the transpose of the matrix B.