Interpreting Meta-Regression: Application to Recent Controversies in Antidepressants’ Efficacy

Abstract

A recent meta-regression of antidepressant efficacy on baseline depression severity has caused considerable controversy in the popular media. A central source of the controversy is a lack of clarity about the relation of meta-regression parameters to corresponding parameters in models for subject-level data. This paper focuses on a linear regression with continuous outcome and predictor, a case that is often considered less problematic. We frame meta-regression in a general mixture setting that encompasses both finite and infinite mixture models. In many applications of meta-analysis the goal is to evaluate the efficacy of a treatment from several studies and meta-regression on grouped data is used to explain variations in the treatment efficacy by study features. When the study feature is a characteristic that has been averaged over subjects, it is difficult not to interpret the meta-regression results on a subject level, a practice that is still widespread in medical research. While much of the attention in the literature is on methods of estimating meta-regression model parameters, our results illustrate that estimation methods cannot protect against erroneous interpretations of meta-regression on grouped data. We derive relations between meta-regression parameters and within-study model parameters and show that the conditions under which slopes from these models are equal cannot be verified based on group-level information only. The effects of these model violations cannot be known without subject level data. We conclude that interpretations of meta-regression results are highly problematic when the predictor is a subject level characteristic that has been averaged over study subjects.

1. Introduction

A major controversy in mental health research is the efficacy of modern antidepressants. This controversy gained much prominence with the publication of a meta-regression, based on group-level data from studies submitted to the USA Food and Drug Administration, relating the efficacy of antidepressants to baseline depression symptoms of patients, by Kirsch et al. [1]. The authors concluded that efficacy reaches clinical relevance only for individuals with high baseline severity and that this pattern is due to a decrease in response to placebo, rather than an increase in response to medication. Numerous publications followed: [2] came to the same conclusion after reanalyzing studies in [1], while [3] and [4] conducted similar meta-regression analyses using other data and each came to different conclusions – the former that the antidepressants were equally effective at all levels of baseline severity, and the latter that improvement with both drug and placebo treatment increases with baseline severity, but the slope for the drug is steeper. [5] took this controversy further and come to question the approach of Evidence Based Medicine (a term, which has become one of the most important in today’s health system), citing the discrepancy between individual study reports and meta-regression results in the antidepressants field.

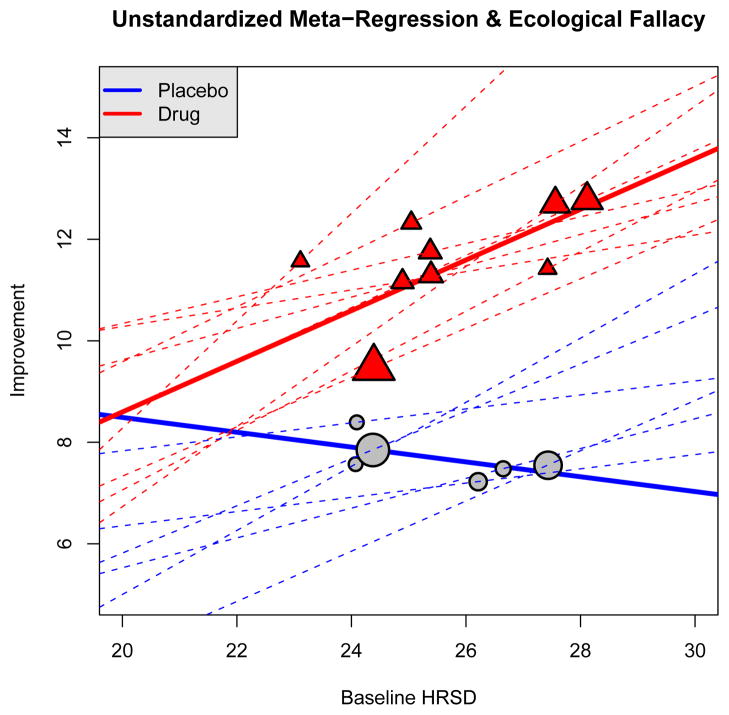
To illustrate how the use of meta-regression is fueling the antidepressant efficacy controversy, we analyzed raw data from ten antidepressant studies both at the subject-level and at the study-level using a meta-regression (see Section 4 for details). The predictor X is the baseline Hamilton Rating Scale for Depression (HRSD), with larger values corresponding to higher depression severity. As was done in the motivating article [1], the outcome Y in the regression is the change in HRSD from baseline to end of treatment. Although using change score as the outcome is known to have numerous shortfalls [6; 7], here it is done to make results comparable to [1], as we illustrate weaknesses related to aggregation (or ecological) bias and the ecological fallacy (e.g., [8; 9]) and discuss the meaning of various regression coefficients. In [1], only studies with 22 < Mean Baseline HRSD < 31 were selected and a weighted least-squares was used to fit the meta-regression model. Figure 1 shows the results of a meta-regression for six of our ten studies (which included nine drug arms) with this restricted baseline range for the means. The (thick) solid lines show the estimated meta-regression lines based on means for the six placebo arms and the nine drug arms (grouped data). The dotted lines in the figure are the regression lines based on subject-level data fit individually for drug and placebo arms. Even though all the subject-level regression lines had positive slopes for the placebo arms, the placebo meta-regression has a negative slope. In a meta-regression, it is very difficult not to interpret the results from meta-regression on a subject level when averaged subject characteristics are used as predictors. In this illustration, a natural interpretation of the meta-regression is that placebo-treated subjects with more severe baseline depression experience less placebo response even though this contradicts the interpretation obtained from subject-level regression lines (shown by the dashed lines in Figure 1).

Figure 1.

Meta-Regression Results: Plot of the study means and meta-regression lines for six studies with baseline mean HRSD restricted to be between 22 and 31 (solid lines). Also plotted are the lines from regressions using subject-level data individually for each of the 6 placebo arms and 9 drug arms in the six studies (dashed lines).

The goal of meta-analysis is to combine several estimates of some quantity of interest (typically a treatment effect) in order to more precisely estimate that quantity. Studies often try to address secondary questions using meta-regression by regressing estimates of treatment effects across studies on study characteristics, such as sample size, sponsorship (e.g. private or federal) or drug dose. As illustrated above, meta-regression has also been used to relate a treatment effect to an averaged patients’ characteristic and proceed to make inferences on a subject-level. Meta-regression methods have been developed that rely on the availability of patient-level data from at least some of the studies in the meta-analysis [e.g., 10; 11; 12; 13; 14; 15]. However, here we discuss meta-regression when subject-level data are not accessible and the available information consists of the observed sample means, standard deviations and sample sizes for each treatment. While regression with a dichotomous outcome has received wide attention and perhaps most scientists are familiar with the problems of meta-regression in that case, the discussion of continuous outcomes and regular linear regression in the literature are few and many researchers consider this situation to be less problematic. This worrisome state of affairs is demonstrated by the publications, in widely read and influential medical journals, of results based on meta-regression with subject-level covariates based only on group level data, including [1]. Regrettably, even in the statistical literature, the threat of ecological bias is often underplayed, as for example, in works discussing power and sample size issues in meta-regression, such as [15] and [12].

This paper focuses on relating meta-regression model parameters to subject-level (or within-study) regression parameters using continuous outcome Y and a continuous predictor X, which is a subject-level characteristic. In the antidepressant studies used for illustration, the meta-regression relates the mean change in depression severity Ȳ_j to the mean baseline severity X̄_j in several trials j = 1, …, K, for treatment T = t, with t = 0 for placebo and t = 1 for active treatment:

$$E({\overline{Y}}_j\mid {\overline{X}}_j,T_j=t)={\gamma }_{t0}+{\gamma }_{t1}{\overline{X}}_j.$$ (1)

If the slopes γ_t1 for t = 0 and t = 1 are not different, the treatment effect would be estimated by the difference between the intercepts γ_t0 and it would be considered constant over the entire range of the mean baseline depression severity (the covariate X̄). A difference between the slopes would indicate that the effect of treatment is different depending on the mean baseline severity. The difference between the slopes γ_t1 for t = 0 and t = 1 measures the magnitude of the interaction between treatment (T) and covariate (X), which will be discussed in Section 4.2. The model for subject-level data is

$$E(Y_{ij}\mid X_{ij},T_{ij}=t)={\beta }_{jt0}+{\beta }_{jt1}{X}_{ij},$$ (2)

where (X_ij, Y_ij, T_ij) are subject level data for the ith subject in the jth study.

From the example above, the fundamental question becomes: what is the relation of meta-regression study-level slopes in (1), to subject-level slopes from (2) that characterize the relationship within the studies? In cases when only group level data are available, another fundamental question is: can one ever use the meta-regression results to make reliable inference on a subject level? In the antidepressant example, if the outcomes for subjects receiving a particular treatment are homogeneous across studies, and subjects are recruited based on a range of X-values, then the studies comprising a meta-regression can be regarded as representative of subpopulations that are slices from the joint distribution of (X, Y) – this scenario is investigated in Section 2.1. A more general mixture model framework is provided in Section 2.2 that encompasses both finite and infinite mixture models. The relations between the outcome and the predictor are derived and compared for (a) the components (subpopulations) of the mixture, (b) the overall mixture population, as well as (c) the relationship between the subpopulations’ means of the outcome and the predictor (i.e., the meta-regression coefficients). Section 3 focuses on the recommended practice of estimating the meta-regression coefficients with random effect models. We return to the analysis and discussion of the antidepressant studies in Section 4 and conclude the paper in Section 5.

2. Heterogeneity of the target population in meta-regression

The literature on meta-analysis has tended to focus almost exclusively on approaches to estimating the regression parameters with little or no regard to the meaning and interpretation of these parameters, except for occasional warnings about committing the ecological fallacy [e.g., 16; 17; 18; 9]. If interest is in the subject-level regression coefficients in (2), it is imperative to understand how the meta-regression parameters relate to the within-study subject-level regression parameters in order to properly interpret the former. This section addresses the questions: Which population one wants to make inferences about when conducting meta-regression and how do parameters estimated in the meta-regression relate to parameters of the population of interest? The emphasis is on clarifying the meaning of meta-regression parameters, rather than on issues of estimation. Because the core focus in this and the next section is the relation of the outcome to the patient-level covariate within treatment groups, in order to simplify the exposition, we drop the treatment index t in (1) and (2) and consider models for just one of the treatment groups in a clinical trial.

The derivations for the results in the the following subsections are given in the eSupplement.

2.1. Slices From One Population

Here we consider an idealized setting where the meta-regression will give results consistent with the analysis of subject-level data. Each study comprising a meta-regression is sampled from a subpopulation of a parent population that is homogeneous with respect to the relationship of Y on X and the jth subpopulation is determined by a restriction on the predictor X, i.e., X ∈ D_j, where D_j denotes a range of x values considered for the jth sub-sample. For example, a depression study may have an inclusion criterion based on HRSD being in some range (e.g. HRSD > 22 or 10 < HRSD < 21). We will assume the D_j are non-degenerate intervals or subsets of intervals on the real line.

Suppose the joint distribution of (X, Y) has density f(x, y), the marginal density of X is f(x) and the regression of Y on X is linear: E[Y |X] = β₀ + β₁X. Let μ_x and μ_y denote the means of X and Y respectively and let

$$\mathbf{\Psi }=\left(\begin{array}{cc}{\sigma }_x^2& {\sigma }_{xy}\\ {\sigma }_{xy}& {\sigma }_y^2\end{array}\right)$$ (3)

denote the covariance matrix for (X, Y). Then, of course, ${\beta }_1={\sigma }_{xy}/{\sigma }_x^2$ and β₀ = μ_y − β₁μ_x.

Letting w_j = P(X ∈ D_j), the joint density of (X, Y) and the marginal density of X for the jth subpopulation are

$$f_j(x,y)=\frac{1}{w_j}f(x,y)I(x\in D_j),\text{and}{f}_j(x)=\frac{1}{w_j}f(x)I(x\in D_j)j=1,\dots ,J.$$

The regression of Y on X ∈ D_j for the jth subpopulation is

$$\begin{array}{l}{E}_j[Y\mid X]={\int }_{-\infty }^{\infty }{yf}_j(y\mid X)dy=\frac{{\int }_{-\infty }^{\infty }{yf}_j(X,y)dy}{f_j(X)}=\frac{{\int }_{-\infty }^{\infty }\frac{1}{w_j}yf(X,y)I(X\in D_j)dy}{\frac{1}{w_j}f(X)I(X\in D_j)}\\ ={\int }_{-\infty }^{\infty }yf(y\mid X)dy={\beta }_0+{\beta }_{1}X,\end{array}$$

and therefore the regression of Y on X in each subpopulation is linear with an intercept β₀ and a slope β₁.

In this scenario, the meta-regression slope γ₁ from (1) will indeed coincide with the common slope within all slices. To see this, note that the mean of Y in the jth slice μ_jy is

$${\mu }_{jy}=E_j[Y]=E_j[E_j[Y\mid X]]=E_j[{\beta }_0+{\beta }_{1}X]={\beta }_0+{\beta }_1{u}_{jx},$$

where μ_jx is the mean of X in the jth slice. Let ${\pi }_j=\frac{w_j}{{\sum }_{h=1}^K{w}_h}$, with Σπ_j = 1. Then the weighted average of the mean responses, μ̃_y is

$${\stackrel{\sim }{\mu }}_y=\sum _{j=1}^K{\pi }_j{\mu }_{jy}=\sum _{j=1}^K{\pi }_j({\beta }_0+{\beta }_1{\mu }_{jx})={\beta }_0+{\beta }_1{\stackrel{\sim }{\mu }}_x,$$

where μ̃_x is the weighted average of the μ_jx’s. Since the slope is the covariance between the response and predictor divided by the variance of the predictor, the meta-regression slope γ₁ is

$$\begin{array}{l}{\gamma }_1=\frac{{\sum }_{j=1}^K{\pi }_j({\mu }_{jx}-{\stackrel{\sim }{\mu }}_x)({\mu }_{jy}-{\stackrel{\sim }{\mu }}_y)}{{\sum }_{j=1}^K{\pi }_j{({\mu }_{jx}-{\stackrel{\sim }{\mu }}_x)}^2}\\ =\frac{{\sum }_{j=1}^K{\pi }_j({\mu }_{jx}-{\stackrel{\sim }{\mu }}_x)({\beta }_0+{\beta }_1{\mu }_{jx}-{\beta }_0-{\beta }_1{\stackrel{\sim }{\mu }}_x)}{{\sum }_{j=1}^K{\pi }_j{({\mu }_{jx}-{\stackrel{\sim }{\mu }}_x)}^2}={\beta }_1.\end{array}$$

Also, the y-intercept of the meta-regression line from (1) is

$${\gamma }_0={\stackrel{\sim }{\mu }}_y-{\gamma }_1{\stackrel{\sim }{\mu }}_x=({\beta }_0+{\beta }_1{\stackrel{\sim }{\mu }}_x)-{\gamma }_1{\stackrel{\sim }{\mu }}_x={\beta }_0.$$

In some settings, this scenario may be plausible, e.g. see Section 4.2. However, in most cases, this scenario is not realistic because studies that typically comprise meta-analyses differ from one another in more ways than just the range of x. For example, if different drugs were used, or different comorbid conditions were exclusion criteria, the joint distributions of baseline depression and improvement (X, Y) are likely to vary across the studies as well.

2.2. Mixture Models

In this section, each study in the meta-analysis represents a random sample from a subpopulation and the collection of subpopulations corresponds to the components in a mixture model. In the antidepressant example, each of the studies comprising the meta-regression would represent a component in the mixture model, where X is the baseline depression severity and Y is the degree of improvement on HRSD. Differences in mean values of X across studies can be due to a variety of factors such as differing inclusion criteria. The collection of subpopulations can be discrete leading to a finite mixture model, or the collection can be regarded as a sample from a hypothetical continuum of studies, leading to an infinite mixture model.

Each study will be parameterized by a vector Θ which we shall endow with a probability density h(θ) to model the distribution of the parameters as they vary across the components (represented by studies) of the mixture. In the case of a random vector (X, Y) having a bivariate normal distribution, Θ = θ can be expressed as $\mathit{\theta }={({\mu }_x,{\mu }_y,{\sigma }_x^2,{\sigma }_y^2,{\sigma }_{xy})}^{\prime }$. An alternative parameterization useful from the standpoint of the regression Y = β₀ + β₁X + ε, is $\mathit{\theta }={({\mu }_x,{\sigma }_x^2,{\beta }_0,{\beta }_1,{\sigma }^2)}^{\prime }$, where σ² is the variance of the error ε. Note, that in this alternative parameterization of Θ, ${\beta }_1={\sigma }_{xy}/{\sigma }_x^2,{\sigma }^2={\sigma }_y^2-{\sigma }_{xy}^2/{\sigma }_x^2$ and μ_y = β₀ + β₁μ_x. A finite mixture with J components is obtained, when Θ = θ_j with probability π_j for j = 1, …, J, where the prior probabilities satisfy π₁ + ··· + π_J = 1. Alternatively, one can obtain an infinite mixture for a continuous density h(θ). A special case of an infinite mixture is when the regression coefficients (β₀, β₁) are assumed to have a bivariate normal distribution. Note, that the standard mixed effects model additionally assumes that μ_x is independent of the slope and intercept.

2.2.1. Conditional and Marginal Regression of Y on X

The slope β₁ denotes the conditional association between X and Y, where conditional is meant with respect to the components of the mixture, e.g., in the case of a finite mixture, conditional on j. Using an approach similar to [19], the joint density of (X, Y, Θ) can be written as f(x, y, θ) = f(x, y|θ)h(θ) from which the marginal density of (X, Y) is the mixture density

$$f(x,y)={\int }_{\theta }f(x,y\mid \mathit{\theta })h(\mathit{\theta })d\mathit{\theta }.$$ (4)

In the case of the finite mixture, where h has J support points, (4) becomes the well-known finite mixture density $f(x,y)={\sum }_{j=1}^J{\pi }_j{f}_j(x,y)$. In order to distinguish within-study parameters from averaged across study parameters, we will write

$${\overline{\mu }}_x=E_{\theta }[{\mu }_x]={\int }_{\theta }{\mu }_{x}h(\mathit{\theta })d\mathit{\theta },\text{and}{\overline{\mu }}_y=E_{\theta }[{\mu }_y]={\int }_{\theta }{\mu }_{x}h(\mathit{\theta })d\mathit{\theta }.$$

Similarly, the regression coefficients averaged across mixture components will be denoted

$$\overline{\mathit{\beta }}=\left(\begin{array}{c}{\overline{\beta }}_0\\ {\overline{\beta }}_1\end{array}\right)=\left(\begin{array}{c}{\int }_{\theta }{\beta }_{0}h(\mathit{\theta })d\mathit{\theta }\\ {\int }_{\theta }{\beta }_{1}h(\mathit{\theta })d\mathit{\theta }\end{array}\right).$$ (5)

It will also be convenient to define mean-zero “random effects” for the y-intercept and slope as

$$\mathit{b}=\left(\begin{array}{c}{b}_0\\ b_1\end{array}\right)=\mathit{\beta }-\overline{\mathit{\beta }}=\left(\begin{array}{c}{\beta }_0\\ {\beta }_1\end{array}\right)-\left(\begin{array}{c}{\overline{\beta }}_0\\ {\overline{\beta }}_1\end{array}\right)$$ (6)

If the conditional Y on X association is linear in the mixture components, the regression of Y on X for the mixture distribution (i.e., the marginal (X, Y) distribution given in (4)) is:

$$E[Y\mid X]={\overline{\beta }}_0+{\overline{\beta }}_{1}X+\frac{{\int }_{\theta }(b_0+b_{1}X)f_x(X\mid \mathit{\theta })h(\mathit{\theta })d\mathit{\theta }}{{\int }_{\theta }{f}_x(X\mid \mathit{\theta })h(\mathit{\theta })d\mathit{\theta }},$$ (7)

which has a linear part plus a generally nonlinear term. This marginal regression of Y on X for the mixture will be linear if the density of X depends only on μ_x and ${\sigma }_x^2$ and if (μ_x, ${\sigma }_x^2$) is independent of the other mixture model parameters in Θ. In particular, if the slopes β₁ and intercepts β₀ are constant across the components of the mixture, the linearity will follow.

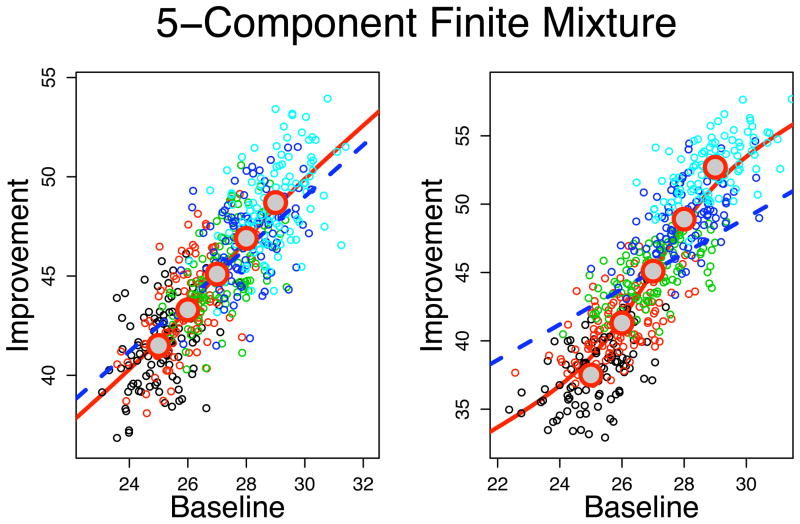
The two panels of Figure 2 show the regression curve E[Y |X] for two 5-component finite mixtures of bivariate normal distributions, each with equal priors of π_j = 1/5, j = 1, …, 5 and a common slope β₁ = 1.3. Also shown are 100 data points simulated independently from each of the five mixture components (for context the observations are color-coded by mixture component). In the left and right panels of the figure, the means of X for the five components are equally spaced from 25 to 29. The two mixtures differ only in the range of their y-intercepts, which are equally spaced: β_j0 = 9, …, 11 for the left frame and β_j0 = 5, …, 15 in the right frame in the order of the means of X. Thus, there is a positive relationship between the mean μ_xj and the intercepts (β_j0) for both mixtures. The dashed line in both frames is the line with slope β₁, and intercept equal to the (weighted) average of the finite mixture component intercepts, ${\overline{\beta }}_0=E_{\theta }[{\beta }_0]={\sum }_{j=1}^K{\pi }_j{\beta }_{j0}$. As Figure 2 illustrates, the marginal relationship between X and Y (the solid curve) is not linear and the deviation from linearity is stronger with more variability in the intercepts β_j0.

Figure 2.

Simulated 5-component equal priors (1/5) finite mixtures of bivariate normal distributions all having the same slope β₁ = 1.3. The solid curve is the regression E[Y|X] for the mixture distribution. The dashed curve is the line with slope β₁ and an intercept equal to the weighted average of mixture component intercepts. The large circles are the actual mixture component means. The means of the x-components are equally spaced from 25 to 29 for each mixture. The mixtures in the left and right frames differ only in the ranges of the equally spaced y-intercepts for the mixture components: left-frame intercepts range from 9–11 and the right frame intercepts are more spread out and range from 5–15. There is perfect positive relationship between the x–means and the y–intercepts.

The large circles are the mixture component means (μ_jx, μ_jy), for which estimates typically exist from the individual studies in a meta-analysis. A key point to make here is that the meta-regression slope, i.e., the slope of the mixture means, does not coincide with the common slope β₁ of the mixture components (i.e., the conditional association between X and Y given j) and also does not represent the regression of Y on X in the entire mixture either (i.e., the marginal association between X and Y).

The parameters of the mixture distribution (i.e., the marginal (X, Y) distribution given in (4)) can be decomposed into within and between-components terms. Let

$$\mathit{\mu }=\left(\begin{array}{c}{\mu }_x\\ {\mu }_y\end{array}\right)\text{and}\mathbf{\Psi }=\left(\begin{array}{cc}{\sigma }_x^2& {\sigma }_{xy}\\ {\sigma }_{xy}& {\sigma }_y^2\end{array}\right),$$

denote mean vector and corresponding covariance matrix and, using the same notation as before, let μ̄ and Ψ̄ denote the mean vector and covariance matrix for the mixture distribution computed by taking expectation with respect to Θ. The finite mixture derivation of the multivariate analysis of variance (MANOVA) equality from [19] readily extends to any general mixture by decomposing the covariance matrix for the mixture distribution, Ψ̄, into within (Ψ̄_W) and between (Ψ̄_B) component covariance matrices as

$$\overline{\mathbf{\Psi }}=\left(\begin{array}{cc}{\overline{\sigma }}_x^2& {\overline{\sigma }}_{xy}\\ {\overline{\sigma }}_{xy}& {\overline{\sigma }}_y^2\end{array}\right)={\int }_{\theta }\mathbf{\Psi }h(\mathit{\theta })d\mathit{\theta }+{\int }_{\theta }(\mathit{\mu }-\overline{\mathit{\mu }}){(\mathit{\mu }-\overline{\mathit{\mu }})}^{\prime }h(\mathit{\theta })d\mathit{\theta }={\overline{\mathbf{\Psi }}}_W+{\overline{\mathbf{\Psi }}}_B.$$ (8)

If the generally nonlinear relationship E[Y |X] given by (7) is approximated by a linear function

$$E[Y\mid X]\approx {\alpha }_0+{\alpha }_{1}X,$$ (9)

then the slope α₁ of this approximation can be expressed as

$${\alpha }_1=\frac{cov(X,Y)}{var(X)}=\frac{E_{\theta }[{\sigma }_{xy}]+{cov}_{\theta }({\mu }_x,{\mu }_y)}{E_{\theta }[{\sigma }_x^2]+{var}_{\theta }({\mu }_x)},$$ (10)

which involves both within- and between-components variances.

2.2.2. Meta-Regression of Y on X

Usually in meta-analysis, the only information available are the sample sizes, the estimated means for X and Y in each component (e.g., study) – these are the large circles in Figure 2 and their standard errors. Typically, estimates of the slopes in the individual mixture components are not available. When investigators perform a meta-regression in such situations, they are attempting to make inferences about the relationship between X and Y (a) either on average over the studies included in the meta-analysis, i.e., average of the conditional (given study j) relationships, β̄₁, or (b) in the marginal (X, Y ) distribution given in (4), which in general is non-linear (see (7)), but has a linear approximation, the slope of which is given in (10).

In the case when the slopes do not vary across studies, i.e., β₁ is constant, the following relationships hold:

$$\begin{array}{l}{\alpha }_1={\beta }_1\frac{\text{Within}X-\text{Variance}}{\text{Total}X-\text{Variance}}+{\gamma }_1\frac{\text{Between}X-\text{Variance}}{\text{Total}X-\text{Variance}}\\ ={\beta }_1+({\gamma }_1-{\beta }_1)\frac{\text{Between}X-\text{Variance}}{\text{Total}X-\text{Variance}}={\gamma }_1+({\beta }_1-{\gamma }_1)\frac{\text{Within}X-\text{Variance}}{\text{Total}X-\text{Variance}}.\end{array}$$ (11)

This shows that the slope of the straight line approximation of the regression of Y on X in the entire mixture distribution, α₁, is a weighted average of within-study slope β₁ and between-studies slope γ₁. It will equal the within-study slope β₁ if all components of the mixture have the same X-mean (i.e., Between X-Variance = 0). Also, γ₁ = α₁ and the meta-regression estimates the slope of the linear regression approximation of the relationship between X and Y in the entire mixture, if the within components variance of X is zero (i.e., Within X-Variance = 0). If γ₁ = β₁, then α₁ is also equal to these parameters.

If the relation at the subject-level (summarized by the within-study average slope β̄₁) is of primary interest, then the principal question becomes: how is the meta-regression slope γ₁ related to β̄₁? The slope γ₁ of the meta-regression line is determined by the between-study covariance matrix Ψ̄_B from (8) and is equal to

$${\gamma }_1=\frac{{cov}_{\theta }({\mu }_x,{\mu }_y)}{{var}_{\theta }({\mu }_x)}=\frac{{\int }_{\theta }({\mu }_x-{\overline{\mu }}_x)({\mu }_y-{\overline{\mu }}_y)h(\mathit{\theta })d\mathit{\theta }}{{\int }_{\theta }{({\mu }_x-{\overline{\mu }}_x)}^{2}h(\mathit{\theta })d\mathit{\theta }}.$$

From this and the identity μ_y = β₀ + β₁μ_x, it follows that

$${\gamma }_1={\overline{\beta }}_1+\frac{{cov}_{\theta }({\mu }_x,{\beta }_0)+E_{\theta }[{({\mu }_x-{\overline{\mu }}_x)}^2({\beta }_1-{\overline{\beta }}_1)]+{\overline{\mu }}_x{\text{cov}}_{\theta }({\mu }_x,{\beta }_1)}{{var}_{\theta }({\mu }_x)},$$ (12)

which extends the finite mixture model result of [20, page 182] to the general mixture setting. Based on (12), there is no clear relation between the meta-regression slope γ₁ and the average within-study slope β̄₁. In particular, it is unclear how γ₁ can be used to quantify the relation of Y to X within studies without making strong assumptions or without within study information regarding β₀ and β₁. To minimize the discrepancy between the average within study slopes and the meta-regression slopes, one could attempt to choose studies with a wide variability in mean baseline values so that var_θ(μ_x) is inflated. If inflating this variance does not also inflate the numerator of the second term in (12), then there should be a greater agreement between the average within study slope and the meta-regression slope. However, what happens with the numerator of the second term in (12) in that case in unknown, unless the individual studies have reported the intercepts and slopes from the regression of Y on X. The additional terms on the right-hand side of (12), besides β̄₁, can be called the ecological-bias terms. The “ecological bias” disappears if μ_x is uncorrelated with the intercepts and slopes and if μ_x has a third central moment of zero (assuming linear conditional expectations).

Even in a “best-case scenario” where all studies share a common slope β₁, the meta-regression slope γ₁ will generally differ from β₁, unless μ_x is uncorrelated with the intercepts. Also, when the within study slopes are all equal, it is illuminating to examine the the variability in the y-intercepts β₀. In the antidepressant studies example, the intercepts correspond to the improvement (with a given treatment) for subjects with baseline severity (X) equal to zero, which is a value outside the range of values in all studies, and in this example the individual intercepts do not have meaningful interpretation. However, we can interpret the variability in the y-intercepts by decomposing it into two parts. The variance of β₀ across studies can be partitioned as

$${var}_{\theta }({\beta }_0)=E_{\theta }[var({\mu }_y\mid {\mu }_x)]+{({\gamma }_1-{\beta }_1)}^2{var}_{\theta }({\mu }_x).$$

The first part corresponds to variability of improvement between subjects with the same value of the baseline severity, but from different studies which can be due to numerous study-level or subject-level factors that are different between the studies. This part is often termed “heterogeneity” in meta-tergression [e.g. 21, page 2693]. However, the variance of the intercepts has a second term, which is directly related to the discrepancy between the meta-regression slope γ₁ and the common within-study slope β₁. Therefore, even when the individual study slopes are equal, the variance of the intercepts cannot be interpreted as variance between the studies with respect to efficacy at given level of X, (see also Section 3.2).

An important reminder here is that even if there is a common within-study slope, the between-study meta-regression slope can have a sign opposite of the common within-study slope of the mixture components, which can occur if the sign of cov(μ_x, β₀) is opposite the sign of the common slope β₁. Figure 3 shows a finite mixture simulation illustration of how the slope of the mixture component means can come out with a sign opposite of the common slope’s sign for the individual mixture components. An actual case was shown in Figure 1 of the Introduction and is discussed in Section 4.3.

Figure 3.

Same as Figure 2 except that the common mixture component slope is β₁ = 0.3 and the y-intercepts are equally spaced from −9 to −11 in 1/2 increments so that mixture component x–means and the y-intercepts are perfectly negatively correlated.

3. Random Effects Model for Meta-Regression

3.1. The assumptions of the model

Perhaps the most commonly used infinite mixture model is the linear mixed effects model with random effects for the intercept and slope. In particular, a vector of fixed effects can be defined as the averaged regression coefficients across studies given by (5) and the random effects defined by (6), which are typically assumed to be bivariate normal. With subject-level data the linear mixed effects model for simple linear regression can be expressed as

$$Y_{ij}=({\overline{\beta }}_0+b_{j0})+({\overline{\beta }}_1+b_{j1})X_{ij}+{\epsilon }_{ij},$$ (13)

where Y_ij is the ith subject’s response in the jth study and the random effects (b_j0, b_j1)′ are assumed to be independent of the (mean zero) error ε_ij whose variance will be denoted ${\sigma }_j^2$.

In addition to the common assumption of normality of the random effects, another very important assumption that is almost always made when fitting mixed effects model, is that the covariate is independent of the random effects [e.g., 22, page 310]. In the meta-regression setting, this translates to independence between μ_x and the regression random effects (b₀, b₁). It is common in meta-regression estimated with random effects models to further simplify model (13) by assuming that there is no random effect for the slope, i.e. the regression slope does not vary among studies (β₁ := constant) [e.g., 17; 21; 18; 9]. Thus, the only random effect is for the intercept, which is sometimes referred to as heterogeneity [e.g. 21, page 2693] (although, in a meta-analysis literature, the meaning of the term heterogeneity is not entirely consistent and one could naturally regard heterogeneity between studies in terms of both slopes and intercepts).

Under these assumptions, the parameterization of Θ can be simplified to $\mathbf{\Theta }={({\mu }_x,{\sigma }_x^2,{\beta }_0,{\sigma }^2)}^{\prime }$, where the non-varying terms have been dropped and β₀ ~ N(β̄₀, τ²), with τ² denoting the variance of the random intercept. The recommended approach to estimating the parameters of the meta-regression model (1) is the random-effects approach [e.g., 16; 17; 18; 9], which acknowledges that variability in the mean responses Ȳ_j is due to the usual variability associated with a sample mean within a given trial, as well as possible heterogeneity due to the fact that the true means can vary among the studies.

The meta-regression random-effects model [e.g. 17, page 397] in the context of a continuous outcome and predictor is

$${\overline{Y}}_j={\gamma }_0+{\gamma }_1{\overline{X}}_j+{\delta }_j+{\epsilon }_j,$$ (14)

where X̄_j is often regarded as fixed and/or known, δ_j ~ N(0, τ²) is a random effect for heterogeneity across studies, ${\epsilon }_j~N(0,{\sigma }_j^2/n_j)$ is considered independent of δ_j and ${\sigma }_j^2$ represents the sampling variability of Ȳ_j within study j.

If μ_x is independent of the intercept, then the covariance between μ_x and β₀ will be zero and (12) implies that the meta-regression slope γ₁ will coincide with the common within-study slope β₁. In this simplified random effects model, the generally non-linear marginal regression of Y on X from (7) is linear with slope equal to β₁:

$$\begin{array}{l}E[Y\mid X]=\int yf(y\mid X)dy=\frac{{\int }_{\theta }\int yf(y\mid X,\mathit{\theta })dyf(X\mid \mathit{\theta })h(\mathit{\theta })d\mathit{\theta }}{f(X)}\\ =\frac{{\int }_{\theta }E[Y\mid X,\mathit{\theta }]f(X\mid \mathit{\theta })h(\mathit{\theta })d\mathit{\theta }}{f(X)}=\frac{{\int }_{\theta }({\beta }_0+{\beta }_{1}X)f(X\mid \mathit{\theta })h(\mathit{\theta })d\mathit{\theta }}{f(X)}={\overline{\beta }}_0+{\beta }_{1}X.\end{array}$$

3.2. When the assumptions are violated

Both assumptions (i) β₁ := constant, and (ii) cor(μ_x, β₀) = 0 are difficult to justify in practice. More importantly, in a typical meta-regression study with only group-level data available, there is no information to evaluate whether any of these conditions hold. In the antidepressant example, which will be reported in Section 4, raw subject-level data from 10 antidepressant studies is available and the drug arms in these studies do not satisfy these assumptions.

To examine the ecological bias in meta-regression estimated by random effect models, data sets were simulated based on the mixed effects model (13) where the tri-variate distribution of (μ_x, β₀, β₁)′ was normal with mean and covariance parameters anchored to the sample statistics from the 17 drug arms in the 10 studies reported in Section 4 which were:

$$E\left[\left(\begin{array}{c}{\mu }_x\\ {\beta }_0\\ {\beta }_1\end{array}\right)\right]=\left(\begin{array}{c}{\overline{\mu }}_x\\ {\overline{\beta }}_0\\ {\overline{\beta }}_1\end{array}\right)=\left(\begin{array}{c}21.78\\ -1.78\\ 0.56\end{array}\right)\text{and}\text{Cov}\left[\left(\begin{array}{c}{\mu }_x\\ {\beta }_0\\ {\beta }_1\end{array}\right)\right]=\left(\begin{array}{ccc}23.27& 1.27& -0.33\\ 1.27& 24.45& -1.07\\ -0.33& -1.07& 0.06\end{array}\right).$$ (15)

For the sake of this illustration, the error variance for ε_ij was set to be constant across all data sets, σ = 0.50 and the standard deviation of the predictors σ_x was also set to be constant, σ_x = 6.60, the standard deviation of the baseline values for all subjects in our studies. The sample sizes for each data set were equal to the actual sample size of the drug arms in our data. For each simulation run, 17 vectors were simulated from (15). For the jth study with sample size n_j, predictor values X_ij were then generated from a normal distribution with mean μ_x and standard deviation σ_x. From each of the 17 generated data sets, the sample means of the outcomes Y and predictors X were obtained along with their standard deviations to be used in estimating parameters in a meta-regression. Meta-regression models were estimated for each simulated data set using three methods: (i) ordinary least-squares (OLS) with no weighting, (ii) a weighed least-squares using weights based on the estimated standard errors of the outcome and (iii) a random effects model (14) estimated using restricted maximum likelihood (REML) [e.g. 17] by implementing the rma function in the R metafor package [23].

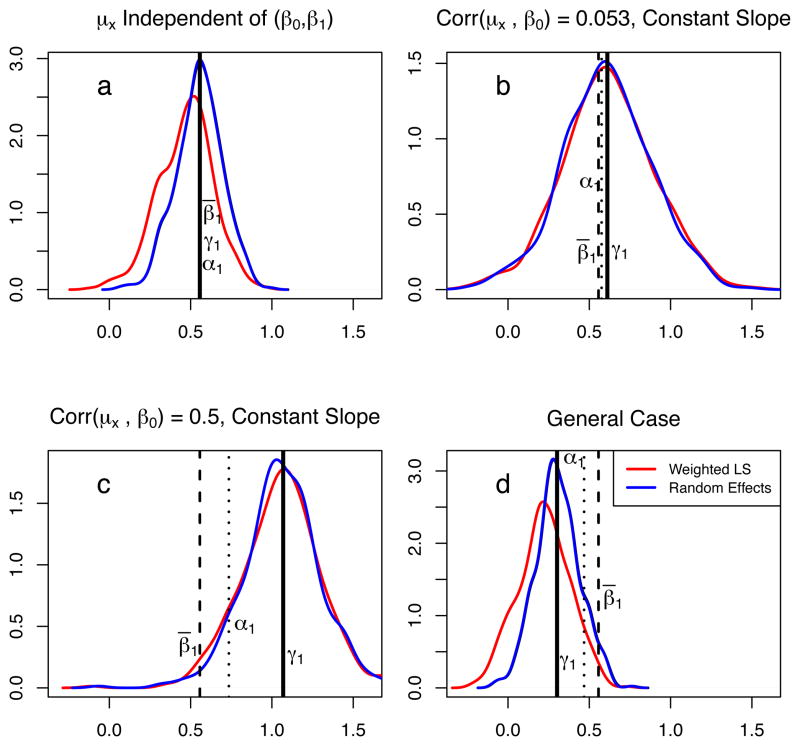
Figure 4 shows slope estimates under four conditions. Top left panel (a) presents the situation when the typical assumptions underlying mixed effects models are satisfied, i.e., the random slope and intercepts (β₀, β₁) are independent of the covariates μ_x. Panels (b) and (c) present the case when the slopes do not vary, i.e., no random effect for slope and no correlation between the slopes and μ_x. The difference between panels (b) and (c) is in the magnitude of corr(μ_x, β₀): the correlation in panel (b) is smaller and equal to the correlation observed in our data, and in panel (c) the correlation is set to 0.5. Panel (d) shows the case, when (β₀, β₁) are correlated with μ_x and the parameters are exactly equal to the observed values given in (15). On each panel, the parameters β̄₁, α₁ and γ₁, estimated from the (known) data generating distribution, are shown as vertical lines. The panels in the plot show nonparametric density estimates of the slope estimates from 500 simulated data sets, where the meta-regression slopes were estimated by one of methods (i), (ii) or (iii) from above. In all of the cases the REML estimates of the random effect variance is much larger (by over an order of magnitude) than the sample variance of the mean responses $s_y^2/n$ and consequently the OLS slopes estimates are nearly equal to the slopes estimated from the random effect models – that is why the OLS densities are not visible on Figure 4 [e.g., 17, page 387].

Figure 4.

Simulation results comparing three methods of meta-regression estimation on data simulated from model (13), based on sample statistics from antidepressant drug arms, given in (15). The dashed vertical line is the fixed effect slope β̄₁, the solid vertical line is the between-study meta-regression slope γ₁ and the dotted line is the slope α₁ of the linear approximation to the marginal relationship (7). The density plots are based on estimates from 500 simulated data sets using weighted least-squares and a random effects model: (a) (β₀, β₁) are independent of μ_x; (b) β₁ is constant, corr(β₀, μ_x) is small; (c) β₁ is constant, corr(β₀, μ_x) is large; (d)(β₀, β₁) and μ_x are not independent and the dependencies are those observed in the actual data.

On panel (a) of Figure 4, where (β₀, β₁) are independent of μ_x, there is no ecological bias and β̄₁ = α₁ = γ₁. In this case all methods are yielding unbiased estimates of these slopes. On panel (b), where the conditional (on study j) slopes β₁ are all equal, but the random intercepts β₀ and μ_x are correlated, γ₁ ≠ β₁. However, because the corr(β₀, μ_x) is small the difference between them is not very large. In contrast, panel (c) shows that the difference between β̄₁ and γ₁ can be quite large when the intercepts and x-means are strongly correlated. Notice, that in all cases α₁ is between β̄₁ and γ₁, since it is a weighted average of the later two parameters, see (12). Finally, panel (d), which is based on the observed data, presents the most realistic situation: the slopes vary and the random intercepts and slopes are correlated with μ_x. There are large discrepancies between the meta-regression slope γ₁ and both β̄₁ and α₁.

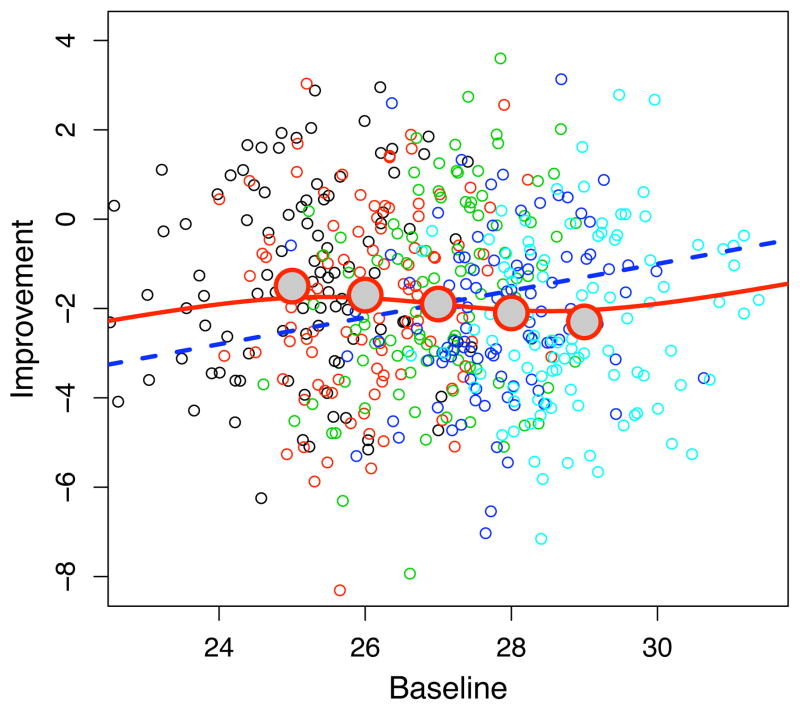
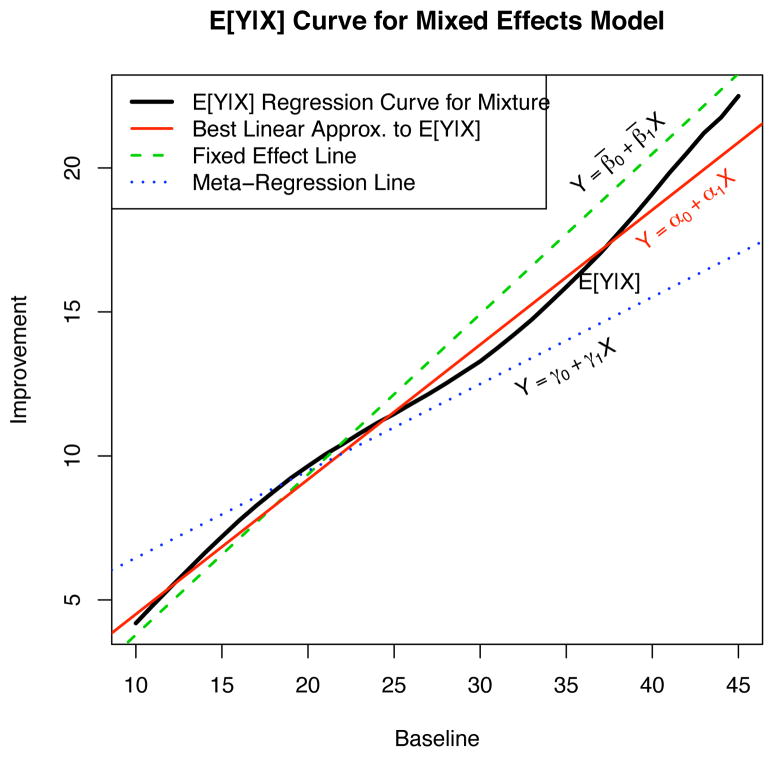
Figure 5 shows the (nonlinear) regression curve E[Y |X] from (7) (which has been generated by a Monte Carlo simulation of 100,000 randomly generated variates from a tri-variate normal distribution with parameters from (15)), and corresponds to the scenario on panel (d) of Figure 4. This figure also shows the line defined by the fixed effects intercept β̄₀ and slope β̄₁ and the best linear approximation y = α₀ + α₁x to the true regression curve, with α₁ given by (10). In addition, the meta-regression line y = γ₀ + γ₁x is also plotted. The figure illustrates that there is a marked difference between the marginal population regression curve and the meta-regression line as well as a large discrepancy between the meta-regression line and the line defined by the fixed effects slope and intercept. The online eSupplement provides derivations relating the slope and intercept parameters used to create this plot for the meta-regression line and the best-fit line in terms of the parameters defining the distribution of Θ in (15).

Figure 5.

The regression curve E[Y |X] for the simulated random effects model based on the drug arm statistics in Section 4 (case presented on Figure 4d). Also shown are the regression lines: (i) the best linear approximation to E[Y |X] given by y = α₀ + α₁x; (ii) the fixed effect line y = β̄₀ + β̄₁x; and (iii) the meta-regression line y = γ₀ + γ₁x.

If the random effects model is correctly specified, the meta-regression slope estimator is estimating the true fixed-effects slope. However, the strong assumptions required for the meta-regression random effects model (14) seem unwarranted in practice and the meta-regression slope γ₁ estimated from a random effects model in that case is estimating something other than β₁.

If the model generating the data is as in (14) with β₁ constant across studies and corr(μ_x, β₀) = 0, then the meta-regression slope from model (14) is equal to the common slope. In this idealized case, the variance of μ_y given μ_x is the variance of the intercepts, estimated by τ̂², the “heterogeneity parameter”. The heterogeneity parameter estimate is regularly used to assess whether the intercepts are all equal, i.e., all regression lines are identical. However, in the frequently occurring situations, where the random effect model assumptions are violated, var(μ_y|μ_x) is given by

$$var({\mu }_y\mid {\mu }_x)={\tau }^2+var(b_1){\mu }_x^2+2{\mu }_x\text{cov}(b_0,b_1),$$ (16)

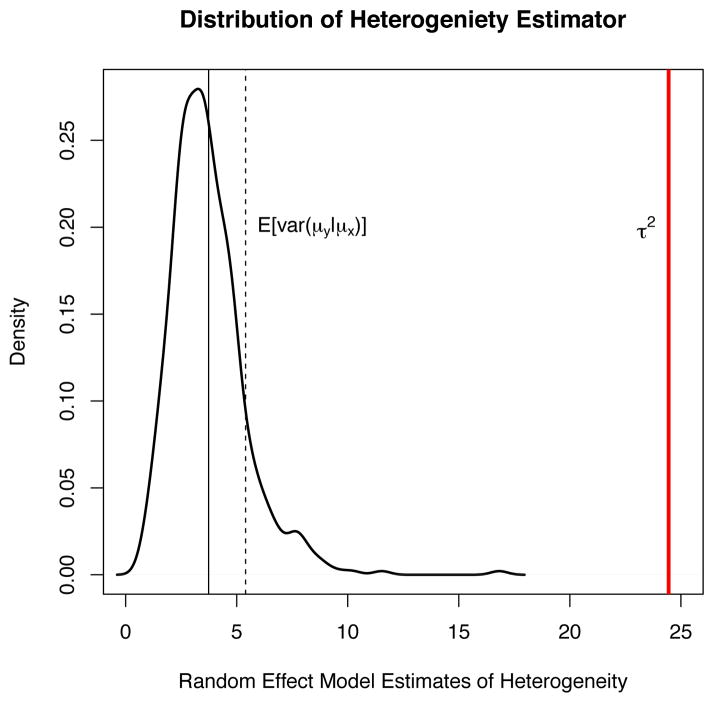
and consequently, τ̂² does not correspond to a measure of intercept heterogeneity and has no clear interpretation. To illustrate the problem, Figure 6 shows the sampling distribution of τ̂² based on the simulations presented in panel (d) of Figure 4. τ̂² grossly underestimates the true intercept variance τ² = 24.45 and also underestimates var(μ_y|μ_x). In fact, τ̂² is estimating some complicated function of the true model parameters which can be determined using the approach in [24]. Thus, when the (misspecified) random effects meta-regression model (14) is used to estimate the relationship between X and Y, not only does the estimated meta-regression slope generally differ from β₁, but also τ̂² has no clear meaning and interpreting it as a measure of heterogeneity is misleading.

Figure 6.

Distribution of τ̂² from the simulations in Figure 4d with its mean (most left solid vertical line), compared to the true τ² = 24.45 (right most solid vertical line) and the average of var(μ_y|μ_x) from (16) (dashed vertical line).

4. Application: Antidepressant Efficacy vs. Baseline Depression Severity

In this section we return to the ten antidepressant studies mentioned in the Introduction to compare the meta-regression results to subject-level regression results. The duration of treatment in the studies varied from 5 weeks to 12 weeks with roughly weekly evaluations. The entire pooled data set consists of 3132 subjects of whom 1080 were treated with a placebo. All studies had a placebo arm and one or more drug arms – either different drugs or different doses of the same drug. The drugs were fluoxetine and imipramine, and in one study there was a phenelzine arm. The baseline depression severity X in all studies was measured by the HRSD. The outcome Y is the improvement in depression severity measured as the change from baseline to end of treatment. Although using the change score as the outcome in evaluating the efficacy in clinical trials in known to have weaknesses [e.g., see 6; 7] and the practice is discouraged in favor of the actual post-treatment scores, this modeling choice is not a focus of this paper and the derivations here do not depend on how Y is defined. Thus, we use Y = “change score” in order to parallel the analysis of [1], which motivated this work. In the analysis of individual studies, the estimated slopes using model (2) of all arms of all studies were positive and significantly so, except for one of the drug arms and one of the placebo arms (from two different studies, notedly, with the smallest sample sizes of fewer than 100 subjects). Analyses were performed on different subsets of subjects: only those with at least 6 weeks of data, or only those with at least 3, 2 or 1 post-baseline assessments. Results varied, but not qualitatively with respect to issues that are the focus of this work, so here we report the analysis of the most inclusive subset – all subjects with at least one post-baseline assessment.

Figure 7, panel (a) shows a scatterplot (improvement versus baseline depression severity) for all subjects in the 10 studies. Due to the discreteness of the data (HRSD is recorded on an integer scale), many of the data points overlapped. Therefore, each point in Figure 7 is a bubble, whose size is directly proportional to the number of subjects that shared the same coordinates. Because the HRSD scores are positive, the improvement (baseline minus end of study HRSD) cannot exceed the baseline and the points in the figure are constrained to lie below the 45° angle line. Nonparametric regression loess curves [25] (solid curves) are plotted for all drug and all placebo treated subjects (ignoring study) with the drug curve laying entirely above the placebo curve. To access the variability of the nonparametric regression, 100 bootstrap samples of each of the placebo and drug arms of each study were obtained and loess curves were computed for each combined bootstrap sample (indicated by the dashed curves in Figure 7). The loess regression curves give an overall impression of the trend of the marginal relationship between baseline symptoms severity and improvement and indicate that drug treated subjects experience a greater degree of improvement than subjects treated with a placebo. In addition, it appears that for subjects with low to mild baseline severity (HRSD < 22), there is less benefit from the drug – the difference in average improvement between drug and placebo is smaller than for subjects with higher baseline severity. Of course, this could be, at least partly, a consequence of the ceiling effect, since subjects with lower baseline HRSD have less room for improvement. There is also a great deal of variability in the nonparametric regression curves at the upper end of the baseline severity, likely due to the small number of subjects with baseline HRSD > 35. Note that the loess curves for drug and placebo arms are nonlinear and the shape of the drug arm curve has the same shape as the simulated regression curve E[Y |X] for the infinite mixture shown in Figure 5 which is to be expected because the random variates in that figure were simulated based on sample statistics from the drug arms.

Figure 7.

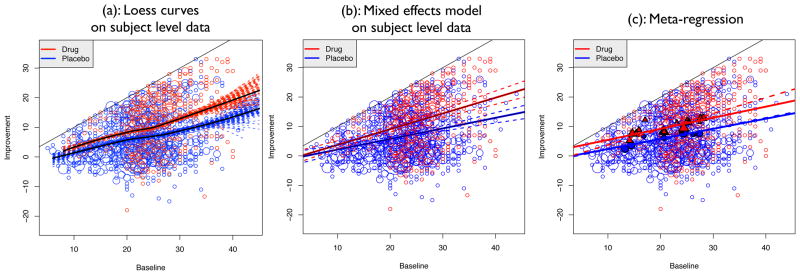
Plot of subject-level data from all studies of improvement versus baseline depression severity. The data points are indicated by the bubbles where the size of the bubble is directly proportional to the number of subjects that share the same coordinates. (a): The solid curves are nonparametric loess smoothers on subject-level data for drug and placebo treated subjects. Loess curves were also generated for 100 bootstrap samples to highlight the variability in the estimated nonparametric curves. (b): The solid lines correspond to the fixed effect regression lines for drug and placebo arms, from a mixed effects model on study-level data with random study effects for treatment, X and treatment by X interactions. The dashed lines are upper and lower 95% pointwise confidence bounds. (c): Meta-Regression Results: Plot of the mean improvement vs. baseline for all arms of all studies (circles are for placebo treated and triangles for drug treated arms), sized according to the inverse of the standard error of the mean response. The solid lines are the meta-regression lines from REML estimation with R-package metafor [23]. For reference, the dashed line is the fixed effect line from panel (b) for drug treated subjects. (The fixed-effect line for placebo treated subjects overlaps with placebo-treated meta-regression line and cannot be seen clearly.)

4.1. Linear Mixed Effects Model Fit to Subject-Level Data

To account for the clustering of subjects within studies, the mixed effects model (13) with the treatment effect T was fit to the subject level data

$$Y_{ij}=({\overline{\beta }}_0+b_{j0})+({\overline{\beta }}_1+b_{j1})X_{ij}+({\overline{\beta }}_2+b_{j2})T_{ij}+({\overline{\beta }}_3+b_{j3})X_{ij}{T}_{ij}+{\epsilon }_{ij},$$ (17)

where Y_ij and X_ij are the change from baseline and the baseline HRSD of the ith subject in the jth study, T_ij is the treatment indicator (T = 0 for placebo and T = 1 for active drug), and the random effects are assumed to be independent of the error ε_ij. The model with random intercepts and slopes allows for different variances of the random effects for placebo and active treatment groups within the same study. The results are plotted in Figure 7 panel (b), which shows the raw data and the regression lines based on the fixed effects for the placebo and drug treated subjects (the dashed lines are parametric pointwise 95% confidence bounds about the lines).

The estimated fixed effect slope for X for the placebo treated subjects is 0.359 with an estimated standard error of 0.049. The fixed effect interaction was estimated to be 0.175 with standard error 0.058 so that the estimated slope for drug treated subjects is 0.543. A 95% bootstrap confidence interval for the fixed effect interaction term is (0.08, 0.27). The slopes and the interaction term in the model were significant. The interaction is clearly manifested by the increasing divergence seen between the placebo and drug lines as baseline severity goes from low to high. We note in passing that lines (not shown), with intercepts and slopes that are given by the weighted averages across studies from (5), coincide very closely with the fixed effects lines estimated by (17) plotted on Figure 7(b).

4.2. Meta-Regression Results

The mean baseline and improvement from each arm in all studies were computed and these means are plotted in Figure 7 panel (c). The circles indicate the placebo means and the triangles are the drug means. In a typical meta-regression, these means along with sample sizes and standard errors would be the only information available instead of the actual subject-level data. The size of the plotting symbols are proportional to the inverse of the standard error of the mean improvement. The solid lines in Figure 7(c) are obtained from a random-effects meta-regression model

$${\overline{Y}}_{jt}={\gamma }_0+{\delta }_j+{\gamma }_1{\overline{X}}_j+{\gamma }_2{T}_j+{\gamma }_3{\overline{X}}_{jt}{T}_j+{\epsilon }_j,$$ (18)

where δ_j ~ N(0, τ²) is a random effect for heterogeneity between studies, considered independent of the error ${\epsilon }_j~N(0,{\sigma }_j^2/n_j)$. The model is fit using restricted maximum likelihood (REML) estimation and the R-package metafor [23]. Even though there are only a few studies, the effect of baseline severity is highly significant in the meta-regression. However, the interaction term is not significant (p-value = 0.75), which is not surprising given the low power of meta-regression to detects interactions between a treatment indicator and a covariate [15; 12]. The estimated common slope in the meta-regression (from a meta-regression model without an interaction between treatment and X) is 0.363. The drug main effect is also highly significant and estimated to be 3.47 with standard error 0.501 indicating that from the meta-regression model, subjects on active treatment have a mean improvement of about 3.47 HRSD units higher than placebo treated subjects for all levels of baseline severity.

For reference, panel (c) of Figure 7 also shows the estimated regression lines (dashed lines) from fitting (17), which are shown on panel (b). The fixed-effects regression line for placebo-treated subjects overlaps almost perfectly with the meta-regression placebo line and cannot be distinguished on the figure. Because the estimated meta-regression line coincides almost exactly with the fixed effects regression line obtained from (17), it appears the placebo arms are consistent with the slice model of Section 2.1. This in not entirely surprising because the treatments across placebo arms are similar and it is conceivable that humans can be (mostly) homogeneous in response to placebo. Unlike the case of a typical meta-regression, because the raw data are available, a test for equality of the intercepts and slopes across the placebo arms of the studies, i.e. test for heterogeneity [26] using estimated intercepts and slopes (and their estimated standard errors) is possible. The p-values from these tests are 0.737 and 0.749 respectively showing that the placebo arms are consistent with the slice model of Section 2.1. As is shown by [27], this test has a very low power to detect heterogeneity and therefore the homogeneity of the placebo regression lines can be viewed with skepticism. However, the conclusion of heterogeneity for the drug arms seems plausible because the p-values of the chi-square tests are 0.135 for intercept and 0.058 for slopes.

The meta-regression results for the drug treated subjects differ fairly substantially from the analysis of the subject-level data. In the analysis of the subject level data, there was a significant interaction indicating that the degree of improvement of drug treated subjects over placebo treated subjects increased on average as baseline severity increased. However, this interaction is very small and not significant in the meta-regression. The difference in the meta-regression slope γ₁ (common for drug and placebo) and the average within study slope β̄₁ for the drug arms is due to the second term in (12) and this term diminishes the interaction effect seen in the subject-level data analysis. We computed the value of the second term from (12) separately for the placebo and drug arms of the studies based on a finite mixture (see (5)): the values were −0.058 and −0.102 respectively, explaining the lack of appreciable difference between the estimates of γ₁ and β̄₁ for placebo and the observed negative bias in the meta-regression coefficient for the drug arms.

4.3. Effect of Variance of μ_x on Meta-Regression

From (12) it can be seen that the difference between the meta-regression slope γ₁ and the average across studies slope β̄₁ depends on the variance of the study means μ_x. Including in the meta-analysis studies with a wide range of average subject characteristics x̄ has the potential of reducing this difference, as discussed at the end of Section 2.2. Conversely, reducing the range of the average baseline levels of x, which is sometimes done to ensure similar patient populations for the meta-analysis, might result in a larger discrepancy of the meta-regression slope γ₁ from β̄₁.

As was shown in Figure 1 in the Introduction, using only the six studies with a restricted range 22 < Baseline HRSD < 31 changed the meta-regression results dramatically from the meta-regression on all ten studies. Despite the small meta-regression sample size, the interaction term is now significant (p = 0.0443), with the slope for the nine drug arms being positive with an estimate of 0.499 and the slope for the six placebo arms being negative with an estimate of −0.146, although not significantly different from zero (p = 0.539). Recall that Figure 1 also showed individual subject-level regression lines estimated from model (2) which all had positive slopes even though the meta-regression line for the placebo arms had a negative slope.

We maintain that in practice it is very difficult not to interpret the results from meta-regression on a subject level and to restrict the inferences to study-level characteristics. Thus, the interpretation of the meta-regression that would likely be given in this case is that the relative efficacy of the drug compared to placebo increases with baseline depression severity and this is due to both a small decline in placebo effect and a significant rise of drug effect associated with higher baseline levels of symptom severity. Of course, as was reported in the previous sections, analysis of the subject-level data shows that the average improvement increases as baseline severity increases for both placebo and drug treated subjects.

4.4. General Comments

There are numerous modifications that can be made to the analysis presented here which will inevitably lead to differing results (e.g. distinguishing different drugs and doses in the model, restricting analysis to subjects at least two or three post-randomization observations, etc). Covariates such as sex and age could have been included. Sex did not appear to have an effect on the outcome, but age was significant, with older patients tending to have weaker response to the medications and we could have included that as well. Each of the studies were longitudinal where subjects were evaluated over several weeks and we could have compared the results of a longitudinal data analysis with the meta-regression results as well as was done in [28]. Although the effects of all these factors are potentially interesting, we have focused the scope of this paper on shortcomings with using meta-regression models.

5. Discussion

The goal of this paper is to elucidate the statistical issues underlying current controversies in public media as well as in the psychiatric literature regarding the efficacy of antidepressants, much of which has stemmed from the use of meta-regression. It is clear that for a collection of studies, the relationship between the means of the outcome and the means of a subject level covariate is usually not the same as the relationship between the outcome and the covariate in the individual studies, nor is it the same as the relationship over the entire collection of studies (i.e., ignoring study). In other words the meta-regression relationship (γ₁) from (1) is not the same as the conditional study relationships (β₁) from (2) or the marginal relationship over all studies (α₁) from (9). Based on numerous publications in the medical literature (including the motivating antidepressant paper [1]) it is evident that many investigators conduct meta-regression with the goal of making inferences about the conditional relationship (β₁) between the outcome and the covariate, although it is possible that the marginal association (α₁) might be of interest also. We take the view that the relationship that is most intuitive is the conditional relationship (which might be different across the studies). Table 1 shows how the meta-regression relationship and the marginal relationship depend on the parameters of the conditional relationships (β₀, β₁), as well as on the other parameters characterizing the distributions of the outcome and the covariate within and between studies (which are derived in the eSupplement C under some reasonable simplifying assumptions).

Table 1.

The connection between the marginal relation, the slope of its linear approximation (α₁) and meta-regression slope (γ₁) to individual-level parameters (β₀, β₁)

Relations and Parameters	(β0, β1) across studies
	β0, β1 constants	β1 constant, β0 vary		β0, β1 vary
	cov(μx, β0) = 0 & cov(μx, β1) = 0	cov(μx, β0) = 0	cov(μx, β0) ≠ 0	cov(μx, β0) = 0 & cov(μx, β1) = 0	cov(μx, β0) ≠ 0&/or cov(μx, β1) ≠ 0
Marginal	Linear, slope β1	Linear, slope β1	Nonlinear	Linear, slope β̄1	Nonlinear
α1	α1 = β1	α1 = β1	${\alpha }_1={\beta }_1+B_1^{\ast }$	α1 = β̄1	α1 = β̄1 + B1 + B2
γ1	γ1 = β1	γ1 = β1	γ1 = β1 + B3	γ1 = β̄1	α1 = β̄1 + B3 + B4
α1 (to β1 and γ1)	α1 = β1 = γ1	α1 =β1= γ1	Weighted average of β1 and γ1	α1 = β̄1 = γ1	Weighted average of β̄1 and γ1

^*

$$B_1=\frac{{cov}_{\theta }({\mu }_x,{\beta }_0)}{E_{\theta }[{\sigma }_x^2]+{var}_{\theta }({\mu }_x)},B_2=\frac{{\overline{\mu }}_x{\text{cov}}_{\theta }({\mu }_x,{\beta }_1)}{E_{\theta }[{\sigma }_x^2]+{var}_{\theta }({\mu }_x)},B_3=\frac{{cov}_{\theta }({\mu }_x,{\beta }_0)}{{var}_{\theta }({\mu }_x)}\text{and}{B}_4=\frac{{\overline{\mu }}_x{\text{cov}}_{\theta }({\mu }_x,{\beta }_1)}{{var}_{\theta }({\mu }_x)}$$

From Table 1 it is clear that the slope of the meta-regression relationship (γ₁) is equal to the common slope (or the average of the slopes) of the individual studies relationships when the distribution of the studies is such that the means of the covariate are not correlated with the study intercepts and slopes. However, if only means and standard deviations for the outcome and the covariate are available from the studies, these conditions cannot be verified. Columns 4 and 6 of Table 1 present the cases when the slope of the meta-regression does not equal the common study slopes (or the average of the study slopes). In those cases, the meta-regression slope equals β₁ (or β̄₁) plus extra non-zero “bias” terms (B₁ to B₄ from the table), but are unknown in typical meta-analysis situations. These conclusions do not depend on the estimation methods, but rather they concern the parameters that characterize the relationship between outcome and covariate, and the association between these parameters.

Let us now consider estimation. The currently recommended approach for meta-regression estimation – a random effects meta-regression model [e.g., 16; 17; 18; 9] – makes the assumptions that (i) β₁ are all equal, and (ii) the random intercepts are independent of the mean covariate, i.e., cov(μ_x, β₀) = 0. These assumptions are given in the third column of Table 1 and if they hold true, then the meta-regression slope is estimating the common study slope β₁. In fact, even if (i) from above is not satisfied, but (iii) cov(μ_x, β₁) = 0 (see the fifth column), the meta-regression model will be unbiased for the average study slope β̄₁. However, the conditions (i)–(iii) cannot be verified without estimates of (β₀, β₁) from the individual studies and therefore, when conducting meta-regression there is no way of knowing how the estimate of γ₁ relates to β₁, β̄₁, or α₁.

Methods for estimating meta-regression depend on restrictive and usually unverifiable assumptions when only group level data is available and this can lead to results that are quite misleading when the assumptions are violated. Moreover, a meta-regression slope can have a different sign than slopes from subject-level analysis and this situation, contrary to common wisdom, is not that unusual, as investigators try to include only similar studies in the meta-analysis, thus restricting the range of mean covariate values.

In summary, meta-regression inferences can be valid when the covariate is a study-level characteristic, such as drug dose or treatment duration. However, using meta-regression when the covariate is an average subject-level characteristic (such proportion of women, or average age, or average baseline symptoms severity) is extremely risky when no information is available about the association between the covariate and the outcome on subject level from the individual studies. A major difficulty is the fact that when the covariate is a subject characteristic, it is quite impossible not to interpret results from meta-regression on a subject-level.