Low Demographic Variability in Wild Primate Populations: Fitness Impacts of Variation, Covariation, and Serial Correlation in Vital Rates

Abstract

In a stochastic environment, long-term fitness can be influenced by variation, covariation, and serial correlation in vital rates (survival and fertility). Yet no study of an animal population has parsed the contributions of these three aspects of variability to long-term fitness. We do so using a unique database that includes complete life-history information for wild-living individuals of seven primate species that have been the subjects of long-term (22–45 years) behavioral studies. Overall, the estimated levels of vital rate variation had only minor effects on long-term fitness, and the effects of vital rate covariation and serial correlation were even weaker. To explore why, we compared estimated variances of adult survival in primates with values for other vertebrates in the literature and found that adult survival is significantly less variable in primates than it is in the other vertebrates. Finally, we tested the prediction that adult survival, because it more strongly influences fitness in a constant environment, will be less variable than newborn survival, and we found only mixed support for the prediction. Our results suggest that wild primates may be buffered against detrimental fitness effects of environmental stochasticity by their highly developed cognitive abilities, social networks, and broad, flexible diets.

Introduction

A fundamental tenet of life-history theory is that fitness in a stochastic environment can differ substantially from fitness under average environmental conditions (Lewontin and Cohen 1969; Gillespie 1977). In a structured population in which individuals differ in their contributions to population growth as a function of their age, size, or life stage, fitness of an entire life history is determined by multiple vital rates (e.g., survival and reproduction at each life stage). Depending on the importance of each vital rate for fitness and on how different rates vary and covary over time, fitness in a stochastic environment can be less or greater than fitness in the average environment (Tuljapurkar 1982). Recently, Tuljapurkar et al. (2009) reemphasized three aspects of demographic variability that jointly determine the impact of environmental stochasticity on long-term fitness (i.e., the growth rate of a lineage over many years in a stochastic environment): (1) the variance of each vital rate over time, (2) covariation between pairs of vital rates in the same year, and (3) serial correlations of single vital rates and vital rate pairs between successive years.

Both covariation within years and serial correlation between years can be positive or negative. Positive within-year covariation occurs when, during years in which one vital rate (e.g., adult survival) is above average, a second rate (e.g., newborn survival or adult fertility) is also likely to be above average, perhaps because the two vital rates respond in the same way to environmental conditions. Negative within-year covariation may arise due to life-history trade-offs that are expressed within a single year (e.g., high reproduction leads to lower survival to the next census). Negative serial correlations may reflect trade-offs expressed across years (e.g., high reproduction in one year is followed by low reproduction or low survival in the following year[s]), whereas positive serial correlations may result from fluctuations in environmental conditions with a period longer than 1 year or from effects of especially good or bad conditions that persist for more than 1 year.

Although the potential importance of variation, covariation, and serial correlation between vital rates has been appreciated by theoretical biologists for nearly 30 years (since Tuljapurkar 1982), we are not aware of any empirical studies that have disentangled the fitness effects of these three aspects of demographic variability for an animal species (see chap. 8 in Morris and Doak 2002 for the only plant example of which we are aware). One impediment to doing so has been the need for long-term data to estimate components of variability, particularly serial correlations across time.

In this article, we take advantage of long-term life-history data to assess the fitness effects of demographic variation, covariation, and serial correlation for populations of seven species of primates in the wild (listed from smallest to largest female body mass): sifaka, capuchin monkey, blue monkey, muriqui, yellow baboon, chimpanzee, and gorilla (table 1). These species are the subjects of ongoing behavioral studies that, as of the end of 2008, had lasted for 22–45 years. Complete information on the life histories of all individual animals in these studies, including dates of birth (or appearance) and death (or disappearance), as well as reproductive information for all females, has been compiled into a single data archive known as the Primate Life History Database (Strier et al. 2010; http://demo.plhdb.org/). This resource represents the best comparative data on demographic variability in wild primates, and it enables us to estimate the means and all three components of variation for all vital rates. Importantly, the seven study populations are all wild feeding and live in natural habitats. None have experienced more than a few interventions, which include limited provisioning and occasional medical treatment (all interventions are listed in Strier et al. 2010). Hence, the degree of demographic variation in these data should be little influenced by direct human activities.

Table 1.

Characteristics of the behavioral studies and study sites

Species (species code)	Date of first census	No. years of data	No. individual animals	Annual rainfall
				Mean (SD)	Coefficient of variation
Verreaux’s sifaka, Propithecus verreauxi (Sif)	December 31, 1984	24	756	562.9a (109.5)	.311a
White-faced capuchin monkey, Cebus capucinus (Cap)	December 15, 1986	22	167	1,721.1 (487.5)	.466
Blue monkey, Cercopithecus mitis stuhlmanni (Blu)	December 31, 1980	28b	412c	1,963.6 (186.5)	.166
Northern muriqui, Brachyteles hypoxanthus (Mur)	November 26, 1983	25	407	1,199.2 (157.5)	.255
Yellow baboon, Papio cynocephalus (Bab)	December 31, 1971	37	1,055	344.4 (73.9)	.342
Eastern chimpanzee, Pan troglodytes schweinfurthii (Chi)	December 31, 1963	45	285	1,329.6 (231.2)	.207
Mountain gorilla, Gorilla beringei beringei (Gor)	December 31, 1967	41	269	1,358.6 (214.5)d	.158

^aData are from Lawler et al. 2009.

^bFertilities could be estimated only starting June 15, 1997, because animals were followed seasonally at the beginning of the study.

^cThis study does not include adult males, which could not be monitored after emigration from the natal group.

^dThese data were collected several kilometers from the field site, at a lower elevation.

Stochastic demography of wild primate populations is of inherent interest for at least two reasons. First, primates possess complex behavioral repertoires and are capable of sharing information within persistent social groups. These traits may reduce the impact of environmental stochasticity on their long-term fitness compared with other taxa. Second, as they are close relatives of humans, demographic studies of other primates inform us about the role that environmental stochasticity may have played in human evolution.

Perhaps the most important question about demographic variation, covariation, and serial correlation is whether each component of variability increases or decreases fitness compared with what it would be in a constant environment. However, whether each aspect of variability increases or decreases fitness depends on which other aspects are operating. For example, in the absence of covariation and serial correlation (i.e., when all rates are independently and identically distributed [IID]), variation in vital rates, particularly those that most strongly influence fitness in a constant environment, reduces long-term fitness. This relationship is the basis of the hypothesis that more influential vital rates should exhibit less temporal variability (Pfister 1998; Gaillard et al. 2000; Gaillard and Yoccoz 2003; Morris and Doak 2004). But when vital rates covary, increasing the variation of less influential vital rates might increase fitness if those rates covary negatively with more influential vital rates. Such negative covariation cancels out some of the negative fitness effects of variation in the more influential rates (Doak et al. 2005). Similarly, positive serial correlations in the environment can favor greater vital rate variances, reflecting synchronization of the vital rates with partially predictable sequences of environmental states (Tuljapurkar et al. 2003; Morris et al. 2006). Thus, which aspects of variability operate also determine the applicability of specific hypotheses regarding demographic variation. For example, strictly speaking, the prediction of Pfister (1998; that more influential vital rates should exhibit less temporal variability) assumes that all vital rates are IID.

To quantify how the three components of demographic variability influence fitness, we use the estimates of these components for the seven primate study populations to examine three nested stochastic scenarios: (1) vital rate variation in the absence of covariation and serial correlations (the strict IID case), (2) vital rate variation and covariation in the absence of serial correlations, and (3) all three components of variability operating simultaneously. We compare long-term fitness in each stochastic scenario to fitness in a constant environment to assess whether demographic variability increases or decreases fitness.

In summary, we address five questions in this article. First, how much variation, covariation, and serial correlation in vital rates do wild primate populations exhibit? Second, do the components of demographic variability (in the three nested scenarios described in the preceding paragraph) increase or decrease estimated long-term fitness in the study populations, and if so, by how much? Third, do the primate demographic data show evidence that the vital rates that would most influence fitness in a constant environment exhibit less temporal variability (Pfister 1998)? Fourth, how does the degree of demographic variability we estimated for primate populations compare with estimates for other taxa in the literature? Fifth, do the fitness impacts of demographic variability in the seven primate species correlate with differences in body mass, life history, or extrinsic environmental variability?

Methods

Estimating Vital Rates and Correcting for Sampling Variation

We estimated vital rates using life-history data for individual animals in the Primate Life History Database (PLHD), which is described in detail by Strier et al. (2010) and illustrated at http://demo.plhdb.org/. Briefly, the database includes information for thousands of individuals about their birth dates, dates of entry and departure from the study, type of entry (i.e., birth, presence at onset of study, or immigration) and departure (i.e., death, emigration, or presence at the last field census), sex, mother’s identity, and whether they were their mothers’ first live-born offspring. For each female, the start and end dates of all time periods in which her fertility was intensively monitored are also recorded in the database.

Because the database includes complete individual life histories through 2008, we could establish a series of hypothetical censuses at 1-year intervals and then determine for each vital rate and intercensus interval the numbers of “trials” (e.g., adults alive at the first census) and “successes” (e.g., the number of those adults surviving to the second census). We used the information about entry type and departure type in the PLHD to adjust the numbers of trials and successes for left and right censoring, as described in appendix A.

We used the same three life-history stages (newborn, juvenile, and adult) to standardize vital rates across species despite differences in life expectancy and generation time. Using fewer stages also increases the sample sizes for estimating vital rates relative to using more stages with fewer individuals per stage. Newborns in each intercensus interval were individuals born between the two censuses, juveniles were individuals alive at the first census but younger than the median age at first reproduction (i.e., first live birth) for females of that species (estimated from the PLHD; table 2), and adults were all older individuals. We then estimated the same set of three survival rates and two fertilities for all species: S_n (the probability that a newborn survives to the first census after its birth), S_j and S_a (the probabilities of survival over 1 year for juveniles and adults, respectively), and F_j and F_a (the mean number of daughters produced by a juvenile or adult female, respectively, during the following year). Juvenile fertility is not zero, because some females begin reproducing in the last juvenile age class, which includes the median age at first reproduction. Survival in each life stage was estimated using both females and males. We used the sex ratio of infants surviving long enough to be sexed to estimate the number of daughters per female. For none of the species did the mean number of daughters per juvenile or adult female per year exceed a value of 1, so it was legitimate to treat both the survival probabilities and the fertilities as binomial vital rates.

Table 2.

Body mass and life-history characteristics of the study species

Species (species code)	Mean adult female body mass (kg)	Median age (years) at first reproduction for females	Life-history traits computed from the mean projection matrix
			Deterministic population growth rate, λ1	Net reproductive rate, R0	Cohort generation time, G (years)	Life expectancy conditional on reaching adult stage, Λ (years)
Sifaka (Sif)	2.8	6.0	.9882	.78	19.5	20.7
Capuchin (Cap)	3.0	6.4	1.0209	1.8	35.2	36.4
Blue monkey (Blu)	4.2	7.2	1.0361	2.1	25.1	26.3
Muriqui (Mur)	8.3	8.7	1.0512	6.4	70.1	71.3
Baboon (Bab)	12.8	6.0	1.0628	3.4	28.1	29.3
Chimpanzee (Chi)	31.3	15.2	.9823	.51	34.0	35.3
Gorilla (Gor)	97.7	9.9	1.0268	2.8	52.9	54.1

Note: Life-history traits were computed from the mean projection matrix using methods in Cochran and Ellner (1992), except where indicated. Cohort generation time is the average time between the birth of a female and the birth of her daughters. Mean adult female body mass and cohort generation time values are unpublished data from the study populations, except for the values for sifaka (from Richard et al. 2000), muriqui (from Lemos de Sá and Glander 1993), and chimpanzee (from Pusey et al. 2005). Median age at first reproduction for females is computed from the Primate Life History Database (http://demo.plhdb.org/). Net productive rate (R₀) is lifetime number of daughters per female. Because cohort generation time and conditional life expectancy are calculated from the stage-based projection matrices used in this article, they do not account for changes in mortality as adults age, as a full age-based life table would do. Therefore, these values are likely to overestimate the true values; however, we are using them in this article only in a comparative sense.

Although the studies in the PLHD are long term by the standards of most demographic studies, several of them include relatively few individuals (table 1), for two reasons. First, in intensive behavioral studies—such as those in the PLHD—in which social groups are followed on a near-daily basis for years on end, following large numbers of individuals is logistically and financially infeasible. Second, several of the local populations in which the study individuals reside are in fact small, as is true of populations of many primates. With small sample sizes, it is especially important to take sampling variation into account when estimating levels of temporal variability in vital rates (Gould and Nichols 1998; Kendall 1998; White 2000; Morris and Doak 2002). We discounted for sampling variability by estimating annual vital rates with a generalized linear mixed model, using the lmer procedure in R (R Development Team 2005; cf. Altwegg et al. 2007). We assumed that errors were binomially distributed, using the numbers of trials and successes for each year as described above, and we fit a model with an intercept and a random effect of year as the only independent variable. The intercept is the mean vital rate (weighted by sample size in each year), and the year coefficients give the corrected vital rate values in each year. Years with small sample sizes will have estimates that are pulled toward the mean relative to the raw estimates. Consequently, the variance of the year estimates will be less than the variance of the raw annual estimates because the effect of sampling variation has been removed. Thus, the variance of the year estimates approximates the true temporal variance, also called the “process variance.” If the apparent variation among years can be completely explained by sampling variation, all years will have the same vital rate value (i.e., the mean) and the estimated process variance will be zero.

Construction of Projection Matrices

We used projection matrices with a 1-year projection interval to integrate the effects of all vital rates on fitness. Although we applied the single estimate of juvenile survival to all juveniles, regardless of their age, to incorporate differences among species in the delay between birth and the onset of reproduction, we varied the number of juvenile classes among species such that the median age at first reproduction as estimated from the database fell within the last juvenile class. For example, for species in which the median age at first reproduction falls between ages 6 and 7 years (i.e., sifaka, capuchin, and baboon; table 2), we constructed the projection matrix A with one newborn (class 1) and six juvenile age classes:

$$\mathbf{A}=\left[\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& F_{\text{j}}\times S_{\text{n}}& F_{\text{a}}\times S_{\text{n}}\\ S_{\text{j}}& 0& 0& 0& 0& 0& 0& 0\\ 0& S_{\text{j}}& 0& 0& 0& 0& 0& 0\\ 0& 0& S_{\text{j}}& 0& 0& 0& 0& 0\\ 0& 0& 0& S_{\text{j}}& 0& 0& 0& 0\\ 0& 0& 0& 0& S_{\text{j}}& 0& 0& 0\\ 0& 0& 0& 0& 0& S_{\text{j}}& 0& 0\\ 0& 0& 0& 0& 0& 0& S_{\text{j}}& S_{\text{a}}\end{array}\right].$$ (1)

We computed the sensitivities of the deterministic population growth rate to the five vital rates for each species. One goal in doing so was to assess Pfister’s (1998) hypothesis that vital rates with a stronger influence on fitness will show less variation over time. The sensitivities measure the influence of each vital rate on fitness in a constant environment and form the basis for Pfister’s hypothesis. A second goal was to interpret more broadly the influence of vital rate variation, covariation, and serial correlation on long-term fitness. We first computed the mean projection matrix by constructing a matrix for each year and averaging them. We then computed the sensitivity of the dominant eigenvalue of the mean matrix to the vital rates, using the standard eigenvector method and the chain rule (Caswell 2001; as a result, the sensitivity to juvenile survival is the sum of the sensitivities of the elements on the principal subdiagonal of the projection matrix [see eq. (1)]). To compare levels of variation between species or between different vital rates in the same species independent of differences in vital rate means, we used the relative variability for each vital rate, computed as the process variance divided by its maximum value, M × (1 − M), given the vital rate’s mean, M. In assessing Pfister’s hypothesis, this procedure accounts for the fact that high mean survival in long-lived species restricts the range of possible variation in survival, which could lead to a spurious negative correlation between absolute variance and sensitivity (see Morris and Doak 2004).

Calculating Long-Term Fitness in Stochastic Environments

We calculated long-term fitness by first generating 50,000 sets of random vital rates with the estimated means, process variances and covariances, and serial correlations using the method described by Morris and Doak (2002, chap. 8). Details are provided in appendix A. Importantly, we assumed that serial correlations between vital rate values separated by two or more years were produced by the 1-year serial correlations. This need not be true (e.g., environmental conditions may fluctuate with a period longer than 1 year), but it is difficult to accurately estimate serial correlations with longer lag times, even with data sets as long as those that we had for primates. We then used the series of random vital rates to construct a sequence of annual projection matrices, and with this we calculated numerically the long-term stochastic population growth rate as described by Caswell (2001).

Results

Mean Vital Rates

The sex ratio of surviving infants could not be distinguished from 50:50 in any species except capuchin, which had a male-biased sex ratio (table 3). For all species, the mean survival probability across years was higher for juveniles and adults than for newborns (fig. 1; table 3), but in three species (sifaka, blue monkey, and chimpanzee), juveniles had an average survival probability that was slightly higher than that of adults. Average survival probabilities of adults and newborns were highest in muriquis and lowest in sifaka, while average survival of juveniles was highest in gorillas and lowest in capuchins and baboons. Mean fertility of adults (new daughters per female per year) ranged from 0.29 in baboons to 0.068 in chimpanzees, with lower mean fertilities in all species for females in the last year of the juvenile period than for adult females (a simple consequence of our definition of the juvenile period).

Table 3.

Estimates of the infant sex ratio and of the means and temporal variances (corrected for sampling variation) of five other vital rates for seven primate species

Vital rate	Species
	Sifaka	Capuchin	Blue monkey	Muriqui	Baboon	Chimpanzee	Gorilla
A. Sex ratio of infants (proportion female, with 95% binomial confidence limits):
Sex ratio	.48 (.41, .54)	.33 (.23, .44)	.51 (.45, .58)	.50 (.44, .57)	.53 (.49, .56)	.47 (.39, .56)	.43 (.36, .51)
B. Vital rate means:
Sn	.527	.793	.809	.941	.875	.828	.830
Sj	.930	.921	.961	.954	.920	.956	.972
Sa	.927	.965	.942	.984	.955	.945	.977
Fj	.0264	.0195	.0494	.0396	.0469	.0205	.0198
Fa	.164	.145	.206	.170	.287	.0677	.103
C. Vital rate variances (corrected for sampling variation):
Sn	.0229	.00440	.00252	0	3.58 × 10−5	.00250	.000841
Sj	.000279	.00177	.000165	.000353	.000228	1.08 × 10−5	.000109
Sa	9.87 × 10−5	7.14 × 10−5	1.33 × 10−5	0	.000625	.00139	6.68 × 10−5
Fj	8.02 × 10−5	0	0	0	0	0	0
Fa	.00305	0	0	0	0	0	0

Figure 1.

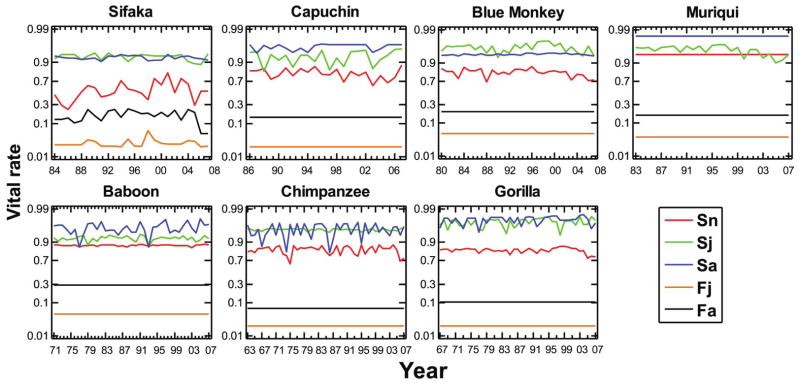
Estimated vital rates (logit scale) for all species in all years. Sn, Sj, and Sa are survival of newborns, juveniles, and adults, respectively; Fj and Fa are fertilities (mean number of new daughters per female per year) for juveniles and adults, respectively. Estimates are corrected for sampling variation (see text); a flat line indicates that the variability in the raw estimates could not be distinguished from pure sampling variation, so the mean value is shown for all years. In this and all other figures and tables, species are presented in order of mean female adult body size (table 2) from smallest (sifaka) to largest (gorilla). S_n is the probability that a newborn survives to the first census after its birth; S_j and S_a are the probabilities of survival over 1 year for juveniles and adults, respectively; and F_j and F_a are the mean number of daughters produced by a juvenile or adult female, respectively, during the following year.

Variances, Covariances, and Serial Correlations of Vital Rates

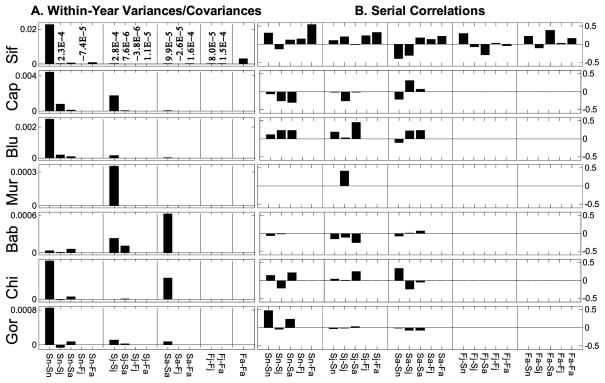
We could not detect temporal variability of adult or juvenile fertility beyond pure sampling variability for any of the species except sifaka (figs. 1, 2; table 3). In contrast, we detected significant temporal process variability in survival for all three life stages in all species except muriqui, which showed detectable temporal variation in survival of juveniles only.

Figure 2.

Process variances, covariances, and serial (between-year) correlations for pairs of vital rates shown at the bottom. A, The first bar in each group is the variance of the specified rate, and subsequent bars are covariances between that rate and the other rates. Nonzero variances and covariances that are too small to be visible at the scale of the Y-axis are written in scientific notation. B, The correlation between the first vital rate of a pair in year t and the second vital rate in year t + 1. All measures of variability are based on vital rate estimates that have been corrected for sampling variation. Sif = sifaka, Cap = capuchin, Blu = blue monkey, Mur = muriqui, Bab = baboon, Chi = chimpanzee, Gor = gorilla. S_n is the probability that a newborn survives to the first census after its birth; S_j and S_a are the probabilities of survival over 1 year for juveniles and adults, respectively; and F_j and F_a are the mean number of daughters produced by a juvenile or adult female, respectively, during the following year.

Covariation between vital rates was weak (fig. 2). When present, covariation was mostly positive, although there were small negative covariances between juvenile fertility and each of the three survival rates in sifaka and between newborn and juvenile survival in gorillas.

Serial correlations between the values of a single vital rate and between pairs of vital rates in successive years were in some cases positive and in other cases negative (fig. 2). Negative correlations between successive values of a single vital rate (e.g., juvenile survival of capuchins) indicate a tendency for that rate to flip between lower-than-average and higher-than-average values in successive years (fig. 1). Positive serial correlation in a single vital rate may indicate a trend over time (juvenile survival in muriquis and newborn survival in gorillas). Positive serial correlations between vital rate pairs (e.g., newborn survival and adult fertility in sifaka) imply that when one rate is above its average in one year, the second rate is likely to be above its average the following year. Some species (sifaka, blue monkey) showed more positive than negative serial correlations, some roughly equal numbers (chimpanzee, gorilla), and others (capuchin, baboon) more negative than positive values.

Influence of Variation, Covariation, and Serial Correlation on Long-Term Fitness

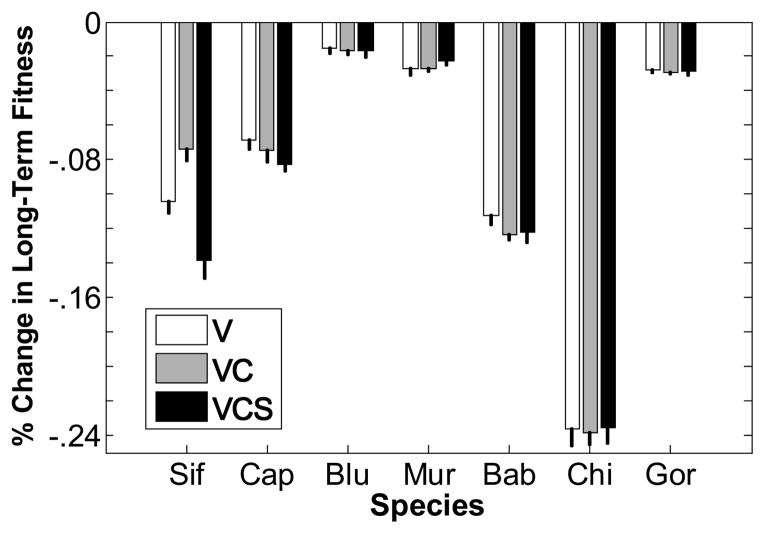
Including temporal demographic variability decreases the estimated long-term fitness of all seven species relative to expected fitness in a constant environment (fig. 3, white bars). The strongest reduction is seen in chimpanzee, which shows the highest temporal variance in adult survival of the seven species (figs. 1, 2; table 3). Temporal variation has more moderate effects on long-term fitness in sifaka, capuchins, and baboons, and it has the smallest effects on blue monkeys, muriquis, and gorillas.

Figure 3.

Percent change in fitness in a stochastic environment relative to fitness in a constant environment. Three scenarios are shown: V is variation in vital rates with no covariation or serial (between-year) correlations; VC is variation and covariation with no serial correlations; VCS is variation, covariation, and serial correlations. Percent change is 100(λ_s − λ₁)/λ₁, where λ_s is the stochastic growth rate and λ₁ is the deterministic growth rate in a constant environment (i.e., the dominant eigenvalue of the mean projection matrix). Error bars are 2 SEs around the mean of 10 simulations, each of 50,000 years. Sif = sifaka, Cap = capuchin, Blu = blue monkey, Mur = muriqui, Bab = baboon, Chi = chimpanzee, Gor = gorilla.

By comparing the white and gray bars in figure 3, we can assess the impact of adding vital rate covariation to the effect of vital rate variation alone (still in the absence of serial correlations). The effect of vital rate covariation differs among species. In capuchins and baboons, vital rate covariation decreases fitness slightly more than does vital rate variation alone. But in sifaka, negative covariation increases long-term fitness compared with the IID case. In all other species, including the estimated levels of covariation has negligible effects on long-term fitness compared with the effects of vital rate variation alone (i.e., the mean percent fitness reduction with covariation falls within the confidence interval of the mean reduction with variation only, and vice versa).

Finally, we can assess the impact of adding the estimated serial correlations by comparing the black and gray bars in figure 3. For sifaka and capuchins, serial correlation in vital rates reduces long-term fitness relative to the case of variation and covariation alone, and it may slightly increase long-term fitness in muriquis. For all other species, the effects of serial correlations are minor.

Overall, the effect of temporal variation in demography, accounting for variation, covariation, and serial correlation, is minor for all seven species, on the order of a 0.02%–0.2% reduction in long-term fitness relative to a constant environment (note Y-axis scale in fig. 3).

Demographic Variability in Primates Compared with Other Vertebrates

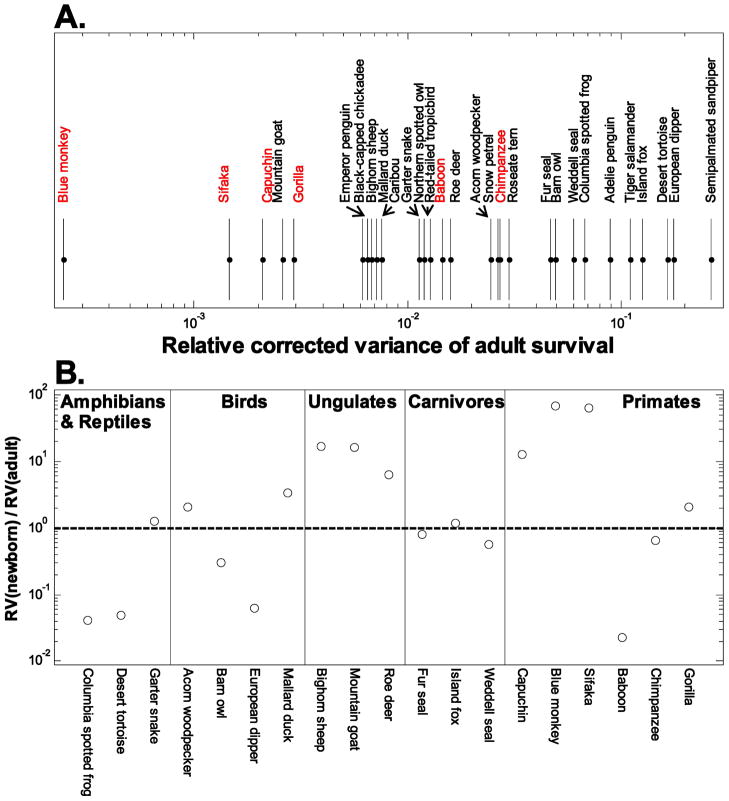
One reason why temporal variation may have weak fitness effects in primates could be that the variation is itself minor. To see how the levels of demographic variability we have estimated here for primates compare with levels in other vertebrate species, we scoured the literature for studies that reported estimates of the temporal variance of survival for newborn and/or adult vertebrates and that corrected the estimates for sampling variation by any one of several methods (Gould and Nichols 1998; Kendall 1998; White and Burnham 1999; White 2000; Altwegg et al. 2007). We excluded many studies that reported only raw estimates of temporal variance uncorrected for sampling variation, because raw variances are not directly comparable to the estimated process variances we report here for our sample of primates. Altogether, we found literature estimates of temporal process variance in adult survival for 23 vertebrate species (see list of studies in app. B). For 15 of these species, process variances for survival of newborns were also reported in the original studies. To compare levels of variability in survival across species while accounting for the fact that mean survival also differs, we converted the process variances in survival to relative variances, as explained in “Methods.”

Of the 29 vertebrate species (including six primates from this study) with estimates of relative variability in adult survival, four of the five species with the lowest levels of variability were primates (fig. 4A). Two other primates (baboon and chimpanzee) fell in the middle of the range of estimates we found. We did not include muriqui in figure 4A, even though the estimated process variance in adult survival was zero. The true variance is unlikely to be zero, but the actual value may have been too low to detect given the sample size and high mean survival in muriquis (table 3, pt. B), as the variance must decrease as the mean approaches 1 (the same holds for moose; see app. B). As a group, primates show significantly less temporal variation in adult survival than do the other vertebrates in figure 4A (Wilcoxon’s rank sum = 43, P = .012; including muriqui and moose with zero variance results in an even lower P value).

Figure 4.

Levels of temporal variability in survival for primates estimated in this study compared with published values for other vertebrates. A, Process variance in survival of adults relative to its maximum possible value given mean survival. Primates are shown in red. Note that relative process variance is shown on a one-dimensional logarithmic scale. B, The ratio (log scale) of relative process variance of newborn survival (RV(newborn)) to relative process variance of adult survival (RV(adult)) for all studies that provided nonzero estimates of both process variances. The horizontal dashed line indicates equal relative process variances for the two survival rates; points above the line therefore show higher relative variability in newborn survival than in adult survival. Muriqui is not included, because the estimated process variance in survival was zero for both newborns and adults. Details of literature estimates are provided in appendix B.

Sensitivities of the Population Growth Rate to Mean Vital Rates

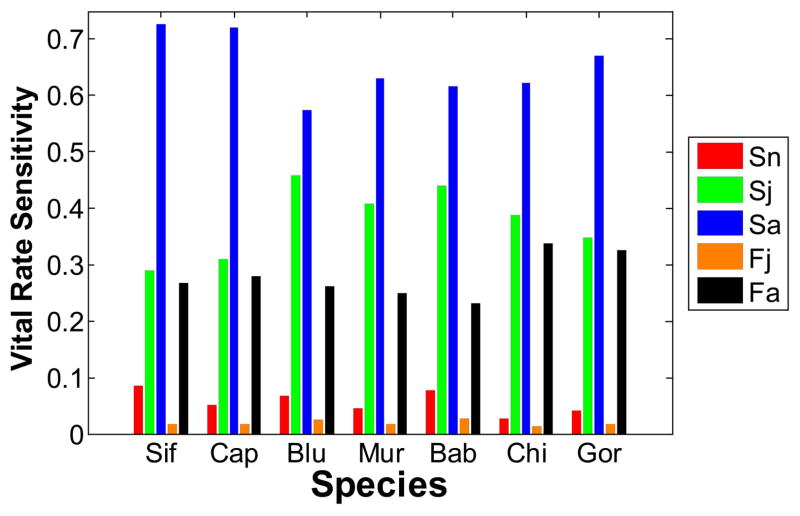
Sensitivities of the deterministic population growth rate to the underlying vital rates followed the pattern typical of a stage-structured projection matrix for a long-lived species (fig. 5). Specifically, for all species, the population growth rate was most sensitive to adult survival and least sensitive to juvenile fertility.

Figure 5.

Deterministic sensitivities of the population growth rate (dominant eigenvalue of the mean projection matrix) to the underlying vital rates. Sif = sifaka, Cap = capuchin, Blu = blue monkey, Mur = muriqui, Bab = baboon, Chi = chimpanzee, Gor = gorilla. S_n is the probability that a newborn survives to the first census after its birth; S_j and S_a are the probabilities of survival over 1 year for juveniles and adults, respectively; and F_j and F_a are the mean number of daughters produced by a juvenile or adult female, respectively, during the following year.

Relationship between Vital Rate Variability and Sensitivity

Given the high sensitivity of population growth to adult survival (fig. 5), Pfister’s (1998) hypothesis would suggest that the relative process variability of adult survival should be low compared with that of the other vital rates. As we did not detect any variability in fertility beyond what could be accounted for by pure sampling variability (except for sifaka), we were not able to assess the relationship between process variation and sensitivity for fertilities. However, we were able to estimate the level of process variation for both newborn and adult survival for six of seven primates (all but muriqui). Given the sensitivities in figure 5, Pfister’s hypothesis would predict that the ratio of the relative process variances of newborn and adult survival rates should be >1 (cf. Gaillard and Yoccoz 2003). We did observe this result for four of six primate species: sifaka, capuchin, blue monkey, and gorilla (fig. 4B). In fact, blue monkey had the highest ratio of relative process variances when compared with any of the other primates and with the other vertebrates in figure 4B. However, the other two primates (baboon and chimpanzee) did not show the predicted higher variability in newborn survival. Support for the predicted ratio is mixed across the other vertebrate groups, and it is strongest for ungulates, although numbers of species in all groups are small (fig. 4B).

Potential Correlates of Demographic Variability in Primates

Finally, we assessed whether demographic variability in primate vital rates is associated with body mass, life-history features, or the level of variability in climate across the study sites. Among the seven primate species in our database, life-history features such as age at first reproduction, generation time, and life expectancy were not correlated with body mass (tables 2, 4). In particular, muriquis have a longer generation time and a longer life expectancy than gorillas, which are 11 times larger (table 2). Median age at first reproduction was significantly correlated with generation time, and measures of generation time and life expectancy were all positively correlated (significantly or nearly so) with one another (table 4). However, the percent reduction in fitness due to temporal variation (variance, covariance, and serial correlation combined) was not significantly correlated with body mass or with any of the life-history metrics we computed (table 4).

Table 4.

Among-species correlations (N = 7) between percent reduction in fitness (fig. 3, black bars) and four life-history metrics from table 2

	PRF	M	A	R0	G	T	Λ
Percent reduction in fitness, PRF	…	−.036	.071	.643	.321	.107	.321
Body mass, M	.963	…	.607	.250	.500	.607	.500
Median age at first reproduction, A	.906	.167	…	−.179	.536	.929	.536
Net reproductive rate, R0	.139	.595	.713	…	.5	−.0714	.5
Cohort generation time, G	.498	.267	.236	.267	…	.714	1
Generation time, T	.840	.167	.007	.906	.0881	…	.714
Conditional total life span, Λ	.498	.267	.236	.267	.0004	.0881	…

Note: Numbers above the diagonal are Spearman rank correlations; numbers below the diagonal are P values. For numbers in bold type, P < .05; for numbers in italics, .05 < P < .1. Generation time, T = log (R₀)/log (λ₁), is the time required for the population to grow by an amount equal to R₀, and it accounts for differences in population growth rate, λ₁ (unlike cohort generation time).

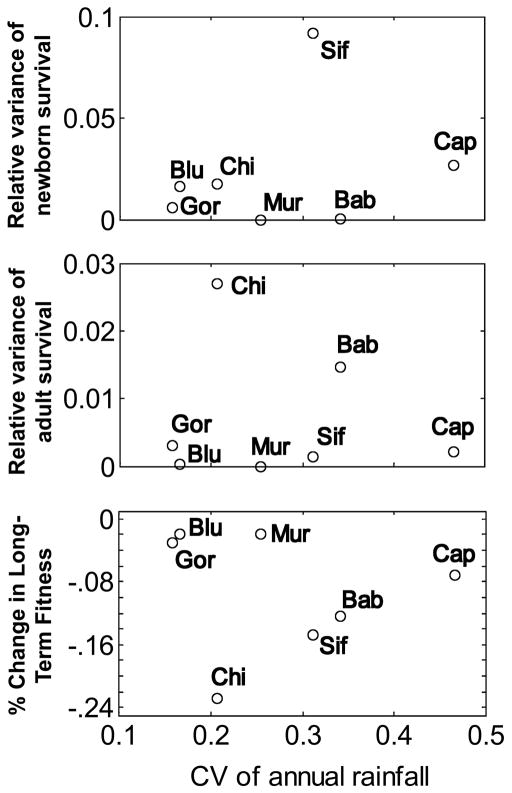
To test for an association between demographic variability and climate, we used mean annual rainfall as the climate variable, justified by the following logic. Net primary productivity (NPP) is likely to be a reasonable, general measure of the availability of food in the environments these primates inhabit. In turn, food availability is likely to affect survival and fertility. On a global scale, the strongest predictor of NPP is actual evapotranspiration (Rosenzweig 1968), which is positively correlated with both precipitation and temperature (i.e., NPP is highest under warm, moist conditions). As all of the primate study sites reported here are in warm tropical or subtropical (sifaka) locales, the primary climatic axis on which NPP is likely to vary among years within sites is rainfall. We measure variability in rainfall as the coefficient of variation (standard deviation divided by the mean) of annual rainfall across the same years for which we estimated vital rates (table 1). By this measure, capuchins inhabit the most variable environment (likely due to strong El Niño effects on rainfall variation on the western slope of Costa Rica) and gorillas inhabit the least variable environment. However, there is no clear relationship between rainfall variability and any metric of demographic variability that we estimated (fig. 6), including the degree to which demographic variability depresses long-term fitness. Supporting the absence of a strong relationship between demographic variability and rainfall variability, only five of the 35 species by vital rate combinations showed a significant (.005 < P < .05) rainfall effect in a generalized linear model (with binomial errors) regressing annual vital rate values against annual rainfall (results not shown).

Figure 6.

Relationship between climate variability (coefficient of variation in annual rainfall) and relative variance in newborn survival (A), relative variance in adult survival (B), and the effect of variability on long-term fitness (C; these are the same values shown for the VCS case in fig. 3). Sif = sifaka, Cap = capuchin, Blu = blue monkey, Mur = muriqui, Bab = baboon, Chi = chimpanzee, Gor = gorilla.

Discussion

Although life-history theory highlights the potential impact of temporal demographic variation for long-term fitness, few empirical studies have assessed the fitness impacts of estimated levels of variation, covariation (but see Coulson et al. 2005), and, especially, serial correlation. While we found evidence that covariation and serial correlation in vital rates can influence long-term fitness for some primate species (fig. 3), the overwhelming impression that emerges from our analyses is that temporal demographic variability of any kind has only minor influence on long-term fitness in wild primate populations. Levels of demographic variability in the primates we examined were generally low compared with those of other vertebrates for which process variability has been reported. Below we discuss (1) potential causes of low demographic variability in primates, (2) causes underlying the few cases in which covariation and serial correlation influenced fitness, (3) the lack of an association between rainfall variability and demographic variability, (4) our results in relation to Pfister’s (1998) hypothesis that more influential vital rates will be less variable, and (5) future directions.

Potential Causes of Low Demographic Variability in Primates

In addition to long generation times, primates also have long life spans (table 2). Long lives can be achieved only by high mean annual survival. As the upper limit of the variance of a survival rate must decline as its mean approaches 1 (Morris and Doak 2004), primates can be expected to have lower year-to-year variance in survival than other species with shorter life spans. But even when we account for this built-in relationship between the mean and the variance of survival by dividing the absolute process variance by its maximum value given the mean, primates still show low variability in survival relative to other vertebrates (fig. 4A), some of which (e.g., desert tortoise, Weddell seal) also have long lives. An obvious possibility is that the well-developed cognitive abilities of primates and their capacity to share information within complex social groups, in combination with a broad and flexible diet, allows them to obtain resources consistently and thus maintain high and more constant survival despite fluctuations in their environment. Cognition and information sharing are certainly better developed in the primates than in the other vertebrates in figure 4A (Roth and Dicke 2005). It is tempting to speculate that similar abilities may have buffered early human populations against environmental stochasticity and thus improved their success. Indeed, selection to reduce the demographic impact of a fluctuating environment may have favored the evolution of encephalized brains, complex sociality, bipedalism, and a broad diet in humans (Potts 1996, 1998).

A complicating factor in comparing levels of demographic variability in the species in figure 4 is that, in addition to differences in longevity, cognition, social systems, and diet, these species inhabit a wide range of environments, from tropical rainforests to deserts to Antarctic seas, that may also differ in their inherent environmental variability. As we are unlikely to find many pairs of sympatric vertebrates with similar life spans but that differ in cognitive ability, sociality, and diet breadth, testing this hypothesis further may require a multiple regression approach, with demographic variability as the dependent variable and degree of cognitive complexity, social interaction, diet breadth, longevity, and extrinsic environmental variability as independent variables. Weighing the contributions of so many predictor variables will necessitate more data than are presently available. Alternatively, our hypothesis would predict that other vertebrate groups with well-developed cognition and social networks, especially elephants and cetaceans (Roth and Dicke 2005), for which estimates are not currently available would also show low demographic variability.

Fitness Effects of Variation, Covariation, and Serial Correlation

We have concluded that the effects of demographic variability on fitness in the primate species we studied are likely to be minor because the additions of the estimated levels of vital rate variation change the population growth rate only slightly relative to the deterministic rate in the average environment. In support of this conclusion, we note that quantitative information indicates that four of the study populations (capuchins [Fedigan and Jack 2001], muriquis [Strier et al. 2006], baboons [Alberts and Altmann 2003], and gorillas) are actually growing and one (sifaka; Lawler et al. 2009) is slowly declining, which is in agreement with the deterministic population growth rates predicted by our projection matrices (table 2). Anecdotal evidence suggests that blue monkey populations are also increasing, as our model predicts. However, our model predicts a slow decline in the chimpanzee study population, whereas numbers in the study groups from which the vital rate estimates were made have increased by about 2% per year from 2002 to 2009 (Rudicell et al. 2010). Thus, although the models are not perfect, there is reasonable agreement between the observed recent behavior of the study populations and the predictions of our deterministic population models, bolstering the conclusion that variability effects are likely to be weak.

Nonetheless, adding the estimated level of covariation between vital rates did increase slightly the estimate of long-term fitness in sifaka relative to the case of independent variation in vital rates (cf. white bars and gray bars in fig. 3). This effect is predicted by the negative covariances between juvenile fertility and the three survival rates in sifaka (fig. 2). Even though juvenile fertility has a relatively small influence on population growth (fig. 5), by fluctuating out of synchrony with three more influential vital rates, it tends to reduce the fitness impact of variation in those rates (Doak et al. 2005). We also observed some positive covariation between vital rates. For example, newborn and juvenile survival covary positively in capuchins, as do newborn and juvenile survival with adult survival in baboons, which tends to decrease long-term fitness (fig. 3), also as expected (Doak et al. 2005).

Accounting for the estimated serial correlations in vital rates also had mostly minor effects on long-term fitness. Again, the largest effect was for sifaka (fig. 3). Pinpointing which of the many positive and negative serial correlations among sifaka vital rates (fig. 2) may be responsible for this effect is challenging, especially because, as for within-year covariances, the effect of serial correlation in one vital rate or a pair of rates depends on the sensitivity of the population growth rate to the vital rate(s) involved (Tuljapurkar 1982). Tuljapurkar et al. (2009) used simulations to explore the effects of serial correlations in fertility (in the absence of within-year covariation) on long-term fit-ness. While they found that both positive and negative serial correlation can either increase or decrease long-term fitness, depending on details of the life history, they also found that the magnitude of the effect of serial correlation on long-term fitness diminishes with increasing generation time (see fig. 4b in Tuljapurkar et al. 2009). We are not aware of other simulations that have included serial correlation in both fertilities and survival rates, but it seems likely that longer generation times will also buffer long-term fitness against serial correlation in survival. Should this be so, the absence of strong effects of serial correlation on fitness in primates, which have long generation times relative to the scenarios explored by Tuljapurkar et al. (2009), would be consistent with their theoretical results. Interestingly, sifaka, for which we saw the largest impact on fitness of serial correlation (in all vital rates), is also the species in our database with the shortest generation time (table 2).

Demographic Variability versus Rainfall Variability

Within our sample of primates, we did not find a correlation between demographic variability or its fitness effects and extrinsic variability in the environments our study species inhabit (at least as measured by the coefficient of variation in annual rainfall; fig. 6). In contrast, some vital rates have been shown to be correlated with identified environmental drivers in some of our species, including capuchin (Fedigan et al. 2008), sifaka (Richard et al. 2000, 2002; Dewar and Richard 2007; Lawler et al. 2009), and muriqui (Strier 1999). These results are not necessarily incompatible, for at least three reasons. First, if demographic variability is driven by factors other than rainfall variability in some of our study species, the overall correlation between demographic and climatic variability would be weakened. For example, outbreaks of respiratory disease lowered adult survival in the Gombe chimpanzee population in 1968, 1987, and 1996 (Pusey et al. 2008; Williams et al. 2008), and low newborn survival in 1975 was at least in part a consequence of females killing infants (Goodall 1977). Similarly, predation may strongly impact primate survival in a climate-independent fashion (Anderson 1986; Isbell 1994). Second, for those species that do exhibit demographic sensitivity to climate drivers, the slope of the relationship between a vital rate and rainfall may differ among species, so that rainfall variability is amplified in the demography of some species more than in others. Such differential amplification would also add noise to the overall relationship between demographic and climatic variability. Third, different vital rates may be rainfall dependent in different species. As the impact of variation in a vital rate on long-term fitness depends on the sensitivity of population growth to that vital rate, some rainfall-driven variation in vital rates might have little effect on long-term fitness. It is important to emphasize that even if demographic variability is not correlated with climate variability across species, the search for climatic drivers of demography in individual populations is still valuable, as it provides a means to project how future climate change may influence the viability of those populations.

Assessing Predicted Patterns of Variability among Vital Rates

For primates, we found only mixed support for Pfister’s (1998) hypothesis that vital rates with greater influence on the rate of population growth should be less variable in time, a pattern that Morris and Doak (2004) referred to as “buffering” of vital rates. We assessed this prediction by comparing variability in newborn and adult survival, because we could not estimate process variability in fertility for most species. While four species showed higher variability in newborn survival as predicted, two others did not. Furthermore, we found only limited support for this particular prediction in other vertebrate groups (fig. 4B). When demographic variability is low in all vital rates, as we have shown it to be in primates (figs. 3, 4B), there may be little scope for selection to act differentially on the levels of variability in different vital rates. As noted in the “Introduction,” Pfister’s hypothesis strictly assumes that all vital rates vary independently. Thus, a second possible explanation for the apparent absence of buffering in some taxa is that covariation and serial correlation in vital rates alter the selection to reduce vital rate variability posited by Pfister (Doak et al. 2005; Morris et al. 2006). A future challenge is to understand how simultaneous selection on all aspects of demographic variability shape the evolution of life histories in stochastic environments (Tuljapurkar et al. 2009). The number of species within each larger taxonomic group in figure 4B is small, making the possibly higher prevalence of buffering in some groups (ungulates and primates) only a suggestion. But if this pattern should hold up with more species, seeking to explain why only some groups show widespread buffering would be a priority.

Future Directions

Here we have assumed that all serial correlations between vital rate values separated by two or more years were produced by the estimated correlations between adjacent years. Additional long-term serial correlations could be produced by long-period fluctuations in the environment or longer-term life-history trade-offs. Long-term correlations are difficult to estimate even with such long-term data sets, but as all of the demographic studies we report here are ongoing, we hope to better estimate long-term serial correlations in the future.

Our analysis also assumes that vital rates are density independent. Some of the negative serial correlations we observed could be produced by short-term density feedback rather than by environmental autocorrelation or life-history trade-offs. Positive serial correlations could be produced by longer-term density feedback (i.e., as density slowly increases, a downward trend in a vital rate would produce above-average values in early years and below-average values in later years, making adjacent deviations from the mean more similar than expected at random). Another future challenge is to assess fitness impacts of demographic variability accounting for density-dependent feedback.