Abstract
A counterintuitive and theoretically important pattern of results in the visual word recognition literature is that both word frequency and stimulus quality produce large, but additive effects in lexical decision performance. The additive nature of these effects has recently been called into question by Masson and Kliegl (2012), who used linear mixed effects modeling to provide evidence that the additive effects were actually being driven by previous trial history. Because Masson and Kliegl also included semantic priming as a factor in their study and there is recent evidence that semantic priming can moderate the additivity of word frequency and stimulus quality (Scaltritti, Balota, & Peressotti, 2012), we re-analyzed data from three published studies to determine if previous trial history moderated the additive pattern when semantic priming was not also manipulated. The results indicated that previous trial history did not influence the joint influence of word frequency and stimulus quality. Importantly, and independent of the Masson and Kliegl conclusions, we also show how a common transformation used in linear mixed effects analyses to normalize the residuals can systematically alter the way in which two variables combine to influence performance. Specifically, using transformed, compared to raw reaction times, consistently produces more underadditive patterns.
A common approach in experimental psychology is to investigate the joint influence of two or more independent variables on some dependent measure. When two variables are manipulated, researchers are interested in whether there is an interaction between the two variables or whether the two variables produce additive effects, i.e., two main effects, but no evidence of an interaction. This latter pattern initially received considerable interest in studies of mental chronometry, because Sternberg (1969) argued that additivity may suggest independent stages of processing, wherein the two factors influence separate stages. Although there are some limitations to the strong inferences that Sternberg drew from additive effects (e.g., McClelland 1979), there are also compelling reasons why some patterns of additivity in response latency data are most consistent with distinct stages (see for example, Roberts & Sternberg, 1993; Yap & Balota, 2007).
The nature in which variables produce additive or interactive effects in response latency data has been a central focus in a number of studies in visual word recognition (e.g., Borowsky & Besner, 1993; O’Malley, Reynolds, & Besner, 2007; Scaltritti, Balota, and Peressotti, 2012; Yap & Balota, 2007). This interest has been nurtured by the intriguing conundrum regarding the pattern of effects produced by semantic priming, word frequency, and stimulus quality. The conundrum is as follows: Semantic priming interacts with both word frequency and stimulus quality, but word frequency and stimulus quality have repeatedly been shown to produce additive effects. This pattern has been interpreted as suggesting there are at least two separable stages, an early stage that is influenced by both stimulus quality and semantic priming and a later lexical stage that is influenced by word frequency and semantic priming. Although there have been attempts to interpret these effects within a single-process model (see Plaut & Booth, 2000), the full pattern of results remains problematic for such attempts (see Borowsky & Besner, 2006 and reply by Plaut & Booth, 2006; see also Yap, Tse, & Balota, 2009).
The present research focuses on the additive effects of frequency and stimulus quality. As noted, this simple additive pattern appears to support serially organized stages and is challenging for the currently most successful models of visual word recognition, where there is a heavy reliance on interactive activation mechanisms (e.g., McClelland & Rumelhart, 1981). Such interactive activation mechanisms are central to the dual-route cascaded (DRC) model (Coltheart, Rastle, Perry, Langdon, Ziegler, 2001) and the connectionist dual process (CDP+) model (e.g., Perry, Ziegler, & Zorzi, 2007). The most straightforward prediction from the interactive activation framework is that the word frequency effect should be larger for visually degraded input compared to clear input, since the slower uptake of featural letter information should have more of an influence for representations that are further from threshold, i.e., low-frequency words. As noted, however, the effect of word frequency is of the same size for words presented in clear fashion and words that are visually degraded in some manner. This pattern was originally reported by Stanners, Jastrzembski, and Westbrook (1975), and has been replicated many times. Independent of the interactive activation framework, it is indeed counterintuitive that the influence of stimulus quality would be comparable for uncommon low frequency words (e.g., SILO) and common high-frequency words (FARM).
Although the additive effects of word frequency and stimulus quality on lexical decision performance have been replicated many times, the basic counterintuitive pattern, and the high degree of interactivity in the lexical processing architecture suggests that there may be an alternative interpretation underlying this pattern. Recently, Masson and Kliegl (2012) have reported a study which suggests that this is indeed the case. They reported two experiments which not only bring into question the additive effects of stimulus quality and word frequency but the manner in which one makes inferences regarding additive and interactive effects from standard factorial ANOVA designs. Because of the importance of this contribution, we attempted to explore their approach in greater depth.
Masson and Kliegl (2012) argued that in order to fully interpret the influence of different variables on a given trial, one must also consider the effects of trial history within an experimental design. Indeed, there is accumulating evidence indicating that the response latencies on previous trials within a standard reaction time study can influence the pattern obtained (see Lupker, Kinoshita, Coltheart & Taylor, 2003; Kinoshita, Forster & Mozer, 2008). Specifically, it is possible that the apparent additive effects observed in the reaction time data actually reflect tradeoffs between previous trial history and the nature of the current trial. Hence, it is important to consider trial history in order to directly demonstrate truly additive effects. Masson and Kliegl’s approach reflects a recent movement in psycholinguistics, and other domains, of conducting linear mixed-effects modeling (LME; Baayen, Davidson, & Bates, 2008), which allows by-subjects and by-items effects to be explored within the same analysis.
Masson and Kliegl (2012) reported two lexical decision experiments that factorially crossed semantic priming, stimulus quality, and word frequency to further examine the joint effects of stimulus quality and word frequency. The results from their first experiment yielded an interaction amongst previous trial stimulus quality, current trial stimulus quality, and word frequency. When this interaction was further examined, they reported a significant underadditive interaction when the previous trial was clear, but a non-significant overadditive interaction when the previous trial was degraded. Hence, the stimulus quality by word frequency interactions moved in opposite directions as a function of previous trial stimulus quality. When one collapses across previous trial history, (spuriously) additive effects of stimulus quality and word frequency are yielded. In their second experiment, Masson and Kliegl manipulated stimulus quality between different blocks of trials, and so could not examine the interaction of previous trial stimulus quality and current trial stimulus quality and word frequency. However, Masson and Kliegl did obtain via the LME a reliable four-way interaction amongst previous trial lexicality, current trial stimulus quality, word frequency, and semantic priming. Based on this complex interaction, they argued that the joint effects of stimulus quality and word frequency are modulated by previous trial lexicality and semantic priming, which again calls into question the presumed additive effects of these two variables.
Masson and Kliegl (2012) interpreted their results as suggesting that the additive effects that have been observed in the past studies are confounded by trial history effects, and so do not truly reflect additive effects. Consequently, such additivity does not pose a serious problem for interactive activation or parallel distributed processing perspectives. They correctly note that one needs to be cautious in interpreting additive effects, when previous trial history is not taken into account. This is a critical observation that does not merely have relevance to the effects of stimulus quality and word frequency but also to extensions of the interpretation of how multiple variables combine to influence performance in any study. Although Masson and Kliegl did not strongly endorse a particular theoretical perspective, they believe their results are most consistent with a dynamic continuous function relating input and output, similar to the nonlinear function described by Plaut and Booth (2000). This framework can handle interactive or additive effects depending on where one is on the input output function. According to Masson and Kliegl, it is also possible that the previous trial may influence where one is on the input output function on the current trial, and hence, one needs to take into consideration previous trial history when interpreting interactive or additive effects. In addition, Masson and Kliegl also point out that their results are consistent with the Adaptation to the Statistics of the Environment (ASE) model developed by Kinoshita et al. (2008; 2011), based on a Bayesian framework in which participants take advantage of trial history. Clearly, these perspectives are inconsistent with any notion that the purported additive effects of word frequency and stimulus quality provide evidence in support of separable processing stages in visual word recognition.
In the present study, we address two issues: First, there were aspects of Masson and Kliegl’s design which may limit the generalizability of their findings to the many studies in the literature that have replicated the additive effects of stimulus quality and word frequency. Second, in the course of reanalyzing data from our previous studies, we uncovered a concern in which a standard procedure of transforming data in LME modeling can influence the pattern of results obtained via the analyses. Specifically, in such analyses, one often transforms the individual subject RT data so that the residuals are more normally distributed. This rescaling of raw reaction time can actually influence the pattern of results when examining multiple variables. Although such transformations do not appear to be a critical factor influencing the results in the Masson and Kliegl study, it is clear that the data transformation has a clear and systematic influence in the present reanalyses. We now discuss each of these issues in turn.
Semantic Priming and the Additive Effects of Word Frequency and Stimulus Quality
Masson and Kliegl (2012) not only manipulated word frequency and stimulus quality in their study, but also included a third factor, semantic priming. This indeed is quite reasonable given the original conundrum described earlier regarding the complex pattern of interactivity and additivity amongst the three variables. However, it has recently become clear that the additive effects of word frequency and stimulus quality can be modulated by the presence of semantically related primes within the experimental context. Specifically, Scaltritti et al. (2012) have shown that one obtains additive effects of word frequency and stimulus quality only following related primes, when semantic priming is manipulated within the experiment (also see Borowsky & Besner, 1993). They argued that the presence of semantically related primes induces a list wide retrospective checking process which has its greatest influence on the most difficult low-frequency words presented in a degraded fashion. When a match is found between this checking process and a related prime, one finds additivity, however, when no match is found, the low-frequency degraded words are especially compromised, leading to the overadditive interaction. Critically, in a second experiment, Scaltritti et al. eliminated the semantically related primes, thus including only unrelated primes, and found that the overadditive interaction in the presence of related primes reverted back to additivity when those primes were removed. Indeed, the list wide retrospective checking process is consistent with recent arguments by Balota et al. (2008), Thomas, Neely, and O’Connor (2012), and Yap, Balota, and Tan (2012) in studies examining stimulus degradation and semantic priming. The analyses provided by Masson and Kliegl actually provide some support for the influence of semantic priming in their study. In both experiments, there was evidence of higher order interactions when semantic priming was included in the analyses. Thus, because of the theoretical importance of additive effects of stimulus quality and word frequency, and the Scaltritti et al. results, it is important to directly address whether the additive effects hold up in LME when only word frequency and stimulus quality are manipulated, without semantic priming.
In order to directly address this issue, we present re-analyses of three recently published studies that have directly addressed the influence of word frequency and stimulus quality in lexical decision performance. The first study (Yap & Balota, 2007) involved a between participants manipulation of stimulus quality, along with a within participants manipulation of word frequency. This replicated the original study by Stanners et al. (1977) demonstrating additive effects of the two variables in a between participants manipulation. The second study included a within participants manipulation of both frequency and stimulus quality with pronounceable nonwords (e.g., FLIRP, Yap et al., 2008, Experiment 1), while the third study included a within participants manipulation of both variables with pseudohomophones (e.g., BRANE, Yap et al., 2008, Experiment 2). To preview our results, none of the studies demonstrate that the previous trial moderates the additive effects of word frequency and stimulus quality.
The Influence of Transformations on Additive and Interactive Effects
The second issue that we explore in the present study is the influence of transforming response time data. This issue has a rich history in mental chronometry (see Baayen & Milin, 2010, Kliegl, Masson, & Richter, 2010; Rouder et al. 2008, for thorough discussions of the issue). With the advent of LME modeling, there has been an increased emphasis on transforming raw RT data in order to produce residuals that are more normally distributed. Because the target of LME is trial level data, and because RT distributions are almost always positively skewed, researchers have applied transformations to normalize the data. For example, Masson and Kliegl (2012) used the reciprocal transformation (i.e., −1/RT), which is commonly used in word recognition research (e.g. Andrews & Lo, 2012; Kinoshita, Mozer & Forster, 2011), although the logarithmic transformation is also used (see Baayen et al., 2008). Indeed, based on the Box-Cox procedure (Box & Cox, 1964), the reciprocal transformation most closely approximated normality in all of our re-analyses presented below.
In our LME reanalyses of previous studies to examine trial history effects (see below), we consistently observe a tendency towards underadditivity in the influence of stimulus quality and word frequency when the inverse transformation is used, but not when the raw RTs are analyzed. As discussed later, this is a natural consequence of the slower conditions in the design matrix being more influenced by the inverse RT condition than the remaining faster conditions. We should emphasize here that this observation does not appear to be a major problem with the Masson and Kliegl conclusions because they note in their Footnote 1: “ We repeated the LMM analyses reported below using response time instead of the reciprocal transformation and found essentially the same results. This was true for both Experiment 1 and Experiment 2. A few interactions that were significant with the reciprocal measure were not significant in the response time analysis, probably because of lower statistical power due to heterogeneity of residuals.” Therefore, it is important to consider this second observation about reaction time transformations as independent of the Kliegl and Masson study per se.
Overview of the Experiments
As noted, the goal of the present study is to examine if the additive effects of word frequency and stimulus quality persist when one conducts LME analyses to examine trial history and semantic priming is not included in the design. We examine three published studies that only manipulated stimulus quality and word frequency, and obtained large effects of both variables, but no hint of an interaction in the standard ANOVAs. All experiments were conducted at Washington University in St. Louis. Because RT distributional analyses were conducted, each experiment included a large number of observations per participant cell, which we briefly describe here, but full details are available in the published reports.
Yap and Balota (2007) included a between participant manipulation of stimulus quality, with 100 HF words and 100 LF words randomly interspersed within a lexical decision task with 200 pronounceable nonwords. Thirty seven individuals were in the clear condition and 35 were in the degraded condition. Yap, Balota, Tse and Besner (2008, Experiment 1) included a within participants manipulation of stimulus quality with each participant receiving 50 words in each of the four cells produced by crossing frequency and stimulus quality, along with 200 pronounceable nonwords (e.g., FLIRP). Yap, et al. (2008, Experiment 2) included the same stimuli used in Experiment 1, but now included 200 pseudohomophones (e.g., BRANE).
Results
The data were analyzed using Proc Mixed in SAS version 9.3. The data were trimmed in the same fashion as the original studies. Specifically, RTs on error trials, as well as any latency faster than 200 ms or slower than 3000 ms were initially removed. Of the remaining trials, any latency that was 2.5 standard deviations away from the individual mean was also removed.1 The data were then submitted to a LME analyses with subject and items treated as crossed random effects (Baayen et al. 2008, Quené & van den Bergh 2008). For the Yap and Balota (2007) data set, stimulus quality, word frequency, previous trial lexicality and all the two- and three-way interactions were included as fixed effects. Since stimulus quality was manipulated between subjects, the effect of previous trial quality could not be assessed. For the Yap et al. (2008) datasets, stimulus quality was a within subjects factor, and hence, previous trial quality was also included as a fixed effect in addition to all the remaining interactions.2 Analyses were conducted on both the raw reaction times as well as the reciprocal transformation (−1000/ RT).
The results of the LME analyses of each experiment are displayed in Table 1–3. In the left half of each Table, the analyses are displayed for the raw RT data, and in the right half of each table the data are displayed for the inverse transformed data. Of course, the critical aspects of these analyses are (a) the additive effects of frequency and stimulus quality in the raw and transformed data, and (b) if these additive effects of frequency and stimulus quality are modified when previous trial effects are added into the LME analyses.
Table 1.
Linear Mixed effects Analyses for Yap and Balota (2007)
| Untransformed RTs | Transformed RTs |
|||
|---|---|---|---|---|
| Fixed Effects | F | p-value | F | p-value |
| Stimulus Quality (Q) | 33.24 | <.0001 | 35.03 | <.0001 |
| Frequency (F) | 73.87 | <.0001 | 97.03 | <.0001 |
| Previous Lexicality (PL) | 81.63 | <.0001 | 186.07 | <.0001 |
| Q*F | .37 | .5454 | 17.3 | <.0001 |
| Q*PL | .51 | .4768 | 6.68 | .0098 |
| F*PL | 3.61 | .0573 | 9.6 | .0019 |
| Q*F*PL | .32 | .5686 | .52 | .4708 |
| Random Effects | Estimate | St Error | Estimate | St Error |
| Subject | 10634 | 1823.43 | .0519 | .0089 |
| Item | 1649.65 | 213.34 | .0079 | .0009 |
| Residual | 27534 | 345.22 | .089 | .0011 |
Table 3.
Linear Mixed Effects Analyses for Yap et al. (2008, Experiment 2)
| Untransformed RTs | Transformed RTs |
|||
|---|---|---|---|---|
| Fixed Effects | F | p-value | F | p-value |
| Stimulus Quality (Q) | 739.71 | <.0001 | 1121.5 | <.0001 |
| Frequency (F) | 31.52 | <.0001 | 34.55 | <.0001 |
| Previous Lexicality (PL) | 88.25 | <.0001 | 189.28 | <.0001 |
| Previous Quality (PQ) | 4.06 | .044 | 5.58 | .0181 |
| Q*F | 0 | .9818 | 3.94 | .0471 |
| Q*PL | .38 | .5381 | 4.78 | .0288 |
| Q*PQ | 2.15 | .1424 | 5.22 | .0224 |
| F*PL | .21 | .6495 | .38 | .5366 |
| F*PQ | 0 | .9925 | .01 | .9117 |
| PL*PQ | 0 | .9511 | 3.86 | .0494 |
| Q*F*PL | 1.58 | .2095 | .39 | .5306 |
| Q*F*PQ | .16 | .6934 | 1.21 | .2713 |
| F*PL*PQ | .26 | .6093 | .89 | .3457 |
| Q*PL*PQ | 14.71 | .0001 | 35.44 | <.0001 |
| Q*F*PL*PQ | .03 | .8722 | .07 | .7843 |
| Random Effects | Estimate | St Error | Estimate | St Error |
| Subject | 11503 | 2236 | .0369 | .0071 |
| Item | 3266.46 | 445.97 | .0124 | .0016 |
| Residual | 40352 | 573.16 | .1038 | .0015 |
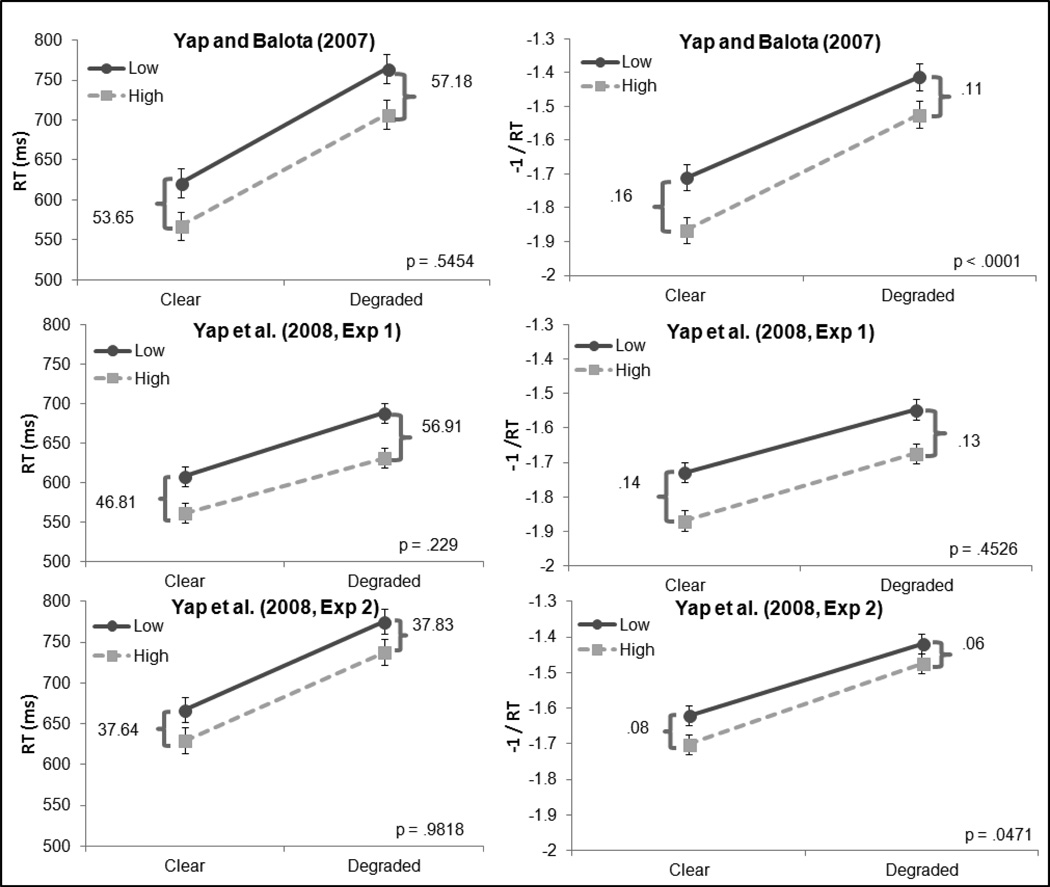
First, consider the analyses of the Yap and Balota (2007) study with the between participants manipulation of stimulus quality. As shown in the analyses of the raw RT data, there is clear additivity of stimulus quality and word frequency, as reported in the original paper. Importantly, these two variables do not interact in higher order interactions with previous trial history in the LME analyses. Interestingly, turning to the inverse transformed data, there is actually an underadditive interaction between stimulus quality and frequency, which, as argued below, is likely due to the data transformation. Importantly, this interactive effect is again not modulated by the inclusion of previous trial history.
The differing patterns of SQ and Frequency in the inverse transformed and untransformed data are displayed in the top panel of Figure 1. As shown here, the interaction indicates that transforming the additive effects in the raw data actually leads to an underadditive interaction, i.e., low frequency words are less disrupted by stimulus quality than high frequency words. As discussed below, we believe that this is a predictable effect in that the slow RTs (for degraded low-frequency words) are more influenced by the transformation than the fast RTs and hence the tail of the RT distribution is diminished for this condition. Thus, an additive effect in the raw response latencies becomes underadditive once the data is transformed.
Figure 1.
Mean performance as a function of stimulus quality and word frequency from Yap and Balota (2007, top panel), Yap et al. (2008, Experiment 1, middle panel) and Yap et al. (2008, Experiment 2, bottom panel). The untransformed data are presented on the left and inverse transformed data on the right. The p-value represents the test of the interaction.
Turning to the Yap et al. (2008, Experiment 1), with pronounceable nonwords, the results from the LME analyses are shown in Table 2. In this study, there is again clear additivity in the untransformed data which does not interact with previous trial history. The additive pattern also occurs in the inverse transformed data and again is not influenced by previous trial history. However, as shown in middle panel of Figure 1, there is evidence that there is again a tendency toward underadditivity in the inverse transformed data. Specifically, the hint of an overadditive interaction in the raw reaction time data becomes slightly underadditive in the transformed data, but neither of these produced reliable interactions.
Table 2.
Linear Mixed Effects Analyses for Yap et al. (2008, Experiment 1)
| Untransformed RTs | Transformed RTs |
|||
|---|---|---|---|---|
| Fixed Effects | F | p-value | F | p-value |
| Stimulus Quality (Q) | 320.56 | <.0001 | 447.79 | <.0001 |
| Frequency (F) | 59.66 | <.0001 | 76.07 | <.0001 |
| Previous Lexicality (PL) | 31.65 | <.0001 | 66.92 | <.0001 |
| Previous Quality (PQ) | 5.38 | .0204 | 4.44 | .0351 |
| Q*F | 1.45 | .229 | .56 | .4526 |
| Q*PL | 0 | .9481 | .35 | .5551 |
| Q*PQ | .25 | .62 | .26 | .6118 |
| F*PL | .02 | .8948 | 1.05 | .3061 |
| F*PQ | .43 | .5101 | .03 | .8634 |
| PL*PQ | 1.23 | .2668 | .4 | .5247 |
| Q*F*PL | .71 | .3979 | 1.35 | .2455 |
| Q*F*PQ | 1.15 | .2828 | 1.9 | .1682 |
| F*PL*PQ | .07 | .7846 | .22 | .636 |
| Q*PL*PQ | 26.2 | <.0001 | 29.36 | <.0001 |
| Q*F*PL*PQ | .15 | .6977 | .03 | .854 |
| Random Effects | Estimate | St Error | Estimate | St Error |
| Subject | 3581.07 | 1007.91 | .0207 | .0058 |
| Item | 1369.37 | 232.98 | .0079 | .0012 |
| Residual | 22560 | 455.94 | .1019 | .0021 |
The results from the LME analyses of the Yap et al. (2008) study, with the pseudohomophones, are shown in Table 3. The results again indicate that there are additive effects in the raw RTs, which were not influenced by previous trial history. Interestingly, as in the analysis of the Yap and Balota (2007, Experiment 1) data indicated, one again finds a reliable interaction between frequency and stimulus quality in the transformed data. This interactive pattern is displayed in the bottom panel of Figure 1. Again, the same pattern is found. Specifically, the inverse transformed data produced a reliable underadditive interaction, whereas the analysis of the raw data produced the expected additivity. Importantly, there is no hint of an interaction with previous trial history.
Summary
The results from the analyses of three previous published studies that have manipulated word frequency and stimulus quality are quite clear. First, regarding the relevance to the Masson and Kliegl study, there is no evidence that previous trial history influences either the raw RT effects or the inverse transformed RT effects. Second, regarding the influence of the inverse data transformation, there is consistent evidence of additive effects of frequency and stimulus quality in the raw RTs, which becomes more underadditive in the transformed data.
Before discussing the implications of these results, we now turn to the influence of lexicality (word vs. nonword) and stimulus quality in the same three studies. Our goal here is to determine if the tendency towards a more underadditive pattern when the data are transformed extends beyond word frequency and stimulus quality.
Lexicality and Stimulus Quality: Further Examination of the Effect of the inverse RT Transformation
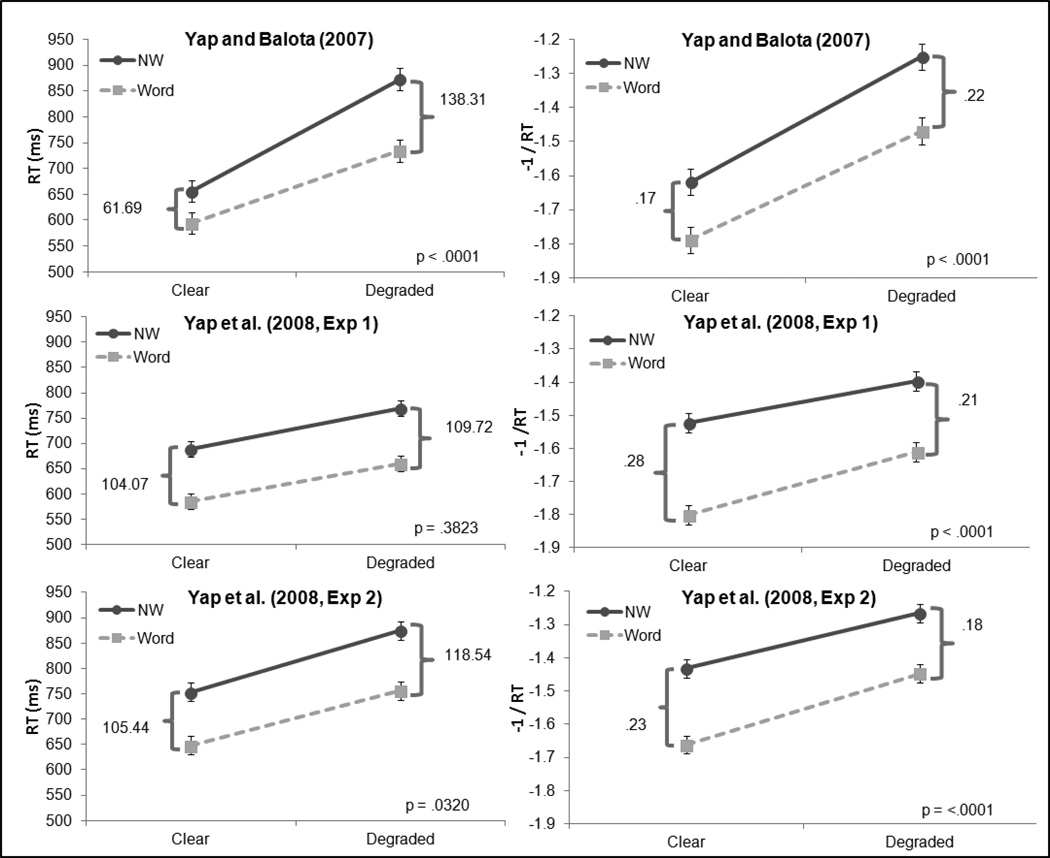
Figure 2 displays the untransformed and inverse transformed data for lexicality and stimulus quality, in the same manner that word frequency and stimulus quality were displayed in Figure 1. As shown in the top panel of Figure 2, the results from Yap and Balota (2007) produced a larger overadditive interaction between lexicality and stimulus quality in the untransformed data. Specifically, the effect of lexicality was two times as large in the degraded condition compared to the clear condition when one considers the raw RTs. However, in the transformed data, the effect of lexicality is only 1.2 times larger in the degraded condition compared to the clear condition.
Figure 2.
Mean performance as a function of stimulus quality and lexicality from Yap and Balota (2007, top panel), Yap et al. (2008, Experiment 1, middle panel), and Yap et al. (2008, Experiment 2, bottom panel). The untransformed data are presented on the left and the inverse transformed data on the right. Thep-value represents the test of the interaction.
The results from Yap et al. (2008) with pronounceable nonwords are displayed in the middle panel. Here one can see that there is evidence of additive effects of lexicality and stimulus quality in the untransformed data. However, in the transformed data, there is a highly reliable underadditive interaction, indicating that for degraded stimuli, there is a smaller effect of lexicality than for clear stimuli.
The results from the Yap et al. (2008) study with pseudohomophones are displayed in the bottom panel. Here one can see a reliable, albeit small, overadditive effect of lexicality and stimulus quality in the raw RT data. Importantly, in the transformed data, one finds a highly reliable underadditive interaction of lexicality and stimulus quality. Hence, the very nature of the interaction reverses.
In summary, across the three experiments examining stimulus quality and lexicality, one again finds a consistent pattern towards more underadditive interactions in the inverse transformed data than in the raw data. This is exemplified by (a) a highly significant overadditive interaction in the untransformed data that becomes more additive in the transformed data; (b) an additive pattern in the untransformed data becomes highly underadditive, and (c) a small overadditive interaction in the untransformed data becomes underadditive. Clearly, these results converge on the analyses from the influence of word frequency and stimulus quality indicating that there is a greater reduction in the slowest condition than the remaining conditions in the inverse transformed data compared to the untransformed data.
General Discussion
The present set of analyses were initially motivated by an important observation by Masson and Kliegl (2012) indicating that the apparent additive effects of word frequency and stimulus quality do not reflect true additivity but more likely reflect subtle trial history effects that are best uncovered by LME analyses. Because of the importance of the consistent additive effects of these two variables for extant models, we further explored this pattern using data from three published experiments. We were motivated to further explore the Masson and Kliegl results because of there is now evidence that the presence of semantic primes (which were included in the Masson & Kliegl study) actually induces a list wide retrospective checking process that indeed can moderate the presence of additive or interactive effects of word frequency and stimulus quality (Scaltritti et al., 2012, see also Borowsky & Besner, 1993). Of course, because the Scaltritti et al. and the Masson and Kliegl studies were under review at the same time, there was no way for Masson and Kliegl to have known about the Scaltritti et al. (2012) results. The present re-analyses of three previously published experiments indicate that additive effects of frequency and stimulus quality do not interact with previous trial history when semantic priming is not included in the study. O’Malley and Besner (2013) have recently come to the same conclusion from a reanalysis of a previous speeded pronunciation study that only manipulated word frequency and stimulus quality.
The observation that the effects of frequency and stimulus quality are not moderated by previous trial history further points to the robustness of the additive effects of these two variables in visual word recognition. As noted earlier, models that incorporate interactive activation mechanisms (e.g., Coltheart et al., 2001; Perry, Ziegler, & Zorzi, 2007) and connectionist principles (e.g., Plaut & Booth, 2000) cannot easily, if at all, accommodate these additive effects. These results appear to be most compatible at present with serially organized stages. For example, one way to account for these effects is that there is an early normalization process which cleans up the stimulus, which is followed by a second stage that involves lexical access. The second lexical access process is where word frequency modulates performance (see Yap & Balota, 2007). It is indeed interesting that the original Sternberg (1969) additive effects of set size and stimulus quality also involved a binary decision task and a hypothesized initial normalization (clean up) stage before memory search.
In pursuing these analyses, we also observed a consistent influence of using a standard inverse transformation of raw reaction data3. Because LME analyses directly address subject by item level data, one needs to insure that the residuals are normally distributed. Since RT distributions at the subject level are almost always highly skewed, one often transforms the data to normalize the residuals for the mixed effects analyses. However, by doing this, one is losing potentially important aspects of the RT distribution. For example, there is now evidence that some variables can have isolated effects on different components of the RT distribution, e.g., semantic priming has been shown to shift the RT distribution (see Balota et al., 2008), whereas, word frequency both shifts and increases the skew (e.g., see Yap & Balota, 2007). Moreover, there are important models of performance in reaction time tasks, which capitalize on the shape of the underlying RT distribution (e.g., Ratcliff, 1978, diffusion model). By transforming the skewed RT distribution in order to normalize the residuals, one may be obscuring important aspects of that distribution.
Importantly, the influence of the inverse transformation was quite powerful in the present results at the factor level. When examining the joint effects of word frequency and stimulus quality, additive patterns in the raw data consistently became more underadditive in the inverse transformed data. Turning to the joint effects of lexicality and stimulus quality, the pattern was also quite consistent. Specifically, the slowest condition in the inverse transformed data was relatively more influenced by the transformation than the remaining three conditions. This resulted in large overadditive interactions becoming less overadditive, additive effects becoming underadditive, and small overadditive interactions becoming highly underadditive.
Why would one expect a tendency towards underadditivity when transforming raw RT data? This naturally follows from the influence of the transformation at different levels of the scale. Specifically, the difference between inverse transformations becomes smaller at longer reaction times. Consider the simplest example, in which one observes additive effects of Factors A and B with the following means: A1B1 = 500 ms, A2B1 = 600 ms, Factor A1B2 = 600 ms and A2B2 = 700 ms. Here one can see main effects of 100 ms for both Factors A and B with no evidence of an interaction. However, if one now considers the inverse transformed data, one now has the following means: A1B1 = −2, A2B1 = −1.67, A1B2 = −1.67, and A2B2 = −1.43. Now an underadditive interaction emerges where the effect of Factor B is smaller for the slower level in Factor A (−1.67 + 1.43 = .24) than for the faster level in Factor A (−2.00 + 1.67 = .33). Clearly, such transformations will be biased towards decreasing the difference in the slower conditions of the untransformed data.
It is worth noting that the tendency towards underadditivity is also difficult to reconcile with the predictions from extant interactive activation models. For example, consider the influence of stimulus quality and word frequency, within a simple interactive activation framework. One would assume a priori that stimulus quality would influence the rate of accumulation of featural information per unit of time, whereas, word frequency should influence the thresholds (or resting activations) for recognition of a lexical representation. For example, if the rate of accumulation of features is 30 per time unit for clear stimuli and 20 per time unit for degraded stimuli, and high-frequency words have a threshold of 90 and low-frequency words have a threshold of 120, then one should expect the influence of stimulus quality to be larger for low-frequency words (2 time units) than high frequency words (1.5 time units). Thus, the obvious predictions from the interactive activation model would be an overadditive interaction (Reynolds & Besner, 2004, come to the same conclusion from interactive activation simulations). The observation that one finds the opposite underadditive pattern with inverse transformed data further brings into question the influence of the transformation.
The influence of data transformations on the pattern of additive and interactive effects is also quite important when considering the non-linear input output function developed by Plaut and Booth (2000). Specifically, Plaut and Booth argued that one can find underadditive, additive, or overadditive patterns, depending upon where one is on this function. This is an important theoretical observation. However, given the influence of the data transformation on producing a tendency towards underadditivity, one would need to be careful to consider whether the transformation is placing individuals at different points along the input-output function or whether this reflects the actual input-output function of the model.
Finally, one may argue that the inverse transformation may reflect processing speed and this is indeed a better metric than raw reaction time when considering the influence of variables. Even if this were the case, one would need a principled argument regarding the different patterns in raw RT data vs transformed data. Importantly, as mentioned earlier there are extant models that rely on the underlying RT distributions (e.g., Ratcliff’s, 1978, diffusion model), and by transforming the data one will lose important constraints for such models.
In summary, Masson and Kliegl (2012) is an important paper that uses LME analyses to examine the joint effects of word frequency, stimulus quality, and semantic priming. Indeed, there are a number of aspects of this paper which are important contributions to the literature, and this is the first study which has examined all three variables with LME analyses. Here we focused on the simple observation that the additive influence of word frequency and stimulus quality are a reflection of trial history. The present results provide no support for the argument that trial history influences the joint effects of word frequency and stimulus quality when semantic priming is not included as a factor. In this light, the present study further points to the robustness of the additive effects of these two variables, and the important theoretical ramifications noted earlier. Moreover, although we are sympathetic to the goals of LME analyses, we also provided evidence suggesting that inverse transformations of raw reaction time data to normalize the residuals in LME analyses can have quite dramatic effects on the pattern of means. Hence, we believe that at the very least, one needs to explore both the raw data and the transformed data when making inferences about how variables combine to influence performance.
Acknowledgements
This work was supported by NIA T32 AG000030-32, NIA PO1 AG03881, and NIA PO1 AGO26276. We thank Sachiko Kinoshita, Michael Masson, and Dennis Norris for helpful comments on an earlier version of this manuscript.
Footnotes
The following manuscript is the final accepted manuscript. It has not been subjected to the final copyediting, fact-checking, and proofreading required for formal publication. It is not the definitive, publisher-authenticated version. The American Psychological Association and its Council of Editors disclaim any responsibility or liabilities for errors or omissions of this manuscript version, any version derived from this manuscript by NIH, or other third parties. The published version is available at www.apa.org/pubs/journals/xlm
Because Kliegl and Masson used a relatively liberal screening in their study (only screened approximately .5% of RT observations, we also explored the possibility that differences in screening could have lead to the differences in results. Thus, we trimmed at 3 seconds (which eliminated overall .4% of the RTs), and still found no evidence that previous trial history modulated the additive effects of stimulus quality and word frequency.
We also explored a variety of random effect structures in these analyses, and again, the previous trial history did not modulate the additive effects of stimulus quality and word frequency in these analyses.
We also examined the log transform of the raw RT data, and as expected, a similar tendency towards underadditivity was observed.
Contributor Information
David A. Balota, Washington University in St. Louis
Andrew J. Aschenbrenner, Washington University in St. Louis
Melvin J. Yap, National University of Singapore
References
- Andrews S, Lo S. Not all skilled readers have cracked the code: Individual differences in masked form priming. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2012;38(1):152–163. doi: 10.1037/a0024953. [DOI] [PubMed] [Google Scholar]
- Baayen RH, Davidson DJ, Bates DM. Mixed-effects modeling with crossed random effects for subjects and items. Journal of Memory and Language. 2008;59(4):390–412. [Google Scholar]
- Baayen RH, Milin P. Analyzing reaction times. International Journal of Psychological Research. 2010;3(2):12–28. [Google Scholar]
- Balota DA, Yap MJ. Moving beyond the mean in studies of mental chronometry: The power of response time distributional analyses. Current Directions in Psychological Science. 2011;20(3):160–166. [Google Scholar]
- Balota DA, Yap MJ, Cortese MJ, Watson JM. Beyond mean response latency: Response time distributional analyses of semantic priming. Journal of Memory and Language. 2008;59(4):495–523. [Google Scholar]
- Borowsky R, Besner D. Visual word recognition: A multistage activation model. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1993;19(4):813–840. doi: 10.1037//0278-7393.19.4.813. [DOI] [PubMed] [Google Scholar]
- Borowsky R, Besner D. Parallel distributed processing and lexical-semantic effects in visual word recognition: Are a few stages necessary? Psychological Review. 2006;113(1):181–193. doi: 10.1037/0033-295X.113.1.181. [DOI] [PubMed] [Google Scholar]
- Box GEP, Cox DR. An analysis of transformations. Journal of the Royal Statistical Society, Series B (Methodological) 1964;26:211–252. [Google Scholar]
- Coltheart M, Rastle K, Perry C, Langdon R, Ziegler J. DRC: A dual route cascaded model of visual word recognition and reading aloud. Psychological Review. 2001;108(1):204–256. doi: 10.1037/0033-295x.108.1.204. [DOI] [PubMed] [Google Scholar]
- Heathcote A, Popiel SJ, Mewhort DJ. Analysis of response time distributions: An example using the Stroop task. Psychological Bulletin. 1991;109:340–347/. [Google Scholar]
- Kinoshita S, Forster KI, Mozer MC. Unconscious cognition isn’t that smart: Modulation of masked repetition priming effect in the word naming task. Cognition. 2008;107(2):623–649. doi: 10.1016/j.cognition.2007.11.011. [DOI] [PubMed] [Google Scholar]
- Kinoshita S, Mozer MC, Forster KI. Dynamic adaptation to history of trial difficulty explains the effect of congruency proportion on masked priming. Journal of Experimental Psychology: General. 2011;140(4):622–636. doi: 10.1037/a0024230. [DOI] [PubMed] [Google Scholar]
- Kliegl R, Masson MEJ, Richter EM. A linear mixed model analysis of masked repetition priming. Visual Cognition. 2010;18(5):655–681. [Google Scholar]
- Luce RD. Response times: Their role in inferring elementary mental organization. 1986 [Google Scholar]
- Lupker SJ, Kinoshita S, Coltheart M, Taylor TE. Mixing costs and mixing benefits in naming words, pictures, and sums. Journal of Memory and Language. 2003;49(4):556–575. [Google Scholar]
- Masson MEJ, Kliegl R. Modulation of additive and interactive effects in lexical decision by trial history. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2012 doi: 10.1037/a0029180. in press. [DOI] [PubMed] [Google Scholar]
- McClelland JL. On the time relations of mental processes: An examination of systems of processes in cascade. Psychological Review. 1979;86(4):287–330. [Google Scholar]
- McClelland JL, Rumelhart DE. An interactive activation model of context effects in letter perception: I. An account of basic findings. Psychological Review. 1981;88(5):375–407. [PubMed] [Google Scholar]
- O'Malley S, Besner D. Reading aloud: Does previous trial history modulate the joint effects of stimulus quality and word frequency? Journal of Experimental Psychology: Learning, Memory & Cognition. 2013 doi: 10.1037/a0031673. in press. [DOI] [PubMed] [Google Scholar]
- O’Malley S, Reynolds MG, Besner D. Qualitative differences between the joint effects of stimulus quality and word frequency in reading aloud and lexical decision: Extensions to Yap and Balota (2007) Journal of Experimental Psychology: Learning, Memory, and Cognition. 2007;33(2):451–458. doi: 10.1037/0278-7393.33.2.451. [DOI] [PubMed] [Google Scholar]
- Perry C, Ziegler JC, Zorzi M. Nested incremental modeling in the development of computational theories: The CDP+ model of reading aloud. Psychological Review. 2007;114(2):273–315. doi: 10.1037/0033-295X.114.2.273. [DOI] [PubMed] [Google Scholar]
- Plaut DC, Booth JR. Individual and developmental differences in semantic priming: Empirical and computational support for a single-mechanism account of lexical processing. Psychological Review. 2000;107(4):786–823. doi: 10.1037/0033-295x.107.4.786. [DOI] [PubMed] [Google Scholar]
- Plaut DC, Booth JR. More modeling but still no stages: Reply to Borowsky and Besner. Psychological Review. 2006;113(1):196–200. [Google Scholar]
- Quené H, van den Bergh H. Examples of mixed-effects modeling with crossed random effects and with binomial data. Journal of Memory and Language. 2008;59(4):413–425. [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychological Review. 1978;85:59–108. [Google Scholar]
- Roberts S, Sternberg S. The meaning of additive reaction-time effects: Tests of three alternatives. In: Meyer DE, Kornblum S, editors. Attention and performance XIV: Synergies in experimental psychology, artificial intelligence, and cognitive neuroscience. Cambridge, MA: MIT Press; 1993. pp. 611–653. [Google Scholar]
- Rouder JN, Tuerlinckx F, Speckman P, Lu J, Gomez P. A hierarchical approach for fitting curves to response time measurements. Psychonomic Bulletin & Review. 2008;15(6):1201–1208. doi: 10.3758/PBR.15.6.1201. [DOI] [PubMed] [Google Scholar]
- Scaltritti M, Balota DA, Peressotti F. Exploring the additive effects of stimulus quality and word frequency: The influence of local and list-wide prime relatedness. The Quarterly Journal of Experimental Psychology. 2012 doi: 10.1080/17470218.2012.698628. [DOI] [PubMed] [Google Scholar]
- Stanners RF, Jastrzembski JE, Westbrook A. Frequency and visual quality in a word-nonword classification task. Journal of Verbal Learning and Verbal Behavior. 1975;14(3):259–264. [Google Scholar]
- Sternberg S. Memory-scanning: Mental processes revealed by reaction-time experiments. American Scientist. 1969;57(4):421–457. [PubMed] [Google Scholar]
- Thomas MA, Neely JH, O’Connor P. When word identification gets tough, retrospective semantic processing comes to the rescue. Journal of Memory and Language. 2012;66(4):623–643. [Google Scholar]
- Yap MJ, Balota DA. Additive and interactive effects on response time distributions in visual word recognition. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2007;33(2):274–296. doi: 10.1037/0278-7393.33.2.274. [DOI] [PubMed] [Google Scholar]
- Yap MJ, Balota DA, Tan SE. Additive and interactive effects in semantic priming: Isolating lexical and decision processes in the lexical decision task. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2012 doi: 10.1037/a0028520. in press. [DOI] [PubMed] [Google Scholar]
- Yap MJ, Balota DA, Tse CS, Besner D. On the additive effects of stimulus quality and word frequency in lexical decision: Evidence for opposing interactive influences revealed by RT distributional analyses. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2008;34(3):495–513. doi: 10.1037/0278-7393.34.3.495. [DOI] [PubMed] [Google Scholar]
- Yap MJ, Tse CS, Balota DA. Individual differences in the joint effects of semantic priming and word frequency revealed by RT distributional analyses: The role of lexical integrity. Journal of Memory and Language. 2009;61:303–325. doi: 10.1016/j.jml.2009.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]