Compressed Sensing Reconstruction for Undersampled Breath-Hold Radial Cine Imaging with Auxiliary Free-Breathing Data

Abstract

Purpose

To improve compressed sensing reconstruction of accelerated breath-hold (BH) radial cine MRI by exploiting auxiliary data acquired between different BHs.

Materials and Methods

Cardiac function is usually assessed using segmented cine acquisitions over multiple BHs to cover the entire left ventricle (LV). Subjects are given a resting period between adjacent BHs, when conventionally no data is acquired and subjects rest in the scanner. In this study, the resting periods between BHs are utilized to acquire additional free-breathing (FB) data, which are subsequently used to generate a sparsity constraint for each cardiac phase. Images reconstructed using the proposed sparsity constraint were compared with conventional compressed sensing (CS) using a composite image generated by averaging different cardiac phases. The efficacy of the proposed reconstruction is compared using indices of LV function and blood-myocardium sharpness.

Results

The proposed method provides accurate LV ejection fraction measurements for 33% and 20% sampled data sets compared with fully-sampled reference images, and shows 14% and 11% higher blood-myocardium border sharpness scores compared to the conventional CS.

Conclusion

The FB data acquired during rest periods can be efficiently used to improve the image quality of the undersampled BH data without increasing the total scan time.

INTRODUCTION

Segmented cine magnetic resonance imaging (MRI) allows non-invasive and reproducible evaluation of the cardiac function. Clinically, cine imaging is acquired in a multi-slice breath-hold acquisition where one or two slices are acquired within a breath-hold (BH) and the patient will breathe normally for a period of 20-30 second between BHs. As the spatiotemporal resolution of the cine imaging increases, the number of heartbeats required for the segmented acquisition and the duration of the BHs increase. To improve the imaging throughput, multiple slices are acquired within a BH to reduce the total scan time for the evaluation of cardiac function. In patients with difficulty in breath-holding or in pediatric patients, real-time cine or segmented cine in short BHs is used. For multiple-BH acquisitions to cover the entire left ventricle (LV), the majority of time is devoted to the resting period between scans so as the patient can recover from the BH. In a typical patient for a 10 second BH, 20-30 seconds is unused in between BHs, which results in substantially low acquisition efficiency of 25-33%. Therefore, this unused time between BHs can be used to accelerate image acquisition with a higher acceleration factor, which can be traded off to improve the spatial or temporal resolution or increase the number of slices that can be acquired within a single BH.

Acceleration techniques for dynamic or cine MRI have been widely studied. Unaliasing by Fourier-encoding the overlaps using the temporal dimension (UNFOLD) utilizes temporal filtering to remove the aliasing undersampling artifacts (1), temporal sensitivity encoding (TSENSE) exploits coil sensitivity information and temporal filtering (2), and k-t Broad-use Linear Acquisition Speed-up Technique (k-t BLAST) utilizes object-specific information obtained from the training data (3). More recently, compressed sensing (CS) (4) has been applied for various MRI reconstruction problems by using the compressibility of MR images in appropriate transform domains. The feasibility of the use of CS for reconstruction of dynamic images exploiting x-f space as the sparsifying transform domain was also presented (5). The use of object-specific prior information has been extended in CS framework via sparsifying images for diffusion-weighted neuroimaging, where the sparsifying composite image is obtained by sliding window reconstruction of an interleaved radial dataset (6). Similarly, reference image based CS has been proposed in dynamic contrast enhanced breast MRI (7) and in brain imaging using low resolution approximation (8), and also been incorporated with k-t SENSE to adaptively regularize the reconstructed image (9).

Although Cartesian trajectories are often used for cardiac cine imaging, non-Cartesian trajectories such as radial (10) can also be used (11-13). Radial trajectories have different imaging properties that may be favorable to cine imaging: it has inherent advantages for object motion (14-16), radial undersampling does not yield a substantial decrease in spatial resolution as the spatial resolution is mainly determined by the k-space coverage (11), and the streaking artifacts in an undersampled radial acquisition are more tolerable compared to the ghosting artifacts in an undersampled Cartesian acquisition (17). Acceleration techniques for radial trajectories have also been proposed including radial focal undetermined system solver (FOCUSS) (18) which asymptotically provides l₁-minimized CS reconstruction, CS reconstruction utilizing temporally averaged composite dataset for real-time radial cardiac imaging (19), and using total variation constraint for undersampled radial data with multiple coils in (20). k-t BLAST and k-t FOCUSS have been extended to radial trajectories in (21) and (12), respectively. For those algorithms that utilize object-specific prior information for successful reconstruction of the accelerated acquisition, it is often necessary to acquire additional data during a separate training phase, or use a time averaged image from a set of undersampled dynamic time frame images if one does not intend to use extra time for the training phase. However, the additional data can be acquired between different BHs without any scan time penalty and may be able to further enhance the image reconstruction, which has not been previously investigated.

In this study, we propose to exploit the free-breathing radial cine data acquired between different BHs of a conventional cine MRI protocol to generate the sparsifying constraint for CS reconstruction of undersampled radial cine acquisitions. LV cardiac function measurements including ejection fraction and end diastolic and systolic volume, and the blood-myocardium border sharpness are used to evaluate the efficacy of the proposed reconstruction.

MATERIALS AND METHODS

All healthy subject data were obtained using 1.5T Achieva magnet (Philips Healthcare, Best, The Netherlands) with a 5-channel phased-array coil. The acquired MR data were transferred to a stand-alone computer and the image reconstruction was performed off-line. All in vivo studies were approved by our institutional review board, and all subjects provided consent prior to participation in the study.

Radial Cine Acquisition and the CS Reconstruction

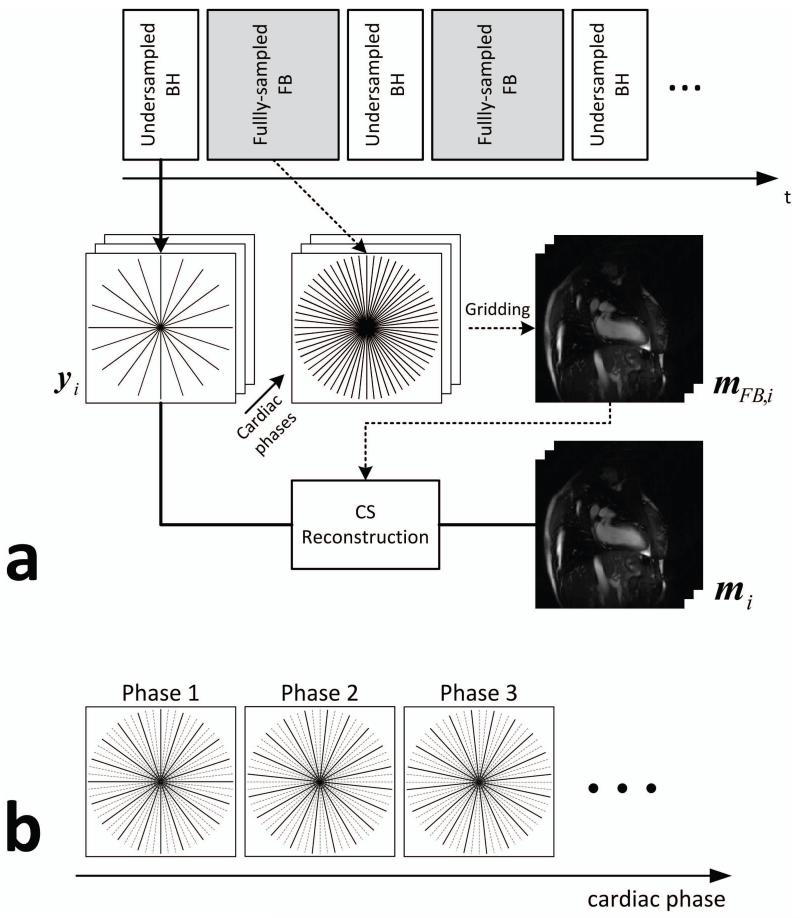
The acquisition and the CS reconstruction of the radial cine imaging are illustrated in Figure 1.a. An undersampled BH acquisition is followed by a fully-sampled FB acquisition during the resting period between BH acquisitions. The undersampled radial cine data is reconstructed using CS by minimizing the following objective function:

$$J\left({\mathbf{m}}_i\right)={\mid \mid {\mathbf{Am}}_i-\mathrm{y}\mid \mid }_2^2+\lambda \Psi \left({\mathbf{m}}_i\right),$$ [1]

where m_i denotes the i-th cardiac phase image, y_i denotes the undersampled radial k-space measurement for i-th cardiac phase, A is the encoding matrix of the radial acquisition, Ψ is a transform operator that sparsifies the image in the transform domain, and λ is a positive scalar parameter that determines the tradeoff between the consistency of the measured k-space data and the sparsity level of the reconstructed image. In this paper, the difference image from the additionally-acquired fully-sampled FB data is used as the sparsifying operator as $\Psi \left({\mathbf{m}}_i\right)={\mid \mid {\mathbf{m}}_i-{\mathbf{m}}_{FB,i}\mid \mid }_1$, where m_FB,i is the i-th cardiac phase image from the fully-sampled FB acquisition and ||·||_p denotes the l_p norm of the input vector which is defined as ${\mid \mid \mathbf{s}\mid \mid }_p={\left({\Sigma }_{i=1}^n{\mid s_i\mid }^p\right)}^{1∕p}$. Each cardiac phase image is sparsified by subtracting the image reconstructed from the fully-sampled FB acquisition with the same cardiac phase for successful CS reconstruction. The fully-sampled FB images are reconstructed by the conventional gridding algorithm (22). In the absence of respiratory motion, FB images are fully-sampled and thus do not have the streaking artifacts coming from the undersampling of the radial trajectory. In the presence of substantial motion, projection signals would be inconsistent due to respiratory motion that could result in streaks, especially, from bright fat signal. However, the FB images in this study are acquired while the patient is breathing normally with a shallow pattern, and the respiratory motion is averaged over multiple cardiac cycles resulting in blurry images without substantial streaking artifacts. For the conventional CS reconstruction, the sparsifying operator is changed to ${\Psi }_{conv}\left({\mathbf{m}}_i\right)={\mid \mid {\mathbf{m}}_i-{\stackrel{‒}{\mathbf{m}}}_{BH}\mid \mid }_1$, where ${\overline{\mathbf{m}}}_{BH}$ denote the composite image temporally averaged from the undersampled BH acquisitions over all cardiac phases. The difference images contain non-zero elements only in the areas where there are cardiac and/or respiratory motion, because the static regions from the BH, FB, and the composite images have similar signals and cancelled each other out. To minimize the objective function in Eq. [1], we adopt an iterative method which alternately enforces the data consistency and the sparsity of the image estimate at every iteration (23). The intermediate image update m_i (t +1) at the (t+1)-th iteration is obtained by solving the following two sub-problems:

$${\mathbf{u}}_i\left(t\right)={\mathbf{m}}_i\left(t\right)+\frac{1}{{\alpha }_t}+{\mathbf{A}}^{\ast }({\mathrm{y}}_i-{\mathbf{Am}}_i(t\left)\right),$$ [2]

which is called the data consistency step and

$${\mathbf{m}}_i(t+1)=\underset{\mathrm{m}}{\mathrm{argmin}}\frac{1}{2}{\mid \mid \mathbf{m}-{\mathbf{u}}_i\left(t\right)\mid \mid }_2^2+\frac{\lambda }{{\alpha }_t}\Psi \left(\mathbf{m}\right),$$ [3]

which is called the thresholding step. Equation [3] can be efficiently solved by a coefficient-wise thresholding function for the case of the difference operator $\Psi \left({\mathbf{m}}_i\right)={\mid \mid {\mathbf{m}}_i-{\mathbf{m}}_{FB,i}\mid \mid }_1$ as

$$m_i^n(t+1)=m_{FB,i}^n+\frac{u_i^n\left(t\right)-m_{FB,i}^n}{\mid u_i^n\left(t\right)-m_{FB,i}^n\mid }\max \left(\mid u_i^n\left(t\right)-m_{FB,i}^n\mid -\frac{\lambda }{{\alpha }_t},0\right),$$ [4]

where the superscript n denotes the n-th element of the input image vector. For the step size parameter α_t, we adopt the update rule from (23). We note that the CS reconstruction is performed for each coil, and the final cine image is obtained by root-sum-of-squares of the individual coil images.

Figure 1.

a) Illustration of the proposed radial cine acquisition. The undersampled BH acquisition is followed by a fully-sampled FB acquisition between BH acquisitions. The fully-sampled FB data is reconstructed by the conventional gridding algorithm and then used for the CS reconstruction of the undersampled BH data for each cardiac phase. b) Undersampling pattern for different cardiac phases of the BH acquisition. The sampling pattern is rotated by one sampling angle per cardiac phase.

Undersampling Pattern

For the undersampled BH acquisition, the radial trajectory is uniformly undersampled to have a constant angle between adjacent projection lines, since it has been shown that uniform undersampling provides superior image quality compared to random undersampling with CS reconstruction (24). The sampling pattern is varied for different cardiac phases and it is rotated by $\frac{{180}^{°}}{N_{\text{Full}}}$ per cardiac phase where N_Full is the number of projection lines in the fully-sampled radial trajectory as illustrated in Figure 1.b. This time-varying undersampling is not required for the proposed CS reconstruction as the proposed method reconstructs each cardiac phase image independently and does not utilize any temporal dependency between different cardiac phases. This sampling pattern is used in order to create a fully-sampled BH composite image by averaging all undersampled cardiac phase images over the BH period for the reconstruction of the conventional CS using the composite image.

In Vivo Study

Ten healthy subjects were imaged with an ECG-triggered steady-state free precession (SSFP) sequence. The scan parameters were as follows: number of cardiac phases = 20, field-of-view (FOV) = 320×320 mm², spatial resolution = 1.7×1.7 mm², TR/TE/α = 3.1/1.5/55°. All BH and FB acquisitions were acquired fully-sampled, and the BH acquisition was retrospectively undersampled to undersampling rates of R = 3 and 5, which yield 33% and 20% sampled data sets. A total of four fully-sampled data sets were acquired for each imaging plane: the first data set was acquired during BH and the remaining three data sets were acquired during FB. The three FB data sets were averaged and then used for the reconstruction of m_FB,i. The reference images were obtained from the fully-sampled BH data sets by using the conventional gridding reconstruction algorithm, and the undersampled BH data sets were reconstructed by the gridding algorithm, the conventional CS reconstruction using the composite image, and the proposed CS reconstruction with the auxiliary FB data sets.

Data Analysis

For the quantitative assessment of the study, the sharpness of the blood-myocardium border was measured and compared on the images reconstructed by the gridding algorithm with fully sampled reference BH data, the conventional CS reconstruction using the composite image with the undersampled BH data, and the proposed CS reconstruction with the undersampled BH data and the auxiliary FB data. The sharpness was measured from the signal intensity profile of a straight line perpendicularly crossing the blood-myocardium border. The sharpness score was defined as the reciprocal of the distance (mm) between the two points which have 20% and 80% of the signal intensity of the profile (25).

The performance of the proposed CS reconstruction was further evaluated by measuring the cardiac volumes and the ejection fraction of the left ventricle (LV). The reconstructed cine images were written into DICOM format and transferred to the ViewForum workstation (Philips Healthcare, Best, the Netherlands) for analysis. The LV end-diastolic volume (LVEDV), LV end-systolic volume (LVESV) and LV ejection fraction (LVEF) were measured by a board certified cardiologist with level 3 training in cardiac MRI blinded to the method of reconstruction using a commercially available software included in the ViewForum workstation.

RESULTS

Sparsifying Images

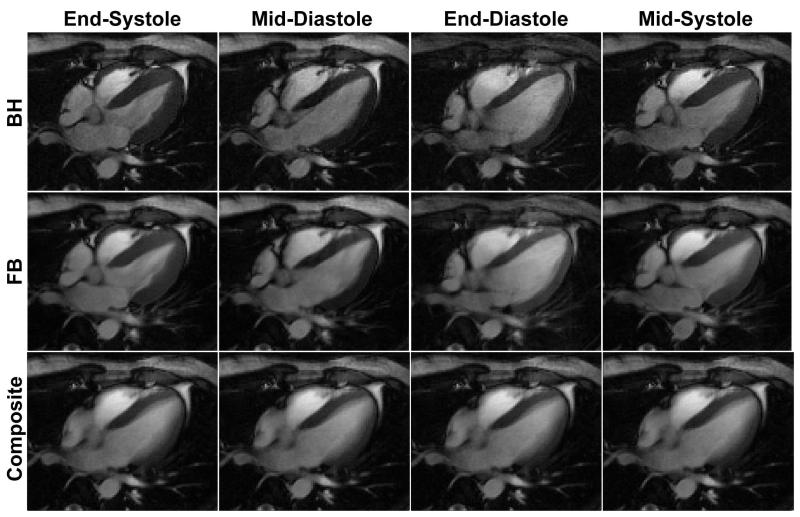
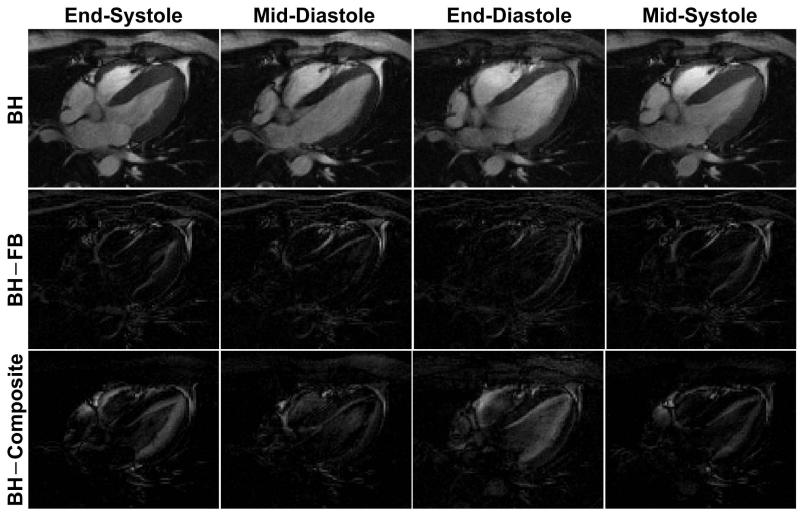
Figure 2 illustrates example cardiac phases from fully-sampled BH and FB acquisition with the temporally averaged composite image from the BH acquisition shown for comparison. The FB acquisition yields blurry images due to the respiratory motion compared to the BH acquisition, but provides very similar cardiac phase images to the BH acquisition, while the composite image appears blurred due to the cardiac motion as it is averaged over multiple cardiac phases. However, due to the superior motion robustness of radial acquisitions, neither the FB images nor the composite image suffers from severe motion artifacts even though they are respiratory-motion averaged and cardiac-motion averaged, respectively, and both can be used to sparsify the BH images in the CS reconstruction. It is more clearly visualized in Figure 3 where the difference images between the reference BH images and the FB images (BH – FB), and between the reference BH images and the composite image (BH – Composite) are shown. Due to the respiratory motion in the FB images, (BH – FB) exhibits non-zero signal near the chest wall and myocardium borders, while (BH – Composite) shows strong signal inside the blood pool due to the averaged cardiac motion in the composite image. Overall, (BH – FB) provides sparser images compared with (BH – Composite).

Figure 2.

Example cardiac phase images from fully-sampled BH acquisition and fully-sampled FB acquisition, and the composite image from BH acquisition. The images from the FB acquisition are blurred due to the respiratory motion, while the composite image is blurred due to the cardiac motion.

Figure 3.

Example cardiac phase images from fully-sampled BH acquisition and the difference images between the reference BH acquisition and the FB acquisition (BH – FB), and between the reference BH acquisition and the composite image from BH acquisition. The difference images are sparse and contain non-zero elements only in the areas where there is respiratory or cardiac motion.

Sharpness Measurements

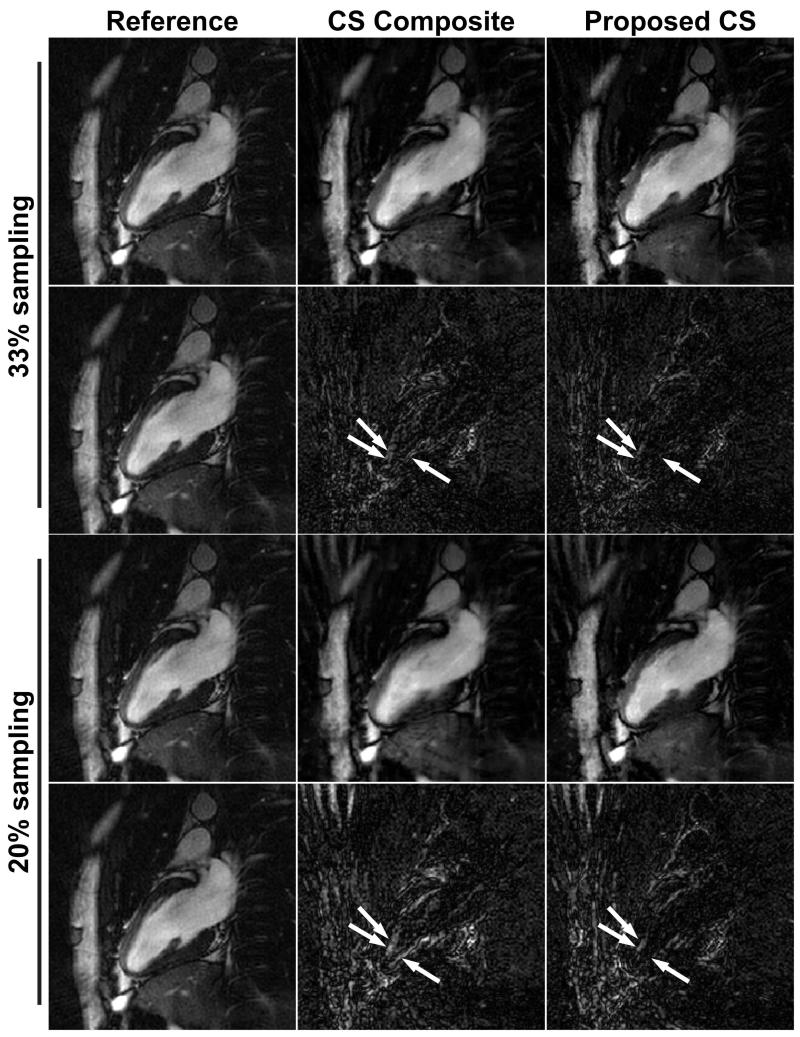
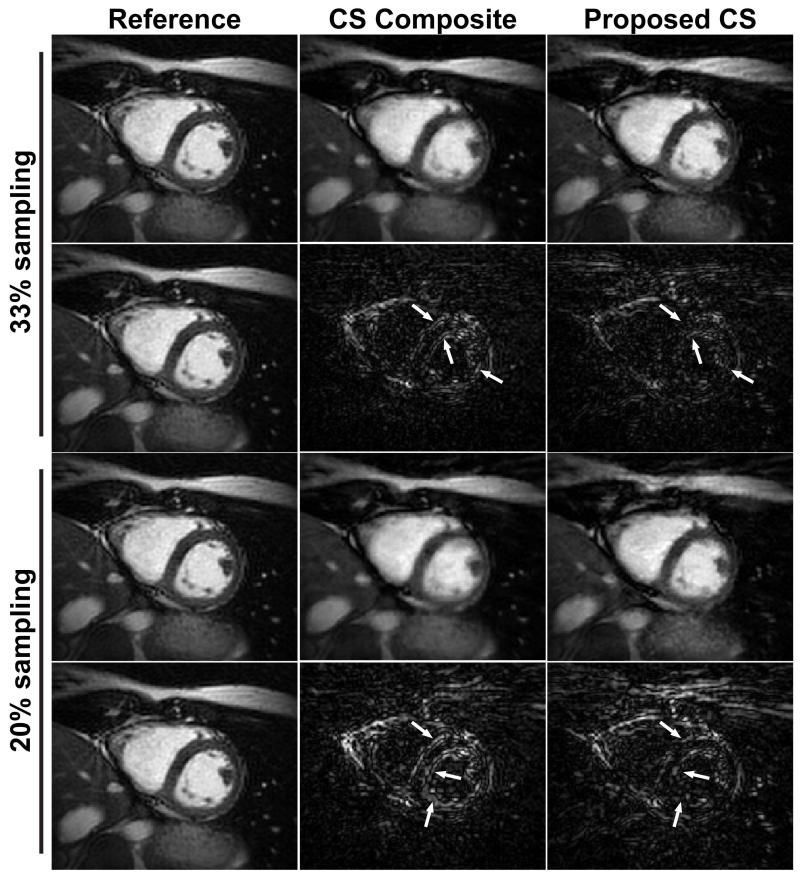
Figure 4 and 5 show example cardiac phase images in 2-chamber (2CH) and short axis (SAX) views reconstructed by the conventional CS algorithm using the composite image and the proposed CS algorithm. The reference images reconstructed by the gridding algorithm from the fully-sampled data set and the difference images between the reference images and the CS reconstructed images were also included for comparison. The BH data are undersampled to have 33% and 20% of projections from fully-sampled data. While most of the streaking artifacts are well suppressed in both CS reconstructions, the proposed CS reconstruction exhibits sharper blood-myocardium borders and improved image quality compared with the conventional CS reconstruction. There are some remaining artifacts in the reconstructed images emanating from the chest wall due to the undersampling especially in the images with 20% sampling density, but they are located outside the region of interest (i.e. the heart). The difference images show that the proposed CS reconstruction has less structured artifacts and improved sharpness on the left ventricular endocardial border, and septal wall and endocardium in 2CH and SAX views, respectively, compared with the CS composite (arrows).

Figure 4.

Example cardiac phase images in 2-chamber (2CH) view from 33% sampled and 20% sampled data sets reconstructed by the conventional CS reconstruction using composite image (CS composite), and the proposed CS reconstruction with additional FB data. The reference images are reconstructed by the conventional gridding algorithm from fully-sampled data set. The difference images from the fully-sampled reference image are also shown. The proposed CS reconstructions provide improved sharpness and improved image quality in the anatomy of interest compared with the conventional CS reconstruction, while they exhibit slightly more streaking artifacts near the chest wall. The difference images show that the proposed CS reconstruction has less structured artifacts on the LV endocardial border compared with the CS composite (arrows).

Figure 5.

Example cardiac phase images in short axis (SAX) view from 33% sampled and 20% sampled data sets reconstructed by the conventional CS reconstruction using the composite image (CS composite), and the proposed CS reconstruction with additional FB data. The reference images are reconstructed by the conventional gridding algorithm from the fully-sampled data set. The difference images from the fully-sampled reference image are also shown. The proposed CS reconstructions provide improved sharpness and improved image quality in the anatomy of interest compared with the conventional CS reconstruction, while they exhibit slightly more streaking artifacts near the chest wall. The difference images show that the proposed CS reconstruction has less structured artifacts on the septal wall and endocardium compared with the CS composite (arrows).

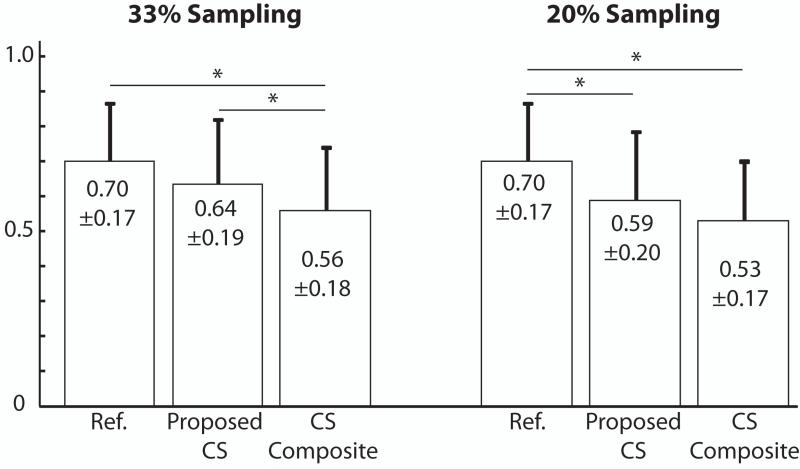
The blood-myocardium border sharpness scores are measured on the images reconstructed by the gridding reconstruction with the fully-sampled BH data, the conventional CS reconstruction using the composite image with the undersampled BH data and the proposed CS reconstruction with the undersampled BH data and the additional FB data. The measured blood-myocardium border sharpness scores are summarized in Figure 6. The sharpness scores for the reference images from the fully-sampled BH data and the proposed CS reconstructions were both significantly higher than the conventional CS reconstructions using the composite image with 33% sampled data set. The sharpness score for the proposed CS reconstruction with 33% sampled data set was similar to that of the reference image. The sharpness score for the proposed CS reconstruction with 20% sampled data set was significantly lower than that of the reference image but it was higher than that of the conventional CS reconstruction with 20% sampled data set (P = 0.12).

Figure 6.

The blood-myocardium border sharpness scores of the reference images from the fully-sampled BH data, the proposed CS reconstructions, and the conventional CS reconstructions using composite image (CS Composite) with 33% and 20% sampled data sets. (*: P < 0.05)

Left Ventricle Measurements

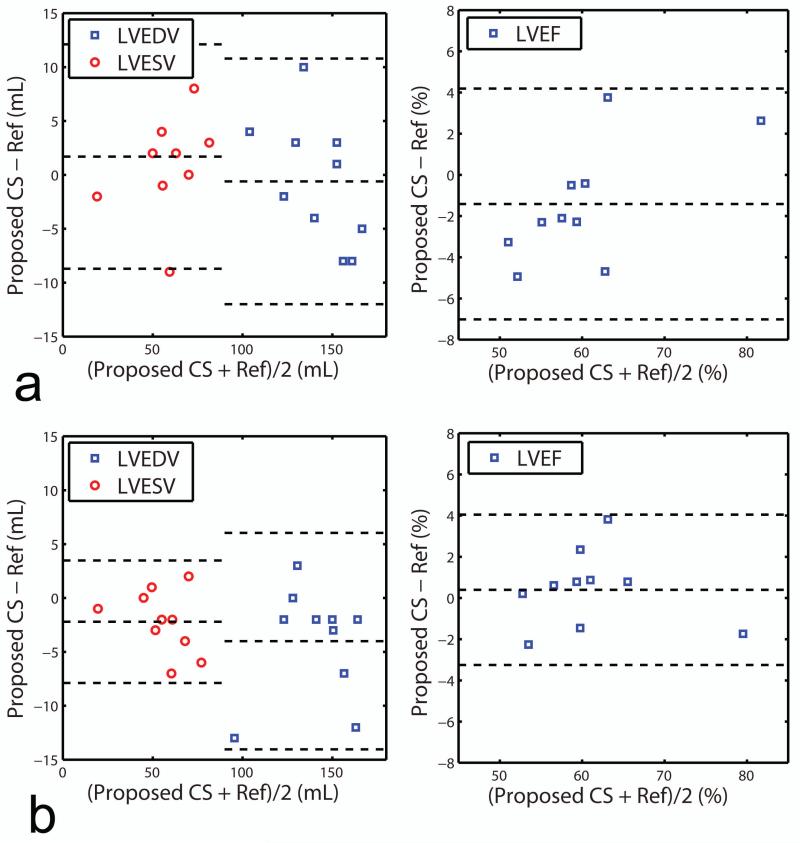
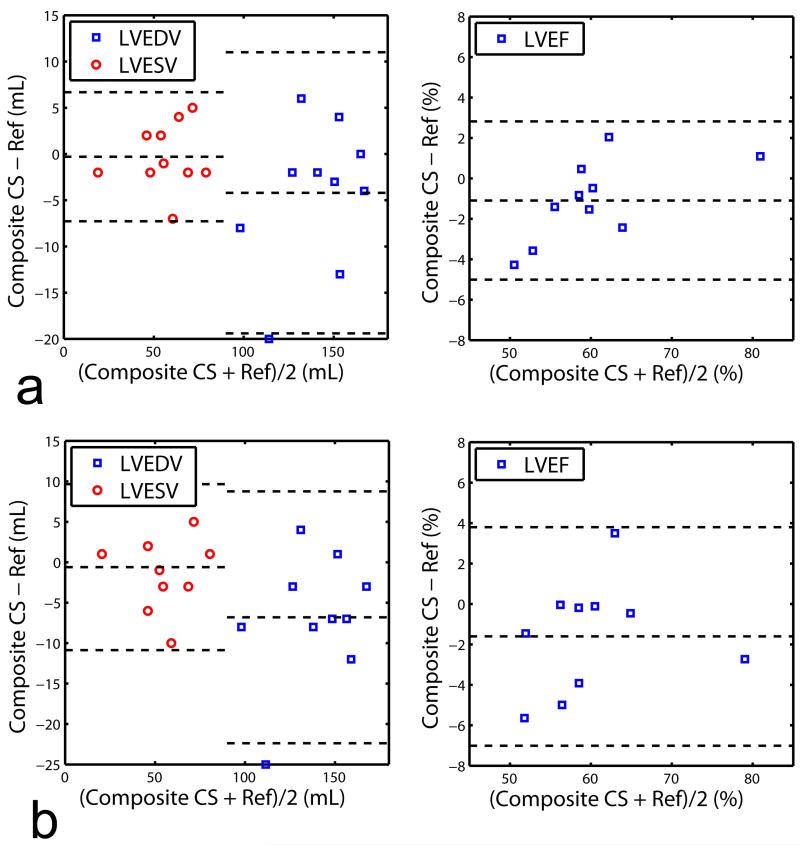
The LVEDV, LVESV, and LVEF were measured from the SAX images reconstructed by the four reconstruction methods (gridding reconstruction with fully-sampled data, gridding reconstruction with undersampled data, conventional CS reconstruction using the composite image with undersampled data, and proposed CS reconstruction with the undersampled data), and the results are summarized in Table 1. All three reconstructions of 33% sampled data provided LVEDV, LVESV and LVEF values similar to the fully-sampled (reference) images. For higher undersampling rate of 20%, there were no differences between the LVEF of the proposed reconstruction and references and differences between the reconstructions using composite image vs. references was marginally significant (P = 0.049). The Bland-Altman plots of the LVEDV, LVESV, and LVEF for the proposed CS reconstructed images vs. the fully-sampled reference images and CS with composite images vs. fully sampled are given in Figure 7 and 8 respectively. The Bland-Altman analysis indicates that the agreement between the fully-sampled reference images and the proposed CS reconstructed images with 95% confidence interval were −0.6±5.8 mL for LVEDV, 1.7±5.3 mL for LVESV and −1.4±2.9 % for LVEF with 33% sampled data sets, and −4±5.1 mL for LVEDV, −2.2±2.9 mL for LVESV and 0.4±1.9 % for LVEF with 20% sampled data sets. Linear regression analysis on the LV measurements for the proposed CS reconstruction vs. fully-sampled reference revealed slopes of 0.9924, 1.029, and 0.9800 for LVEDV, LVESV, and LVEF with 33% sampled data, and 0.9477, 0.9587, and 0.9892 for LVEDV, LVESV, and LVEF with 20% sampled data, respectively. The corresponding R² values were 0.8984, 0.9106, and 0.9051 with 33% sampled data and 0.9393, 0.9708, and 0.9225 with 20% sampled data, respectively. Similar Bland-Altman analysis between the fully-sampled reference images and the CS with composite images shows that the agreement with 95% confidence interval were −4.2±7.8 mL for LVEDV, −0.3±3.6 mL for LVESV and 1.1±2.0 % for LVEF with 33% sampled data sets, and −6.8±7.9 mL for LVEDV, −0.6±5.2 mL for LVESV and −1.6±2.8 % for LVEF with 20% sampled data sets. Linear regression coefficients between the fully-sampled reference images and the CS with composite images were 0.9725, 0.9956, and 0.9843 for LVEDV, LVESV and LVEF with 33% sampled data, and 0.9542, 0.9904, and 0.9742 for LVEDV, LVESV, and LVEF with 20% sampled data, respectively. The corresponding R² values were 0.8919, 0.9570, and 0.9469 with 33% sampled data and 0.8823, 0.9109, and 0.8877 with 20% sampled data, respectively. Similar to the observation with the paired t-test result in Table 1, the Bland-Altman plot shows that the CS with composite images have slightly larger bias and deviation from the reference images than the proposed CS images for 20% sampled data sets (−1.6±2.8 % vs. 0.4±1.9 %).

Table 1.

LV function measurements: Comparison of the measured LVEDV (mL), LVESV (mL), and LVEF (%) reconstructed by the gridding reconstruction, conventional CS reconstruction with composite image (CS composite) and the proposed CS reconstruction for 33% and 20% undersampled data sets.

	Reference	Gridding		CS composite		Proposed CS
Density	100%	33%	20%	33%	20%	33%	20%
LVEDV	142.2±21.2	140.7±17.3	133.9±21.3*	138.0±24.0	135.4±23.8*	141.6±18.0	134.6±22.0*
LVESV	56.8±16.7	57.5±16.4	59.0±17.8#	56.5±17.2#	56.2±17.5	58.5±17.8	54.6±15.7*
LVEF	0.61±0.08	0.60±0.09	0.57±0.11*#	0.60±0.09	0.59±0.08*	0.59±0.10	0.60±0.07

^*P < 0.05 from the reference

^#P < 0.05 from the proposed CS

Figure 7.

Comparison of LVEDV, LVESV and LVEF measurements of the fully-sampled reference images and the proposed CS reconstructed images based on Bland-Altman plot. The proposed CS reconstruction is performed on a) 33% sampled data sets and b) 20% sampled data sets.

Figure 8.

Comparison of LVEDV, LVESV and LVEF measurements of the fully-sampled reference images and the CS with composite images based on Bland-Altman plot. The CS reconstruction with composite images is performed on a) 33% sampled data sets and b) 20% sampled data sets.

DISCUSSION

In this study, we have proposed an accelerated radial cine acquisition strategy and a CS reconstruction algorithm, where the additional FB acquisition acquired during the resting period is utilized to improve the CS reconstruction of the BH acquisition. We have evaluated the performance of the proposed CS reconstruction and compared it to the conventional CS reconstruction using the composite image and conventional gridding. The reconstructed images show that the proposed CS reconstruction yields sharper blood-myocardium border scores and provides better image quality for the assessment of LV volumes and LVEF than the conventional CS reconstruction.

Many CS reconstruction methods have been proposed to improve the reconstruction of undersampled MRI data in various applications. Most of the CS reconstruction methods utilize a predetermined sparsifying transform such as wavelet, finite differences or x-f space. It is not possible, however, to predict whether a given transform can efficiently represent the underlying image characteristic and provide a sufficiently sparse image. More sophisticated techniques have been proposed that can adaptively capture objective-specific sparsity nature (26-29). The proposed method in this paper utilizes the fully-sampled FB acquisition of the same cardiac phase for the reconstruction of the undersampled BH acquisition, thereby providing object-specific sparse representation in a simple way to improve the CS reconstruction, based on the basic assumption of segmented cine acquisition that the cardiac motion is consistent over different cardiac cycles.

The proposed CS reconstruction produces sharper images, while the conventional CS reconstruction using the composite image produces slightly blurred images. The improved image quality of the proposed CS reconstruction over conventional CS reconstruction is due to the fact that the FB images create sparser difference images than the composite image when subtracted from the BH images. It is observed that the sparseness of the difference images is heavily dependent on the breathing pattern on the subject. A subject with a shallow breathing pattern produces FB images with good image quality and the difference from the BH images will also be small, resulting in good image quality of the CS reconstruction. A subject with a deep breathing pattern will have blurry FB images and strong signal in the difference images, degrading the image quality of the CS reconstruction. In such case, the conventional CS reconstruction may provide better image quality. Further study with more patient data with different breathing patterns is needed to further evaluate which reconstruction should be used for different respiratory patterns. Our data also shows that some high-frequency features are still missing from the reconstructed images at 20% sampling, and the reconstructed images display a certain blur for both CS composite and the proposed CS, indicating an insufficient sparsification in both techniques. Therefore, additional studies in improving the sparsification is warranted to further improve the reconstruction.

We have shown that utilizing the fully-sampled FB images is effective to sparsify the difference images in radial acquisitions. It is well-known that radial acquisitions have superior performance with respect to object motion compared with Cartesian acquisitions (15,16). While the standard two-dimensional Cartesian acquisition spreads the motion artifacts mainly in the phase-encoding direction, resulting in a severe ghosting artifact in that direction, the radial acquisition changes the phase-encoding direction over the entire two-dimensional space and the motion artifacts appear as two-dimensional blurring and streaks, which are less objectionable and of lower intensity. We have observed blurred images from the fully-sampled FB acquisitions in most of our cases, but the streaking artifacts were not significant as shown in Figure 2. Using a Cartesian trajectory may not be suitable for the proposed CS reconstruction since the difference images from the FB images may not be sparse enough for the successful CS reconstruction due to the severe motion artifact in the fully-sampled FB images.

The proposed acquisition strategy does not increase the total scan time because the auxiliary FB acquisition is acquired during the resting period which has not been used for acquiring data conventionally. The proposed CS reconstruction allows undersampling of the BH acquisition by a factor of three to five without severely degrading the quality of the cine images. As the undersampling factor increases, the BH duration is reduced accordingly. It is also possible to acquire undersampled data for multiple slices in one BH.

In our study, we have focused on comparing the proposed reconstruction to another commonly used CS reconstruction strategy, which uses composite images from all cardiac phases for sparsification. In this technique, data from all phases are used which results in additional blurring. A sliding window approach using a composite image consisting of only a fraction of consecutive cardiac phases, may be another technique to reduce this blurring, however this was not studied and needs further validation. We did not compare the results from either of CS based reconstructions to parallel imaging and instead used fully-sampled data as the reference standard. This comparison is needed to further investigate the pros and cons of each of these methods. Furthermore, due to low number of phased array coils (5-channel), we did not combine CS with parallel imaging. It is expected with higher number of coil elements, higher acceleration or improved noise performance to be achieved; however this was not studied.

We have performed two different image assessments using a) myocardium-blood border sharpness and b) LV indices of EF, EDV, and ESV for all reconstructions. Although, images reconstructed with the proposed reconstruction have higher myocardium-blood sharpness, the improved sharpness did not necessarily result in more accurate LV measurements, especially for highly undersampled datasets. This could be associated with how image sharpness and artifacts can influence LV measurements, which are calculated by manually drawing regions of interest (ROI) delineating LV blood and myocardium over different cardiac phases. For example, even in the presence of moderate streaking artifacts, LV measurements can be performed accurately since sharp blood-myocardium border can be seen for drawing the LV ROIs. Furthermore, our sample size is relatively small and all subjects had normal EF, therefore, the statistical analysis could be influenced by measurements from as few as one or two subjects. Further studies in a larger cohort including patients with low EF are needed to further evaluate each of these reconstructions.

CONCLUSION

The data acquired during the rest period between multiple BHs of cine MRI can be used to improve the image reconstruction of accelerated radial cine MRI without increasing the total scan time.