In vivo 3D molecular imaging with BIRDS at high spatiotemporal resolution

Abstract

Spectroscopic signals which emanate from complexes between paramagnetic lanthanide III ions (e.g., Tm³⁺) and macrocyclic chelates (e.g., 1,4,7,10-tetramethyl 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetate, or DOTMA⁴⁻) are sensitive to physiology (e.g., temperature and/or pH). Because non-exchanging protons from these lanthanide-based macrocyclic agents have relaxation times on the order of a few milliseconds, rapid data acquisition is possible with chemical shift imaging (CSI). Thus Biosensor Imaging of Redundant Deviation in Shifts (BIRDS) which originate from non-exchanging protons of these paramagnetic agents, but exclude water proton detection, can allow molecular imaging. Previous 2D CSI experiments with such lanthanide-based macrocyclics allowed acquisition from ~12 µL voxels in rat brain within 5 minutes using rectangular encoding of k-space. Because cubical encoding of k-space in 3D for whole brain coverage increases CSI acquisition time to several tens of minutes or more, a faster CSI technique is required for BIRDS to be of practical use. Here we demonstrate a CSI acquisition method to improve 3D molecular imaging capabilities with lanthanide-based macrocyclics. Using TmDOTMA⁻, we show datasets from a 20×20×20 mm³ field-of-view with voxels of ~1 µL effective volume acquired within 5 minutes (at 11.7T) for temperature mapping. By employing reduced spherical encoding with Gaussian weighting (RESEGAW) instead of cubical encoding of k-space, a significant increase in CSI signal is obtained. In vitro and in vivo 3D CSI data with TmDOTMA⁻, and presumably similar lanthanide-based macrocyclics, suggest that acquisition using RESEGAW can be used for high spatiotemporal molecular mapping with BIRDS.

Introduction

Lanthanide-based complexes are widely used as magnetic resonance imaging (MRI) contrast agents due to their ubiquitous effect on water relaxation mainly because of the paramagnetic ionic core in the molecular probe. However magnetic resonance spectroscopy (MRS) signals which emanate from these probes (i.e., not their effect on water) are also quite sensitive to physiology (e.g., temperature and/or pH). Based on the possibility that acquisition of these paramagnetically-shifted signals could have potential for molecular imaging, we recently showed that Biosensor Imaging of Redundant Deviation in Shifts (BIRDS) which originate from these molecular probes can be used for pH and/or temperature mapping in rat brain (1,2). The BIRDS method is based on strong dependence of temperature and/or pH on chemical shifts of proton (or other nuclei) from complexes between lanthanide III ions (e.g., Tm³⁺) and macrocyclic chelates of 1,4,7,10-tetraazacyclododecane-N,N’,N’’,N’’’-tetra (methylene phosphonate) or TmDOTP⁵⁻ and 1,4,7,10-tetraazacyclododecane-1,4,7,10- tetramethyl-1,4,7,10-tetraacetate or TmDOTMA⁻. Because the non-exchanging protons of paramagnetic agents have relaxation times on the order of just a few milliseconds, very fast data acquisition is achievable with conventional CSI.

Previous work with TmDOTP⁵⁻ and TmDOTMA⁻ in rat’s cerebral cortex used rectangular encoding of k-space in conjunction with high speed 2D CSI at 11.7T to allow BIRDS effective spatial resolution of 12.1 µL (nominal resolution of 10.2 µL) within 5 minutes of data acquisition (1,2). However future applications of BIRDS may require whole brain coverage and/or higher spatial resolution. For example, somatosensory stimulation, depending on types of anesthesia and/or stimuli, leads to cortical activation volumes in the range of 5–30 µL (3,4) and thus localized temperature mapping during functional activation (5) would require fast acquisition of quite small CSI voxels. Moreover, for selective brain cooling experiments (6–9) it is important to know the effectiveness of temperature lowering within a region as well as throughout the whole brain, thereby requiring 3D CSI of the whole brain with small voxels. All of these requirements are currently unachievable with present 2D CSI technology. For these types of experiments with BIRDS, a CSI method capable of 3D coverage of entire rat brain with spatial resolution of several µL is required. Since cubical encoding of k-space in 3D increases CSI acquisition time to several tens of minutes, we need a faster 3D CSI technique for practical use with BIRDS.

Replacing cubical encoding with uniform spherical encoding of k-space (10) significantly reduces the time of measurement, but results in an increase of the effective voxel volume. However, spherical encoding is preferred because it reduces the amplitude of the Gibbs ringing (10,11). Spherical encoding of k-space was successfully applied in human calf muscle and human breast to obtain 3D ³¹P CSI datasets at 7 T using an adiabatic multi-echo spectroscopic imaging (AMESING) pulse sequence (12). A spherical stack of spirals trajectories in k-space was used to achieve reduced loss of spatial information in single shot whole brain imaging, compared to acquisitions using concentric shells trajectories (13). Higher signal-to-noise ratio and higher contrast-to-noise ratio within a shorter scan time were obtained using spherical k-space encoding with 3D stack-of-rings trajectory than compared to 3D Cartesian encoding (14).

Sensitivity per unit time can be improved by introducing weighting of k-space, in which less time is spent acquiring high k-space coordinates without a large loss of pixel resolution due to optimization of the point spread function (PSF) (11,15,16). Moreover, a smoother k-space weighting function significantly decreases the Gibbs ringing artifacts (15). The optimal filter for maximum ripple reduction with minimum effect on the point spread function is given by the Dolph-Chebyshev window function (17). However, a more widely used window function is the Hamming function which represents a good approximation of the Dolph-Chebyshev window function (17). A Gaussian window function represents another commonly used window function to provide improved signal-to-noise ratio (SNR) and data collection efficiency (11) with reduced Gibbs ringing (18). Weighting of k-space can also be achieved by making the repetition time TR dependent on the k-space position, resulting in a significant reduction of measurement time (19). A significant reduction in measurement time can be achieved also by compressed sensing acquisitions, in which an appropriate nonlinear recovery scheme is used to recover images with a sparse representation obtained from randomly undersampled k-space acquisitions (20). Although k-space weighting provides some advantages compared to uniform encoding, the method is applicable only when signal averaging is required (e.g., ³¹P CSI or ¹H CSI requiring more than one average). [R1.1][R1.3][R1.5][R3.4]

In the current study we employed a 3D CSI method where the temporal resolution is kept at 5 minutes using reduced spherical encoding with gaussian weighting (RESEGAW) of k-space, allowing us to achieve an effective voxel resolution of ~1µL. Feasibility of obtaining high spatiotemporal resolution temperature maps in rat brain was demonstrated with TmDOTMA⁻ as a temperature sensor (Fig. 1A), due to high SNR of its –CH₃ group (1).

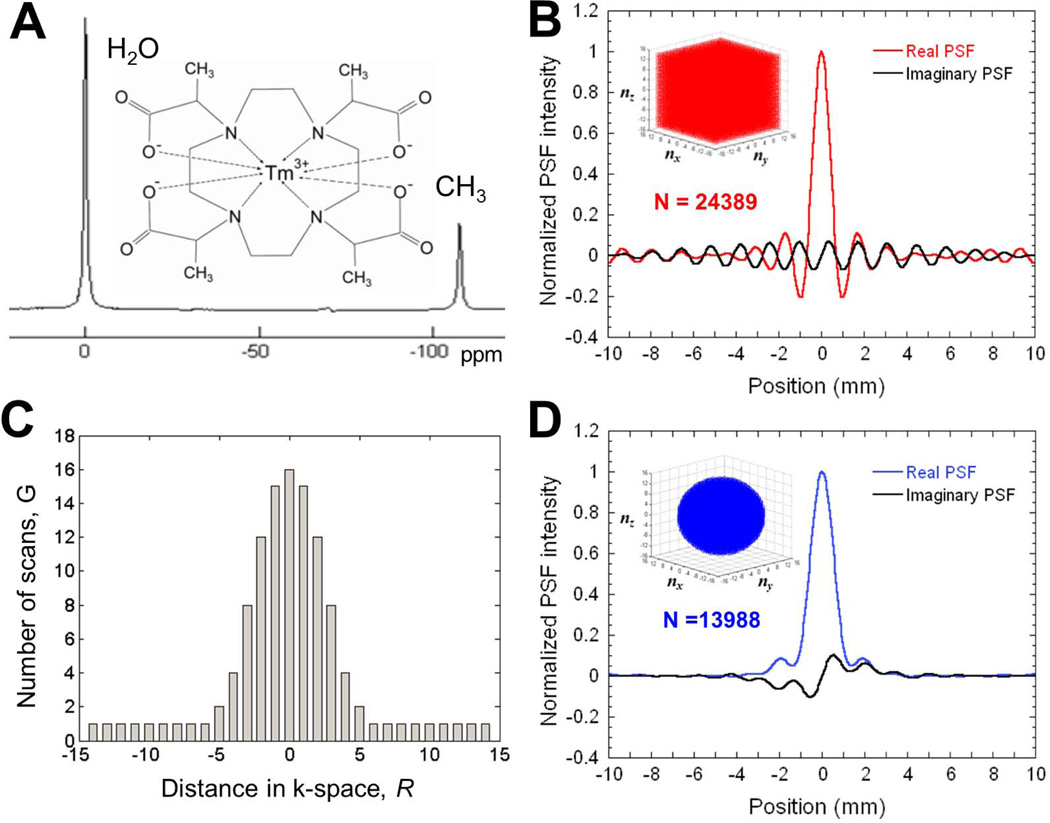
Figure 1. In vitro 3D CSI with TmDOTMA⁻.

(A) Structure and ¹H spectrum of TmDOTMA⁻. (B) The real and imaginary parts of the PSF for 29×29×29 = 24389 cubical encoding along 1D (the other two directions have coordinates zero). The effective voxel volume estimated using the 3D PSF for cubical encoding is 0.33 µL. (C) For the RESEGAW encoding, the number of scans acquired for each k-space point follows a Gaussian distribution based on its distance R to the center of k-space. (D) The real and imaginary parts of the PSF for RESEGAW encoding with 13988 steps along 1D (the other two directions have coordinates zero). The effective voxel volume estimated using the 3D PSF for RESEGAW encoding is 1.0 µL. Thus, acquisition of 3D CSI maps using RESEGAW encoding results in 3-fold increase of a voxel effective volume compared to cubical encoding, but decreases the acquisition time by ~40%.

Materials and Methods

Construction of a 3D sampling function for 1 µL effective resolution

Estimation of the effective volume of a voxel was obtained by calculating the PSF for the cubical and RESEGAW encoding of k-space. For the 29×29×29 cubical encoding (Fig. 1B, inset), a 3D sampling function of k-space was constructed, with unity assigned to all values. However, for the RESEGAW encoding, the proposed sampling function G(R) was constructed using a Gaussian distribution of k-space sampling, with maximum number of scans (N_c) in the center of k-space (Fig. 1C):

$$G(R)=N_C{e}^{-{\left(\frac{R}{R_d}\right)}^2}$$ [1]

where R_d determines the width of the G(R) distribution and R represents the distance from the center of k-space to a k-space position described by the indices n_x, n_y and n_z in the three encoding directions,:

$$R=\sqrt{n_x^2+n_y^2+n_z^2}.$$ [2]

The G(R) distribution was rounded to the closest integer value and for encoding steps corresponding to G(R) < 1, a minimum value of 1 scan was assigned (Fig. 1C). However, based on spectral analysis of the 3D CSI dataset with 29×29×29 cubical encoding (Fig. 1B), the encoding steps corresponding to R > 14 have negligible contribution to total signal (Supplementary Fig. 1). Therefore, G(R) was set to 0 for encoding steps corresponding to R > 14, resulting in a “spherical” encoding of k-space (Fig. 1D, inset).

The PSF (normalized to unity) was obtained for both cubical (Fig. 1B) and RESEGAW encoding (Fig. 1D) by spatial Fourier transformation of the sampling function zero filled to a higher resolution (257×257×257). The effective volume of a voxel was calculated by counting the number of PSF points which have a normalized intensity larger than 0.5, which provides a measure of the PSF width (18). For example, for a 1D PSF, this number provides the width at half maximum (Fig. 1B and 1D), while for a 2D (or 3D) PSF, this number provides the area (or volume) at half maximum. Since the height of the PSF function is normalized to unity and the volume of each PSF point can be expressed in volume units (µL), the number of PSF points with intensity larger than 0.5 provides the effective volume of a voxel.

In vitro ¹H CSI

The 3D CSI datasets of a phantom containing 5 mM TmDOTMA⁻ were obtained on a modified 11.7T Agilent horizontal-bore spectrometer using a ¹H resonator/surface radio frequency (RF) probe (1.4 cm). Two 3D CSI datasets were acquired, one with cubical encoding (24389 encoding steps, Fig. 2A) and the other with RESEGAW encoding (13988 encoding steps, Fig. 2B). A single-banded refocused 90° Shinnar-Le Roux (SLR) RF pulse of 40 kHz bandwidth and 205 µs duration was used for selective excitation of the –CH₃ group of TmDOTMA⁻ (1). The datasets were acquired with a recycle time (TR) of 10 ms and a field of view (FOV) of 20×20×20 mm³. The phase encode gradient duration was 100 µs and the acquisition time of the FID was 4.1 ms [R3.1]. The spectrum for each encoding step was line broadened (300 Hz), phased (zero order), and baseline corrected (first order). The 3D CSI maps were obtained by spatial Fourier transformation of k-space spectra using these two CSI datasets.

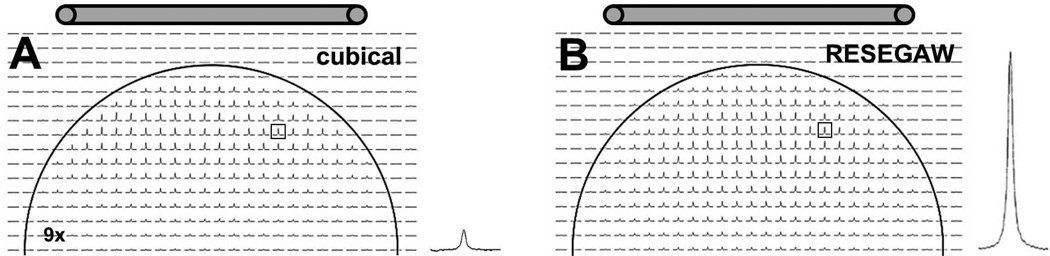
Figure 2. In vitro comparison between 3D CSI with cubical encoding versus RESEGAW encoding of k-space with TmDOTMA⁻.

(A) Example of a ¹H CSI slice (z = 0) obtained using cubical encoding. The spectrum on the right [R1.7][R3.5] of the CSI dataset show the signal of the –CH₃ resonance from the voxel boxed in the CSI dataset. (B) The same ¹H CSI slice as in (A), obtained using RESEGAW encoding. The spectrum on right [R1.7][R3.5] of the CSI dataset show the signal of the –CH₃ resonance in the same voxel as in (A). The CSI spectral intensities of the cubical dataset were multiplied by 9 to match that of the RESEGAW dataset. The location of the surface coil relative to the phantom is also indicated. [R2.2]

In vivo ¹H CSI

All animal experimental procedures on rats were approved by the Institutional Animal Care and Use Committee (IACUC) and similar to procedures described previously (1,2,9). Sprague-Dawley rats (n = 4; 200–300 g) were tracheotomized and artificially ventilated (70% N₂O, 30% O₂). Isoflurane (3%) was used for induction and surgery. An intraperitoneal line was inserted for administration of α-chloralose (46±4 mg/kg/hr) and an intravenous line was used for administration of D-tubocurarine chloride (1 mg/kg/hr) and TmDOTMA⁻ (0.5 mmol/kg). The infusion rate was adjusted to keep the animal within the autoregulatory range of cerebral perfusion. An arterial line was used for monitoring physiology (blood pH, pO₂, pCO₂) throughout the experiment. The anesthetized rats were renaly ligated. A water-heating blanket was used to control and maintain the body temperature. In vivo 3D CSI acquisition and processing parameters were the same as for the in vitro experiments (see above). The temperature, T, was calculated from the chemical shift of the –CH₃ protons (δ_CH3) according to

$$T=a_0+a_1({\delta }_{C{H}_3}-{\delta }_0)+a_2{({\delta }_{C{H}_3}-{\delta }_0)}^2$$ [3]

where δ₀ = − 103.0 ppm and the coefficients a₀ (34.45±0.01), a₁ (1.460±0.003), and a₂ (0.0152±0.0009) were calculated from linear least-squares fit of temperature as a function of chemical shift δ_CH3 as previously described (1).

Results

Comparison of cubical and RESEGAW encodings

Since detailed analysis of ¹H spectra of TmDOTMA⁻ has been demonstrated earlier (1), only a brief summary follows. Of the four detectable proton resonances, the –CH₃ group has the highest SNR compared to other ¹H signals which emanate from this molecular probe (Fig.1A). Moreover, chemical shift of the –CH₃ group has high temperature sensitivity (0.7 ppm/°C) and very short relaxation times (i.e., T₁ and T₂ of less than 5 ms). Together, these reasons enable high SNR molecular imaging for TmDOTMA⁻ with high spatiotemporal resolution (1).

The acquisition of a cubical 29×29×29 3D CSI dataset requires 24389 encoding steps where each of the three orthogonal indices of k-space (n_x, n_y, n_z) are incremented sequentially (by 1 from −14 to 14) with maximum intensity in center of k-space (18). Spectral analysis for all 24389 encoding steps before spatial 3D Fourier transformation indicates that the intensity of the –CH₃ group is higher near the center of k-space and decreases steeply away from the k-space center, as R becomes larger (Supplementary Fig. 1). As a result, the encoding steps corresponding to R > R₀, where R₀=14 represents the cutoff distance (indicated by the arrow in Supplementary Fig. 1) have negligible contribution to total signal thereby suggesting that acquisition of these data points in the case of spherical encoding of k-space may be avoided without compromising SNR significantly. However, this will reduce the number of encoding steps acquired. Thus, for uniform spherical encoding with R < R₀, the number of encoding steps can be decreased from 24389 (Fig. 1B) to 12770, while the addition of Gaussian weighting of spherical k-space increases slightly the number of encoding steps to 13988 (Figs. 1C and 1D). The reduction in the number of encoding steps from cubical 29×29×29 3D CSI to uniform spherical encoding results in a decrease by 48% of the experimental time, while the inclusion of the additional 1218 encoding steps to achieve Gaussian weighting of spherical k-space results in an increase of the experimental time by 5%. Thus, RESEGAW encoding scheme requires only 57% of the experimental time of a cubical 29×29×29 3D CSI encoding scheme. [R1.2] [R1.4]

However reduced sampling of k-space has a detrimental effect on the effective volume of a voxel. Thus calculation of the corresponding PSF for each of the three k-space encoding schemes shows that the width of the PSF increases when the number of encoding steps is decreased. To exemplify this effect, the profile of the real and imaginary parts of the PSF along one of the three directions (corresponding to coordinate zero for the other two directions) was calculated for 29×29×29 cubical encoding (Fig. 1B; red = real PSF, black = imaginary PSF) and RESEGAW encoding (Fig. 1D; blue = real PSF, black = imaginary PSF). Using these two PSF, the effective voxel volume in each case was estimated (see Materials and Methods). Our calculations indicate that for a FOV of 20 mm, the effective volume increases from 0.33 µL for cubical encoding to 0.75 µL for uniform spherical encoding and to 1.0 µL for RESEGAW encoding. In addition, PSF calculation for a reduced 15×15×15 cubical k-space indicates that the effective voxel volume increases to 2.37 µL, although the experimental time is reduced by 86% compared to the 29×29×29 cubical encoding. Moreover, using a reduced 15×15×15 cubical encoding scheme results in enhanced Gibbs ringing artifacts. Therefore, 3D CSI with RESEGAW encoding represents a compromise between spatial and temporal resolutions in order to keep the temporal resolution to a reasonable value (5 minutes) with high SNR. [R1.4]

To compare the cubical and RESEGAW 3D CSI acquisitions in vitro, we calculated the ratio ρ between the signal intensity of RESEGAW and cubical datasets, for 1251 voxels for which the signal was larger than 40% of the maximum signal in the cubical dataset. The average signal ratio over all these voxels was ρ = 9.3 ± 2.3. To further exemplify this result, we extracted the central CSI slice corresponding to position z = 0 for the cubical (Fig. 2A) and RESEGAW (Fig. 2B) datasets. The signal of the cubical dataset was increased 9-fold (Fig. 2A) to match that of the RESEGAW dataset (Fig. 2B). Moreover, comparison of signal intensity in the same CSI voxel from the two CSI datasets indicate almost a 10-fold intensity enhancement for the RESEGAW acquisition (Fig. 2A right and 2B right) [R1.7][R3.5]. However, the effective volume of a voxel in the RESEGAW encoding is 3-fold larger than that for cubical encoding. Therefore, the enhancement factor per unit of volume is 3.1 (=9.3/3) indicating that the signal for the RESEGAW is about 3-fold larger than for the cubical encoding. This increase in the signal is likely due to the shape of the RESEGAW PSF which is mostly positive (Fig. 1D) compared to a more sinc-like shape with alternating positive and negative contributions for cubical encoding (Fig. 1B). The effective voxel volume is calculated at 50% of the PSF (which is a common way to calculate the PSF) but the entire PSF function contributes to the MR signal. Thus, while the PSF for cubical stretches on forever, but is largely self-canceling (Fig. 1B), the PSF for RESEGAW is much more localized, but is all positive (Fig. 1D). [R1.7][R3.5] Moreover, acquisition of a RESEGAW dataset is 1.7-fold (=24389/13988) faster than that of a cubical 3D CSI dataset. These results suggest that RESEGAW encoding should be preferable to cubical encoding when acquiring 3D CSI for BIRDS.

In vivo 3D CSI with RESEGAW encoding

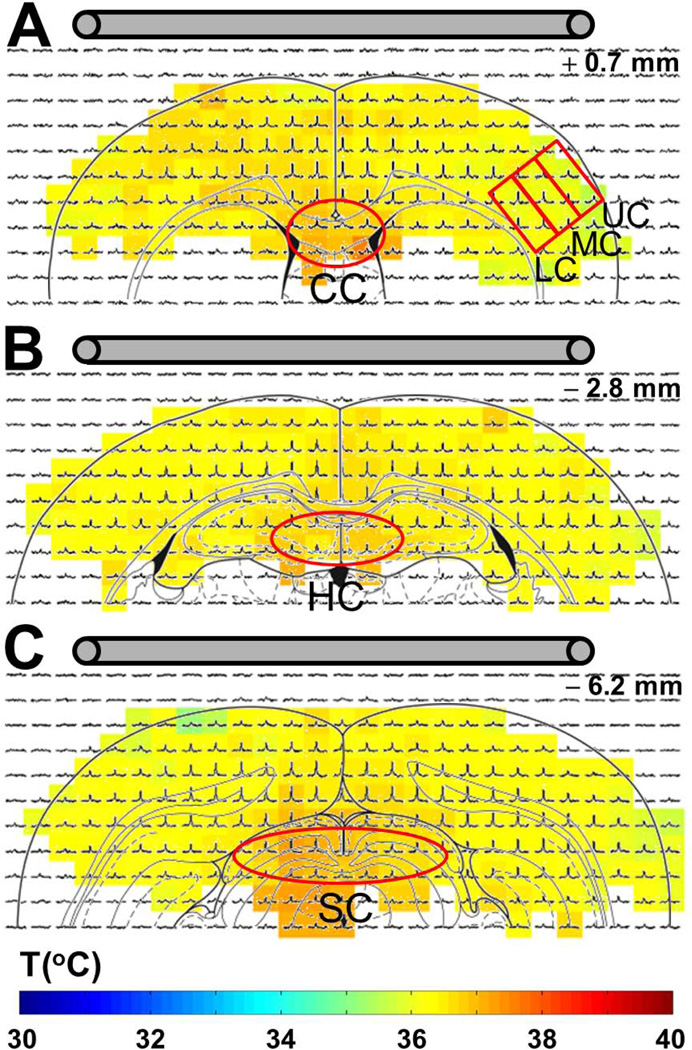
To demonstrate in vivo feasibility of acquiring 3D CSI experimental data with high spatiotemporal resolution, CSI datasets of rat brain with 20 mm FOV in each direction were obtained using RESEGAW encoding of k-space with 13988 encoding steps, similar to the in vitro data shown in Fig. 2. The 13988 encoding steps were acquired in less than 5 minutes using a TR of 10 ms and 2 averages. To exemplify 3D CSI mapping of rat brain, spectra from three CSI slices positioned at +0.7 mm, − 2.8 mm, and − 6.2 mm from bregma, are shown respectively in top, middle and bottom of Fig. 3. The chemical shift of the –CH₃ group of TmDOTMA⁻ was measured in each voxel and eq. [3] [R1.8] was used to calculate the temperature distribution in each slice. The three maps, overlaid on the CSI datasets show a relatively homogenous temperature distribution in rat’s cerebral cortex with an average temperature of 36.4 ± 0.3 °C, 36.5 ± 0.2 °C and 36.3 ± 0.3 °C for the three slices. Temperature measurements over the entire brain indicate a relatively symmetrical distribution with an average value of 36.4 ± 0.6 °C. The temperature values span a relatively narrow range, with 85% of the values between 36 and 37 °C (Supplementary Fig. 2). However closer inspection of smaller regions show heterogeneity across cortical layers and the inner core of the brain (e.g., corpus callosum, hippocampus, superior colliculus), as shown in Fig. 2 and Table 1, where the temperature is progressively warmer from the outer surface to the deeper brain tissues. [R1.6]

Figure 3. In vivo 3D CSI with TmDOTMA⁻ using reduced spherical encoding.

Examples of three ¹H CSI slices from a 3D CSI RESEGAW dataset in rat brain, positioned at +0.7 mm (A), −2.8 mm (B) and −6.2 mm (C) from bregma. The temperature distribution in these three slices was calculated using eq. [1]. The average temperature was 36.4 ± 0.3 °C, 36.5 ± 0.2 °C and 36.3 ± 0.3 °C, respectively. The presence of a temperature gradient of ~0.3°C across cortex was demonstrated by measuring the average temperatures in the upper (UC), middle (MC) and lower (LC) cortical layers, indicated by the three red boxes in (A). Moreover, significantly higher temperatures (>0.5°C compared to cortex) were measured in corpus callosum (CC, red oval in (A)), hippocampus (HC, red oval in (B)) and superior colliculus (SC, red oval in (C)). [R1.6] The location of the surface coil relative to the animal brain is also indicated. [R2.2]

Table 1.

Regional average temperatures measured in rat brain, in the upper, middle and lower cortical layers (Fig.3A, red boxes, UC, MC, and LC), corpus callosum (Fig.3A, red oval, CC), hippocampus (Fig.3B, red oval, HC) and superior colliculus (Fig.3C, red oval, SC).

Region	Average temperature (°C)a
Upper cortical layer	36.0 ± 0.2
Middle cortical layer	36.2 ± 0.2
Lower cortical layer	36.3 ± 0.2
Corpus callosum	36.8 ± 0.3
Hippocampus	36.8 ± 0.1
Superior colliculus	36.9 ± 0.2

^a)T-test analysis using two tailed distributions with unequal variance indicates statistical significant differences with p < 0.02 when comparing the upper cortical layer with the other regions investigated. [R1.6]

Discussion

In the present work we report in vivo feasibility of obtaining high spatiotemporal resolution 3D CSI mapping of rat brain using a lanthanide-containing macrocyclic complex, TmDOTMA⁻. Previous BIRDS experiments in our laboratory used TmDOTMA⁻ as a temperature sensor based on its high temperature sensitivity (0.7 ppm/°C) and very high SNR of the –CH₃ resonance (1). The 2D CSI data of a 4 mm slice were acquired using 16×16 encoding steps with an FOV of 25.6×25.6 mm², a TR of 11 ms, and 100 averages, thus resulting in total acquisition time of 5 minutes and a nominal voxel volume of 10.2 µL (effective voxel volume of 12.1 µL). In the current study we acquired high SNR 3D CSI datasets with effective voxel volume of 1µL (nominal voxel volume of 0.33 µL) in 5 minutes using a reduced k-space spherical encoding with Gaussian weighting (named RESEGAW). The lower number of averages required for the 3D CSI with RESEGAW experiment compared to our previous 2D CSI experiments was a consequence of signal acquisition from the entire animal brain. In addition, Gaussian weighting with increased averaging of encoding steps from the center of the k-space results in significant signal enhancement (Fig. 2). However, the effective voxel volume is 3-fold larger (1 µL) compared with the nominal voxel volume (0.33 µL).

Determination of the number of k-space encoding steps with significant contribution to total signal, involving estimation of the cutoff distance R₀, depends on the distribution of signal intensity in k-space. This distribution is dependent on various factors, such as local agent concentration, shape and size of sample investigated, FOV, etc. Thus in vitro 3D CSI experiments were designed to closely mimic the in vivo situation. The spherical shape, size and location of the in vitro sample are similar to that of the animal brain, leading to similar distributions of signal intensity in the k-space. Moreover the in vitro agent concentration (5 mM) was similar with the estimated TmDOTMA⁻ concentration of about 3 to 4 mM in rat brain (1). The use of in vitro samples with higher TmDOTMA⁻ concentration would have resulted in better SNR and thus a wider region of k-space with significant contribution to the total signal. Therefore based on the in vitro results, we expected that the 3D CSI method using RESEGAW encoding will be successfully applied to obtain 3D CSI datasets of rat brain. Indeed, the analysis of signal distribution in the k-space for the in vivo 3D CSI datasets indicate that a cutoff distance R₀=14 provides a good compromise between the desired fast acquisition (which requires a smaller number of encoding steps) and increased spatial resolution (which requires a larger number of encoding steps).

Extremely fast CSI data acquisition with a very short TR (10 ms) is possible because the T₁ of TmDOTMA⁻ is so short (< 5 ms). However, this TR limit is spectrometer based, which if reduced in the future, would significantly enhance the sensitivity of BIRDS, especially for agents with extremely short T₁ (e.g., smaller than 1 ms). Based on the previously measured T₂ value of 4.17 ms for the TmDOTMA⁻ methyl group (1), the signal decay during the phase encoding (0.1 ms) is only 2.5% of the signal, indicating that signal decay during the phase encoding due to T₂ relaxation prior to FID collection is minimal. Moreover, the short acquisition time of 4.1 ms does not produce any ringing artifacts in the spectra of TmDOTMA⁻. [R3.1]

Multi-slice 20×20 2D ¹H-[¹³C] edited CSI experiments with 1 µL nominal voxel resolution (1.7 µL effective resolution) in microwaved rat brains have been obtained previously to allow generation of ex vivo metabolic maps of [4-¹³C]-glutamate, [4-¹³C]-glutamine and of other ¹³C-labeled molecules (21). Dynamics of lactate generation in focal ischemic rat brain was also estimated using ¹H-[¹³C] edited CSI experiments with 1.9 µL nominal voxel resolution (2.2 µL effective resolution) (22). Detection of ¹³C-labeled brain metabolites requires a relatively long TR (1.5 s or longer) which results in a long CSI experiment (30 minutes or more). Similarly, high resolution quantitative ¹H metabolite maps of more than 10 metabolites from rat brain were obtained in ~1 hour by using a 2D CSI experiment with a nominal resolution of 1.1 µL and an effective voxel size of 1.7 µL (23). While spectroscopic imaging of these metabolites can be sped up significantly using echo-planar imaging schemes (24), whole brain CSI maps would still require quite long acquisition times with superior outer volume suppression (25). Thus ¹H detection of signals from lanthanide-based macrocyclics such as TmDOTMA⁻ at high temporal resolution (~5 minutes) represents a direct consequence of their short T₁ and T₂ relaxation times on the order of milliseconds (1,2,9).

The average brain temperature measured in the current study, 36.4 ± 0.6 °C, (Supplementary Fig. 2) is slightly higher than our previous measurements, where average temperatures of 34.6±0.4 and 34.8±0.4 °C were estimated using 2D CSI of 4mm slices with TmDOTP⁵⁻ and TmDOTMA⁻, respectively (1). However, this result can be easily explained by the strong correlation we always observe between the brain and the body temperatures (data not shown). Thus, in our previous measurements, the rat’s body temperature during 2D CSI acquisition was 35.8 ± 0.1 °C and 36.1 ± 0.1 °C for TmDOTP⁵⁻ and TmDOTMA⁻, respectively, while during the CSI acquisition with RESEGAW encoding, the core temperature was 37.4 ± 0.1 °C. A very important consequence of obtaining high resolution temperature maps in rat brain is that measurement of temperature differences between various brain regions is now possible. These types of regional differences were previously measured by thermocouple wires only (26). Temperature measurements in specific cortical regions indicate a gradual increase in the temperature by ~0.3°C when going from upper to lower cortical layers (Fig. 3A, red boxes and Tab. 1). Moreover, average temperatures in the inner core of the brain were higher by more than 0.5°C compared to cortex (Tab.1) as indicated by the “warmer” colors in corpus callosum (red oval in Fig.3A), hippocampus (red oval in Fig.3B) and superior colliculus (red oval in Fig.3C). [R1.6][R3.4]

TmDOTMA⁻ concentration during a typical in vivo experiment is about 3 to 4 mM in the blood and 3 mM in the extracellular space, as previously measured for the protocol used in current the study (1). This relatively high TmDOTMA⁻ concentration achieved in the brain’s extracellular space is due to increased blood-brain concentration gradient, which presumably helps to facilitate its passive diffusion. However given the high SNR of 3D CSI data shown here, we believe that the TmDOTMA⁻ infusion dose can be decreased. This method requires renal ligation. To overcome this surgical limitation, we are currently conducting studies to implement pharmacological means to temporarily inhibit renal clearance. Future biodistribution studies with surgical and pharmacological renal intervention could allow detailed examination of how ubiquitously TmDOTMA⁻ is distributed in different tissues. Prior studies from other laboratories have shown that agents similar to TmDOTMA⁻ are widely distributed throughout the body (27,28). The relatively homogenous biodistribution of these lanthanide-based agents suggest that BIRDS can be successfully applied not only for brain but also for BIRDS measurements in other organs. [R2.1][R3.2][R3.3][R3.4]

RF or B₁ variations due to use of a surface coil (Fig. 2 and Fig.3) were observed in the TmDOTMA⁻ intensity. This is precisely the reason why the TmDOTMA⁻ signal is not observed further beyond the hippocampus or superior colliculus. However no B₁ corrections were necessary as long as the chemical shift of TmDOTMA⁻ could be measured accurately with sufficient SNR. Moreover, because the T₂ of TmDOTMA⁻ is extremely short (< 5 ms), the TmDOTMA⁻ signal is not significantly sensitive to static field inhomogeneity or B₀ shim effects, (i.e., linewidth of >100 Hz). The smaller intensities of TmDOTMA⁻ at the top of the phantom (Fig. 2) and in the outermost layers of the cortex (Fig. 3) are due to partial volume effects. However, these smaller intensities do not affect the results because the BIRDS estimate of temperature is only dependent on chemical shift. [R2.2] [R2.3]

In summary, current results demonstrate a significant improvement in 3D spatial resolution for BIRDS compared with the previously obtained 2D CSI experiments, while keeping the same temporal resolution at 5 minutes. 3D CSI acquisition with RESEGAW encoding increases the spatial resolution by one order of magnitude, by decreasing the effective voxel size from 12 µL to 1 µL. Acquisition of high spatiotemporal resolution isotropic 3D CSI datasets from whole rat brain has numerous applications for physiological imaging, such as functional activation during somatosensory stimulation and/or selective brain cooling. The high spatiotemporal resolution achieved with TmDOTMA⁻, and presumably similar agents (1,2,9,29), demonstrates that 3D CSI acquisition with RESEGAW encoding could be successfully used for molecular mapping with BIRDS.

Abbreviations

BIRDS

biosensor imaging of redundant deviation in shifts

DOTP⁵⁻

1,4,7,10-tetraazacyclododecane-N,N’,N’’,N’’’-tetra methylene phosphonate

DOTMA⁴⁻

1,4,7,10-tetramethyl 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetate

CSI

chemical shift imaging

MRI

magnetic resonance imaging

MRS

magnetic resonance spectroscopy

SNR

signal-to-noise ratio

PSF

point spread function

RF

radio frequency

RESEGAW

reduced spherical encoding with gaussian weighting

SLR

Shinnar-Le Roux

TR

recycle time

FOV

field of view