Multiple Echo Diffusion Tensor Acquisition Technique (MEDITATE) on a 3T clinical scanner

Abstract

This paper describes the concepts and implementation of an MRI method, Multiple Echo Diffusion Tensor Acquisition Technique (MEDITATE), which is capable of acquiring apparent diffusion tensor maps in two scans on a 3T clinical scanner. In each MEDITATE scan, a set of RF-pulses generates multiple echoes whose amplitudes are diffusion-weighted in both magnitude and direction by a pattern of diffusion gradients. As a result, two scans acquired with different diffusion weighting strengths suffice for accurate estimation of diffusion tensor imaging (DTI)-parameters. The MEDITATE variation presented here expands previous MEDITATE approaches to adapt to the clinical scanner platform, such as exploiting longitudinal magnetization storage to reduce T₂-weighting. Fully segmented multi-shot Cartesian encoding is used for image encoding. MEDITATE was tested on isotropic (agar gel), anisotropic diffusion phantoms (asparagus), and in vivo skeletal muscle in healthy volunteers with cardiac-gating. Comparisons of accuracy were performed with standard twice-refocused spin echo (TRSE) DTI in each case and good quantitative agreement was found between diffusion eigenvalues, mean diffusivity, and fractional anisotropy derived from TRSE-DTI and from the MEDITATE sequence. Orientation patterns were correctly reproduced in both isotropic and anisotropic phantoms, and approximately so for in vivo imaging. This illustrates that the MEDITATE method of compressed diffusion encoding is feasible on the clinical scanner platform. With future development and employment of appropriate view-sharing image encoding this technique may be used in clinical applications requiring time-sensitive acquisition of DTI parameters such as dynamical DTI in muscle.

Introduction

Diffusion tensor imaging (DTI) [1, 2] provides biomarkers of tissue anisotropy and microstructure (principal diffusivities (λ₁, λ₂ and λ₃), mean diffusivity (MD) and fractional anisotropy (FA)), which have many applications in oriented biological tissue (e.g. neural fibers [3], renal tubules [4], muscle fibers [5–7]). Typically, the DTI parameters are derived from a set of diffusion-weighted images, most commonly collected with echo-planar imaging (EPI) [8]. Often, each of these images probes diffusion in one direction with one weighting magnitude [9, 10]. The diffusion information encoded in the set of sequential acquisitions is decoded in post-processing in order to estimate a full 3D diffusion tensor.

In an alternative approach, several diffusion directions and/or weightings can be sampled in one acquisition [11–13]. Initial work obtained additional diffusion sampling by adding diffusion gradients to a train of refocused gradient and spin echoes [11]. This was later extended in the Difftrain-approach [14], using a stimulated echo rather than a spin echo preparation. Another possible approach is the generation of several echoes which are subsequently refocused, as in a DANTE-preparation [15] and more comprehensively with the Multiple-Modulation-Multiple-Echo (MMME)-approach [12, 16]. A related class of techniques involve multiple diffusion-weighted coherence pathways that are temporally superposed into steady state composite signals [17–19]. Multiple such signals can be acquired for improved efficiency and quantification [20].

The MMME-pulse sequence family, reviewed in [16], employs multiple echoes in one acquisition to quickly measure multiple MR parameters. MMME applications have included fast imaging [21], flow measurement [22, 23] and most notably, diffusion imaging [12, 16, 24–26]. In the latter approach, dubbed MEDITATE for Multiple Echo Diffusion Tensor Acquisition Technique, a pattern of diffusion gradients between the multiple RF-pulses encodes a train of echoes with each echo having a different diffusion weighting and direction. In a pre-clinical setting, the MEDITATE-sequence was shown to estimate full three-dimensional diffusion tensor maps in five encodings [25]. A subsequent non-spatially resolved variant showed that the diffusion tensor can be acquired in two shots [26]. However, translation of the latter to a clinical setting is nontrivial due to hardware and SNR limitations. Most importantly, the lower gradient strengths available in a clinical setting necessarily lengthen the sequence timing. This limits the SNR attainable with the MEDITATE method in materials with a short T₂, a problem which affects the common EPI DTI method less severely.

In this study, we introduce a variation of the MEDITATE sequence, expanding the possibilities of the MMME-pulse sequence family. This method overcomes the limitations of scanner hardware and in vivo short T₂-relaxation time (e.g. in muscle tissue [27]) present in previous versions of the MEDITATE sequence, by exploiting longitudinal magnetization decay. Multiple stimulated and spin echoes are diffusion encoded utilizing a MMME magnetization preparation module. The resulting longitudinal magnetization is then read out by a train of pulses. Additional diffusion gradients further add to the diffusion weighting of the echoes and expand their directional sensitivity. The diffusion contrast is isolated from flip angle and relaxation effects via a weighted reference scan. This approach allows an estimation of the apparent 3D diffusion tensor in as few as two acquisitions, one diffusion weighted scan and one reference scan. Multiple diffusion-weighted echo sets with complementary encoding patterns can be included in the inversion if time permits their collection. In the present work, we consider two cases: 2 diffusion-weighted scans and 1 reference scan, and the minimal 1 diffusion-weighted scan and 1 reference scan (referred to herein as the three and two dataset methods). When combined with appropriate k-space trajectories, the compressed diffusion encoding approach may allow time-resolved DTI.

In this paper, we will describe the adaptation of the original MEDITATE-method [16, 25, 26] to the current method (Figure 1a). First, in the Theory section, we will discuss the diffusion weighting encoding and its optimization. Secondly, we will present simulations of the impact of noise and time-dependent diffusion on the apparent diffusion contrast and of the directional variance of MEDITATE. Next, the feasibility and results of the method will be demonstrated in an isotropic phantom, a fibrous phantom, and within in vivo human skeletal muscle using a clinical MRI scanner. Finally, in the discussion section, we will summarize results, comment on limitations, and consider future applications of this encoding scheme.

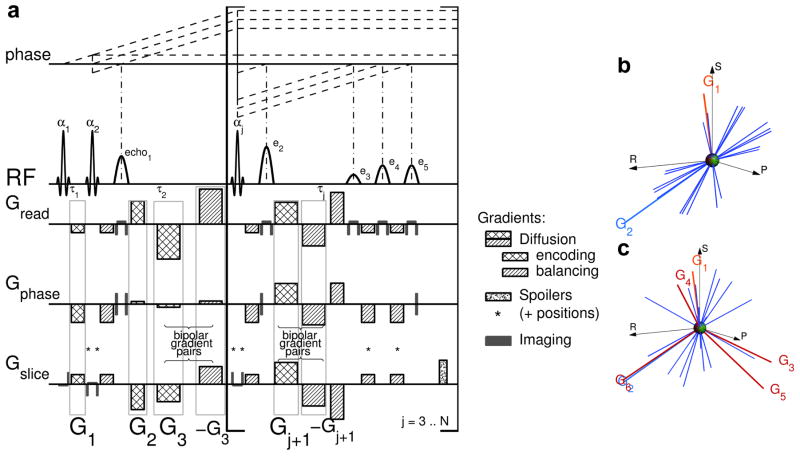
Figure 1.

MEDITATE diffusion tensor acquisition technique. a) The N sinc-shaped slice selective RF-pulses with flip angles α_j separated by time constants τ_j generate a series of (N − 2) × 4 + 1 separate echoes, according to the plotted coherence pathways (dashed lines, only reflecting RF induced phase changes and only including eventually refocused echoes). Each of these echoes carries a different diffusion weighting and direction, as encoded by the diffusion gradient vectors G⃗_j, j = 1..(N + 1) (checkered areas) and their associated rebalancing gradients (hatched areas). Spoiler gradients (speckled areas and included in other gradients on positions labeled *) spoil the remainders of the not retained coherence pathways. (The gradient areas reflect the actual gradient moments whose durations along different physical axes are slightly unequal to minimize slew rate gradient stimulation effects.) b,c) Visual representation of the gradient vectors and the normalized diffusion directions (blue lines, ${\nu }_{b,Q}=(\sqrt{b_{xx,Q}},\sqrt{b_{yy,Q}},\sqrt{b_{zz,Q}})/\Vert (\sqrt{b_{xx,Q}},\sqrt{b_{yy,Q}},\sqrt{b_{zz,Q}})\Vert$ [25,26]) encoded by only G⃗₁ and G⃗₂ (b) and by all diffusion gradients G⃗_j, j = 1..(N +1) (c). In (b), the diffusion directions populate a single plane determined by G⃗₁ and G⃗₂, gradients G⃗_j, j = 3..(N + 1) push the diffusion directions out of this plane (c) in order to sample all diffusion directions.

Theory

Coherence pathway formalism

In this paper, we will use the coherence pathway formalism [12,16,28–32], an alternative but formally equivalent notation to the echo pathway description [33, 34], to calculate the echo times, relaxation, and diffusion weighting of each echo in the sequence. In short, the amplitude of each echo in the sequence can be expressed as a product of the total magnetization M₀ with three factors

$$M_Q=M_0·A_Q·B_Q·C_Q$$ (1)

each a function of the coherence pathway Q leading to the echo. Neglecting off-resonance effects, A_Q depends only on the RF-flip angles α_i and phases φ_i, B_Q depends on spin relaxation weighting (T₁, T₂) and the time-spacing τ_j between the RF-pulses and C_Q accounts for the diffusion weighting experienced along the coherence pathway

$$C_Q=exp\left(-\sum _{mn}{b}_{mn,Q}{D}_{mn}\right)$$ (2)

with D_mn the diffusion tensor elements and m and n = x, y, z. The diffusion weighting factors b_mn,Q can be calculated in the standard way [12,25]

$$b_{mn,Q}={\int }_0^{{TE}_Q}{k}_{m,Q}(t)k_{n,Q}(t)\text{d}t$$ (3)

$$k_{m,Q}(t)=\gamma {\int }_0^t\mu (t^{\prime })G_m(t^{\prime }){\text{d}t}^{\prime },$$ (4)

with G⃗ the gradient waveform including imaging and spoiler gradients, TE_Q the echo formation time and μ(t) the instantaneous value of the magnetization state of Q (0, +1 or −1 for the three states of spin magnetization of an ensemble of spin-1/2 nuclei M₀ = M_z, $M_{+}=(M_x+{iM}_y)/\sqrt{2}$ and $M_{-}=(M_x-{iM}_y)/\sqrt{2}$). When choosing the amplitude and timing of diffusion gradients in this method, the echo formation condition expands to [25]

$${\int }_0^{{TE}_Q}\mu (t)\overrightarrow{G}(t)\text{d}t=0.$$ (5)

Equation (5) needs to be fulfilled for each coherence pathway Q generating a measured echo.

In order to analyze the diffusion effects encoded in the echo amplitudes, C_Q needs to be separated from the nondiffusive elements in Eq. (1) [12,25]. Although the RF- and relaxation factors A_Q and B_Q can be directly calculated when flip angles and relaxation times are known, this approach fails in the presence of B₁-field inhomogeneities. A more robust method [26] acquires a reference experiment M_Q,0 with low diffusion weighting and identical RF-pulses and timing as the weighted experiment M_Q. As a result the factors A_Q and B_Q in (1), i.e. the effects of spin relaxation (T₁, T₂), RF-flip angles α_i and flip angle inhomogeneities, can be normalized out

$$\frac{M_Q}{M_{Q,0}}=\frac{A_Q·B_Q·C_Q}{A_Q·B_Q·C_{Q,0}}=\frac{C_Q}{C_{Q,0}}=exp\left(-\sum _{mn}(b_{mn,Q}-b_{mn,Q,0})D_{mn}\right).$$ (6)

The RF-pulse flip angles α_i are chosen to minimize variations of the product of the magnetization fraction A_Q and the relaxation weighting B_Q between the coherence pathways. That is, optimal RF-flip angles maximally equalize the analytical expressions of A_Q ×B_Q for all retained echoes, in contrast to earlier work which did not consider the relaxation weighting B_Q in the flip angle optimization [12, 16, 25]. For the 5 RF-pulse sequence (Figure 1a; human muscle T₁ = 1420 ms, T₂ = 32 ms at 3T [27]) the optimal angles are calculated to be 61°-73°-100°-45°-90°.

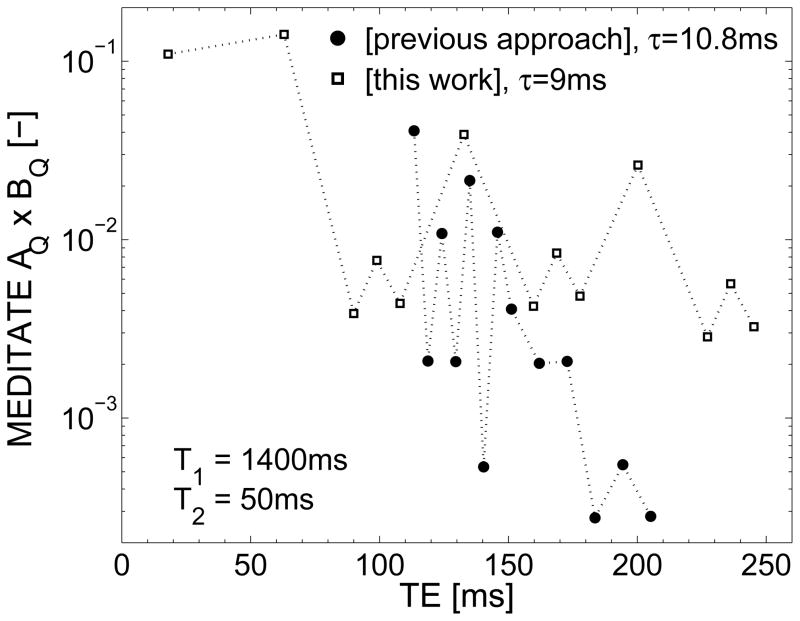
In previous work on the MEDITATE diffusion sequence [16, 25, 26], it was shown that the full apparent diffusion tensor can be estimated in two shots in a spectroscopic approach [26]. However, the lower gradient strengths available on clinical scanners require longer timing τ_i to achieve the same diffusion weighting. In combination with the low T₂ of e.g. human muscle (muscle T₂ = 32±2 ms at 3T [27]), this proved to be detrimental for the SNR of the latter 9 echoes in the measurement (Figure 2).

Figure 2.

The magnetization fraction remaining after relaxation effects A_Q × B_Q (Equation (1), T₁ = 1400 ms and T₂ = 50 ms) of each echo of the previous version [16, 25, 26] and the new variation (with 5 RF-pulses, figure 1a) of the MEDITATE sequence, using typical timing schemes. By utilizing longitudinal magnetization storage, more magnetization is retained in the latter echoes of the MEDITATE variation presented in this work.

Diffusion and spoiler gradients

Here, we introduce a new variation of the MEDITATE method (Figure 1a). This variation discards the coherence pathways which experience long periods of transversal magnetization decay in favor of coherence pathways dominated by longitudinal magnetization decay. That is, the first two RF-pulses generate a set of 4 coherence pathways (Figure 1a), each split by the third RF-pulse into three different pathways. One set of four pathways is refocused and generates echoes 2–5 (Table 1). A second set of four coherence pathways experiences transversal magnetization decay (not plotted in Figure 1a) and when T₂ is short, any future echoes generated from these latter coherence pathways will suffer from low SNR. In contrast, the third set of coherence pathways undergoes longitudinal magnetization decay and is subsequently refocused to generate echoes 6–9 (Table 1). This can be repeated several times to generate a train of echoes, each RF-pulse adding 4 echoes. A similar method retaining all echoes, called stimulated MMME, was suggested earlier by Song et al [12].

Table 1.

Coherence pathways Q of the MEDITATE method described here with N = 5 RF-pulses. μ(t), the instantaneous value of the magnetization state of Q, is piecewise constant with values μ_j in the interval between the RF-pulses j and j + 1, where μ_j can be 0, +1 or −1 for the three states of spin magnetization of an ensemble of spin-1/2 nuclei M₀ = M_z, $M_{+}=(M_x+{iM}_y)/\sqrt{2}$ and $M_{-}=(M_x-{iM}_y)/\sqrt{2}$. When N > 5, the last four coherence pathways are repeated with {μ₃ ··· μ_N−1 μ_N} = {0 ···0 −1}.

Echo Number	Q = {μ0 μ1 μ2 μ3 ··· μN}
	μ0	μ1	μ2	μ3	μ4	μ5
1	0	1	−1
2	0	1	0	−1
3	0	−1	1	−1
4	0	0	1	−1
5	0	1	1	−1
6	0	1	0	0	−1
7	0	−1	1	0	−1
8	0	0	1	0	−1
9	0	1	1	0	−1
10	0	1	0	0	0	−1
11	0	−1	1	0	0	−1
12	0	0	1	0	0	−1
13	0	1	1	0	0	−1

The diffusion gradients, on three axes (Figure 1a, checkered and hatched areas), encode the diffusion weighting and direction of each coherence pathway according to Equation (3). The diffusion encoding of each echo is determined by the choice of 3 × (N + 1) diffusion gradient amplitudes (G_1x, G_1y, G_1z, G_2x, G_2y, G_2z, …, checkered areas in Figure 1a) where N is the number of RF-pulses. All other gradient lobes (Figure 1a, hatched areas) follow from the coherence pathways (Table 1) and the echo formation condition (Equation (5)) [24,25]. These diffusion gradients comprise N + 1 three-dimensional encoding vectors G⃗_j = (G_jx, G_jy, G_jz)/||(G_jx, G_jy, G_jz)|| (Figure 1b). In this pictorial representation, the diffusion gradient vectors G⃗₁ and G⃗₂ define a plane in which the normalized diffusion vectors ${\nu }_{b,Q}=\left(\sqrt{b_{xx,Q}},\sqrt{b_{yy,Q}},\sqrt{b_{zz,Q}}\right)/\Vert \left(\sqrt{b_{xx,Q}},\sqrt{b_{yy,Q}},\sqrt{b_{zz,Q}}\right)\Vert$, an approximate representation of the effective diffusion-weighting direction of each echo [25, 26], are directionally distributed. Indeed, G⃗₁ and G⃗₂ encode two diffusion directions in the spin magnetization which form a basis for each group of four echoes. While the representation using the diffusion vectors ν_b,Q is not formally equivalent to that used for more conventional diffusion sampling, this representation gives a useful intuition of the diffusion encoding.

In addition to the diffusion gradient vectors G⃗₁ and G⃗₂, a second group of diffusion gradients (Figure 1a, G⃗₃ to $\overrightarrow{G_{N+1}}$), was added to the sequence. These bipolar gradients, grouped in diffusion gradient vectors $\overrightarrow{G_j}=\left(\overrightarrow{G_{jx}},\overrightarrow{G_{jy}},\overrightarrow{G_{jz}}\right)$, add to the diffusion encoding in arbitrary directions. Since the bipolar gradient waveform is self-refocused, they do not disturb the balanced gradient pattern of G⃗₁ and G⃗₂. G⃗₃ impacts all but the first coherence pathway, whilst vectors G⃗₄ to G⃗_N+1 only change the diffusion encoding of the three coherence pathways, which are transversal at that time and subsequently form echoes. As depicted in Figure 1c, these diffusion gradients help to push the effective diffusion directions out of the plane determined by G⃗₁ and G⃗₂ (Figure 1b). They are accommodated by a time τ_G added to each RF-time interval except the first.

In this method, echoes are discarded when they experience long periods of transversal magnetization decay along their coherence pathway. Nevertheless, remainders of these coherence pathways and other free induction decays must be spoiled to prevent interference with desired signals. Spoiler gradients are added before RF-pulses number 4 to N (Figure 1a, speckled areas), to the de- and rephasers of the slice selective gradients of RF-pulses number 2 and 3, and wherever needed to balance the gradients of each coherence pathway [13,35] (Figure 1a, *). Furthermore, potential coincident echoes are minimized by a slight delay added to some of the latter RF-pulse time intervals (e.g. when N > 4, ${\tau }_3\to {\tau }_3+\frac{1}{4}{\tau }_1$, when N > 5, ${\tau }_4\to {\tau }_4+\frac{1}{8}{\tau }_1$, …). The calculation of the diffusion weighting factors b_mn,Q (Equation (3)) is straightforward, and must incorporate the imaging and spoiler gradients [36].

Diffusion gradient pattern optimization

Optimal diffusion sampling schemes, optimization methods and comparison metrics are the subject of much research [8–10, 37, 38] and include some guiding features as geometrical considerations, minimum repulsion energy of the diffusion directions or minimal noise propagation. More recently, diffusion sampling schemes have been devised for higher order tensor fitting or specific applications (e.g. [39, 40]). The MEDITATE method exhibits a more limited flexibility in the choice of diffusion sampling directions than conventional diffusion tensor sequences. Despite this limitation, favorable diffusion sampling schemes can be obtained, as described in this section.

The diffusion tensor elements D_mn can be extracted from measurements M_Q and M_Q,0 (Equation (6)), following the conventional processing. This equation can be written in linear form

$$\overrightarrow{m}=B·\overrightarrow{D}$$ (7)

when considering P echoes and where m⃗ = [−ln(M_Q/M_Q,0)₁, …, −ln(M_Q/M_Q,0)_P]′, D⃗ = [D_xx, D_yy, D_zz, D_xy, D_yz, D_xz]′ and

$$B=\left(\begin{array}{cccccc}{b}_{xx,1}& b_{yy,1}& b_{zz,1}& 2b_{xy,1}& 2b_{yz,1}& 2b_{xz,1}\\ ⋮& ⋮& & & & ⋮\\ b_{xx,P}& b_{yy,P}& b_{zz,P}& 2b_{xy,P}& 2b_{yz,P}& 2b_{xz,P}\end{array}\right)$$ (8)

with each element b_mn,Q representing b_mn,Q – b_mn,Q,0. One scalar metric quantifying the quality of the diffusion sampling scheme [8, 9] is the condition number of the matrix B [37] which measures how the relative errors propagate from the observed signals (δm⃗) to the calculated parameters (δD⃗)

$$\Vert \frac{\delta \overrightarrow{m}}{\overrightarrow{m}}\Vert \le \text{cond}(B)\Vert \frac{\delta \overrightarrow{D}}{\overrightarrow{D}}\Vert$$ (9)

as derived from the standard theory of error propagation [8,37], with

$$\text{cond}(B)=\Vert B\Vert \Vert B^{-1}\Vert .$$ (10)

Here ||B|| equals the largest singular value of B and B⁻¹ may represent the pseudoinverse if B is not a square matrix. In practice, condition numbers for conventional DTI sampling schemes were shown to lie in the range of 1.3 to 2 [8,9,37].

The variables for optimization in the variation of the MEDITATE method are the 3 × (N + 1) elements of the diffusion gradient vectors G⃗₁ to $\overrightarrow{G_{N+1}}$ (Figure 1a, 18 optimization variables for a 5 RF-pulse version of MEDITATE). An extra optimization variable was added to represent the relative amplitude of the gradients in the reference experiment M_Q,0. The main optimization parameter was the condition number (Equation (10)). In addition, the optimization was constrained by adding penalty terms to the optimization parameter to guide the mean isotropic b-value ([1], $\overline{b_{\mathit{iso}}}=\overline{(b_{xx,Q}+b_{yy,Q}+b_{zz,Q})}$ with Q = 1..P) to a preset value, as well as to warrant minimum gradient strengths for the elements of the diffusion gradient vectors. It is clear that in this large parameter space any optimization algorithm will only find local minima. In order to close in on the absolute minimum more seed points are chosen and/or the calculation time is increased. We used a direct search optimization algorithm [41] combined with a mesh adaptive search algorithm [42], as implemented in Matlab (The Mathworks, Natick, MA, USA), to optimize the condition number of the encoding matrix B. In a first step, ~ 500 seed points were tried in short optimizations with high termination tolerance, generating the 50 most promising seed points for a more profound optimization with low termination tolerance in the second step. Although we cannot be sure that the absolute minimum condition number was reached, we conjecture that some of the lower local minima were found as several of the optimizations in the second step returned similar endpoints. For the setup described below the lowest condition numbers found were 4.42 (two dataset method) and 3.77 (three dataset method).

Simulations: Time-dependent diffusion and noise impact

The different echo times in this method can influence the resulting apparent diffusion parameters when the diffusion coefficient is time-dependent, e.g. for restricted diffusion. To estimate the extent of this influence, echo amplitudes, simulated using Equation (2) and the sequence parameters from table 2, were fitted with the signal Equation (7). Input diffusion parameters D(t), used to derive diffusion tensor parameters at each echo time t = TE, are calculated according to the short-time $\sqrt{t}$-expansion [43–45]

Table 2.

Pulse sequence parameters of the MEDITATE sequence (3 and 2 datasets of 13 directions, that is, two or one diffusion weighted datasets and one reference dataset) with timing parameters τ₁ = 9.0 ms and τ_G = 18.0 ms and echo times TE = 18.0–245.2 ms. In each combination, the first diffusion gradient set is used for the reference dataset.

datasets	biso [s/mm2]	cond(B) [−]	Diffusion gradient moments [mT/m·ms]
			G⃗1	G⃗2	G⃗3
3	8–810	3.77	(−16,−11,−10)	(−11,11,11)	(193,−66,−35)
			(−66,60,−97)	(88,124,−98)	(−35,−22,−87)
			(−63,−88,32)	(97,−83,−65)	(142,−58,−135)
			G⃗4	G⃗5	G⃗6
			(9,−33,110)	(108,131,−6)	(−20,−10,−25)
			(−61,−428,259)	(284,142,−349)	(261,263,−256)
			(−14,−366,−10)	(35,−33,−22)	(86,−264,−23)
			G⃗1	G⃗2	G⃗3
2	10–790	4.42	(−15, −29,14)	(28, −11, −46)	(−6,250,30)
			(−52, −110,58)	(87, −94, −96)	(−367,229, −312)
			G⃗4	G⃗5	G⃗6
			(−60,62,135)	(−30, −77,10)	(−221,119,44)
			(315, −32,217)	(22, −313, −184)	(228, −296, −315)

$${\lambda }_{\mathit{axial}}\simeq {\lambda }_{\mathit{axial},0},{\lambda }_{\mathit{rad}}(t)\simeq {\lambda }_{\mathit{rad},0}\left[1-\frac{S}{Vd}\left(\frac{4\sqrt{{\lambda }_{\mathit{rad},0}t}}{3\sqrt{\pi }}-\kappa t\right)\right]$$ (11)

with λ_axial the primary diffusion eigenvalue and λ_rad = (λ₂ + λ₃)/2 the radial diffusion value, using male human calf muscle parameters derived from time-dependent MR diffusion measurements [8, 45] (fiber size a 61μm ( $a=\frac{2Vd}{S}$, where $\frac{S}{V}$ is the surface-to-volume ratio and d the dimensionality, 2 for diffusion in a cylinder), membrane permeability κ 20 μm/s, D₀ 1.52 μm²/ms (D₀ = (λ_axial + 2λ_rad)/3) and FA 0.4 (parameters for t = 1s); assuming mono-exponential T₁ and T₂-relaxation). Similar analysis of an isotropic (water) and an anisotropic medium (asparagus stalks (fiber size a 50μm, κ 0.01 10⁻⁶ μm/s, D₀ 1.9 μm²/ms, simulation parameters chosen based on asparagus D(t) measurements and consistent with both MRI and microscopic imaging [22,46]) ) allows for the comparison between time-dependent diffusion D(t) (asparagus stalks) and time-independent diffusion (water).

Simulations were repeated for different SNR-levels with Rician noise added to the echo amplitudes at every iteration. At each SNR-level, 400 samples were generated, the actual SNR was determined, and each sample was fitted individually to Equation (7). The resulting apparent diffusion parameters and their standard deviation across the 400 trials were compared with the diffusion parameters at one diffusion time (Δ = 140 ms, average of the echo times, Table 2).

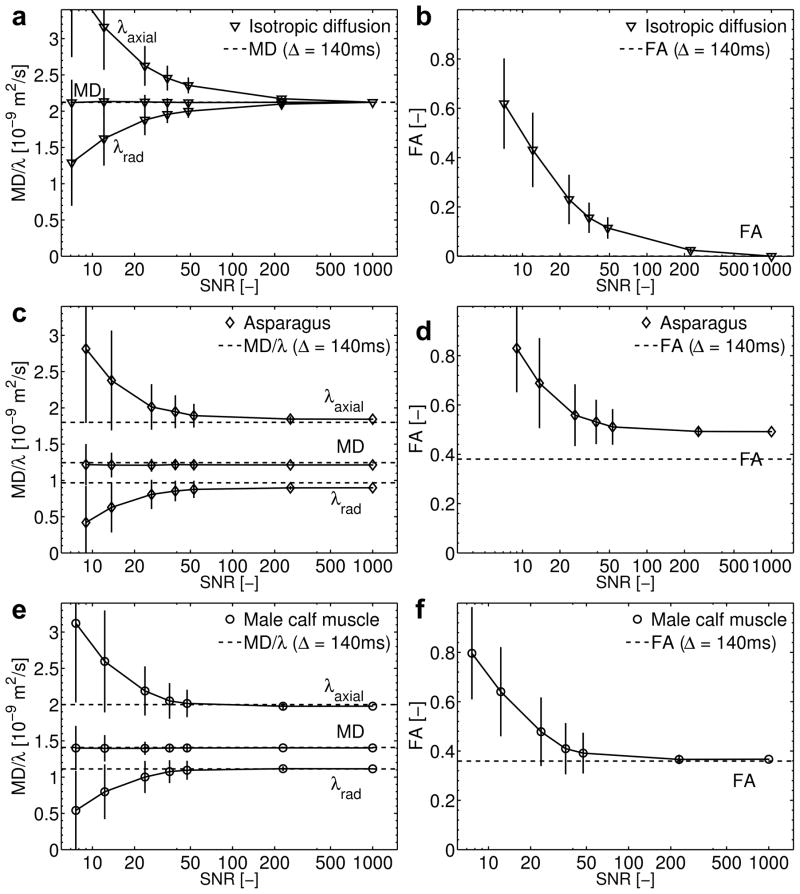
The apparent diffusion parameters derived from the simulation results are summarized in Figure 3. As the SNR-level decreases, the fitted apparent diffusion parameters deviate from the noiseless results; the FA and λ_axial increase and λ_rad decreases. Despite this eigenvalue splitting, the MD remains stable at lower SNR levels.

Figure 3.

Simulations of the impact of time-dependent diffusion and noise on diffusion parameters as would be measured with the MEDITATE sequence (2 series of 13 echoes): Mean Diffusivity (MD)/Eigenvalues (λ_axial and λ_radial) and Fractional Anisotropy (FA) as a function of measurement SNR of a,b) an isotropic medium (water), c,d) an anisotropic medium (asparagus stalks) [46] and e,f) in vivo (male) calf muscle [8,45]. The derived apparent diffusion parameters (mean and standard deviation calculated from 400 samples) are compared to input diffusion parameters (MD and FA) at a diffusion time of 140 ms (dashed lines).

Notwithstanding the range of echo times (Table 2), the fitted apparent diffusion parameters approach the diffusion parameters at Δ = 140 ms with an accuracy depending on the measurement subject. That is, the diffusion parameters are estimated precisely when diffusion is not restricted (water) and SNR is high (water, error of estimate at SNR = 1000, MD: 0%). As the SNR decreases or diffusion time-dependence becomes more pronounced over the time range measured, which occurs more strongly in asparagus stalks (Figure 3c) than in human calf muscle (Figure 3e), the accuracy of the diffusion parameter estimates decreases (error of estimate at SNR = 1000; asparagus, MD: 2.5%, FA: 29%; muscle, MD: 0.06 %, FA: 3%). Hence, depending on the precise nature of the diffusion parameter time dependence, FA and the diffusion eigenvalues might be estimated differently than conventional methods; these simulations suggest that FA might be overestimated. However, we expect that relative differences in scalar DTI metrics between successive measurements acquired with the same protocol will be robust imaging markers for individual or group evaluations.

Simulations: Directional variance

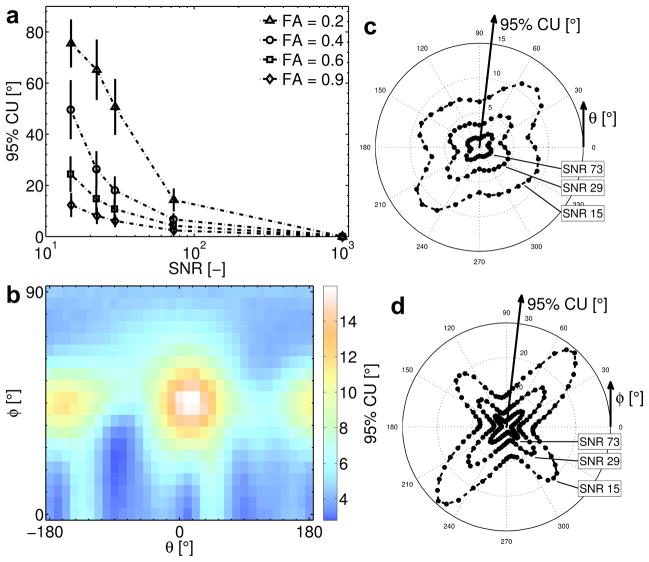
In the MEDITATE sequence, the diffusion encoding directions can not be chosen arbitrarily, rather they are the result of an optimization procedure which also considers timing and maximum gradient strength (see above). As a result, diffusion tensor orientation estimates might be influenced by the diffusion directions selected. The extent of this influence is assessed by computing for each tensor orientation with the 95% cone of uncertainty [47], which is the 95% percentile of the angular deviation between the principal eigenvector of 5000 simulated noisy datasets and their dyadic mean tensor. For these calculations, the tensors (constant MD of 1.5 10⁻⁹ m²/s, varying FA and SNR [47]) were rotated using a similarity transform to 660 different orientations uniformly spaced over the hemisphere. The echo amplitudes of each tensor were simulated using Equation (2) and the sequence parameters from table 2; Rician noise was added to 5000 copies of this dataset and the resulting echo amplitudes were fitted with the signal Equation (7). From the estimated (noisy) diffusion tensors, the 95% confidence intervals were calculated [47].

The computed 95% cone of uncertainty values (Figure 4) indicate that the directional variance will increase with decreasing SNR and decreasing FA (Figure 4a) as can be expected. In addition, the confidence angle of the estimated tensor orientation depends on the it’s orientation relative to the diffusion gradients, with a better performance along the main axes (Read θ/φ = 0/0, Phase θ/φ = 90/0 and Slice θ/φ = 0/90) than along the Read = Phase (θ/φ = 45/0) and Read = Slice (θ/φ = 45/45) directions.

Figure 4.

Simulations of the directional variance of the diffusion encoding scheme of the MEDITATE sequence (2 series of 13 echoes): 95% confidence angles or cone of uncertainty [47] a) averaged over all tensor orientations as a function of measurement SNR and FA; b,c,d) as a function of the azimuth and elevation angles (θ and φ) of the tensor (FA = 0.9, MD = 1.5 10⁻⁹ m²/s) in surface (c, SNR = 29) and polar plots (b,d). 95% cones of uncertainty are taken as the 95% percentile over 5000 samples for each tensor orientation.

Methods

All images in this work were acquired using a 3T wide-bore Siemens Skyra scanner (Erlangen, Germany) with a 15-channel knee coil (QED, Mayfield Village, OH, USA). For comparison of the accuracy and directional diffusion sensitivity of the MEDITATE-method (not the time efficiency) axial DTI was performed using a Spectral Adiabatic Inversion Recovery (SPAIR) fat-saturated twice refocused spin echo diffusion sequence (TRSE) with echo-planar imaging readout [48] (TR / TE = 7400 ms / 59 ms, 64 × 64 × 5 matrix, 3 × 3 × 10 mm resolution, 6 directions, b = 0,500 s/mm², 3 averages, scan time 2:59 min (not optimized for time)).

The MEDITATE-sequences were implemented with a fully segmented Cartesian acquisition scheme, i.e. one k-space line for all echoes was collected per shot. All MEDITATE-acquisitions had a TR of 4000 ms, a 64 × 64 matrix, 3 × 3 mm resolution and a slice thickness of 10 mm (scan time 4:16 min per diffusion gradient set, hence 8:32 min for the two dataset MEDITATE with one weighted and one unweighted dataset). The mean isotropic b-value encoded in the echoes was 450 s/mm², in accordance with the literature of in vivo skeletal muscle DWI [5–7,49–52]. After optimization, optimal sets of diffusion gradient vector moments G⃗₁ to G⃗_N+1 (Figure 1a) were found as listed in Table 2. The spoiler gradients (speckled areas and included in other gradients on positions labeled with * in Figure 1) were chosen to generate a dephasing of 50π (speckled areas) and 20π (*) respectively over the slice width (e.g. the moment is $\frac{50\pi }{\gamma \mathrm{\Delta }z}$, with Δz the slice thickness). The flip angles α_i were chosen as described above and the RF-timing intervals were (τ₁) - (3 × τ₁ + τ_G) - (4.75 × τ₁ + τ_G) - (4.625 × τ₁ + τ_G) with τ₁ and τ_G as listed in Table 2. The echo time ranges quoted in Table 2 refer to the total time between the first RF pulse and the echo formation time.

The resulting datasets were processed offline in three steps (Matlab, Mathworks). In the first step, a Rician noise-correction algorithm was applied to the diffusion-weighted images [52, 53]. Subsequently, Equation (7) was solved pixelwise to generate maps of diffusion eigenvalues (λ_axial and λ_rad), MD, FA, and FA-weighted color maps. Finally, the diffusion parameters in regions of interest (ROIs) were evaluated by calculating the average and standard deviation over the ROI. Mean axial diffusion eigenvectors were used to calculate the difference angles between the diffusion directions of the TRSE and MEDITATE DTI estimates.

The 5 RF-pulse MEDITATE sequence was validated in three systems: an isotropic sample (agar gel), an anisotropic phantom (asparagus stalks) and in vivo in healthy volunteers. The isotropic sample agar gel was made by dissolving 3.5%(w/w) agar (UltraPure Agarose, Invitrogen, Carlsbad, CA, USA) in tap water (25°C), heating the solution to 80°C and pouring the slightly cooled solution (55°C) into a plastic container. Asparagus stalks have been shown [24,25,46] to exhibit diffusion anisotropy in accordance to their prolate cell structure. More precisely, diffusion along the stalk is approximately 30% larger than transverse to the stalk. In this work, asparagus stalks (fresh from a local grocery store; Organic produce from Peru) were submerged in tap water (1h), after which they were cut to length, and stacked in three directions in a plastic container. The voids were filled with agar gel.

The levels of the right calves with the largest cross-sectional area of five healthy volunteers (3 male and 2 female, age 33.0 ± 3.4 y/o) were scanned under a research protocol approved by the local institutional review board. For the in vivo scan, frequency selective fat saturation was used and the acquisition was triggered using ECG gating (trigger delay of 600ms from the R-wave) [54]. The latter increased the scan time from 4:16 to approximately 5:30 per diffusion gradient set in a subject-specific manner. Regions of interest were manually drawn on both TRSE and MEDITATE images enclosing the anterior tibialis (AT), the posterior tibialis (PT) and gastrocnemius medialis (GM) compartments. Results of DTI metrics were averaged over these ROIs for each subject. The mean and standard deviation of these values across all 5 subjects was computed for each sequence.

Results

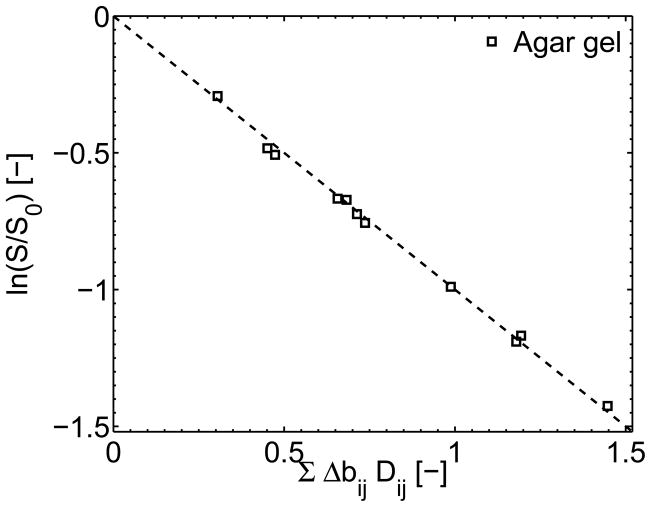
Figure 5 shows the normalized agar gel signal amplitude of the latter 13 echoes of a two-scan 5 RF-pulse MEDITATE sequence as a function of the full diffusion weighting argument, demonstrating the quality of the fit estimating the diffusion tensor D⃗.

Figure 5.

The amplitude ratios of the weighted and unweighted signal of the isotropic diffusion in an agar gel sample as measured with a two dataset 5 RF-pulse MEDITATE sequence plotted versus the full diffusion weighting argument.

The raw images in Figure 6 were acquired with the two-scan 5 RF-pulse MEDITATE sequence (Table 2). In these images, magnitude variations include effects from diffusion, RF pulse flip angles, and relaxation. The effect of relaxation on the signal magnitude can be seen in the stronger T₂ weighting for the in-plane stalks perpendicular to the main magnetic field. These effects are eliminated by forming ratio images, which reflect diffusion contrast alone (Figure 6c).

Figure 6.

Raw images of the 13 last echoes in a MEDITATE sequence with 5 RF-pulses of an anisotropic phantom (asparagus stalks in agar gel) depicted and labeled in order of increasing echo time TE. The mean isotropic b-value $\overline{(b_{xx,Q}+b_{yy,Q}+b_{zz,Q})}$ is 50 s/mm² in the reference scan (a) and 500 s/mm² in the diffusion weighted scan (b). The ratios of (b) and (a) are shown in (c) in order of increasing isotropic b-value.

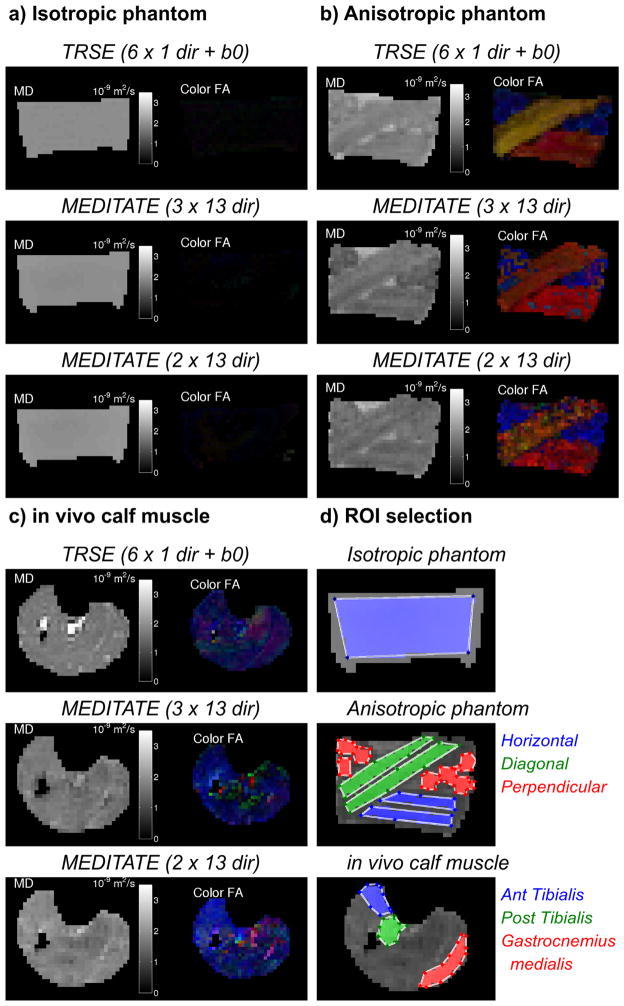
Diffusion-weighted images such as in Figure 6 were analyzed pixelwise with Equation (7). Examples of this DTI-analysis are plotted in Figure 7 which gives an overview of DTI parameter maps as estimated by the conventional TRSE-DTI and 5 RF-pulse MEDITATE-sequences (Table 2). Figure 7 depicts estimated diffusion parameter maps of an isotropic phantom (agar gel), an anisotropic phantom (asparagus stalks) and in vivo calf muscle. ROI analysis of these estimated diffusion parameter maps are plotted in Figure 9, while Figure 8 visualizes the diffusion tensors of the anisotropic phantom with ellipsoidal glyphs (Matlab, fanDTasia toolbox [55]).

Figure 7.

Diffusion tensor parameter maps of the Mean Diffusivity (MD) and Color coded Fractional Anisotropy (Color FA; Red left-right, green anterior-posterior, blue superior-inferior) of an isotropic phantom (a), an anisotropic phantom (b) and in vivo healthy calf muscle of one volunteer (c). DTI-analysis was performed on images obtained with a TRSE-sequence (6 directions + b₀) and the MEDITATE sequence (3 and 2 series of 13 directions, one series is a reference series). (d) ROIs used for further analysis (Figure 9).

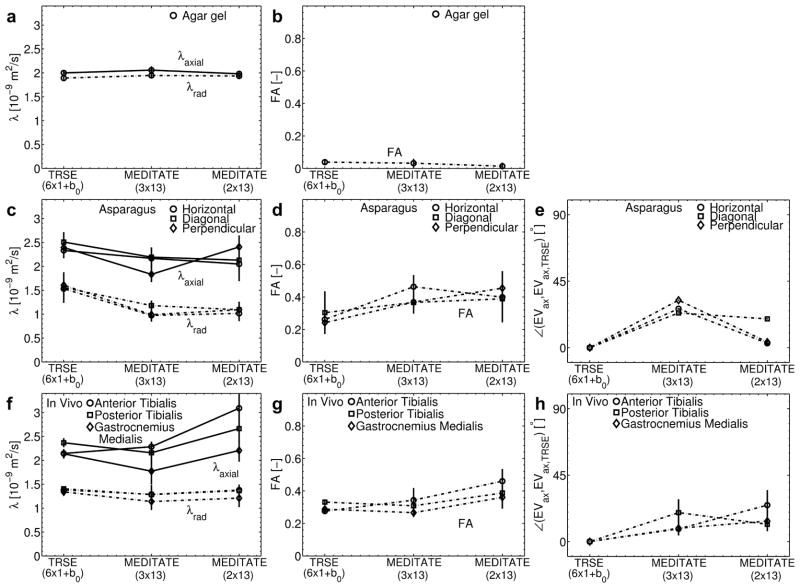
Figure 9.

Comparison of the eigenvalues (λ_axial and λ_radial), Fractional Anisotropy (FA) and the axial diffusion direction (difference angle with the axial eigenvector estimated with the TRSE-sequence) of an isotropic phantom (agar gel) (a,b), an anisotropic phantom (asparagus stalks in horizontal and diagonal in-plane and perpendicular out-of-plane directions) (c,d,e) and in vivo calf muscle (5 volunteers; f,g,h) sampled over a ROI in DTI parameter maps obtained from a TRSE-sequence (6 directions + b₀) and the MEDITATE sequence (3 and 2 series of 13 directions, one series is a reference series) (Example ROIs illustrated in Figure 7d). Phantom eigenvalues and FA are displayed as the mean and standard deviation of values taken from ROIs in the same phantom; the phantom diffusion direction is calculated using the mean axial eigenvector of ROIs. The in vivo results are the mean and standard deviation of DTI parameters across all 5 subjects in the designated ROI.

Figure 8.

Ellipsoidal visualization of the diffusion tensors of an anisotropic phantom superimposed on a b₀-image. DTI-analysis was performed on images obtained with (a) a TRSE-sequence (6 directions + b₀) and (b) the MEDITATE sequence (2 series of 13 directions, one series is a reference series).

Figures 7, 8 and 9 illustrate the agreement between the diffusion tensor parameters estimated with MEDITATE and TRSE-DTI. In the isotropic agar gel (Figure 7a and Figures 9a and 9b), the diffusion eigenvalues are homogeneously high and the FA homogeneously low as expected. The asparagus samples (Figure 7b and Figures 9c, 9d) exhibit λ_axial, λ_radial and FA values in approximate agreement with earlier work [25] for both sequences. Additionally, the asparagus stalk directivity (horizontal, diagonal, or perpendicular to the image plane) is correctly identified in all segments (Figure 9e), however, less accurately in the diagonal direction due to the increased directional variance (Figure 4). In comparison with the diffusion eigenvalues of TRSE-DTI, the diffusion eigenvalues of the asparagus stalks derived from MEDITATE are slightly lower (Figure 9c, λ_axial −10.2%, λ_rad −31.7%), a consequence of the longer diffusion time in the MEDITATE sequence. In general, the asparagus diffusion parameter estimates are relatively robust for the variations of the MEDITATE-sequences tested.

The mean diffusion eigenvalues in the in vivo calf muscle estimated with the 3 and 2 dataset MEDITATE-sequences are, lower (Figure 9f, λ_axial −10.8%, λ_rad −10.2%) and higher (Figure 9f, λ_axial +20.0%, λ_rad −4.2%), respectively, than that of the TRSE-DTI sequence. In addition, the FA is higher in the 2 dataset MEDITATE muscle results, possibly due in part to a residual ghosting artifact in the segmented Cartesian imaging trajectory which is not fully suppressed by the cardiac gating, and in part to higher variance from the higher condition number. However, overall, the estimated diffusion parameters are robust and similar to those found in the conventional TRSE-EPI sequence.

Discussion

In this paper, we present an MRI sequence capable of acquiring apparent diffusion tensor maps in two scans. This method, an adaptation of the MEDITATE-method [12, 24–26], employs a series of diffusion gradients to modulate several echoes with diffusion weighting in both magnitude and direction (Figure 1). Figures 7 and 9 illustrate the capability of MEDITATE to estimate DTI parameters with just three or two encodings. This is a significant compression in diffusion encoding in comparison with more common DTI schemes, which acquire separate scans for at least 6 diffusion encodings and a reference scan,albeit with a faster image encoding.

The diffusion gradient vectors G⃗₃ to $\overrightarrow{G_{N-1}}$ introduced in the MEDITATE sequence increase flexibility in the directional sensitivity of the diffusion weighting. Their impact on the diffusion encoding directivity can be intuitively understood from the pictorial representations of the normalized diffusion vectors in Figures 1b and 1c. In a slightly different approach, the bipolar gradients (G⃗₃ to $\overrightarrow{G_{N-1}}$) can be replaced by monopolar diffusion gradients, adjusting all subsequent diffusion gradients according to the echo formation condition (Equation (5)).

It is interesting to note that, in the MEDITATE sequence family, the diffusion time is not well defined [12]. In the more uniform case of a multiple pulsed gradient spin echo (PGSE), Fordham et al. [56] succeeded in deriving an effective diffusion time. Although an effective diffusion time can be derived for each individual coherence pathway [57], the specific multiple echo structure of the MEDITATE sequence prohibits the definition of a single effective diffusion time. Notwithstanding the lack of well defined diffusion time, the diffusion weighting and direction encoded in each echo are determined very precisely by the diffusion weighting factors (Equation (3)); this information suffices for DTI analysis within the Gaussian diffusion tensor approximation.

In the case of samples with a time-dependent diffusion coefficient D(t), the MEDITATE-sequence has been shown to overestimate [26] or underestimate (Figure 3) the mean diffusivity. Although no diffusion time is defined in this paper for each echo in the MEDITATE sequence, it is clear that each echo will sample a different portion of D(t). This might limit the accuracy of the estimation of diffusion parameters with the MEDITATE sequence [25, 43, 58]. Computer simulations (Figure 3) suggest that the extent of this effect depends on the precise nature of D(t) relative to the diffusion gradient pattern and sequence timing with a larger effect as diffusion time-dependence is more pronounced over the time range measured. At the same time, the computer simulations show that the effect is limited for the systems considered in this study, and that it can possibly be further reduced by incorporating a model for the tissue under study in the optimizations of the diffusion gradient sets. The 2 dataset MEDITATE-sequence underestimates most of the eigenvalues of the measurements with restricted time-dependent diffusion compared to the TRSE-sequence (Figures 9c and 9f). This underestimation relative to the TRSE-sequence stems largely from the difference in diffusion times (TRSE TE = 59 ms, mean MEDITATE TE = 148.2 ms). Simultaneously, computer simulations of the MEDITATE sequence (Figure 3) predict an increased FA and eigenvalue splitting at the measurement SNR levels (asparagus SNR 28.24, in vivo male calf muscle SNR 13.34). An alternative approach might take diffusion time dependence into account with an explicit model in the MEDITATE tensor inversion, but the assumptions and optimizations of such a strategy have not yet been explored.

The DTI parameter estimates obtained with the MEDITATE-method (Figure 9) are fairly robust in spite of a number of limitations. While the differences in magnetization fractions and relaxation weightings are eliminated by the reference experiment (Equation 6) and the differences in diffusion weighting are accounted for by the precise calculation of the diffusion weighting factors (Equation 3), a possible limitation is that some echoes are stimulated echoes and some echoes are spin echoes. Correspondingly, all echoes experience different periods of transverse and longitudinal relaxation. Thus, local magnetic field deviations originating e.g. in magnetic susceptibility differences, might influence the diffusion weighting of the echoes differently. Similarly, for systems like skeletal muscle whose compartmental complexity gives rise to multi-exponential relaxation, the relative importance of the components might vary amongst echoes and thus affect quantification [14]. Further, the MEDITATE analysis assumes Gaussian diffusion behavior and uses b-values within that regime; higher order models (Intravoxel Incoherent Motion (IVIM) [59], Diffusional Kurtosis Imaging (DKI) [60], q-space [61]) are not considered. Likewise, as mentioned above, time-dependent diffusion is not explicitly accounted for in the tensor inversion. Finally, although the echoes display different SNR, no weighting factors were applied in the analysis.

An additional possible limitation of the MEDITATE-method is the resemblance to double wave vector (DWV) experiments [62, 63]. In such DWV experiments, two consecutive PGSE blocks, each with a pair of diffusion gradients, are intended to probe microscopic anisotropy and/or pore ellipticity, where the single PGSE lacks sensitivity [62, 63]. Hence, also the MEDITATE sequence could be susceptible to pore shape and size sensitivities. However, since the sequence was not designed to this end, it does not readily lend itself to the existing formalism. In addition, in the low-q regime, the Gaussian component of the diffusion is the dominating factor. Moreover, as the departure from the underlying Gaussian assumption in the time-dependent diffusion has a limited effect on the DTI estimates, and given formal relationships between this time-dependence and some of the restriction-induced angular modulation inherent to DWV contrast [64], it is conjectured that also the DWV-effects originating from compartment size will have a limited effect on the DTI estimates; i.e. the MEDITATE sequence supplies a fairly robust though approximate estimate of the DTI parameters. However, a full study of the DWV-effects in MEDITATE is beyond the scope of this paper.

The segmented Cartesian sampling scheme used in this implementation of the MEDITATE-method is sensitive to ghosting in the phase encoding direction for the in vivo muscle acquisitions due to motion and cardiac pulsatility of the skeletal musculature [65]. Even though ECG triggering was used to minimize the cardiac pulsatility for the in vivo scans, minimal ghosting could be seen in the raw images. This effect might partially explain the deviations in the estimated in vivo eigenvalues and the higher anisotropy in the in vivo scans (Figures 7 and 9).

The two acquisition 5 RF-pulse MEDITATE sequence significantly compresses the diffusion encoding in comparison to standard DTI acquisition schemes. That is, MEDITATE acquires 13 diffusion encodings of a k-space line in two repetitions where standard DTI acquisition schemes sense one diffusion encoding of the whole k-space per repetition. However, the compressed diffusion encoding has thus far been developed independently from the image encoding scheme, which means that the MEDITATE sequence, with the current segmented Cartesian image encoding, has a lower imaging efficiency than the TRSE sequence (e.g. in vivo SNR = 34.0 versus 54.5 and imaging efficiency γ = 1.07 versus 4.42, with $\gamma =(\text{SNR}/\text{voxel})/\sqrt{T_T}$, T_T the total acquisition time [34]). To reduce the overall scan time in a spatially resolved approach, the suggested compressed diffusion encoding can be combined with an appropriate k-space trajectory, e.g. a radial sampling scheme [66–68]. When also including self-navigation with phase corrections [66,68] and view-sharing [69,70], this sequence may potentially allow time-resolved DTI acquisition in dynamic systems such as mobile skeletal muscle.

The diffusion gradient vector sets for the MEDITATE-sequence (Table 2) constitute diffusion encoding schemes sufficient for 3D DTI. Calculations of the 95% cone of uncertainty (Figure 4) illustrate that the directional variance of the MEDITATE diffusion encoding scheme is higher than e.g. the 6 direction dual-gradient sampling scheme of the TRSE sequence [47]. However, this is mainly problematic in specific tensor directions, e.g. the diagonal direction in the asparagus phantom (Figures 7b and 8b). Whilst the optimization of the diffusion gradient vector sets aimed for a low condition number, additional scalar optimization indices can be considered, such as rotational invariance [38] or minimal DTI parameter variance in a sample set of directions (e.g. [10, 39, 40]). The latter approach could reduce the direction variance of the diffusion sampling and also allow for specialized diffusion sampling optimized for prior knowledge.

In conclusion, we presented an MRI method which compresses the diffusion encoding for DTI. This MRI method is capable of acquiring apparent diffusion tensor maps in two scans, utilizing a slow segmented Cartesian image encoding scheme. The compression of the diffusion encoding is accomplished by modulating multiple echoes, generated by a train of RF-pulses, with diffusion weighting in both magnitude and direction by a pattern of diffusion gradients. The presented MRI sequence is an adaptation of earlier work, limited by low SNR in systems with low T₂, on the Multiple Echo Diffusion Tensor Acquisition Technique (MEDITATE). MEDITATE is adapted here to exploit the longer longitudinal magnetization storage and additional diffusion gradients are added to allow the necessary flexibility in the directional sensitivity of the diffusion weighting. The method is demonstrated in an isotropic phantom, an anisotropic fibrous phantom and within in vivo human skeletal muscle. With future development, this technique may be used in clinical applications requiring time-sensitive acquisition of DTI parameters such as dynamical DTI in muscle.

Abbreviations

MEDITATE

Multiple Echo Diffusion Tensor Acquisition Technique

MMME

Multiple-Modulation-Multiple-Echo

PGSE

Pulsed Gradient Spin Echo

TRSE

twice-refocused spin echo

DTI

Diffusion Tensor Imaging

DWI

Diffusion Weighted Imaging

MD

Mean diffusivity

FA

Fractional Anisotropy

EPI

Echo-planar Imaging

DWV

Double Wave Vector

SNR

Signal to Noise Ratio

ROI

Region Of Interest