Does model-free forecasting really outperform the true model?

Estimating population models from uncertain observations is an important problem in ecology. Perretti et al. observed that standard Bayesian state–space solutions to this problem may provide biased parameter estimates when the underlying dynamics are chaotic (1). Consequently, forecasts based on these estimates showed poor predictive accuracy compared with simple “model-free” methods, which lead Perretti et al. to conclude that “Model-free forecasting outperforms the correct mechanistic model for simulated and experimental data.” However, a simple modification of the statistical methods also suffices to remove the bias and reverse their results.

The instability of both maximum-likelihood and Bayesian inference for chaotic models has been recognized before (2). Deterministic chaos produces quasirandom trajectories that are extremely sensitive to changes in parameters and initial conditions. Likelihoods are therefore often highly irregular in shape (3). Moreover, if there is sufficient noise in either process or observation, “true” chaotic parameters may have lower likelihood than alternative parameters with stable trajectories, effectively devaluating maximum-likelihood as a consistent estimator for chaotic dynamical systems (4). The reason is that, for chaotic models, the smallest amount of noise leads to diverging population trajectories, so that simulations from the same parameters may be further apart from each other in the long run than from a stable trajectory at the time-series mean (Fig. 1B).

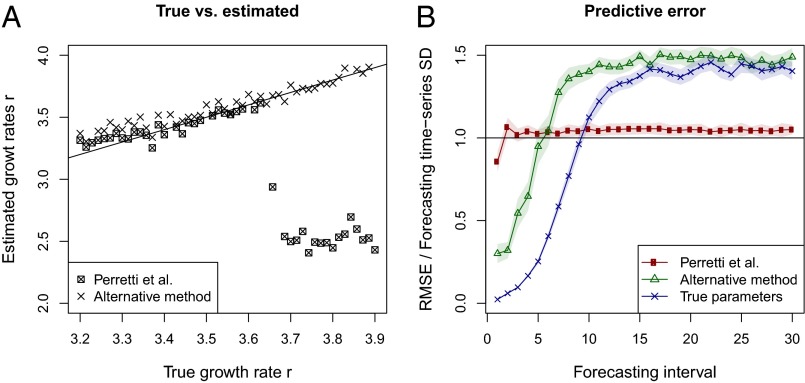
Fig. 1.

Comparison of median posterior parameter estimates for different values of the growth rate r (A) and predictive error for r = 3.7 (B) for the estimation method used by Perretti et al. (1) and our alternative estimation method. For B, we additionally show the predictive error of the true parameters. Predictive error is measured by standardized root mean-square error (RMSE) (1). The shaded area depicts the 95% confidence interval. Note that biased, but stable r values estimated by Perretti et al. have larger short-term but smaller long-term error than the true values.

There are a number of known methods to bypass these problems. Using summary statistics, potentially in an approximate Bayesian framework, is one of them (3, 5). In the case of the chaotic models presented by Perretti et al. (1), however, there is a simpler solution. Because the bias arises from the long-term divergence of the chaotic population dynamics, a simple solution is to divide the time series in smaller subsets and fit the model to those individually (2). We applied this method to the example of the logistic model used in Perretti et al. (1) and obtained parameter estimates that are virtually unbiased. Technical details and code are available at http://arxiv.org/abs/1305.3544. The resulting median parameter estimates show similar dynamics and predictive uncertainty as the “true” model, with lower short-term error than the statistical alternatives (Fig. 1). It seems likely to us that similar results could also be obtained for the other model types examined in Perretti et al. (1).

Perretti et al. (1) highlight a statistical problem in inferring parameters of chaotic dynamics, which is very important, as it is conceivable that the described bias may have gone unnoticed when working with empirical data only. However, our simulations question Perretti et al.’s conclusion that these problems fundamentally render “model-free” approaches superior. As we show, using a simple modification of the statistical method provides a better solution to the problem, without having to give up other advantages of mechanistic models that might also benefit forecasting in the long run, such as transferability and theoretical understanding.