We have shown that statistical methods widely used in ecology and wildlife management to estimate parameters and forecast population sizes fail when the underlying ecological system is chaotic (1). Although we noted that alternative methods exist (1), their general applicability has not been demonstrated. Hartig and Dormann (2) show that the Pisarenko and Sornette method (3) can apply to the logistic model in particular, and can provide reasonable parameter estimates.
Such results satisfy our intuitive expectation that the “true model” ought to work the best, provided we know the true model to begin with. However, one must question whether we ever know the true model in ecology. Rather, we routinely acknowledge that all models are ultimately wrong yet hope that some models provide a useful approximation. Therefore, an extremely relevant issue arising from our original work is the question of how well any explicit model-fitting methods improve our ability to forecast with an approximate but ultimately incorrect model.
To simulate this situation, we generated time series using the theta-logistic model 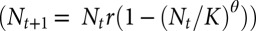 , and then fit the logistic model applying the method used by Hartig and Dormann (2) (source code available at www.arxiv.org/abs/1307.5747). The functional form of the theta-logistic is identical to that of the logistic when a single parameter, θ = 1. We expect, therefore, that the logistic should be a reasonable approximating model.
, and then fit the logistic model applying the method used by Hartig and Dormann (2) (source code available at www.arxiv.org/abs/1307.5747). The functional form of the theta-logistic is identical to that of the logistic when a single parameter, θ = 1. We expect, therefore, that the logistic should be a reasonable approximating model.
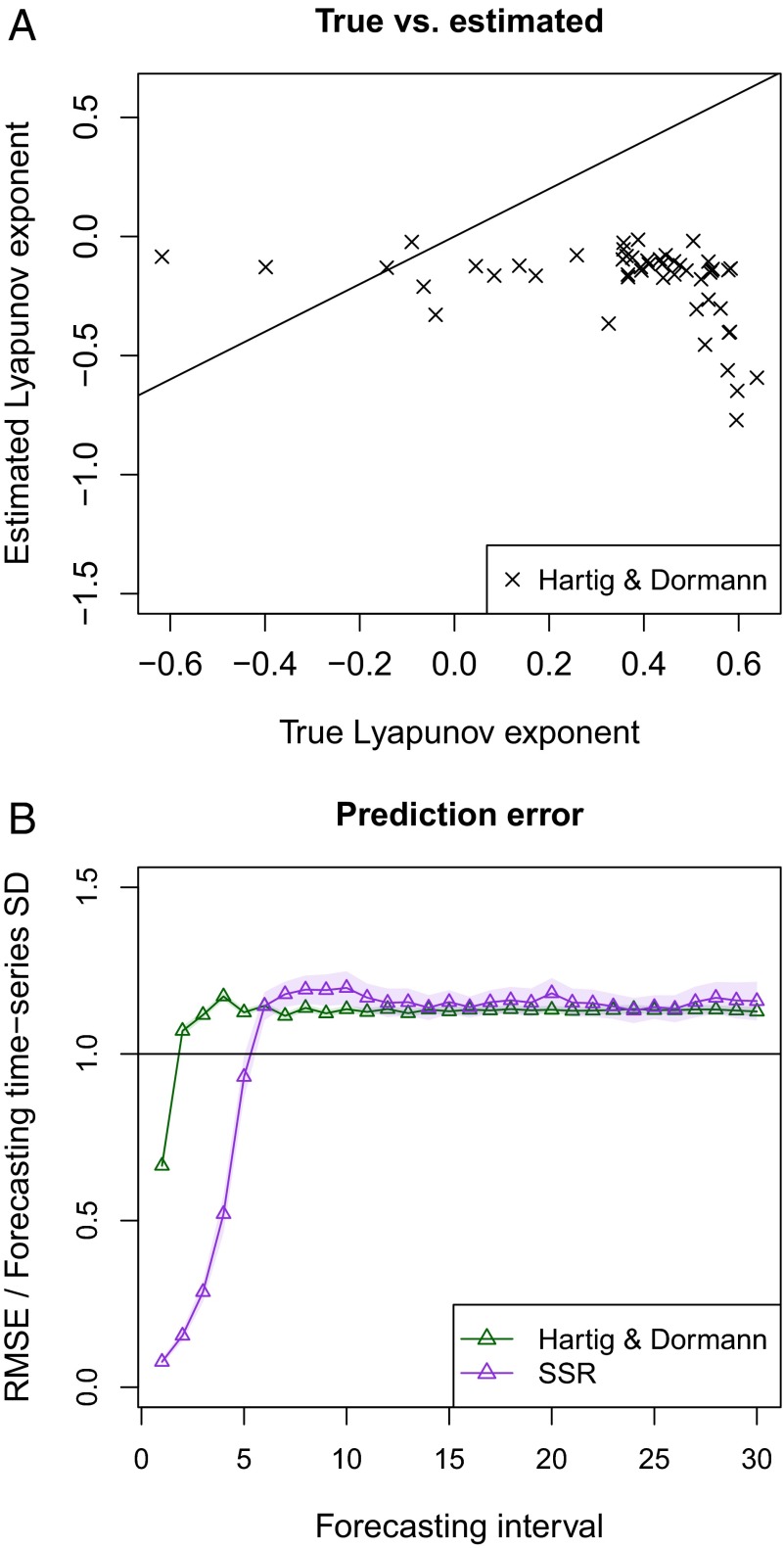
Similar to previous work (4), we find that the model-fitting method suggested by Hartig and Dormann (2) provides inaccurate predictions and severely biased estimates of the dynamics (Fig. 1). This result occurs in the absence of observation error, and despite model-fit diagnostics that suggest convergence to a correct model. In contrast, the model-free method of state–space reconstruction avoids any requirement for ad hoc assumptions as to model structure, and provides useful short-term forecasts that can be validated empirically. Moreover, a simple extension of the model-free method allows one to test potential mechanisms and causal drivers (5), thus promoting a better mechanistic understanding without reliance on a mythical true model.
Fig. 1.
Estimated Lyapunov exponent of the logistic model (A), and predictive accuracy (B) when the true model is the theta-logistic model (for r = 1.8, and q = 4.0). Similar to standard maximum likelihood estimates, the Lyapunov exponent estimates using the method proposed by Hartig and Dormann (2) are consistently biased toward stable dynamics (Lyapunov exponent < 0) when the true dynamics were often chaotic (Lyapunov exponent > 0). In addition, the state–space reconstruction (SSR) method exhibits substantially lower forecast error than the fitted logistic model (B). Forecast error is represented by standardized root mean-square error (RMSE); the shaded interval represents the 95% confidence interval.
Footnotes
The authors declare no conflict of interest.
References
- 1.Perretti CT, Munch SB, Sugihara G. Model-free forecasting outperforms the correct mechanistic model for simulated and experimental data. Proc Natl Acad Sci USA. 2013;110(13):5253–5257. doi: 10.1073/pnas.1216076110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hartig F, Dormann CF. Does model-free forecasting really outperform the true model? Proc Natl Acad Sci USA. 2013;110:E3975. doi: 10.1073/pnas.1308603110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pisarenko VF, Sornette D. Statistical methods of parameter estimation for deterministically chaotic time series. Phys Rev E Stat Nonlin Soft Matter Phys. 2004;69(3 Pt 2):036122. doi: 10.1103/PhysRevE.69.036122. [DOI] [PubMed] [Google Scholar]
- 4.Perretti CT, Sugihara G, Munch SB. Nonparametric forecasting outperforms parametric methods for a simulated multispecies system. Ecology. 2013;94(4):794–800. [Google Scholar]
- 5.Sugihara G, et al. Detecting causality in complex ecosystems. Science. 2012;338(6106):496–500. doi: 10.1126/science.1227079. [DOI] [PubMed] [Google Scholar]