Significance
Marking animals avoid locations recently visited by others. We conceptualized this time nonlocal avoidance behavior as stigmergy, a form of mediated interaction that gives rise to coordinated behavior from seemingly independent individuals. In so doing, the concept of stigmergy is used beyond the realm of eusocial insects. To link the population spatiotemporal patterns that emerge from the individual nonlocal rules of interaction, we construct a collective movement model whereby randomly moving animals have the tendency to avoid marks left by a conspecific, depending on the age of the mark. As a result, we are able to quantify animal decision-making processes in terms of current and past locations of other individuals, linking behavior to history-dependent actions.
Keywords: movement ecology, animal space use, delayed response, territoriality, home range
Abstract
Collective animal behavior studies have led the way in developing models that account for a large number of individuals, but mostly have considered situations in which alignment and attraction play a key role, such as in schooling and flocking. By quantifying how animals react to one another’s presence, when interaction is via conspecific avoidance rather than alignment or attraction, we present a mechanistic insight that enables us to link individual behavior and space use patterns. As animals respond to both current and past positions of their neighbors, the assumption that the relative location of individuals is statistically and history independent is not tenable, underscoring the limitations of traditional space use studies. We move beyond that assumption by constructing a framework to analyze spatial segregation of mobile animals when neighbor proximity may elicit a retreat, and by linking conspecific encounter rate to history-dependent avoidance behavior. Our approach rests on the knowledge that animals communicate by modifying the environment in which they live, providing a method to analyze social cohesion as stigmergy, a form of mediated animal–animal interaction. By considering a population of animals that mark the terrain as they move, we predict how the spatiotemporal patterns that emerge depend on the degree of stigmergy of the interaction processes. We find in particular that nonlocal decision rules may generate a nonmonotonic dependence of the animal encounter rate as a function of the tendency to retreat from locations recently visited by other conspecifics, which has fundamental implications for epidemic disease spread and animal sociality.
Animals of the same species often are found either clustered together, e.g., in herds, or spread apart. Understanding the principles behind this heterogeneity is one of the central tenets in animal ecology with fundamental implications for population regulation, ecosystem functioning, and species evolution (1). Recent mechanistic modeling approaches (2) have produced landmark studies for the interpretation and analysis of animal spacing. Despite these fundamental advances, quantitative analyses often assume that individuals respond to one another’s presence instantaneously. Although computationally advantageous, such an approach may fail to capture the nonlocality, when present, of animal interactions. One such example occurs when individuals react to one another’s presence from a distance rather than only upon direct encounter. For this to occur, animals either use long-range communication, e.g., sound signals, or they acquire information about the past locations of other individuals. In the first case, the interaction is nonlocal in space, whereas in the second, the interaction is nonlocal in time. The latter is the focus of our investigation.
How nonlocal individual interactions affect the spatial distribution of sedentary, i.e., neither nomadic nor migratory, animals remains an open question. Recent studies (3, 4) advocate the need to develop a general framework to explain the broad spectrum of spacing behavior we observe: from one extreme condition, with full territorial exclusion, to an intermediate situation, with overlapping home ranges, to the other extreme, with free-ranging animals that fully share the available space. Animals that deposit marks over the terrain represent a model animal system to develop such a framework. As individuals react to the encounter of foreign marks, they respond to the locations where other conspecifics have been in the past, making the interaction nonlocal in time. Recent studies on scent-marking animals (5–7) have taken into account nonlocal interactions, but they have investigated the formation of territorial patterns. Here, we move beyond that limitation by analyzing the collective emergence of spacing patterns resulting from animals’ avoidance. We chose to focus on the endogenous mechanisms of how patterns are generated rather than asking why animals do it, which depends on the resources they aim to defend (3).
As with other collective movement phenomena, e.g., in herding (8) or schooling and flocking (9), the key to understanding the emerging dynamics is the interaction between individuals. Here, we consider the strength of the interaction as dependent on the degree of nonlocality, which we accomplish by having the probability of an individual to retreat from the encountered active foreign marks depending on how long ago the marks were deposited.
Conceptual Framework
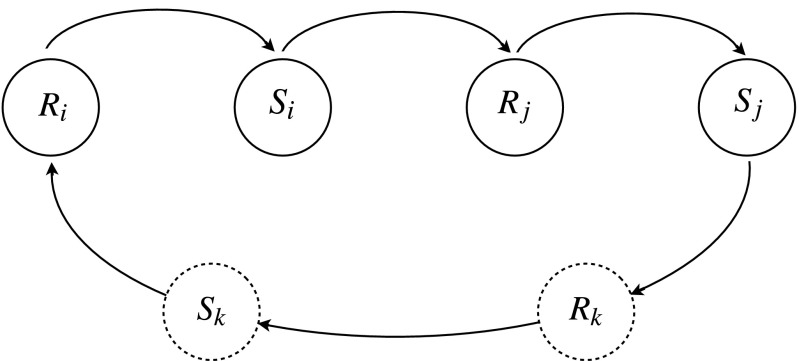
The delayed response between mark deposition, the action of an individual, and conspecific retreat, the reaction of another conspecific, is a basic ingredient of stigmergy (10, 11), a mediated interaction mechanism whereby the changes produced endogenously in the environment by the marks of one individual elicit a response in the neighbors, which in turn respond, affecting their nearest neighbors. This cascade of events creates a feedback mechanism for the entire population, which self-organizes into a dynamic spatiotemporal pattern. Fig. 1 depicts a schematic diagram representing the feedback and interaction processes among individuals, with animal i responding to some foreign marks initially present in the environment by producing a spatiotemporal arrangement of its own marks, the stimulus Si. This stimulus is detected by another individual j whose reaction produces stimuli for other members of the population. Because marking is a broadcasting mechanism, the stimulus generated by individual j eventually induces a response from individual i, which in turn acts to modify the profile of its marked area, therefore creating a feedback onto the original stimulus Si. This feedback may require two steps or a cascade of interactions via various k individuals, and thus act indirectly onto Si.
Fig. 1.
Schematic representation of stigmergy in marking animals. When the animal i detects the presence of active foreign marks, it responds by retreating from the locations of the foreign marks (Ri). At the same time, the animal i itself deposits marks over the terrain, whose active set constitutes the stimulus Si that another member j of the population detects, inducing the response Rj. In turn, animal j deposits its own marks (Sj), whose locations affect animal i again or individual k, which will react and itself produce a stimulus. The number of individuals involved in this feedback loop may be as a large as the entire population or as small as just individuals i and j, depending on the locations the animals visit after their response. The dashed lines around Rk and Sk represent the fact that the number of steps necessary to affect individual i may vary because of the random nature of the movement process and, thus, of the probability of animal i encountering the stimulus (Sj).
The shrinking and growth of Si are controlled, respectively, by the aging of the marks and the movement of the animals. The transience of the deposited cues tends to reduce the size of a marked area, because inactive marks are ignored by conspecifics. An aging mark at a given location reduces the propensity of other conspecifics to retreat from that location, which in turn increases the pressure onto individual i to move further inside its own marked area, reducing even further the spatial extent of Si. Because a decrease in the size of Si further reduces its spatial extent, the decay of the marks acts as a positive feedback. The other positive feedback is the movement of the animals, which helps the growth of Si. As animals deposit marks by exploring regions beyond their inner-core areas, they increase the extent of Si and pressure neighbors into moving away to avoid confrontation. This in turn allows them to explore even larger areas, thus further increasing the size of their marked areas. Positive feedback mechanisms act to reinforce a given process and are the key to explaining various forms of aggregation and pattern formation (see, e.g., ref. 12 for the application of reinforced random walks to represent some types of positive feedback). On the other hand, the negative feedback acts in the opposite direction of the variation of Si whether it is a decrease or increase in its spatial extent. As marked areas get smaller, animals may traverse them quicker and thus slow their shrinking. Similarly, as marked areas get bigger, animals take longer to move across them, preventing individuals from re-marking aging marks. This results in a reduction of the growth rate of Si.
We choose to interpret the space use of marking animals as a stigmergic interaction for three reasons. The first is that animal marking is a widespread behavior in the animal kingdom, and although each species has evolved specialized means of communication by depositing cues on the terrain, it serves the general function of broadcasting an animal’s presence. Marks contain information about identity and relative dominance (13), with many vertebrates (14) and eusocial insects (15) making use of chemical signals but also with examples in which visual marks are used, such as feathers and feces by birds. Stigmergy represents a well-developed concept that would help in studying animal space use from a general theoretical perspective, independent of the types of signals present in the marks that get deposited or the sensory modalities required for the detection of those signals. The second reason is that stigmergy makes interactive processes history dependent, which captures the fact—often neglected in quantitative analyses of animal space use—that individuals do not respond simply to the current position of other conspecifics, but also to where they have been in the recent past. A mark, when detected, represents a record of an individual’s past activity in a specific location to which other conspecifics eventually respond. The third reason is that stigmergic stimulus–response association relies upon modification of the environment. As environmental heterogeneity may also affect how individuals move in space, our approach yields a method to quantify another form of spatial heterogeneity, the one generated endogenously from animal interactions. It thus may be possible to extend our current framework to provide a common currency to interpret animal space use as a function of the most important endogenous and exogenous features of the ecosystem, respectively, conspecific avoidance and environmental covariates. Promising approaches in that respect already are available and may help link population spatial distribution to animal spatial memory and landscape persistence (16), as well as to prey distribution and terrain steepness (17, 18).
In this framework of socially interacting animals, we are interested in determining how the individual movement response to the presence of conspecifics shapes the degree of segregation in the population. A useful tool to characterize the emerging spatiotemporal pattern of the population is the encounter rate of mobile animals, an instrument of broad ecological applicability (19). Most encounter estimates have relied upon basic animal movement models, in which displacement is ballistic and individuals are completely independent, which amounts to considering animals as “ideal gas” particles. This approach has been taken as a null model to estimate the frequency of meeting or associations among mobile animals (20) and has been used recently to estimate, with the help of allometric considerations in a spatially implicit context, how home range size scales with body mass (21). Here, to capture the key biological features of the movement and interaction processes that underlie animal spacing, we consider a spatially explicit scenario to determine how individual behavior affects animal space use. The focus of our analysis is the quantification of the average encounter rate, home range size, and degree of exclusivity as a function of the degree of stigmergy.
Model and Results
To study how individual-level interaction affects spacing patterns, we need to take into account the discreteness of the population and the mediated interaction events (22). We do so with an individual-based simulation in continuous time and discrete space (2D lattice) with periodic boundary conditions (see SI Appendix for mode details). Animals move at random among nearest-neighbor lattice sites and leave marks everywhere they go. By depositing marks, each member of the population tends to acquire space at the expense of other conspecifics. This spatial competition occurs because upon the encounter of an active foreign mark, i.e., a mark that has been deposited within a time 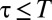 in the past, an individual reacts by retreating with some probability p. The direction in which an animal retreats is the centroid of its own marked area (see SI Appendix to see how p enters explicitly in the computation of the movement direction). That probability is a value between
in the past, an individual reacts by retreating with some probability p. The direction in which an animal retreats is the centroid of its own marked area (see SI Appendix to see how p enters explicitly in the computation of the movement direction). That probability is a value between 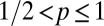 up until time T and becomes 1/2 when
up until time T and becomes 1/2 when 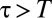 , which corresponds to ignoring foreign marks. Because
, which corresponds to ignoring foreign marks. Because 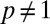 , except when individuals encounter one another, the marked areas of each individual at each instant in time may overlap; the higher the overlap, the smaller the value of p. An example of the overlapping spatiotemporal dynamics of the individual marked areas of three neighboring animals (in a population of 25) when
, except when individuals encounter one another, the marked areas of each individual at each instant in time may overlap; the higher the overlap, the smaller the value of p. An example of the overlapping spatiotemporal dynamics of the individual marked areas of three neighboring animals (in a population of 25) when 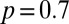 is shown in Movie S1. From this movie, it is clear that the number of marked areas that overlap and the extent of the overlap continuously change in time.
is shown in Movie S1. From this movie, it is clear that the number of marked areas that overlap and the extent of the overlap continuously change in time.
The presence of a maximum time T captures the common feature that animals will ignore a foreign mark when the message contained in it has decayed or has become uninformative, because it affects the perception of the encounter probability with a conspecific (23). Although the actual value of T for each species changes according to the sensory modalities used to acquire information from the environment (24), there is a natural dimensionless quantity that characterizes the collective dynamics of the system (6): 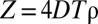 , with D being the animal’s diffusion constant, characterizing the rate of movement of the individuals, and ρ the population density; 4DT represents the average area that a freely diffusing animal would tend to cover during a time T (ref. 9, pp. 10–27), whereas ρ−1 is the average area each animal would occupy if the terrain were equally divided into exclusive regions among the individuals of the population. For a constant population density, an increase in T makes the boundary location marks persist longer, thus reducing encroachment of conspecifics. A reduction in foreign intrusion also occurs by increasing ρ (while keeping T constant), causing each individual to encounter the edge of its marked area more frequently, on average. As larger values of Z increase the pressure an animal imposes on the neighbors in preventing conspecifics from acquiring additional space, we call Z the (spatial) competition parameter in the population. This provides an intuitive interpretation of the parameter Z, except when the probability of retreat upon foreign marks is very low, whereby spatial mixing of the population is considerable.
, with D being the animal’s diffusion constant, characterizing the rate of movement of the individuals, and ρ the population density; 4DT represents the average area that a freely diffusing animal would tend to cover during a time T (ref. 9, pp. 10–27), whereas ρ−1 is the average area each animal would occupy if the terrain were equally divided into exclusive regions among the individuals of the population. For a constant population density, an increase in T makes the boundary location marks persist longer, thus reducing encroachment of conspecifics. A reduction in foreign intrusion also occurs by increasing ρ (while keeping T constant), causing each individual to encounter the edge of its marked area more frequently, on average. As larger values of Z increase the pressure an animal imposes on the neighbors in preventing conspecifics from acquiring additional space, we call Z the (spatial) competition parameter in the population. This provides an intuitive interpretation of the parameter Z, except when the probability of retreat upon foreign marks is very low, whereby spatial mixing of the population is considerable.
Although a response function to the encounter of foreign marks with constant p for 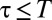 may reproduce qualitatively the effects of conspecific avoidance, a more realistic scenario is one in which animals react differently depending on how long ago a conspecific was present at a given location (25). We thus have considered a response function
may reproduce qualitatively the effects of conspecific avoidance, a more realistic scenario is one in which animals react differently depending on how long ago a conspecific was present at a given location (25). We thus have considered a response function 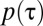 that changes as a function of the time
that changes as a function of the time 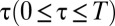 since the mark was deposited. For this purpose, we considered the functional form
since the mark was deposited. For this purpose, we considered the functional form 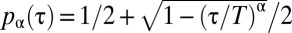 for
for 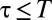 and
and 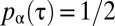 for
for 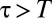 , which we plotted in Fig. 2A for different values of the parameter α. Although many other choices were possible, the specific functional form of the function
, which we plotted in Fig. 2A for different values of the parameter α. Although many other choices were possible, the specific functional form of the function 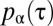 was dictated by mathematical convenience, with the single parameter
was dictated by mathematical convenience, with the single parameter 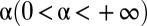 representing the degree of reactivity to the encounter of foreign marks; the larger the α, the more likely an animal is to retreat upon encountering a foreign mark. Because the stimulus–response association in our model animals corresponds to the deposition of a mark, and subsequent retreat of another individual, α represents the strength with which individuals mediate their interactions through the environment. We thus have called α the “degree of stigmergy” of the interaction process. In the limit
representing the degree of reactivity to the encounter of foreign marks; the larger the α, the more likely an animal is to retreat upon encountering a foreign mark. Because the stimulus–response association in our model animals corresponds to the deposition of a mark, and subsequent retreat of another individual, α represents the strength with which individuals mediate their interactions through the environment. We thus have called α the “degree of stigmergy” of the interaction process. In the limit 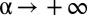 , animals have a very strong reaction, as they always retreat upon encountering a foreign mark. The response function in this limit reduces to a step function with
, animals have a very strong reaction, as they always retreat upon encountering a foreign mark. The response function in this limit reduces to a step function with 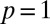 for
for 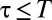 and
and 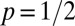 for
for 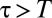 , corresponding to the formation of territories that overlap the neighboring ones only at the boundaries. This is the scenario of exclusive territory formation analyzed in the past (5) and shown to provide a successful explanation of the mechanisms underlying a wide-reaching 80-y-old hypothesis about the elasticity of territorial patterns (7). For finite α values, each animal roams a spatial region covered with its own marks and from which neighbors are only partially excluded, and in the limit
, corresponding to the formation of territories that overlap the neighboring ones only at the boundaries. This is the scenario of exclusive territory formation analyzed in the past (5) and shown to provide a successful explanation of the mechanisms underlying a wide-reaching 80-y-old hypothesis about the elasticity of territorial patterns (7). For finite α values, each animal roams a spatial region covered with its own marks and from which neighbors are only partially excluded, and in the limit 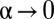 ,
, 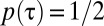 for any τ and animals ignore one another; thus, no stimulus–response association is present.
for any τ and animals ignore one another; thus, no stimulus–response association is present.
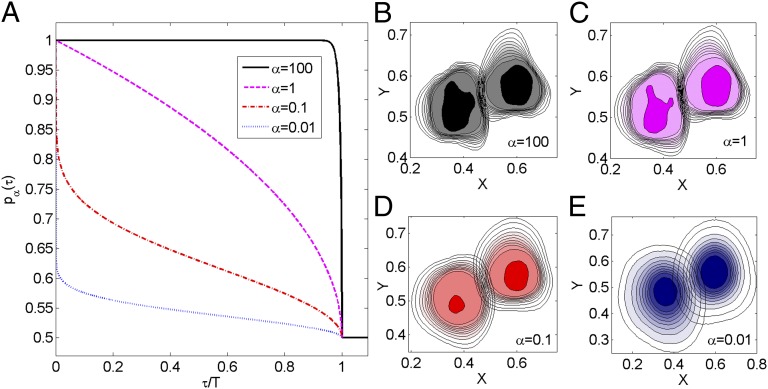
Fig. 2.
Relation between the degree of stigmergy and the animal occupation probability. The animal response function to the encounter of conspecific marks is depicted in A, with the resulting spatial pattern of two representative neighboring individuals in the population shown in B. (A) Response functions 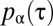 for different values of the degree of stigmergy α as a function of τ, the time in the past when an encountered (foreign) mark was deposited. (B–E) Utilization distributions (i.e., time-integrated position distributions) of two neighbors with spatial coordinates in arbitrary units for different degrees of stigmergy α. The competition parameter Z (see text) has been set equal to 32 in all three cases. The left and right neighboring individuals shown here are selected from a population composed of 16 animals, with simulations integrated over a time equal to 2.5T, and with their utilization distributions colored purple and red, respectively, in the corresponding four panels displayed in SI Appendix, Fig. S1. The fraction of time an individual has occupied a lattice site is given by the contour level values (not shown), ranging from 0.008 for the innermost ones to 10−4 for the outermost ones. In sequentially observing B through E, the spacing between contours increases, indicating a decrease in the steepness of the utilization distribution at the boundaries. In E, the probability of occupying a site is never more than 0.008, so there is one less contour than in B–D, and the innermost contour is at height 0.004.
for different values of the degree of stigmergy α as a function of τ, the time in the past when an encountered (foreign) mark was deposited. (B–E) Utilization distributions (i.e., time-integrated position distributions) of two neighbors with spatial coordinates in arbitrary units for different degrees of stigmergy α. The competition parameter Z (see text) has been set equal to 32 in all three cases. The left and right neighboring individuals shown here are selected from a population composed of 16 animals, with simulations integrated over a time equal to 2.5T, and with their utilization distributions colored purple and red, respectively, in the corresponding four panels displayed in SI Appendix, Fig. S1. The fraction of time an individual has occupied a lattice site is given by the contour level values (not shown), ranging from 0.008 for the innermost ones to 10−4 for the outermost ones. In sequentially observing B through E, the spacing between contours increases, indicating a decrease in the steepness of the utilization distribution at the boundaries. In E, the probability of occupying a site is never more than 0.008, so there is one less contour than in B–D, and the innermost contour is at height 0.004.
The spatial heterogeneity emerging from the interactions among the animals is controlled by the shape factor α of the response function. The degree of stigmergy thus determines the spatial profile of the occupation probability of two neighboring conspecifics. For the same strength of spatial competition Z, when a foreign mark of age τ is encountered, a larger α will make animals retreat more often. Over time, this has the effect of reducing the amount of space that can be shared with the neighbors, thus segregating each individual within its own marked area. In Fig. 2 B and C, one can see that for large α, sharply decreasing sides of the utilization distribution—the time-integrated probability distribution of the animals—emerge with exclusive core areas. Those sides become shallower by decreasing α, as shown in Fig. 2D, and eventually no exclusive regions appear for sufficiently small values of α, as depicted in Fig. 2E. Because the competition parameter also controls the rate of movement of the marked areas, the utilization distribution changes depending on the choice of Z: the smaller Z, the longer the time for an individual to cover its marked area relative to the time required for the marks to decay. As a result, for a given degree of stigmergy, the steepness of the utilization distribution decreases with decreasing Z. (See SI Appendix and Movie S2 and S3 to observe the dynamics of the individuals for different α and Z values.)
A quantity that may be associated directly with the amount of social cohesion is the rate of encounters among individuals. In Fig. 3, we study how the average rate R with which an individual meets conspecifics varies as a function of α for different values of Z. In Fig. 3A, for small values of α, all animals are diffusing with minimal constraint on their movement and share all the space available to them. The population in that case is “well mixed.” In this situation, the average encounter may be computed analytically through 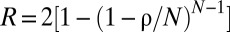 (26), which reduces to
(26), which reduces to 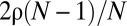 for small population density ρ. This limit explains why all curves in Fig. 3A converge to
for small population density ρ. This limit explains why all curves in Fig. 3A converge to 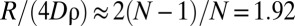 , where we used
, where we used 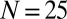 animals and
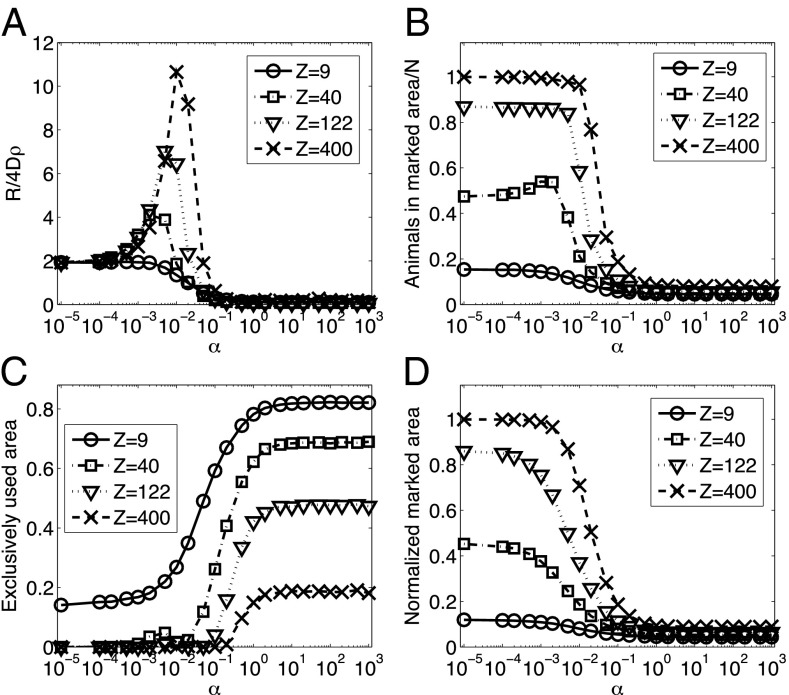
animals and 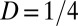 . As α increases beyond about 10−4, the chance of retreating from locations recently visited by other conspecifics increases and each animal starts to be slightly confined, as shown in Fig. 3D, in which the average size of an individual’s marked area, which we may call its home range, is plotted versus α. Because the encounter rate between a random walker and a set of targets—in this case, the other individuals of the population—is to a first approximation inversely proportional to the size of the confining domain (27), initially R increases as the size of the home range shrinks, explaining the initial increase in the encounter rate as a function of α. From Fig. 3D, it is clear that the extent and steepness of the variation of home range size as a function of α depend on the spatial competition parameter. In Fig. 3D, the normalized marked area plot, which indicates the average size of a home range relative to the size of the 2D domain, starts at increasingly higher values the larger the parameter Z for small α. This is a result of the space-filling nature of the diffusive movement, which tends to make individuals occupy larger regions of space the stronger their spatial competition. The range of reduction of home range size as a function of α also depends on the competition parameter, with larger reduction for larger Z. This explains why, in the encounter rate plot, the initial increase in R is further to the right for bigger values of Z.
. As α increases beyond about 10−4, the chance of retreating from locations recently visited by other conspecifics increases and each animal starts to be slightly confined, as shown in Fig. 3D, in which the average size of an individual’s marked area, which we may call its home range, is plotted versus α. Because the encounter rate between a random walker and a set of targets—in this case, the other individuals of the population—is to a first approximation inversely proportional to the size of the confining domain (27), initially R increases as the size of the home range shrinks, explaining the initial increase in the encounter rate as a function of α. From Fig. 3D, it is clear that the extent and steepness of the variation of home range size as a function of α depend on the spatial competition parameter. In Fig. 3D, the normalized marked area plot, which indicates the average size of a home range relative to the size of the 2D domain, starts at increasingly higher values the larger the parameter Z for small α. This is a result of the space-filling nature of the diffusive movement, which tends to make individuals occupy larger regions of space the stronger their spatial competition. The range of reduction of home range size as a function of α also depends on the competition parameter, with larger reduction for larger Z. This explains why, in the encounter rate plot, the initial increase in R is further to the right for bigger values of Z.
Fig. 3.
Encounter rate and other demographic characteristics as a function of the degree of stigmergy. (A) Average encounter rate, (B) fraction of the average number of individuals inside a marked area, (C) fraction of the terrain used by exactly one animal, and (D) average size of a single marked area. The normalization in A is with respect to the population density and diffusion constant—more precisely, to the average diffusive rate 4Dρ, that is, the rate for an animal to cover an area equal to the inverse of the population density ρ−1. In B, we normalize the measured quantity by dividing by N, the total number of individuals in each simulation. The normalization in C and D is with respect to the size of the box (with periodic boundary conditions) that has been used in the stochastic simulations. When α is small, retreat events upon the encounter of foreign marks are reduced to a minimum, with individuals moving nearly unbounded and having no exclusive use of space, except for very low Z (C). With few constraints on their movement, an increase in Z corresponds to an increase in the diffusive area that individuals would cover, resulting in larger home ranges (D). For larger α, on the other hand, we obtain a reduction in the size of the exclusive area with increased neighbor competition, that is, with larger Z (C), without an appreciable change in home range size (D).
Although a further increase in the degree of stigmergy reduces the size of the home ranges even more, beyond the value of α where 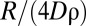 achieves its maximum, which we call
achieves its maximum, which we call 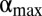 , the number of individuals inside a home range decreases, as shown in Fig. 3B. By comparing Fig. 3 B and D, it is apparent that the number of individuals decreases more steeply than the decrease in home range size. Therefore, their ratio, the local population density,
, the number of individuals inside a home range decreases, as shown in Fig. 3B. By comparing Fig. 3 B and D, it is apparent that the number of individuals decreases more steeply than the decrease in home range size. Therefore, their ratio, the local population density, 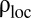 , decreases for
, decreases for 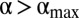 . As the encounter rate is positively correlated to
. As the encounter rate is positively correlated to 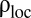 , we thus observe a decrease in
, we thus observe a decrease in 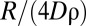 for
for 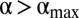 (Fig. 3A). This is amplified further by the formation of increasingly large exclusive areas inside each home range as α increases (Fig. 3C), causing the number of possible locations where animals can encounter one another to diminish. The presence of this nonmonotonicity in the encounter rate also has been confirmed by using a flat response function, where
(Fig. 3A). This is amplified further by the formation of increasingly large exclusive areas inside each home range as α increases (Fig. 3C), causing the number of possible locations where animals can encounter one another to diminish. The presence of this nonmonotonicity in the encounter rate also has been confirmed by using a flat response function, where 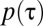 is constant for
is constant for 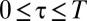 . It is an intrinsic feature of the system and a result of the interplay among the movement of the animals in partially confined spaces, the size of the confining domains, and the stigmergic interaction among the members of the population.
. It is an intrinsic feature of the system and a result of the interplay among the movement of the animals in partially confined spaces, the size of the confining domains, and the stigmergic interaction among the members of the population.
The value of the competition parameter also determines the relative magnitude of the fraction of the terrain used by an animal (exclusivity), shown in Fig. 3C, compared with the average size of an animal’s marked area, displayed in Fig. 3D. As explained earlier, for the same degree of stigmergy, spatial competition affects the overall size of an animal’s marked area; the stronger the competition, the larger the region each individual occupies, as clearly shown in Fig. 3D for low α values. As Z is reduced, the amount of area an animal can mark within a time T decreases, resulting in more interstitial regions and a smaller marked area. If each marked area takes up a large proportion of the total terrain, then animals are forced to have very large overlaps with their neighbors, resulting in little exclusive area, whereas smaller marked areas allow for a larger proportion of exclusivity. This causes the order of the curves in Fig. 3D to be the reverse of that in Fig. 3C.
Discussion
We have identified similarities between the mechanisms of environment-mediated interaction with which an insect colony may find resources and those with which a population of territorial animals segregate in space. In so doing, we can view animal space use processes as a decentralized coordination of tasks, a problem of utmost importance in the realm of eusocial insects as well as to the world of artificial intelligence and interactive robots in experimental biology (28). This opens the possibility of devising adaptive control procedures that are well developed in swarm intelligence studies (29), which may prove applicable to management and conservation problems. At the same time, tessellation algorithms developed from a solid quantitative understanding of animal territorial behavior might be used to improve the so-called digital hormone strategies being developed for the coordination of swarming autonomous vehicles (30). Other aspects of group foraging optimization (31), which have been quantified extensively in social insect colonies, also may provide fundamental insights into the advantage and disadvantage of space sharing.
Although various models of spatial distribution in a population do account for individual interactions, the retreat response of an animal to the presence of conspecifics often is considered for simplicity as being local in time. Although this approximation may be sufficient in some cases, it is seriously violated when animal interactions are mediated through the environment, that is, in the presence of stigmergy. By modeling animals as individuals that mark the terrain with visual or olfactory cues, we determine how the response to the encounter of foreign marks determines the degree of social cohesion in a population. Our study shows how the spatial segregation of the individuals depends on the degree of stigmergy of the interaction. The resulting spatial profile ranges from uniformity, when animals are completely gregarious, to individuals partially sharing regions of space within overlapping home ranges, all the way to defended territories that are fully exclusive.
A salient feature of our framework is the ability to represent the spectrum of spacing patterns commonly observed in the field. Reversal of dominance in space (1), whereby animals are asymmetric competitors with negotiating strategies (32, 33), has been proposed to explain this spectrum of variation. In most taxa, few individuals exclude competitors at all times. Instead, control of space depends on relative dominance, which in turn is related to asymmetries in fighting abilities. In birds, whose ease of transport makes sharp territorial boundaries the norm, detection of competitors may occur at large distances. In mammals, however, for which visual detection might be more difficult in structurally complex habitats, individuals often cover ground traveled by others. Individuals thus are likely to rely on lingering marks, and the relative value of space declines with distance from a core area. The degree of stigmergy in marking animals thus may be interpreted as representing the strength of this dominance relation in space.
Similar to eusocial insects that use chemicals to interact with other members of the population, our model system has all the ingredients of a stigmergic process (10, 11): amplification of fluctuations, multiple interactions, and positive and negative feedback. The randomness inherent in the movement processes induces spatiotemporal fluctuations in the animals’ interaction with foreign marks. These fluctuations generate correlations in the individuals’ and marked areas’ locations, which are propagated via multiple nearest-neighbor “transmission” events to all individuals of the population. The stability in the spatial structures is down-regulated via a negative feedback mechanism, the time it takes for an individual to re-mark its own marks, which makes it shrink if the marked area is too large or grow if too small. Up-regulation is a result of the fade-out of the marks and the animal diffusion, which tend to further reduce or increase the size of an individual’s marked area, respectively, constituting a positive feedback. The response of the individuals to the detection of foreign marks is a probabilistic rule to retreat, depending on the age of the stimulus. Stigmergy in marking animals is another example in which the stimulus–response association follows probabilistic rather than deterministic rules, similar to the classic example of nest construction in Polistes wasp colonies (34).
Unlike eusocial insects, which often respond collectively through a movement or an action toward a certain direction or location, e.g., trail following in ants, in our case each animal’s retreat upon the encounter of foreign marks is in a different direction, toward the interior of its own marked area, causing segregation rather than aggregation. For this reason, the response of an individual to the encounter of its own marks does not play a role here, as conspecific avoidance relies upon detecting and responding to the presence of other members of the population. As a result, as shown in Fig. 1, the feedback onto one’s own marks is only indirect via the response and subsequent stimulus deposition of other individuals. The positive and negative feedback depends, respectively, on T, the time during which a mark remains active, and the rate Dρ of movement of an individual around a marked area of average size. The spatial competition parameter 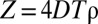 thus quantifies the feedback mechanisms via a product of the parameters controlling positive and negative feedback.
thus quantifies the feedback mechanisms via a product of the parameters controlling positive and negative feedback.
At the behavioral level, our results show that the frequency of animal encounters may depend nonmonotonically on the propensity of an individual to ignore foreign marks. When spatial competition is strong, two distinct regimes of interaction appear. For a high probability of retreat from foreign marks, animals remain mainly segregated within their own exclusive areas, sharing only a small fraction of space with their neighbors. For a small probability of retreat, exclusivity is nearly absent and animals possess very large home ranges, sharing most of the terrain with conspecifics. In the former regime, animal encounters are relatively infrequent, being controlled by pairwise interaction events that occur in the narrow regions of overlap between marked areas. In the latter, the frequency of encounter is greater because at any location, one individual may meet many other members of the population. Between, there is a regime in which encounters are even more frequent owing to each home range being smaller than in the latter case, thus confining the individual’s movement but still overlapping significantly with many other home ranges.
Because Z is proportional to the time decay T of a mark, it also indicates the degree of history dependence of the interaction. For a given magnitude of the diffusion constant D and population density ρ, when values of T are small, animals would quickly consider foreign marks to be uninformative and their spatial positions would be correlated only over a short period, reacting to one another only when in close proximity. For large values of T, instead, an animal’s decision to move more likely would be influenced by where other conspecifics have been in the past. This generates correlations between the positions of the individuals that persist for long periods, making animals interact from a distance and thus altering the spacing patterns we would observe if decisions were instantaneous.
To account for the discreteness of the interactions, which include the meeting of individuals and the encounters of foreign marks that decay in a finite amount of time, we have used an agent-based approach, as coarser descriptions that do not track encounter events may provide inaccurate descriptions of the individual avoidance response (6). To single out the endogenous causes of the spatiotemporal patterns observed in a variety of animal population distributions, we have assumed for simplicity that resources are uniform and abundant, and thus do not play any role in the dynamics. Our choice of resource homogeneity also has simplified our selection of the response function, whose parameters, α and T and, as a consequence, Z, have been considered independent. Future directions should address their interdependence, as animal stigmergy may be the result of different types of mediated conspecific interactions. To understand how endogenous features of the environment affect the exogenously generated spacing pattern presented here, one should include animal competition resulting from resource heterogeneity. In this case, α and Z may not be independent anymore: animals may compete fiercely for their space (large Z) and react very strongly (large α) to conspecifics’ presence when food is scarce, or animals may respond weakly to foreign marks (small α) and minimize interactions (small Z) when resources become very abundant. Because competition and avoidance response between conspecifics vary throughout the year, intruder pressure and response function may be explicitly time dependent or even change the nature of their interaction, e.g., during the mating season, during which animals may be attracted by foreign marks rather than avoiding them. Future studies should try to address this aspect. Other aspects, such as the energetic expenditure to the deposition of marks, also should be taken into account. Such an approach would help reveal movement strategies that optimize the placement of cues over the terrain.
Our approach to the collective formation of spacing patterns in marking animals is relevant to many taxa among vertebrates and invertebrates and represents the first mechanistic explanation of the emergence of home ranges with areas of exclusivity and home range overlap, as conceptualized in the seminal work by William Burt 70 years ago (35). The observations of moving and interacting animals with ever-increasing resolution will provide the appropriate data to link movement data to the theory developed here. A recent study showed how to apply wavelet transform to movement trajectory data and to extract correlations between moving animal pairs (36). That approach could be extended to extract anticorrelations resulting from conspecific avoidance. Mapping the strength of the negative correlations emerging from the model animal trajectories with different degrees of stigmergy may then allow future studies to associate the degree of anticorrelation in trajectory data with the strength of the mark-avoidance response.
By associating a cost with the encounter of conspecifics, e.g., as a result of aggressive confrontations, and including foraging processes, it would be possible to study how species adapt their behavior to the distribution of resources in the environment. This ultimately would help answer questions related to the profitability of a population’s social spacing, depending on the spatiotemporal distribution of resources. The striking nonmonotonicity in encounter rates we have uncovered may provide the mechanistic basis to explain the when and where of sociality vs. territorial defense (37), a classic example being the African golden-wing sunbird, which illustrates how territorial defense or sharing of flowers depends on the relative amount of nectar and the intensity of intrusions by competitors (38). Similar findings also were shown in laboratory studies in pygmy sunfish in response to changes in competition intensity (39). Our development will provide spatially explicit explanations for recent findings that relate the scaling of home range size and overlap to animal body mass (21) and help interpret allometric variability of space use across species. Finally, by considering the exchange dynamics of individuals among different social units, the neighboring marked areas, it would be possible to shed light on how the spatial extent of an epidemic outbreak is affected by the degree of spatial overlap of the individuals in a population (40).
Supplementary Material
Acknowledgments
L.G. thanks Guy Theraulaz for fruitful discussions about aspects of the research. L.G. acknowledges financial support from Engineering and Physical Sciences Research Council (EPSRC) Grants EP/K004581/1 and EP/I013717/1. J.R.P. acknowledges support from EPSRC Grant EP/E501214/1. D.I.R. acknowledges financial support from National Science Foundation Grants IBN-9874523, CNS-025214, and IOB-9874523. S.A.L. acknowledges financial support from Army Research Office Grant W911NG-11-1-0385.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: The data reported in this paper have been deposited in the Dryad Digital Repository, http://datadryad.org (DOI: 10.5061/dryad.v60r7).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1307071110/-/DCSupplemental.
References
- 1.Brown JL, Orians GH. Spacing patterns in mobile animals. Annu Rev Ecol Syst. 1970;1:239–262. [Google Scholar]
- 2.Moorcroft PR, Lewis MA. Mechanistic Home Range Analysis. Princeton, NJ: Princeton Univ Press; 2006. [Google Scholar]
- 3.Adams ES. Approaches to the study of territory size and shape. Annu Rev Ecol Syst. 2001;32:277–303. [Google Scholar]
- 4.Bөrger L, Dalziel BD, Fryxell JM. Are there general mechanisms of animal home range behaviour? A review and prospects for future research. Ecol Lett. 2008;11(6):637–650. doi: 10.1111/j.1461-0248.2008.01182.x. [DOI] [PubMed] [Google Scholar]
- 5.Giuggioli L, Potts JR, Harris S. Animal interactions and the emergence of territoriality. PLOS Comput Biol. 2011;7(3):e1002008. doi: 10.1371/journal.pcbi.1002008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Potts JR, Harris S, Giuggioli L. Territorial dynamics and stable home range formation for central place foragers. PLoS ONE. 2012;7(3):e34033. doi: 10.1371/journal.pone.0034033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Potts JR, Harris S, Giuggioli L. Quantifying behavioral changes in territorial animals caused by sudden population declines. Am Nat. 2013;182(3):E73–E82. doi: 10.1086/671260. [DOI] [PubMed] [Google Scholar]
- 8.Gueron S, Levin SA, Rubenstein DI. The dynamics of herds: From individuals to aggregations. J Theor Biol. 1996;182(1):85–98. [Google Scholar]
- 9.Okubo A, Levin SA. Diffusion and Ecological Problems: Modern Perspectives. 2nd Ed. New York: Springer; 2001. [Google Scholar]
- 10.Theraulaz G, Bonabeau E. A brief history of stigmergy. Artif Life. 1999;5(2):97–116. doi: 10.1162/106454699568700. [DOI] [PubMed] [Google Scholar]
- 11.Holland O, Melhuish C. Stigmergy, self-organization, and sorting in collective robotics. Artif Life. 1999;5(2):173–202. doi: 10.1162/106454699568737. [DOI] [PubMed] [Google Scholar]
- 12.Codling EA, Plank MJ, Benhamou S. Random walk models in biology. J R Soc Interface. 2008;5(25):813–834. doi: 10.1098/rsif.2008.0014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rubenstein DI, Hack M. Horse signals: The sounds and scents of fury. Evol Ecol. 1992;6(3):254–260. [Google Scholar]
- 14.Müller-Schwarze D. Chemical Ecology of Vertebrates. New York: Cambridge Univ Press; 2006. [Google Scholar]
- 15.Hölldobler B, Wilson E. Colony-specific territorial pheromone in the African weaver ant Oecophylla longinoda (Latreille) Proc Natl Acad Sci USA. 1977;74:2072–2075. doi: 10.1073/pnas.74.5.2072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Berbert JM, Fagan WF. How the interplay between individual spatial memory and landscape persistence can generate population distribution patterns. Ecol Complex. 2012;12(5):1–12. [Google Scholar]
- 17.Moorcroft PR, Lewis MA, Crabtree RL. Home range analysis using mechanistic home range model. Ecology. 1999;80(5):1656–1665. [Google Scholar]
- 18.Moorcroft PR, Lewis MA, Crabtree RL. Mechanistic home range models capture spatial patterns and dynamics of coyote territories in Yellowstone. Proc Biol Sci. 2006;273(1594):1651–1659. doi: 10.1098/rspb.2005.3439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Morales JM, et al. Building the bridge between animal movement and population dynamics. Philos Trans R Soc Lond B Biol Sci. 2010;365(1550):2289–2301. doi: 10.1098/rstb.2010.0082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hutchinson JMC, Waser PM. Use, misuse and extensions of “ideal gas” models of animal encounter. Biol Rev Camb Philos Soc. 2007;82(3):335–359. doi: 10.1111/j.1469-185X.2007.00014.x. [DOI] [PubMed] [Google Scholar]
- 21.Jetz W, Carbone C, Fulford J, Brown JH. The scaling of animal space use. Science. 2004;306(5694):266–268. doi: 10.1126/science.1102138. [DOI] [PubMed] [Google Scholar]
- 22.Durrett R, Levin SA. The importance of being discrete (and spatial) Theor Popul Biol. 1994;46(3):363–394. [Google Scholar]
- 23.Alberts AC. Constraints on the design of chemical communication systems in terrestrial vertebrates. Am Nat. 1992;139:S62–S89. [Google Scholar]
- 24.Warburton K. Social forces in animal congregations: Interactive, motivational, and sensory aspects. In: Parrish JK, Hammer WM, editors. Animal Groups in Three Dimensions. Cambridge, UK: Cambridge Univ Press; 1997. pp. 313–336. [Google Scholar]
- 25.Gosling LM, Roberts SC. Scent-marking by male mammals: Cheat-proof signals to competitors and mates. Adv Stud Behav. 2001;30:169–217. [Google Scholar]
- 26.Sanders DP. Exact encounter times for many random walkers on regular and complex networks. Phys Rev E Stat Nonlin Soft Matter Phys. 2009;80(3 Pt 2):036119. doi: 10.1103/PhysRevE.80.036119. [DOI] [PubMed] [Google Scholar]
- 27.Chevalier C, Bénichou O, Meyer B, Voituriez R. First-passage quantities of brownian motion in a bounded domain with multiple targets: A unified approach. J Phys A Math Theor. 2011;44:025002. [Google Scholar]
- 28.Krause J, Winfield AFT, Deneubourg JL. Interactive robots in experimental biology. Trends Ecol Evol. 2011;26(7):369–375. doi: 10.1016/j.tree.2011.03.015. [DOI] [PubMed] [Google Scholar]
- 29.Bonabeau E, Dorigo M, Theraulaz G. Swarm Intelligence: From Natural to Artificial Systems. New York: Oxford Univ Press; 1999. [Google Scholar]
- 30.Bullo F, et al. Hormone-inspired self-organisation and distributed control of robotic swarm. Auton Robots. 2004;17:93–105. [Google Scholar]
- 31.Dorigo M, Maniezzo V, Colorni A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans Syst Man Cybern B Cybern. 1996;26(1):29–41. doi: 10.1109/3477.484436. [DOI] [PubMed] [Google Scholar]
- 32.Parker GA, Rubenstein DI. Role assessment, reserve strategy and acquisition of information in asymmetric animal conflicts. Anim Behav. 1981;29:221–240. [Google Scholar]
- 33.Stamps JA, Krishnan VV. How territorial animals compete for divisible space: A learning-based model with unequal competitors. Am Nat. 2001;157(2):154–169. doi: 10.1086/318634. [DOI] [PubMed] [Google Scholar]
- 34.Kansai I, Pénzes Z. Comb building in social wasps: Self-organization and stigmergic script. J Theor Biol. 1993;161(4):83–113. [Google Scholar]
- 35.Burt WH. Territoriality and home range concepts as applied to mammals. J Mammal. 1943;24(3):346–352. [Google Scholar]
- 36.Polansky L, Wittemyer G. A framework for understanding the architecture of collective movements using pairwise analyses of animal movement data. J R Soc Interface. 2011;8(56):322–333. doi: 10.1098/rsif.2010.0389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Waser PM. Sociality or territorial defense? The influence of resource renewal. Behav Ecol Sociobiol. 1981;8:231–237. [Google Scholar]
- 38.Pyke GH. The economics of territory size and time budget in the golden-winged sunbird. Am Nat. 1979;114(1):131–145. [Google Scholar]
- 39.Rubenstein DI. Individual variation and competition in the everglades pygmy sunfish. J Anim Ecol. 1981;50(2):337–350. [Google Scholar]
- 40.Giuggioli L, Pérez-Becker S, Sanders DP. Encounter times in overlapping domains: Application to epidemic spread in a population of territorial animals. Phys Rev Lett. 2013;110(5):058103. doi: 10.1103/PhysRevLett.110.058103. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.