RNA does the folding dance of twist, turn, stack

RNA molecules have long been known to adopt unusual conformations. The first crystal structure of an RNA was that of yeast tRNA^phe (1, 2), which provided a portent of what was to come. With more structures available now from X-ray crystallography and NMR, that promise has been met beyond expectations. The RNAs that are folded in molecular dynamics simulations by Chen and Garcia (3) are tetraloops (RNA hairpin loops of only four nucleotides) that are among the most unusual small structures known today. Although or because they are unusual with atypical thermal stability, these loops are also ubiquitous in longer RNA strands [rUUCG (4); rGNRA and rCUUG (5)]; they were first identified as the most abundant hairpins in prokaryotic rRNA. The function of these loops varies: the GNRA tetraloops (where N is any base and R is a purine) is often found in RNA:RNA tertiary interactions to anchor a global fold. The UUCG tetraloop is solitary, with no known interactions with RNA or proteins: it is thought to nucleate folding and so direct in vivo RNA folding patterns. These little hairpins have been the objects of considerable in vitro experimental structural characterization by NMR and X-ray crystallography, and are found to consistently form a single unique structure. The rUUCG tetraloop in particular has been subjected to many thermodynamic investigations to measure the sources of its unusual stability (6). The rCUUG hairpin is structurally the most flexible, because it tucks its first U into the minor groove but its second U is relatively unconstrained. Among the three tetraloops, CUUG has a propensity for significant conformational exchange (7). Although the three tetraloops used in the Chen and Garcia (3) computational folding experiments are all unusually stable, they achieve their stability by very different means. Their structural diversity makes them excellent candidates for folding studies, because no one mechanism dominates their ability to adopt their unique structures.

The myriad of conformations that an RNA molecule can adopt makes RNA structural predictions very challenging, even now as the biology of RNA molecules is exploding. It is not an exaggeration to say that RNA molecules are involved at every level of gene regulation, so the accuracy with which their structures can be predicted or determined has become a critical problem for biology. The structures of the three tetraloops here could not have been predicted a priori today, given the intricate hydrogen bonding and base-stacking arrangements that they contain. These tetraloops are but a microcosm of what an RNA molecule can do, and because an RNA structure is an intricate part of its function, there are major research efforts devoted to develop predictive algorithms (8).

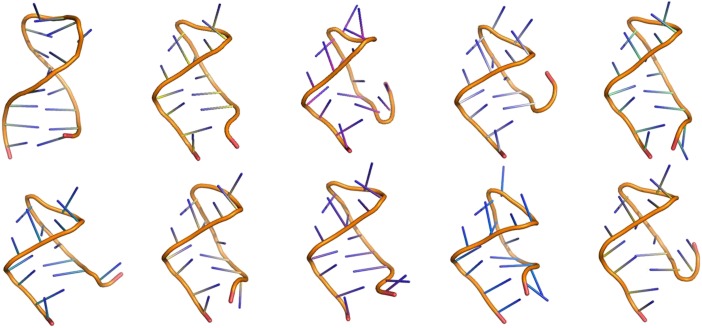
The static structure of an RNA is only a part of its characterization, though, because its dynamic motions are also linked to its function. RNAs are typically single-stranded, with short double-stranded (duplex) regions interspersed among local unstructured sequences. The short duplexes can lead to the formation of hairpin loops, internal bulges flanked by duplexes, three-way junctions, four-way junctions, and beyond. It is easy to imagine how the nucleotides in a loop could move, because the constraints on their conformation and consequent motions are greatly reduced from the strictures of a double strand (Fig. 1). The seven degrees-of-freedom of a nucleotide (including backbone torsions and glycosidic bond) allow it in theory to adopt many conformations. One of the experimental challenges is to describe the motions of nucleotides in nonduplex regions, because nucleotides in these regions control RNA folding, tertiary structure formation, and interactions with other molecules (proteins, small molecules, and other RNAs).

Fig. 1.

Although the dance of this RNA hairpin is too exuberant, its torsion angle twists and turns, its sugar repuckering, and its base stacking all contribute to its conformational flexibility. Chen and Garcia (3) examine how these properties lead to folding of RNA tetraloops, but they also allow an RNA molecule to do catalysis and bind ligands.

Unfortunately, experimental methods to measure dynamic motions and their consequences for RNA properties are rather limited by their timescales and probes. NMR methods are the most versatile for measurements of changes in the ribose pucker, stacking interactions between nucleobases and phosphate backbone flexing, but not every RNA is amenable to NMR experiments, and there are too many biologically functional RNAs that need investigation. Computational methods are ideally suited to explore the structure and dynamics of an RNA, given their timescales, which now range from picoseconds to microseconds in all atom molecular dynamics simulations with explicit solvent, and the implementation of clever sampling methods that bypass linear time lines. One such method, replica exchange molecular dynamics, is used by Chen and Garcia (3) for their RNA folding experiments.

Applications of molecular dynamics simulations to protein structure, dynamics, ligand binding, and folding have become standard, although certainly questions remain about force-field stability, water models that give correct protein correlation times, and sampling methods. In contrast, the need for accurate computational methods to describe RNA molecules has become acute, but molecular dynamics simulations of nucleic acids, in particular of RNAs, have lagged behind protein applications. Many of the questions related to accurate depictions of RNAs in silico remain unanswered. Several groups are making substantial contributions to RNA computational methods, as shown by recent reports from Denning et al. (9), using CHARMM36 to address the contributions of the ribose 2′ OH, and Tubbs et al. (10), incorporating revisions to the glycosidic angle χ using AMBER; AMBER applications for nucleic acids are reviewed in a perspective by Cheatham and Case (11).

The report by Chen and Garcia (3) is unique in successfully describing folding of an RNA to its experimentally determined structure. This achievement is exciting not only for what it promises for computational experiments that are sure to follow, but for the underlying reasons for its success.

One of the driving forces for RNA structure and dynamics is the stacking of nucleobases. Base stacking in the most common force fields, AMBER and CHARMM, has been a source of considerable trouble in practical and theoretical terms. AMBER is generally known to overstack nucleobases (3), which limits conformational sampling and leads to duplexes that are too stable. In contrast, CHARMM is known to understack bases (9), leading to disruption of duplexes and instability of noncanonical structures that are known to stack (such as tetraloops). Experimentally, nucleobase stacking is known to be enthalpically driven; it is not hydrophobic, and is generally considered to be described in chemical physics terms by London dispersion forces. As expressed by the Lennard–Jones potential, V = 4ε[(σ/r)¹²−(σ/r)⁶], r(σ) is the distance between molecules, ε the well depth, and σ the distance at which the potential is zero (the van der Waals radius). The first term is the repulsive term, and the second term the attractive term. This potential is heuristic, and the variables must be determined by measurement or fitting. In the RNA folding experiment by Chen and Garcia (3), one of the keys to their success was the optimization of ε and σ for base stacking in the AMBER force field.

As folding targets, Chen and Garcia (3) chose three RNA tetraloops, including the ubiquitous UUCG and GCAA loops, and the CUUG loop. By choosing to look at folding rather than describe the time-dependent motions of the nucleotides, the authors set themselves a more difficult task. Biological RNA folding is notorious for its off-pathway excursions to alternative structures; there is often no single low-energy well at the bottom of a steep folding funnel. Rather, the funnel is rugged, with nooks and crannies that trap the molecule, and the bottom of the funnel is shallow and broad (12–14). Although Chen and Garcia facilitated their task by the selection of three unusually stable hairpin loops, even these RNAs displayed complications. The authors found that the UUCG tetraloop adopted its unusual loop structure via several paths that involved intermediates, in agreement with spectroscopic experiments from the Gruebele laboratory (15). Chen and Garcia’s simulations also predict multiple folding pathways for the GCAA loop, again in agreement with several different in vitro experiments. In vitro folding experiments can identify kinetic intermediates, but are typically unable to assign a specific conformation to them. In silico folding experiments have the potential to provide that information, which can be subsequently used to design modified molecules to test that pathway. The Chen and Garcia experiments using replica exchange molecular dynamics have no kinetic data, so correspondence between their structural intermediates and those inferred from experiment will need to be tested. Their third chosen tetraloop, CUUG, remained recalcitrant; the experimentally determined folded structure evaded capture. When the structure of the CUUG tetraloop was solved by NMR, the investigators noted that its bases underwent considerable internal motion, especially the second U, so perhaps its performance in the simulations is not too far removed from its solution reality. By any criteria, the success of these computational folding experiments brings the field one step closer to accurate simulations of RNAs.

What RNA questions can be addressed now, with this improved AMBER force field? The DNA field has been obsessed with the timescales and geometries of bases that flip out of DNA duplexes. The analogous scenario for RNA is the dynamics of unpaired bases in asymmetric internal bulges. These are difficult to measure experimentally, but are important sites for binding to ligands; TAR:tat is a famous example (16). Beyond repeating computational experiments where RNA conformations are important for RNA function, fundamental questions relating RNA structure/dynamics are everywhere: how does a three-way junction become a site for small-molecule binding (riboswitches) or how does it fold to form a catalytic pocket (hammerhead ribozyme)? How are unpaired nucleotides accommodated in miRNA duplexes and bound to Argonaut proteins? Nature provides many more examples that await examination. RNAs will continue to be challenging molecules to describe experimentally, both in vitro and in silico. The prize when the puzzle is solved is a window into the world of RNA.