Bounded population sizes, fluctuating selection and the tempo and mode of coexistence

Significance

Habitats vary over time, but the influence of temporal variability on biodiversity is largely unknown. We develop a simple theory that shows temporal fluctuations in the direction of selection alone can promote biodiversity, and we confirm this prediction by direct experiment. Our work provides fundamental insights into the structure of competition and lays a conceptual foundation unifying competition theory in population genetics and ecology.

Abstract

Existing theory predicts competitors (species or genetic clones) cannot coexist in a fluctuating environment unless relative fitness is negatively frequency-dependent (relative fitness declines as the frequency of a competitor increases). We develop simple theory to show coexistence does not require frequency-dependent selection, and we confirm this prediction by direct experiment. The conditions for coexistence in a fluctuating environment are precisely the same as those for coexistence in a spatially variable environment, conditions that arise naturally whenever population abundances are bounded. Simulations show the likelihood of coexistence increases with environmental uncertainty. The capacity of temporally variable environments to maintain biological diversity is far broader than generally envisaged.

The great paradox of ecology is why so many species coexist in seemingly uniform environments (1) when the competitive exclusion principle asserts that only one should persist and the others be driven to extinction (2, 3). Of the various solutions that have been shown to promote coexistence, including mutualistic symbioses (4) competition for multiple resources (5, 6) and niche construction (7), all involve negative frequency-dependent selection wherein the relative fitness [the ratio of Malthusian parameters (8)] of a species declines as it increases in frequency. Temporal variability in the direction of selection might also contribute (1, 9). However, in the absence of rigorous experiments, it is not clear whether temporal variability adds anything other than noise to negative frequency-dependent fitness effects (10, 11).

Competition among species is conceptually identical to competition among asexual clones—in both cases reproductively isolated populations vie for limiting resources. Population genetic theory predicts that temporal variation in the direction of selection cannot protect clonal polymorphisms (12–17). Consider an infinitely large population of two asexual clones, A and B, with fitnesses W_A.i and W_B.i in generation i. The eventual fate of the competitors is determined by the product of their relative fitnesses, 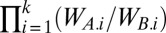(12). A wins the competition if the product is larger than one, B wins if it is smaller than one, and either A or B will randomly fix if it equals one (13). There is no tendency to maintain a polymorphism in the absence of negative frequency-dependent selection. Considered fundamental to all work on variable selection (18), classic population genetics theory suggests that alone fluctuating selection cannot maintain biodiversity.

More recently, a chemostat model of microbial competition (19) made a surprising prediction; competing clones can coexist in a fluctuating environment in the absence of frequency-dependent selection when population density is limited by resource availability. Ecologists have shown that species abundances are, in general, regulated (20, 21), yet population genetic models rarely specify whether or not this is so. Here, we demonstrate that classic population genetics theory predicts competitive exclusion as a consequence of an implicit assumption—that clonal growth is unbounded. Bounded growth enables fluctuating selection to promote coexistence in the absence of frequency-dependent selection.

Results

Theory.

We recast the previous model of fluctuating selection in a chemostat (19) into a model of fluctuating selection in serial transfer, which is experimentally more tractable. Malthusian parameters (growth rates) are independent of competitor densities and frequencies. The total population size is bounded because competitors cease to grow when the limiting resource runs out. Growth resumes upon dilution into fresh medium.

Let μ_X.i be the Malthusian parameter of competitor X (A or B) in environment i and let its initial frequency be p_X.i(0). Assume that a constant fraction of the total population, f, is transferred into each environment. Then

where t_i is the time available for growth (until the limiting resource is fully consumed) in environment i and 1/f is the fold increase in total population density in each environment. When competitor A is exceedingly rare, the time available for growth is 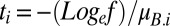, whereas when competitor B is exceeding rare, the time available for growth is 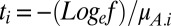. Evidently, the time available for growth depends on competitor frequencies in a population whose size is bounded by resource availability. As we shall see, the effect is to bias selection in favor of the rare competitor because more time is spent growing in environments favorable to it (because the common competitor grows more slowly, taking longer to exhaust the limiting resource) while less time is spent growing in environments that are unfavorable to it (the common competitor grows more quickly, taking less time to exhaust the limiting resource).

Rather than consider the time for growth, which is a dependent variable, it is much more convenient to handle the number of doublings by competitor X in environment i, d_X.i = μ_X.it_i /(Log_e2). The relative number of doublings equals the ratio of Malthusian parameters, d_A.i/d_B.i = μ_A.i/μ_B.i, a definition of relative fitness that is independent of competitor densities and frequencies and of the time available for growth. A rare competitor A increases in frequency across n environments when its doublings exceed those of the common competitor B, 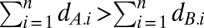. In a serial transfer experiment, each 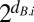of the common competitor equals the dilution factor (usually 1/f = 100). With 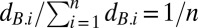, the condition for A to increase in frequency is that its arithmetic mean relative fitness be greater than one:

A will decrease in frequency when common (and rare B increase in frequency) if its harmonic mean relative fitness is less than one:

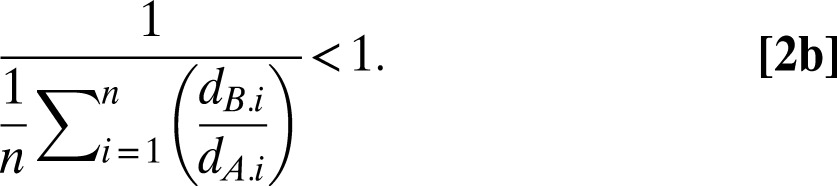These conditions, previously derived for a chemostat model of fluctuating selection in microbial populations (19), ensure coexistence because each competitor will increase in frequency when rare and will decrease in frequency when common.

That both competitors increase in frequency when rare and decrease in frequency when common is also predicted by negative frequency-dependent selection (22). However, inspecting inequalities 2a and 2b reveals that the relative fitnesses (ratio of Malthusian parameters, ratios of doublings, relative growth rates) (23, 24) are independent of competitor frequencies. Thus, the coexistence predicted by our model is not attributable to negative frequency-dependent selection.

That so simple a model predicts coexistence stands in contrast to more complex ecological theory, while the prediction of coexistence itself is at variance with classic population genetics theory (12).

Experiments.

To determine if our theory is valid, we conducted competition experiments between two populations of Escherichia coli, one resistant to chloramphenicol (Clm^r) and the other resistant to tetracycline (Tet^r). We enforced fluctuating selection by alternating between sublethal dosages of each antibiotic in minimal medium with glucose as the sole source of carbon and energy. On reaching an OD₆₀₀ of 0.3 (37.5 Klett units, or approximately K = 2.5 × 10⁸ cells per milliliter), mixed populations were diluted 100-fold into fresh medium containing the alternative antibiotic. This procedure imposed a bound on population size and avoided any physiological complications associated with entering and exiting stationary phase.

Competitions were conducted between a Clm^r.T5R strain resistant to the bacteriophage T5 and a Tet^r.T5S strain that was sensitive to T5. T5 resistance (fhuA) serves as a selectively neutral marker that allows the progress of competition to be monitored by counting individual cells from each population using flow cytometry (6). This assay is far more rapid and accurate than counting colonies on selective plates.

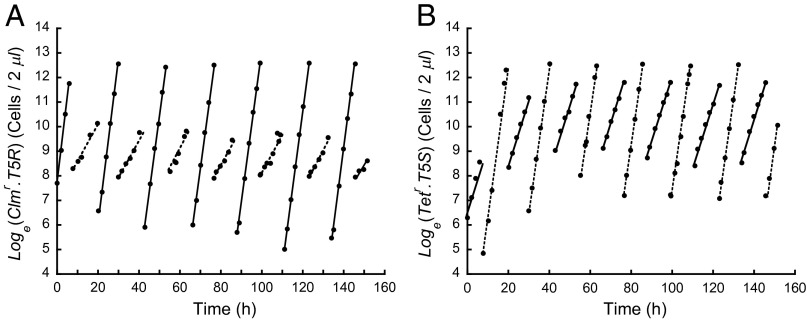
Pure cultures growing at sublethal antibiotic concentrations of 0.12 μg/mL chloramphenicol (Clm) and 0.55 μg/mL tetracycline (Tet) predict an arithmetic mean relative fitness greater than one and a harmonic mean relative fitness less than one—conditions sufficient for coexistence (Table 1). As predicted, populations competing in mixed culture under these conditions converge on a stable oscillatory coexistence regardless of their initial frequencies (Fig. 1A). Changing the antibiotic concentrations shifts the equilibrium midpoint of the oscillations up and down (Fig. 1B). This shows that coexistence is robust to perturbations. The selection is neither frequency- nor density-dependent because Malthusian parameters remain constant regardless of competitor frequencies and densities (Fig. 2).

Table 1.

Predicted and observed relative fitnesses

Antibiotic	Pure cultures			Mixed cultures
	μ, h−1*		Predicted relative fitness	μ, h−1*		Observed relative fitness
	Clmr.T5R	Tetr.T5S		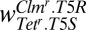Clmr.T5R	Tetr.T5S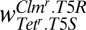
Chloramphenicol	0.62	0.28	2.21	0.64	0.29	2.21
Tetracycline	0.30	0.59	0.51	0.30	0.59	0.51
Arithmetic mean			1.36			1.36
Harmonic mean			0.83			0.83
Geometric mean			1.06			1.06

Antibiotic concentrations are 0.12 μg/mL chloramphenicol and 0.55 μg/mL tetracycline.

^*SEs are less than 1.5% of all estimates.

Fig. 1.

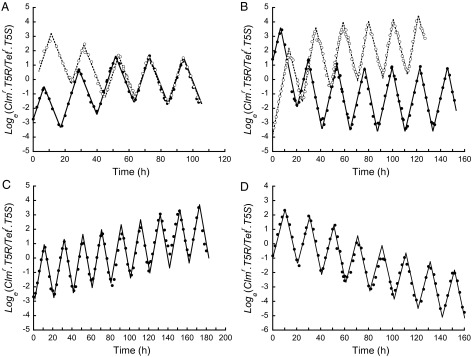
The outcome of competition with alternating directional selection depends on the mechanism of population regulation. (A and B) Transferring cultures to fresh medium at a fixed population density leads to coexistence. (A) Two mixed cultures (open circles and filled circles), initiated at different clone frequencies, converge rapidly onto the same stable oscillation (alternating 0.12 μg/mL chloramphenicol and 0.55 μg/mL tetracycline). On reaching a density of 2.4 × 10⁸ cells per milliliter, cultures were immediately diluted 1/100 into fresh medium containing the alternate antibiotic. (B) Changing the concentrations of the antibiotics changes the selection intensities and shifts the stable oscillation up (open circles, chloramphenicol now 0.22 μg/mL) and down (filled circles, tetracycline now 0.65 μg/mL). (C and D) Transferring cultures to fresh medium every 10 h regardless of population density leads to competitive exclusion. (C) Antibiotic concentrations identical to A. (D) Antibiotic concentrations identical to B (filled circles). The selection coefficients per hour (slopes) depend only on antibiotic concentrations and remain invariant regardless of clone frequencies, culture densities, and mechanisms of population regulation.

Fig. 2.

Growth rates of clones (A) Clm^r.T5R and (B) Tet^r.T5S are log-linear showing that the Malthusian parameters remain invariant at 0.12 μg/mL chloramphenicol (lines) and 0.65 μg/mL tetracycline (dashes) demonstrating that they are neither frequency- nor density-dependent. Data from Fig. 1B (filled circles).

We can recover the behavior predicted by classic population genetic theory if, instead of transferring the mixed culture at a predetermined population size, we transfer it after a fixed period. The Clm^r.T5R population has the larger geometric mean fitness and is now predicted to win the competition (Table 1). Under precisely the same environmental conditions that led to coexistence in Fig. 1A, but now with transfers every t = 10 h regardless of population density, the Clm^r.T5R population is destined for fixation (Fig. 1C). And under precisely the same environmental conditions that led to coexistence in Fig. 1B (filled circles), the Clm^r.T5R population is now destined for extinction (Fig. 1D) with transfers every t = 10 h. Coexistence and competitive exclusion depend on the transfer regime.

Discussion

Carrying Capacities Are Critical to Coexistence.

To understand the role of bounded population size in promoting coexistence we have only to consider a serial transfer experiment in which a mixed culture is diluted, say 2¹⁰-fold, and grown to full density. If competitor B is common and a fitter competitor A (μ_A/μ_B = d_A/d_B > 1) is rare, then it follows that the number of doublings by B is 10, and that the number of doublings by A is 10 · d_A/d_B > 10. However, if A is common and B is rare, then it follows that the number of doublings by A is 10, and that the number of doublings by B is 10 · d_B/d_A < 10. In resource-limited environments, competitors experience more doublings when the least fit competitor is most common. It is not relative fitness that is frequency-dependent; it is the number of generations (i.e., the number of doublings) per dilution that is frequency-dependent.

Now suppose the fitness of A relative to B is 2 in environment 1 and 0.5 in environment 2. When common, B experiences 10 doublings in each environment following dilution and growth to carrying capacity, while the rare A experiences 20 doublings in environment 1 (where it is twice as fit) and 5 doublings in environment 2 (where it is only half as fit). For every cycle of two environments, B experiences 20 doublings whereas A experiences 25 doublings. The argument is symmetrical with respect to A and B; when A is common it experiences 20 doublings while the rare B experiences 25 doublings (Table 2). Hence, each competitor invades when rare because it experiences more doublings than its common rival whose doublings are strictly resource limited.

Table 2.

Doublings in a fluctuating environment

Competitor	Frequency	Doublings
		Environment		Sum
		1	2
A	Rare	20	5	25
B	Common	10	10	20
A	Common	10	10	20
B	Rare	5	20	25

Fitness of A relative to B (μ_A/μ_B = d_A/d_B) is 2 in environment 1 and 0.5 in environment 2 in this hypothetical serial transfer experiment with 2¹⁰-fold dilutions.

With fixed time periods, as in classic population genetics, the doublings in each environment by each competitor are fixed. A rare competitor A invading a population B, whose doublings precisely match the 2¹⁰-fold dilution at each transfer, must grow to infinity since 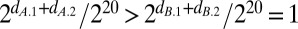. The assumption that resources are infinite was introduced to population genetics when it was supposed that continuous time overlapping generation population growth could be accurately represented by a discrete generation time model with normalized Malthusian parameters (i.e., relative fitnesses). Far from describing competition, the population genetic model instead describes ecological neutralism, for without limiting resources there is no competition, no struggle for existence. The clones never interact. They simply reproduce and die.

Synthesis.

Temporal variability has been considered either unimportant (25, 26) or detrimental (27) to promoting coexistence because the necessary conditions were thought to be either too restrictive or impossible to meet (12–18). Recent theoretical and field observations (9, 28, 29) challenge this view, suggesting instead that temporal variability might play a major role in maintaining diversity. Our result cannot be attributed to the storage effect (9, 29), because E. coli has no equivalent of a seed bank or means to diapause to help it through harsh times, nor to nonlinearities in competition (9, 30–34), because Malthusian parameters remain constant in each environment. Rather, our result is the inevitable consequence of bounded population growth passively biasing competition in favor of rare competitors, and in so doing, promoting coexistence.

Inequalities 2a and 2b for coexistence in a temporally variable environment are identical to those for coexistence in a spatial model of competing clones that disperse randomly into habitats at each generation (35). In a randomly mating diploid population, coexistence of two alleles is ensured when the harmonic mean fitnesses of both homozygotes, with respect to the heterozygote, are less than one. This condition, which prevents fixation of either allele, is identical to Levene’s (36) spatial model of selection with random dispersal of zygotes to different habitats each generation. We conclude that, in the absence of restrictions to migration among habitats, temporal and spatial environmental variability have similar capacities to maintain genetic diversity.

The probability that two competitors coexist in two environments is 0.193 when Malthusian parameters are chosen randomly from a uniform distribution, although it differs when sampling from other distributions (e.g., with a normal distribution or a gamma distribution the probability of coexistence depends on SD and the shape parameter). The probability of coexistence increases with more environments and decreases with the number of species that must coexist (Fig. 3A). Tradeoffs among Malthusian parameters increase the likelihood of coexistence (Fig. 3B). The probability that two competitors coexist in two environments is 0.5 with a linear tradeoff. The impact can be dramatic—coexistence is guaranteed for two species in two environments when the fitness tradeoff has the form w₁ = 1/w₂. We assert that temporal variability in competition is as important as spatial variability in promoting biological diversity.

Fig. 3.

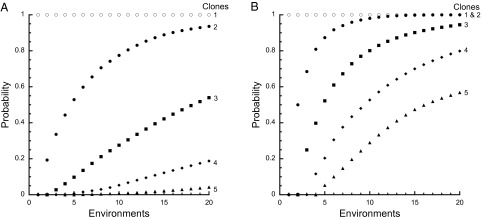
Probability of coexistence in variable environments. (A) The probability of coexistence increases with the number of environments but decreases rapidly with the number of clones (1, open circles; 2, filled circles; 3, filled squares; 4, filled diamonds; 5, filled triangles) in the absence of fitness tradeoffs. Malthusian parameters for each species in each environment were drawn independently and randomly from a uniform distribution. (B) Coexistence is much more likely in the presence of fitness tradeoffs. Summing and normalizing the Malthusian parameters of each species introduces fitness tradeoffs.

Competition among species is equivalent to competition among asexual clones—in both cases reproductively isolated populations compete for limiting resources. Despite sharing this commonality, theoretical ecology and population genetics have taken dissimilar approaches to assessing the impact of competition on biological diversity. Ecological models describe population growth rates in terms of resource abundances, population densities, and interactions between species. Population genetic models treat relative fitnesses as independent variables and not as the emergent properties of underlying ecological and organismal processes. Our theory provides a conceptual foundation that unifies these two fields, while at the same time striking a balance between realism and clarity. Our experiments demonstrate that temporal fluctuations in selection are sufficient to promote coexistence during competition for a single limiting resource in the absence of negative frequency-dependent selection.

Materials and Methods

Media.

For rich medium, we used Luria-Bertani medium (LB; 10 g Bacto trytone, 5 g Bacto yeast extract, 10 g NaCl in 1 L ddH₂O) with 15 g/L Bacto agar for solid medium and 8 g/L for soft agar. For minimal medium, we used minimal Davis medium (MD; 7 g K₂HPO₄, 2 g KH₂PO₄, 1 g (NH₄)₂SO₄, and 0.5 g of sodium citrate in 1 L ddH₂O) with 1 mL of 1 M MgSO₄⋅7H₂O, 0.5 mL of 1% thiamine, 2 mL of 20% (wt/vol) glucose stock solution, and 1 mL of 50-mg/mL kanamycin (Kan) added after autoclaving. Tet and Clm were added at various sublethal concentrations as required.

Strain Construction.

Tet^r and Kan^r resistance cassettes were PCR amplified from pBR322 (NEB) and pKD13 (37) and fused together. The paired Tet^r–Kan^r cassettes were ligated between 1-kb fragments upstream of lacI and downstream of lacA (PCR amplified from the E. coli MG1655 chromosome) and then ligated into plasmid pRD007 (38) using standard molecular cloning procedures (39) and propagated in strain DH5α [fhuA2 Δ(argF-lacZ)U169 phoA glnV44 Φ80 Δ(lacZ)M15 gyrA96 recA1 relA1 endA1 thi-1 hsdR17]. The MG1655 lac operon was then replaced by the Tet^r–Kan^r construct using the lambda red recombination system (37). The construct was PCR amplified from the plasmid and transformed into MG1655 cells carrying pKD46 using electroporation (MicroPuler Electroporator, Bio-Rad; 1,800 V, 5.0 ms). Recombinants were selected on LB–Kan plates, screened for Tet resistance (LB plates with 20 μg/mL tetracycline), and the insert confirmed by sequencing. The Clm^r strain was similarly constructed except Tet^r was replaced by Clm^r amplified from pRD007. Note that the derived plasmid was propagated in RecA⁻ strain DH5α in the presence of Kan to prevent loss by deletion.

T5 phage-resistant mutants of both strains were isolated by the method of Dykhuizen and coworkers (6); and 10¹⁰ T5 phage (100 μL of lysate) were added to 10⁸ cells (100 μL of stationary phase culture grown in LB–Kan) and the mixture added to 4 mL of soft LB–Kan agar (50 °C) and plated immediately onto LB–Kan plates. After overnight incubation at 37 °C, T5-resistant colonies were streaked on fresh LB–Kan plates, then grown in liquid LB–Kan and frozen at −80 °C in the presence of 15% (vol/vol) glycerol.

Competition.

T5-sensitive Tet^r (Tet^r.T5S) and T5-resistant Clm^r (Clm^r.T5R) strains from −80 °C stocks were streaked on LB plates supplemented with Kan and incubated overnight at 37 °C. A single colony from each strain was used to inoculate 1 mL MD media and incubated at 37 °C with vigorous shaking (250 rpm) until moderately turbid (OD₆₀₀ between 0.3–0.6, 1-cm light path). Strains were mixed in the ratio desired based on OD₆₀₀ readings and used to inoculate a 250 mL sidearm flask with 10 mL MD medium supplemented with a sublethal dose of chloramphenicol. Competitions were carried out by incubating flasks at 37 °C with vigorous shaking. Every 2 h, 200 μL of culture were transferred to a sterile 1.5-mL Eppendorf microcentrifuge tube and stored on ice. At the same time, the population density was determined using a Klett spectrophotometer (with our set up, 125 Klett units with a D35 filter (540 nm) is equivalent to 1 OD₆₀₀, 1-cm light path, or 8 × 10⁸ cells per milliliter). In competition experiments with fixed carrying capacities, population densities above 25 Klett units were monitored frequently and, upon reaching 37.5 Klett units (2.4 × 10⁸ cells per milliliter), 100 μL of culture inoculated into a second flask of fresh 10 mL MD medium supplemented with a sublethal dosage of tetracycline. This transfer procedure was repeated exposing the mixed culture to alternating chloramphenicol and tetracycline with a carrying capacity of 2.4 × 10⁸ cells per milliliter. The procedures were similar for competition experiments with transfers at fixed 10-h intervals.

Flow Cytometery.

The progress of competition was monitored by the T5 method of Lunzer et al. (6) with modification. Every 10 h, ice-kept samples were analyzed in a single batch. To each 200-μL sample were added 42 μL buffer I [equal volumes of fresh LB and T5 lysate (>10¹¹ phage per milliliter) with 5% 20 mg/mL choremphenicol] and 58 μL buffer II [50 μL phosphate buffer (7 g of K₂HPO₄ and 2 g of KH₂PO₄ in 1 L ddH₂O), 7 μL 62.5 mM Na₂EDTA, and 1 μL of 1 mM TO-PRO-3 (Invitrogen) dissolved in DMSO]. The mixture was vortexed and incubated at 37 °C for 30 min. After appropriate dilution (to bring the sample density to ∼10⁶ cells per milliliter) in fresh phosphate buffer, cells were counted using a FACSCalibur (BD Sciences) flow cytometer equipped with a 635-nm red diode laser and a 670-nm low-pass filter.

The staining procedure allows T5-sensitive and -resistant cells to be distinguished. Attachment of T5 phage to sensitive cells depolarizes the cell membranes making them permeable to the TO-PRO-3, which enters and binds to double-stranded nucleic acid. Bound TO-PRO-3 emits in the far-red (660 nm) upon excitation at 635 nm by a red diode laser. T5-resistant cells remain unstained. Forward scatter and side scatter channels were used together to gate out noise. Typically, data were collected for 50 s (30,000–75,000 events). The density of each strain in the mixed culture was calculated as cell counts per second × dilution factor ÷ flow rate (0.2 μL/s) after correction for background counts.

Experimental Predictions and Data Analysis.

The predicted trajectories of the competitions were calculated using Mathematica (Version 8.0, Wolfram Research, Inc.). The predictions require nine input parameters: two starting densities of each strain at time 0, four Malthusian parameters in each environment, the carrying capacity, the number of environmental shifts, and the fold dilution at each shift.

New, fitter mutants arising during the competitions would compromise results. Their presence is usually detected between 60 and 80 h after the start of the competition as a sudden deviation from the predicted growth trajectory. Because we can accurately predict the strain densities far into the future, each competition experiment was initiated at several time points along the expected trajectory, usually at 0, 40, and 80 h. These data were then spliced together, with a minimum 20-h overlap, to reveal the overall trajectory of the competition.

Analytical Solutions.

Assume the Malthusian parameters of two competitors (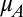 and 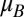) are independent variables drawn from a common uniform distribution on the interval [0, 1]. The probability density function of the relative fitnes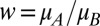s () is

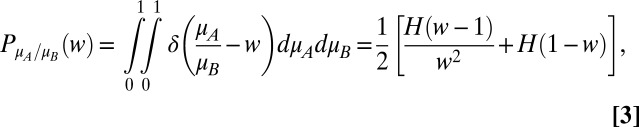where 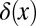is a delta function and 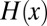is a Heaviside step function. The probability density of a pair of relative fitnesses in an environment alternating between two states is the joint distribution of a pair of Eq. 3s

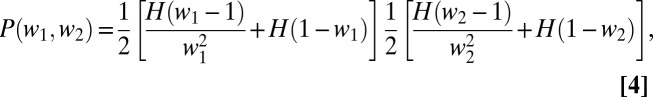where 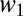and 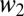are the relative fitnesses in environments 1 and 2. The assumption of independence means there are no tradeoffs in fitness. The probability of coexistence can be calculated by imposing inequalities 2a and 2b on Eq. 4 and integrating with respect to 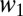and 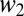over the interval [0, ∞]. The probability that two clones can coexist in a two-season environment is then found numerically to be 0.193.

With a linear tradeoff, we have 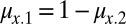. For x = A and x = B to coexist, each must be able to invade when rare. Inequalities 2a and 2b become

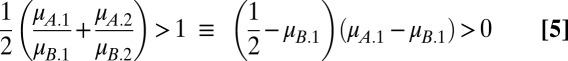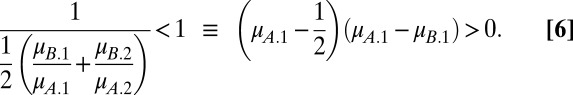When 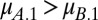, coexistence requires that 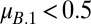and 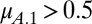. Alternatively, when 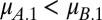, coexistence requires that 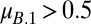and 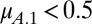. Evidently, coexistence is guaranteed when the Malthusian parameters of the competitors lie either side of 1/2. Hence, the probability that two clones can coexist in a two-season environment is 0.5 when tradeoffs are linear.

Simulations.

Analytical solutions with more than two species are formidably complex and were not attempted. Instead, we simulated competition in Mathematica by drawing Malthusian parameters at random from a uniform distribution on the interval [0, 1] for n clones in m cyclical environments and using the FindRoot algorithm (incorporating a damped Newton’s method, the secant method, and Brent’s method) to numerically solve for t_j the time spent growing in each environment j,

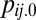is the frequency of clone i in environment j at time 0, μ_ij is its ratio of Malthusian parameter, and d is the natural logarithm of the fold dilution (usually 100) at each transfer. Inserting t_j renders each term under the summation as the frequency of clone i in the next environment j + 1 at time 0, 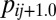. The FindRoot algorithm is once again applied for the next environment. The cycle is repeated across the m cyclical environments until no clone frequency changes more than ±10⁻¹² (from environment j to j + m) or a clone with a frequency below 10⁻⁶ is declared extinct. The simulation was repeated 10,000 times each for n clones in m environments and the number of times n clones coexist recorded.