High-resolution reversible folding of hyperstable RNA tetraloops using molecular dynamics simulations

Significance

We report atomistic simulations describing the spontaneous folding of three RNA tetraloops from the unfolded state to within 1–3 Å of their experimentally determined structures. These common and highly stable motifs serve as building blocks for large structured RNA molecules. This success is caused by the reparameterization of the energy function used to describe the interatomic interactions, which was obtained by calibrating the energy function to reproduce known thermodynamic and kinetic measurements of RNA monomers and dimers. In particular, the accurate recapitulation of the characteristic loop configurations responsible for the thermodynamic hyperstability of these motifs represents a significant milestone to the accurate description of RNA tertiary structure using unbiased all-atom molecular dynamics simulations.

Abstract

We report the de novo folding of three hyperstable RNA tetraloops to 1–3 Å rmsd from their experimentally determined structures using molecular dynamics simulations initialized in the unfolded state. RNA tetraloops with loop sequences UUCG, GCAA, or CUUG are hyperstable because of the formation of noncanonical loop-stabilizing interactions, and they are all faithfully reproduced to angstrom-level accuracy in replica exchange molecular dynamics simulations, including explicit solvent and ion molecules. This accuracy is accomplished using unique RNA parameters, in which biases that favor rigid, highly stacked conformations are corrected to accurately capture the inherent flexibility of ssRNA loops, accurate base stacking energetics, and purine syn-anti interconversions. In a departure from traditional quantum chemistrycentric approaches to force field optimization, our parameters are calibrated directly from thermodynamic and kinetic measurements of intra- and internucleotide structural transitions. The ability to recapitulate the signature noncanonical interactions of the three most abundant hyperstable stem loop motifs represents a significant milestone to the accurate prediction of RNA tertiary structure using unbiased all-atom molecular dynamics simulations.

Structured RNAs exhibit a distinct preference for loops of precisely 4 nt, which was originally noted by Woese et al. (1) using comparative sequence analysis of ribosomes. Approximately 70% of these tetraloops are comprised of just three specific loop sequences: UUCG, GCAA, or CUUG. The abundance of these sequences is thermodynamic in origin, because each motif forms a unique network of noncanonical interactions within their loops that stabilizes the folded state. The abundance of high-resolution structural and thermodynamic data available for these motifs coupled with their characteristic noncanonical signatures make them ideal for adjudicating the accuracy of RNA folding simulations.

RNA folding is understood to be hierarchical in nature, with secondary and tertiary folds stabilized by distinct thermodynamic driving forces (2). Secondary structure (the formation of canonical helices stabilized by Watson–Crick base pairs) can be accurately predicted from the nucleotide sequence alone using simple nearest neighbor thermodynamic models (3). In contrast, tertiary structure formation is a subtle competition between intrinsic flexibility of single-stranded segments, rigidity imparted from base-stacking interactions, stabilization of noncanonical hydrogen bonding patterns, and site-specific ion binding. In principle, a molecular dynamics simulation using a properly calibrated force field should capture all of the physicochemical properties of ribonucleotides relevant to the RNA folding process. Up until now, however, even small, fast-folding tetraloops cannot be accurately and reversibly folded from the unfolded state (4–6). In contrast, numerous documented successes have been reported using de novo protein folding with all-atom molecular dynamics simulations (7).

In this work, we present the results of replica exchange molecular dynamics (REMD) simulations that are consistently able to correctly fold all three hyperstable tetraloops from random unfolded states to 1–3 Å rmsd from their experimentally determined structures, using optimized RNA parameters. These parameters feature van der Waals interactions that have been calibrated against high-level quantum mechanics (QM) dispersion calculations in conjunction with a suite of experimental measurements of aqueous nucleoside and dinucleotide interactions. The resulting RNA parameters reproduce the experimentally measured clustering propensities of aqueous nucleoside solutions as a function of concentration, the thermodynamics of base stacking as a function of temperature, and the population and lifetimes of syn-anti glycosidic transitions; in contrast, we find that the default AMBER-99 RNA (8) parameters fail all of these same tests. We find that these degrees of freedom are intrinsically coupled and that only a simultaneous global reparameterization results in the ability to reversibly fold hyperstable tetraloops with their signature noncanonical interactions. The ability to fold small model RNAs de novo enables future computational studies of larger biologically interesting RNAs, such as riboswitches, ribozymes, and mRNA UTRs.

Results

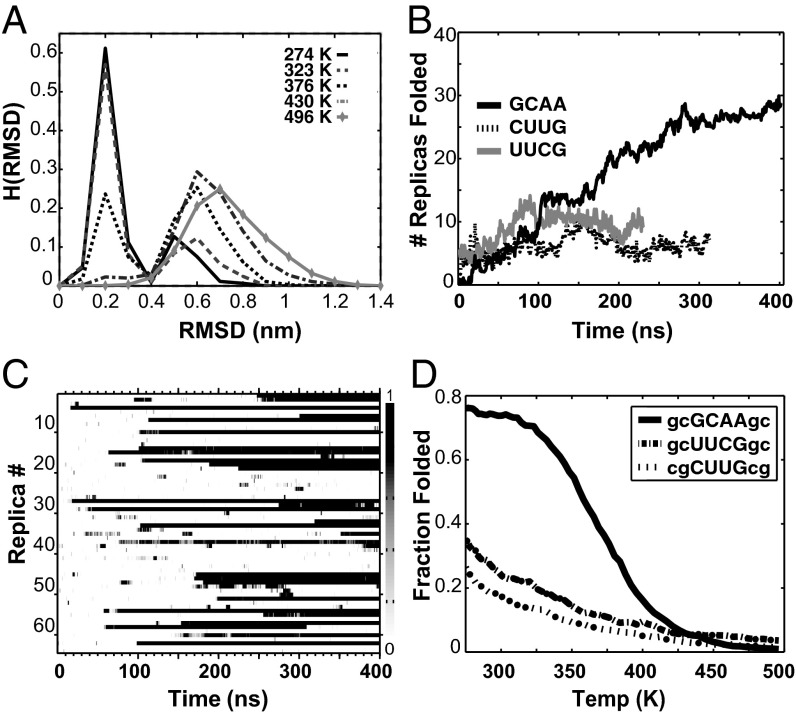
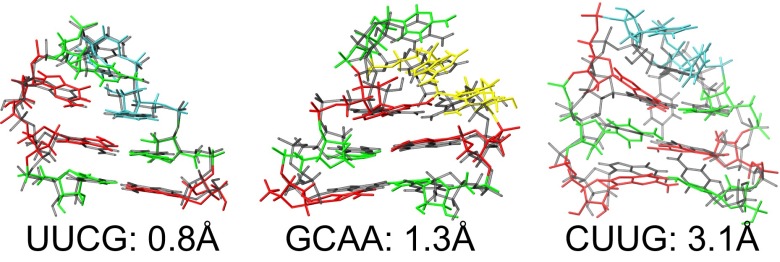
In each REMD simulation, dozens of folding events are observed, which can be seen in Fig. 1C; the resulting melting curves for all three tetraloops are shown in Fig. 1D. The folded states calculated for the three tetraloops, which are shown in Fig. 2, are superimposed against their experimentally determined structures, which are shown in Fig. 2, gray. Each calculated structure is the centroid of the most highly populated cluster from the trajectory found at the lowest REMD temperature (274 K)—not the structure with the lowest rmsd. This cluster identifies the most thermodynamically stable configuration from the REMD ensemble without introducing any artificial bias to the experimental structure during the selection process. The centroid structures capture all of the unique noncanonical signatures of hyperstable tetraloops, which are detailed below. In all cases, hydrogen bonding interactions between the first (L1) and fourth (L4) base in the loop form a distorted base pair constrained by the reduced interstrand distance of the loop, whereas the second (L2) and third (L3) loop bases are either weakly stacked or completely unrestrained by virtue of being flipped out into solution.

Fig. 1.

Tetraloop folding simulations. (A) Histograms of GCAA rmsd vs. temperature. The folded fraction is taken as rmsd < 0.4 nm. (B) Number of folded replicas vs. time. UUCG and CUUG both equilibrate within 100 ns, whereas GCAA requires 275 ns before steady state is reached. (C) Fraction of each 0.5-ns block spent in the folded state for all 64 replicas of the GCAA folding simulation. (D) Fraction folded vs. temperature for all three tetraloop sequences.

Fig. 2.

Folded state predictions (colored) vs. experimental structure (gray) for all three hyperstable tetraloops and their rmsd values from the experimentally determined structures. Predictions are centroids from the most populated cluster of the trajectory visiting the lowest REMD temperature. Nucleosides are colored as red (guanine), green (cytosine), yellow (adenine), and cyan (uracil).

The centroid structure for the UUCG tetraloop is just 0.8 Å all heavy-atom rmsd from the X-ray structure (Fig. 2, Left), with a closest cluster conformation of 0.6 Å rmsd. The folded state correctly captures the transwobble GU base pair as well as the correct orientation of the middle loop bases U_L2 and C_L3. The transwobble GU pair requires G_L4 to adopt an unusual syn conformation and is stabilized by a hydrogen bond between the N1 of G_L4 and the 2′OH of U_L1 but not with N2. U_L2 is highly mobile and flipped out into solution, and the amino group of C_L3 is observed to form a hydrogen bond to the O1P of U_L2, which are all in agreement with the high-resolution NMR structure (9). Additionally, we observe hydrogen bonds from the N2 of G_L4 to the O2 of C_L3 and from the O6 of G_L4 to the 2′OH of U_L2, which tend to form when the other two hydrogen bonds to G_L4 are broken, resulting in a cage of weak hydrogen bonds that cumulatively maintain the highly mobile G₄ in its unusual syn conformation.

Our simulations also accurately fold the GCAA tetraloop, where the most populated cluster centroid is 1.3 Å (all heavy atom) rmsd from the NMR structure (Fig. 2, Center), with a closest conformation of 0.8 Å rmsd. The folded state correctly captures the unusual sheared GA loop base pair, with exocyclic amino group of G_L1 alternately hydrogen bonding with the N7 of A_L4 or the O2P of A_L3. The putative hydrogen bond between N7 of A_L3 and the 2′OH of G_L1 suggested by NMR studies (10) is also observed, which stabilizes the stacked conformation of A_L3 on top of A_L4, whereas C_L2 is flipped out into the solvent and largely unrestricted. G_L1 exhibits strong cross-stacking with the G of the closing base pair, whereas A_L3 is more solvent-exposed and does not interact strongly with the closing base pair. It can be seen in Fig. 2, Center that the slightly rotated conformation of A_L4 is the only significant deviation from the 1ZIH NMR structure. However, it has been shown in the work by Mohan et al. (11) that GNRA (where N = C or U and R = A or G) tetraloops within the 70s ribosome crystal structure consistently exhibit similarly repositioned A_L4 conformations on account of torsional stress within the loop backbone. If these structures (2JJ0) are used as a reference rather than the NMR structure, the centroid rmsd drops to <1.0 Å.

Additionally, we are also able to fold the CUUG tetraloop, albeit with less accuracy than either the UUCG or GCAA tetraloop. The centroid rmsd is 3.1 Å (Fig. 2, Right), with the closest observed conformation at 2.0 Å rmsd from the experimental structure. The buckled CG base pair between C_L1 and G_L4 of the loop is correctly recapitulated, essentially creating a 3-bp helix topped by an effective biloop. The primary discrepancy is the predicted position of U_L2, which does not get inserted into the minor groove as experimentally observed; consequently, the predicted position of the neighboring U₃ is also perturbed. This unusual U_L2 conformation is known to be stabilized by hydrogen bonds to the exocyclic amino group of G_L4 as well as two additional hydrogen bonds to the proximal stem CG base pair, none of which are observed in our simulations. It should be noted that U_L3, unlike U_L2, is poorly restrained by existing NMR NOE restraints, because it does not participate in any hydrogen bonds and undergoes fast chemical exchange (12). Therefore, it is just the predicted position of U_L2 that is at odds with the experimental data and not the arbitrary conformation of U_L3 as represented in the experimental structure. If U_L3 is excluded from the rmsd calculation, the centroid is ∼2.0 Å rmsd from the experimental structure.

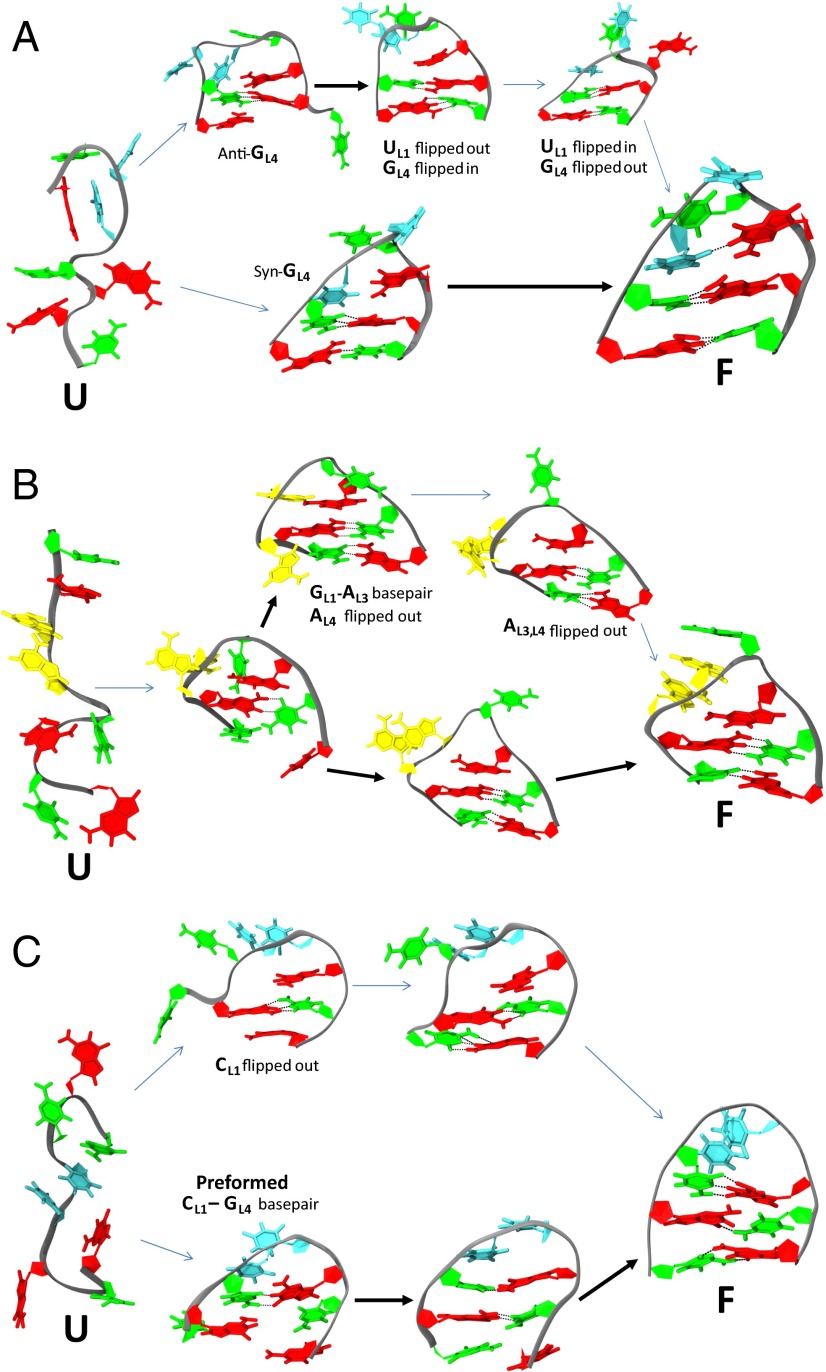
At intermediate temperatures, clustering analysis reveals that the folded ensemble consists of multiple interconverting substates that are not as optimally packed as the native state but still possess 2 stem bp. The sequence of events from the observed folding trajectories sheds light on how each loop sequence dictates the overall RNA folding pathway. It should be noted, however, that individual REMD trajectories rapidly swap temperatures, and therefore, the observed pathways may not be identical to the pathways observed at constant temperature. Surprisingly similar folding pathways are observed for all three tetraloop sequences. Each productive folding event always originates from a high-temperature replica, where it is fully extended and unstructured. The initiation of folding from expended conformations does not imply that mispaired or collapsed conformations are not sampled, but rather that they were not observed as on-pathway intermediates for productive folding. These extended high-temperature states undergo rapid fluctuations that bring base pairs on opposing ends of the RNA in close proximity, resulting in many transiently formed single base pairs (including nonnative ones). Mispaired, nonnative base pairs tend to rapidly dissociate, whereas the occasional formation of an in-register stem base pair results in the immediate formation of the neighboring second stem base pair (facilitated by a cross-stacked purine). After it is formed, the doubly base-paired stem remains intact for the remainder of the simulation. At this point, the loop bases are in a disordered, collapsed state and begin a restricted search for a more optimal packing arrangement. If the loop happened to collapse very close to the native state, the noncanonical hydrogen bonds between loop bases L1 and L4 are able to rapidly find their folded state. If the loop collapsed with a suboptimal base packing, the search is a slow, multistep process involving successive flipping out and in of the bases at the L1 and L4 positions until the proper noncanonical hydrogen bonds are realized. Only then can the loop bases at positions L2 and L3 properly adjust their stacking to complete the folded tetraloop motif.

For the UUCG tetraloop, a handful of trajectories collapse with G_L4 already in the syn conformation, and therefore, the trans G-U wobble interaction forms quickly (Fig. 3A). However, typical trajectories collapse with G_L4 in the anti conformation and are stacked against the inner stem CG base pair. In these cases, the G₄ will not fit sterically in the narrow, collapsed loop at the same time as U_L1, and therefore, one or the other is forced to flip out into solution. For the GU trans wobble to form_, U_L1 must be flipped in, whereas G_L4 is flipped out and transitions to the syn conformation. This slow, multistep process does not always complete for every folded trajectory within the simulation timescale. In fact, clustering analysis reveals that these kinetically trapped conformations are highly populated in intermediate temperature trajectories. However, the fact the native state is at all reachable is a direct consequence of our revised force field, which correctly captures both the relative populations of syn-anti conformers and the correct transition rates between them.

Fig. 3.

Tetraloop folding pathways. Two alternate folding pathways are observed for all three hyperstable tetraloops. Thick and thin arrows depict rapid and slow transitions, respectively. Bases are colored the same as in Fig. 2. (A) UUCG folds rapidly if G_L4 is already in syn before collapse, which is required to form the trans-GU wobble base pair (lower pathway). In contrast, misfolds containing the anti-G_L4 must flip G_L4 out of the loop to access the syn conformation and then flip back in to pair with U_L4 (upper pathway). (B) GCAA folds rapidly when G_L1 correctly pairs with A_L4 after loop collapse to form a sheared base pair (lower pathway), but it can also form a nonnative G_L1-A_L3 base pair (upper pathway). A_L3 must flip out before the native G_L1-A_L4 base pair can form. (C) The CUUG tetraloop rapidly folds when the C_L1-G_L4 base pair is preformed before collapse (lower pathway); otherwise, C_L1 is initially flipped out and must flip back into the loop to reach the native state (upper pathway).

GCAA folding events also begin with the formation of the inner stem CG base pair stabilized by cross-stacking from G_L1 (Fig. 3B). After it has collapsed, G_L1 and A_L4 can form the characteristic sheared GA base pair, and then, A₃ stacks on top are stabilized by a hydrogen bond to the 2′OH of G_L1; the noninteracting C₂ remains flipped out into solution, completing the motif. However, there is the possibility that a sheared GA base pair can also form between G_L1 and A_L3 on loop collapse, forcing A_L4 to flip out into solution to accommodate the shortened loop. This nonnative, misfolded conformation can eventually find the native state if A_L3 flips out and then A_L4 flips in to form the correct sheared GA base pair. This multistep search process proceeds much slower than the first route, resulting in the unusually slow overall equilibration rate observed for the GCAA simulation (Fig. 1B).

Lastly, the CUUG motif involves the formation of a buckled CG base pair involving C_L1 and G_L4 of the loop, effectively creating a biloop (Fig. 3C). Unlike either UUCG or GCAA, it is observed that there is a possibility of C_L1-G_L4 base pair formation preceding stem formation, because Watson–Crick base pairs can form outside the context of the collapsed loop. The primary pathway, however, is similar to the other two tetraloops, where the inner stem base pair forms first (aided by a cross-stacked G₄), then the outer base pair forms, and finally, the loop CG base pair forms. The experimental CUUG structure indicates that U_L2 should then pack vertically into the minor groove to form hydrogen bonds with both the loop and inner stem CG base pair; however, in our simulations, we do not observe the U₂ base to adopt this configuration, possibly indicating an interaction not properly modeled by our RNA parameters. In particular, we have not attempted any modification of the default AMBER-99 phosphate backbone torsions, which have been shown in prior work by Pérez et al. (13) to result in distortions of B-form DNA helices in long molecular dynamics simulations. An incorrect description of RNA backbone flexibility combined with the unusually strained CUUG loop backbone may explain the inability of the CUUG simulations to adopt the experimentally observed minor grove interaction.

Discussion

Our findings indicate that the folding of a minimal RNA motif (hyperstable tetraloops) exhibits many of the hallmarks of hierarchical folding observed for larger, structured RNAs. Secondary structure formation (in this case, the formation of two Watson–Crick stem base pairs) occurs very rapidly (<100 ps) with high cooperation in a canonical two-state fashion. The noncanonical loop interactions, however, often involve a slow conformational search through isoenergetic intermediates that cannot even begin until after the stem is completely formed, indicating the existence of a rough free energy landscape, even for minimal hyperstable RNA motifs.

The existence of multiple substates with suboptimal loop conformations in our REMD simulations is consistent with prior experimental reports of not two-state behavior in tetraloop folding. Menger et al. (14) found that 2-aminopurine stacking at the L2 and L3 positions of the GAAA tetraloop displayed distinctly different relaxation lifetimes on the microsecond timescale using fluorescence-detected temperature jump experiments. Intriguingly, Menger et al. (14) also found that fluorescence changes at either position were anticorrelated with changes at the other position as a function of temperature, indicating a population shift involving competing stacking rearrangements of A_L2 and A_L3. Similarly, Johnson and Hoogstraten (15), using NMR relaxation, observed a puzzling temperature-dependent multisite exchange process for the C2′ of A_L3 that they hypothesized could be caused by extrusion of A_L4 at higher temperatures. Zhao and Xia (16), using femtosecond time-resolved fluorescence, concluded that multiple loop conformations are possible for GNRA tetraloops, including a state where A_L3 is partially stacked with G_L1 but not stacked with A_L4 as in the native state. These observations are all potentially explained by the two interconverting loop conformations that we observe for the GCAA tetraloop (Fig. 3B), in which either the G_L1-A_L4 sheared base pair is formed, allowing A_L3 to stack on top at low temperatures, or an alternate form is formed at higher temperatures where a G_L1-A_L3 base pair forms, resulting in the concomitant flipping out of A_L4 and allowing A_L2 to stack on top.

For the UUCG tetraloop, Ma et al. (17), using temperature jump experiments, observed three distinct relaxation processes requiring four distinct states to describe the folding process. Ma et al. (17) conclude that one on-pathway and one off-pathway intermediate must be present, with the on-pathway intermediate disappearing for either a UUUU tetraloop or a UUCG with a bromonated G_L4. The interpretation by Ma et al. (17) is that this on-pathway intermediate corresponds to a nonnatively packed loop transitioning to a native loop. The disappearance of this transition can, therefore, be explained by the fact that UUUU lacks a native loop packing, whereas the 8-Br-G bypasses the nonnative loop state altogether by preorganizing the G_L4 in the syn conformer. An extension of this work by Sarkar et al. (18) raises the possibility that the four states could be arranged in two parallel pathways, which could also explain the observed kinetic data. In related work, Proctor et al. (19) showed that incorporation of 8-Br-G in UUCG results in a 4.1 times faster folding rate, indicating that preorganization of the syn G_L4 conformer accelerates the conformational search for the native state. These observations are entirely consistent with the two pathways that we observe for UUCG folding (Fig. 3A): a rapid pathway, in which an syn-G_L4 is preformed on loop collapse, and a much slower pathway, where G_L4 and U_L1 alternate flipping out of the loop until G_L4 is able to transition to the syn rotamer. It should be noted that not all mispacked loop conformations were able to reach the native state within the timescale of our simulations, and therefore, it is possible that some pathological packing is actually an off-pathway intermediate requiring complete unfolding and refolding to reach the native state. However, we cannot ascertain this for certain without extensive kinetic simulations, which are beyond the scope of this study.

The observed folding pathways also explain the observed closing base pair preferences for the three tetraloops sequences. For both gCUUGc and cGCAAg, when the closing stem G is on the opposite side of the loop as the consensus loop G, the resulting RNA is measurably more stable than RNA sequences in which the stem G is on the same side (20). We observe that, for both cGCAAg and gCUUGc, a cross-stacked G-G interaction is able to preorganize the formation of the correct in-register upper stem base pair, which always forms before the lower stem base pair (Fig. 3C). Although cUUCGg would seem to break this rule, in this case, G_L4 must adopt an syn conformer in the native state as opposed to the anti conformer stabilized by cross-stacking, which must then undergo a slow search to find the native syn rotamer (Fig. 3A).

In prior attempts to fold hyperstable tetraloops from the unfolded state with atomistic detail, none of the noncanonical loop interactions were correctly predicted in the folded state conformation. The ROSETTA suite of knowledge-based potentials routinely ranks among the best performers in the critical assessment of protein structure prediction (CASP) blind protein structure prediction contests, but related efforts to predict RNA structure could not reproduce any of the hydrogen bonds or stacking patterns within the UUCG tetraloop (5). The GCAA motif has been extensively studied using the massively parallel distributed computing resources of the Folding@Home project, which was only able to capture 19 heterogeneous folding events among 10,000 folding simulations involving ∼475 µs of cumulative sampling, with majority of the trajectories kinetically trapped in nonspecific collapsed states (21). A follow-up study used 2,800 serial replica exchange simulations designed to facilitate rapid equilibration with stochastic heating and cooling; however, reversible folding still could not be achieved, despite ∼55 µs of cumulative REMD sampling (4). In a recent study, both the UUCG and GAGA tetraloops were simulated for ∼19 µs of cumulative REMD sampling from both the folded and unfolded state; however, equilibrium folding was not achieved, and the folded state was only transiently sampled (6). The lone claim of reversible tetraloop folding from the unfolded state originated from our own laboratory using extensive temperature replica exchange simulations of the UUCG motif, resulting in native state folds that averaged 4–6 Å rmsd from the experimental structure (22). However, the folded states observed in those simulations did not recapitulate any of the signature loop-stabilizing noncanonical interactions characteristic of the UUCG motif. Furthermore, the single most populated structure obtained from clustering analysis of the ensemble was, in fact, a hyperstacked, interdigitated structure with zero base pairs, for which there is no experimental evidence. These hyperstacked structures were caused by the erroneously strong base-stacking propensity exhibited by the AMBER force field (23–25), which we corrected in the parameters used for this work. These results cumulatively indicate that gross inaccuracies in the underlying physical description of RNA interactions themselves and not merely extent or method of sampling are likely to blame for the poor performance of RNA folding simulations to date.

Multiple prior studies of tetraloops have simulated the equilibrium unfolding using REMD simulations initialized from the native state (26–28). It is argued that, after equilibrated, the multicanonical ensemble is thermodynamically equivalent to an REMD simulation initialized from the unfolded state, and therefore, the (un)folding process can still be accurately observed. This assumption would be rigorously correct if the simulation parameters unambiguously recapitulated the correct tetraloop native state as the global free energy minimum, an assumption that has never been proven. In fact, a recent study has explicitly tested the convergence of the UUCG and GAGA tetraloops simulated from both the folded and unfolded states in REMD simulations (6), and it concluded that convergence was not achieved, even at ∼400 ns per replica. In this study, we found that significant revisions to the underlying RNA parameters themselves were needed before equilibrium folding could be achieved, after which rapid folding was observed, even within the initial 100-ns REMD equilibration period. The ability of the improved force field to accurately recapitulate the signature noncanonical interactions of hyperstable tetraloops is a key step to the eventual simulation of the folding and dynamics of larger, biologically interesting RNAs in the near future.

Methods

The three hyperstable tetraloop sequences gcUUCGgc, gcGCAAgc, and cgCUUGcg were initialized in random unfolded states taken from an excluded-volume ensemble with no bias to the folded conformation. These conformations were solvated in a cubic simulation cell of 5.5 nm on each side with explicit water and ions (5,300 TIP3P, 100 K⁺, and 93 Cl⁻) to approximate ionic conditions of 1 M excess KCl. This large box size is a departure from the minimal simulation boxes previously used for simulations of an 8-nt RNA, because fully extended states with end-to-end distances of ∼4 nm are readily realized at high temperatures using the newly modified RNA parameters. These initial conformations were equilibrated in short constant pressure simulations at ambient conditions, from which snapshots with instantaneous pressures of ∼1 bar were used as initial seeds for a constant volume REMD simulation. Each REMD simulation consisted of 64 replicas with a temperature schedule chosen to maintain an ∼20% exchange rate from 274 to 498 K, with temperature swaps every 2 ps. Simulations were propagated for 200–400 ns per replica depending on the observed equilibration rate, and a total of ∼58 µs of cumulative REMD sampling for all three tetraloops was combined.

Conformations were considered folded if the rmsd to the experimental structure was less than 4 Å rmsd, a cutoff chosen based on the apparent two-state behavior exhibited by rmsd vs. temperature shown in Fig. 1A. This definition of the folded state is conservative, in that it essentially requires that both stem CG base pairs be correctly formed, a criterion that excludes nonspecifically collapsed structures and the highly interdigitated, nonbase-paired structures previously observed in the work by Garcia and Paschek (22). Convergence was ascertained by the asymptotic behavior of the number of folded replicas as a function of time (Fig. 1B), with the first 100 ns discarded as equilibration for UUCG and CUUG and the first 275 ns discarded for GCAA. Configurational clustering of the sampled ensemble was performed with the Daura algorithm (29), with a cutoff of 1.2 Å. The use of cluster centroids to characterize the folded state is highly insensitive to the specific clustering algorithm used, because folded states in low-temperature trajectories were long-lived and undergo only minor fluctuations around the native state after folding. The following Protein Data Bank (PDB) entries were used as reference structures only for rmsd calculations: UUCG, PDB ID code 1F7Y (30); GCAA, PDB ID code 1ZIH (31); 2J00 nucleotides 897–902 (32) and CUUG, PDB ID code 1RNG (11).

RNA parameters are based on a significant revision to the AMBER-99 force field for nucleic acids based on detailed calibrations against a wide range of experimental data, which are described in detail in Supporting Information. It has been previously shown that the default AMBER nucleic acid parameters dramatically overestimate base-stacking propensities (23–25, 33), do not correctly balance the syn-anti glycosidic rotamers (34, 35), and violate the close contact distances calculated by dispersion-corrected quantum chemical calculations (36, 37). These deficiencies in the parameters are all consequences of the inappropriate reuse of van der Waals parameters developed for protein model compounds (8), resulting in bloated nucleobases that do not accurately reflect the physicochemical properties of aqueous heterocycles.

To derive parameters sufficiently accurate for de novo RNA folding, the Lennard–Jones (L-J) σ-parameters for base–base interactions were uniformly reduced to match close contact distances observed from high-level dispersion-corrected coupled cluster theory including singlet, doublet, and triplet excitations quantum calculations of gas-phase nucleobases (38). The L-J well-depth parameter-ε was then adjusted to achieve the correct stacking propensity in solution, which was adjudicated by clustering propensities of aqueous nucleosides (39). The base–water interaction was also adjusted to reproduce the correct enthalpy and entropy decomposition for dinucleotide stacking. The refinement of parameters was accomplished by comparing stacking free energies calculated from potentials of mean force with circular dichroism measurements as a function of temperature (39). Finally, the glycosidic torsion, χ, was adjusted to optimize the syn-anti populations and transition frequencies as measured by NMR (40) and ultrasonic absorption (41). It should be noted that torsion optimization can only be performed after optimization of the L-J parameters because of their intrinsic interdependency. Details of the parameters and optimization strategy are included in SI Methods.