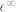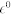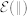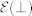Dielectric properties and Raman spectra of ZnO from a first principles finite-differences/finite-fields approach

Abstract

Using first principles calculations based on density functional theory and a coupled finite-fields/finite-differences approach, we study the dielectric properties, phonon dispersions and Raman spectra of ZnO, a material whose internal polarization fields require special treatment to correctly reproduce the ground state electronic structure and the coupling with external fields. Our results are in excellent agreement with existing experimental measurements and provide an essential reference for the characterization of crystallinity, composition, piezo- and thermo-electricity of the plethora of ZnO-derived nanostructured materials used in optoelectronics and sensor devices.

ZnO is a wide-band gap, transparent, polar semiconductor with unparalleled optolectronic, piezoelectric, thermal and transport properties, which make it the material of choice for a wide range of applications such as blue/UV optoelectronics, energy conversion, transparent electronics, spintronic, plasmonic and sensor devices¹. Understanding the infra-red (IR) properties of the bulk crystal is crucial for the intrinsic characterization of the material and is a prerequisite for the viable application of all ZnO-derived systems (e.g. nanostructures, interfaces, alloys) that are now the leading edge of research in many optoelectronic fields. In fact, at IR wavelengths, the vibrational polar modes affect also the dielectric response of the material (i.e. the optical properties), and thus its final performance. This justifies the uninterrupted sequence of experimental reports on vibrational properties of wurtzite ZnO crystal, which started in the sixties and continues nowadays²,³,⁴,⁵,⁶,⁷,⁸.

Raman spectroscopy is one of the most common investigation techniques exploited for this purpose because it provides information on the structural and chemical properties such as orientation, crystallinity and existence of defects and impurities. However, despite the profuse research efforts pursued in the last decades, there are still open questions on the unambiguous identification of high-frequency phonon modes or unusual line-width variations⁴ and the interpretation of angular-dependent Raman spectra of ZnO: The uniaxial crystal structure along with the pronounced mass difference and the strong bond polarity imparts a large LO-TO splitting that mixes phonon bands and makes the interaction with external radiation largely anisotropic. Clearly, a unified theoretical approach able to treat at the same level of accuracy both the phonon dispersion and the Raman spectra is highly desirable. Although semiempirical approaches could provide a simple and computationally inexpensive way to treat this problem⁹,¹⁰, the parameterization of the force fields strongly reduces the transferability of the interatomic potentials, which must be carefully tested for each specific system and morphology especially in the presence of doping, defects and impurities. On the other hand, while a few attempts to reproduce ZnO phonon bands through ab initio techniques exist⁷, no simulations of Raman spectra have appeared so far. The challenge resides in the proper treatment of the response of a highly polar material like ZnO to external electric fields.

In principle, Density Functional Perturbation Theory (DFPT)¹¹,¹² is an elegant and accurate approach for simulation of both phonon and Raman spectra¹⁴. In practice, the required computational effort, and the difficulty in improving the description of the electronic structure beyond the common functional approximations (LDA, PBE, etc.) prevent the application of this techniques for a large class of realistic structures and materials. ZnO is a prototypical example: a standard Density Functional Theory (DFT) description of the band structure of bulk ZnO severely underestimates repetition the band gap (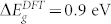 vs 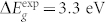). This is not simply due to the lack of many-body corrections typical of DFT, but rather to an unphysical enhancement of the covalent character of the Zn-O bonds¹⁵. In turn, the wrong description of the electronic structure affects the electrostatic properties of the system and thus the phonon distribution and the coupling with the external fields. This problem may be easily overcome by including Hubbard-like corrections¹⁶ or using hybrid functionals¹⁷. However, these features are not readily accessible in DFPT approaches for their large computational cost¹⁸.

In this paper we have solved the problem of simulating with comparable accuracy both the electronic and vibrational spectrum of ZnO using a unified finite-fields/finite-differences approach that is independent of the choice of the functional. This allows us to simulate the phonons, the high and low-frequency dielectric constant and the nonresonant Raman spectra of any material through a finite set of electronic structure and force calculations using the finite displacement method¹⁹.

Results

Unified finite-fields/finite-differences theory

The interatomic Force Constants (IFCs) K and the electronic susceptibility χ are obtained as finite differences of forces and polarizations with respect to atomic displacements or external electric fields²⁰.

IFCs are the second derivatives at equilibrium of the total energy versus the displacements of the ions u(R), or alternatively, the derivative of the atomic forces F versus the ionic displacements:

where R and R′ are Bravais lattice vectors, I, J are the I-th and J-th atom of the unit cell, and α and β represent the Cartesian components. Phonon frequencies (ω_ph) and normal modes (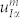) are routinely obtained from the resolution of the eigenvalue equation: 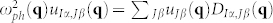, where the dynamical matrix D_Iα,Jβ(q) is the Fourier transform of the IFC. The acoustic sum rule (ASR) in real space is defined as in Ref. 12, while long-wavelength dipole-dipole effects are included by means of specific non-analytical correction to the IFCs, as proposed by Yi Wang et al.²¹.

The proper treatment of the long wavelength macroscopic polarization field requires also the evaluation of the dielectric tensor and of the Born effective charges. For this purpose we consider the electronic susceptibility:

where 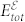is the total energy in the presence of electric field 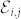and P^el is the electronic polarization along the direction of 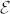. Here, 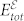and P^el are evaluated following the method proposed by Umari and Pasquarello²⁰, where the introduction of a non local energy functional 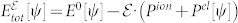allows electronic structure calculations for periodic systems under finite homogeneous electric fields. E⁰ is the ground state total energy in the absence of external electric fields; P^ion is the usual ionic polarization, and P^el is given as a Berry phase of the manifold of the occupied bands²².

The high-frequency dielectric tensor 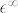is then computed as 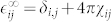, and the Born effective charge tensor 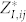is defined as the induced polarization along the direction i by a unitary displacement of the I-th atom in the j direction, or alternatively in terms of atomic forces in the presence of the electric field :

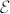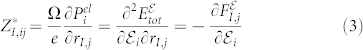Finally, the contribution of the polar optical modes to the static dielectric constant 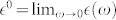is computed using the Lyddane-Sachs-Teller relation¹²,¹³: 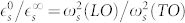where ω(LO) (ω(TO)) are the LO (TO) phonon frequencies and s denotes the electric field polarizations parallel (||) and perpendicular (⊥) to the polar axis. This alternative method is implemented and fully integrated in the Quantum ESPRESSO suite of codes²³ (www.quantum-espresso.org; the finite-fields/finite-differences approach is implemented in the package FD in PHonon.).

The calculation of the Raman spectra proceeds along similar lines. The non-resonant Raman intensity for a Stokes process is described by the Placzek's expression²⁴:

where e_i (e_s) are the polarization of the incident (scattered) radiation, ω_m is the frequency of the generated optical phonon, n_m is the Bose-Einstein distribution, and 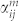is the Raman tensor, defined as:

Within the finite-field approach, the third rank tensor 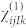is evaluated in terms of finite differences of atomic forces in the presence of two electric fields²⁵:

In practice, the tensor 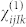is obtained from a set 19 calculations, which combine the finite electric fields 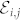along the cartesian coordinates. 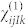is then symmetrized to recover the full C_6v symmetry of the wurtzite structure.

Dielectric and vibrational properties

The calculated high and low frequency dielectric constants, summarized in Table I, are in agreement with experimental spectroscopic ellipsometry data³, as well as Hartree-Fock calculations²⁶. Born effective charges (Table I) are also in agreement with values extracted from transverse IR reflectance spectra²⁷, and may be easily associated to piezolectric properties of ZnO and its modifications under pressure²⁸.

Table 1. High-frequency (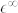) and static (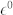) dielectric constant and effective Born charges (Z*) of wurtzite ZnO, for electric field polarization parallel and perpendicular to the c-axis. Corresponding experimental values are reported in parenthesis.

			Z*
	3.14 (3.78)a	7.76 (8.91)a	2.12
	3.08 (3.70)a	6.98 (7.77)a	2.06 (2.02)b

^afrom Ref. 3.

^bfrom Ref. 27.

PBE and PBE + U phonon dispersions are reported in Fig. 1 and phonon frequencies at the Brillouin Zone center (Γ) are summarized in Table II, where we also display the LDA values for comparison. Experimental Inelastic Neutron Scattering (red diamond and blue circles) and Raman (green squares) data are extracted from Ref. 7 and superimposed in Fig. 1 to the first principles data. While LDA and PBE results clearly underestimate the experimental frequencies, mostly in the optical branches, with PBE + U the agreement is very good. Here only the highest-frequency LO bands are slightly overestimated. Notably, these phonon branches suffer of anharmonic renormalization effects, which are not included in the present approach. Furthermore, the error bar on the experimental Raman results is higher for these bands, due to the low cross-section of the corresponding phonon-photon scattering processes (see below).

Figure 1. Calculated (black lines) phonon dispersions for wurtzite ZnO calculated with (a) PBE and (b) PBE + U. Solid/open diamonds (red) and open circles (blue) represent experimental INS data, green squares represent Raman frequencies.

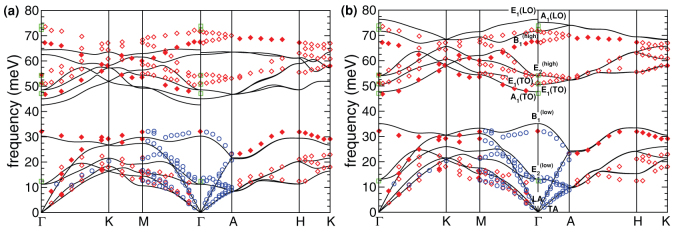
Experimental data reproduced from Ref. 7.

Table 2. Phonon frequencies (in cm⁻¹) of ZnO at Brillouin Zone center (Γ), calculated with LDA, PBE, PBE + U and compared to experimental Raman data from Ref. 7.

Mode (Γ)	LDA	PBE	PBE + U	Exp (Raman)
TA/TA	0	0	0	0
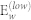	87	89	106	100
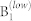	258	243	283	-
A1(TO)	398	343	384	380
E1(TO)	420	363	408	410
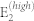	446	392	436	438
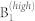	539	505	578	-
A1(LO)	547	498	607	(584)
E1(LO)	560	508	615	(595)

Following the irreducible representation of the wurtzite symmetry group C_6v, the phonon modes of ZnO can be classified as Γ = 2A₁ + 2B₁ + 2E₁ + 2E₂. One low energy A₁ and one double E₁ modes correspond to the transverse and longitudinal acoustic branches, the others are optical modes. B₁ modes are IR and Raman inactive. The two E₂ modes are non polar IR inactive but Raman active. In A₁ and E₁ polar modes, atoms move parallel and perpendicular to the c-axis respectively and are the ones responsible for the LO-TO splitting. The labeling in Fig. 1 and Table II is based on the direct analysis of the phonon eigenmodes and their underlying symmetry. Note that PBE calculations give an incorrect ordering of the B₁ and A₁(LO) modes that is instead correct in PBE + U (see Table II).

Raman spectroscopy

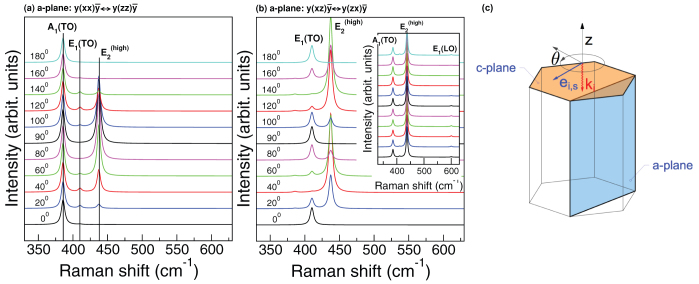
We calculated the Raman spectra for different propagation (k) and polarization (e_i,s) directions of the incoming and scattering light, as shown in Fig. 2. We simulated the Raman spectra for different rotation angles (θ) of the polarization vectors in the planes parallel (a-plane) and perpendicular (c-plane) to the c-axis. Following the standard experimental setups, for c-plane spectra we considered only parallel polarization of the incoming and scattered light 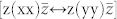. We used the Porto notation: symbols inside the parentheses indicate the direction of e_i and e_s, while symbols outside the parentheses indicate the directions of propagation of light (k). In the a-plane case, two different orientations of e_i,s can be experimentally detecte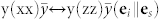d: and .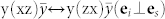

Figure 2.

Calculated Raman spectra for different rotation angles on the a-plane in the parallel (a) and perpendicular polarization vector configurations. The inset of panel (b) shows the modification of the spectrum upon relaxation of the ideal scattering geometry. (c) Scheme of the wurtzite lattice and high symmetry planes perpendicular (c-plane) and parallel (a-plane) to the polar (0001) c-axis. k_i indicates the propagation direction of light, e_i,s are the incident and scattered polarization vectors; θ is the rotation angle in the plane perpendicular to the k_i direction.

Results for room temperature boson distribution are summarized in Fig. 2. Panel (a) shows the a-plane spectra for parallel polarization vector configurations, which reproduces the angular modification of experimental spectra³,⁸ and the reciprocal intensity ratio of the main peaks. The spectra are, in fact, dominated by Stokes processes due to the A₁(TO) and 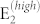phonon modes at 384 and 436 cm⁻¹, respectively, only 2 cm⁻¹ from the experimental values. The intensity of the A₁(TO) peak is independent from the orientation of incident polarization, while the 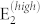peak reaches a maximum at 90° and minima at 0° and 180°. For 20°, 40°, 120°, and 140° a small contribution from E₁(TO) also appears at 410 cm⁻¹. The 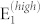phonon mode at 106 cm⁻¹ is not visible in this energy scale, the LO modes are not allowed by symmetry for this incident light direction.

Similar arguments apply for the a-plane spectra for e_i ⊥ e_s polarizations, as displayed in panel (b). Here the main contributions stem from the E₁(TO) and 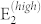modes, whose reciprocal intensity depends on the θ angle. The two peaks are in counter phase: the former has maxima at 0°, 90° and 180°, where the latter reaches the minimum, and vice versa. Besides these two peaks, experimental results for crossed polarization vectors exhibit small, angular-dependent features associated to A₁(TO) and E₁(LO) that should be symmetry forbidden in this geometry. This is indeed a consequence of the deviation from the ideal geometry set-up and/or a deviation from perfect hexagonal crystallinity of the sample. Following Ref. 8 we considered non-orthogonal polarization vectors,

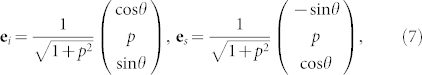through the inclusion of an arbitrary constant p. The angular distribution and intensity of the peaks depend on the choice of the p factor, i.e. on the characteristic crystallinity of the sample. Results for p = 0.5 are reported in the inset of panel (b) where the A₁(TO) peak and a small contribution from E₁(LO) appear.

From the spectra of Fig. 2 we can also extract the relative intensity ratio between the main Stokes peaks, which are univocally related to the non-zero matrix elements of the Raman tensor for the C_6v point group (see for instance Ref. 29). Calculated ratios between A₁ (E₁) and 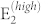, taken as reference, are 0.54 and 0.23, respectively; the corresponding experimental values are 0.6 and 0.4⁸. The agreement is quite satisfactory for A₁, while it is slightly worse for E₁. However, in the latter case the experimental value is extracted from e_i ⊥ e_s polarizations spectra, which may suffer of non-ideal hexagonal symmetry, as discussed above (Fig. 2b).

Discussion

Our results demonstrate that the coupled finite-fields/finite-differences DFT approach is essential to accurately evaluate the dielectric properties, phonon dispersions and Raman spectra of ZnO. By reducing high order derivatives of the total energy (i.e. of the charge density) to lower order differences of polarizations and forces obtained from a limited set of self-consistent DFT simulations, it favors the inclusion of advanced corrections to the ground-state electronic structure that are essential for the proper description of the system. In particular, the ground state electronic structure and the coupling with external fields in ZnO require the use of ad hoc corrections to the position of the d-bands of Zn that can be achieved with a DFT + U treatment, as summarized in Fig. 3. In the case of standard LDA and PBE calculations we observe a severe underestimation of the bandgap (E_gap) and a wrong energy position of the d-bands of the Zn atoms, that in turn give an inadequate description of the phonon dispersions (see Fig. 1(b) and discussion therein). The choice of functional influences directly the electrostatics and thus also the characteristics of the vibrational response of the system. In fact, the IFCs are the sum of two contributions:

where 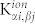are the second derivatives of Ewald sums corresponding to the ion-ion repulsion potential, while the electronic contributions 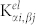are the second derivatives of the electron-electron and electron-ion terms in the ground state energy. It is the last term that reflects directly in the vibrational spectrum the wrong position of the d-states and the dramatic underestimation of the gap. On the other hand, LDA, with its overestimation of the bonding (shorter lattice parameter and stiffer IFCs) accidentally gives results that are marginally closer to the experimental data thanks to a fortuitous cancellation of errors. The inclusion of the Hubbard U, by correcting the d-Zn p-O hybridization, properly describes not only the electronic bands but also the vibrational and dielectric properties in agreement with the experimental results¹⁵. Notably, the values of the dielectric constants obtained with LDA (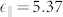, 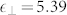) and PBE (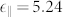, 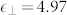) are much higher than in experiments, a clear indication of a lesser polarity of the system in these approximations.

Figure 3. Density of states of hexagonal ZnO crystal with LDA, PBE and PBE + U (from top to bottom).

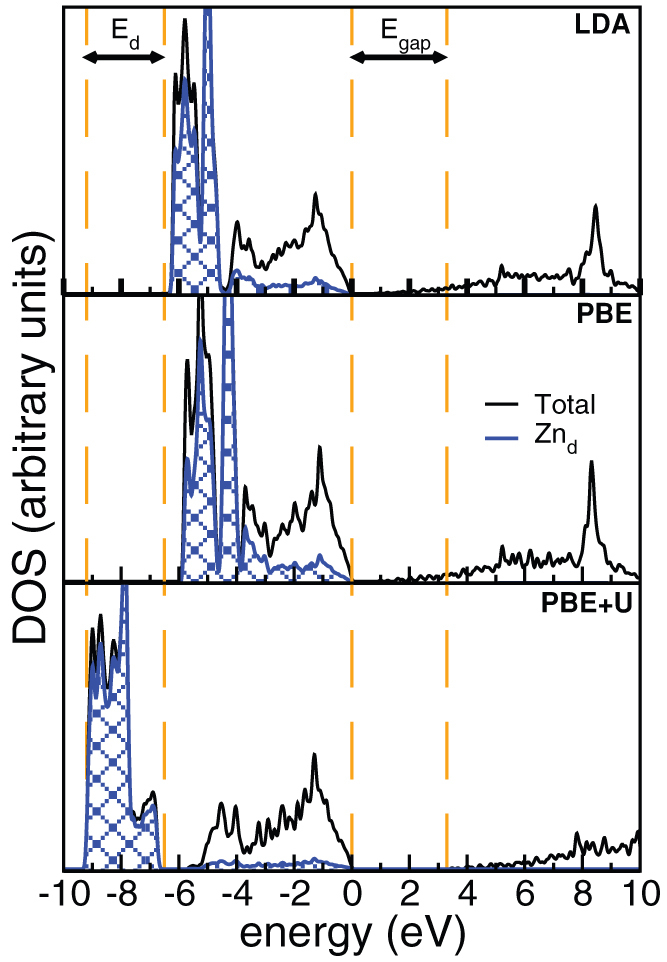
Energies are referred to the respective top of valence bands. The vertical lines indicate the experimental energy gap (E_gap) and 3d-band width (E_d) from Ref. 15.

Finally, the finite-fields/finite-differences framework allows straightforward developments of the theory to include 3rd order terms in the IFCs (i.e. anharmonic contribution to phonons) or susceptibility χ⁽²⁾ for the simulation of non-linear optical properties such as hyper-Raman or electro-optic effects. One example of the latter is the Raman signal along the parallel c-plane , shown in Fig. 4, where the A₁(LO) and modes dominate the spectrum for all angles (0–180°) (black solid line). However, although allowed by symmetry, A₁(LO) is invisible or hardly visible in most experimental data collections²,³,⁶,⁸. This effect is due to a competitive interaction with the Fröhlich term², which couples with the macroscopic field generated by the A₁(LO) mode and cancels most of the deformation potential contributions. This effect may be evaluated including a non-linear correction to the tensor for the longitudinal q_l mode³⁰

where the third order tensor 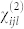may be straightforwardly calculated extending the finite field approach to the case of three electric fields, or alternatively:

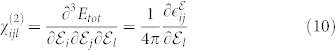Indeed, the inclusion of the Fröhlich term suppresses the A₁(LO) (red dashed line) in agreement with experiments.

Figure 4. Calculated Raman spectra of c-plane sample in the parallel polarization vector configuration with (red) and without (black) Fröhlich correction to longitudinal optical phonons.

In conclusion, we have demonstrated that our unified finite-fields/finite-differences technique provides a general framework for the calculation of the vibrational, dielectric and Raman properties of materials, without any limitation in the choice of the DFT framework. We have applied this method to the study of ZnO, a material that for its complex electronic structure requires a special treatment in order to obtain a faithful representation of its properties. Our results are in excellent agreement with available experimental data.

Methods

Computational details

We calculated vibrational and Raman spectra of wurtzite ZnO bulk using PBE-GGA³¹ ultrasoft pseudopotentials³² for all the atomic species, a 28 (280) Ry energy cut off in the plane wave expansion of wavefunctions (charge) and a (12 × 12 × 8) regular k-point mesh. LDA calculations have been done with norm-conserving Troullier-Martins pseudopotentials³³, with a kinetic energy cutoff of 100 Ry. 3d electrons of Zn have been explicitly included in the valence for both cases. For PBE + U, a Hubbard-like potential with U = 12.0 eV and U = 6.5 eV is applied on the 3d orbitals of zinc and on the 2p orbitals of oxygen, respectively¹⁶. Note that the Hubbard U values included in the calculations do not have to be considered as physical on-site electron-electron screened potentials, in the sense of the many-body Hubbard Hamiltonian, but as empirical parameters introduced to correct the gap. This is an efficient and computationally inexpensive way to correct for the severe underestimation of the bandgap and the wrong energy position of the d-bands of the Zn atoms¹⁵,³⁴. This procedure has also been applied to other similar systems³⁵,³⁶,³⁷,³⁸. P^el and α^m are obtained applying a.u along the cartesian axes. All calculations have been run with lattice parameters optimized for each functional¹⁶.

For the calculation of phonon modes we considered a (8 × 8 × 2) hexagonal supercell (512 atoms) and we calculated forces (i.e. IFC) displacing only 2 atoms in primitive ZnO cell along the two inequivalent directions. This corresponds to a set of 4 DFT calculations. The Raman tensor has been calculated on the primitive wurtzite cell.

Author Contributions

A.C. and M.B.N. designed the research, performed the calculations, analyzed the data and co-wrote the paper. M.B.N. wrote the finite-difference codes for phonon calculations. A.C. wrote the code for the finite-field calculation of the Raman tensor.