Early-photon fluorescence tomography: spatial resolution improvements and noise stability considerations

Abstract

In vivo tissue imaging using near-infrared light suffers from low spatial resolution and poor contrast recovery because of highly scattered photon transport. For diffuse optical tomography (DOT) and fluorescence molecular tomography (FMT), the resolution is limited to about 5–10% of the diameter of the tissue being imaged, which puts it in the range of performance seen in nuclear medicine. This paper introduces the mathematical formalism explaining why the resolution of FMT can be significantly improved when using instruments acquiring fast time-domain optical signals. This is achieved through singular-value analysis of the time-gated inverse problem based on weakly diffused photons. Simulations relevant to mouse imaging are presented showing that, in stark contrast to steady-state imaging, early time-gated intensities (within 200 ps or 400 ps) can in principle be used to resolve small fluorescent targets (radii from 1.5 to 2.5 mm) separated by less than 1.5 mm.

1. INTRODUCTION

Optical tomography refers to an ensemble of imaging methods designed to interrogate tissue using near-infrared light (NIR) transmission, where the transport process interacts with its microscopic components. There are two main categories of tomographic imaging applications, with each potentially probing different biological mechanisms. Fluorescence molecular tomography (FMT) is used to localize optical contrast associated with the accumulation or retention of fluorescent reporters, which can be used to image specific cellular or organ-specific processes [1–16]. The second approach, based on transmission alone, is often referred to as diffuse optical tomography (DOT), and is used to study how light interacts with tissue based on absorption contrast from molecules such as hemoglobin and water [17–19]. Both approaches use diffuse light measurement, which is known to lead to low resolution and blurry images. Typically, the resolution of optical tomography is limited to several millimeters depending on the thickness of the tissue being imaged, which is comparable to nuclear imaging resolution. Mainly, there are three factors determining the resolution: (1) the physical properties of light-matter transport, (2) the instrument design, and (3) the image reconstruction method. The optimal combination of light transport with time-gated data, optimal instrument design, and an appropriate image reconstruction algorithm can lead to dramatic improvements in image resolution. This subject is analyzed here through numerical analysis studies of the signal and inversion process.

Photons propagating through tissue are either absorbed or scattered, making it possible to model this with general bulk tissue interaction coefficients. The absorption coefficient μ_a and scattering coefficient μ_s describe their probability of interaction per unit length. The average distance covered by a photon between two scattering sites in tissue (mean free path) is typically near 100 μm, but when isotropic scattering is approximated, then the transport (or reduced) scattering coefficient μ_s′ is defined for approximate isotropic scattering. The transport scattering distance in tissue (or transport mean free path) is approximately 0.5 mm to 1.0 mm. This sets a fundamental limit on the spatial resolution that can be attained when using diffuse optical imaging.

The second consideration that can degrade this resolution limit further is determined by the instrument design. It has been shown that different combinations of sources and detectors will lead to different reconstruction image quality [20]. In particular, singular-value analysis of the DOT and FMT forward model has been performed in order to design mathematical criteria that might be used to optimize the source–detector design [21–24]. However, it is generally expected that an optimal configuration for optical tomography will be one which mimics x-ray computed tomography (CT), where there is as much circular symmetry as possible at the periphery of the tissue being imaged.

An inherent characteristic of optical tomography is the fact that, even for excellent tissue sampling detection geometries, the inverse problem is ill-conditioned [25]. In practice, this means that the problem is underdetermined, implying that a large number of solutions exist for a given optical data set. By using an ideal tissue sampling geometry, the symptomatic linear dependency of the measurements is minimized, thereby improving the conditioning of the problem. Then, a least-squares solver would be expected to converge to a unique solution corresponding to a high-fidelity image for which the spatial resolution is set by the aforementioned fundamental limit imposed by diffuse imaging. However, this is not the case for diffuse optical tomography, as is well known, and will be analyzed further here. In reality, reconstructing optical images is typically attained by finding a balance between minimization of the residual norm and the size of the solution through regularization. Here, size of the solution should be understood broadly as representing a mathematical norm that can be used to include prior information of the problem. For example, the main trend in optical imaging consists of using structural anatomical information from segmented CT or MR images as a way to improve the conditioning of the optical imaging problem [26–30]. Another approach consists of using multi-spectral optical data to improve image quality [31,32].

An important consequence of the ill-posed nature of the problem is that the inversion is hypersensitive to noise. Therefore, the problem cannot be solved uniquely no matter how many diffuse measurements are added to the data vector, even if it becomes an overconditioned problem. Reducing the sensitivity to noise can be partially attained by using regularization methods or using different data types. Here, the approach of choice consists of using a modeling method that allows the user a choice to improve the conditioning of the matrix inversion problem without the use of spatial or spectral priors, hence reducing the sensitivity to noise. To do this, the optical tomography inversion is formulated with the ability to analyze the effect of different optical data types that correspond to modified light transport paths. Niedre et al. [33] have shown that image reconstructions based on so-called early photons lead to significant resolution improvements in the FMT images when imaging lung tumors in mice in vivo. The forward modeling approach they use is based on analytic solutions to the radiative-transfer-equation (RTE) [34,35]. In effect, this approach allows capture of early photons that are highly scattered in the forward direction and so deviate very little from the direction of travel. For any given source–detector pair, the path of travel of photons in the earliest time windows is much narrower than the path that would have held for all time gates. Decreasing time gates directly translate into narrower more direct path photons, and this inherently improves the resolution of imaging with this data set. DOT approaches have also been developed to reconstruct images based on early photons associated with nonfluorescent optical signals [36,37].

The main aim of this paper is to explain why a combination of appropriate light-transport modeling techniques, photon detection technology, and image reconstruction methods can lead to tomography with intrinsically higher spatial resolution as compared with the majority of approaches that have been used in the past. The approach outlined is based on the FMT forward model constructed using a time-dependent finite-element method (FEM) solution to the diffusion equation. The model is used to show that the forward problem for weakly diffused photons produces a significantly improved conditioning of the inversion matrix when compared with that associated with a steady-state diffuse signal. Evidence for this is provided through computation of the condition number of the forward problem matrix as well as through detailed singular-value analysis (SVA). The results of the SVA provide an intuitive explanation for why the spatial resolution of optical tomography can be improved so dramatically. Those findings are supported by actual image reconstructions performed for simulated fluorescence data of a multiple target phantom with different levels of contrast.

Section 2 briefly presents the outline for time-domain FMT as well as a description of the preclinical instrument motivating the detection geometry used in this work. Then, Section 3 presents the general formulation of the time-dependent optical tomography problem, with the derivation of the forward problem for time-gated diffused fluorescence signals and the inverse problem resolution methods used for image reconstruction. Section 4 presents the main results of this paper in the form of a SVA of the problem with image recovery. The paper is concluded in Section 5 with discussions pertaining to limitations and potential extensions of the results.

2. BACKGROUND

A. Fan-Beam Detection of Time-Domain Signals

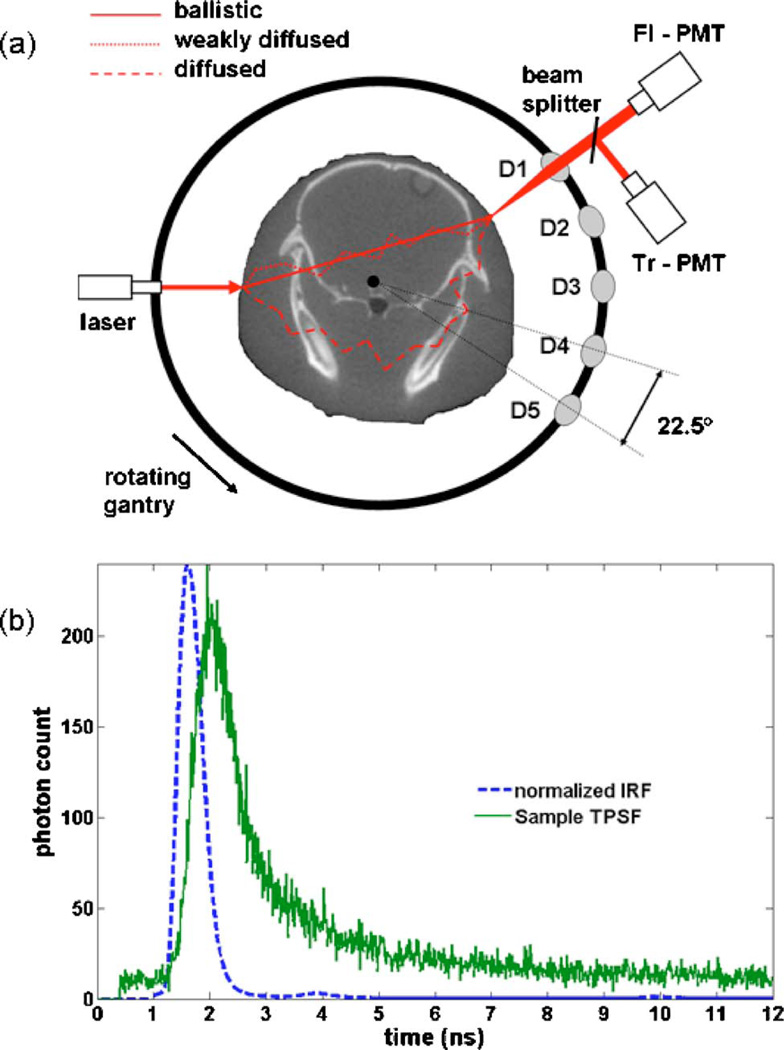
The simulation results presented in this paper are performed based on a detection geometry mimicking a newly developed time-domain tomography system [38]. The system utilizes a bed compatible for both FMT and x-ray CT instruments for small animal studies. FMT images complement the anatomical information from CT with molecular information pertaining to extracellular and intracellular processes highlighted by either endogenous or exogenous fluorophores. A schematic of the optical system is shown in Fig. 1(a). The system was designed to utilize a rotating gantry, allowing use of a single source with a fan beam configuration of photomultiplier tube (PMT) detectors that rotate around the surface of the specimen. In this configuration, fully noncontact excitation and detection is achieved, and a flexible number of measurements can be obtained. Five optical channels (labeled D1 to D5 in the figure) use focused detection to collect the diffuse transmission of excitation and fluorescence signals from the surface of the specimen.

Fig. 1.

(Color online) Schematic representation of the optical instrument. Shown is a single excitation source position and the five channels. Diffuse light signals at the surface of the specimen are collected using focalized detection. The detected signals are then separated and directed to two sets of PMTs dedicated to fluorescence and excitation signals at each fiber channel. This detection geometry is that used for the simulations presented in this paper. (b) Impulse-response-function (IRF) and sample fluorescence time-resolved signal acquired for one of the channels.

In this work, optical tomography resolution improvements are examined using data associated with time-gated signals. The optical system design is based on time-correlated single photon counting (TCSPC) instrumentation cards (Becker and Hickl, Berlin, Germany) and a laser diode driver module (PicoQuant, Berlin, Germany) controlling a 635 nm pulsed diode laser operating at 80 MHz and delivered to the rotating gantry by fiber optics and focused through free space onto the animal tissue. Diffusely transmitted fluorescence and excitation signals are then collected from five lenses with an angular separation of 22.5°. These couple through fibers to the transmission (Tr) and fluorescence (Fl) channels, respectively. The light is then collimated and spectrally separated using filters. Hamamatsu H7422P-50 PMTs detect the incident photons and generate a single analog pulse for each detected photon. Fig. 1(b) shows a sample temporal-point-spread function (TPSF) acquired with the optical system as well as the corresponding impulse-response-function (IRF). Time-referencing of the signals is accomplished by approximating the initial time when photons hit the specimen surface as the mean time of the IRF. This approach allows sampling of the light into 12.5 ps time bins, and while the temporal response function of the laser through the system is close to 400 ps, calibration allows accurate sampling of data down to near the time resolution of the bins. Relative to photon detection based on ICCD cameras, PMT-based detection has an increased sensitivity due to internal gain factors that are one or two orders of magnitude larger.

As schematically illustrated in Fig. 1(a), the photons making up a time-domain signal can be divided into three conceptual categories: (1) ballistic photons, (2) weakly scattered photons (WSP), and (3) diffused photons. The ballistic photons correspond to those particles that propagate from the source to the detector without going through scattering events, while the WSPs are those photons suffering only a limited number of scattering events prior to detection.

As shown in the figure, the WSPs are associated with travel paths remaining relatively close to the direct line-of-sight between the source and the detector. They correspond to photons that were almost ballistic and ultimately propagated in a highly forward directed manner, largely because each scattering event is anisotropic with the highest probability of scatter being in the forward direction. In contrast to this, the diffuse photons are those that go through a large number of scattering events before being detected. Light transport for the diffuse photons can be modeled as a diffusion process. Indeed, it has been shown that in the high scattering limit where μ_a⪢ μ_s and when light transport distances are large enough compared to the photon transport mean free path, the RTE effectively reduces to the diffusion equation (see, for example, [39]). Diffused photons are the main contributors to a TPSF whenever those two physical conditions are satisfied.

Evidently, the smaller the number of scattering events a photon suffers, the earlier it can be picked up by one of the detectors. For example, [34] shows, based on analytic solutions to the RTE, that the experimental signature of ballistic photons should be in the form of a prepulse in the TPSF centered around t_b=n d/c, where d is the distance between the source and the detector on the surface, n is the index of refraction of the medium, and c is the speed of light. For all practical purposes, the contribution of ballistic photons is negligible in situations relevant for tissue imaging [34,40]. However, there are situations where the contribution of WSPs can be relevant. For example, consider the case of small-animal imaging, which is the main focus of study here. Typically, the absorption in small animals is rather large, and the distances between sources and detectors can be of the order of a few centimeters. Both of these facts make it unlikely that the diffusion approximation to the RTE is valid for precisely modeling early photons. Therefore, several of the time bins after t_b could be dominated by highly forward directed WSPs. Nevertheless, in this paper light transport modeling is done by solving the diffusion equation, because it allows an examination of the transition between diffuse and WSP photons with continuous variation of the time bins used. The assumption made is that the conclusions that are reached studying the forward problem for early diffused photons time-gates are relevant for the WSPs, and at the very least, the trends observed are expected to be indicative of what would be seen if completed with a more exhaustive transport model. A discussion pertaining to the generalization of the diffusion-based results and how they relate to radiation transport modeling is presented in section 5.

B. Tissue Heterogeneities and Data Normalization

One of the key features associated with FMT and, in particular, with the instrument described in Subsection 2.A is the fact that it acquires light signals at two different wavelengths. Indeed, the consensus that seems to have emerged in FMT consists of using the so-called Born normalization approach [41]. This consists of reconstructing images based on raw fluorescence measurements normalized by a measurement acquired at the light source excitation wavelength. Formally, it can be shown that for appropriate detection geometries this normalization process partially reduces the effect of high photon attenuation from the fluorescence signal, thereby significantly reducing the importance of precisely knowing the optical tissue properties of the interrogated specimen [42–44]. This implies that when using Born-normalized data sets it is relatively safe to use a forward model assuming homogeneous optical properties. An educated guess for the average values is then used based either on the literature or on average background values obtained by TPSF fitting prior to image reconstruction [45–47]. This approach considerably simplifies the procedure by making it easier to model light propagation and by reducing the number of unknowns to be reconstructed. In addition, these ratio data provide a normalization of the signal which reduces modeling errors when the diffusion model used does not exactly mimic the tissue shape, or when the fibers used for imaging do not have consistent contact with the tissue. This boundary error minimization provides an inherent stability to the signal used which is critical for routine application.

The critical feature that is required for the Born approach to work is that the tissue region that is producing the fluorescence signal should be similar to that sampled by the photons in the transmitted signal. In effect, the ideal geometry that satisfies this criterion is one where the signal acquisition is done in transmission across the imaged specimen in a manner mimicking 360° x-ray acquisition as performed in CT devices [see Fig. 1(a)].

In the remainder of this work, the assumption is made that the simulated input measurement vectors always consist of Born-normalized data. In the case of time-gated signals, the fluorescence and transmitted signals prior to taking the ratio are assumed to be computed for the same time-gates. As will be evidenced in Subsection 3.B, the tissue sampled by time-gates corresponding to early photons is much narrower than for conventional steady-state signals. This implies that the tissue volume sampled by fluorescence and transmission early photons are then even more similar, thereby further increasing the potential of the Born ratio to reduce the impact of optical property heterogeneities and boundary errors when compared with imaging based on steady-state measurements.

3. MODELING METHODS AND ALGORITHMS

In this section, the basic formalism to model time-dependent light transport in tissue is introduced within the scope of a tomographic approach. Then, this notation is applied to develop the formalism for the forward problem associated with time-gated signals in FMT. The section ends with important features of the inverse problem resolution methods that emphasize those aspects relevant to improving the image spatial resolution.

A. Formulation for Time-Dependent Optical Tomography

In the diffusion approximation limit, the modeled optical properties consist of a family of local tissue parameters including the absorption coefficient μ_a and the reduced scattering coefficient μ_s′ of the chromophores, the index of refraction (n), the absorption coefficient associated with fluorophores (μ_a^F), as well as the quantum yield Q_F and the lifetime of the fluorophores (τ). It should be noted that all these parameters will typically have a nontrivial spectral dependence in tissue. For example, in the case of DOT imaging it is usually assumed that the only variables in the forward problem are μ_a(λ) and μ_s′(λ). In the case of FMT, an approximation is usually made that the only variable affecting the fluorescence signal is μ_a^F. Oftentimes, the lifetime is set to a constant close to that of the value of the main fluorophore under study, and the tissue optical properties at the emission and excitation wavelengths are assumed constant and sometimes equal in value [48]. Significant work has been done assuming that lifetime is the main variable of interest [49–51]. However, in the case examined here, the early time behavior of the time-resolved pulsed laser signal is used as the principal data type to set up the inverse problem.

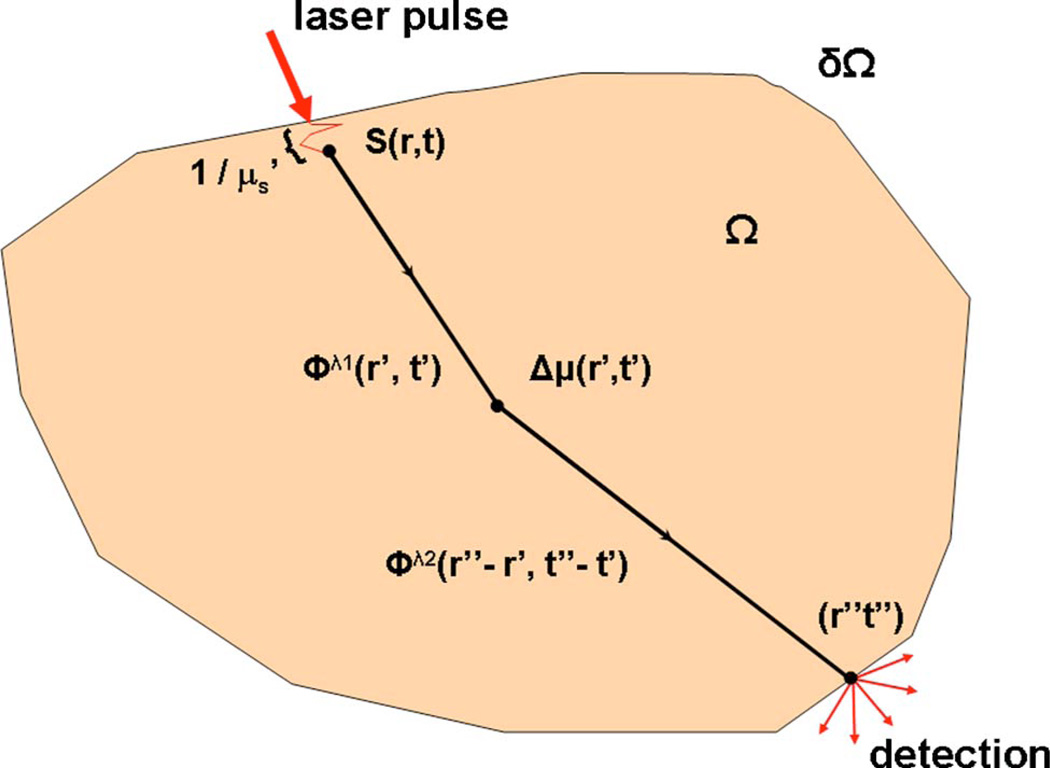
Figure 2 shows a general tissue domain Ω where light injection is assumed to be in the form of a collimated beam sourced either by a steady-state, a frequency-modulated, or a pulsed laser. For diffusion modeling purposes, an isotropic time-dependent source term S(r,t) is inserted one reduced scattering distance (1/μ_s′) under the tissue boundary δΩ at (r,t). Light collection is performed from a region including the point (r″,t″). Unless otherwise noted, it is assumed that both illumination and light detection are performed locally. This is done for simplicity in order not to obscure the main results with mathematical formalism. It should be noted that the numerical method described can model arbitrary illumination and detection geometries.

Fig. 2.

(Color online) Schematic representation of a turbid medium Ω with boundary δΩ. The spatial distribution of optical properties is represented by μ while a local perturbation over this background is represented by Δμ. For modeling purposes, an isotropic source term S(r,t) is inserted under the tissue surface at the place of entry of a collimated laser beam. The light transport solutions between different space-time locations are labeled Φ.

The optical tomography forward problem is set up in the form of an update equation predicting how much tissue property variation will affect a signal, namely,

$$\delta S_{\mathrm{\Omega }}=\sum _{J=1}^{N_V}{A}_J[{\mu }_J]\delta {\mu }_J,$$ (1)

where μ_J=(μ_a, μ_s′,μ_a^F,n, Q_F,_τ) collectively represents all modeled tissue properties at voxels labeled J, and δμ_J stands for the local variations responsible for predicted signal variations δS_Ω over the signal S_Ω associated with background properties μ_J. A_J is the Jacobian for the transformation between δS_Ω with respect to δμ_J. Effectively, an optical tomography method consists of using a large number of measurements on ∂Ω to find those values of μ_j minimizing the mismatch between experimental measurements and signals that are predicted by the model based on the update equation. For problems where the matrix A depends nonlinearly on the properties targeted for reconstruction (as in DOT), nonlinear iterative solvers are used, whereas if an approximation can be made to the effect that signal variations are linearly related to the reconstructed properties (as is the case for FMT), simpler linear reconstruction techniques can be used [41].

More specifically, the update equation associated with one optical measurement takes the form

$$\delta S_{\partial \mathrm{\Omega }}(\overrightarrow{r}″,t″)=N{\int }_{\mathrm{\Omega }}{\mathrm{d}}^{3}r\prime \int \mathrm{d}t\prime \langle {\prod }_1{\mathrm{\Phi }}^{{\lambda }_1}(\overrightarrow{r}\prime ,t\prime )\rangle \delta \mu (\overrightarrow{r}\prime ,t\prime )\times \langle {\prod }_2{\mathrm{\Phi }}^{{\lambda }_2}(\overrightarrow{r}″-\overrightarrow{r}\prime ;t″-t\prime )\rangle ,$$ (2)

where the ∏’s are mathematical operators, and Φ^λ is a solution to the diffusion equation at wavelength λ. N is a model-dependent normalization constant, and the integral runs over all space–time points potentially contributing to the signal perturbation. For example, in the case of DOT the update equation takes the form

$$\delta S_{\partial \mathrm{\Omega }}(\overrightarrow{r}″,t″)~{\int }_{\mathrm{\Omega }}{\mathrm{d}}^{3}r\prime \mathrm{d}t\prime [\mathrm{\Phi }(\overrightarrow{r}\prime ,t\prime )\delta {\mu }_{\mathrm{a}}(\overrightarrow{r}\prime )G(\overrightarrow{r}″-\overrightarrow{r}\prime ,t″-t\prime )+\nabla \mathrm{\Phi }(\overrightarrow{r}\prime ,t\prime )\delta {\mu }_{\mathrm{S}}\prime (\overrightarrow{r}\prime )·\nabla G(\overrightarrow{r}″-\overrightarrow{r}\prime ,t″-t\prime )],$$ (3)

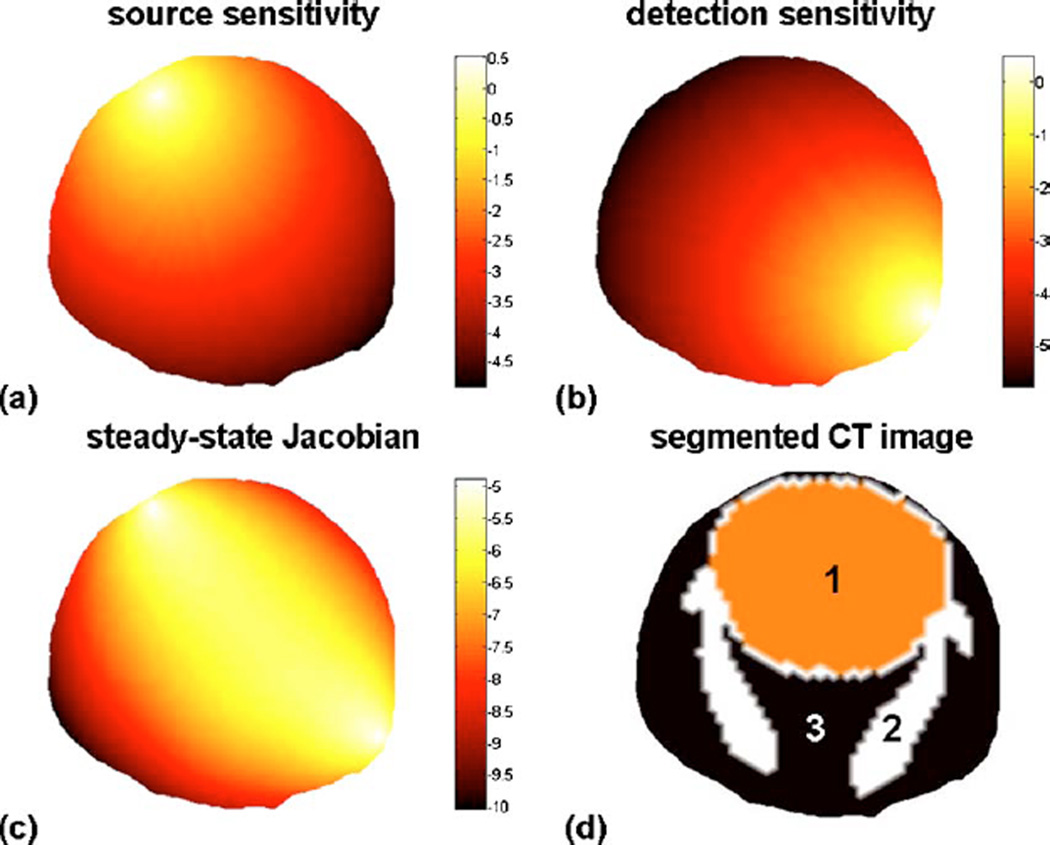
where Φ is a solution to the diffusion equation, while G is a Green’s function. Here construction of the update equation is attained numerically evaluating the photon probability distribution based on FEM [52,53]. Figure 3 illustrates this in the case of the evaluation of the steady-state Jacobian corresponding to perturbations in μ_a—the first term in δS_Ω in Eq. (3). This also corresponds to the steady-state Jacobian used in FMT. In the case shown in Fig. 3, the local optical properties associated with each node of the mesh were set based on a segmented CT image of a mouse head shown in Fig. 3(d).Figure 3(a) shows the photon fluence Φ(r′) associated with the source term, while Fig. 3(b) corresponds to the light sensitivity of the detector G(r′,r″), which effectively corresponds to a solution to the diffusion equation with a delta-function source term. Figure 3(c) illustrates the corresponding Jacobian which, as shown in Eq. (3), is simply the product of the fields shown in Fig. 3(a) and Fig. 3(b).

Fig. 3.

(Color online) Steady-state photon distribution associated with a diffusive light source inserted one reduced scattering distance under the tissue surface. (b) Steady-sate photon sensitivity distribution associated with a light collection point located on the surface of the mouse head. (c) Photon sensitivity distribution associated with the source and detector location shown in (a) and (b). (d) Segmented CT image (1, brain; 2, skull; 3, rest of tissues) used to project sources and detectors as well as to tag different anatomical regions with different optical properties.

B. Time-Gated Fluorescence Molecular Tomography

Subsection 3.A defined time-dependent update equations for general optical tomography in cases where light transport is modeled as a diffusive process, and this is now extended within the case of a forward model for time-gated FMT signals.

Fluorescence from tissue can be modeled as a two-step process beginning with the propagation of light from a collimated source to the fluorescent molecular targets followed by re-emission at a different wavelength. The first step is modeled by solving the differential equation

$$\frac{n}{c}\frac{\partial {\mathrm{\Phi }}^{\mathrm{x}}(\overrightarrow{r}\prime ,t\prime )}{\partial t\prime }-\nabla D_{\mathrm{x}}(\overrightarrow{r}\prime )·\nabla {\mathrm{\Phi }}^{\mathrm{x}}(\overrightarrow{r}\prime ,t\prime )+{\mu }_{\mathrm{a}}^{\mathrm{x}}(\overrightarrow{r}\prime ){\mathrm{\Phi }}^{\mathrm{x}}(\overrightarrow{r}\prime ,t\prime )=S(\overrightarrow{r}\prime ,t\prime ),$$ (4)

where D = 1/3(μ_a + μ_s′). In Eq. (4), the photon fluence and the optical properties are evaluated at the laser excitation wavelength λ_x. Subsequent re-emission of light by the fluorophores at a longer wavelength is modeled by a second coupled differential equation, where the source term is time-dependent corresponding to the exponential decay of the fluorescence excited by the photon field Φ^x [54],

$$\frac{n}{c}\frac{\partial {\mathrm{\Phi }}^{\mathrm{e}}(\overrightarrow{r}″,t″)}{\partial t″}-\nabla D_{\mathrm{e}}(\overrightarrow{r}″)·\nabla {\mathrm{\Phi }}^{\mathrm{e}}(\overrightarrow{r}″,t″)+{\mu }_{\mathrm{a}}^{\mathrm{e}}{\mathrm{\Phi }}^{\mathrm{e}}(\overrightarrow{r}″,t″)=\sum _{l=1}^{N_{\mathrm{F}}}[Q_{\mathrm{F}}^l{\epsilon }_{\mathrm{F}}^l\int \mathrm{d}t\prime ″{\mathrm{\Phi }}^{\mathrm{x}}(\overrightarrow{r}″,t\prime ″)C_{\mathrm{F}}^l(\overrightarrow{r}″)e^{-(t\prime ″-t″)/{\tau }_l}],$$ (5)

where the photon fluence and the optical properties are evaluated at the re-emission wavelength λ_e. The summation on the right-hand-side of Eq. (5) is included to account for the possibility of there being different fluorescent species (l = 1,…,N_F, where N_F is the number of species). The photophysical properties of these species are the fluorescent quantum yield Q_F, the extinction coefficient μ_F, the lifetime τ, and the local concentration of fluorophores C_F(μ^F_a = Q_Fμ_FC_F). The formal solution to the system of Eqs. (4) and (5) is obtained using Greens’ theorem [54],

$${\mathrm{\Phi }}^{\mathrm{e}}(\overrightarrow{r}″,t″)=Q_{\mathrm{F}}{\epsilon }_{\mathrm{F}}{\int }_{\mathrm{\Omega }}{\mathrm{d}}^{3}r\prime \int \mathrm{d}t\prime (\int \mathrm{d}t\prime ″{\mathrm{\Phi }}^{\mathrm{x}}(\overrightarrow{r}\prime ,t\prime ″)C_{\mathrm{F}}(\overrightarrow{r}\prime )e^{-(t\prime ″-t\prime )/\tau })\times G^{\mathrm{e}}(\overrightarrow{r}\prime -\overrightarrow{r}″,t\prime -t″),$$ (6)

where it is assumed for simplicity that there is only one type of fluorophore (N_F=1).

In order to bring the forward model Eq. (6) to a form where it can be used as part of an inverse problem, an N_V node FEM mesh of the tissue volume Ω is created followed by discretization of the spatial and time integrals. The spatial resolution is set by that of the created mesh while the temporal resolution is thenceforth set to Δt = 10 ps in the numerical simulations. Assuming a large number of measurements N_m is collected, the forward problem associated with the signal in time-gate t″ can be written in the matrix form

$$\left[\begin{array}{c}\hfill {\mathrm{\Phi }}_1^{\mathrm{e}}\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathrm{\Phi }}_{N_{\mathrm{m}}}^{\mathrm{e}}\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill A_1^{t″}({\overrightarrow{r}}_1)\hfill & \hfill \cdots \hfill & \hfill A_1^{t″}({\overrightarrow{r}}_{N_{\mathrm{V}}})\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill A_{N_{\mathrm{m}}}^{t″}({\overrightarrow{r}}_1)\hfill & \hfill \cdots \hfill & \hfill A_{N_{\mathrm{m}}}^{t″}({\overrightarrow{r}}_{N_{\mathrm{V}}})\hfill \end{array}\right]\times \left[\begin{array}{c}\hfill C_{\mathrm{F}}({\overrightarrow{r}}_1)\hfill \\ \hfill ⋮\hfill \\ \hfill C_{\mathrm{F}}({\overrightarrow{r}}_{N_{\mathrm{V}}})\hfill \end{array}\right],$$ (7)

where A_k^t″ (r_i) is an element of the Jacobian matrix corresponding to measurement k (k =1,…,N_m) and voxel with spatial location r_i (i = 1,…,N_V):

$$A_{\mathrm{k}}^{t″}({\overrightarrow{r}}_{\mathrm{i}})Q_{\mathrm{F}}{\epsilon }_{\mathrm{F}}\int \mathrm{d}t\prime (\int \mathrm{d}t\prime ″{\mathrm{\Phi }}^{\mathrm{x}}({\overrightarrow{r}}_{\mathrm{i}},t\prime ″)e^{-(t\prime ″-t\prime )/\tau })\times G^{\mathrm{e}}({\overrightarrow{r}}_{\mathrm{i}}-{\overrightarrow{r}}_{\mathrm{k}},t\prime -t″).$$ (8)

Similarly, inspection of Eq. (8) shows that the Jacobian for one time bin, here t″, can be generalized to model the signal corresponding to any combination of time bins. For example, the forward model for a time-gate between t₁ and t₂ is obtained with the following substitution in Eq. (7):

$$A_{\mathrm{k}}^{t″}({\overrightarrow{r}}_{\mathrm{i}})\to \sum _{t″=t_1}^{t_2}{A}_{\mathrm{k}}^{t″}({\overrightarrow{r}}_{\mathrm{i}}).$$ (9)

Riley et al. have shown in [55] that the use of local data types, such as the slope of the rising TPSF, lead to more stable FMT reconstructions with an approach where the forward model was based on an analytic expression for a simple geometry. The more general approach used here can be used to compute the Jacobian associated with the data type corresponding to the slope of the time-domain signal around t ″ located anywhere in the TPSF. This is implemented by the following substitution into Eq. (7):

$$A_{\mathrm{k}}^{t″}({\overrightarrow{r}}_{\mathrm{i}})\to \frac{A_{\mathrm{k}}^{t″-\mathrm{\Delta }t}({\overrightarrow{r}}_{\mathrm{i}})-A_{\mathrm{k}}^{t″+\mathrm{\Delta }t}({\overrightarrow{r}}_{\mathrm{i}})}{2\mathrm{\Delta }t}.$$ (10)

The fluence distributions G^e and Φ^x in Eq. (8) are computed by solving the time-dependent diffusion equation with the finite-element method. The solutions correspond to N_V probabilistic weights, one for each node in the mesh. The steady-state limit of the Jacobian consists of evaluating Eq. (9) for t₁ = 0 ns and t₂ = 10ns. The t₂ = 10 ns time limit corresponds to the end point of the simulated time-window, where signals have decreased to zero, as shown by inspection of the simulated TPSF in Fig. 6(a) below. Evaluating the Jacobian for one time bin involves numerically performing two convolutions in time: one between the detector sensitivity function and the exponential decay term of the fluorophore, and one between the resulting time-dependent expression and the time-dependent fluence produced from the light source. Finally, time-gated forward models are evaluated by performing the sum of the Jacobians for all time bins from t₁ to t₂.

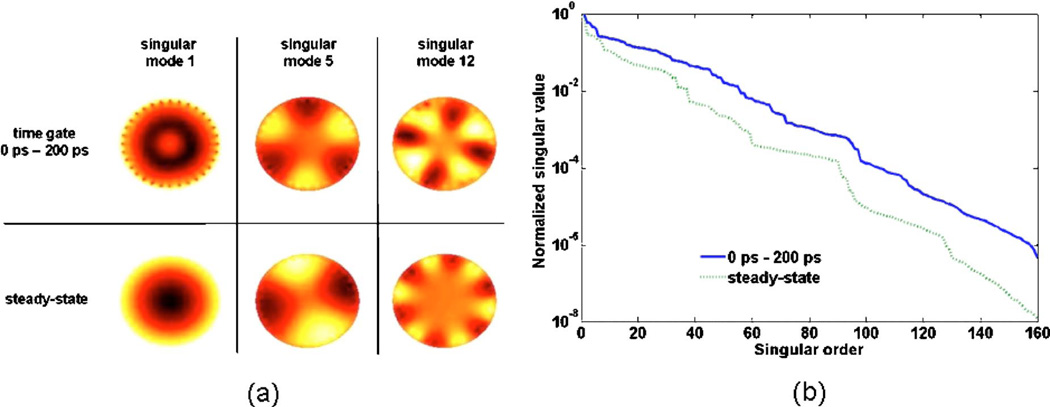
Fig. 6.

(Color online) Decay curve of singular values (log-scale) as a function of their order i for two FMT forward model matrices corresponding to weakly diffused photons (0–200 ps time-gate) as well as steady-state signal. The decay rate for the weakly diffuse photons is significantly less favorable to noise propagation in the images. (b) Illustration of some image-singular modes for the same two forward models. At the same order, the spatial frequency of the modes associated with weakly diffused photons is typically smaller than those associated with steady-state signal, again affording more leeway in reconstructing high-spatial-resolution images.

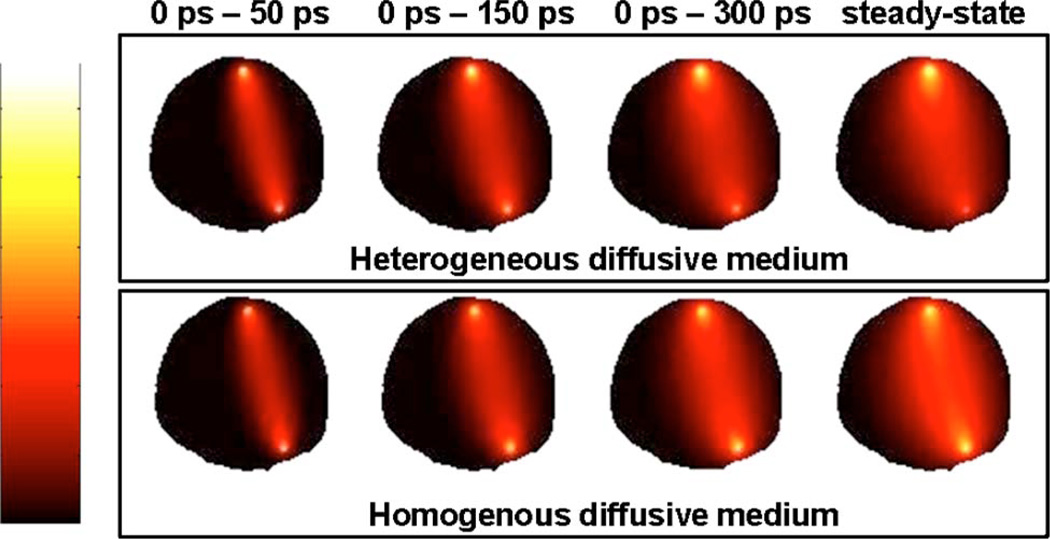
Figure 4 illustrates Jacobians numerically computed for different time gates with t₁ = 0 ns and τ = 1 ns. Specifically, the figure shows Jacobians associated with t₂ = 50 ps, t₂ = 150ps, t₂ = 300 ps and t₂ = 10ns. The first three time gates correspond to increasingly diffused photons, while the last one effectively corresponds to the steady-state signal equivalent to that of a continuous-wave source. For a given source–detector pair, inspection of Fig. 4 clearly shows that the tissue sampled by propagating photons is significantly reduced for early photons as compared with the highly scattered steady-state signal. Moreover, comparison of the Jacobians for homogeneous and heterogeneous optical properties highlights the fact that early photon signals appear less sensitive to the presence of optical absorption heterogeneities.

Fig. 4.

(Color online) Diffusion photon sensitivity distributions for the imaging geometry represented in Fig. 2 for a given source–detector pair. From left to right, sensitivity plots for increasingly large time gates are shown with the last image corresponding to a steady-state signal. The upper row shows distributions computed assuming that the diffusive medium has homogeneous optical properties, while the bottom row of images corresponds to a medium with heterogeneous optical properties.

C. Inverse Problem Resolution Algorithms

Linear systems of equations can be solved based on iterative regularization approaches such as those based on conjugate gradient methods. The end result then consists of a sequence of iteration vectors x_a, a = 1,2,3…, that converge to the desired solution. Such methods are generally preferable to direct methods when the coefficient matrix is so large that it is too time-consuming or too memory-demanding to work with an explicit decomposition of the Jacobian matrix A. In FMT, the linear inverse problem is often solved based on iterative regularization methods and, in this way, a regularized solution is computed. Here, we use the bound-constrained least-squares (BCLS) algorithm [44,56] for solving problems corresponding to the generic objective function problem:

$$\underset{C_{\mathrm{F}}\mathrm{s}.\mathrm{t}.l\le C_{\mathrm{F}}\le u}{\text{argmin}}{\Vert A{C}_{\mathrm{F}}-\mathrm{\Phi }\Vert }^2+{\gamma }^2{\Vert L{C}_{\mathrm{F}}\Vert }^2,$$ (11)

where the N_V-dimensional vectors l and u are lower and upper bounds on the optimization variables C_F. The parameter γ is a regularization coefficient that is used to control the norm ||LC_F||² while balancing it against the residual norm ║A C_F-Φ║². Typically, the matrix L can be engineered to play a wide variety of roles including the inclusion of prior spatial information in the reconstruction process.

Linear problems can also be solved using direct methods such as the singular-value decomposition (SVD) and its generalization to the matrix pair involved here (A, L). SVD decompositions are useful because they allow one to understand the underlying problem in terms of vectors, allowing direct manipulation of the fundamental spectral units from which tomography images are built. However, using direct methods is usually not practical in tomography because most problems are associated with large datasets. In fact, numerical algorithms performing decompositions of large matrices are memory-consuming and usually cannot be run on individual processors. However, here we are considering smaller datasets that can be used with SVD decomposition of the forward model matrices. This approach illustrates how the reconstructions based on the SVD decomposition work and is used to show generalizations of more conventional and practical iterative regularization methods. Hence, SVA is used only to gain an intuitive understanding of the underlying problem here.

Basic SVD decomposition reformulates a forward model matrix A ∈R^m×n into the form

$$A=U\mathrm{\Sigma }{V}^T=\sum _{i=1}^n{u}_{\mathrm{i}}{\sigma }_{\mathrm{i}}{v}_{\mathrm{i}}^{\mathrm{T}}$$ (12)

where U =(u₁,…,u_n) ∈R^m×n and V = (v₁,…,v_n) ∈R^m×n are orthonormal norm matrices, and where the diagonal matrix Σ = diag(σ₁,…,σ_n) has non-negative diagonal elements appearing in non-increasing order (σ₁ ≥ σ₂ ≥ … ≥ σ_n ≥ 0). The numbers σ_i are the singular values of A, while the vectors u_i and v_i are the so-called image and data singular vectors of A, respectively. A critical aspect to solving a tomography inverse problem consists of finding methods allowing us to minimize as much as possible the impact of the intrinsic ill-conditioning of the forward model matrix. The degree of ill-conditioning can be used as a measure of how much noise and intrinsic data-model mismatch propagate into the solutions [57]. To a large extent the degree of ill-posedness can be evaluated by studying the decay rate of the singular values, which in turn significantly affects how noise propagates into the regularized solutions. Using the SVD decomposition, the solution to the inverse problem can be rewritten as the sum over image singular vectors,

$$C_{\mathrm{F}}=\sum _{\mathrm{i}=1}^{N_{\mathrm{S}\mathrm{V}\mathrm{D}}}\frac{f({\sigma }_{\mathrm{i}})}{{\sigma }_{\mathrm{i}}}(v_{\mathrm{i}}^{\mathrm{T}}\mathrm{\Phi })u_{\mathrm{i}},$$ (13)

where N_SVD corresponds to the number of modes used to build the solution, and f(σ) is a regularization function. Essentially, this expression is a spectral decomposition of the solution as a sum over image singular vectors weighted by a spectral coefficient. As a general rule, the singular values decrease with increasing values of the order i, and the spatial frequency of the modes ui increases with i.

4. RESULTS

Here the time-gated modeling approach presented in Section 3 is used to show how reconstructing fluorescence images based on early diffused photon signals can significantly improve the intrinsically poor resolution of optical tomography.

A. In silico Fluorescence Phantoms

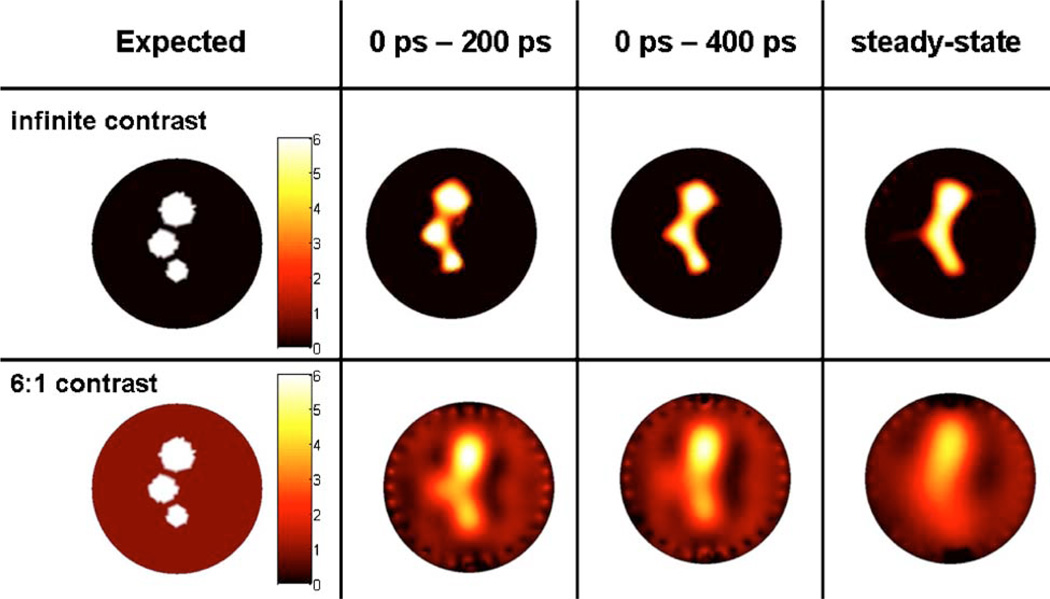
Simulated optical data sets were generated for two cylindrical phantoms, both containing three small fluorescent inclusions. As seen in Fig. 5 (left-most column), one numerical phantom has infinite fluorescent contrast, and the other one has a more realistic contrast-to-background ratio of 6 to 1. The phantoms were designed with features making their use relevant in deriving conclusions applicable to mouse imaging. The radius of the phantom is R = 12.5 mm and the optical properties of the bulk diffusive medium are μ_a = 0.02 mm⁻¹ and μ_s′ =1 mm⁻¹—both for the excitation and the emission wavelengths. The fluorescent inclusions have radii R_I = 2.5 mm, R_II = 2.0 mm, and R_III = 1.5 mm. The radii were chosen for consistency with animal model tumors routinely imaged with FMT The size of the smallest inclusion was determined because it roughly corresponds to the fundamental spatial resolution limit set by diffusion theory. The centers-of-mass of adjacent inclusions in the phantom are separated by a distance of δ_CM = 2.5 mm, while the minimum distance between the edges is δ_e = 1 mm.

Fig. 5.

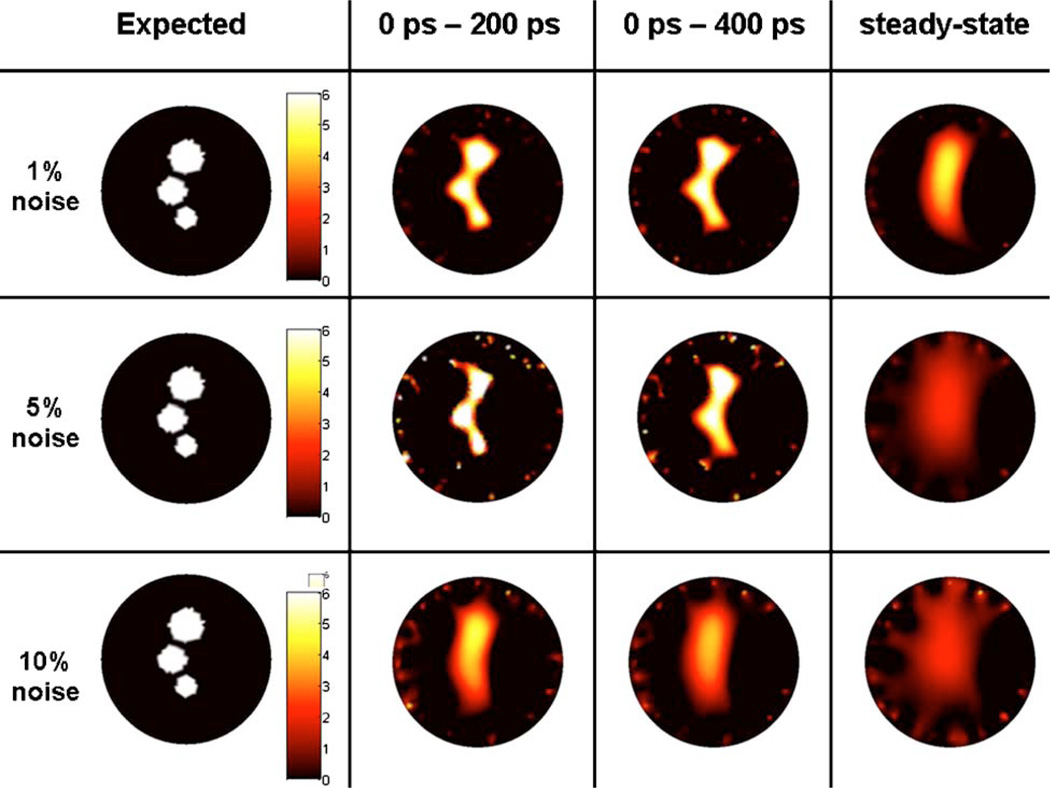
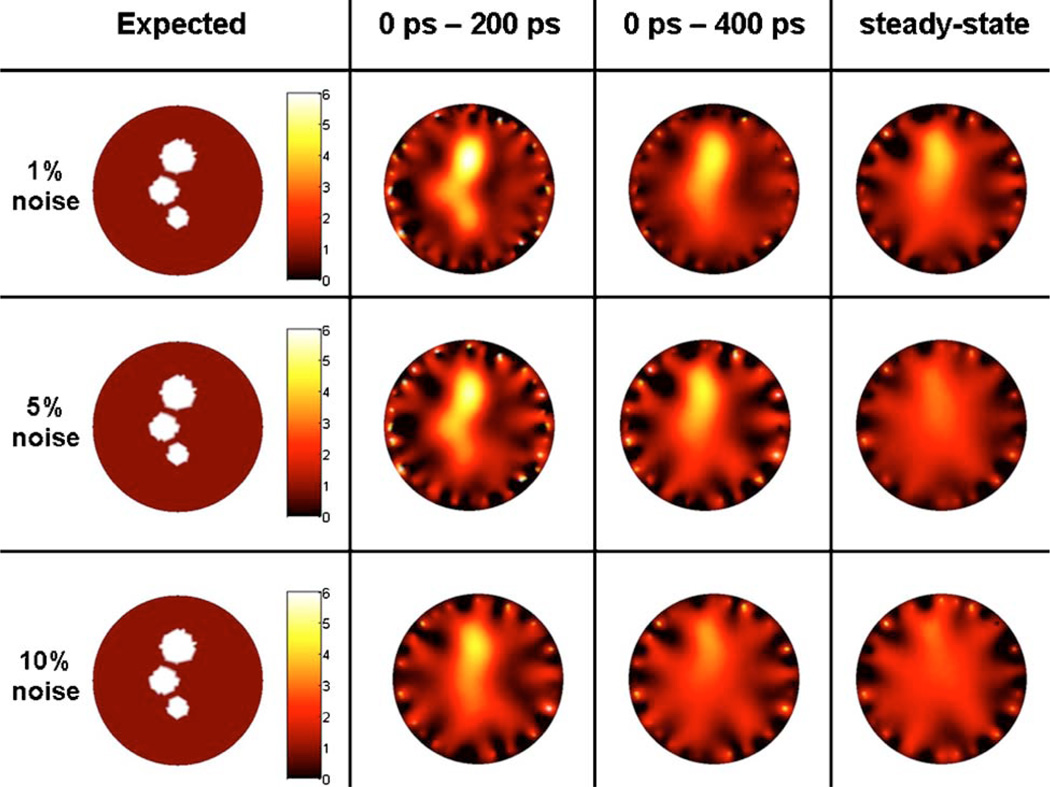
(Color online) Target images reconstructed with the iterative regularization method BCLS. The first column corresponds to the target images used to generate synthetic data for different time-gates. In the upper images, the fluorescence contrast is infinite, while in the lower ones the contrast is 6 to 1. Reconstructed images shown are for weakly diffused photon time-gates 0–200 ps and 0–400 ps as well as for simulated steady-state signal for comparison purposes. No noise was added in the simulated data for these reconstructions.

Forward model data were calculated with the 2D diffusion equation for a medium with homogeneous optical properties μ_a and μ_s′ [53,58]. The choice of doing light transport simulations in 2D was made for simplicity and to reduce simulation time. FMT matrices for three different time-gated signals were generated, namely, T_{200 ps} = 0 ps–200 ps, T400 ps = 0 ps–400 ps and the steady-state case T_CW covering the full time window. As shown in Subsection 3.B, the FMT inverse problem for any type of data can be cast in the matrix form

$${\mathrm{\Phi }}^{\mathrm{T}}=A^{\mathrm{T}}{C}_{\mathrm{F}},$$ (14)

where, in this case, T labels the time-gate under consideration. Simulated data are generated for each time-gate by multiplying the Jacobian, A^T with the target fluorescence images shown in Fig. 5. Then, statistical noise following a Gaussian distribution around the signal amplitude is added to the synthetic data vectors. Four levels of noise are considered, namely, 0%, 1%, 5%, and 10%.

B. Singular-Value Analysis and Spatial Resolution Improvement

Experimental data Φ^T always contain noise, and the most critical aspect of solving an optical tomography inverse problem is controlling how much this noise is allowed to propagate into the reconstructed images. When using iterative reconstruction methods, one or several regulariza-tion parameters are carefully chosen to allow convergence toward those solutions that represent the better possible compromise between minimization of the residual norm and minimization of noise propagation in the final solution. An intuitive understanding of this is shown through SVA of the forward problem matrices for time-gated data relative to steady-state.

As explained in subsection 3.C, reconstructed fluorescence images can be built by summing image singular vectors of increasingly high spatial frequencies. The spatial frequency of the modes increases with the order of the singular values i. Consequently, the number of modes Nsvd that are used to build the solution can effectively be regarded as a parameter controlling the spatial resolution of the resulting fluorescence images. For example, Fig. 6(a) shows the image singular vectors for i = 1, 5 and 10 in the case of FMT matrices for time-gates T_{200 ps} and T_CW. When forming a fluorescence image, those image singular vectors u_i are weighted against each other according to the values taken by the spectral coefficient (v_i^TΦ^T)/σ_i. As explained further below, it is the behavior of those coefficients combined with the spatial frequency of the corresponding image singular modes that is setting an absolute spatial resolution limit to optical tomography.

Maximizing the spatial resolution of a fluorescence image is attained by keeping as many high-spatial-frequency image singular modes u_i in the solution as possible. This can be accomplished by truncating the sum in Eq. (13) for i = N_SVD as large as possible. The problem is that noise in the data vector limits the number of modes that can effectively be used when reconstructing an image. Indeed, when noisy data are used the spectral coefficients typically diverge for finite values of i. This implies that if the corresponding modes are kept in the solution, they will be the only ones contributing, potentially making it appear, incorrectly, that the solution has a very high resolution. However, all information pertaining to the underlying physical content of the image has been lost. Cutting off the divergent modes appropriately then amounts to regularization of the solution.

Another possibility for obtaining a yet smoother regularized solution consists of introducing a smoothing function f(σ) that is continuously decreasing from one to zero as the singular-value order increases. The inflexion point of the smoothing function is then located around the value where the spectral coefficients begin to misbehave. It can be shown analytically that this approach is equivalent to an iterative regularization Tikhonov method (for example, see [57]). In fact, an important point here is that any iterative method that is used to solve a linear inverse problem can, in principle, be formulated in terms of a SVD or a generalized SVD decomposition associated with a specific smoothing function. The reason this is so important is that any conclusion that is derived based on SVA considerations can in principle be translated to other more conventional approaches used to solve optical tomography problems.

To a large extent, the degree of ill-posedness of a problem can be quantified by the decay rate of the singular values [57]. The importance of the decay rate can be traced back to the fact that the computation of the spectral coefficients involves evaluating the ratio 1/σ_i, which tends to become very large for small singular values. If the singular values are decreasing rapidly, then the spectral coefficients weighting the image singular vectors will have a tendency to blow up for small values of i, thereby compromising the stability of the solution. Consequently, the sensitivity to noise is going to be more important for cases where the decay rate of the singular values is larger. Figure 6(b) shows the decay curves of the singular values for two different time-gates, namely T_{200 ps} and T_Cw. Inspection of this log-scale figure clearly reveals that the decay rate associated with the steady-state forward model is significantly larger than that associated with early photons. This implies that the solutions for early photon data are more stable. This also means that the divergence of the spectral coefficients will typically occur for larger values of i in the case of early photon forward models when compared to steady-state. Therefore, more high-frequency image singular modes can be used in a given early-photon solution, potentially leading to improved resolution when compared with steady-state-based reconstructions.

As mentioned earlier, for a given singular order i, the spatial frequency of a mode appears higher for early photons than it does for steady-state [Fig. 6(a)]. This further illustrates there is an increase in spatial resolution for images reconstructed based on early-photon signals. Finally, it can also be shown based on perturbation bound theorems [57] that the error committed when solving an inverse problem using a truncated SVD (at i=N_SVD)—due to noise and bad modeling—is proportional to the ratio σ₁/σN_svd Again, this emphasizes the importance of insuring that the singular-value decay rate is as slow as possible when choosing a forward model.

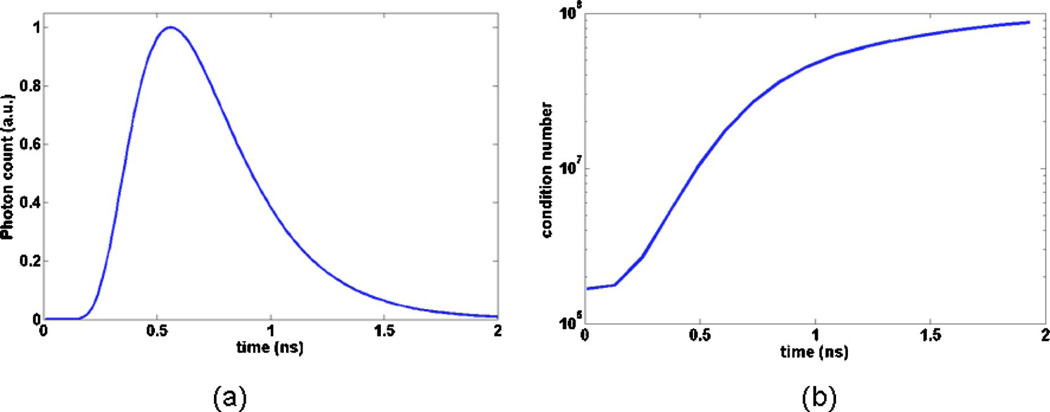
A measure that is often used to quantify the degree of ill-conditioning of a system of linear equations is the condition number of the Jacobian, which consists of the ratio between the largest and the smallest singular values. Linear systems associated with large condition number matrices typically have a large number of linear dependencies, which makes them more susceptible to noise. Figure 7(a) shows a transmission TPSF that was generated numerically for the in silico phantom described in Subsection 4.A for the coaxial detection channel in Fig. 1(a). Then, Fig. 7(b) shows the condition number of the corresponding forward model matrix A^T for different time-gate sizes. The time-gates considered here start at t₁ = 0 ps. The x-axis on the graph corresponds to increasing values of t₂, that is, increasingly large time-gates with the largest one (t₂ = 2 ns) effectively corresponding to the steady-state signal. Inspection of Fig. 7(b) shows that the degree of ill-posedness as measured by the condition number increases exponentially as a function of the time-gate size. This is certainly consistent with the results derived in Subsection 4.B based on a singular-value decomposition approach. However, analyzing the ill-conditioning of the optical tomography problem solely based on the condition number is not sufficient to gain a clear intuitive understanding of the basic mechanisms at play.

Fig. 7.

(Color online) Illustration of the FMT forward model matrix condition number as a function of the time-gates that are included in the signal: (a) simulated time-domain signal, (b) graph showing the condition number of the matrix for time-gates from 0 ns to t ns, where t is the x-axis value on the graph.

C. Fluorescence Reconstructions with Weakly Diffused Photons

Reconstruction results are now presented based on simulations performed with the in silico phantoms described in Subsection 4.A. As mentioned earlier, different levels of noise were added to the time-gated data prior to inversion including 0%, 1%, 5%, and 10%. A discussion relating to noise propagation in early-photon time-gates is presented at the end of this section, placing these values in a more appropriate experimental context.

Throughout this section, inverse problem resolution results are presented only for tomography images obtained with the BCLS solver described in Subsection 3.C. It was found that the reconstruction results obtained with the BCLS solver are consistent with expectations gained by performing the SVA. Indeed, every reconstruction we have performed with BCLS was also performed using the truncated SVD approach as well as the SVD method with Tikhonov smoothing function. The trends, in terms of stability to noise and spatial resolution improvements, were maintained for all approaches. We are limiting the presentation to BCLS results partly for conciseness and partly because of the improved quality of the fluorescence images. In this case, our main criterion for judging the quality of an image is based on a qualitative assessment of the number of artifacts present in the solutions.

Part of the reason BCLS images are of better quality might be the non-negativity constraint that is imposed through the merit function in Eq. (11)—l = 0 and v = ∞. Indeed, it has been observed repeatedly in the past that FMT images reconstructed using non-bound-constrained iterative regularization methods have a tendency to imbue images with nonphysical negative intensity values. Ill-conditioned systems of linear differential equations are associated with a high degree of linear dependencies, which implies that for a given data vector there exist a lot of candidate solutions with comparable residual norms. Among that large number of solutions composing the degenerate landscape, non-bound-constrained solvers seem to favor those solutions containing a subset of negative intensity values. Imposing convergence toward positive-definite solutions is therefore also found to indirectly improve the conditioning of the inverse problem.

In what follows the regularization parameter γ is set to zero in the objective function Eq. (11). The only regularization parameter used in BCLS is the tolerance factor itself, which corresponds to the targeted convergence value of the residual norm of the solution. This regularization parameter is henceforth referred to as λ. Comparison with direct SVD-based inversion methods provides evidence that λ plays a role similar to that of the truncation order (N_svd) in the singular-value analysis presented in Subsection 4.B. In this case though, smaller values of λ lead to solutions with higher intrinsic spatial resolution. Also, the more noise there is in the data vector, the larger λ needs to be to prevent noise from propagating into and dominating the solution. This is in accord with the intuitive SVA arguments presented in Subsection 4.B: solutions with a larger residual norm are built with a smaller number of high-spatial-frequency modes than solutions having a smaller residual norm.

Figure 5 shows reconstructions performed for different time-gates when no noise (0%) was added to the in silico data vectors. In a way, since these reconstructions were without any noise, the results can be interpreted as the best possible result based on the detection geometry shown in Fig. 1(a): 32 sources, 5 detectors per source. In the infinite fluorescent contrast case, clear spatial resolution improvements can be seen to have been achieved by using a time-gate consisting of photons as weakly diffused as possible. The improvement is quite dramatic since steady-state imaging cannot be used to resolve the targets, while individual fluorescent sources can be distinguished on the image reconstructed based on the T_{200 ps} time-gate. Clear image improvements are also noted for the T_{400 ps} time-gate when compared with the steady-state case. Indeed, the fluorescence intensity for the smallest inclusion (R_III = 1.5 mm) is correctly recovered for T_{400 ps} yet it is not when using T_CW.

In optical tomography, it is notoriously more difficult to reconstruct finite contrast targets [59]. The bottom row of images in Fig. 5 shows the 0% noise reconstructions for the multiple targets phantom where the contrast associated with the inclusions is 6 to 1. Comparison with the infinite contrast results (upper row of images in Fig. 5) shows that the reconstructed images are in general much more diffuse for finite contrast values even when early-photon time-gates are considered. Nonetheless, we find that although they cannot be distinguished, all three targets can be seen when using a weakly diffused signal corresponding to the 0 ps–200 ps time-gate. The T_CW image shows a single diffuse blob with its highest intensity located around the center of mass of the largest inclusion (R_I = 2.5 mm). Then, comparison with the T_{200 ps} and T_{400 ps} images shows that decreasing the size of the time-gate allows the other inclusions to start taking form. In no way should these results be interpreted as a fundamental limit of early photon optical tomography. In fact, improving tissue sampling by increasing the number of measurements is likely to further improve the quality of the fidelity of the tomography images.

D. Noise Propagation in Time-Domain Signals

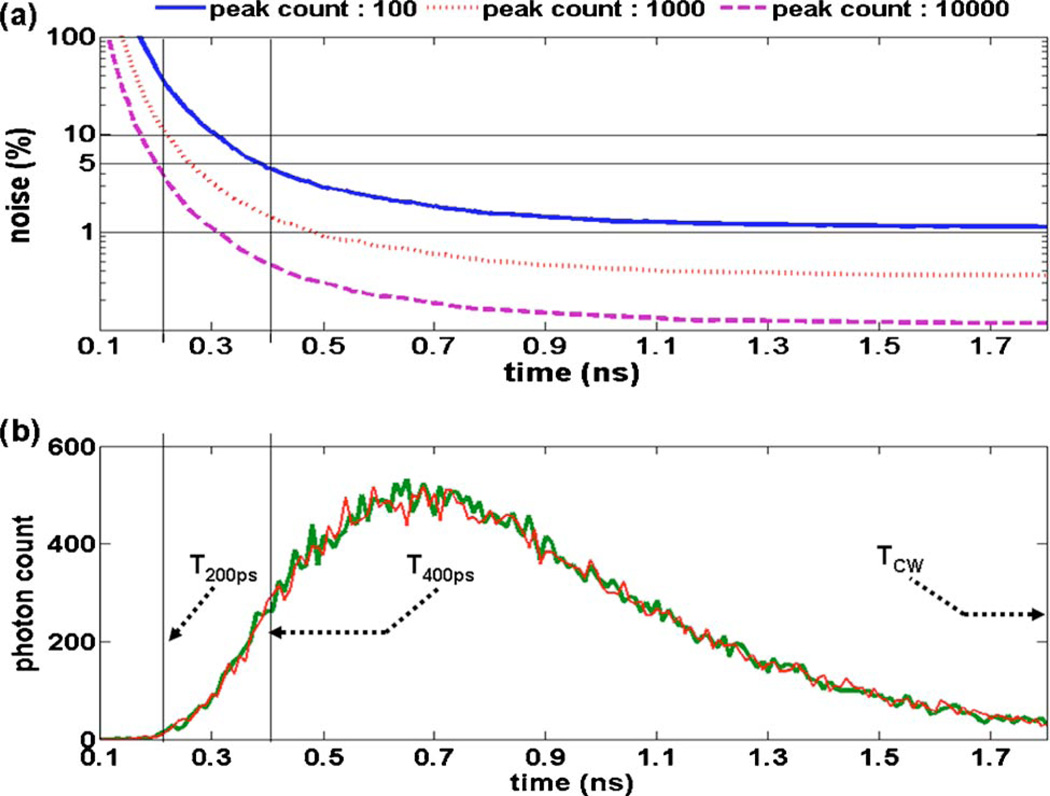
In the scope of early diffused photon simulations, it is important to understand the limitations of early times windows in terms of inherent noise limits on imaging through thick tissues. The stochastic noise associated with TCSPC-based PMT detection can be modeled by adding to each time bin a random value according to a Poisson distribution with the mean corresponding to the total number of photon counts in each time bin. Then, the stochastic noise in each bin is associated with the SNR as

$$\mathrm{S}\mathrm{N}\mathrm{R}=\sqrt{N},$$ (15)

where N is the number of photons collected for a given time bin of the TPSF. For example, Fig. 8(b) shows two different simulated TPSFs for which stochastic noise was added. Therefore, increasing the total number of photons collected to build a TPSF increases the overall SNR of the signal. Often, the quality of a TPSF in terms of stochastic noise is measured by the number of counts at the curve peak corresponding to where the signal is maximal. Henceforth, this quantity is referred to as the peak count of a TPSF. The experimental parameters that can be varied in order to improve the SNR for a given data set are the laser power and the illumination/collection integration time when acquiring each measurement. Imaging through thick and highly absorbing tissue requires increasing either or both of these instrument parameters.

Fig. 8.

(Color online) Stochastic noise propagation in time-gated TPSF signals. The lower graph shows two curves (peak count of 500) where noise following a Poisson distribution with mean N (number of counts in individual time bins) was added. Time-gates T_{200 ps,} T_{400 ps}, and T_CW are highlighted. The upper image shows how noise propagates into the time-gates for different TPSF peak counts. The x-axis for both pictures corresponds to the end-point of the time-gate (t₂). The initial point of the time-gates was always t₁ = 0 ns.

Figure 8(a) shows how stochastic noise propagates into different time-gate sizes for different levels of photon peak count, namely, 10², 10³, and 10⁴. The variable on the x-axis of the figure corresponds to t₂. The initial time in the gate always corresponds to t₁ = 0 ns. Inspection of the graph shows that the exponential signal increase that is typical of early time bins of a TPSF leads to an exponential increase of the noise propagating in the early time-gates. From a practical point of view, it is therefore expected that the product of laser integration time and power required to obtain good SNR datasets will also increase exponentially as the size of the time-gates decreases. However, the modeled signal here is purely diffusive and it is likely that in situations involving mouse imaging, for example, there will be a non-negligible WSP component in the signal improving the count rate. This is mentioned here to clarify that the results shown in Fig. 8(a) should be used only as an example illustrating the trends associated with considering different count levels.

Based on the noise analysis presented above, the shorter the early-photon time-gate is, the smaller the corresponding SNR will be. This can be problematic for tomography since the relevant inverse problem methods tend to be very sensitive to noise. The optimization game that needs to be played when considering early photon tomography consists of acquiring signals that have a good enough SNR so the benefits discussed earlier—stability to noise and improved spatial resolution—can be preserved at a reasonable cost in terms of laser power and integration time.

Figures 9 and 10 show more realistic reconstruction results where different levels of noise are added to the simulated data vectors. In agreement with the 0% noise results (Fig. 5), improvements in imaging fidelity are found for reconstruction based on weakly diffused signals. Perhaps the most salient feature of both the infinite and 6 to 1 contrast images is that the steady-state images are particularly sensitive to noise. Indeed, all T_CW images that were reconstructed with more than 1% noise have lost all information relating to the original image, both in terms of target localization and recovered fluorescence intensity. Only in the case of 1% added noise can the approximate center of mass of the larger inclusion be recovered. In this case, it would be very difficult to predict that there are other smaller inclusions.

Fig. 9.

(Color online) Infinite contrast target image reconstructed with the iterative regularization method BCLS for different levels of noise. The first column corresponds to the target image used to generate synthetic data for different time-gates. Reconstructed images shown are for weakly diffused photon time-gates 0–200 ps and 0–400 ps as well as for simulated steady-state signal for comparison purposes. Three different levels of noise are shown: 1%, 5%, 10%.

Fig. 10.

(Color online) 6 to 1 contrast target image reconstructed with the iterative regularization method BCLS for different levels of noise. The first column corresponds to the target image used to generate synthetic data for different time-gates. Reconstructed images shown are for weakly diffused photon time-gates 0–200 ps and 0–400 ps as well as for simulated steady-state signal for comparison purposes. Three different levels of noise are shown: 1%, 5%, 10%.

There is another interesting observation that can be made by inspecting the 1% and 5% noise rows in Fig. 9. In this case, the quality of the reconstructions for both T_{200 ps} and T_{400 ps} appear to be able to localize the center of mass of all inclusions as well as to recover the correct fluorescence intensity. This is a sharp difference with the results obtained with the steady-state signal. On the other hand, the information content in the 10% noise images for the early-photon time-gates in Fig. 9 is essentially equivalent to what is contained in the 1% T_CW time-gate. In other words, it does not appear that doing early-photon imaging with 10% noise would significantly improve the results obtained with steady-state imaging at 1% noise level. Those findings for the infinite contrast cases can essentially be transposed to the 6:1 contrast results shown in Fig. 10. The only exception is that in the presence of a fluorescence background the fidelity of the images obtained with T_{200 ps} is significantly improved when compared with those corresponding to T_{400 ps}.

5. DISCUSSION

A. Spatial Resolution and Sensitivity to Noise

Using arguments derived from inverse problem considerations, the analysis here illustrates why an instrument designed with tomographic fan-beam detection geometry and single-photon-counting technology can significantly increase the spatial resolution of FMT if the data type is chosen appropriately. This is an important prospect because optical tomography is a modality that has traditionally been plagued with low resolution, low contrast recovery, and ultimately low predictive power, when used as a stand-alone imaging modality.

The main conclusions of this work are with respect to the use of early-time photons in the FMT inverse problem. Better conditioned inversion can be gained with time-gated data as compared with steady-state data. A useful numerical measure of this behavior is found to be the condition number of the Jacobian. For cases relevant to small-animal imaging, this number was found to grow exponentially with increasing size of the time-gates. For example, in Fig. 7 the condition number going from T_{200 ps} to the steady-state forward model matrix increases by a factor of 450. Reconstructions using synthetic data from a realistic in silico phantom were performed and used to show that, in accord with condition number analysis, the early-photon fluorescence tomography problem is significantly less sensitive to noise than its steady-state counterpart. It is observed that this increased stability to noise is accompanied by an improved intrinsic spatial resolution. In fact, early-photon tomography was shown to have the potential to resolve small fluorescence inclusions having their center of mass separated by a distance of 2.5 mm. More precisely, as shown in Fig. 5, inclusions having a distance between their edges δ_e=1 mm could be resolved in ideal conditions when using early-photon time-gates with no stochastic noise added. Even in such ideal situations, steady-state imaging is incapable of resolving the targets to a level that is comparable with early-photon imaging.

The prognostic analysis based on the condition number of the Jacobian matrix is insufficient to gain a full understanding of the underlying principles behind the enhanced spatial resolution and limited noise sensitivity associated with early-photon fluorescence tomography. In particular, the analysis does not allow one to disentangle the cause of two main aspects affecting the quality of tomography images, namely, sensitivity to noise and intrinsic spatial resolution. Therefore, as a complement to condition-number considerations, a singular-value analysis of the time-gated FMT inverse problem was performed.

As a general rule, the spatial resolution of a reconstructed optical image is related to the number and the spatial frequency of the image-singular mode vectors that can be used to build the solution. An analysis of the image-singular vectors associated with inverse problems for different time-gates was performed. In general, it was found that for the same singular order (i) the spatial frequency of the image vectors was usually larger for smaller time-gate matrices. This implies that if one were to use a finite number of singular modes to reconstruct an image (N_svd), then the resolution associated with early time-gate images would be improved compared with larger time-gates and, in particular, with steady-state imaging.

However, one might argue that if the number of modes that are kept in the solution is not limited but kept as large as is possible—for the cases of N_m×N_V matrices, this number is min(N_m,N_V)—then the resolution of early-photon images and steady-state images could be equivalent. However, as illustrated in Fig. 5, this is found not to be the case. Part of the reason for this might have been explained by the fact that the decay rate of the singular values associated with the steady-state problem is much larger when compared with the early time-gated case [see Fig. 6(b)]. This implies that, even in the absence of noise, the high-spatial-frequency components of the SVD solutions will have an increased tendency to diverge because of divisions by small numbers 1/σ_i, where i is large. Diverging high-frequency modes should not, of course, be part of the solution because they would dominate over the lower-frequency modes in which much of the physical information is contained. Inspection of Fig. 6(b) shows that the smallest singular value for the 0 ps–200 ps time-gate is about two orders of magnitude larger than that corresponding to the steady-state signal. This makes the high-spatial-frequency components potentially more sensitive to both noise in the data vector as well as to the machine precision value. Indeed, were the singular values associated with higher-frequency modes smaller than the machine precision, then those modes would diverge and be rendered nonaccessible for image reconstruction. However, for the particular inverse problems considered in this work, the smallest singular values that were considered are always safely above the machine precision value. Issues relating to machine precision divergence will be encountered when considering denser data sets leading to rank-deficient inverse problems that are associated with high content of redundant information.

Based on this argument, the increased intrinsic spatial resolution of early-photon tomography can be thought of mathematically as being due to there being more high-frequency modes available for image reconstruction. Similarly, a combination of slower singular-value decay rate and higher spatial frequency of the corresponding image-singular vectors can be used to explain the improved stability to noise associated with early-photon tomography.

B. Generalization to Weakly Scattered Photons

The main challenge in early-photon imaging consists of using time-domain detection technology to collect signals associated with those photons that have traveled along paths that are as straight as possible between the source and the detector [33,36,37]. Ideally, the ballistic component of the signal should be used in order to maximally improve on the poor spatial resolution of diffuse optical imaging. This is expected, of course, based on our intuition developed working with x-ray CT systems. However, for small-animal optical imaging, sampled tissue volumes are usually such that the ballistic component of the signal is negligible.

Typically then, as described in Subsection 2.A, early-photon signals are composed of a mixture of WSPs and of weakly diffused photons. The main difference between these two types of particles is that the WSPs are highly forward directed while the weakly diffused photons can be modeled as a purely diffusive process. The key question one needs to answer when devising a model for early photons consists in determining how much of the signal is composed of weakly scattered photons compared with weakly diffused photons. Their relative proportion is going to be affected by the thickness of tissue being imaged as well as by the magnitude of the absorption. Also, increasing the size of the early-photon time-gate will reduce the proportion of WSP up to a point where diffused photons dominate the signal. Evidence is provided in [33] that the T_{200 ps} time-gate contains a large fraction of WSPs in the case of an application that images lung tumors with FMT.

In [33], light transport for WSPs is modeled with analytic solutions obtained from the cumulant approximation to the RTE [35]. This allows the authors to build forward models with photon sensitivity functions that are thinner, with more of the photon weights localized along the direct line of sight between sources and detectors. This is to be contrasted with the diffusion model used in the work here where the photon sensitivity distributions remained comparatively broad even in the case of the 0 ps–50 ps time-gate, as shown in Fig. 4. This is simply a manifestation of the fact that WSPs and ballistic photons are not modeled by solutions to the diffusion equation. Of course, the frontier between WSPs and weakly diffused photons is not a discrete one, and there is a smooth continuation between diffusion-based solutions and RTE-based solutions. The results found here in terms of improved spatial resolution and increased stability to noise apply as well to inverse problems associated with RTE-based light transport modeling.

In conclusion, there are two types of information a fluorescence tomography approach is expected to provide. Ideally, the method should afford localization of small targets and it should quantify their relative fluorescence intensities. Often, appropriately calibrated FMT instruments are able to measure only the total fluorescence emitted from a tissue without providing clear delineation of the fluorescence sources such as tumors. Here, we have shown how and why the spatial resolution and quantitative power of FMT can be significantly improved by optimizing tissue sampling and using time-domain technology to acquire early-photon signals.