Statistical Estimation & Inference of Cell Counts from ELISPOT Limiting Dilution Assays

Abstract

The ELISPOT Assay is often used for cell count determination in immunological studies. Automated methods are needed to estimate cell concentrations from spot counts obtained from the assay. Three major distributions are assumed for observational cell counts. For each assumed distribution, individual least squares (LS)/maximum likelihood, and/or individual robust least squares (RLS) are applied for parameter estimation. Distributions of study endpoints (derived variables), defined as percentages of antigen-specific memory cell per total IgG, are investigated to provide a basis for hypothesis testing. We show, under some weak conditions, the distribution of endpoint estimates across subjects is approximately the same within a group. Thus the t-test or the Wilcoxon Rank Sum test can be applied to detect group differences. These methods are compared through simulations and application to real data.

1 Introduction

Immunological assays based on 96-well (or greater) plate technologies are pervasive in the research community. Although there are several types of these assays, many depend on replicate wells of certain culture conditions, often with one of the assay components set in a limiting dilution series. With samples appropriately diluted, the target cells will be neither limiting nor in excess of the detection range of the assay. The Enzyme Linked Immuno-Spot (ELISPOT) assay is one such approach. The unique aspect of the ELISPOT is that the 96-well plate is constructed with a nitrocellulose or similar filter membrane upon which a capture agent, either an antibody or antigen, is bound. Secretion of the specific product by the cell of interest results in the capture of this product on the filter. Secondary reagents (usually another antibody and enzyme) are used to develop the spots through the deposition of a colored precipitate that can be visualized on the filter. Sophisticated instruments have been devised to count the spots within each well.

The question becomes how to best determine the total cell number in a sample from the numbers of spots, observed over a range of limiting dilutions. Recent statistical methods have been proposed for statistical issues related to binary response (presence or absence of a cell type) based on the ELISPOT readout or other limiting dilution assays (Wang et al., 2008; Wang and Soong, 2008; Hudgens et al., 2004; Moodie et al., 2006). There has been extensive research on statistical analysis of Radioimmunosassy and ELISA data where responses are continuous, for example, optical densities; see Rodbard (1974, 1975), Finney (1976) and others. Little study has been particularly focused on the count responses (total number of cells in the sample), although accurate measurement of cellular immune responses are critical, for example, in the study of infectious diseases.

An influenza vaccine study was designed to determine whether a subject with prior immunization of an antigenic variant could be primed for immune responses to a single dose of study vaccine representing the current pandemic threat (Goji et al., 2008). Of the 37 subjects enrolled in the parent study, ELISPOT data on 28 subjects were available to investigate memory B cell responses to vaccination. Peripheral blood mononuclear cells (PBMC) were obtained for assessment of antigen-specific memory B cells prior to vaccination (baseline) and on days 7, 28, and 56 after vaccination. A study objective was to determine the numbers of antigen-specific memory B cells changed after immunization. The ELISPOT memory B cell assay was described by Crotty et al. (2003), and involves coating a 96-well plate with viral antigen (H5VN influenza epitope). Samples used to detect all IgG-secreting cells (measure of total memory B cells) undergo 1 : 5 to 1 : 40 initial dilutions, and then one-half serial dilutions for seven times. Samples for antigen-specific memory cell determinations are directly serially diluted 1 : (k +1) at the kth dilution (k = 1, …, 7). The diluted samples are then applied to 96-well plates prepared with influenza antigen. The number of total IgG and antigen-specific antibody secreting cells (ABS) in each diluted sample well are counted by the Eli Scan system (A EL Vi S, Hannover Germany).

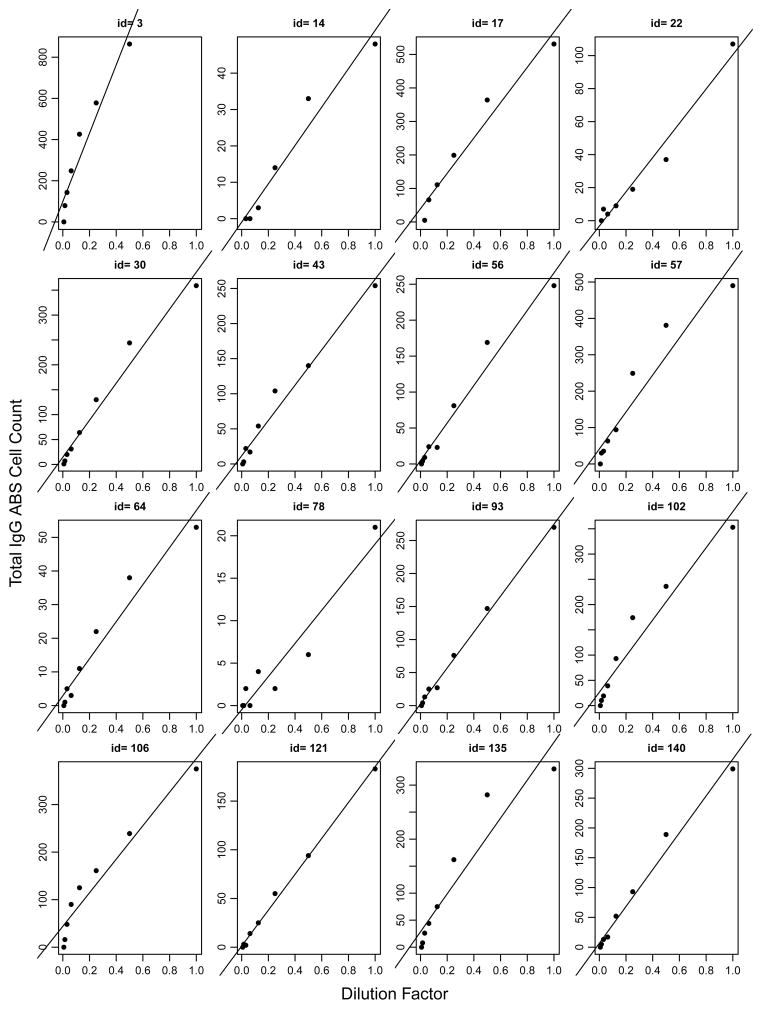
Figure (1) presents 16 of 28 donors’ baseline observations of the total IgG ABS cells over the corresponding dilution factors. A monotonically increasing trend of IgG measurements over the dilution factors is observed suggesting that least squares (LS) or robust procedures can be used to estimate total cell counts. For these donors, a normal distribution can be assumed for the observed cell numbers, either with the same variance or with heteroscedastic variance. For each assumption, both individual least squares (LS) and individual robust least squares (RLS) are applied to estimate parameters. In addition, the Poisson distribution can be assumed for cell numbers. Actually for cells with large counts, a Poisson distribution with parameter λ is approximately equivalent to a normal distribution with mean and variance being λ, because Poisson(λ) is well approximated by N(λ, λ) if λ is not small. Under the Poisson assumption, β_i is estimated by the MLE.

Figure 1.

Number of total IgG antibody secreting (ABS) cells by serial dilution of PBMC samples from 16 donors from an influenza vaccine study.

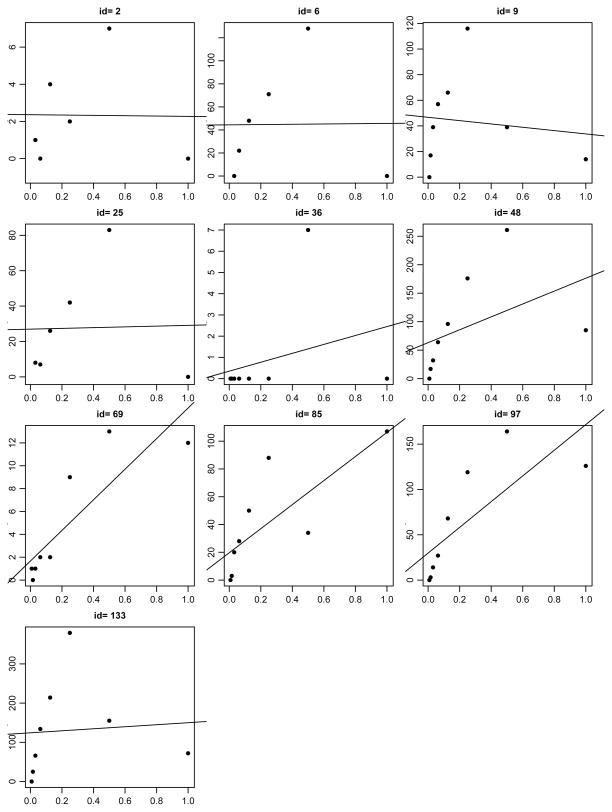
However, as demonstrated in Figure (2), the remaining donors (two donors didn’t have valid observations) had cell counts with irregular patterns. For these donors, fewer number of cells were observed in the undiluted (1 : 1) and/or the first diluted sample (1 : 2) compared to the more diluted samples. An examination of corresponding ELISPOT plate well images shows that this type of irregular cell counts usually comes with variable background staining intensity problems, which more often occur to less diluted samples. If we include these probable errors in the estimation, the LS estimator of cell counts will be seriously biased, as shown in the plots. On the other hand, these observations may not be outliers. If so, the RLS approach may not be able to detect them. We propose to apply the same methods after the probable errors associated with the undiluted or half-diluted samples are removed. It is possible that errors may also occur to highly diluted samples, but in that case, they can not exert much influence on parameter estimation.

Figure 2.

Numbers of total IgG antibody secreting (ABS) cells by serial dilution from 10 donors where non-linear patterned cell counts were observed.

For the example study, one of the interesting endpoints was the percent (%) H5VN-specific memory B cells per total IgG memory B cells, to take into account the non-specific stimulation of the culture used in the assays. To assess the effect of interesting factors, such as prior immunization, on the endpoint, the t-test or its non-parametric analogy of the Wilcoxon Rank Sum test can be used to detect group differences. But generally these tests require that observations within each group be independent and identically distributed (i.i.d.). We investigate the distributions of the study endpoints, and show that within-group endpoints have approximately the same distribution across subjects under some weak conditions. Thus these tests can be used with the reasonable assumption of independence among subjects.

The performance of these methods is evaluated numerically through simulations, and illustrated by data from the immune response to flu vaccination study. Recommendations are made for cell count determinations for future ELISPOT assays. The conclusions of this study may not be applicable to other assays, because they are solely based on quantitative ELISPOT assays. In addition, the focus of this study is not new methodology development or theoretical property deduction, but the application of existing methods to new fields.

In summary, we introduce the estimation methods for cell counts from ELISPOT assays in Section 2. We investigate the distribution of study endpoints in Section 3. We demonstrate the performance of the proposed methods by simulations and real data analysis in Section 4. Finally in Section 5 we give recommendations on estimation methods of cell counts for data from similar ELISPOT assays.

2 Estimation Methods for Cell Counts from ELISPOT Assays

The relationships between cell counts and their corresponding dilution factors can be characterized by the linear model

$$Y_k=X_k\beta +{\epsilon }_k,$$ (1)

where Y_k and X_k denote cell count and dilution factor at the kth dilution level, respectively, and the error term ε_k is from a pre-assumed distribution. We assume that k has a range of (1, K). The coefficient β corresponds to the cell count for an undiluted sample, which is the study interest. For subject i, the cell count will be estimated from model

$$Y_{ik}=X_{ik}{\beta }_i+{\epsilon }_{ik}.$$ (2)

The estimation of β_i is fully based on the distributional assumption about error terms ε_ik. A classical assumption is that ${\epsilon }_{ik}\stackrel{i.i.d}{\sim }N(0,{\sigma }^2)$. Under this assumption, the LS estimator β̂_LS is obtained as the solution to the minimization of sum of residual squares, with

$${\widehat{\beta }}_{i_{LS}}=\frac{{\sum }_{k=1}^K{X}_{ik}{Y}_{ik}}{{\sum }_{k=1}^K{X}_{ik}^2}.$$ (3)

In practice, there commonly exist outliers in responses or covariates. The independent variable of limiting dilution factor is fixed in advance, so we do not consider leverage points. For outliers in the dependent direction, the Huber-type M-estimation is a common robust approach. The robust linear square (RLS) estimator is obtained by minimizing:

$${\widehat{\beta }}_{i_{\mathit{RLS}}}=\underset{\beta }{min}\sum _{k=1}^K\rho (\frac{r_{ik}}{\sigma }),$$ (4)

where r_ik = Y_ik − X_ikβ̂_i, and ρ is a less rapidly increasing function of residuals, in contrast to the quadratic function for the ordinary least square estimation. The RLS estimator will be solved by the iteratively re-weighted least squares (IRLS) with updating form

$${\widehat{\beta }}_{1i}=\frac{{\sum }_{k=1}^K{X}_{ik}w\left(\frac{Y_{ik}-X_{ik}{\widehat{\beta }}_{0i}}{\sigma }\right)Y_{ik}}{{\sum }_{k=1}^K{X}_{ik}w\left(\frac{Y_{ik}-X_{ik}{\widehat{\beta }}_{0i}}{\sigma }\right)X_{ik}},$$ (5)

where w(·) is a weight function defined as $w(r)=\frac{{\rho }^{\prime }(r)}{r}$ with ρ′ being the derivative of ρ. As a special type of robust regression, the ordinary least squares approach assigns equal weight to each observation. The computational algorithm for the IRLS was given in Holland and Welsch (1977).

The bisquare weight function is defined as

$$w(r)=\{\begin{array}{cc}{(1-{(\frac{r}{c})}^2)}^2& \mid r\mid \le c\\ 0& \mid r\mid >c.\end{array}$$ (6)

This weight function has flexibility in choosing the tuning constant c, with smaller c providing more resistance to outliers, though at the expense of low efficiency for the normal case. Generally c is chosen in a way such that the related M-estimator achieves 95% asymptotic efficiency for normal observations. Given its robustness to unusual data, we apply the bisquare weight to estimate β_i.

The strong assumption of identical distribution of error terms may not always be appropriate. It is highly possible that measurement errors may depend on dilution factors, for example, $\mathit{Var}({\epsilon }_{ik})=X_{ik}^2{\sigma }^2$. Under this scenario, an easy calculation finds that

$$\frac{Y_{ik}}{X_{ik}}\stackrel{i.i.d}{\sim }N({\beta }_i,{\sigma }^2).$$ (7)

For a sample of K normally distributed observations $\frac{Y_{ik}}{X_{ik}}$, the LS estimator of β_i is the sample mean (which is also the UMVUE)

$${\widehat{\beta }}_{i_{ME}}=\frac{{\sum }_{k=1}^K\frac{Y_{ik}}{X_{ik}}}{K}.$$ (8)

We name β̂_iME as the ME estimator.

Chen and Tyler (2002) showed that Tukey’s median is highly robust in terms of both influence function and maximum contamination bias function. Tukey’s median is the sample median for a one-dimensional sample. Hence the sample median is used as the robust estimator when measurement errors depend on dilution factors:

$${\widehat{\beta }}_{i_{MD}}=\mathit{median}\{\frac{Y_{ik}}{X_{ik}},k=1,\dots ,K\}.$$ (9)

Hence β̂_iMD is called the MD estimator.

Furthermore, we applied Huber-type M-estimation to get another robust estimator under the scenario (7)

$${\widehat{\beta }}_{i_{\mathit{RPOI}}}=\underset{\beta }{min}\sum _{k=1}^K\rho (\frac{{\gamma }_{ik}}{\sigma }),$$ (10)

with ${\gamma }_{ik}=\frac{Y_{ik}}{X_{ik}}-{\widehat{\beta }}_i$. We call β̂_iRPOI as the RPOI estimator.

The third distributional assumption about cell measurements is $Y_{ik}\stackrel{i.i.d}{\sim }\mathit{Poisson}(X_{ik}{\beta }_i)$, to take account of the response as counts. Thus the cell count for subject i can be estimated by the maximum likelihood estimator as

$${\widehat{\beta }}_{i_{\mathit{POI}}}=\frac{{\sum }_{k=1}^K{Y}_{ik}}{{\sum }_{k=1}^K{X}_{ik}}.$$ (11)

This estimator is correspondingly called the POI estimator.

As mentioned previously, undiluted or half-diluted samples are often associated with background staining intensity problems, which lead to fewer spots counted by the scan system than in subsequently diluted samples. These observations are likely errors, and thus are not best dealt with by robust procedures. We modify our methods to take these probable errors into account. Specifically, for samples from each donor, we order the observations in descending dilution values, and remove the first and/or second observations if the first observation and/or the second observation is not greater than subsequent diluting observations. The proposed methods are applied after likely errors are removed.

In summary, we propose six methods (simplified as MD, ME, LS, RLS, RPOI and POI) using all data to estimate total cell counts and the same six methods excluding likely errors occurring in undiluted or half-diluted observations. Their performance are evaluated numerically through simulations and with an application to real data.

3 Distribution of Study Endpoint

The culture used in the limiting dilution assays is non-specific in that it stimulates all memory cells present at the time of the blood draw. For the immune response study, the total IgG is a measurement of the overall number of B cells that respond in the assay (defined as memory B cells) and the H5VN is a measure of the proportion that are specific to H5VN. By expressing the results as a ratio of the H5VN over the total IgG, we end up with a frequency of H5VN-specific/total ABS memory B cells, with this ratio expected to increase after immunization.

Investigation of the distribution of the endpoints is important. For example, in the pre-mentioned vaccine study, an interesting question is whether a history of seasonal flu vaccination affects the H5VN-specific response at day 7. The t-test or the Wilcoxon Rank Sum test may be used to detect the group differences (with or without history of seasonal flu vaccination), but both require observations from each group to be i.i.d. The endpoints are uniquely associated with subjects, and thus can be reasonably assumed to be independent of each other. Are they also identically distributed? The LS estimators are obtained under the assumption that cell counts are normally distributed, and thus have normal distribution. Under some regular conditions, the RLS estimator by M-estimation is asymptotically consistent and normally distributed (Huber, 1973). The population mean and the population median coincide with each other, and thus the robust estimators using medians are also normally distributed. Under the independent Poisson assumption, ${\sum }_{k=1}^K{Y}_{ik}~\mathit{Poisson}({\sum }_{k=1}^K{X}_{ik}{\beta }_i)$, and ${\sum }_{k=1}^K{X}_{ik}{\beta }_i$ is expected to be large. Thus $\mathit{Poisson}({\sum }_{k=1}^K{X}_{ik}{\beta }_i)$ can be well approximated by a normal distribution, and the MLEs by the Poisson approach also have an approximately normal distribution. Based on these arguments, next we will show that the β̂_LS in equation (3) are distributed approximately the same across subjects. Similarly we can show that estimates obtained by each of other approaches have approximately the same distribution across subjects.

For simplicity of explanation, all the letters and symbols with subscript of 1 are associated with the interested H5VN-specific cell, and those with subscript of 2 are associated with total IgG. To take account of between subject variations, we further assume that

$${\beta }_i=\beta +b_i,$$ (12)

where β_i = (β_1i, β_2i)′, β = (β₁, β₂)′, and the random effect b_i = (b_1i, b_2i)′ are independent variables from a normal distribution with mean zero and variance ${\sigma }_{b_1}^2,{\sigma }_{b_2}^2$ and a correlation coefficient of ρ. In addition, b_i are independent of ε_i.

The endpoint estimator for subject i is

$${\stackrel{\sim }{z}}_i=100\frac{{\widehat{\beta }}_{1i}}{{\widehat{\beta }}_{2i}}.$$ (13)

Under models (2) and (12), β̂_pi ~ N(β_p, V_pi) for p = 1, 2, with $V_{pi}=\frac{{\sigma }_{b_p}^2{\sum }_k{x}_{\mathit{pik}}^4+{\sigma }_p^2{\sum }_k{x}_{\mathit{pik}}^2}{{({\sum }_k{x}_{\mathit{pik}}^2)}^2}$, and $\mathit{cov}({\widehat{\beta }}_{1i},{\widehat{\beta }}_{2i})=\frac{{\sum }_k{\sum }_{k^{\prime }}{x}_{1ik}^2{x}_{2{ik}^{\prime }}^2}{{\sum }_k{x}_{1ik}^2{\sum }_{k^{\prime }}{x}_{1{ik}^{\prime }}^2}\rho {\sigma }_{b_1}{\sigma }_{b_2}$. For the data example, the between subject variations are much smaller than the related assay variations, which suggests that ${\sigma }_1^2\gg {\sigma }_{b_1}^2$ and ${\sigma }_2^2\gg {\sigma }_{b_2}^2$. Hence $V_1\approx {\sigma }_1^2/{\sum }_{k=1}^K{x}_{1ik}^2$ and $V_2\approx {\sigma }_2^2/{\sum }_{k^{\prime }}{x}_{2{ik}^{\prime }}^2$.

Hinkley (1969) showed that the ratio of two correlated random variables $z_1~N({\mu }_1,{\sigma }_{z_1}^2)$ and $z_2~N({\mu }_2,{\sigma }_{z_2}^2)$ with correlation coefficient ϱ has a complicated distribution, but its CDF (cumulative distribution function) can be approximated by a simpler form under some conditions. Specifically, as Pr(z₂ > 0) → 1,

$$F(z)\to \mathrm{\Phi }\left\{\frac{{\mu }_{2}z-{\mu }_1}{{\sigma }_{z_1}{\sigma }_{z_2}a(z)}\right\},$$ (14)

where F(·) is the CDF of the ratio z = z₁/z₂, Φ is the CDF of a standard normal variable, and $a(z)=\sqrt{\frac{z^2}{{\sigma }_{z_1}^2}-\frac{2\mathrm{\varrho }z}{{\sigma }_1{\sigma }_2}+\frac{1}{{\sigma }_{z_2}^2}}$. Therefore, if Pr(β̂_2i > 0) → 1, then the CDF of $z_i=\frac{{\widehat{\beta }}_{1i}}{{\widehat{\beta }}_{2i}}$ will go to

$$\mathrm{\Phi }\left(\frac{{\beta }_{2}z-{\beta }_1}{\sqrt{\sqrt{V_{2i}}{z}^2-2\mathit{cov}({\widehat{\beta }}_{1i},{\widehat{\beta }}_{2i})z+\sqrt{V_{1i}}}}\right).$$ (15)

In reality, Pr(β̂_2i > 0) = 1, with total IgG counts being very large (in the vaccine study, the total IgG counts are estimated over 2500 on average by all the approaches), which means the nonconstant part z_i has a distribution approximately the same as a random variable with CDF (15).

For z̃_i and z̃_j to have the same distribution, the following have to be true: V_1i = V_1j, V_2i = V_2j and cov(β̂_1i, β̂_2i) = cov(β̂_1j, β̂_2j). In other words,

$$\begin{array}{lll}\hfill \sum _k{x}_{1ik}^2& =\hfill & \sum _k{x}_{1jk}^2,\hfill \\ \hfill \sum _{k^{\prime }}{x}_{2{ik}^{\prime }}^2& =\hfill & \sum _{k^{\prime }}{x}_{2j{k}^{\prime }}^2,\hfill \\ \hfill \sum _k\sum _{k^{\prime }}{x}_{1ik}^2{x}_{2{ik}^{\prime }}^2& =\hfill & \sum _k\sum _{k^{\prime }}{x}_{1jk}^2{x}_{2j{k}^{\prime }}^2.\hfill \end{array}$$ (16)

In practice, the design matrix is the same for all subjects. When there are no missing values for either of the two subjects, z̃_i and z̃_j have the same distribution. When missing problems do occur to one subject or both, we show below that under some weak conditions, z̃_i still has approximately the same distribution as z̃_j.

Let x_1ik = x_1jk + c_1k and x_2ik′ = x_2jk′ + c_2k′. Here c_1k and c_2k′ are induced by missing values. Specifically, they will be zeroes when the values are not missing, and equal the missing values otherwise. Plugging them into the first two equations of (16) yields

$$\begin{array}{rrr}\hfill \sum _k{c}_{1k}(c_{1k}+2x_{1jk})& \hfill =& \hfill 0,\\ \hfill \sum _{k^{\prime }}{c}_{2k^{\prime }}(c_{2k^{\prime }}+2x_{2j{k}^{\prime }})& \hfill =& \hfill 0.\end{array}$$ (17)

When c_1k ≈ 0 and c_2k′ ≈ 0, equations in system (16) will be true. This suggests that when missing problems occur only to highly-diluted samples, the endpoint estimators for subject i and j will be distributed approximately the same. Hence those tests can be applied to detect group differences.

4 Numerical Study

4.1 Monte Carlo Simulations

We conducted Monte Carlo simulations to study the finite sample properties of the proposed methods. Data are simulated based on the study design of immune response to a single dose of H5VN vaccine (Goji et al., 2008). In assays, the limiting dilution factors for total IgG ABS cells are usually smaller than those for antigen-specific cells, due to their large counts. In the immune response study, the limiting dilution factors are 2^−(g−1) for total IgG after its primary dilution factor of 1/5 to 1/40, and 1/g for antigen-specific cells, with g = 1, …, 8. The same dilution factors as the real data problem are used to generate the simulation data set. In the mentioned study, the observations are counts, and the estimated variance is about a tenth of the estimated cell count. Then at each dilution factor x, cell count y is generated from 0.9βx + Poisson(0.1βx), where β denotes the mean IgG or H5VN-specific cell count. The performance of proposed methods may be different when cell counts vary. We select a wide range of counts for both total IgG and H5VN-specific cell based on the real data. For the real data, the estimated ranges for total IgG and H5VN-specific cell counts by the Poisson approach, which is revealed to perform best, are 200 to 12300 and 3 to 90, respectively. In our simulation study we let the mean counts of IgG change from 200 to 20100, with an increase of 100 each time, and the mean numbers of H5VN cell change from 10 to 408, with an increase of 2 each time. This means both mean IgG and H5VN cell have 200 values for each simulation run. The simulation size is 500.

We investigate the performance stability of the proposed methods by applying them to the simulated data without probable staining errors on the first two dilutions and the data with the problems. The generation of staining error observations are also based on the real data. In the aforementioned data set, about 40% of donors have probable staining errors associated with the first two dilution factors in total IgG, and about 60% of donors have the same problem with H5VN-specific cell counts. In our study we simulate this type of error for both IgG and H5VN-specific cell with an error rate set at 50%. For randomly selected subjects, their observations for IgG and/or H5VN-specific cell of undiluted or half-diluted samples are randomly selected to contain errors. The selected observations are multiplied by 0.01 for IgG and 0.1 for H5VN-specific cell counts, in consideration of the large counts of total IgG and small counts of H5VN-specific cell. The primary dilutions are applied to the simulated IgG counts as done in real practice. Before the application of the proposed methods, the simulated IgG counts are shrunk to 1/5 to 1/40 depending on the sizes, with counts shrunk to 1/5 if less than or equal to 5100, to 1/10 if less than or equal to 10100, to 1/20 if less than or equal to 15100, and to 1/40 otherwise.

For each proposed method h (h = 1, …, 6), its performance is assessed by two criteria: 1. average relative error (ARE), calculated as

$$\mathit{ARE}=\frac{1}{500}\sum _{b=1}^{500}\mid \frac{{\widehat{\beta }}_{h_b}-\beta }{\beta }\mid$$ (18)

for a cell count of β; 2. proportion of yielding estimates with smallest absolute error (PSAE) among 500 runs at each mean level, calculated as

$$\mathit{PSAE}=\frac{{\sum }_{b=1}^{500}I(\mid {\widehat{\beta }}_{h_b}-\beta \mid \le \mid {\widehat{\beta }}_{j_b}-\beta \mid )}{500}$$ (19)

for a cell count of β and j = 1, …, 6 but j ≠ h, where I is an indicator function. The ARE gives the absolute estimation error per unit, which takes into account cell difference across the selected ranges.

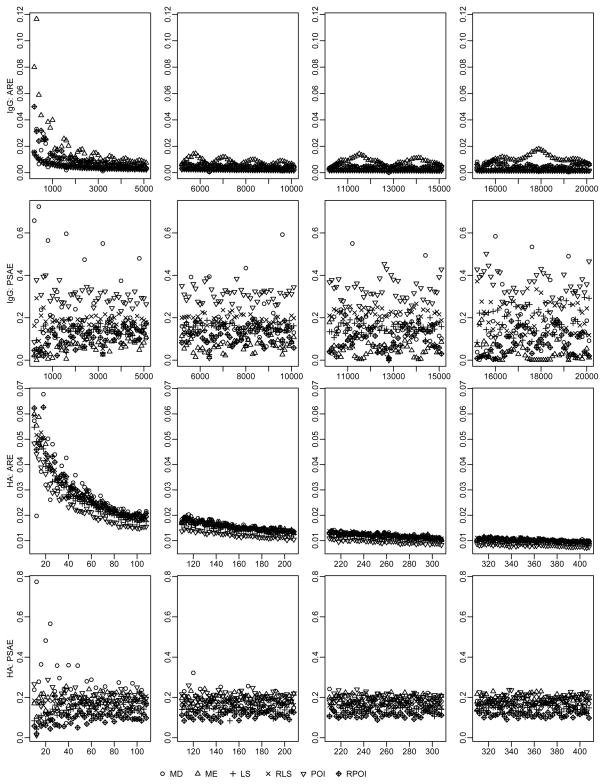
For the scenario of no staining errors on the first two dilution levels, Figure (3) demonstrates the AREs and the PSAEs of the proposed methods in estimating both IgG andb H5VN-specific cell with their mean cell counts varying over wide ranges. The POI estimators consistently have the smallest AREs and the largest PSAEs, although seldom the MD estimators produce larger PSAEs. Overall, the POI approach yields the best cell count estimators when no unusual observations exist on the first two dilution levels.

Figure 3.

ARE and PSAE under scenario of no staining errors associated with undiluted or half-diluted samples for total IgG (on top two rows, with mean cell counts varying from 200 to 12300) and H5VN-specific (on bottom two rows, with mean cell counts varying from 10 to 408) ABS cells. ARE, average relative error; PSAE, proportion of yielding estimates with smallest absolute error among 500 runs; MD, median approach; ME, mean approach; LS, least squares; RLS, robust least squares; POI, poisson approach; RPOI, robust least squares when measurement errors depend on dilution levels.

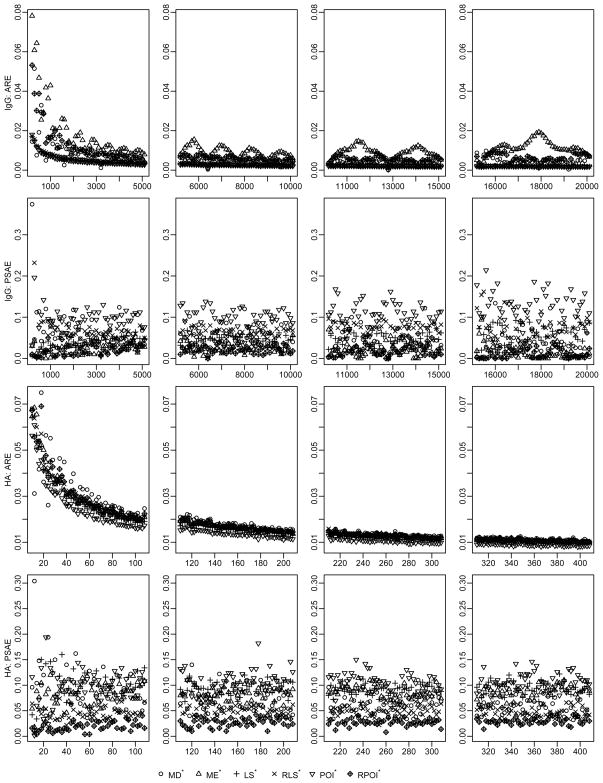
Under the scenario of having unusual observations on the first two dilution levels, we use two algorithms to estimate cell counts: 1. directly applying the proposed methods; 2. firstly removing the unusual observations on the top two dilution levels and then applying the proposed methods. Hereafter the methods with ^* sign indicate the second algorithm. Table (1) presents the performance ranking of the proposed methods in terms of both ARE and the PSAE under this scenario, with smaller numbers denoting better performance. The smaller rankings in both ARE and PSAE for the estimators with order errors removed indicate that the proposed methods work better after the probable errors are deleted. Irrespective of sizes of cell counts, the POI with probable staining errors removed has the smallest ranking in both ARE and PSAE and thus yields the best cell count estimators. The optimal performance of the POI is also shown in Figure (4). Overall, the Poisson approach has uniformly the best performance regardless of the cell counts. Thus we recommend the Poisson approach for cell count determination in real data analysis.

Table 1.

Orderings of proposed methods in terms of both ARE and PSAE. ARE, average relative error; PSAE, proportion of yielding estimates with smallest absolute error among 500 runs; MD, median approach; ME, mean approach; LS, least squares; RLS, robust least squares; POI, poisson approach. RPOI, robust least squares when measurement errors depend on dilution levels;

		MD	ME	LS	RLS	POI	RPOI	MD*	ME*	LS*	RLS*	POI*	RPOI*
Total IgG	ARE	5	9	11	12	10	7	4	8	2	3	1	6
	PSAE	5	11	12	9	10	8	3	6	4	2	1	7
H5VN-specific	ARE	8	9	12	10	11	5	7	3	2	4	1	6
	PSAE	6	10	8	12	5	11	4	3	2	7	1	9

^*Method applied after probable staining errors on first two dilutions removed

Figure 4.

ARE and PSAE under scenario of having staining errors associated with undiluted or half-diluted samples for total IgG (on top two rows, with mean cell counts varying from 200 to 12300) and H5VN-specific (on bottom two rows, with mean cell counts varying from 10 to 408) ABS cells. ARE, average relative error; PSAE, proportion of yielding estimates with smallest absolute error among 500 runs; MD, median approach; ME, mean approach; LS, least squares; RLS, robust least squares; POI, poisson approach; RPOI, robust least squares when measurement errors depend on dilution levels.

^*Methods applied after probable staining errors on first two dilutions removed.

4.2 Real Data Application

We demonstrate the proposed methods by applying them to the study of memory B cell responses to vaccination (Goji et al., 2008). For illustration purposes, only following two donors’ results at baseline are presented: ID = 43, whose B cell observations didn’t have probable staining errors, and ID = 85, whose observations were associated with the problem.

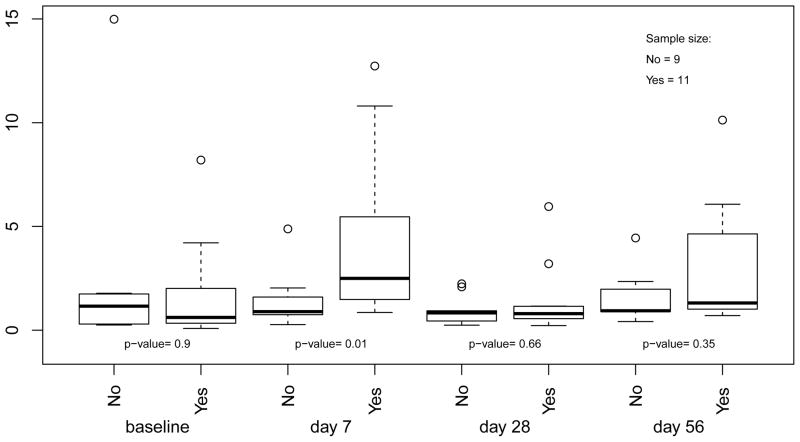
If no probable errors were observed in total IgG or H5VN-specific cell counts, the estimators with ^* would be same as those corresponding estimators without the sign. Table (2) indicates that, probable errors were observed not in the first donor’s observations, but in the second donor’s observations, because for ID = 43 the six estimators with ^* are same to their corresponding estimators without the sign, but for ID = 85 this is not true. Since the Poisson approach is the recommended method for cell count determination, we would expect the cell counts of total IgG and H5VN-specific ABS cells at baseline were, respectively, 1348 and 8 for the first donor, and 1021 and 12 for the second donor. The study endpoint of interest is % H5VN ABS cells per total IgG ABS cells. In consideration of the non-normality of the endpoints, the Wilcoxon Rank Sum test is applied to test whether prior seasonal vaccination has a significant effect on the immune response characterized by H5VN-specific cell counts. Figure (5) shows that at baseline, there was no difference in % H5VN memory B cell per total memory B cell between the group with history of seasonal flu vaccination and the group without it. However, at day 7, the subjects with a history of seasonal flu vaccination had significantly (p-value= 0.01) larger proportion of H5VN-specific cells than those without reported history, although the difference between groups vanished over time. The same trend was observed in group difference in the change of % H5VN memory B cell from the baseline.

Table 2.

Cell count and endpoint estimates for donors with ID = 43 and ID = 85 at baseline. MD, median approach; ME, mean approach; LS, least squares; RLS, robust least squares; POI, poisson approach; RPOI, robust least squares when measurement errors depend on dilution levels;

		MD	ME	LS	RLS	POI	RPOI	MD*	ME*	LS*	RLS*	POI*	RPOI*
ID=43	Total IgG	1920	1784	1144	1356	1348	1717	1920	1784	1144	1356	1348	1717
	H5VN-specific	7	7	8	8	8	7	7	7	8	8	8	7
	Endpoint	0.36	0.39	0.69	0.58	0.56	0.41	0.36	0.39	0.69	0.58	0.56	0.41
ID=85	Total IgG	1520	1458	501	504	747	1441	1760	1650	689	673	1021	1626
	H5VN-specific	12	10	6	6	8	10	12	12	12	12	12	12
	Endpoint	0.79	0.70	1.29	1.28	1.11	0.72	0.68	0.71	1.70	1.76	1.15	0.73

^*Method applied after probable staining errors on first two dilutions removed

Figure 5.

Effect of history of seasonal flu vaccine on % H5VN/total IgG ABS cells over time. No, no history of seasonal flu vaccination; Yes, with history of seasonal flu vaccination.

5 Discussion

The ELISPOT assays have been an invaluable tool for detecting the number of ABS lymphocytes, which can be present in very low frequencies in general populations. Automated ways are needed to estimate cell counts in samples from the limiting diluted assays. The individual least squares/maximum likelihood and/or the individual robust least squares are applied to automatically estimate cell counts under three distributional assumptions. Under some weak conditions, we show that the derived endpoints within each group are distributed approximately the same across subjects, which provides a basis for statistical hypothesis testing in the derived endpoints by standard approaches. Monte Carlo studies show that the Poisson approach has optimal performance regardless of probable staining errors associated with the less diluted samples. In practice, we recommend using the Poisson approach to estimate cell counts from ELISPOT assays after removal of probable staining errors.

The impact of serial dilution on the covariance structure has been investigated for other types of limiting dilution assay data, such as Elisa data. But there is much difference between ELISPOT data and Elisa data. Study the similar problem in ELISPOT data could be a future research direction.