Abstract
Rating scales are a standard measurement tool in psychological research. However, research suggests that the cognitive burden involved in maintaining the criteria used to parcel subjective evidence into ratings introduces decision noise and affects estimates of performance in the underlying task. There has been debate over whether such decision noise is evident in recognition, with some authors arguing that it is substantial and others arguing that it is trivial or nonexistent. Here we directly assess the presence of decision noise by evaluating whether the length of a rating scale on which recognition judgments are provided is inversely related to performance on the recognition task. That prediction was confirmed: rating scales with more options led to lower estimates of recognition than scales with fewer options. This result supports the claim that decision noise contributes to recognition judgments and additionally suggests that caution is warranted when using rating scales more generally.
Rating scales are among the most widely used measurement tools in psychology. They provide the basis for a majority of absolute and relative judgment tasks in perception and cognition, often provide the fundamental data for exercises in scaling, and, most importantly for present purposes, provide a means of estimating multiple points on a single detection or discrimination function. That function is often called an isosensitivity function, or receiver-operating characteristic, and the points along it represent equivalent discrimination but different underlying decision criteria. Isosensitivity functions play a prominent role in theoretical development, particularly in research on recognition memory, so it is important to examine closely the assumptions that underlie the translation between the shape and location of the isosensitivity function and the nature of the evidence that yields that function.
Here we consider the contrasting implications of the standard view of the decision process being static and nonvariable, as in classical Theory of Signal Detection (TSD; Green & Swets, 1966; Macmillan & Creelman, 2005) and a view with a noisy decision process (Benjamin, Diaz, & Wee, 2009; Malmberg & Xu, 2006; Mueller & Weidemann, 2008). In particular, we test the prediction of the Noisy Decision Theory of Signal Detection (ND-TSD; Benjamin et al., 2009) that the location of the isosensitivity function should vary with the length of the rating scale used to assess it. The claim that recognition involves a noisy decision process has been controversial (Kellen, Klauer, & Singmann, 2012), so a direct evaluation of the predictions of ND-TSD is important. First, we briefly review the rating-scale methodology in recognition research and the way in which isosensitivity functions are generated from those data.
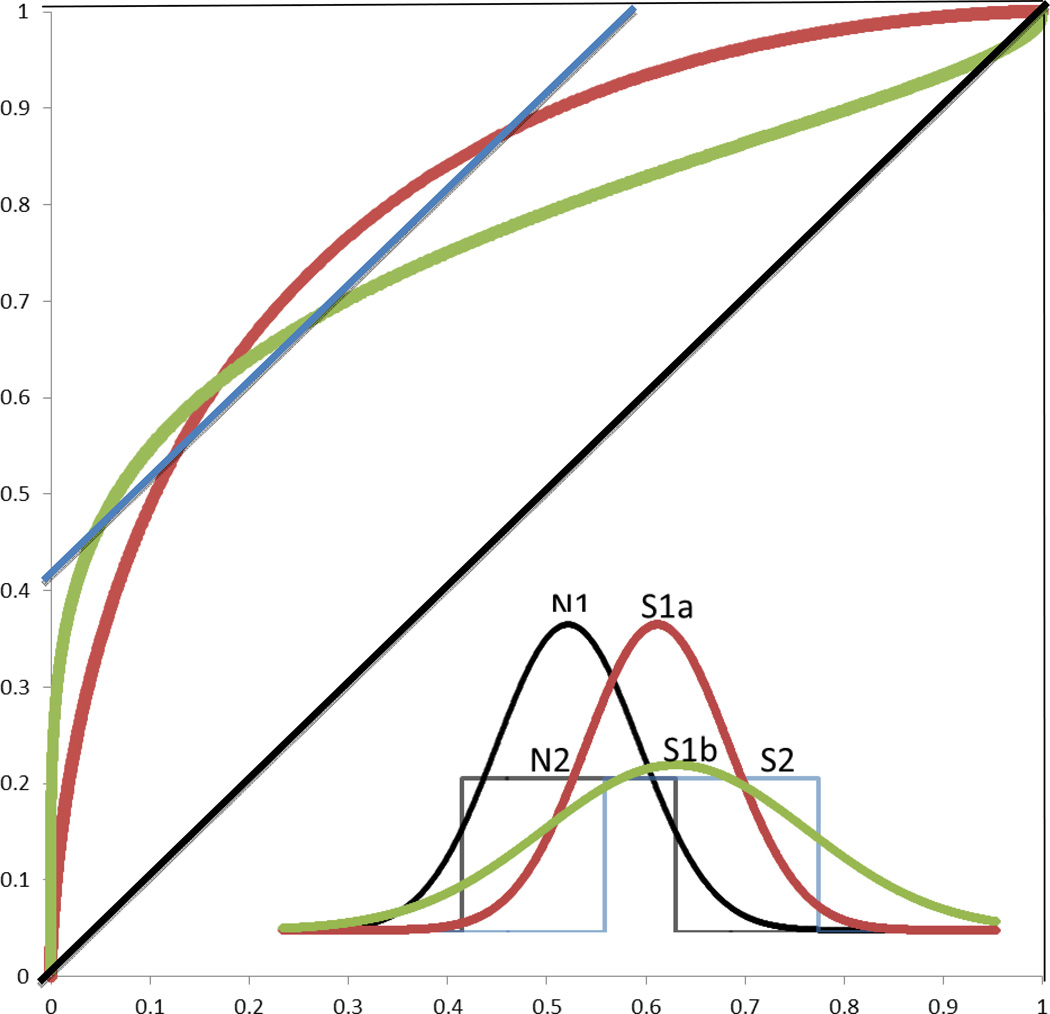
The isosensitivity function is a theoretical function relating true and false positives across the range of all potential decision criteria. It is useful because the shape and location of that function can be related to the shapes and locations of probabilistic evidence distributions that are thought to underlie the decision. Examples are provided in Figure 1, in which different isosensitivity functions are shown, along with the probabilistic distributions of noise and signal that generated them. Rectangular distributions with thresholds yield functions that are linear and intersect the axes away from one or both of the corners. Gaussian distributions yield curvilinear functions, with the degree of asymmetry indexing differences in variability between the distributions.
Figure 1.
Theoretical isosensitivity functions and their generating distributions. Gaussian signal and noise distributions of equal variance (N1 and S1a) yield bowed and symmetric isosensitivity functions (red curve). Gaussian signal and noise distributions of unequal variance (N1 and S1b) yield bowed and asymmetric functions (green curve). Rectangular threshold functions (N2 and S2) yield straight functions (blue line).
The isosensitivity function is estimated by collecting multiple points along the function in one of two ways. In one procedure, bias is manipulated by having subjects respond under different payoff procedures; these payoffs induce more conservative or liberal responding by virtue of the cost/benefit tradeoff of different types of errors. In the second procedure, more common in recognition research, confidence ratings are taken during the response task, and these ratings are treated as criteria partitioning the evidence space. Some have argued that the inclusion of ratings so perverts the shape of the isosensitivity function that the broad consensus that evidence is graded rather than thresholded is wrong (Bröder & Schütz, 2009). However, there is compelling evidence that isosensitivity functions are in fact curvilinear even when estimated from manipulations of bias (Dube & Rotello, 2012; Koen & Yonelinas, 2011), indicating that the assumption of graded evidence is indeed correct. However, the exact shape of isosensitivity functions estimated from ratings does differ across conditions of differential bias (Van Zandt, 2000), so there is reason for concern that the underlying information available to the recognizer might not be equivalent in the two cases.
Malmberg and Xu (2006; Malmberg, 2002) noted that variations and suboptimalities in the decision process corrode the relationship between the isosensitivity function and the underlying evidence, and suggested that the theoretical agenda of trying to discern the nature of the evidence in recognition from the isosensitivity function may be fundamentally flawed, particularly when that function is estimated from confidence ratings.Benjamin et al. (2009) echoed this sentiment and further provided estimates of decision noise within recognition that were sufficiently large to merit concern. In their study, decision noise was estimated to be of approximately the same magnitude as stimulus noise—that is, decision noise contributed as much to the recognition decision as did the differences across stimuli within the experiment.
Kellen et al. (2012) provided new data, using a direct comparison between forced-choice and yes-no recognition, and came to the opposite conclusion: that decision noise played no meaningful role in recognition judgments. The goal of the present experiment is to examine in as directly a manner as possible the claim that the criteria that recognizers set have some variability, or noisiness, associated with them. We do so by evaluating whether rating scales with more options, and consequently more criteria to discriminate between those options, yield “poorer” recognition performance than scales with fewer options. If this prediction is confirmed, it suggests that the higher number of criteria engender a greater amount of decision noise that plays out in estimates of “poorer” performance. “Poorer” is placed in scare quotes here because the core process of recognition is not presumed to be impaired by the use of rating scales, only the translation of that evidence into judgments via a noisy decision process.
Wickelgren (1968) suggested that noisy criteria could lead the point corresponding to yes-no discrimination to lay above the isosensitivity function estimated from multiple points, indicating “poorer” performance in the multiple-rating than the two-rating case. The small amount of research on this topic is mixed and almost entirely from research in perception, with some results confirming this claim (Swets et al., 1961, Figure 14) and others that do not (Baranski & Petrusic, 2001; Egan et al., 1959). Complicating the issue further is the fact that, even when comparisons do not yield evidence for differences in discriminability, they may lead to different response times (Petrusic & Baranski, 2003). The closest result in the literature comes from a report by Koen and Yonelinas (2011), in which they directly compared isosensitivity functions estimated confidence ratings with ones estimated from yes/no responses with a payoff manipulation between conditions. They found similar functions across those two conditions but several aspects of their procedure are not ideal for our purposes. First, the payoff manipulation may invite a novel memory demand that depresses performance in that yes/no condition relative to a case in which payoffs are unvaried. Second, their study had relatively low power due to the between-subjects nature of the manipulation and the relatively small sample size (n = 20 and 22 in the two relevant conditions). Here we provide a means of evaluating the effects of rating-scale length powerfully and incisively, without additional manipulations of payoff. We measure recognition performance for previously studied words under conditions in which subjects make yes/no judgments (a 2-point rating scale), 4-point confidence rating scale judgments, and 8-point confidence rating scale judgments.
Method
Participants
Sixty undergraduate students from the University of Illinois participated in this experiment as a part of a course requirement.
Materials
Six hundred words were chosen from the English Lexicon Project (Balota et al., 2002). To ensure a wide range of pre-experimental familiarities, half of the words were chosen to be of relatively high frequency (mean log HAL frequency 11.66), and half were chosen to be of relatively low frequency (mean log HAL frequency 8.84). The words ranged in length between 4 and 8 letters (mean-high = 5.44, mean-low = 5.59). A total of six sets of sixty words were chosen pseudo-randomly from the pool without replacement for each participant with the condition that half of each set of words was high frequency and the other half low frequency. Three of the six subsets were designated to be study lists, and the remaining lists served as distractors for the tests.
Design and procedure
Participants experienced three study-test cycles, each of which implemented a different rating scale condition—either 2-alternative (yes/no), 4-alternative, or 8-alternative. The order of the conditions was counterbalanced, and participants were informed of the nature of the rating scale immediately prior to the relevant test.
Participants were individually placed in a well-lit room, seated approximately 40cm away from a computer monitor. Presentation of stimuli and recording of responses was controlled by Matlab with the Psychophysics Toolbox (Brainerd, 1997; Pelli, 1997). Before the first study phase, participants were told that they would study a list of words for a later memory test. During the study phase, each word was presented for 3000 msec in white in the center of the black screen, with a 300 msec ISI. After each study phase, participants were given another set of instructions telling them that they would now be tested on the words they had just studied. Participants were told to choose a boxed number that corresponded to their response decision regarding their memory of a given word.
During the test, participants were presented with either a previously studied or a previously unstudied word, and asked to pick a response to the question: “Do you remember studying this word?” The response options, which were presented as boxed numbers, were presented right below the word being tested and remained on the screen until a response was made. Only the cues “sure no” (on the far left) and “sure yes” (on the far right) were presented below the boxed numbers, to ensure that the order of the rating scale was clear. Test stimuli remained on the screen until a response was provided.
The presentation of words in both study and test blocks was designed so that no more than four words from the same frequency category were presented in a row. Also, the presentation of studied and non-studied words in each test block was pseudo-randomly ordered so that no more than four studied or non-studied words were presented in a row.
Results
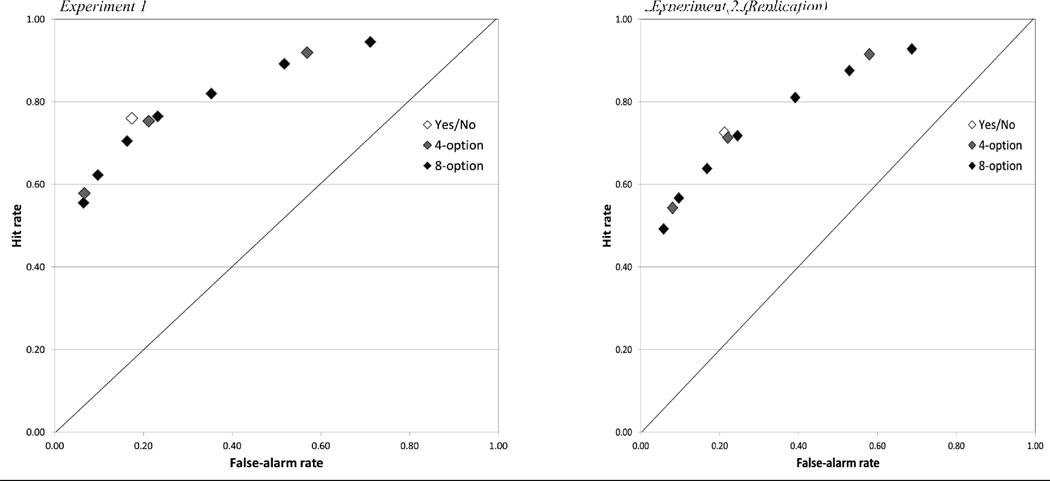
The data are shown in the left panel of Figure 2. The data points show the average hit rates and false-alarm rates averaged across subjects for the three conditions.1 It can be seen that the performance level for yes/no discrimination is higher (that is, lies further in the upper left quadrant of the space) than the points from the 4-point judgments, and that performance for the 4-point judgments is higher than for the 8-point judgments. However, direct comparison is difficult. Performance in the conditions with more than two options on the rating scales is traditionally summarized with a measure of performance that takes into account the (potential) differential variability between the signal and noise evidences (such as da), but that measure cannot be computed for performance in the two-option condition. To ensure that all conditions could be compared against one another on equal footing, we developed a novel technique for comparison.
Figure 2.
Mean performance as a function of rating scale length for Experiment 1 (left) and Experiment 2 (right). Endorsement rates are averaged over subjects.
The logic of this test is as follows. For each subject, we compare the obtained hit rate for a given condition (and for a given rating value, when appropriate) to the predicted hit rate estimated from the isosensitivity function for a condition with a higher number of ratings. Equivalently, we take a given point (say, the yes/no point), draw a vertical line to the isosensitivity function with a higher number of ratings (say the 4-rating condition), and compare the y-values of those two points. If the predicted hit rates are reliably lower than the obtained hit rates—that is, if the isosensitivity function from the condition with the higher number of ratings lies consistently below the obtained score—then those conditions differ in discriminability in the predicted direction. Because the conditions with higher ratings are hypothesized to involve more decision noise, those conditions should yield lower performance and thus underestimate performance in conditions with fewer rating options.
This technique has the quality that it conditionalizes on an exact false-alarm rate for each comparison. This is an advantage because the conditions may induce different response biases, rendering direct comparison between the empirically obtained hit/false-alarm rate pairs across conditions difficult.
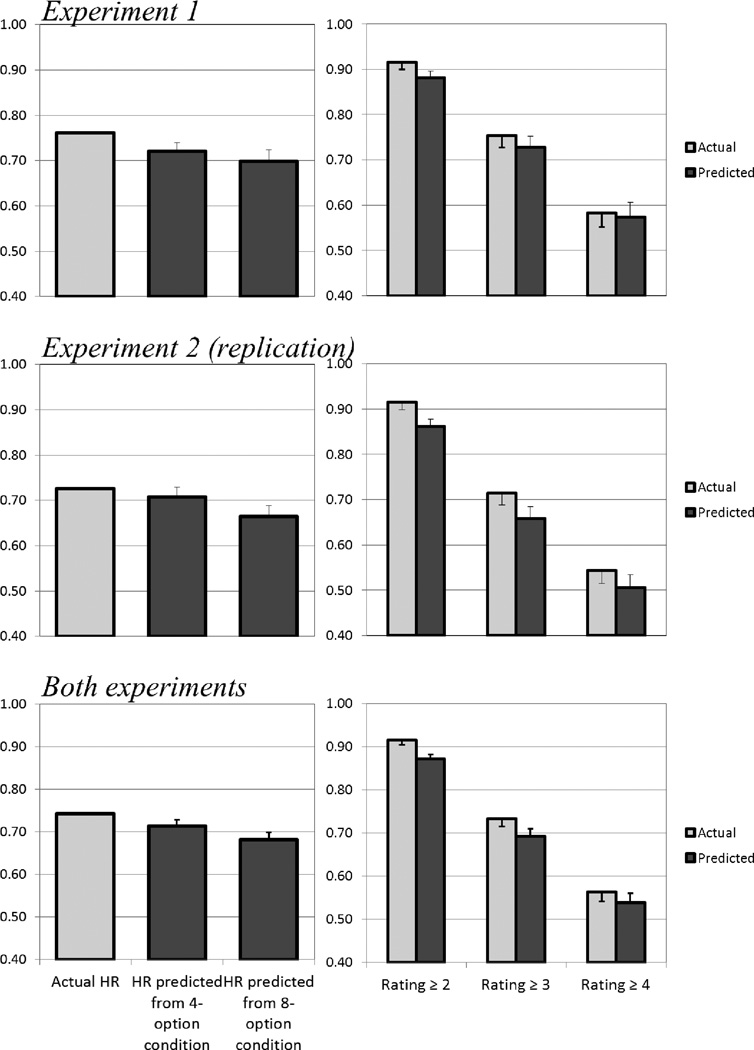
The results from this analysis are shown in Figure 4. For the yes/no condition, theoretical hit rates estimated from the isosensitivity functions of the 4-option (t[59] = 2.17) and the 8-option (t[59] = 2.37) conditions underestimated performance. The average effect size d for these two comparisons was 0.30, indicating a small-to-medium effect (Cohen, 1988). For the 4-option condition, estimates from the 8-option condition underestimated the most liberal cumulative ratings category (t[59] = 2.24), but not the other two (ts[59] = 1.04, 0.28). The effect size d for these three tests was 0.16, indicating a small effect.
Figure 4.
Actual and predicted hit rates for yes/no (left panels) and 4-option (right panels) rating scales. Error bars represent one standard error of the mean of the within-subject difference score.
One potential concern here lies in the self-paced nature of the test: as noted in our earlier review, longer rating scales might elicit longer response times (Petrusic & Baranski, 2003). This did occur in this experiment (MRT = 1.29s, 1.60s, and 1.80s, for the 2-, 4- and 8-rating conditions, respectively). There are several effects this confound could have on our results. First, longer scales might foster the use of more conservative points on the speed-accuracy tradeoff function. Second, longer scales might introduce a sufficiently large delay to induce a functionally greater retention interval. The first possibility can be ruled out because it makes a prediction opposite to what actually occurred in the experiment: longer ratings scales led to lower, not higher, accuracy. To evaluate whether retention interval played a role in the effect reported here, we directly compared da across the 4- and 8-rating conditions for the first and second halves of the test. If each individual test trial introduces a longer delay in the longer than the shorter rating scale conditions, then the advantage for shorter rating scales should be greater in the second half of the test, when a greater difference owing to this differential “slack” has accumulated. However, the effect of rating scale was actually numerically greater in the first half (Δda = 0.34) than the second half (Δda = 0.27) of the test, thus allaying any concern that differences in retention interval played a role in the effect described above.
Results of Replication (Experiment 2)
In order to ensure the validity of the claim that shorter rating scales induce poorer performance, we conducted an exact replication of the experiment. Only one replication was conducted (i.e., we did not conduct multiple tests and select the one with the most promising results), and the only difference between the two experiments is that 64 subjects were included in the replication.
The right panel in Figure 2 and the middle panels in Figure 4 display the results from the replication experiment. In the replication, theoretical hit rates estimated from the isosensitivity functions of the 4-option (t[63] = 0.86) and the 8-option (t[63] = 2.54) conditions underestimated performance, but only the latter was significant. The average effect size d for these two comparisons was 0.22, indicating a small effect (Cohen, 1988). For the 4-option condition, estimates from the 8-option condition underestimated the most liberal cumulative ratings category (t[63] = 3.33) and the middle category (t[63] = 2.16), but not the most conservative category (t[63] = 1.33). The effect size d across the three tests was 0.29, indicating a small-to-medium effect.
Combined analysis
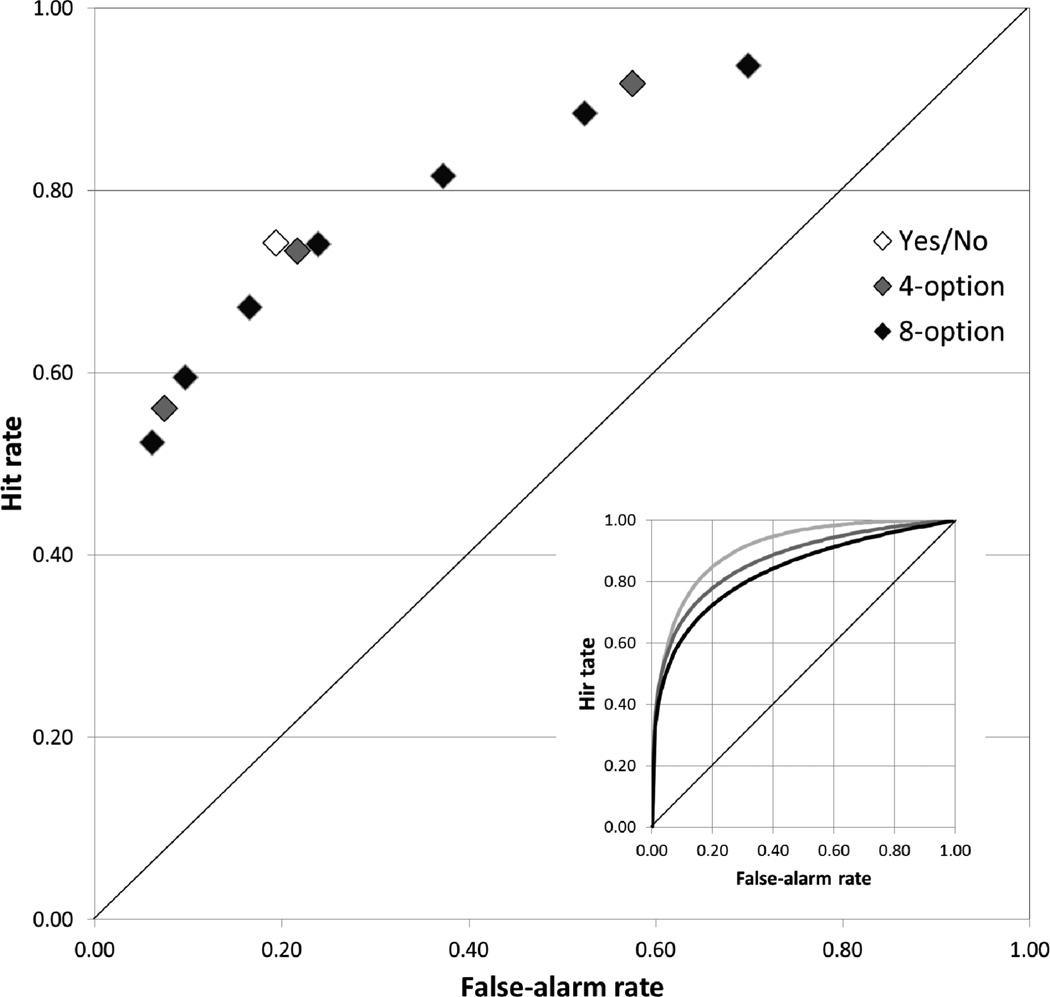
The data from both experiments were combined in order to increase power for each of the component comparisons. The results are shown in Figure 3 and in the bottom panel of Figure 4. In that analysis, obtained hit rates for the yes/no condition were higher than theoretical hit rates estimated from either the 4-option (t[123] = 2.02) or the 8-option (t[123] = 3.49) condition. In addition, obtained hit rates were higher in the 4-option condition than those predicted by the 8-option condition for all cumulative rating categories (ts[123] = 3.98, 2.29) except for the most conservative one (t[123] = 1.13). The effect sizes (d) for each of these comparisons were: 0.18, 0.31, 0.29, 0.14, and 0.04, respectively. These results indicate that the comparison across more distant conditions (two scale options versus eight) yielded larger effects, and also that effects are more pronounced in the more liberal response portion of the scale (the higher side of the isosensitivity function). As a final check on the effect of interest, da ratings were directly compared between the 4-option (M = 1.54) and the 8-option (M = 1.33) condition, and they were significantly higher in the 4-rating condition (t[123] = 3.43).
Figure 3.
Mean performance as a function of rating scale length, collapsed across both experiments. Larger figure shows endorsement rates averaged over subjects; inset shows the functions from the average parameters estimated from the model fit to individual subjects. Median parameter values were used because the model occasionally failed to converge on reasonable solutions for the 8-option condition.
The inset of Figure 3 shows the isosensitivity functions based on the median parameters generated from a maximum-likelihood fit of the unequal-variance signal-detection (UVSD) model to the 4- and 8-rating condition and generated from a fit of the equal-variance signal-detection (EVSD) model to the yes/no condition. The yes/no curve is symmetric because the EVSD model cannot support the estimation of differential variance between signal and noise. These group isosensitivity functions are shown only for ease of visualization, not for analysis, but it can also be seen in those functions that scales with a higher number of options led to poorer performance.
Discussion
The fact that rating scales with more options lead to lower estimates of recognition performance has major implications for theoretical views of the decision process underlying recognition and for the practical value of using rating scales in psychological experiments. Here we must conclude either that the nature of the rating scale somehow affects memory for the material being tested—an unlikely option—or, as suggested by Benjamin et al. (2009), that each point on the rating scale introduces some amount of variability to the decision process and undermines recognition performance.
The idea that maintaining criteria poses a burden to memory—and thus that maintaining more criteria poses a greater burden—is consistent with a large range of evidence in memory and psychophysics, including response autocorrelations (Treisman & Williams, 1984), inconsistencies in the relationship between forced-choice and yes/no recognition procedures (Green & Moses, 1966), variability in the slope of the function across learning conditions (Glanzer, Kim, Hilford, & Adams, 1999), differences between confidence-rating and bias-induction recognition procedures (Van Zandt, 2000), probability matching (Lee, 1963), response conservatism in response to manipulations of base rates (Healy & Kubovy, 1978), effects of aging (Kapucu, Rotello, Ready, & Seidl, 2008), and variation in the slope of the zROC for “remembered” items (Wixted & Stretch, 2004). In addition, criterion variability has been revealed in perceptual tasks (Bonnel & Miller, 1994; Nosofsky, 1983) and is incorporated into sampling models of recognition (Ratcliff & Rouder, 1998). Though the traditional application of TSD to perceptual and mnemonic tasks leaves no room for such decision noise, models incorporating a role for decision noise are available (e.g., Benjamin et al., 2009; Nosofsky, 1983; Wickelgren, 1968) that are entirely consistent with the spirit of detection theory.
If criteria do place a burden on memory, what is the nature of that burden? ND-TSD treats criteria as random samples from normal distributions but is agnostic with respect to the nature of the source of variance. There is good evidence that criteria are not maintained as singular entities but rather tied to the range of evidence that the recognizer experiences (e.g., Benjamin, 2003, 2005; Hirshman, 1995; Stretch & Wixted, 1998; Tullis & Benjamin, 2012; Turner, Van Zandt, & Brown, 2012). Mapping evidence onto responses thus requires a plan in which quantiles are determined from the number of response options available and are updated as the range of evidence changes. This updating is one source of noise, and the shifting of criteria induced by changes in range may also introduce memory failures in which, for example, a recognizer mistakenly fails to use an updated criterion value. Such a process would also be consistent with the presence of response dependencies (Malmberg & Annis, 2012; Treisman & Williams, 1984). In our original experiment, sequential dependencies were apparent and reliable (mean response autocorrelation = 0.06; SEM = 0.015) but did not differ across the ratings conditions. It would thus be difficult to attribute our condition effect exclusively to any source of noise that would lead to different levels of sequential dependencies.
The fact that decision noise can influence the shape and location of the isosensitivity function does suggest limits on the use of those functions in theoretical development. In recognition memory research, major theoretical debates over the number and nature of the processes that contribute to recognition have played out on a battlefield of isosensitivity functions (e.g., Wixted, 2007; Yonelinas, 1999), in which relatively subtle variations in form are taken to have substantial theoretical relevance. The presence of decision noise, and the unknown individual differences it brings with it, suggests that an overreliance on such methodological tools may be dangerous.
We do not wish to suggest that the general use of rating scales in psychology is fundamentally flawed. In many cases, the addition of an unknown amount of decision noise does not meaningfully affect the types of conclusions researchers wish to draw from their data. The problems introduced by decision noise can perhaps be characterized best as a bias in estimation rather than comparison. Measures of performance that include decision noise are likely inaccurate estimators of the underlying perceptual or mnemonic skill. But comparisons between similar conditions that are affected to the same degree by decision noise should not be dramatically hampered by the presence of that noise. More accurately, such comparisons are affected by criterion noise in the same way that they are affected by the many other unavoidable forms of uncontrolled noise in such experiments.
We end by noting that the decision noise debate echoes an earlier debate over the use of rating scales in individual-difference research (e.g., Garner, 1960). There it has been known for a long time that rating scales with many options provide little benefit for measurement when compared to scales with fewer options (Symonds, 1924). Some authors have even shown a loss in reliability with a higher number of scale options (Bendig, 1953), and others have argued that any increases in reliability that might come from increasing the scale length do not benefit the validity of the instrument (Cronbach, 1950).
As in that field, it is worth remembering that the best scale is the one that optimizes the tradeoff between the coarseness of the measurement and the limited discriminating precision of the rater. Discriminating among levels of subjective confidence or evidence in service of a recognition decision is certainly no less fraught with uncertainty over the boundary between response categories than discriminating among options in response to a personality or educational instrument. The seminal paper by Miller (1956) is often remembered for its review of limitations on short-term memory, but was in fact more substantively concerned with limits on absolute identification—a limitation that would be profitable to remember when designing response instruments. We ignore decision noise at our own peril.
Footnotes
Publisher's Disclaimer: The following manuscript is the final accepted manuscript. It has not been subjected to the final copyediting, fact-checking, and proofreading required for formal publication. It is not the definitive, publisher-authenticated version. The American Psychological Association and its Council of Editors disclaim any responsibility or liabilities for errors or omissions of this manuscript version, any version derived from this manuscript by NIH, or other third parties. The published version is available at www.apa.org/pubs/journals/xlm
Scores were adjusted by adding 0.5 to the count of hits and false alarms, and adding one to the total number of relevant items.
Contributor Information
Aaron S. Benjamin, University of Illinois at Urbana-Champaign
Jonathan G. Tullis, University of Illinois at Urbana-Champaign
Ji Hae Lee, Washington University in St. Louis.
References
- Balota DA, Cortese MJ, Hutchison KA, Neely JH, Nelson D, Simpson GB, Treiman R. The English Lexicon Project: A web-based repository of descriptive and behavioral measures for 40,481 English words and nonwords. Washington University; 2002. from http://elexicon.wustl.edu/ [Google Scholar]
- Baranski JV, Petrusic WM. Testing architectures of the decision-confidence relation. Canadian Journal of Experimental Psychology. 2001;55:195–206. doi: 10.1037/h0087366. [DOI] [PubMed] [Google Scholar]
- Bendig AW. The reliability of self-ratings as a function of the amount of verbal anchoring and the number of categories on the scale. Journal of Applied Psychology. 1953;37:38–41. [Google Scholar]
- Benjamin AS. Predicting and postdicting the effects of word frequency on memory. Memory & Cognition. 2003;31:297–305. doi: 10.3758/bf03194388. [DOI] [PubMed] [Google Scholar]
- Benjamin AS. Recognition memory and introspective remember/know judgments: Evidence for the influence of distractor plausibility on "remembering" and a caution about purportedly nonparametric measures. Memory & Cognition. 2005;33:261–269. doi: 10.3758/bf03195315. [DOI] [PubMed] [Google Scholar]
- Benjamin AS, Diaz ML, Wee S. Signal detection with criterion noise: Applications to recognition memory. Psychological Review. 2009;116(1):84–115. doi: 10.1037/a0014351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonnel A-M, Miller J. Attentional effects on concurrent psychophysical discriminations: Investigations of a sample-size model. Perception & Psychophysics. 1994;55:162–179. doi: 10.3758/bf03211664. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The psychophysics toolbox. Spatial Vision. 1997;10:433–436. [PubMed] [Google Scholar]
- Bröder A, Schütz J. Recognition ROCs are curvilinear— or are they? On premature arguments against the two-high-threshold model of recognition. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2009;35:587–606. doi: 10.1037/a0015279. [DOI] [PubMed] [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. Hillsdale, New Jersey: Lawrence Erlbaum Associates; 1988. [Google Scholar]
- Cronbach LJ. Further evidence on response sets and test design. Educational and Psychological Measurement. 1950;10:3–31. [Google Scholar]
- Dube C, Rotello CM. Binary ROCs in perception and recognition memory are curved. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2012;38:130–151. doi: 10.1037/a0024957. [DOI] [PubMed] [Google Scholar]
- Egan JP, Schulman AI, Greenberg GZ. Operating characteristics determined by binary decisions and by ratings. Journal of the Acoustical Society of America. 1959;31 [Google Scholar]
- Garner WR. Rating scales, discriminability, and information transmission. Psychological Review. 1960;67:343–352. doi: 10.1037/h0043047. [DOI] [PubMed] [Google Scholar]
- Glanzer M, Kim K, Hilford A, Adams JK. Slope of the receiver-operating characteristic in recognition memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1999;25:500–513. [Google Scholar]
- Green DM, Moses FL. On the equivalence of two recognition measures of shortterm memory. Psychological Bulletin. 1966;66:228–234. doi: 10.1037/h0023645. [DOI] [PubMed] [Google Scholar]
- Green DM, Swets JA. Signal Detection Theory and Psychophysics. England: John Wiley; 1966. [Google Scholar]
- Healy AF, Kubovy M. The effects of payoffs and prior probabilities on indices of performance and cutoff location in recognition memory. Memory & Cognition. 1978;6:544–553. doi: 10.3758/BF03198243. [DOI] [PubMed] [Google Scholar]
- Kapucu A, Rotello CM, Ready RE, Seidl KN. Response bias in ‘remembering’ emotional stimuli: A new perspective on age differences. Journal of Experimental Psychology: Learning, Memory, & Cognition. doi: 10.1037/0278-7393.34.3.703. (in press) [DOI] [PubMed] [Google Scholar]
- Kellen D, Klauer KC, Singmann H. On the measurement of criterion noise in Signal Detection Theory: The case of recognition memory. Psychological Review. 2012 doi: 10.1037/a0027727. [DOI] [PubMed] [Google Scholar]
- Koen JD, Yonelinas AP. From humans to rats and back again: Bridging the divide between human and animal studies of recognition memory with receiver operating characteristics. Learning & Memory. 2011;18:519–522. doi: 10.1101/lm.2214511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee W. Choosing among confusably distributed stimuli with specified likelihood ratios. Perceptual and Motor Skills. 1963;16:445–467. doi: 10.2466/pms.1963.16.2.445. [DOI] [PubMed] [Google Scholar]
- Macmillan NA, Creelman CD. Detection theory: A user's guide. 2nd ed. NJ, US: Lawrence Erlbaum Associates; 2005. [Google Scholar]
- Malmberg KJ. On the form of ROCs constructed from confidence ratings. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2002;28:380–387. [PubMed] [Google Scholar]
- Malmberg KJ, Annis J. On the relationship between memory and perception: sequential dependencies in recognition memory testing. Journal of Experimental Psychology: General. 2012;141:233–259. doi: 10.1037/a0025277. [DOI] [PubMed] [Google Scholar]
- Malmberg KJ, Xu J. The influence of averaging and noisy decision strategies on the recognition memory ROC. Psychonomic Bulletin & Review. 2006;13:99–105. doi: 10.3758/bf03193819. [DOI] [PubMed] [Google Scholar]
- Mueller ST, Weidemann CT. Decision noise: An explanation for observed violations of Signal Detection Theory. Psychonomic Bulletin and Review. 2008;15:465–494. doi: 10.3758/pbr.15.3.465. [DOI] [PubMed] [Google Scholar]
- Nosofsky RM. Information integration and the identification of stimulus noise and criterial noise in absolute judgment. Journal of Experimental Psychology: Human Perception & Performance. 1983;9:299–309. doi: 10.1037//0096-1523.9.2.299. [DOI] [PubMed] [Google Scholar]
- Pelli DG. The Video Toolbox software for visual psychophysics: Transforming numbers into movies. Spatial Vision. 1997;10:437–442. [PubMed] [Google Scholar]
- Petrusic WM, Baranski JV. Judging confidence influences decision processing in comparative judgments. Psychonomic Bulletin & Review. 2003;10:177–183. doi: 10.3758/bf03196482. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Rouder JN. Modeling response times for two-choice decisions. Psychological Science. 1998;9:347–356. [Google Scholar]
- Swets JA, Tanner WP, Jr, Birdsall TG. Decision processes in perception. Psychological Review. 1961;68:301–340. [PubMed] [Google Scholar]
- Stretch V, Wixted JT. Decision rules for recognition memory confidence judgments. Journal of Experimental Psychology: Learning, Memory & Cognition. 1998;24:1397–1410. doi: 10.1037//0278-7393.24.6.1397. [DOI] [PubMed] [Google Scholar]
- Symonds PM. On the loss of reliability due to coarseness of the scale. Journal of Experimental Psychology. 1924;7:456–461. [Google Scholar]
- Treisman M, Williams TC. A theory of criterion setting with an application to sequential dependencies. Psychological Review. 1984;91:68–111. [Google Scholar]
- Tullis JG, Benjamin AS. The effectiveness of updating metacognitive knowledge in the elderly: Evidence from metamnemonic judgments of word frequency. Psychology and Aging. doi: 10.1037/a0025838. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner BM, Van Zandt T, Brown S. A dynamic, stimulus-driven model of signal detection. Psychological Review. 2011;118:583–613. doi: 10.1037/a0025191. [DOI] [PubMed] [Google Scholar]
- Van Zandt T. ROC curves and confidence judgments in recognition memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2000;26:582–600. doi: 10.1037//0278-7393.26.3.582. [DOI] [PubMed] [Google Scholar]
- Wickelgren WA. Unidimensional Strength Theory and Component Analysis of Noise in Absolute and Comparative Judgments. Journal of Mathematical Psychology. 1968;5:102–122. [Google Scholar]
- Wixted JT. Dual-process theory and signal-detection theory of recognition memory. Psychological Review. 2007;114:152–176. doi: 10.1037/0033-295X.114.1.152. [DOI] [PubMed] [Google Scholar]
- Wixted JT, Stretch V. In defense of the signal detection interpretation of remember/know judgments. Psychonomic Bulletin & Review. 2004;11:616–641. doi: 10.3758/bf03196616. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP. The contribution of recollection and familiarity to recognition and source-memory judgments: A formal dual-process model and an analysis of receiver operating characteristics. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1999;25:1415–1434. doi: 10.1037//0278-7393.25.6.1415. [DOI] [PubMed] [Google Scholar]