Abstract
Drug delivery using nanoparticles as drug carriers has recently attracted the attention of many investigators. Targeted delivery of nanoparticles to lymph nodes is especially important to prevent cancer metastasis or infection, and to diagnose disease stage. However, systemic injection of nanoparticles often results in organ toxicity because they reach and accumulate in all the lymph nodes in the body. An attractive strategy would be to deliver the drug-loaded nanoparticles to a subset of draining lymph nodes corresponding to a specific site or organ to minimize systemic toxicity. In this respect, mucosal delivery of nanoparticles to regional draining lymph nodes of a selected site creates a new opportunity to accomplish this task with minimal toxicity. One example is the delivery of nanoparticles from the vaginal lumen to draining lymph nodes to prevent the transmission of HIV in women. Other known examples include mucosal delivery of vaccines to induce immunity. In all cases, molecular and particle transport by means of diffusion and convective diffusion play a major role. The corresponding transport processes have common inherent regularities and are addressed in this review. Here we use nanoparticles delivery from the vaginal lumen to lymph nodes as an example to address the many aspects of associated transport processes. In this case, nanoparticles penetrate the epithelial barrier and move through the interstitium (tissue) to the initial lymphatics until they finally reach the lymph nodes.
Since the movement of interstitial liquid near the epithelial barrier is retarded, nanoparticles transport was found to take place through special foci present in the epithelium. Immediately after nanoparticles emerge from the foci, they move through the interstitium due to diffusion affected by convection (convective diffusion). Specifically, the convective transport of nanoparticles occurs due to their convection together with interstitial fluid through the interstitium towards the initial lymph capillaries. Afterwards, nanoparticles move together with the lymph flow along the initial lymph capillaries and then enter the afferent lymphatics and ultimately reach the lymph node. As the liquid moves through the interstitium towards the initial lymph capillaries due to the axial movement of lymph along the lymphatics, the theory for coupling between lymph flow and concomitant flow through the interstitium is developed to describe this general case.
The developed theory is applied to interpret the large uptake of Qdots by lymph nodes during inflammation, which is induced by pre-treating mouse vagina with the surfactant Nonoxynol-9 prior to instilling the Qdots. Inflammation is viewed here to cause broadening of the pores within the interstitium with the concomitant formation of transport channels which function as conduits to transport the nanoparticles to the initial lymph capillaries. We introduced the term “effective channels” to denote those channels which interconnect with foci present in the epithelial barrier and which function to transport nanoparticles to initial lymph capillaries. The time of transport towards the lymph node, predicated by the theory, increases rapidly with increasing the distance y0 between the epithelial barrier and the initial lymph capillaries. Transport time is only a few hours, when y0 is small, about some R (where R is the initial lymph capillary radius), due to the predomination of a rather rapid convection in this case. This transport time to lymph nodes may be tens of hours (or longer) when y0 is essentially larger and the slow diffusion controls the transport rate in a zone not far from the epithelial barrier, where convection is weak at large y0. Accounting for transport by diffusion only, which is mainly considered in many relevant publications, is not sufficient to explain our nanoparticles uptake kinetics because the possibility of fast transport due to convection is overlooked. Our systematic investigations have revealed that the information about the main transport conditions, namely, y0 and the pore broadening up to the dimension of the interstitial transport channels, is necessary to create the quantitative model of enhanced transport during inflammation with the use of the proposed model as a prerequisite.
The modeling for convective diffusion of nanoparticles from the epithelial barrier to the lymph node has been mainly accomplished here, while the diffusion only scenario is accounted for in other studies. This first modeling is a semi-quantitative one. A more rigorous mathematical approach is almost impossible at this stage because the transport properties of the model are introduced here for the first time. These properties include: discovery of foci in the epithelium, formation of transport channels, definition of channels interconnecting with foci (effective foci and channels), generation of flow in the interstitium towards the initial lymph capillaries due to axial flow within afferent lymphatics, deformation of this flow due to hydrodynamic impermeability of the squamous layer with the formation of the hydrodynamic stagnation zone near the epithelial barrier, predomination of slow diffusion transport within the above zone, and predomination of fast convection of nanoparticles near the initial lymph capillaries.
1. Introduction
Problems associated with nanoparticles penetration through an epithelial barrier (EB), their subsequent convective diffusion through the interstitium (tissue between EB and lymphatics) to initial lymph capillaries (ILCs) and their final transport to regional lymph nodes (LNs) have recently attracted considerable attention because their potential use as drug or immunogen carriers presents new opportunities in mucosal immunization and prevention of infections. Many authors have investigated delivery of micro- and nanoparticle drug carriers to achieve gastrointestinal transport (GIT), and to treat or prevent cancer and viral infections. In order to develop such applications, transport modeling is mandatory because it allows one to predict the optimal properties of the nanoparticles (NPs) (size, charge, hydrophobicity/hydrophilicity, etc.) and to estimate the dependence of transport properties in the interstitium and lymphatics on system parameters. Although the desired transport properties will depend on the targeted application, there are general regularities that control convective diffusion of NPs to regional LNs. This topic will be characterized here using particle transport from the vaginal lumen to regional LNs to prevent sexual transmission of the HIV virus as an example.
According to the currently accepted mechanism of HIV sexual transmission (Figure 1), dendritic cells (DCs) and Langerhans cells (LCs) present in the vaginal mucosa are the first cells to encounter cell-free HIV virus particles [1]. According to this mechanism, the HIV virus is ferried by DCs across the cervico-vaginal epithelium, even in the absence of injury or lesions. The DC-associated virus is then transported to the lamina propia (interstitium between the epithelium and the lymphatics) to adjacent draining lymph nodes, where it replicates exponentially by infecting CD4+ T cells, and is then transmitted to other host tissues and organs. These processes ultimately lead to HIV dissemination and infection. Means to intercept or disrupt these events are being seriously explored to prevent HIV infections around the world. We hypothesize that mucosal delivery of nanoparticles containing either an antiviral drug or an immunogen via the vaginal lumen to draining LNs will decrease the incidence of such infection. If this can be achieved, the accumulation of such nanoparticles within LNs with concomitant long-term drug release may be considered as a new prophylactic strategy to prevent HIV transmission. In order to examine the above hypothesis, we developed a mouse model [2] to study the transport process of NTR-emitting nanoparticles (Qdots) [3] from the vagina by visualizing their penetration through the epithelial barrier and by assessing their accumulation in regional draining LNs [4].
Figure 1.
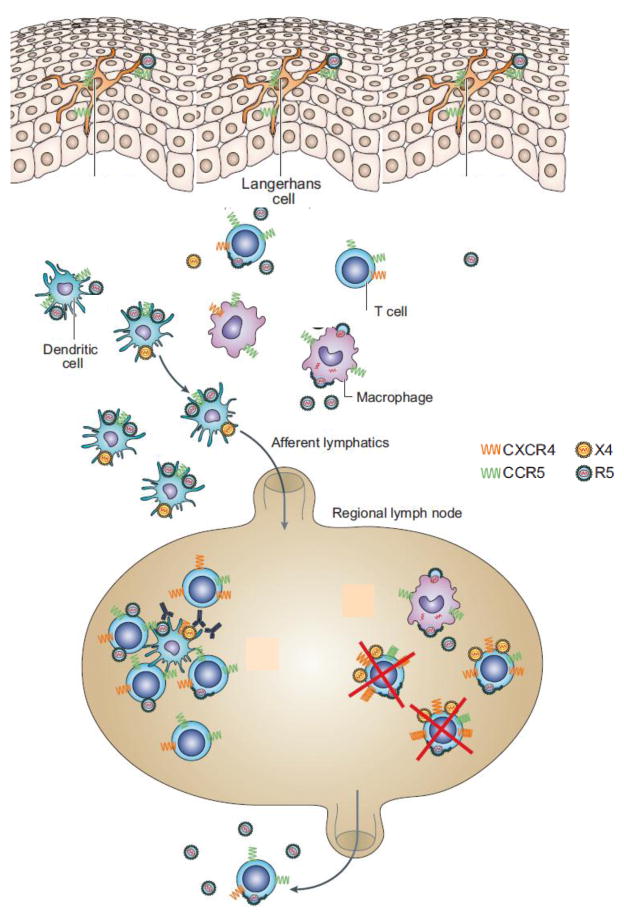
Schematic showing the currently accepted mechanism for the transmission of the HIV virus through the vaginal epithelial barrier via cellular carrier transport, adapted from [59]. X4 or R5 HIV virus is captured by Langerhans cells at the vaginal surface and then handed over to dendritic cells. The HIV virus can also replicate in macrophages or in CD4+ T cells in the interstitium and can then be captured by dendritic cells. According to this mechanism, the HIV virus is ferried by dendritic cells to regional draining lymph nodes where it replicates in CD4+ T cells and then disseminates to host organs resulting in full HIV infection.
The following is a summary of our experimental findings: 1) The majority of Qdots transport occurs via isolated foci in the epithelial barrier (EB) and not from the entire interior surface of the vagina/cervix as was originally assumed; 2) The majority of Qdots diffusing through foci in the squamous layer (portion of EB) appears to be extracellular and not associated with dendritic cells (DCs), i.e., they emerge from foci into the lamina propia (interstitium); 3) The majority of Qdots found in LNs was also extracellular as evidenced by microscopic examination and by FACS analysis; and 4) Surprisingly, the amounts of DCs detected in the interstitium on the boundary with the squamous layer and within the LN were negligible despite numerous microscopic observations to explain the significant transport achieved. In this review, foci may represent either a singular or plural state.
Our experimental findings may not contradict the aforesaid notion that virus penetration, transport and accumulation within LNs occurs by DC carriers. It is known that DCs are able to internalize viruses and perhaps capture more viruses due to specific receptor-ligand binding, while on the other hand, Qdots do not possess such ligands. At least doubt arises regarding whether the strategy of LN targeting with Qdots may be realized by DCs as particle carriers. Indeed, the notion regarding the major role of cell-associated transport of antigens to LNs was revised in a recent review [5] with respect to mucosal vaccine delivery. According to such revisions, only a small fraction of antigens will result in the formation of DC-antigen associates since the number of DCs is small within the epithelium. Hence, the majority of antigens remains free and moves towards regional LNs according to colloid transport mechanisms.
Recently, attention has been paid in the literature concerning the identification of the conditions needed for antigens transport towards LNs, which is favorable for the transport of NPs either in the free form or due to association with carrier cells. Macromolecules about 20-200 nm efficiently enter the lymphatic system, with an optimal size being ∼40 nm [6-8]. Consequently, particles and macromolecules that are smaller than 100-200 nm can enter the lymphatic system at distal sites of the lymph vessels [9]. By contrast, particles that are larger than 200-500 nm do not efficiently enter lymph capillaries in the free form [10, 11]. Instead, such large particles need to be carried into the lymphatic system by specialized cells such as DCs which can squeeze through openings between overlapping endothelial cells of lymph capillaries [12]. A conclusion is made that free versus cell-associated drainage of vaccines/antigens has a crucial effect on the targeting of cell populations by using different size particles as delivery vehicles [5]. This new information provides additional confirmation regarding our observation that transport of NPs to LNs can take place in the free form because Qdots dimensions are less than 200 nm, even if they are aggregated.
Since the role of DCs in particle transport is ruled out as the primary mechanism, understanding the transport of nanoparticles to LNs becomes possible on the basis of colloid transport in porous media [13]. The latter are always considered as adsorbing media where the transport mechanism normally takes place by diffusion and/or convective diffusion. In the present system, particle penetration through the epithelial barrier occurs by means of diffusion, while interstitial transport and transport within LNs are controlled by convective diffusion (Figure 2). Accordingly, this mode of transport attains new features due to the coupling between diffusion (convective diffusion) and adsorption processes.
Figure 2.
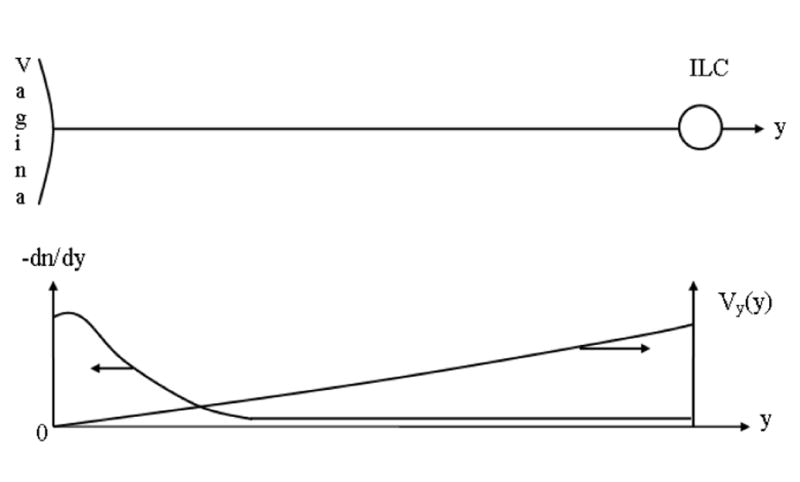
Convective diffusion of Qdots within the interstitium from foci in the epithelial barrier (EB) towards an initial lymph capillary (ILC). The Brownian diffusion predominates near the epithelial barrier (EB) because the interstitial fluid is immobilized in this zone. The velocity of interstitial fluid V increases with its approach to the initial lymph capillary (ILC), which causes the predomination of convection. The nanoparticle concentration n(y) is maximal near the exits of foci and decreases rapidly under the influence of increasing velocity Vy(y), which is the usual case in convective diffusion. Correspondingly, dn/dy decreases downstream with concomitant decrease in the diffusion flux.
While the notions of colloid science may be sufficient for understanding the mechanism of transport processes, detailed biophysics of the system will be needed to define some of its important variables. This includes, for example, biophysics related to flow in the afferent lymphatics such as contractility, one-way valve system, etc. [14], and other characteristics that define the flow of interstitial liquid towards initial lymph capillaries.
The diffusivity of a 50-nm hydrodynamic radius nanoparticle in water is about 10-8 m2/sec. The diffusive properties of the interstitium have been described in [15] according to the pore theory for plasma proteins with the molecular dimension of 3-10 nm assuming pore radii of about 12-20 nm for a normally hydrated umbilical cord or for subcutaneous tissue. Plasma proteins are reported to have a diffusion coefficient in the interstitium of about 10-25% of that found in water [16]. As therapeutic nanoparticles are several times larger than the largest among proteins, and because pores will affect strongly their diffusivity, we believe 10-9 cm2/sec may be considered a crude estimation of the time necessary for diffusion when the distance to the initial lymph capillaries [l] is about 300 microns. Then the transport time would be about 5.105 sec or 5 days, according to the Einstein equation. One concludes that only interstitial flow may provide nanoparticles transport to lymph capillaries at a very small mean velocity of interstitial liquid of about 0.02 micron/sec, which cannot explain the observed experimental results where the onset of the uptake within the LN takes place about 4 hours from instillation. It will be shown that the necessary velocity may be essentially higher because of nanoparticle adsorption on the extracellular surfaces.
There is another factor that forces us to pay attention to interstitial transport. This relates to the adsorption of nanoparticles on the extracellular surfaces during their transport towards the initial lymph capillaries. In the case of polyarginine-coated Qdots, this adsorption is caused by the electrostatic attraction of polycations to the negatively-charged extracellular surface [17]. This is defined as Qdots uptake by extracellular surface. Hence, nanoparticles transport considers two steps: 1) uptake within the interstitium, and 2) uptake by lymph nodes.
The kinetics of transport processes in the extracellular surface and in the lymph nodes may have important therapeutic applications when considering drug-carrying nanoparticles. The release of drugs or immunogens from nanoparticles may have therapeutic functions during their penetration through the epithelial barrier, interstitium and within the lymph nodes.
Other research groups have not confirmed the exact role of phagocytosis on nanoparticles transport to lymph nodes, and attention has recently been placed on the physicochemical aspects of lymphatic delivery [18]. Since the leading role of cellular phagocytosis of particle transport has not been fully confirmed in these researches, a new concept called “Novel-Modified Nano-System-Based Targeting” is proposed in [18].
Several sub-processes and properties are mentioned as important for solute uptake by the lymphatic system and are discussed in [18]. “Since solute must travel at least some distance through the interstitium before entering the initial lymphatics, the interstitial resistance to molecular transport greatly affects the apparent lymphatic uptake rate. The rate of particle uptake from an interstitial injection site is dictated by its rate of diffusion through the interstitium which is dependent on the physiological properties of the interstitium, including: the anatomical site of injection and the physiochemical properties of the delivered particles. The latter include: size, number of particles, surface charge, molecular weight and surface hydrophobicity. Molecules smaller than 10 nm are preferentially re-absorbed into the blood capillaries, while the optimal particle size for lymphatic uptake is found between 10 and 100 nm.” The size, shape, charge and lipophilicity of a molecule (or particle) which affect its uptake rate into the lymphatics may also reflect its interstitial hindrance characteristics prior to lymphatic uptake [19-21].
A similar statement may be made on the basis of the physicochemical theory of colloid transport in porous adsorbing media. This justifies the possibility of applying this theory to modeling lymphatic uptake of nanoparticles. The application of this theory immediately reveals, even on a qualitative level, that there is an unacceptable omission of important sub-processes in the picture described by the reproduced citations, as follows:
While the term adsorption is used in [18], the significance of its reversibility is not mentioned. A solute cannot propagate through porous media if the adsorption is irreversible, i.e., if there is no desorption act after an adsorption act, which is termed as its reversibility. A macromolecule or nanoparticle only attains the possibility of further propagation after a desorption act. The notion of local adsorption-desorption quasi-equilibrium is a central one in the theory of colloid transport in porous media.
While the importance of the physicochemical properties of nanoparticles regarding their transport towards lymph nodes and their retention within the nodes is emphasized, and the relevant strategy for their surface engineering/modification is discussed, no mention is made that the requirements of adsorption properties are controversial. This is important because in order to facilitate overall transport, the adsorption within the interstitium has to be suppressed and the adsorption within the LN has to be enhanced. The strong bonding of nanoparticles inside the lymph node is required for their retention because desorbed nanoparticles become involved in lymph flow and can be easily lost via the efferent duct. Modification of the surface of nanoparticles may enhance their binding within the node, and extend their residence time within it with a concomitant increase in uptake. However, a similar increase in nanoparticles uptake may occur within the interstitium prior to their entering into the lymphatics. Therefore, increasing the adsorption bond may simultaneously decrease nanoparticles loss from the node caused by their outflow into the efferent capillary and increase their loss due to their immobilization in the interstitium. Hence, an essential correction in the strategy of particle surface modification [18] is necessary. Thus, in order to achieve effective transport, strengthening of the adsorption binding within the lymph node has to be achieved without a concomitant strengthening of the adsorption binding within the interstitium.
Although diffusion is mentioned in [18] as the single mechanism responsible for the transport of NPs through the interstitium towards the initial lymphatics, the existence of interstitial liquid flow towards the initial lymph capillaries with a concomitant transport of nanoparticles is overlooked. Meanwhile, the overlooked stage of convective transport towards the initial lymphatics is very important for such transport; were it absent, transport through the interstitium would take days while the experimental measurements show that it would take only hours [4].
The “novel-modified nanosystem-based targeting” elaborated in [18] generalizes the experience of many groups and demonstrates that novel strategies to advance this field can be made by the application of physical chemistry. In fact, a branch of physical chemistry, namely colloid and interface science, describes colloid transport within porous-adsorbing media with concomitant retention of adsorbed species. The major role in this transport is played by processes involving convective diffusion, reversible adsorption and their coupling. The application of theories for convective diffusion and reversible adsorption and their coupling to the modeling of nanoparticles transport from the epithelium towards regional lymph nodes and their retention within such nodes is the objective of our research.
The goal of this review is to address the convective diffusion of NPs through the interstitium when the effect of adsorption on extra-cellular surfaces is negligible and to define the conditions needed for optimal drug delivery to lymph nodes. Harmful adsorption during convective diffusion through the interstitium, i.e., the coupling between convective diffusion and adsorption, will be considered in the next review. The general utility of successful particle transport to lymphatics is relevant to decreasing HIV transmission and to preventing cancer metastasis among other applications in biology.
2. Coupling between lymph hydrodynamics and hydrodynamics in interstitium
2.1. Qualitative description and mathematical models for transport through the interstitium
Investigation in this area started some decades ago and is generalized in the very informative review [22]. Among the many relevant topics, we shall briefly consider the following: transport properties of the interstitium, pre-nodal lymphatics, mechanisms for the onset of liquid transport and the most advanced recent mathematical models [23-25].
a. Transport properties
Transport properties were addressed in connection with the composition of the interstitium (collagen, glycosaminoglycan, etc.) in [22]. Interstitium composition affects its hydration, where upon hydration, the calculated pore radius can double with about a three to five times increase in interstitial fluid volume [22]. Another relevant example of the effect of interstitium composition is that “a major portion of hyaluronans is easily mobilized by increased interstitial fluid flux” [22], which also increases pores. The composition of the interstitium affects tissue elasticity, which may manifest itself when considering the hydrodynamic permeability. In spite of these complexities, the concept of the interstitium as a static structure predominates in the description of transport properties and this would thus influence the modeling which is primarily based on the Darcy law [26]. The application of the Darcy Law [27] has revealed that none of the interstitial components is present in sufficient amounts to account for the observed hydraulic conductivities alone; however, their combined effect is required to explain the available experimental data. Specifically, 1.5. 10-9 cm4 dyn-1 sec-1 [28] and 5.10-12 cm4 dyn-1 sec-1 [29] are reported for hydraulic conductivity of normally hydrated tissue.
b. Pre-nodal lymphatics
The lymphatic system is composed of a network of vessels, termed lymphatics, which include lymph nodes and lymphoid organs. Pre-nodal lymphatics consist of initial lymphatics, pre-collecting lymphatics and collecting lymphatics. Interstitial fluid enters through the small lymph capillaries (also called initial or terminal lymphatics) that gradually combine to form larger diameter vessels, namely the pre-collectors, or simply collectors. The terms capillary filling and lymph propulsion describe two sequent stages of liquid transport from the interstitium through the pre-nodal lymphatics towards a regional draining node. Capillary filling occurs only within the initial lymphatics. Lymph propulsion towards a lymph node only occurs within the collecting lymphatics.
c. Mechanisms of interstitial fluid mobilization
Interstitial fluid originates when blood plasma leaves the arterioles and flows into tissue, where it becomes tissue fluid - also known as interstitial fluid. When this interstitial liquid enters the initial lymph capillaries, it is called “lymph,” and this transition process is called the lymph formation. This path points to the role of increased blood pressure on interstitial fluid movement. However, how this mechanism affects the transport of nanoparticles into lymph capillaries is not clear. Moreover, this mechanism affects lymph transport if an arteriole is located between a lymph capillary and the epithelial barrier. When the arteriole is distant respective to the lymph capillary, its influence may be weak or non-existing depending on the distance.
Oncotic pressure caused by the gradient of protein concentration and hydrostatic pressure may contribute to lymph formation. However, there are many unanswered questions regarding the role of oncotic pressure in lymph formation which need to be answered [14].
The hydrostatic pressure theory of lymph formation relies on the development of hydrostatic pressure differences between the interstitium and the lumen of the initial lymphatic. Normally, the average pressures in the interstitial space are near zero or slightly negative with respect to atmospheric pressure, while most pressures measured in the lymphatics are slightly positive. Thus, the net pressure gradient does not favor entry of fluid into the initial lymphatics. However, there is a growing body of evidence that indicates transient development of pressure gradients is favorable to the movement of fluid into the lymphatics [14, 15 and 19]. This favorable transient pressure gradient coupled with the presence of the primary and secondary valve systems [14, 15, 19] within the lymphatics allow for the generation of lymph formation within the initial lymphatics, with a corresponding net central flow of lymph into venous circulation. This theory relies on the contraction/compression and relaxation cycle of either the intrinsic (Figure 3) or extrinsic lymph pump in initial or collecting lymphatics, and on the function of one-way valves (Figure 4) in the initial and collecting lymphatics. These one-way valves allow for the transient entry of fluid into the initial lymphatics during the expansion/relaxation phase and prevent fluid loss during the contraction/compression phase.
Figure 3.
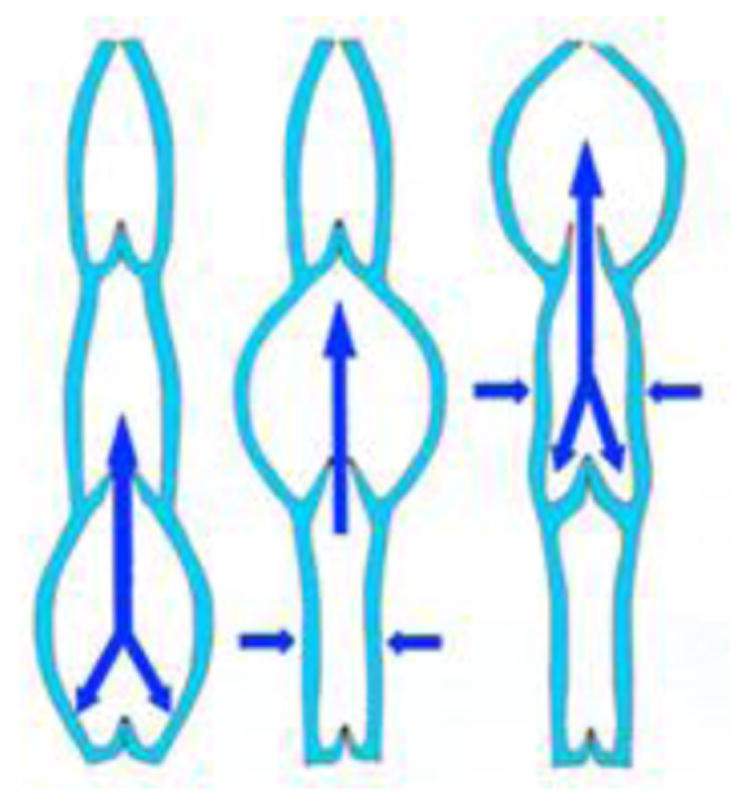
- Like veins, lymphatic afferent vessels, which are known as lymphangions, have one-way valves to prevent any backward flow.
- Each angion is a segment created by the space between two sets of valves.
- Smooth muscles in the walls of the lymphatic vessels cause the angions to contract sequentially to aid the flow of lymph toward the thoracic region.
Figure 4.
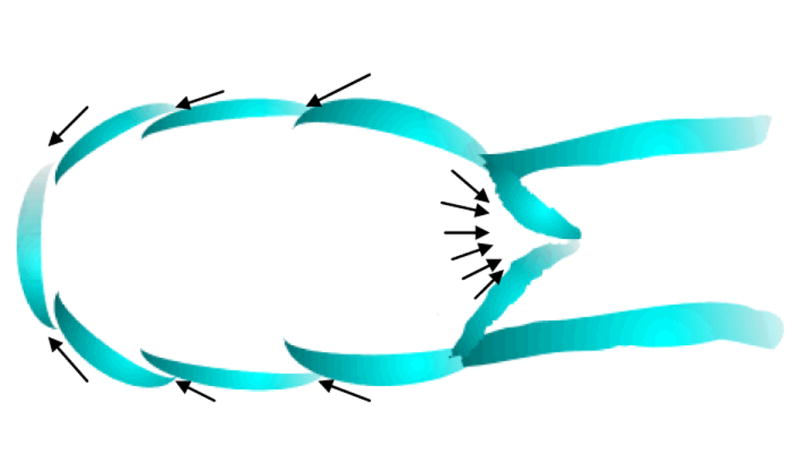
Lymph entering an initial lymph capillary through primary valves. Lymphatic capillaries begin as blind-ended tubes that are only a single cell in thickness. These cells are arranged in a slightly overlapping pattern, much like the shingles on a roof. Each of these individual cells is fastened to nearby tissues by an anchoring filament. The pressure from the fluid surrounding the capillary forces these cells to separate for a moment to allow lymph to enter the capillary. Then the cells of the wall close together. This does not allow the lymph to leave the capillary. Instead, this forces the lymph to move downstream.
Recently [30, 31], measurements of pressure inside single isolated bovine mesenteric lymphangions have been performed with the diastolic pressure inside the lymphangions set to 0 cm H2O. Pressure tracings obtained in this study demonstrated the development of negative fluctuations of pressure inside the lymphangions of up to ∼5 cm H2O, which were associated with the contraction of the lymphatic wall. Such events may produce suction in the lymphangions, so energy from the active lymphatic pump may be used to not only empty the lymphangions, but also to drive lymphangion filling at the same time.
The term “passive” or “extrinsic” lymph pump combines all the extra-lymphatic forces that influence lymph flow. Extrinsic lymph-driving forces include the driving force of lymph formation (historically also named as “vis a tergo”), influences of cardiac and arteriol pulsations on neighboring lymphatics, contractions of skeletal muscles adjacent to the lymphatics, central venous pressure fluctuations, gastrointestinal peristalsis and respiration. All of these forces may produce hydrostatic gradients in the lymphatic network, which could effectively move lymph, even in the absence of intrinsic lymphatic contractions. Lymph flow directly depends on the magnitude of lymph formation. In turn, interstitial flow is connected with lymph formation. One concludes that interstitial flow depends on the contractile activity of lymphangions as well as the action of extrinsic forces.
d. Mathematical models
Distinct from the large efforts in modeling of propulsion [30, 31, 33], in particular propulsion within collecting lymphatics, little attention has been paid to modeling the filling of initial lymphatics, especially with respect to its coupling with interstitial flow. In particular, there is coupling of capillary filling with lymph propulsion along the initial capillaries.
As convective transport through the interstitium is an important stage in nanoparticles transport towards lymph nodes, the coupling of propulsion along the initial capillaries with the concomitant flow of interstitial fluid around such capillaries is one of the tasks whose solution is required for modeling particle uptake in lymph nodes. While earlier attempts to model the hydrodynamics of interstitial fluid movement were accomplished for understanding the mechanism of edema and are referred to in [14, 15], a recent investigation explored the delivery of protein drugs to lymphatics via subcutaneous injection as the primary delivery route [23]. Since there is no subcutaneous injection in our case, it will be shown that this will lead to an essential modification of the task when considering both the movement of interstitial liquid and the convective transport of nanoparticles. Nevertheless, the fundamentals in our approach cannot differ from those described in the literature [23]. The bases for our modeling are: i) the conservation laws which govern the transport of interstitial fluid and nanoparticles, ii) the transport properties of the interstitium, iii) the hydrodynamics of afferent lymphatics, and iv) the equations which interconnect lymph flow and the flow of interstitial liquid, as follows:
-
The conservation law for incompressible fluids is:
(2.1) where v is velocity distribution in space.
The conservation law for momentum is the Darcy law for the interstitium(2.2) where p is pressure distribution in space, η is viscosity of the interstitial fluid and Kin is the hydraulic conductivity of the interstitium.
The conservation law for the momentum for propulsion in the initial capillaries is the Navier-Stokes equation.
ii) The transport properties of the interstitium were discussed earlier, i.e., Kin is sufficient.
The hydrodynamics of afferent lymphatics has already been discussed. Information about the flow rate on the boundary between afferent lymphatics and an initial lymph capillary is sufficient as a boundary condition for quantifying the hydrodynamics of the initial lymph capillary.
The peculiarity about interstitial fluid flow is that its modeling requires the joint description of both interstitial fluid flow and lymph flow. This coupling must be accounted for regarding both laws of conservation. With respect to the conservation law for fluid flow, the openings in the wall of the initial lymphatics are outlets for the interstitial flow, while the openings within the arteriol wall are inlets of the interstitial flow. This leads to the generalization of Eq. (2.1). Two terms, corresponding to inlet and outlet, are introduced on the right-hand side of Eq. (2.1) (see for example, Eq.(a.1) in [23]).
With respect to momentum conservation, there must be an interconnection between the pressure inside the initial lymph capillary p(z) and the pressure in the interstitium on the external wall of the capillary pin(z) at the same z, where z is the axial coordinate along the capillary. The smaller the hydrodynamic permeability on the wall, the larger the differences between the pressures will become. However, the value of such pressure difference may be negligible, i.e.,
| (2.3) |
This same condition is applied in [23]. As a result, the final equation (namely, Eq. (2) in [23]) does not depend on the permeability of the capillary wall.
An essential simplification in the description of lymph propulsion through the initial lymph capillary occurs due to the small Reynolds number (Re). This is because initial lymph capillaries have a diameter of approximately 10-60 microns [15]. The corresponding high hydrodynamic resistance results in a very low lymph velocity and consequently a low Re. This means that the non-linear term in the Navier-Stokes equation can be omitted. The second important sequence is that the joint influence of both the intrinsic and extrinsic pumps may be described by means of linear superposition of velocity distributions arising due to the intrinsic pump only or to the extrinsic pump only.
As secondary and primary valves are either in an open or closed state, the flows of lymph and interstitial fluids are non-steady. However, the so-called quasi-steady approximation can be used. This means that the distributions in space may be considered as steady ones in spite of their change in time. Liquid movement at any moment is similar to steady movement corresponding to a momentary external condition [32]. As the external conditions depend on time, the quasi-steady distributions change in time as well. In other words, the distribution in space can be determined by solving it as a steady task, while the time dependence is the same as that of the boundary conditions.
The equation for hydrodynamic relaxation time, i.e., the time necessary for the onset of the quasi-steady hydrodynamic mode is [32]:
| (2.4) |
where ν is kinematic viscosity. This yields T=10-4to 3.6.10-3 sec for d=10 to d=60 microns. With respect to the intrinsic pump, Tumer et al. [33] observed that contractions occur at a frequency of 0.09-0.14 Hz and smaller. This corresponds to a period of about 10 seconds and higher. As the relaxation time according to Eq. (2.4) is in orders of magnitude shorter, the quasi-steady approximation can be used for the coupling between the propulsion in the initial lymph capillary and the flow of interstitial fluid in the surrounding interstitium.
2.2. Modeling fluid flow in the interstitium around an initial lymph capillary initiated by the intrinsic pump
Since the fundamentals for the above modeling (Section 2.1) have been mainly developed in [23], this simplifies our task which must be formulated in the framework of existing fundamentals taking into account the essential distinction regarding conditions of transport compared to the delivery of an injectable drug [23]. The route of an injectable drug is very long because the drug stream meets many arterioles and lymph capillaries along its route. This means that the equation for liquid conservation has to account for the inlets and outlets, which is provided by Eq. (A.1) in [23]. In our case, however, a nanoparticle route from the vaginal surface to the nearest initial lymph capillary is short. The conservation equation in its simplest form (Eq.1) may be used if there are no arterioles present between the initial lymph capillary and the epithelial barrier.
Since the distance between the interstitium zone and the nearest lymph capillary is very short, the influence of the intrinsic pump is expected to predominate within this zone. This is a completely new situation because the factors nominated as the extrinsic pump [14,15] are considered in the existing models [23] for the interstitial fluid movement.
While the small distance to the afferent lymphatics determines the force which basically moves the interstitial fluid, the small distance to the epithelial barrier suppresses this movement because the fluid flow does not penetrate through the barrier, i.e., the normal component of the velocity equals zero:
| (2.5) |
where SEB is the surface of the epithelial barrier. This boundary condition causes additional mathematical difficulty and will be initially disregarded. In order to account for this condition a posteriori, we assume that a single initial lymph capillary is oriented parallel to the vagina axis. As the interstitium around the initial capillary is considered not confined, the hydrodynamic task attains cylindrical symmetry with the vaginal axis, which coincides with the lymph capillary axis (Figure 5).
Figure 5.
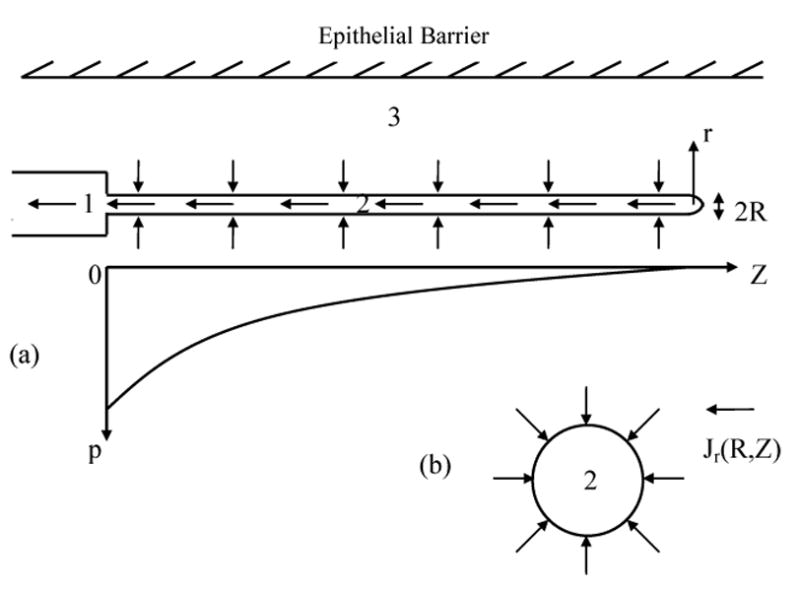
- Schematic showing the decreased pressure inside an ILC and the axial dependence of pressure.
- Interstitial fluid flow towards an initial lymph capillary; Jr(R,r) is the flux density in the radial direction around the ILC with axial symmetry.
There is no information in the literature to precisely describe how interstitial fluid may enter the afferent vessel directly through its wall; however, it is accepted that interstitial fluid enters through openings in the initial lymph capillaries, while the valve of the last afferent vessel creates an axial flow along the initial capillary connected to it. Volumetric velocity Qaf on the boundary between an initial lymph capillary and the afferent capillary will be considered in our task as a known value.
As the initial capillary is blind ended, the axial volumetric velocity Q is small at this end and gradually increases downstream due to the uptake of the surrounding interstitial fluid up to a maximal known value Q(z=0)=Qaf, where z = 0 corresponds to the location of the last lymphangion. The axial dependence Q(z) is determined by its coupling with the radial flux in the interstitium, characterized by the flux density jr (r,z). The mathematical representation of this coupling is expressed through the equation for fluid conservation, specified for a section of the lymph capillary between (z+Δz) and z. The increase in Q(z) with the decrease in Δz is caused by the interstitial liquid flow through the section of the capillary wall with the area 2πRΔ z which is proportional to jr(R,z). The equation for this balance is:
| (2.6) |
Both sides of this equation may be expressed through one sought function, namely, the axial dependence of pressure inside the capillary, p(z). With this aim, the Darcy law may be used within the interstitium and inside the capillary. Inside the capillary, it may be specified as the Poisseuille law:
| (2.7) |
where η is the liquid viscosity, assuming that the variation of the capillary cross-section with z is not large.
The substitution according to Eq. (2.7) into Eq. (2.6) yields
| (2.8) |
We only consider the regime which is most important for the drug delivery process under consideration, when the axial component of the interstitial fluid flow may be disregarded, i.e.,
| (2.9) |
The necessary condition will be established a posteriori. Then the equation of the interstitial fluid conservation (1) takes the form:
| (2.10) |
where the right-hand side may be expressed using the Darcy law
| (2.11) |
that yields after integration
| (2.12) |
In this derivation, we do not account for the pressure difference across the capillary wall which is justified for the case when Kin is small and when the major resistance to flow occurs within the interstitium. A more general formula which accounts for this pressure drop will be obtained a posteriori.
With r*→∞, p(r) diverges, which is the manifestation of the well-known phenomenon of divergence of the solution for the mass conservation equation when there is exact cylindrical symmetry. In contrast, the divergence is absent at spherical symmetry, when the dependence is 1/r. We need to take into account that the real capillary length lic is a finite one and that at the distance r≫lic, the symmetry becomes approximately spherical. This means at r*>lic, p(r*) decreases very rapidly and may be omitted, while r* in the right-hand side of Eq. (2.12) may be taken as lic. Although this estimate for r* is a very crude one, this does not lead to a large mistake because the logarithmic dependence is very weak.
The substitution
| (2.13) |
into Eq. (2.8) yields a differential equation for the determination of the axial dependence of the pressure inside the initial lymph capillary
| (2.14) |
| (2.15) |
The solution of Eq. (2.14) is
| (2.16) |
where
| (2.17) |
A is the coefficient. The dependence (2.16) satisfies the boundary condition
| (2.18) |
which originates from the obvious condition Q(lic)=0 and Eq. (2.7). The condition for the determination of A is expressed through Qaf, which is Q on the boundary between the afferent and initial capillaries. In turn, Qaf equals the total stream through the cylindrical wall of the initial lymph capillary, which may be obtained by integrating Jr(R,z) over the entire wall or integrating p(R,z), which is seen from Eq. (2.13).
Mainly R affects the ratio λ/lic, while the influence of Kin is weaker. On the other hand, Kin may vary within a broader range. When R is sufficiently large, the hydrodynamic resistance of the capillary is small λ/lic is large and an almost uniform pressure distribution establishes along the initial capillary. Correspondingly, the axial dependence of the interstitial flow is weak. Table 1 illustrates the dependence of λ on R and Kin. The calculations are accomplished for the range of Kin values found in [28, 29] and for a known range of R values.
Table 1.
Estimates for λ [cm] according to Eq. (2.17).
| R (micron) | Kin (cm2) | ||
|---|---|---|---|
| 1.50E-11 | 4.50E-13 | 5.00E-14 | |
| 10 | 0.14 | 0.76 | 2.4 |
| 20 | 0.5 | 2.9 | 8.9 |
| 60 | 3.9 | 23 | 67 |
There is a shortage of information in the literature about the length and length/diameter ratio for the initial lymph capillary. It is stated in [34] that terminal lymphatics are usually about 0.5 mm long. The data in Table 1 are obtained assuming lic= 1mm.
When lic is about 1 mm or less, the important condition
| (2.19) |
is satisfied within the usual ranges for R and Kin, as shown in Table 1 above. This means that almost uniform (with respect to z) distribution for the radial velocity Vr around the capillary takes place, which is seen from the comparison of Eqs. (2.13) and (2.16). Vr(R) may be found from the condition that the total flux through the cylindrical surface of the initial capillary is equal to Qaf. One obtains
| (2.20) |
The substitution according to this equation into the equation
| (2.21) |
describes the velocity distribution around the initial capillary when condition (2.9) is valid.
This condition is satisfied very well at a position not far from the capillary, i.e., for r not very large in comparison with R for all combinations of parameters in Table 1. lic and R are characteristic lengths in axial and radial directions, i.e., Jz∼lic-1 and Jr∼R-1. Hence, condition (2.9) is valid because of Eq. (2.19).
A more general theory is necessary when the distance between the squamous layer and the initial capillary exceeds 300 microns. This theory is also required to describe the portions of the streaming lines at z < 0, i.e., around the afferent capillary and at z>lic.
A finite cylinder is usually replaced by a prolonged spheroid which allows one to apply ellipsoidal coordinates and to overcome the large difficulties arising from the cylinder case. As the ratio (lic/R) is large in our case, this approach is rather rigorous. Hence, the boundary condition must be formulated for the ellipsoidal surface Sell
| (2.22) |
where PILC is almost invariant pressure inside the initial lymph capillary. As the pressure distribution in the interstitium satisfies the Laplace equation, an electrostatic analogy with the potential distribution around the isopotential ellipsoid may be used. Unfortunately, the potential (pressure) distribution presented in the ellipsoidal coordinates is difficult to apply to the next stages of nanoparticles transport.
The Darcy law allows us to introduce the potential for velocity distribution within the interstitium in the general case
| (2.23) |
because
| (2.24) |
and the Darcy law, i.e., Eq. (2.2), are identical. The flow potential ψ satisfies the Laplace equation which follows from Eq. (2.24) and the equation for fluid conservation (Eq.(2.1))
| (2.25) |
i.e.,
| (2.26) |
The derived formula (2.16) may be used as the boundary condition on the cylinder surface r=R.
As flow in the interstitium around an initial lymph capillary is only one among many sub-processes affecting transport to draining lymph nodes, we tried to simplify the modeling with the aim of incorporating it into a general model (scheme) to describe the transport to the lymph node. The major simplification is the choice of Qaf as the boundary condition. In contrast, other models [34-36] are much more complicated because of the complexity in modeling the primary valve dynamics. Although the scientific value for biomechanics is much higher, their incorporation into the general scheme of transport to lymph nodes will cause serious complications because they are mainly numerical while the proposed primitive model here is analytical.
In the pioneering modeling for the initial lymphatics [34], the Darcy law for flow around the capillary was not used. Instead, the hydrodynamic resistance of the primary valve was considered as the factor which affects the flow in the interstitium and in the initial lymph capillary.
Mendoza and Schmid-Schonbein [35] developed a two-dimensional model of the primary lymphatic valves, which was later refined by Galie and Spilker [36]. This model also assumed a two-dimensional flow in contrast to the model described in [35]. The interstitial space was included as a porous medium, neglecting deformations and describing flow with Brinkerman’s equations [37]. The model was completed by appropriate no-slip boundary conditions at the stationary walls, velocity matching at the fluid-structure interface, pressure and velocity continuity at the porous fluid interface and pressure at the boundaries.
Incorporation of the hydrodynamic resistance of the primary valve in our model, following the simple approach of Ref [34], is possible with the preservation of the analytical form of theory. Eq. (2.11) for the conservation of radial flow in the interstitium is generalized by means of the incorporation of the flux through the capillary wall KL(pinw–p) following Ref. [34]
| (2.27) |
where Eq. (2.13) is used and where p(R,z)=pinw
As there is an interruption in pressure distribution during crossing of the capillary wall, the pressure distribution within the interstitium is denoted as pin, its value on the external surface of the capillary wall, pinw, while the nomination p remains for intra-capillary pressure, and KL is the hydraulic conductivity of the terminal lymphatics per its unit length [34]. One obtains after integration
| (2.28) |
where
| (2.29) |
At sufficiently large KL, the radial flux is controlled by Kin, as this was accounted for in the presented theory. Formula (2.28) agrees with this suggestion because γ may be much larger than 1 in this case and pinw= p according to Eq. (2.28), as was assumed in the presented theory. At sufficiently small KL, the radial flux must decrease radial velocity and consequently decrease pinw, which is expressed by Eq. (2.28). The replacement of p(R,z) in Eq. (2.13) by pinw using Eq. (2.15) leads to generalization of Eq. (2.15) and consequently, Eq. (2.17) for λ
| (2.30) |
2.3 Analytical representation of fluid flow in the interstitium towards the initial lymph capillary initiated by the extrinsic pump
In the first theory for liquid flow through terminal lymphatics [34], the influence of a blood capillary adjacent to an initial lymph capillary is analyzed. This numerical theory may be simplified, supplemented and represented in analytical form, although this is beyond the scope of this first presentation. Reddy [34] neglects the pressure drop across the interstitium which corresponds to the condition
| (2.31) |
| (2.32) |
that follows from Eq. (2.28).
When assumption (2.31) is valid, the trans-capillary filtration rate from the blood capillary Qf and the flow rate into the terminal lymphatics from the interstitium may be quantified withoutdetermination of the pressure distribution within the interstitium because the pressure variation within it is small [34]. The net filtration at the blood capillary can be expressed by the Starling-Landis relationship where we omit the oncotic term
| (2.33) |
where Kc is the hydraulic conductivity of the blood capillaries, pc is the capillary pressure and Qfilt is the liquid flow through the blood capillary wall.
The flow into the terminal lymphatic can be obtained by integrating over the length of the lymphatic and multiplying by the hydraulic conductivity of the terminal lymphatic wall.
| (2.34) |
Assuming that p and pc are given, both Qs depend only on pin.
The dynamic changes in the interstitial fluid volume that occur when the normal fluid balance is altered are governed by the instantaneous rates of net trans-capillary filtration and lymph flow.
Therefore,
| (2.35) |
The interstitial fluid pressure is a non-linear function of interstitial fluid volume [22,38]. As soon as this function is known, the system of Eqs. (2.33) to (2.35) allows one to determine pin(t), and afterwards, both volumetric velocities, Qfilt and Qtl. The infusion of liquid from the blood capillary builds up local pressure to a level slightly above normal, which depends on the V increase and the elastic properties of tissue [22, 38].
When the opposite case is under consideration with a small Kin and a large Kl, necessity arises in the determination of pressure distribution. Indeed, local pressure may be large and may cause local swelling of tissue. As the pressure varies along the path towards the initial lymph capillary, the swelling, and consequently the hydraulic conductivity are variable as well. This is another kind of transport problem where the interstitium has to be modeled as an elastoporous medium. The unknown elastic constants become important in this case.
The systematic experimental and theoretical investigations of the Swartz [45] group created the fundamentals for modeling the flow of interstitial fluid through an elastoporous tissue. The experimental models regarding injecting nanoparticles into mouse tail allow one to formulate the mathematical problem as a one-dimensional case to describe the coupling between flows through the lymphatics and through the interstitium, taking into account the elastoporous properties of tissue. In our opinion, there is a perspective to extend this approach over the case of cylindrical symmetry, namely, a capillary with a surrounding interstitium. The pressure (velocity) distribution obtained for the blood capillary and the adjacent lymph capillary may be superimposed, which is necessary for modeling nanoparticles transport from the vaginal squamous layer towards a lymph capillary when there is an arteriole between them.
If tissue swelling is weak, approximation of the rigid porous media with the application of invariant hydraulic conductivity is valid. This means the validity of Eq. (2.21). While a similar equation may be valid for the blood capillary, specifically where the hydrodynamic resistance of the wall of the blood capillary is higher, γ<1 more probable. As linear hydrodynamic equations are valid in this case, the application of linear superposition for velocity distributions around the blood capillary and around the adjacent lymph capillary is possible.
Quantitative description of the influence of the extrinsic pump on flow through the interstitium may be more difficult than that caused by the intrinsic pump (Section 2.2) because in addition to arteriol pulsations, the contractions of the muscles adjacent to the lymphatics, central venous pressure fluctuations, gastrointestinal peristalsis and respiration may play a role [15]. Taking this into account, the conclusion about the relative role of the intrinsic and extrinsic pumps as reviewed in [15] is important.
It is not clear whether extrinsic mechanisms can have a significant or even dominant role in the pumping of lymph. Olszewski [39] considers extrinsic mechanisms to be secondary to intrinsic pumping based on their experimental results in humans.
Passive flow owing to a positive pressure gradient may also occur in edema during which lymph formation is increased [22]. In fact, Gashev et al. [31] report that for low levels of lymph formation, the intrinsic mechanism is dominant, but when the level of production rises, the active lymph pump is inhibited and the vessels become conduits.
2.4. Distribution of fluid velocity in the interstitium between the epithelial barrier and an adjacent initial lymph capillary
The cylindrical symmetry of the found distribution of velocity (Section 2.2) disappears in the presence of the epithelial barrier. However, there is a possibility of satisfying the boundary condition (2.5) taking into account the velocity distribution Eq. (2.21) and the peculiar feature of the flow in the interstitium, that is, the flow potential according to Eqs. (2.23) to (2.26).
At first glance, this opportunity cannot be realized because the velocities within the interstitium are low, i.e., the Reynolds number is small, which corresponds to the regime of viscous flow, and because of the necessity of satisfying the boundary condition for the tangential component νt
| (2.36) |
in addition to the boundary condition (2.5). Fortunately, there is anessential difference regarding the tangential velocity near an impermeable wall (the epithelial barrier) in the case of the interstitium and in the case of viscous flow in spite of the fact that the boundary condition (2.36) is valid in both cases. These velocities differ regarding the rate of ν t increase with increasing distance to the wall. ν t of viscous flow increases slowly with distance y to the wall, namely, proportional to y. As v t is small within the rather broad vicinity of the wall, the boundary condition (2.36) is usually accounted for. In contrast, ν t increases rapidly with increasing y within the interstitium, namely, the tangential flow retardation by the wall disappears on a distance scale of about 1-2 layers of cells, i.e., on a small distance of about few microns. This distance is very small in comparison with the width of the interstitium between the epithelial barrier and the capillary. Hence, we may disregard the boundary condition (2.36), assuming that the rigorous description of tangential flow in the narrow zone with a width of about some microns near the epithelial barrier is not important (Appendix 1).
As soon as the boundary condition (2.36) may be disregarded, the general methods of the theory of potential [41,42] may be applied for modeling fluid movement within the interstitium. In particular, the method of mirror image, well-known in electrostatics [41,42], may be used to satisfy the boundary condition (2.5), which may be formulated as the condition for the potential derivative
| (2.37) |
where n is the normal to surface, and S is the vagina surface, which may be considered approximately as flat regarding its section near the lymph capillary because the vagina diameter very significantly exceeds the capillary diameter. A qualitative picture for the velocity distribution, given in Figure 6, may be obtained taking into account that the y axis is the axis of the symmetry for the velocity distribution and that the streaming lines do not cross each other. The quantitative analysis in Appendix 1 confirms this picture.
Figure 6.
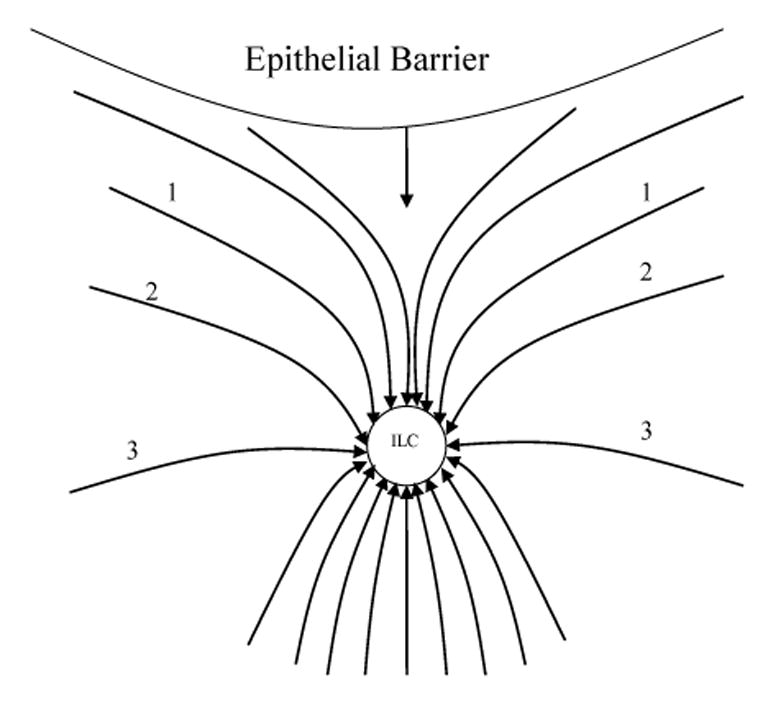
The distribution of interstitial fluid velocity around an initial lymph capillary (ILC) caused by suction due to angion contractility is depicted. Movement towards the surface of the vagina is suppressed because it is impermeable to fluid flow, and this affects flow streamlines 1, 2 and 3.
2.5 Time of transport of nanoparticles through the interstitium to lymph nodes
Colloid transport appears to control the kinetics of nanoparticles uptake by lymph nodes if the particles dimensions are less than 100 to 200 microns [6-8]. This is distinct from larger nanoparticles which are ferried to lymph nodes as associated with certain immune cells [10, 11]. Hence, a perspective arises with respect to smaller nanoparticles to quantify the kinetics of their uptake by lymph nodes when they are delivered intra-vaginally.
Three sequent stages may be considered when nanoparticles transport to lymph nodes from the vagina surface is considered: 1) transport through the epithelial barrier, 2) transport through the interstitium, and 3) transport through pre-nodal lymphatics.
At first glance, modeling for transport through the epithelial barrier is mandatory because this slow stage may control the entire uptake by lymph nodes. The prerequisite for such modeling is poor, although there has been effort regarding the investigation of transport through the mucus layer [43]. Our discovery of discrete foci [4] within the epithelial barrier creates a new and favorable situation for modeling the kinetics of nanoparticles uptake by lymph nodes after vaginal application. Transport through the epithelial barrier may be extremely enhanced due to such foci. In particular, the rate of transport for a foci cross-section may become comparable with the rate of transport through the interstitium. In the meantime, the width of the epithelial barrier is many orders of magnitude thinner than that of the interstitium. In such a situation, the time required for penetration of a nanoparticle through a foci may be short in comparison to the time necessary for such nanoparticle to cross the interstitium and reach an initial lymph capillary.
While foci may not essentially affect the kinetics of uptake by lymph nodes, their small amount (small portion of their area in comparison to the total area of the total vaginal squamous layer) may control the magnitude of uptake. In other words, the difference in concentration of nanoparticles near a foci exit may not differ essentially from the concentration near the foci entrance, or in other words, the concentration per unit surface of squamous layer may be very low.
As to the time it takes to transport nanoparticles along pre-nodal lymphatics, this is controlled by the flow velocity inside the initial lymph capillaries because the linear velocity is rather high inside the afferent capillaries [14,15].
The time of transport along an initial lymph capillary is affected by the axial dependence of lymph velocity, which follows from the results of Section 2.2.
| (2.38) |
where u=exp(lic/λ), ν=exp(z/λ), νic=dz(0)/dt, i.e., lymph velocity on the boundary between the initial lymph capillary and the afferent capillary.
The time of transport from point z, where a nanoparticle enters an initial lymph capillary to the boundary with an afferent capillary is obtained by integrating
| (2.39) |
The time increases from 0 corresponding to z=0 to infinity for z=lic. The infinity arises due to zero velocity near the dead end. This does not mean that nanoparticles entering an initial lymph capillary near its dead end do not contribute to the uptake. They diffuse downstream and afterwards become involved in lymph flow. Even a small difference between lic and z leads to the logarithm value of about 1. If condition (2.19) is met, the bracket in Eq. (2.39) approximately equals 2l/λ, which leads to an obvious result
| (2.40) |
This leads to a rather short time in the order of minutes because lic ∼ 0.5 mm [34], while some papers [44-46] report values for vic in the range between 1 and 15 microns/sec.
The derivation for time required for the transport from a foci to an initial lymph capillary Tlc corresponds to a couple of simplifications regarding the location of an initial lymph capillary and a foci. It is assumed that the initial lymph capillary is oriented parallel to the vagina axis and that the foci location corresponds to the shortest distance between the vagina surface and the initial lymph capillary (Figure 5).
When x=0, r = (y0 – y) and r’ = (y+y0) for nanoparticles trajectory from foci to the initial lymph capillary along the shortest distance, this leads to Eq. (A1.6) and simple integration for Tin.
| (2.41) |
At a certain distance from the foci, nanoparticles move due to diffusion because the convective velocity at y=0 is zero according to Eq. (A1.6). As convection predominates at y>δ, the integration is accomplished, starting from y=δ. The integration is straightforward and its result is
| (2.42) |
where the integration is accomplished, starting from y=δ.
| (2.43) |
Convection dominates when y>δ, while diffusion dominates when y<δ. Their contributions are comparable when y∼δ. This is the condition for the specification of the δ value in Eq. (2.43). The ratio of convective flux to diffusion flux is given by the Peclet number [13,47-51]
| (2.44) |
where L is the characteristic length (in our case is y), and v is vy(y). As Pe is usually expressed through the invariant characteristic length, the introduced Pe(y) is simply just the nomination for a crude estimate of the local ratio of convection flux to diffusion flux, Pe=1 for y=δ This yields an equation for δ estimation
| (2.45) |
where the nomination for maximal Pe, i.e., Pe for r=R is introduced
| (2.46) |
Hence
| (2.47) |
y0 cancels in Eq. (2.47). It takes a very simple form
| (2.48) |
where
| (2.49) |
A more rigorous derivation for δ is described in Appendix 2. The difference between Eqs. (2.48) and (A2.8) is small.
The substitution according to this equation into Eq. (2.43) reveals that G is of order 1 when δ/y0< 0.2. This simplifies the comparison of Eq. (2.39) and Eq. (2.41)
| (2.50) |
One concludes that transport through the interstitium takes one or two orders of magnitude longer time than transport along the initial lymph capillaries.
In spite of the fact that convection essentially decreases the distance remaining for the predominating diffusion, the contribution of the time necessary for diffusion TinD in the total time necessary for transport
| (2.51) |
It is not negligible. It may be estimated by means of the substitution δ according to Eq. (2.49) into the Einstein equation [47,48,51]
| (2.52) |
It is remarkable that D disappeared in the equation for TinD. This became possible because δ depends on D. It is even more surprising that TinD and TinC are expressed through the same dependence on y0, R and vr, if the multiplier G/2 is disregarded in Eq. (2.42). Combining Eqs. (2.42) and (2.52) yields, for total time, a product in which the first multiplier represents the main regularities, while the second multiplier is of secondary significance
| (2.53) |
The next values of parameters may be used in the calculation according to Eq. (2.51): lic -= 0.5 mm [34], vic = 5 microns/sec [44-46]. Three values for R (0, 20 and 30 microns) comprise its range as reported in the literature [44-46]. As to y0 or y0/R, literature data is scarce. The substitution δ/y0 according to Eq. (2.47) into the equation for G leads to its form:
| (2.54) |
which indicates its applicability boundary, namely the condition
| (2.55) |
which is inherent in the proposed method.
In fact, the method is applicable to the case of strong enhancement of diffusion transport due to convection and fails when the mechanism of coupling becomes more complicated. This occurs with decreasing vic or R as well because of the concomitant decrease in PeR(R) The method allows one to account for the convection retardation or enhancement by means of the introduction of the convective coefficient Ψc (Section 2.4) into Eqs. (A1.6), (2.41) and (2.42) as a multiplier. A more general description for the coupling between diffusion and convection is based on the standard method of the equation for convective diffusion [47-51], which will be described in the next publication and which is more complicated.Combining Eqs. (2.53) and (2.54) yields
| (2.56) |
3. Influence of channels on the convective diffusion of nanoparticles towards an initial lymph capillary
Experimental observation of nanoparticles transport with dimensions of about 100nm towards initial lymph capillaries indicates that channels with a similar diameter (about 100nm) exist between the initial lymph capillaries and the epithelial barrier, while the dimension for pore majority is an order of magnitude smaller [22]. Electron micrographs showed that channels between 50 to 100 nm exist in tissue [52]. This supports the presence of “free fluid channels” with diameter in the order of 50-100nm in tissue. Based on these facts, one concludes that the mathematical modeling of interstitial inhomogeneity based on two distinct compartments of tissue may give a more accurate picture [22, 53]. As the existence of the preferential channels is of principal interest for nanoparticles transport, we modified the two-compartment models to describe the case at hand. Only two kinds of cylindrical channels are considered, although real pores are not cylindrical and there is unknown distribution of their dimensions. The cylinder radius R1 and R2 and their amount per unit cross-section are n1 and n2, respectively. The porosity in this model is
| (3.1) |
The volume velocity is
| (3.2) |
where Pouiseille’s law is used. The velocity inside a large pore is
| (3.3) |
where gradp may be expressed in Eq. (3.2) through Q
| (3.4) |
| (3.5) |
it is possible that
| (3.6) |
in spite of
| (3.7) |
For example, R1 = 50 nm, R2= 2.5 nm, (R1/R2)2 = 0.0025 ≪ε1 = 0.025. Hence, the velocity in channels Vch may exceed Vr (according to Eq. (2.20)) by 1-2 orders of magnitude, estimated with the use of volumetric velocity within the lymphatics if the inhomogeneity of the interstitium satisfies conditions (3.5) and (3.6) (Figure 8).
Figure 8.
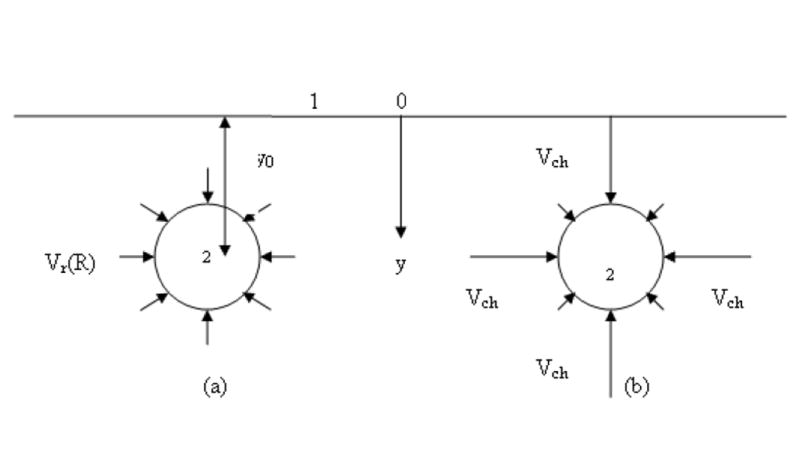
-
(b)uniform axial symmetrical velocity distribution (in the absence of channels).
-
(c)velocity in channels, where the liquid contacting the initial lymph capillary wall is much larger than on the major portion of the wall.
| (3.8) |
where ε ch (or ε 1) is the porosity due to channels. Hence ε ch has to be substituted into equation (2.56)
| (3.9) |
where index ch means that the channel presence is assumed.
Nanoparticle diffusion occurs only due to channel existence. As nanoparticle dimension is comparable with the channel diameter, steric obstruction may cause a decrease in nanoparticle diffusivity within a channel Dch in comparison with that in water D
| (3.10) |
where K ≪ 1. The steady diffusion flux is smaller, the smaller εch is, because the cross-section for diffusion is εch. The effective diffusion coefficient can be introduced which characterizes the steady flux per unit surface
| (3.11) |
This diffusivity may essentially decrease because the product of 2 small numbers, εch and K, is small. Channel presence causes the necessity of classifying foci in 2 groups. We will call a foci effective if it is connected with a channel (Figure 9). A foci without such a connection does not contribute to nanoparticles transport because such particles cannot penetrate a channel after arrival at a foci exit. Only a small portion of the squamous layer is damaged by foci and may be characterized by foci coverage θf; i.e., the ratios of the surface belonging to foci to the total surface area. Consequently, the overlap of a foci with a channel is a rare case, corresponding to effective foci. If there is no correlation in the location of foci and channels, the probability for this case may be estimated as the product
Figure 9.
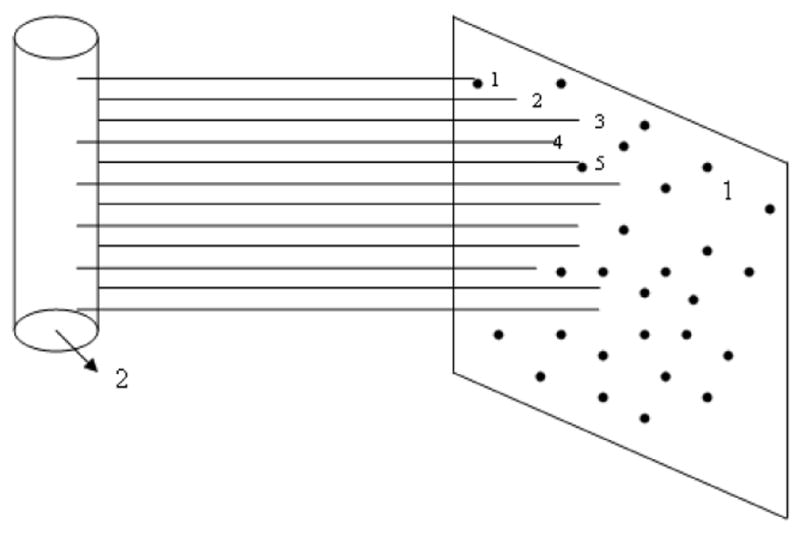
Illustration of the notion of effective foci and effective channels.
1 – section of squamous layer opposite to an initial lymph capillary (ILC); (2) –____ channels with ∼100 nm diameter between the ILC and the squamous layer;
• • • •foci
Only channels 1 and 5 have contact with foci and contribute to nanoparticles transport. Only foci 1 and 5 are effective. Other foci do not contribute to nanoparticles transport. Channels perpendicular to the drawn channels are normally not shown. Channels are normally not straight.
| (3.12) |
| (3.13) |
where Nef and Nf are the amounts of effective foci and their total amounts, respectively. Distinct from foci, all channels may effective, i.e., they contribute to nanoparticles transport if they are interconnected; hence, a drastic decrease in the amount of effective foci, when εch ≪ 1, does not affect the convective transport. In the meantime, in this case the total cross-section for diffusion near the epithelial barrier may decrease essentially.
We consider the kinetics only because a solution of the equation for convective diffusion [47-51] is necessary for the quantification of steady (quasi-steady) flux. It is noteworthy that the obtained equation for T does not depend on the foci amount (θf) because θf does not affect transport kinetics. Although foci were ignored in our kinetics consideration, it is obvious that this makes physical sense only when a certain amount of foci is present. However, the foci amount strongly affects the steady flux, no matter whether the kinetics is rapid or slow.
Assuming that the interstitium structure is isotropic, we consider movement along channels in all directions which allows liquid movement along channels in all directions. In fact, this model for channel structure is necessary to apply the derived equations for liquid velocity distribution around initial lymph capillaries in the presence of an impermeable squamous layer as derived in Appendix 1.
4. Enhancement of nanoparticles transport towards lymph nodes during inflammation
The elaborated primitive model for convective diffusion through the interstitium may be applied to our preliminary experimental results. As the nanoparticles are observed within the lymphatics even without inflammation, this means that there are channels between the initial lymph capillaries and the epithelial barrier with a diameter of 100 nm or larger even without inflammation. Moreover, some of the channels must overlap with squamous layer foci and form “effective foci.” The small amount of nanoparticles detected within the lymphatics (without inflammation) means that the amount of effective foci Nf is small. Eq. (3.13) may be transformed for cases of inflammation
| (4.1) |
The amount of foci may increase due to inflammation
| (4.2) |
| (4.3) |
The porosity caused due to the presence of channels may increase due to inflammation, Eq. (4.3).
Hence
| (4.4) |
because both multipliers in Eq. (4.1) increase. A rather modest swelling during inflammation strongly affects diffusion kinetics. As the diffusivity in the channels may be much smaller than that in unconfined liquid, i.e., K≪1 in Eq. (3.10), the increase in channel dimensions, less than, for example, twice, may increase diffusivity perhaps an order of magnitude during inflammation. This may lead to a large increase in interconnection between channels and foci, i.e., formation of new effective foci with concomitant enhancement of diffusion transport. This may be a major mechanism for enhancement of nanoparticles transport due to inflammation.
Although the absence of information about εchinfl during inflammation does not allow comparing our experimental data with the simple equation (4.3), some conclusions can still be made. With this purpose, we present some information about the measurement method and the results obtained.
We used electron microscopy to estimate the size of quantum dot aggregates that are found in the lymph nodes. We found that the clusters consist of several hundred to several thousand quantum dots, with few, if any, clusters smaller than 50-100 nm. We note that after incubation with biotinylated polyarginine, streptavidin-coated quantum dots form clusters of sizes from two-quantum dot doublets to micron-size monsters; if the original clusters were not broken up or aggregated during transport, then the size of the aggregates we found inside the lymph node would be the size actually transported. It is therefore interesting that most of the nanoparticle aggregates that we observed in the TEM micrographs were 50-200nm in size. This result suggests that large nanoparticles (100-200nm) may be taken up and transported to lymph nodes. Figure 10 shows a thin section of one such cluster from a lymph node, its diameter being about 140 nm. However, if this inference is correct, it poses the question of why smaller aggregates are not taken up. As to larger aggregates, it is known that they do not penetrate into the wall of the lymph capillary. As to smaller aggregates, it must be taken into consideration that the Qdots or other nanoparticles are detected within the lymph node if they are adsorbed there. In the meantime, the energy of adsorption decreases with particle (aggregate) dimension and depends on the physicochemical properties of the particles. For example, nanoparticles treated with polyethylene glycol are almost not adsorbed by blood cells [5]. If smaller nanoparticles with appropriate surface properties are not adsorbed within the lymph node, they leave it together with lymph flow via the efferent duct. The influence of the surface properties of the nanoparticle aggregates on their transport is found in our experiments and characterized in Figure 11. A mouse model of cervico-vaginal toxicity and inflammation for preclinical evaluation of topical vaginal microbicides [55,56,57] was used. 36 hours later after mice instillation with Qdots, mice were necropsied, lymph nodes were removed and clarified, and then the quantum dots were counted. It is obvious that such an approach is not sufficient for the determination of transport time between the instilling site and the lymph node. However, this allows us first of all to detect the transport, and second of all, to conclude that the transport time is shorter than 36 hours. Further, this approach allows us to determine the transport time by means of the decreasing time interval between Qdot instilling and lymph node removal. In the meantime, the purpose of this research was to obtain information about the influence of N-9 application on transport properties, namely, on foci formation and channel appearance due to swelling of tissue concomitant to inflammation. This became possible when our measurements (Figure 12) of Qdot uptake by the lymph nodes at several time intervals between Qdot instilling and pretreatment with N-9 were compared with the information in Refs [55,56,57] about the development of inflammation as a function of time.
Figure 10.
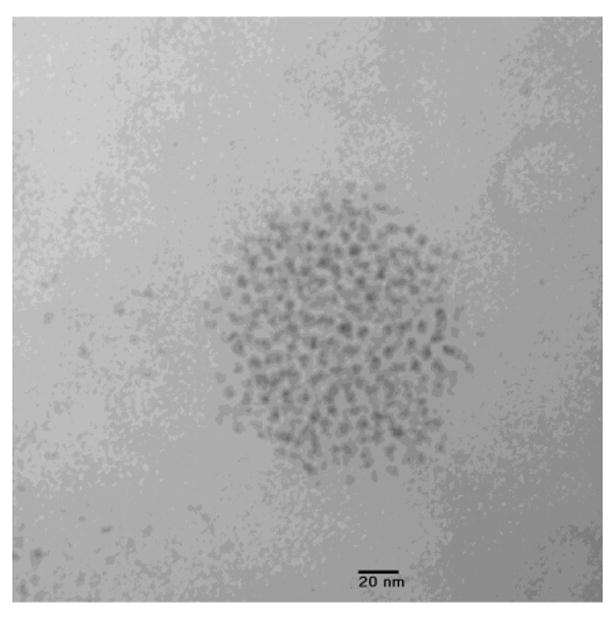
Electron micrograph of quantum dot cluster from lumbar lymph node. Paraformaldehyde fixation, Epon embedding, 10 nm section, unstained [4].
Figure 11.
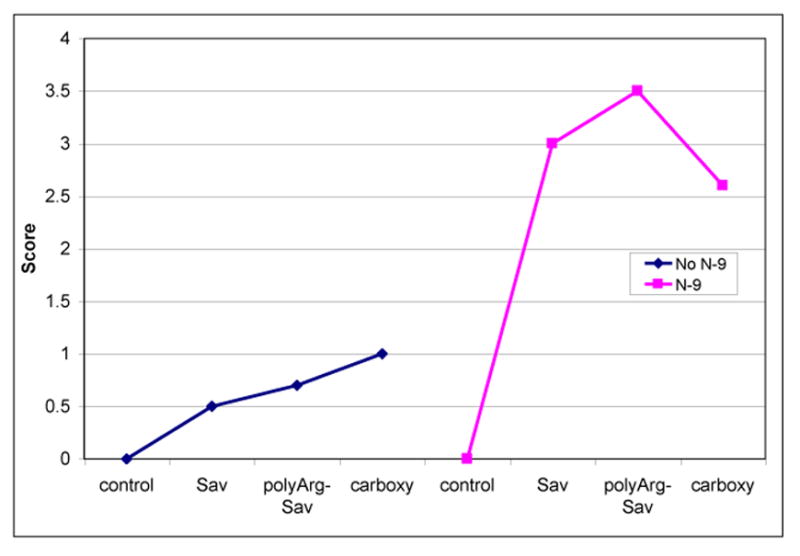
Quantum dots (Qdots) transport from vagina to lumbar lymph nodes. Quantum dots were instilled 12h after treatment with N-9 or saline. Lymph nodes were harvested 36h later, rendered transparent, and quantum dot clusters were counted. Coatings were: carboxyl, streptavidin (SAv), or SAv coupled to biotinylatedpolyarg-nonamer. Scoring: 1=1-10 clusters per node; 2=10-50 clusters per node; 3=50-100 clusters per node; 4=>100 clusters per node [4].
Figure 12.
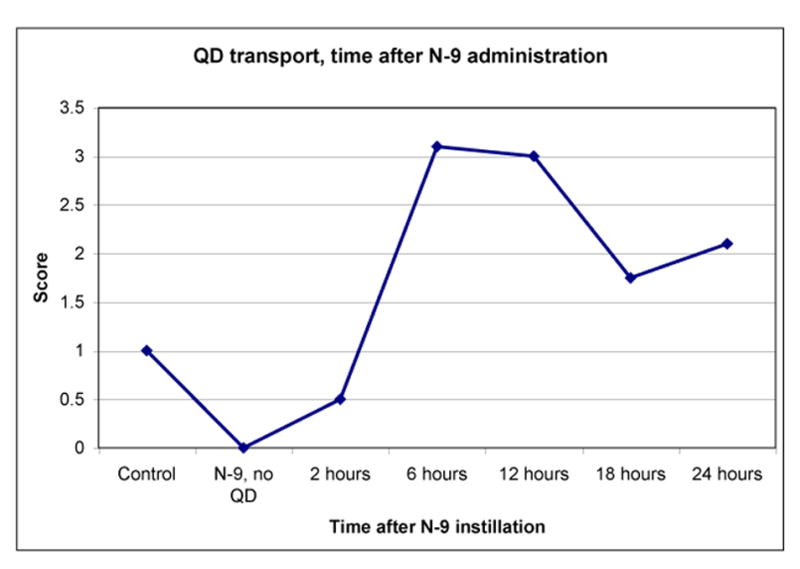
Quantum dots (Qdots or QD) transport at different times following N-9 pretreatment. Mice were treated using 1% N-9 in PBS, then after the stated interval, 30ul 1uM polyarg-Sav-QD were instilled. Lymph nodes were harvested 36h later and scored. Control mice were not treated with N-9 (5 animals per group). Scoring: 1=1-10 clusters per node; 2=10-50 clusters per node; 3=50-100 clusters per node; 4=>100 clusters per node [4].
Moderate epithelial damage was observed [55,56,57] when the time after N-9 pretreatment was 2 to 4 hours, while manifestations of inflammation culminated later, namely, when the time after pretreatment was about 12 to 20 hours. Epithelial disruption leads to foci formation, whose contact with channels leads to an increase in the number of effective foci. Indeed, an uptake into lymph nodes was observed at the time of maximum inflammation (Figure 12). However, the maximal uptake corresponds to Qdot instilling 12 hours after pretreatment with N-9. In the meantime, the inflammation extends more deeply into the interstitium after 12 hours [55,56,57], and we may speculate that a 3-dimensional (3-D) network of channels is formed during this time. Hence, 2-4 hours after treatment by N-9, foci form, and after about 6-12 hours, a 3-D network of channels may form.
More favorable conditions for nanoparticles transport enhancement occur at t=6 to 12 hours because the epithelial barrier damage preserves, although it is not maximal [55,56-58] and there is another stage for the formation of a 3-D network of channels because inflammation leads to swelling of the interstitium between the epithelial barrier and the initial lymph capillaries. Although secretion of fluids at the vaginal surface controls the duration of Qdots presence in the vagina, there is a time interval when Qdots are present in the foci coincidental with the simultaneous existence of a 3-D network of channels, i.e., when the amount of effective foci may strongly increase. Naturally, this interpretation has to be confirmed by observing the appearance of a 3-D network of channels during inflammation.
5. Discussion
Current understanding of HIV sexual transmission is primarily based on binding the virus to dendritic (or Langerhans) cells at the vaginal mucosa, transporting the virus through the interstitium (lamina propia), accumulating the virus within draining lymph nodes where it replicates in CD4+ cells and disseminating the virus to host tissue and organs where it ultimately results in infection. Our direct visualization of Qdots transport to lymph nodes from the vaginal mucosa in a mouse model has not confirmed this generalized scenario. In contrast, we detected the presence of foci within the epithelial barrier which makes it possible for Qdots to be transported to lymph nodes via a process independent of dendritic cells.
Since the cellular-carrier mechanism of nanoparticles transport by dendritic cells could not be confirmed, understanding the transport of nanoparticles to lymph nodes becomes possible on the basis of generalized notions of colloid science [47-51], namely: viruses are considered as a “biocolloid” and transport takes place in a porous medium, representing tissue. The porous medium is always considered as an adsorbing medium, while the transport mechanism of nanoparticles occurs by either diffusion or convective diffusion, or their combination. Penetration of nanoparticles through foci occurs by means of diffusion, while interstitial transport and transport within lymph nodes is controlled by convective diffusion. These transport processes attain new features due to the coupling between diffusion (convective diffusion) and adsorption.
While the notions of colloid science may be sufficient for understanding the mechanism of transport processes, biophysics remains important for defining the transport properties of this system. The biophysics or physiology of afferent lymphatics (contractility of the afferent capillary, etc.) controls the flow of interstitial liquid towards initial lymph capillaries.
The main regularities of convective diffusion are predetermined by the detailed features of the hydrodynamic flow towards initial lymph capillaries (Figures 2 and 6). This leads to the formation a two-zone system: a zone with predominating diffusion near the epithelial barrier where Pe<1, and a zone of predominating convection where Pe>1 near the initial lymph capillaries. When the dimensionless distance y0/R between the epithelial barrier and the initial lymph capillaries is not large (y0/R < 3 or 4), the zone of predominating diffusion is rather thin (Figure 7a). In this case, the diffusion stage of nanoparticles transport does not take a long time and the total time of transport through the interstitium is rather short, as well as the time, Tln, necessary for the onset of nanoparticles uptake by the lymph nodes. Hence, the notion of a mode of rapid transport (Tln in hours) may be introduced and identified as that arising when y0/R is not large. In contrast, an increase in y0/R leads to an increase in the thickness of the zone of predominating diffusion which leads to a large increase in the time necessary for diffusion transport of nanoparticles, and consequently to a long Tln (day or longer) for particles to reach the lymph nodes (Figure 7b). Hence, the mode of slow transport may be introduced corresponding to a sufficiently large y0/R.
Figure 7.
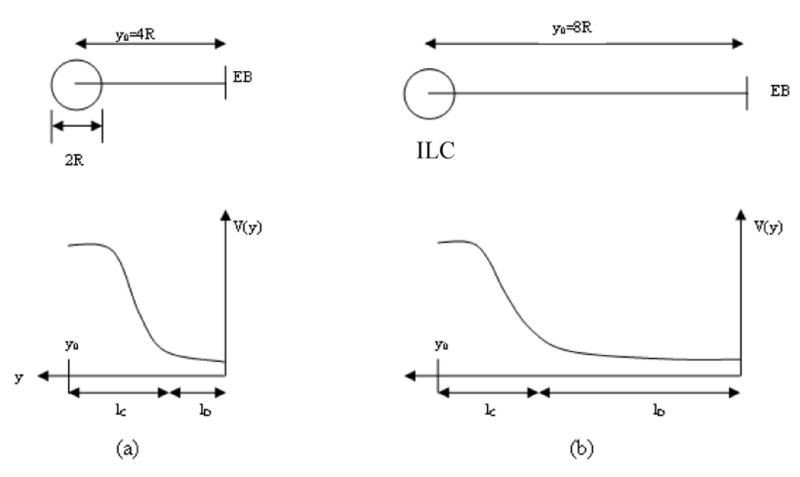
- The distance y0between the epithelial barrier (EB) and the initial lymph capillary (ILC) is rather short, y0=4R, which corresponds to the narrow zone (lD) of predominating diffusion. As lDis not large, the diffusion time is not long and the total time for transport is not long as well due to fast convective diffusion.
- The distance y0is not short, y0=8R, which corresponds to the width of the zone of predominating diffusion lD∼7R and hence, transport takes a long time due to diffusion transport only.
Our direct observations that nanoparticles are transported to lymph nodes from the vaginal mucosa in a mouse model support the fact that such particles must be transported via the initial lymphatics or lymph capillaries. Accordingly, transport of nanoparticles with dimensions of about 100 nm from the epithelial barrier to initial lymph capillaries points to the existence of “channels” of similar diameter connecting the epithelial barrier and the initial lymph capillaries, and that through such channels particle transport takes place. The overlapping or interconnection of a channel with a foci is necessary for the transport of nanoparticles to initial lymph capillaries. Our analysis indicates that only a small portion/fraction of foci overlaps with channels, and it is through such interconnected foci that nanoparticles transport occurs. These may be called “effective foci,” while other foci (which do not connect to channels) do not contribute to transport (Figure 9).
Within channels, the velocity of interstitial fluid may be much higher compared to the case when the radial velocity is uniform over the initial lymph capillaries surface in the absence of a channel. The enhancement of convection within a channel increases with decreasing partial porosity due to the presence of channels, εch, which is expressed by Eq. (3.8). As a result, the convection promotes nanoparticles transport from a larger distance according to this system of channels.
The proposed theory of kinetics of convective diffusion (Section 3) and the derived Eq. (2.56) for time T of nanoparticles transport towards the lymph nodes due to convective diffusion allow us to characterize quantitatively the role of convection by means of comparison of T and an imaginary transport time TD(y0) in the absence of convection, when the transport is caused by diffusion only.
| (5.1) |
As nanoparticles transport occurs only through channels and its velocity is larger within them, we generalized Eq. (2.49) taking into account Eqs. (3.8) and (2.49)
| (5.2) |
Table 2 shows that PeR(R,K,εch)≫1 almost always, that is not valid for PeR(R), when R = 10 micron.
Table 2.
The dependence of Peclet number on initial lymph capillaries radius R and characteristics εch and K depending on channel cross-section and their porosity according to Eq.(5.2).
| R (micron) | |||
|---|---|---|---|
| Kεch | 10 | 20 | 30 |
| 1.0 | 0.5 | 2.0 | 4.5 |
| 0.1 | 5.0 | 20 | 45 |
Eq. (2.55) is easily generalized taking into account for εch and Dch.
| (5.3) |
The multiplier in square brackets demonstrates the decrease in time due to convection.
The small influence of convection is difficult to estimate for R=10 microns because PeR(R, εch, K) is not large for εchK=0.3. The results presented in Table 3 for R=20 and 30 microns show that the time required for nanoparticles transport to lymph nodes decreases more than an order of magnitude due to convective diffusion in comparison with time TD(y0), when diffusion only is accounted for. As found times T(y0) are rather small, it would be important to extend calculations over a larger distance, for example, y0 = 600, 800 microns, etc. Unfortunately, the errors will increase for larger y0 because the dependence of velocity Vr(r) distribution on z becomes important in Eq. (2.21).
Table 3.
Transport time TD(y0) due to diffusion only according to Eq. (5.1) and transport time T due to convection, Eq. (5.3), K=εch=0.3.
| y0 (micron) | TD(y0) (hour) | R (micron) | ||
|---|---|---|---|---|
| 10 | 20 | 30 | ||
| T (hour) | ||||
| 200 | 37 | 34 | 1.8 | 1.0 |
| 300 | 83 | 91 | 5.0 | 2.8 |
| 400 | 150 | 150 | 9.0 | 5.1 |
If y0 is large, enhancement of diffusion flux during inflammation may not be sufficient because the transport time, T, at slow kinetics is long, while this time needs to be shorter than the therapeutic time, Tth, necessary for the therapeutic efficiency of nanoparticles uptake by the lymph nodes,
| (5.4) |
Therapeutic time is defined as the time of virus arrival at the lymph nodes and the beginning of infection.
An estimate for the influence of inflammation on slow kinetics is possible on the basis of Eq. (5.1). A huge decrease in transport time is possible during inflammation because the effective diffusivity, expressed by Eq. (3.11), increases (Eq. (5.1)), which allows the introduction of the characteristic length, y0crD, which characterizes a kinetic constraint with respect to the achievement of a therapeutic effective uptake by the lymph nodes. The time of nanoparticles transport T to the lymph nodes during inflammation as equal to Tth has to be substituted into Eq. (5.2), which transforms into an equation for y0crD
| (5.5) |
Tth specification is independent and not a simple task. Tth has to be shorter than 24 hours perhaps because a portion of viruses arrive at lymph nodes after a time of about 24 hours according to [1].
When nanoparticles transport is slow and viruses arrive at lymph nodes earlier, their replication may start before nanoparticles’ arrival at lymph nodes, or before the amount of nanoparticles accumulated within lymph nodes becomes sufficient to inhibit virus replication. Hence, the necessary condition at slow kinetics
| (5.6) |
has to be satisfied to achieve a therapeutical effect (effective slow kinetics).
A condition which is more exact than Eq. (5.6) accounts for transport enhancement due to convective diffusion which leads to a longer critical distance The equation for follows from the substitution Tth on the left-hand side of Eq. (5.1) and the substitution Tth on the left-hand side of Eq. (5.3) and their comparison
| (5.7) |
| (5.8) |
As the right-hand side of Eqs. (5.7) and (5.8) are equal, one obtains
| (5.9) |
The calculated results according to this equation are given in Table 4.
Table 4.
Maximal distance y0cr between the epithelial barrier and initial lymph capillaries for which transport towards the lymph nodes is possible during time Tth. y0crD and y0crCD are calculated taking into account diffusion only or convective diffusion, respectively.
| εchK | y0crCD (micron) | |||
|---|---|---|---|---|
| y0crD(micron) | R = 20 microns | R = 30 microns | ||
| 170 | 1.0 | 280 | 350 | |
| 170 | 0.3 | 380 | 510 | |
| 170 | 0.1 | 570 | 770 | |
Tth = 12 hours, Dch = 3.10-13 m2/sec
The main constraint is characterized by the y0crD value because it is not clear how condition (5.1) may be satisfied when
| (5.10) |
Naturally, the systematic measurement of y0 is required. The interpretation of our kinetics data (Figure 12) is complicated because our measurements focus on nanoparticles uptake in lymph nodes. In the meantime, a huge amount of initial lymph capillaries collect nanoparticles from their interstitial vicinity. Afterwards, the nanoparticle streams from single initial lymph capillaries are mixed in an afferent capillary and reach a lymph node. The different initial lymph capillaries of the same initial capillary bed are characterized by different distances y0i to the epithelial barrier, where ‘i’ is the number of a certain initial lymph capillary within the initial capillary bed. Hence, different kinetics of uptake by different initial lymph capillaries has to be taken into account for complete interpretation of the kinetics of nanoparticles uptake by a lymph node.
6. Future Directions
The first group of new tasks to be addressed is the further development of the model. The initial lymphatic bed has to be considered as the generator of fluid flow in the interstitium towards the lymph capillaries. The possible adsorption of nanoparticles on the extracellular surface within tissue during their transport through the interstitium has to be incorporated into the model. This adsorption retards the propagation of the convective diffusion front towards the lymph capillaries and causes nanoparticles loss with respect to their ultimate uptake by lymph nodes.
While the described transport processes characterize the conditions which affect the onset of nanoparticles uptake by lymph nodes, control of this uptake and its kinetics is possible only by means of modification of the surface properties of nanoparticles and by controlling inflammation. The stronger adsorption bond for nanoparticles within the lymph node is favorable for decreasing their loss caused by the involvement of a portion of free nanoparticles into the lymph stream towards the efferent capillaries. The weaker adsorption bond within the interstitium is favorable for decreasing nanoparticles loss. In spite of these opposite requirements, they may be (in principle) satisfied if the difference in adsorption properties within the lymph node and within the interstitium is taken into account. Hence, an important prerequisite for optimizing nanoparticles uptake by lymph nodes is the characterization of the adsorption properties of the interfaces within the lymph node and within the interstitium. If the adsorption characteristics are known, the nanoparticles surface could be modified in such a way so that nanoparticles adsorption during transport through the interstitium would be suppressed, while strong adsorption binding within the lymph node would be enhanced.
The second group of tasks to be addressed relates to the application of a more rigorous mathematical apparatus. In fact, a primitive asymptotic approach was used when only the extreme cases of strong predomination of either convection or diffusion were considered. The standard procedure based on the equation for non-steady convective diffusion may allow us to achieve more rigorous quantification. The next step would be the quantification of the coupling between convective diffusion and reversible adsorption of nanoparticles, where great mathematical difficulties are well known.
7. Conclusions
In our experiments, we discovered that the concentration of dendritic cells in the interstitium is too low to explain the high level of Qdots transported to the lymph nodes [4]. Further, our discovery of foci within the epithelial barrier, and Qdots penetration through such foci and their subsequent significant accumulation within the lymph nodes further support our approach that colloid transport plays a central role in this process. The general regularities of colloid transport in porous media control nanoparticles transport, while their long residence within lymph nodes is caused by their physical adsorption onto the interior surfaces of lymph nodes. Thorough review of the relevant research of other groups has shown that currently the role of phagocytosis has not been confirmed and that attention is now being placed on the physicochemical aspect of lymphatic delivery of drugs.
An additional conclusion is that channels with dimensions of about 100 nm or larger must exist between the squamous layer of the epithelial barrier and the initial lymph capillaries to make this nanoparticles transport possible. When the porosity, εch, caused by those channels is low, the contact between a foci and a channel is a rare case which corresponds to “effective foci,” while the majority of foci do not contribute to nanoparticles transport in this case. This explains the weak transport through the interstitium when the epithelial barrier is in the normal intact state, i.e., without pretreatment with N-9. Pore broadening during inflammation leads to the formation of a 3-D network of channels and to a drastic increase in the amount of effective foci because the probability for contact between foci and channels increases when the channel amount increases due to swelling. This explains the observed significant enhancement of nanoparticles transport towards lymph nodes during inflammation.
The transport enhancement due to inflammation found in our case, from the epithelium to lymph nodes, is a general phenomenon which creates the possibility of enhancing the transport of drug-loaded nanoparticles.
According to the developed integrated transport model, diffusion controls nanoparticles transport through the foci since the fluid near a foci is almost stagnant, while axial lymph flow along initial lymphatics induces radial flow in the surrounding interstitium towards a capillary with the concomitant transport of nanoparticles through it. The main result of our modeling is the discrimination of two main modes of nanoparticles transport to lymph nodes: 1) the mode of fast transport (time Tln for the onset of nanoparticles uptake by lymph nodes is some hours), and 2) the mode of slow transport (T is a day or more). The introduction of these modes reflects the existence of a zone with predominating fast convection near initial lymph capillaries, and another zone with predominating slow diffusion at a larger distance y from the initial lymph capillaries near the epithelial barrier. When the distance between an initial lymph capillary and the epithelial barrier (y0) is smaller than a critical thickness y0cr, the zone of slow diffusion is narrow and the diffusion does not retard the transport. This is the mode of fast kinetics (Figure 7a). When y0> y0cr, the slow diffusion within zone y0 – y0cr controls the transport time T, which becomes long. This is the mode of slow kinetics (Figure 7b). With respect to HIV inactivation within lymph nodes, introduction of the notions of effective and delayed (in comparison with viruses) transport of nanoparticles towards lymph nodes and their quantification deserves major attention. When nanoparticles arrive at a lymph node earlier than viruses, nanoparticles transport may be effective in providing, within the lymph node, a concentration of an antiviral drug that can inactivate the virus, either directly or indirectly. In the opposite case, when nanoparticles arrive at the lymph node later than the virus, the application of therapeutic nanoparticles may be in vain (the case of delayed transport).
Two main transport properties which control the time of nanoparticles transport to lymph nodes are: 1) the actual distance between the epithelial barrier and the initial lymph capillary, y0’, and 2) the quantified critical value y0crCD. When y0< y0crCD, nanoparticles transport may be effective. In the opposite case, the idea of preventing virus replication within the lymph nodes with the use of therapeutic nanoparticles fails. The equation for y0crCD as a function of nanoparticles diffusivity, initial lymph capillary radius and time of virus transport to the lymph nodes is derived.
Nanoparticles cannot arrive at lymph nodes during inflammation time Tth about 105 sec and the anti-HIV therapy cannot be provided if the distance between the epithelial barrier and initial lymph capillaries exceeds a critical value y0crCD, as given by Eq. (5.9).
In conclusion, mechanisms of colloid transport and physical adsorption create the premise for a new strategy which may provide much higher uptake of therapeutic nanoparticles by lymph nodes when the optimal properties of nanoparticles (their dimensions and adsorbability within lymph nodes and their concentration in intravaginal microbicides) are predicted by modeling, and then supported by testing in animal models.
Highlights.
Convective diffusion of nanoparticle drug carriers to draining lymph nodes from epithelial barriers, especially from vaginal surface.
Conditions for preventing HIV infection by controlling nanoparticle convective diffusion to lymph nodes.
Nanoparticle transport depends on transport properties of epithelial barrier and convective diffusion in interstitium.
Acknowledgments
The authors acknowledge funding for this research from the National Institute of Allergy and Infectious Diseases, National Institutes of Health (Grant Numbers R21AI082738 and R33AI082738). The authors especially acknowledge the key contributions of Dr. Byron Ballou and Ms. Susan Andreko of Carnegie Mellon University for performing the Qdots uptake experiments in the mouse model and for providing the data to support the development of the models presented in this paper. We would like to thank Dr. Thomas Hope and his laboratory staff at Northwestern University for the results that elucidated the presence of foci in the epithelial barrier. Special thanks are dedicated to Dr. Yacoob Tabani for his great effort in preparing this manuscript and the figures, and to Ms. Anita Labib for editing and enhancing the final version of this review.
Appendix 1. Application of a method of mirror image for modeling lymph flow in the interstitium between an initial lymph capillary and the epithelial barrier
As the potential of lymph flow and its distribution in space is similar to the well-known case of electric potential which is described by the Laplace equation (2.25), we may try to use the method of electrostatic analogy, i.e., use the experience of electrostatic problems.
An analogous situation arises in electrostatics when spherically symmetrical potential distribution around an isolated charge q in vacuum
| (A1.1) |
where r is the distance to charge, is deformed due to the presence of a conducting plate at some distance y0 (Figure A.1). The electrical field of charge q attracts charges of opposite sign in the plate or repulses charges of the same sign which leads to the formation of a distribution of induced charge −qi(x), while at the same time the lines of the electric field in vacuum are distributed between charge q and charges −qi(x), whose total charge is −q.
Figure A1.1.
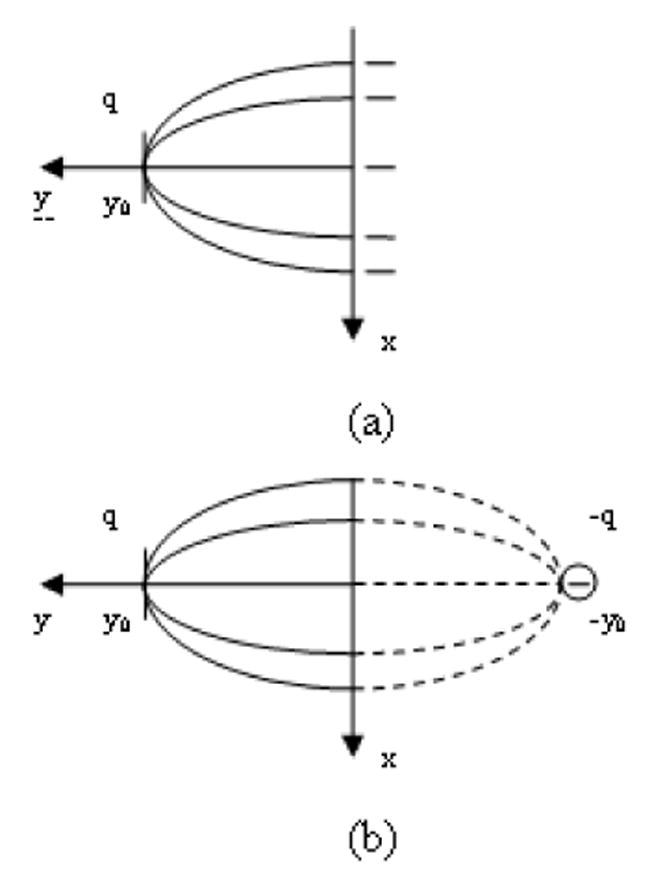
a. Influence of a conducting plane on the distribution of an electric field originated from a positive charge +q, located at distance y0. y=0 within the plate.
b. The same electric distribution is predicted by the mirror image method between the charge q and an imaginary charge –q with location y=-y0, x=0. The real lines of the electric field are shown by solid lines and the imaginary lines of the electricfield are shown by dotted lines.
In electrostatics it was found that the identical distributions in space for an electric field and corresponding potential exists, when in addition to the real charge, an imaginary charge −q is introduced as a mirror image of the charge q (Figure A.1). The advantage of this method, known as the method of mirror image, is that a simple description of the potential distribution arises, namely, the linear superposition of potentials generated by the real charge q and the imaginary charge −q. The boundary condition in this well-known problem is that the conducting plate is isopotential, its potential is zero.
The boundary condition in our case is related to the gradient of potential on the surface S in between the real and mirror charges
| (A1.2) |
It may be satisfied if the equal charges of the same sign are used as the real charge and its mirror image
| (A1.3) |
The normal components of gradient of these potentials on the S surface are equal and directlyopposite to each other: . This shows that the superposition satisfies the boundary condition (A1.2) that isillustrated in Figure A1.3.
Figure A1.3.
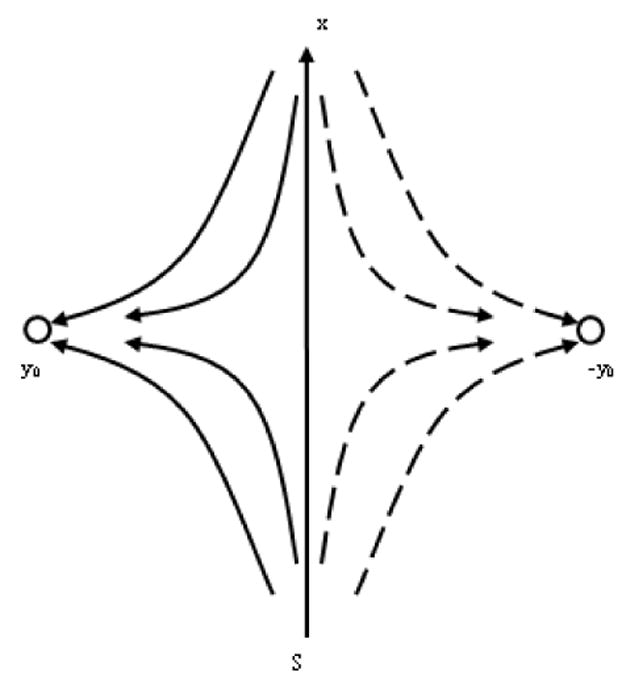
The boundary condition (A.3) of fluid near the impermeable epithelial barrier may be satisfied in the framework of the mirror image method by the introduction of an identical inlet of flow and its location as a mirror image, i.e., at y=-y0, x=0. The surface S is similar to the barrier surface, y0is the distance between the axis of the initial capillary and the barrier. The streaming lines of interstitial flow are shown by solid lines. The streaming lines of imaginary flow are shown by dotted lines.
While this derivation is usually presented for the 3-D case, it is valid for the 2-D case as well, i.e., when a charged needle is considered instead of a single charge, while r and r’ are distances between two points either within the 3-D space or within the 2-D space. r and r’ are illustrated in Figure A1.2, where the plane y=0 coincides with the barrier surface, and y0 is the distance from the lymph capillary axis to the barrier. r and r’ are distances from the real outlet, i.e., lymph capillary and outlet, which is its mirror image, to any point of the interstitium x, y.
Figure A1.2.
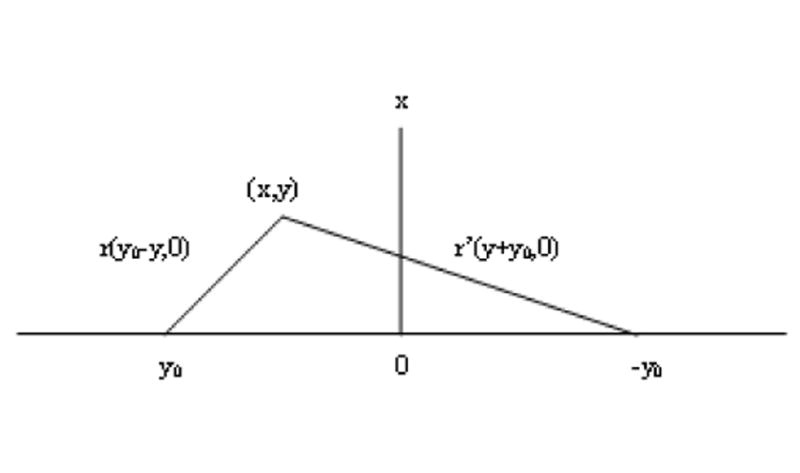
The potential for any point with coordinates x,y is determined by r and r’, where r is its distance to the real charge, located at y=y0, x=0, and r’ is its distance to the imaginary charge, located at y=-y0, x=0.
| (A1.4) |
The axial symmetry is valid for potential distribution around a charged cylindrical needle instead of the spherical one in Eq. (A1.3). The electrical field around the needle decreases with distance as r-1. This regularity exists for velocity distribution formed by ILC, namely Eq. (2.21) where z dependence will be disregarded due to condition (2.19). Taking into account that and that one obtains
| (A1.5) |
The next equation follows from Eq. (A1.5) for normal component of liquid velocity distribution along the shortest distance between EB and ILC, i.e., for x=0
| (A1.6) |
The substitution y=(y0-R) on the right hand side yields reasonable result: .
The derived equation (A1.5) agrees with the qualitative feature of the velocity distribution, as illustrated in Figure 6. The velocity is directed towards the capillary in the vicinity of the axis of symmetry x=0, i.e., Vy>0, at small x and the velocity is directed towards the barrier, i.e., Vy<0 at sufficiently large x. Eq.(A1.5) shows the change of sign at the transition from small x to large x because at small x, the first term predominates, and at large x, the second term predominates, while their signs are opposite. At x=0, the first term in bracket is (y-y0)-1, while the second term (y+y0)-1 is smaller. At large x, r and r' are almost equal, and the ratio of the second term to the first term is about (y+y0)/(y-y0), i.e., the second term predominates.
The method of mirror images is rigorous in application to the fixed charges. If charges are distributed on a conducting surface, the mutual polarization of charges on the real conducting surface and the image charges is unavoidable. Nevertheless, the method remains useful as approximate one, when
| (A1.7) |
The manifestation of this limitation respective to our task is the violation of the necessary condition that pin(R,θ) is invariant over the surface of the initial capillary for fixed z. Indeed, p inside the initial capillary depends on z only, while the boundary condition (2.3) shows that pin(R,θ) has to be invariant as well. This is valid for the first term in superposition (A1.3), while the second term causes angular dependence because of the variation r’ over the lymph capillary surface at constant z. However, the variation of 1/r’ is small in comparison with 1/r, when the condition (A1.7) is valid. Hence, the condition (A1.7) restricts the applicability of the results obtained in this Appendix.
Figure A1.4 presents a semi-quantitative illustration of the statement in Section 2.4 that the account for the boundary condition (2.36) is not important if the description of tangential flow near the EB within zone, including 2-3 layers of extracellular matrix, is not required for quantification of NPs transport. The interstitium between the EB and the ILC includes tens or even hundreds of cell layers because its thickness is larger than 3R which corresponds to the interesting case of not small transport time T. As the diffusion dominates near the EB, even a large error in the description of convection within this zone cannot cause an essential error in T quantification. Hence, although the difference between true Vx(y) and its representation Vx(Ψ(x,y)), based on velocity potential Ψ(x,y), is large near the EB, this cannot cause an essential error in T quantification. However, another question arises, as to whether the introduction of a wrong boundary condition Vt(Svag)≠0 instead of Eq.(2.36) may affect the velocity distribution from the EB, and consequently, affect NPs transport. The refusal from boundary condition (2.36) means its replacement by the boundary condition Vt(y=0)=-Vx(y=0), which is unknown and is illustrated in Figure A1.4. This kind of boundary condition is known in the theory of the so-called hybrid system [37], consisting of a porous half space with a flat interface between it and an adjacent half space where a tangential viscous flow takes place with a velocity Vt(y=0). While this velocity is given, the question arises as to how deep this flow penetrates into the porous media. A notion of penetration depth is introduced in the papers cited in [37]. It turns out that the theory predicts the penetration depth of about 1 to 3 layers of particles, which forms a porous media. This allows one to conclude that an essential difference between Vx(y) and Vx(Ψ(x,y)) is possible only within 1 to 3 layers of cells near the EB.
Figure A1.4.
Illustration for dependencies of true tangential velocity Vx and its approximation Vx(Ψ) on distance y to the EB. The circles on the right show the layers of cells of the extracellular surface. ______Vx(y), --------Vx(Ψ(x,y)).
Appendix 2. Determination of boundary applicability for the equation describing predominating convective transport
The influence of convection is disregarded during the first stage of transport, which is caused mainly by diffusion. The influence of nonsteady diffusion is disregarded during the main second stage of transport which is caused mainly by convection. This means that the nonsteady diffusion is accounted for only within the zone of predominating diffusion 0<y<δ, while the steady convection is accounted for only within the zone of predominating convection δ<y<(y0-δ). The solution of the equation of nonsteady diffusion within half space, when the concentration in y=0 is invariant
| (A2.1) |
is well known
| (A2.2) |
where
The next assymptotics will be used in the derivation
| (A2.3) |
| (A2.4) |
Initially, the diffusion flux (not far from the EB) is very strong and exceeds the convective flux. As the diffusion flux decreases in time, the convective flux of NPs becomes equal to the diffusion flux at certain time t and distance δ. This gives a condition for δ determination
or
| (A2.5) |
When δ/2(Dt)0.5≫1, the right-hand side is exponentially small according to Eq. (A2.5) and the condition (A2.5) cannot be satisfied. Its solution exists when δ/2(Dt)0.5<1, which leads to simplification
| (A2.6) |
due to assymptotics (A2.3)
The velocity distribution (A1.6) simplifies for δ≪y0
| (A2.7) |
t is the time of displacement of the diffusion front on distance δ, which allows one to apply the Einstein equation (2.52). Using this equation, the replacement t with δ in Eq. (A2.6) yields
| (A2.8) |
In spite of the large difference in approach used in the derivation of Eqs. (2.47) and (A2.8), the difference between them is not large. This justifies the developed theory as an approximate one.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.de Witte L, Nabatov A, Geijtenbeek TB. Trends Mol Med. 2008;14:12–19. doi: 10.1016/j.molmed.2007.11.001. [DOI] [PubMed] [Google Scholar]
- 2.Ballou B, et al. Bioconjugate Chemistry. 2007;18:389–396. doi: 10.1021/bc060261j. [DOI] [PubMed] [Google Scholar]
- 3.Kim S, et al. Nat Biotechnol. 2004;22:93–97. doi: 10.1038/nbt920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ballou B, Andreko SK, Osuna-Highley E, McRaven M, Catalone T, Bruchez MP, Hope TJ, Labib ME. PLOS ONE. 2012;7(12) doi: 10.1371/journal.pone.0051995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bachmann MF, Jennings GT. Nature Reviews Immunology. 2010;10:787–796. doi: 10.1038/nri2868. [DOI] [PubMed] [Google Scholar]
- 6.Swartz MA. Adv Drug Deliv Rev. 2001;50:3–20. doi: 10.1016/s0169-409x(01)00150-8. [DOI] [PubMed] [Google Scholar]
- 7.Reddy ST, Rehor A, Schmoekel HG, Hubbell JA, Swartz MA. J Control Release. 2006;112:26–34. doi: 10.1016/j.jconrel.2006.01.006. [DOI] [PubMed] [Google Scholar]
- 8.Oussoren C, Zuidema J, Crommelin DJ, Storm G. Biochem Biophys Acta. 1997;1328:261–272. doi: 10.1016/s0005-2736(97)00122-3. [DOI] [PubMed] [Google Scholar]
- 9.Leak LV. J Cell Biol. 1971;50:300–323. doi: 10.1083/jcb.50.2.300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Reddy ST, et al. Nature Biotech. 2007;25:1159–1164. doi: 10.1038/nbt1332. [DOI] [PubMed] [Google Scholar]
- 11.Swartz MA, Berk DA, Jain RK. Am J Physiol. 1996;270:H324–H329. doi: 10.1152/ajpheart.1996.270.1.H324. [DOI] [PubMed] [Google Scholar]
- 12.Manolova V, et al. Eur J Immunol. 2008;38:1404–1413. doi: 10.1002/eji.200737984. [DOI] [PubMed] [Google Scholar]
- 13.Elimelech M, Gregory J, Jia X, Williams RA. Particle Deposition and Aggregation. Butterworth Heinemann; 1995. [Google Scholar]
- 14.Zawieja DC, von der Weid PY, Gashev AA. Comprehensive Physiology. American Physiological Society by Wiley-Blackwell; 2011. Microlympatic Biology. Chapter 5 in. [Google Scholar]
- 15.Margaris KN, Black RA. J R Soc Interface. 2012;9(69):601–612. doi: 10.1098/rsif.2011.0751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Granger HJ, Dhar J, Chen HI. In: Proceedings of Workshop on Altrumin. Sgouis JT, Rene A, editors. 1975. pp. 114–124. [Google Scholar]
- 17.Parker JC, Gilchrist S, Cartledge JT. J ApplPhysiol. 1985;59:1128–1136. doi: 10.1152/jappl.1985.59.4.1128. [DOI] [PubMed] [Google Scholar]
- 18.Saraf S, Ghosh A, Kaur CD, Saraf S. Research Journal of Nanoscience and Nanotechnology. 2011;1:60–74. [Google Scholar]
- 19.Porter CHJ, Charman WN. Adv Drug Delivery Rev. 2001;50:61–80. doi: 10.1016/s0169-409x(01)00151-x. [DOI] [PubMed] [Google Scholar]
- 20.Hawley AE, Davis SS, Illurn L. Adv Drug Delivery Rev. 1995;17:129–148. [Google Scholar]
- 21.Liu J, et al. Lung Cancer. 2006;51:377–386. doi: 10.1016/j.lungcan.2005.11.006. [DOI] [PubMed] [Google Scholar]
- 22.Aukland K, Reed RK. Physiol Rev. 1993;73:1–78. doi: 10.1152/physrev.1993.73.1.1. [DOI] [PubMed] [Google Scholar]
- 23.Reddy ST, Berk DA, Jain RK, Swartz MA. J ApplPhysiol. 2006;101:1162–1169. doi: 10.1152/japplphysiol.00389.2006. [DOI] [PubMed] [Google Scholar]
- 24.Swartz MA, et al. J Biomech. 1999;32:1297–1307. doi: 10.1016/s0021-9290(99)00125-6. [DOI] [PubMed] [Google Scholar]
- 25.Taylor DG, Bert JL, Bowen BD. J Theory Microvasc Res. 1990;39:253–278. doi: 10.1016/0026-2862(90)90042-p. [DOI] [PubMed] [Google Scholar]
- 26.Happel J, Brenner K. Low Reynolds Number Hydrodynamics. Prentice Hall; 1966. [Google Scholar]
- 27.Lewis GP, Winsey NJ. Br J Pharmacol. 1970;40:446–460. [PMC free article] [PubMed] [Google Scholar]
- 28.Guyton AC, Scheel K, Murphree D. Circ Res. 1966;19:412–419. doi: 10.1161/01.res.19.2.412. [DOI] [PubMed] [Google Scholar]
- 29.Swabb EA, Wei J, Gullino PM. Cancer Res. 1974;34:2814–2822. [PubMed] [Google Scholar]
- 30.Gashev AA, Orlov RS, Zawieja DC. Ross FiziolZh SSSR Im I M Sechenova. 2001;87(1):97–109. (in Russian) [PubMed] [Google Scholar]
- 31.Gashev AA. Ann NY AcadSci. 2002;979:178–187. doi: 10.1111/j.1749-6632.2002.tb04878.x. [DOI] [PubMed] [Google Scholar]
- 32.Landau LD, Lifshitz EM. Fluid Mechanics. Pergamon: 1959. [Google Scholar]
- 33.Tumer A, Ozturkdemir N, Basareroglu C, Noyan A. J Muscle Res Cell Motil. 1983;4:103–113. doi: 10.1007/BF00711961. [DOI] [PubMed] [Google Scholar]
- 34.Reddy NP, Patel K. Med EngPhys. 1995;17:134–140. doi: 10.1016/1350-4533(95)91885-k. [DOI] [PubMed] [Google Scholar]
- 35.Mendoza E, Schmid-Schonbein GW. J Biomech. 2003;21:118–123. [Google Scholar]
- 36.Galie P, Spilker RL. J BiomechEng Trans ASME. 2009;131:111004. doi: 10.1115/1.3212108. [DOI] [PubMed] [Google Scholar]
- 37.Dukhin SS, Zimmermann R, Duval JFL, Werner C. J Colloid Interface Sci. 2010;350:1–4. doi: 10.1016/j.jcis.2010.04.049. [DOI] [PubMed] [Google Scholar]
- 38.Guyton AC. Fed Proc Fed Am SocExpBiol. 1978;35:1861–1865. [Google Scholar]
- 39.Olszewski WL. In: The lymphatic continuum: lymphatic biology and disease. Rockson SG, editor. Vol. 979. Annals of the New York Academy of Sciences; New York, NY: 2002. pp. 52–63. pp. 52-63. [Google Scholar]
- 40.Gashev AA, Davis MJ, Zawieja DC. J PhysiolLond. 2002;540:1023–1037. doi: 10.1113/jphysiol.2001.016642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Landau LD, Lifshitz EM. Electrodynamics of Continuous Media. Pergamon: 1960. Chapters 1 and 3; [Google Scholar]
- 42.Grinberg GA. A collection of problems in the mathematical theory of electrical and magnetic phenomena. Moscow-Leningrad: 1948. (In Russian) [Google Scholar]
- 43.Lai SK, Wang YY, Wirtz D, Hanes J. Adv Drug Deliv Rev. 2009;27:86–100. doi: 10.1016/j.addr.2008.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Leu AJ, Berk DA, Yuan F, Jain RK. Am J Physiol Heart CircPhysiol. 1994;267(4):H1507–H1513. doi: 10.1152/ajpheart.1994.267.4.H1507. [DOI] [PubMed] [Google Scholar]
- 45.Swartz MA, Berk DA, Jain RK. Am J Physiol Heart CircPhysiol. 1996;270(1):H324–H329. doi: 10.1152/ajpheart.1996.270.1.H324. [DOI] [PubMed] [Google Scholar]
- 46.Berk DA, Swartz MA, Leu AJ, Jain RK. Am J Physiol Heart CircPhysiol. 1996;270(1):H330–H337. doi: 10.1152/ajpheart.1996.270.1.H330. [DOI] [PubMed] [Google Scholar]
- 47.Lyklema J. Fundamentals in Colloid and Interface Science. Vol. 1. Academic Press; London – Toronto: 2000. Chapter 6, Section 6.7. [Google Scholar]
- 48.Russel WB, Saville DA, Showalter WR. Colloidal Dispersions. Cambridge University Press; 1989. Chapters 2,3,7,11,13. [Google Scholar]
- 49.Levich VG. Physico-Chemical Hydrodynamics. Prentice Hall; Englewood Cliffs, NJ: 1962. [Google Scholar]
- 50.Probstein RF. Physicochemical Hydrodynamics. Butterworth: 1989. [Google Scholar]
- 51.Van de Ven TG. Colloidal Hydrodynamics. Academic Press; 1989. [Google Scholar]
- 52.Casley-Smith JR, Vincent AH. Tissue Cell. 1978;10:571–584. doi: 10.1016/s0040-8166(16)30350-0. [DOI] [PubMed] [Google Scholar]
- 53.Powers MR, Wallace JC, Bell DR. Am J Physiol, Heart CircPhysiol. 1988;254(23):H89–H101. doi: 10.1152/ajpheart.1988.254.1.H89. [DOI] [PubMed] [Google Scholar]
- 54.Oussoren C, Storm G. Adv Drug Delivery Rev. 2001;50:143–156. doi: 10.1016/s0169-409x(01)00154-5. [DOI] [PubMed] [Google Scholar]
- 55.Catalone BJ, Kish-Catalone TM, Budgeon LR, Neely EB, Ferguson M, Krebs FC, Howett MK, Labib M, Rando R, Wigdahl B. Antimicrob Agents Chemother. 2004;48(5):1837–1847. doi: 10.1128/AAC.48.5.1837-1847.2004. DOI:10-1128/AAC.48.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Cone RA, Hoen T, Wong X, Abusuwwa R, Andersonl DJ, Moench TR. BMC Infectious Diseases. 2006;6(90):1471–2334. doi: 10.1186/1471-2334-6-90. DOI:10-1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Catalone BJ, Kish-Catalone TM, Neely EB, Budgeon LR, Ferguson ML, Stiller C, Miller SR, Malamud D, Krebs FC, Howett MK, Wigdahl B. Antimicrob Agents Chemother. 2005;49(4):1509–1520. doi: 10.1128/AAC.49.4.1509-1520.2005. DOI:10-1128/AAC.49.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Veronese F, Anton P, Fletcher CV, DeGruttola V, McGowan I, Becker S, Zwerski S, Burns D. Aids Research and Human Retroviruses. 2011;27(1):81–90. doi: 10.1089/AID.2010.0226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Klasse PJ, Shattock R, Moore JP. Annu Rev Med. 2008;59:455–471. doi: 10.1146/annurev.med.59.061206.112737. [DOI] [PubMed] [Google Scholar]


