Improved Prediction of Rates of Visual Field Loss in Glaucoma Using Empirical Bayes Estimates of Slopes of Change

Abstract

Purpose

To describe and test a new methodology for estimation of rates of progressive visual field loss in glaucoma.

Methods

This observational cohort study enrolled 643 eyes of 368 patients recruited from the Diagnostic Innovations in Glaucoma Study (DIGS), followed for an average of 6.5 ± 2.0 years. The visual field index (VFI) was used to evaluate degree of visual field loss in standard automated perimetry. Growth mixture models were used to evaluate VFI changes over time. Empirical Bayes estimates of best linear unbiased predictions (BLUPs) were used to obtain slopes of change based on the first 5 visual fields for each eye. These slopes were then used to predict future observations. The same procedure was done for ordinary least squares (OLS) estimates. The mean square error (MSE) of the predictions was used to compare the predictive performance of the different methods.

Results

The growth mixture model successfully identified subpopulations of non-progressors, slow, moderate and fast progressors. The MSE was significantly higher for OLS compared to the BLUP method (32.3 vs. 13.9, respectively; P<0.001), indicating a better performance of the BLUP method to predict future observations. The benefit of BLUP predictions was especially evident in eyes with moderate and fast rates of change.

Conclusion

Empirical Bayes estimates of rates of change performed significantly better than the commonly used technique of OLS regression in predicting future observations. Use of BLUP estimates should be considered when evaluating rates of functional change in glaucoma and predicting future impairment from the disease.

Introduction

Detection of progression plays a central role in the diagnosis and management of glaucoma and standard automated perimetry (SAP) remains the method of choice for monitoring functional changes in the disease. However, although most glaucoma patients will show some evidence of visual field progression if followed long enough, the rate of deterioration can be highly variable among them.^1-2 While most patients progress relatively slowly, others have aggressive disease with fast deterioration which can eventually result in blindness or substantial impairment unless appropriate interventions take place.

The main purpose of calculating rates of visual field loss is to predict future outcomes for an individual patient. That is, it is assumed that current rates of disease progression will remain relatively unchanged unless further interventions take place and, therefore, are good predictors of future observations. For this purpose, rates of change in structural and functional tests in glaucoma have traditionally been estimated using ordinary least squares (OLS) or simple linear regression of the measurements obtained for an individual eye over time.^3-11 The true rate of change, however, is actually a latent or unobservable variable and the slope of change obtained from OLS is just an imprecise estimate that is confounded by noise and influenced by the number and intervals of measurements during follow-up. Therefore, prediction of future observations based on OLS estimates of rates of change may actually be subject to considerable error.

OLS estimates are obtained taking into account only the measurements of an individual patient, without considering the influence of the population where the patient comes from. Although other assembled data are rarely used to improve the accuracy of a patient's estimate, it could be argued that improved accuracy of an individual patient's estimate is possible by using previously longitudinally collected data from other patients. For example, it is reasonable to assume that the best estimator of the rate of change in a patient in whom we do not have any measurements collected over time is the average rate of change in the overall population from where he comes from. As measurements are acquired for this patient, however, his/her rate of change will most likely deviate from the population average. For patients with less measurements, the precision of the estimates can be increased by “borrowing strength” from the population, whereas for patients with large number of measurements, precise estimates can be obtained relying almost only on the individual data and the need to borrow strength from the population decreases.

The principles outlined above correspond to empirical Bayes estimates or best linear unbiased predictors (BLUPs) of slopes of change.^12-14 We have previously used BLUPs to estimate rates of change in structural tests in glaucoma.^15-17 In the current study, we extend this methodology and demonstrate how it can be used to estimate rates of visual field loss and predict future observations. We compare the ability of OLS and BLUP approaches to predict future observations based on slopes of change.

Methods

This was an observational cohort study. Participants from this study were included in a prospective longitudinal study designed to evaluate optic nerve structure and visual function in glaucoma (DIGS – Diagnostic Innovations in Glaucoma Study) conducted at the Hamilton Glaucoma Center, University of California, San Diego. Participants in the DIGS were longitudinally evaluated according to a pre-established protocol that included regular follow-up visits in which patients underwent clinical examination and several other imaging and functional tests. All the data were entered in a computer database. All participants from the DIGS study who met the inclusion criteria described below were enrolled in the current study. Informed consent was obtained from all participants. The University of California San Diego Human Subjects Committee approved all protocols and the methods described adhered to the tenets of the Declaration of Helsinki.

At each visit during follow-up, subjects underwent a comprehensive ophthalmologic examination including review of medical history, best-corrected visual acuity, slit-lamp biomicroscopy, intraocular pressure (IOP) measurement, gonioscopy, dilated fundoscopic examination, stereoscopic optic disc photography, and automated perimetry using Full-threshold or Swedish Interactive Threshold Algorithm (SITA). Only subjects with open angles on gonioscopy were included. Subjects were excluded if they presented best-corrected visual acuity less than 20/40, spherical refraction outside ± 5.0 diopters and/or cylinder correction outside 3.0 diopters, or any other ocular or systemic disease that could affect the optic nerve or the visual field.

The study included a cohort of patients diagnosed with glaucoma and patients suspected of having the disease, as determined on the baseline visit. Eyes were classified as glaucomatous if they had repeatable abnormal visual field test results on the baseline visits, defined as a PSD outside of the 95% normal confidence limits, or a Glaucoma Hemifield Test result outside normal limits, regardless of the appearance of the optic disc. Eyes were classified as glaucoma suspects if they had normal and reliable visual field results on the baseline visits. These eyes were considered glaucoma suspects based on the presence of history of elevated intraocular pressure (>21 mmHg), suspicious or glaucomatous appearance of the optic nerve or family history of glaucoma.

Standard Automated Perimetry

Only reliable tests (≤ 33% fixation losses and false negatives, and < 15% false positives) were included. Evaluation of rates of visual field change during follow-up was performed using the Visual Field Index (VFI).⁴ Details of the calculation of the VFI have been described elsewhere.⁴ In brief, the VFI represents the percent of normal age-corrected visual function and it is intended for use in calculating rates of progression and staging glaucomatous functional damage. Evaluation of rates of functional loss in glaucoma eyes with the VFI has been demonstrated to be less susceptible than the mean deviation to the effects of cataract or diffuse media opacities.⁴ Also, the VFI is supposed to more accurately reflect the relative importance of the central and more peripheral visual fields to patient visual function compared to other available global visual function indexes. The VFI can range from 100% (normal visual field) to 0% (perimetrically blind field).

We required a minimum of 6 reliable visual fields and a minimum of 3 years of follow-up. A total of 6198 visual fields were available for analysis. A median of 10 (first quartile: 8, third quartile: 13) visual fields were available during follow, ranging from 6 to 21.

Growth Mixture Modeling and Empirical Bayes Estimates of Slopes of Change

Empirical Bayes estimates of slopes of change for individual eyes were derived from growth mixture models applied to the longitudinal data.^18-19 These models differ from the conventional linear mixed models by allowing heterogeneity of different subgroups in the population through the use of categorical latent variables. In conventional random effects mixed models, the average evolution of a specific response is described using some function of time, and random intercepts and random slopes introduce subject-specific deviations from this average evolution. ^20-21 In the traditional random effects model, the observations Y_ij for eye i are assumed to follow a trajectory such that:

$${\mathrm{Y}}_{\mathrm{i}\mathrm{j}}={\beta }_1+{\beta }_2{t}_{\mathrm{i}\mathrm{j}}+b_{1\mathrm{i}}+b_{2\mathrm{i}}{t}_{\mathrm{i}\mathrm{j}}+e_{\mathrm{i}\mathrm{j}},\mathrm{j}=1,\dots ,n_{\mathrm{i}}$$

Y_ij corresponds to the measurement Y for the i^th eye at the j^th measurement occasion. β₁ and β₂ correspond to the fixed effects regression parameters for intercept and slope, respectively; and b₁ and b₂ correspond to the random effects for intercept and slope. In the conventional model, the β's are assumed to be the same for all individuals and have population-averaged interpretations, whereas the b_i's correspond to subject-specific regression parameters and indicate how the conditional mean response for an individual deviates from the population average.

The conventional model assumes that the random effects are normally distributed and that the individuals vary around a single mean growth curve. However, previous studies have shown that the general assumption of normally distributed random effects may lead to biased estimates of individual growth parameters when there is heterogeneity in the population.^22-23 In the present application, heterogeneity is to be expected as only a proportion of eyes will show visual field progression over time. Further, in the progressing group, only a small proportion will have relatively fast progression. This can induce considerable non-normality or skeweness in the random effects distribution. In order to address this, we used growth mixture models, also known as heterogeneity models. These models represent unobserved heterogeneity between the subjects using both random effects and finite mixtures.^18-19 This allows different sets of parameter values for mixture components corresponding to different unobserved subgroups of individuals, capturing latent trajectory classes with different patterns of change over time. It relaxes the single population assumption, so that instead of considering individual variation around a single mean growth curve, the growth mixture model allows different classes of individuals to vary around different mean growth curves. Thus, the normality assumption is not imposed on the overall population but merely on the subpopulations, allowing for the possibility of highly nonnormal distributions of responses at the overall population level. Subjects can then be grouped according to the similarities of their trajectories, such as in non-progressors, slow and fast-progressors and they are allowed to have varying intercepts and slopes within the different subgroups. The model is then specified as follows:

Y_kij = β_1k + β_2kt_ij + b_1ki + b_2kit_ij + e_kij, j = 1,…,n_i, where k represents the k latent trajectory classes or subpopulations.

Based on the model-estimated response probabilities and observed data, each eye's estimated probability of class membership or posterior class probability can then be calculated. The precision of the classification can be assessed by how well the eyes are classified into each class. A reliable classification will require an eye to have very high posterior probability of belonging to a single class and very low of belonging to all other classes. The overall quality of the classification can be summarized by an entropy measure varying from 0 to 1 with values close to 1 indicating better classification.¹⁹

After estimates of model parameters for the different classes and posterior class probabilities are obtained, it is possible to obtain best linear unbiased predictors (BLUPs) of slopes of change for each eye using empirical Bayes estimation.^24-25 BLUPs are known as shrinkage estimates because they are shrunken towards the population mean. The amount of shrinkage depends on within-subject and between-subject variabilities. In fact, it can be shown that the prediction of individual-specific regression coefficients is a weighted average of the estimate of population-averaged fixed effects and the corresponding OLS estimate for the particular individual, with the weighting scheme based on within- and between-subject variability estimates and number of observations. BLUPs take into account the results obtained by evaluating the whole sample of eyes giving less weight to individual measurements obtained from eyes with few measurement occasions and/or large within-individual variability (that is, more “noise”).¹³ When OLS estimates are precise they have greater weight; when OLS estimates are imprecise, the population average trajectories have greater weight. Using the finite mixture model, there will be k subpopulations and the shrinkage, if necessary, will occur towards the subpopulation to where the individual eye was determined to belong.

In the present study, individual BLUPs of slopes of VFI values were obtained for each eye included in the study, taking into account the individual measurements and the parameter estimates of the growth mixture model applied to the whole sample. For each individual eye, the BLUP slope of change was calculated taking into account only the first 5 visual fields obtained during follow-up. These rates of change were then used to predict future observations for individual eyes (i.e, 6^th, 7^th, etc VFI values). The same procedure was done for OLS estimates but, as discussed above, OLS estimates use information only from the individual eye. The residual difference, or error, between the actual VFI value and the predicted value was calculated for each observation. The mean square error (MSE) of the predictions was used to evaluate and compare the predictive performance of the different methods.

The choice of the appropriate number of k mixture components was based on the Lo-Mendell-Rubin (LMR) likelihood ratio test and Bayesian Information Criteria (BIC).¹⁹ BIC is calculated as the sum of -2 times the loglikelihood value of the model, plus the number of model parameters times the natural log of the sample size. Lower scores represent better fitting models. In practice, BIC marks the balance between the impact of adding a new class on the loglikelihood value and the penalty for increasing the number of model parameters that results from the addition of that class. Thus, adding a trajectory class is beneficial with respect to BIC only if it has a marked effect on the fit of the model. The LMR likelihood ratio test provides a statistical comparison of the fit of a given model with with a model with one fewer classes. Importantly, the selection of number of classes and the classification of individuals to each one of the subpopulations were based only on the first 5 visual field measurements. The expectation-maximization algorithm was used to obtain maximum likelihood estimates for all parameters of the mixture model.

Statistical Analyses were performed using MPLUS v. 5.0 and MATLAB R2009a (Mathworks, Natick, MA). The alpha level (type I error) was set at 0.05.

Results

The study included 643 eyes of 368 patients with a mean ± SD age of 62 ± 12 years at baseline, and followed for an average of 6.5 ± 2.0 years. Two hundred nineteen patients were female (60%). From the 643 eyes included in the study, 212 (33%) had glaucomatous visual field loss at the baseline visit and 431 (67%) were considered as glaucoma suspects. Median (first quartile, third quartile) MD and PSD of the visual field closest to the baseline imaging test date in glaucomatous eyes were -3.47dB (-6.47dB, -1.68dB) and 3.20dB (2.30dB, 6.90dB). Corresponding values for glaucoma suspect eyes were -0.39dB (-1.43dB, 0.62dB) and 1.49dB (1.32dB, 1.72dB).

Four subpopulations were identified by the growth mixture model, which we named non-progressors, slow progressors, moderate progressors and fast progressors. BIC and LMR likelihood ratio tests supported the 4-class model compared to models with 3, 2 or 1 class. Adding more than 4 classes did not significantly improve the model. The classification of an individual eye to a subgroup was based only on the information available from the first 5 visual fields. The entropy value of the classification was 0.91, indicating clearly distinguishable subpopulations. The subgroup of non-progressors had 301 eyes (47%) and an average slope of VFI change of -0.05%/year (95% CI: -0.10 – 0.1), which was not significantly different than zero (P=0.342). The subgroup of slow progressors had 225 eyes (35%) and an average slope of VFI change of -0.32%/year (95% CI: -0.46 – -0.18), which, albeit small, was significantly different than zero (P<0.01). Moderate progressors constituted 97 eyes (15%) with an average slope of change of -0.94%/year (95% CI: -1.29 - -0.59; P<0.01). Finally, fast progressors were 20 eyes (3%) and had an average rate of change of -3.8%/year (95% CI: -5.47 – -2.13; P<0.01). Mean rates of change in slow, moderate and fast progressors were all significantly different than the mean rate of change in non-progressors (P<0.05 for all comparisons).

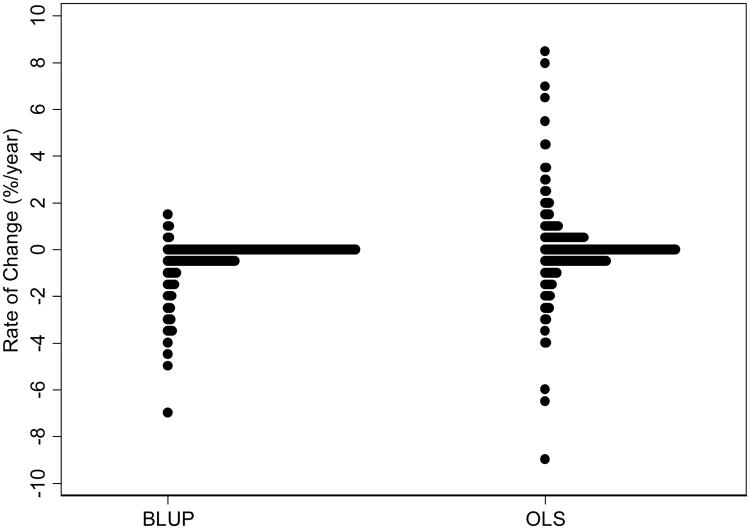
Figure 1 shows the distribution of BLUP estimates of rates of change for individual eyes, as calculated based on the first 5 visual fields. Information from the intercept and slope of change was used to predict future observations for each eye. A total of 2983 visual fields from 643 eyes were available to evaluate predictive ability. The average difference between actual minus predicted value was -0.03 (median: 0.37; first quartile: -0.76; third quartile: 1.14). The mean square error of the predictions was 13.9 (95% CI: 11.2 – 16.6) (Table 1).

Figure 1.

Distributions of empirical Bayes estimates (BLUPs) and ordinary least squares (OLS) slopes of VFI change.

Figure 1 also shows a distribution of estimates of rates of change based on the first 5 visual fields obtained by the OLS method. The majority of eyes had rates of change close to zero, but there was large variability in the estimates with 10% of the eyes with OLS estimates of rates of visual field loss faster than 1%/year. Information from the intercept and OLS slope of change was used to predict future observations for each eye. The average difference between actual minus predicted value was -0.66 (median: 0; first quartile: -1.15; third quartile: 0.98). The mean square error of the predictions was 32.3 (95% CI: 25.0 – 39.6).

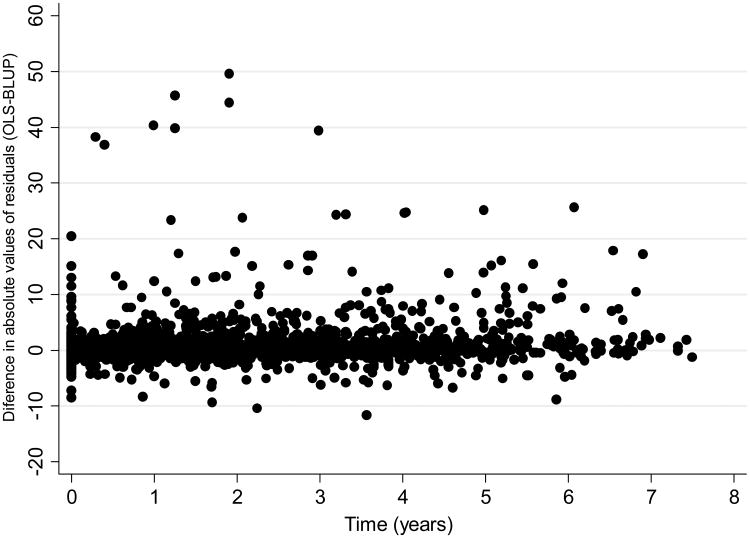
The mean square error of the prediction was statistically significantly lower for BLUP compared to the OLS method (P<0.001), indicating a significantly better performance of the BLUP method to predict future observations (Table 1). Figure 2 shows a scatter plot of the difference between the absolute residuals for each method versus time. In this plot, the initial time in the horizontal axis was set to zero at the first available visual field after the initial 5 visual fields. The plot shows that residuals for OLS estimates tended to be larger than those for BLUP estimates, that is, predictions from OLS estimates were in general worse than those based on BLUPs. When limited to observations occurring up to 5 years after the last visual field that was used for calculation of the slopes of change, BLUP estimates still outperformed OLS estimates (mean square errors of 12.5 vs. 28.9; P<0.001).

Figure 2.

Relationship between differences in absolute values of residuals for OLS and BLUP predictions and time. Positive values indicate that residuals for the OLS method were greater than those from the BLUP method.

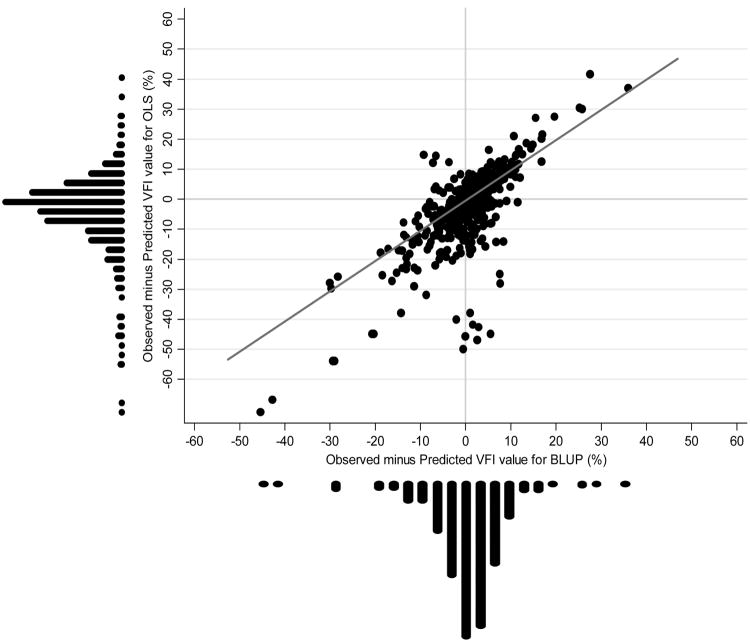
We also tested whether predictions based on BLUP were better than OLS for the different subpopulations of eyes as classified by the mixture model. For eyes classified as non-progressors, there was no statistically significant difference between mean square errors of the predictions for BLUP compared to OLS method (8.7 vs. 9.5, respectively; P = 0.13). For slow progressors, the mean square error of the BLUP predictions was significantly lower than that for OLS, although the difference was of small magnitude (1.7 vs. 2.4, respectively; P<0.001). The greatest benefit of BLUP predictions compared to OLS was seen in moderate and fast progressors. For moderate progressors, mean square error of BLUP predictions was significantly lower than OLS (53.5 vs. 185.1, respectively; P<0.001). For fast progressors, BLUP estimates also significantly outperformed OLS estimates (mean square errors of 59.9 vs. 81.1, respectively; P<0.001). Figure 3 shows a scatterplot of residuals of BLUP and OLS predictions for moderate and fast progressors.

Figure 3.

Scatterplot with marginal distributions of observed minus predicted values of VFI according to BLUP and OLS methods for moderate and fast progressors. Negative values indicate that predicted values were higher (i.e., more normal) than observed values and, therefore, underestimated visual function loss. A reference (45°) line is also plotted.

Predictions that underestimated the amount of damage in future observations (i.e., predicted VFI values were higher than observed values) are of particular concern due to the possibility of underestimating the risk of visual function loss, especially in moderate and fast progressors. Therefore, we evaluated whether BLUP and OLS predictions tended to underestimate the amount of field loss in future observations in moderate and fast progressors. Considering the 535 future visual fields of moderate and fast progressors that were available to check the predictions, OLS predictions underestimated field loss in future observations by more than 10 points in 91 fields (17%). In contrast, BLUP predictions resulted in underestimation of more than 10 points in only 37 (7%) of the visual fields.

We also evaluated the performance of BLUP versus OLS predictions according to the diagnostic category at baseline, i.e., suspect versus glaucoma. For glaucoma eyes, mean square error of BLUP predictions was significantly smaller than that of OLS (32.1 vs. 85.5; P<0.001). For glaucoma suspects, mean square error of BLUP predictions was also significant smaller than that of OLS, but with only a slight difference (4.7 vs. 5.3, respectively; P=0.02).

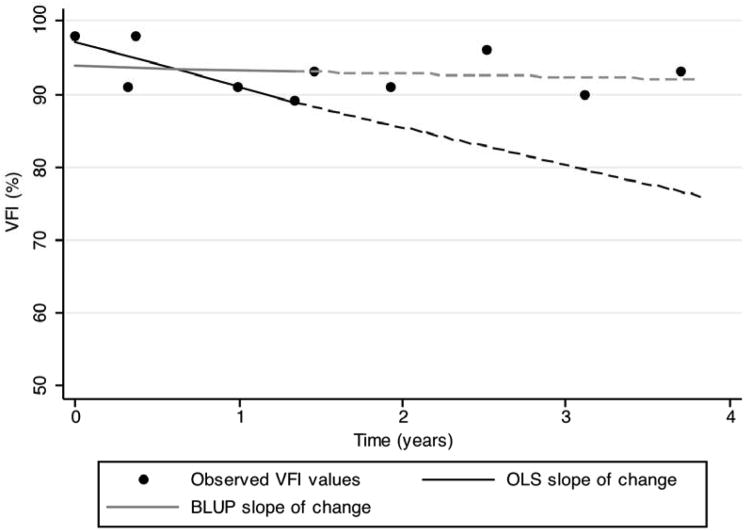
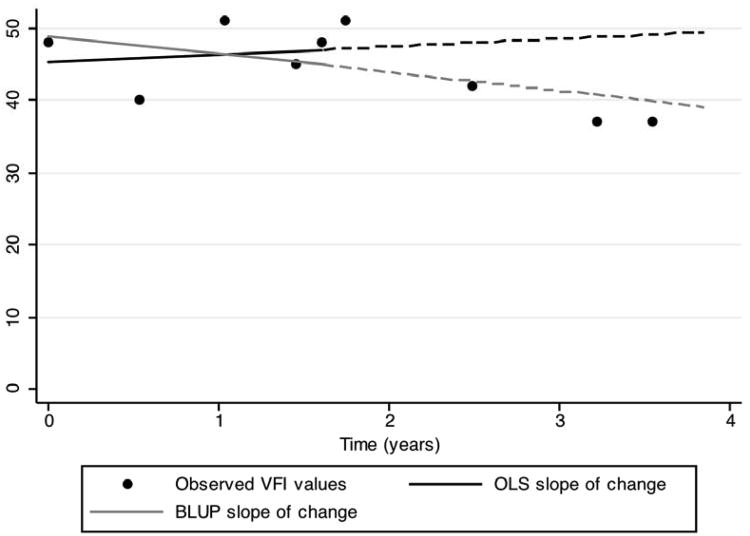
Figures 4 and 5 show examples of eyes followed over time with slopes of change calculated from the first 5 visual fields and used to predict future observations. It can be seen that the extrapolated lines from the BLUP slopes are closer to the actual future observations than those based on OLS slopes.

Figure 4.

VFI results for an eye followed over time. Black and gray continuous lines show OLS and BLUP regression lines, respectively, calculated from the first 5 VFI measurements. The eye was classified as non-progressor. The OLS slope suggests worsening over time, whereas the BLUP slope is close to zero. Dashed lines show predictions from the calculated slopes of change. Predictions from BLUP were closer to actual observed values than those from OLS.

Figure 5.

VFI results for an eye followed over time. Black and gray continuous lines show OLS and BLUP regression lines, respectively, calculated from the first 5 VFI measurements. The eye was classified as moderate progressor. The OLS slope suggests improvement over time, whereas the BLUP slope suggests worsening. Dashed lines show predictions from the calculated slopes of change. Predictions from BLUP were closer to actual observed values than those from OLS.

We also evaluated the impact of the number of initial visual field observations available to obtain BLUP and OLS estimates (Table 1). We recalculated rates of change using the first 6, 7 and 8 visual fields and used the estimated slopes to predict future observations. Mean square errors of predictions of OLS and BLUP were 12.3 vs. 22.6 (P <0.001) using the first 6 visual fields, 11.5 vs. 15.6 (P <0.001) using the first 7 visual fields, and 10.1 vs. 12.8 (P<0.001) using the first 8 visual fields.

Discussion

In the current study, we proposed a method to evaluate rates of visual field loss in glaucoma based on growth mixture models and empirical Bayes estimates of slopes of change. The proposed methodology significantly outperformed the commonly used method of simple linear regression of measurements over time for predicting future visual field observations. These results may have significant implications for the calculation of rates of functional loss in glaucoma and for the management of the disease.

The evaluation of rates of functional loss in glaucoma is one of the most important aspects in the management of the disease. Glaucoma treatment should be based on decreasing the rate of deterioration in order to preserve vision-related quality of life, taking into account the projected life expectancy for the patient. The recent introduction of the VFI has allowed better quantification of rates of visual function in glaucoma due to its decreased dependency on media opacities, compared to indexes such as MD that have been previously used to assess rates of disease progression.⁴ The current Humphrey Glaucoma Progression Analysis (GPA) software (Carl-Zeiss Meditec, Inc., Dublin, CA) shows a plot of VFI changes over time and calculates the rate of VFI loss using OLS regression. The slope of the line is based on the observed measurements for the eye under consideration and it is extrapolated to predict what the future measurements will be up to 3 to 5 years in the future, if the same rate of change persists over time. In our study, we showed that these predictions based on the OLS method could be subject to considerable error, especially in eyes that have apparently faster rates of change over time. The error in OLS predictions for eyes classified as moderate or fast progressors was greater than 10 points in 24% of the visual fields available to check predictions. OLS predictions underestimated field loss in future observations by more than 10 points in 17% of the cases. This result is similar to a recent report by Bengtsson et al.²⁶ where OLS predictions were within 10 points of the observed final VFI in 70% of the cases. Although the authors interpreted this result as indicating a good predictive ability of OLS regression of VFI values, a 10-point difference in VFI actually represents substantial field damage and corresponds to approximately 3 to 4dB loss in mean deviation.

The use of empirical Bayes estimates to calculate individual slopes of VFI change resulted in significant improvement in the prediction of future observations. Predictions obtained by extrapolating slopes of change calculated from BLUP methodology were closer to actual VFI values than those obtained by extrapolating OLS regression lines, as shown by differences in mean square error of the predictions. Importantly, the superior performance of BLUP predictions was most notably seen in eyes that were classified as moderate or fast progressors. These eyes carry special importance as they are the ones most likely to develop significant functional disability over time. Predictions that underestimate damage in future observations in these eyes are particularly worrisome due to the possibility of underestimating the risk of visual function loss. As shown in Figure 3, OLS predictions significantly underestimated field loss in a large number of cases, with 17% of the visual fields showing predictions that were higher than the observed value by more than 10 points. In a significant number of cases, OLS predictions were higher than the future observations by more than 20 points. On the other hand, BLUP predictions were significantly more accurate in moderate and fast progressors, with predictions more than 10 points higher than observed values occurring in only 7% of the visual fields.

Although an improvement in the predictions was seen for both methods with an increase in the number of visual fields used for the initial calculation of the slopes of change, BLUP predictions still outperformed OLS predictions for larger number of tests. It is known that as the number of measurements increases, the OLS estimate approaches the true underlying latent variable. However, in clinical practice, there is a cost associated with obtaining more measurements over time, including the expense of the test itself, the cost in patient time, and the cost related to delaying detection of change. Further, the superior performance of BLUPs to predict visual field loss with smaller number of tests suggests that this methodology could be able to detect progression earlier than the OLS method.

Previous studies have compared BLUP and OLS estimates under other circumstances, but none in the investigation of rates of change in eye diseases.^27-31 Using Monte Carlo simulations, Candel and Winkens³¹ showed that empirical Bayes estimators performed significantly better than OLS estimators. In their study, the gain in decreasing the prediction error with empirical Bayes estimators was relatively higher for lower number of measurement occasions. However, although the two methods became closer with increase in the number of measurements, there was no cross-over in that the OLS estimates became better than empirical Bayes estimates. This is in agreement with our results showing that predictions based on BLUP estimates still outperformed OLS even when up to 8 visual fields were considered for obtaining the estimates of slopes of change. It should be noted that we limited calculation of slopes to a minimum of 5 visual fields. Calculation of slopes of changes using fewer observations actually resulted in even worse performance of OLS estimates and greater difference compared to BLUP predictions. We only showed results from calculations including at least 5 visual fields as the current clinically available Humphrey perimeter software for VFI analysis requires at least 5 visual fields in order to provide an OLS slope.

In addition to improving the clinician's estimate of the patient's rate of visual function loss, the use of growth mixture models and BLUP estimates may have important implications for research design and clinical trials. In clinical trials comparing the effect of different interventions on the rate of disease progression, the use of BLUP estimates will allow more precise and accurate evaluation of rates of change, potentially decreasing the need to collect additional data and reducing the costs of the study.

BLUPs are shrinkage estimates that take into account the results obtained by evaluating the whole sample of eyes giving less weight to estimates obtained from eyes with few measurement occasions and/or large intra-individual variability (that is, more “noise”).¹³ Therefore, one of the important requisites for their calculation is to obtain accurate parameter estimates of the population.³² The use of finite mixture models in our study allowed the identification of clearly distinguishable subpopulations according to the similarities of the trajectories of change over time. The information about these subpopulations was used to improve predictions of slopes of change for individual eyes. In addition, the use of growth mixture modeling with identification of subpopulations of fast progressors provides a framework for identification of the eyes at highest risk for functional impairment and for the evaluation of factors influencing these rates. However, this approach requires an adequate and sufficiently large sample of patients similar to the patients in whom we want to make predictions. In our study, we used a large group of glaucoma and glaucoma suspect patients that have been longitudinally studied according to pre-specified protocols for many years. Construction of similar built-in databases would be required to implement this methodology in currently available instruments.

Although in the current study we applied the BLUP methodology to estimate slopes of change for functional loss in SAP, this methodology could be extended for the estimation of rates of change measured by other functional tests such as frequency doubling technology or short-wavelength automated perimetry. In addition, BLUPs can be used to evaluate rates of change in structural tests. We have previously used the current methodology for evaluation of rates of glaucoma progression using different imaging techniques such as scanning laser polarimetry, optical coherence tomography and confocal scanning laser ophthalmoscopy.^15-17

Although BLUP estimates significantly outperformed OLS estimates in our study, predictions based on BLUP estimates were still subject to error. Therefore, caution should be exercised when attempting to predict future functional losses in glaucoma patients. In fact, due to the logarithmic scaling of visual field data, it is likely that rates of functional loss will not be linear when measured over very long periods of time. Further, patients in our study were treated at the discretion of the attending ophthalmologist. It is possible that modifications in treatment may have induced changes in rates of deterioration during follow-up increasing the error in the predictions. For example, it is possible that a patient who was rapidly deteriorating had an increase in medical treatment or surgical procedure to arrest progression. In such case, initial rates of change could show poor ability to predict future rates of loss due to departure from the linearity. However, this should have exerted a similar influence in the mean square errors of the predictions obtained by both methods, as both were based on linear rates of change over time. Also, it would not explain the large number of eyes that had OLS predictions which underestimated the amount of field loss. Future studies should evaluate whether the application of non-linear methods for the evaluation of rates of change could potentially improve prediction of future observations. Also, although we evaluated rates of change based on the VFI, the application of this index for measuring rates of change over time still require further validation. When we conducted similar analyses using the MD index, we obtained similar results (not shown), which is not surprising due to the very high correlation between VFI and MD values in our dataset (r = 0.94).

In conclusion, empirical Bayes estimates of rates of change derived from growth mixture models performed significantly better than the commonly used technique of OLS regression in predicting future observations. Use of BLUP estimates should be considered when evaluating rates of functional change in glaucoma and predicting future impairment from the disease.