Combining Structural and Functional Measurements to Improve Estimates of Rates of Glaucomatous Progression

Abstract

Purpose

To evaluate whether a combination of topographic optic disc measurements and visual field data may improve the estimation of rates of structural and functional progression in glaucoma and the prediction of future outcomes in the disease.

Design

Observational cohort study.

Methods

The study included 242 eyes of 179 glaucoma patients followed for an average of 6.4 ± 1.1 years. Subjects were longitudinally monitored with standard automated perimetry (SAP) and confocal scanning laser ophthalmoscopy (CSLO). Slopes of functional and structural change over time were evaluated by the parameters mean deviation (MD) and rim area, respectively. For each eye, the follow-up time was divided into two equal periods: the first half was used to obtain the slopes of change and the second period was used to test the predictions. Slopes of change were calculated using two methods, the conventional approach of ordinary least squares linear regression and a Bayesian joint regression model integrating structural and functional information. The mean square error (MSE) of the predictions was used to compare the predictive performance of the different methods.

Results

Bayesian slopes were more accurate than those obtained by the ordinary least squares method in predicting future MD (MSE: 5.13 vs. 11.2, respectively; P<0.001) and rim area values (MSE: 0.016 vs. 0.027, respectively; P<0.01).

Conclusion

A Bayesian joint regression model combining structure and function resulted in more accurate and precise estimates of slopes of change compared to the conventional method of ordinary least squares linear regression.

INTRODUCTION

Detection of progression is paramount to the diagnosis and management of glaucoma, however, although most glaucoma patients will show some evidence of change if followed long enough, the rate of deterioration can be highly variable among them.^1–5 While most patients progress relatively slowly, some have aggressive disease with rapid deterioration that necessitates more aggressive therapeutic intervention. According to the Consensus on Medical Treatment from the World Glaucoma Association, glaucoma treatment is generally indicated for patients whose rates of progression will most likely result in loss of vision-related quality of life over the projected remaining years of life.⁶ Therefore, accurate and precise estimation of rates of change are essential in order to determine the need and/or aggressiveness of treatment.

Standard automated perimetry (SAP) remains the most common method for estimating rates of functional progression. However, there is evidence that many patients can present structural changes in the optic nerve or retinal nerve fiber layer (RNFL) before detectable changes in SAP.^3,7–14 There is also evidence that progressive changes to the optic nerve are highly predictive of future functional deterioration and, therefore, monitoring rates of structural damage becomes essential to improve individualized management of the disease. On the other hand, several patients show evidence of functional deterioration without measurable changes in currently available structural tests, highlighting the need for assessing rates of both structural and functional change throughout the course of the disease.^10,11,15

The disagreement between structural and functional methods for detecting progression could be related to the different algorithms employed to assess change, to the variability of measurements over time, or to the different scales used to assess structure and function.^14–24 While some disagreement is to be expected, we have recently shown that a combination of structural and functional tests can significantly improve detection of glaucoma progression.²⁵ Using Bayesian statistics, we developed a joint model that takes into account the correlation between the different tests in order to integrate the longitudinal information obtained from structural and functional evaluations, allowing the information derived from one test to influence the inferences obtained from the other test. For example, a visual field change that would otherwise be declared non-statistically significant by analysis of visual field data alone may be declared significant after taking into consideration the structural changes occurring in the same eye, and vice-versa. We applied our method to combine SAP and scanning laser polarimetry RNFL measurements and we demonstrated that the method significantly improved detection of glaucoma progression compared to either test used alone or to the use of both tests, but without taking into account the correlation between them.

The main purpose of calculating rates of change is to predict future outcomes for an individual patient. That is, it is assumed that current rates of disease progression will remain relatively unchanged unless further interventions take place and, therefore, are good predictors of future observations. In the current study, we expand our Bayesian methodology to a combination of SAP and topographic optic disc measurements to demonstrate that it can also improve the estimation of rates of structural and functional damage in the disease and prediction of future outcomes in a cohort of glaucoma patients followed over time.

METHODS

This was an observational cohort study. Participants from this study were included in two prospective longitudinal studies designed to evaluate optic nerve structure and visual function in glaucoma (the African Descent and Glaucoma Evaluation Study [ADAGES] and the Diagnostic Innovations in Glaucoma Study [DIGS]). The 3-site ADAGES collaboration includes the Hamilton Glaucoma Center at the Department of Ophthalmology, University of California-San Diego (UCSD) (data coordinating center), the New York Eye and Ear Infirmary and the Department of Ophthalmology, University of Alabama at Birmingham, Birmingham (UAB). Although the DIGS includes only patients recruited at UCSD, the protocol of the two studies are identical. Methodological details have been described previously.²⁶

At each visit during follow-up, subjects underwent a comprehensive ophthalmologic examination including review of medical history, best-corrected visual acuity, slit-lamp biomicroscopy, intraocular pressure (IOP) measurement, gonioscopy, dilated fundoscopic examination, stereoscopic optic disc photography, and automated perimetry using Swedish Interactive Threshold Algorithm (SITA Standard 24-2). Only subjects with open angles on gonioscopy were included. Subjects were excluded if they presented with a best-corrected visual acuity less than 20/40, spherical refraction outside ± 5.0 diopters and/or cylinder correction outside 3.0 diopters, or any other ocular or systemic disease that could affect the optic nerve or the visual field.

The study included 242 eyes of 179 patients diagnosed with glaucoma, as determined on the baseline visit. Seventy-five patients were recruited from the University of California San Diego, 45 from the University of Alabama and 59 from the New York Eye and Ear Infirmary. Eyes were classified as glaucomatous if they had repeatable (two consecutive) abnormal visual field test results on the baseline visits and a glaucomatous appearing optic disc based on masked stereophotograph assessment. An abnormal visual field was defined as a pattern standard deviation (PSD) outside of the 95% normal confidence limits, or a Glaucoma Hemifield Test result outside normal limits.

Standard Automated Perimetry

All visual fields were evaluated by the UCSD Visual Field Assessment Center (VisFACT).²⁷ Visual fields with more than 33% fixation losses or false-negative errors, or more than 15% false-positive errors were excluded. The only exception was the inclusion of visual fields with false-negative errors of more than 33% when the field showed advanced disease. Visual fields exhibiting a learning effect were also excluded. Visual fields were further reviewed for the following artifacts: lid and rim artifacts, fatigue effects, inappropriate fixation, evidence that the visual field results were due to a disease other than glaucoma (such as homonymous hemianopia), and inattention. The VisFACT requested repeats of unreliable visual field test results, and these were obtained whenever possible.

Evaluation of rates of visual field change during follow-up was performed using the mean deviation (MD) global index provided by the Humphrey perimeter (Carl-Zeiss Meditec, Inc., Dublin, CA).

Confocal Scanning Laser Ophthalmoscopy

Topographic optic disc measurements were obtained using confocal scanning laser ophthalmoscopy (CSLO) with the HRT II (software version 3.0, Heidelberg Engineering, Dossenheim, Germany). It uses confocal scanning laser principles to obtain a three-dimensional topographic image of the optic nerve. Its principles of working have been described in detail elsewhere.²⁸ For each patient, three topographical images were obtained and were combined and automatically aligned to make a single mean topography used for analysis. An experienced examiner outlined the optic disc margin on the mean topographic image while viewing stereoscopic photographs of the optic disc. Good quality images required a focused reflectance image with a standard deviation not greater than 50µm. Corneal curvature measurements were used to correct images for magnification error. The CSLO Reading Center at the University of California, San Diego conducted all quality assessment and image processing and certified all operators according to standard protocol.⁴ The parameter rim area was used to evaluate rates of structural change over time.

Data Analysis

A minimum of 4 HRT exams and 4 SAP tests during follow-up were required. Average follow-up time was 6.4 ± 1.1 years (range: 5.0 to 13.1 years). For each eye, the follow-up time was divided into two equal periods: the first half was used to obtain the slopes of change and the second period was used to test the predictions. That is, rates of change were obtained using only the tests available during the first half of follow-up. Subsequently, these rates of change were then used to predict observations for individual eyes during the second half of the follow-up period. Slopes of change were calculated using two methods, the conventional approach of ordinary least squares linear regression and a Bayesian joint regression model. Using ordinary least squares regression, two slopes were obtained for each eye, one representing rim area loss over time and another representing MD change over time. ordinary least squares regression is the standard approach used to calculate slopes of change in commercially available software packages from perimeters and imaging devices and does not take into account the correlation between the results of the two tests. The Bayesian model also provides two slopes for each eye, one for rim area and one for MD, however, the calculation of the slope for MD loss over time takes into account the slope of rim area change and vice-versa, as described below.

For each measurement (rim area and MD) and method (ordinary least squares vs. Bayesian), the residual difference, or error, between the actual value and the predicted value was calculated for each observation available during the second half of the follow-up period. The mean square error (MSE) of the predictions was used to evaluate and compare the predictive performance of the different methods.

Bayesian Joint Regression Model

A joint regression model was implemented using a Bayesian hierarchical modeling framework to integrate the two longitudinal measures obtained over time, i.e., the HRT rim area and SAP MD. Details of the modeling approach have been described in a previous publication.²⁵ In brief, random-intercept random-slope hierarchical models were used to evaluate the evolution of each response over time. In these models, the average evolution of a specific response is described using some function of time, and subject-specific deviations from this average evolution are introduced by random intercepts and random slopes, allowing for different baseline values and different rates of change for each eye. Hierarchical models can also easily handle the correlation structure arising from data coming from both eyes of the same patient.²⁹ In a joint-modeling approach using hierarchical models, random-effects are assumed for each response process and the different processes are associated by imposing a joint multivariate distribution on the random effects. This approach has great flexibility and allows joining models for responses of different types and also with different number of observations, as in our application.³⁰

At the first level, each response process is described using a linear model:

$${\mathrm{Y}}_{1\mathrm{i}}={\mathrm{\alpha }}_{1\mathrm{j}[\mathrm{i}]}+{{\mathrm{\beta }}_{2\mathrm{j}[\mathrm{i}]}}^{*}{\text{time}}_{\mathrm{i}}+{\mathrm{\epsilon }}_{1\mathrm{i},}{\mathrm{\epsilon }}_{1\mathrm{i}}~\mathrm{N}(0,{{\mathrm{\sigma }}_{1\mathrm{y}}}^2)\text{for}\mathrm{i}=1,2,3,4,\dots ,\mathrm{n}$$ (1)

$${\mathrm{Y}}_{2\mathrm{i}}={\mathrm{\alpha }}_{2\mathrm{j}[\mathrm{i}]}+{{\mathrm{\beta }}_{2\mathrm{j}[\mathrm{i}]}}^{*}{\text{time}}_{\mathrm{i}}+{\mathrm{\epsilon }}_{2\mathrm{i},}{\mathrm{\epsilon }}_{2\mathrm{i}}~\mathrm{N}(0,{{\mathrm{\sigma }}_{2\mathrm{y}}}^2)\text{for}\mathrm{i}=1,2,3,4,\dots ,\mathrm{n}$$ (2)

Where Y₁ and Y₂ represent the longitudinal measurements of rim area and MD, respectively, for an eye j taken at time i, α₁ and β₁ correspond to random intercepts and random slopes, respectively, for process 1 (HRT); and α₂ and β₂ correspond to random intercepts and random slopes for process 2 (SAP). At the second level, both response trajectories are tied together through a multivariate distribution of the random effects. That is, in the Bayesian model, the intercepts (α_1j’s and α_2j’s) and slopes (β_1j’s and β_2j’s) were assumed to follow a multivariate t distribution and this multivariate distribution acted as a “prior” for the estimation of the intercepts and slopes for each individual eye. By using a prior that relates functional to structural change over time, it is possible to integrate the results of the two tests. The parameters of this multivariate distribution were estimated from the data, however, in order to carry out Bayesian inference, we also need to specify priors for the parameters of the multivariate distribution (i.e., the hyperparameters). We used non-informative priors for the parameters of the multivariate distribution, as described previously.³¹ Estimates of model parameters were obtained with information from n−1 eyes and applied to obtain the estimates of slopes of change in the n^th eye.

Estimates of the posterior distributions of the parameters of interest, i.e., the random effects, were obtained by Markov chain Monte Carlo (MCMC) procedures. The MCMC sampler was implemented in WinBUGS software.³² We used 10000 iterations after discarding the initial 5000 iterations for burn-in. Convergence of the generated samples was assessed by standard tools in WinBUGS (trace plots, autocorrelation function [ACF] plots) as well as Gelman-Rubin convergence diagnostics. After the posterior distributions were estimated, summary measures were calculated such as mean and credible intervals.

RESULTS

The study included 242 eyes of 179 participants with a mean ± SD age of 63 ± 12 years at baseline. One hundred and seven (60%) patients were female. Median (first quartile, third quartile) MD and PSD of the visual field closest to the baseline imaging test date were −3.36dB (−5.40dB, −1.88dB) and 3.67dB (2.46dB, 5.96dB), respectively. There was a large variation in baseline MD in the eyes included in the study, with values ranging from −30.3dB to 1.11dB. Mean ± SD of rim area at the baseline visit was 1.25 ± 0.37mm², ranging from 0.31mm² to 2.54mm².

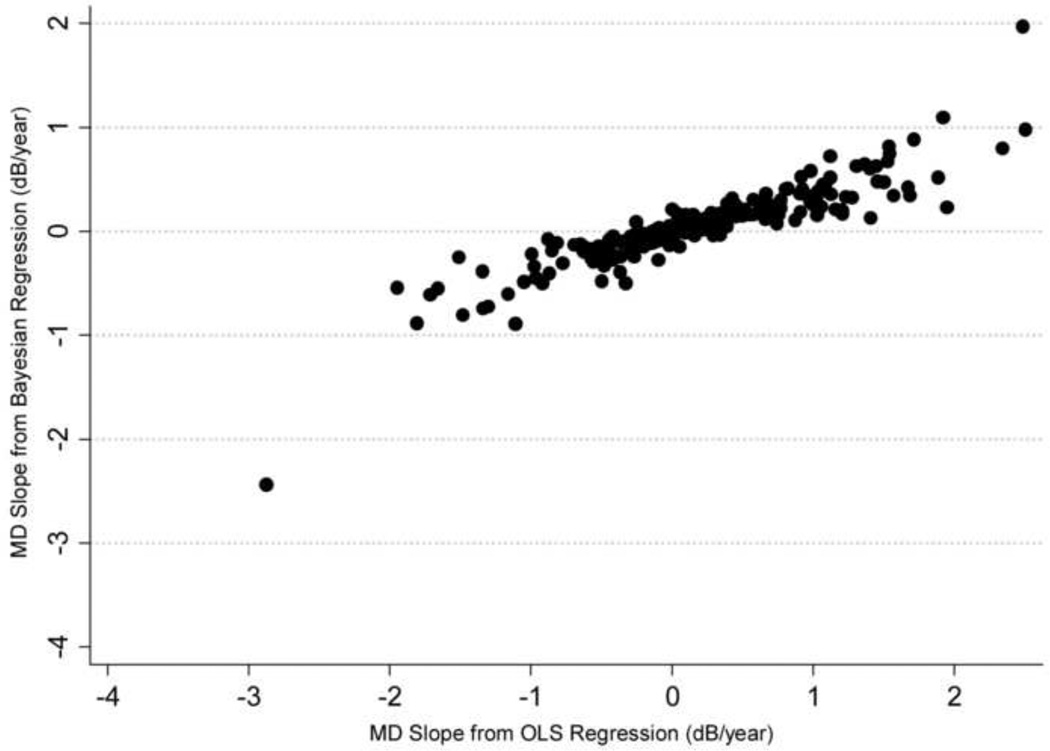
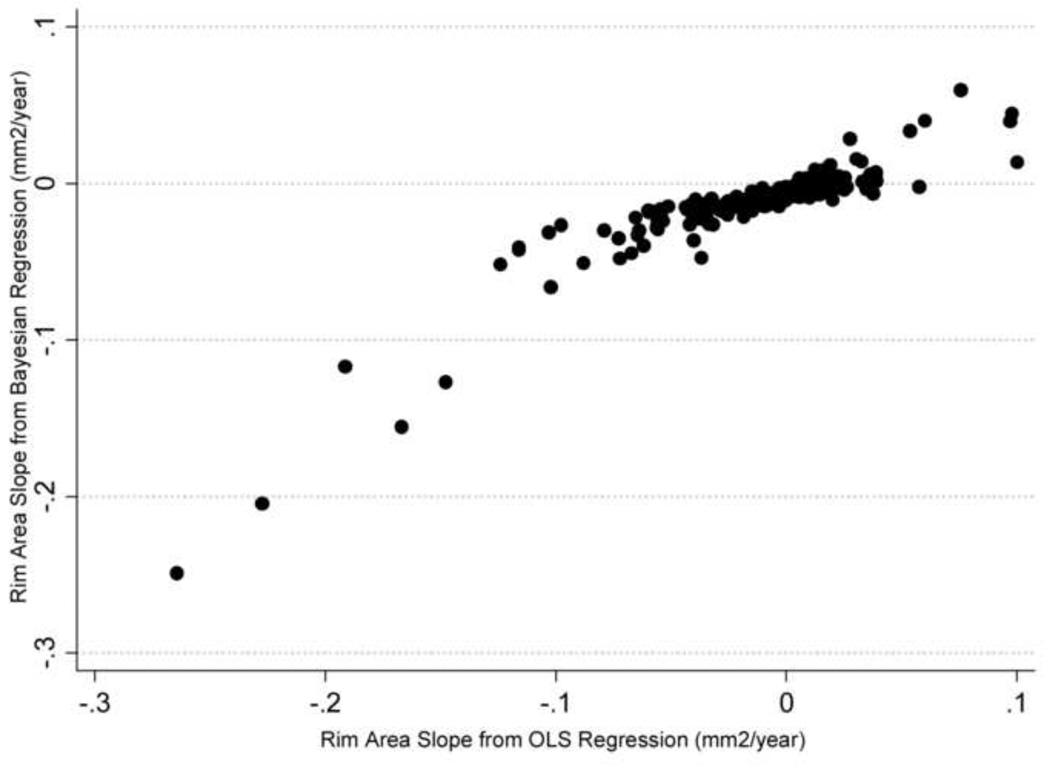
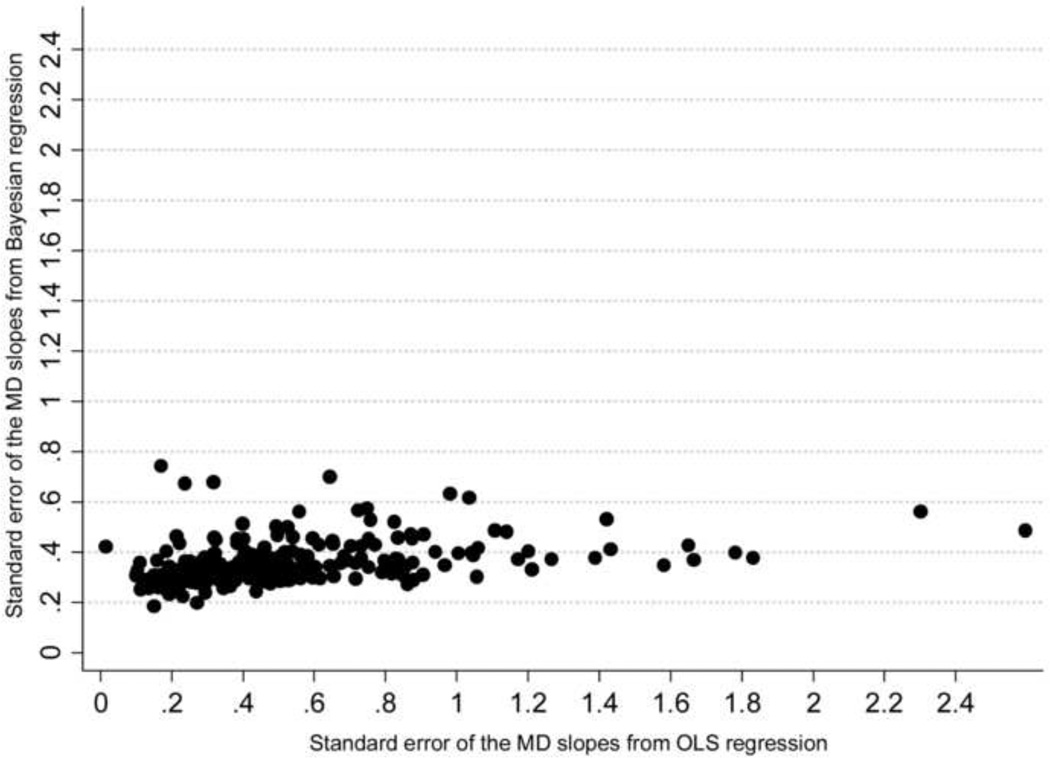
A median number of 5 visual fields (range: 3 to 13) and 5 HRT exams (range 3 to 6) were available during the first period of follow-up and used for calculation of the slopes of MD and rim area change over time. Figure 1 shows a scatterplot of slopes of MD change obtained by the Bayesian and ordinary least squares methods and Figure 2 shows the corresponding scatterplot for slopes of rim area change. There was a stronger relationship between slopes of MD and rim area change calculated by the Bayesian joint regression model (Sperman’s ρ = 0.57) compared to the ordinary least squares method (Spearman’s ρ = 0.19; P<0.001).

Figure 1.

Scatterplot illustrating the relationship between slopes of Mean Deviation (MD) change obtained by the Bayesian joint regression model and by ordinary least squares (OLS) linear regression in glaucoma eyes.

Figure 2.

Scatterplot illustrating the relationship between slopes of rim area change obtained by the Bayesian joint regression model and by ordinary least squares (OLS) linear regression in glaucoma eyes.

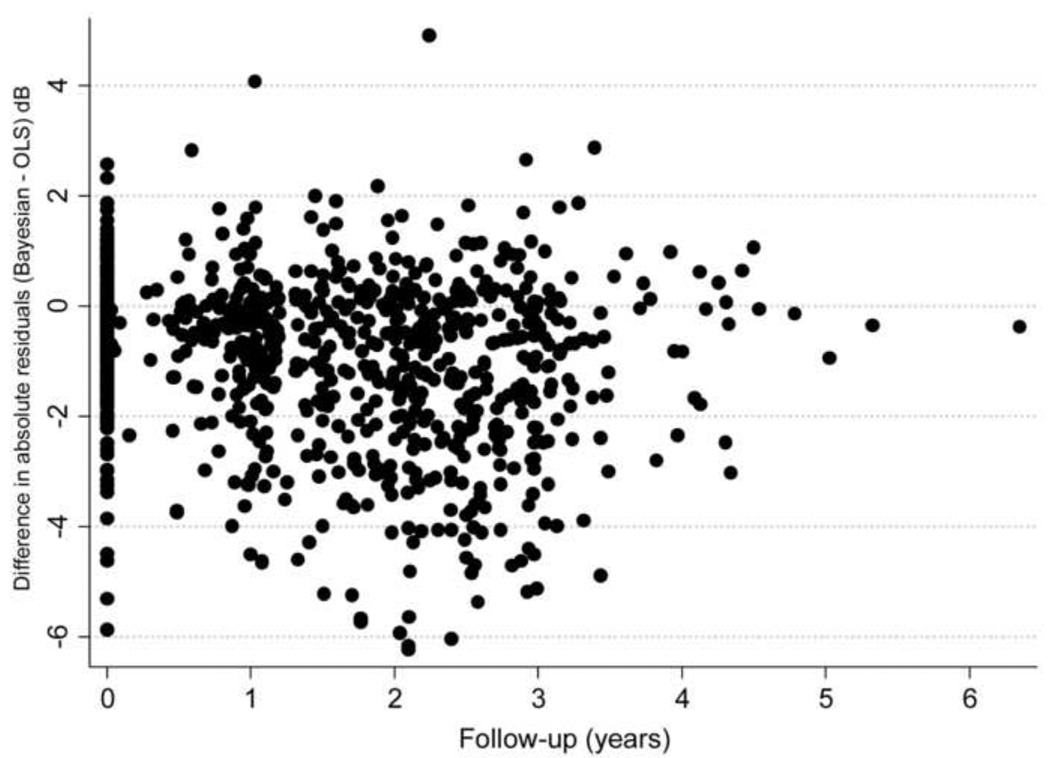
A total of 916 visual fields were available to evaluate the predictions of the Bayesian and ordinary least squares models, with a median number of 4 visual fields per eye. For the ordinary least squares method, the average difference between actual minus predicted MD value was −0.61dB (median: −0.47dB; first quartile: −2.51dB; third quartile: 1.36dB). The mean square error of the ordinary least squares predictions was 11.2 (95% CI: 9.8 – 12.6). For the Bayesian method, the average difference between actual minus predicted MD value was −0.11dB (median: 0.05dB; first quartile: −1.21dB; third quartile: 1.11dB). The mean square error of the Bayesian predictions was 5.13 (95%CI: 4.25 – 6.01). The mean square error of the predictions was significantly lower for the Bayesian compared to the ordinary least squares model (P<0.001). Figure 3 shows a scatter plot of the difference between the absolute residuals for each method versus time. In this plot, the initial time in the horizontal axis was set to zero at the first visual field available to check predictions. The plot shows that residuals for ordinary least squares estimates tended to be larger than those for the Bayesian model, that is, predictions from ordinary least squares regression were in general worse than those based on the Bayesian model.

Figure 3.

Relationship between differences in absolute values of Mean Deviation (MD) residuals in glaucoma eyes for Bayesian and ordinary least squares (OLS) predictions and time. Negative values indicate that residuals for the ordinary least squares method were greater than those from the Bayesian method.

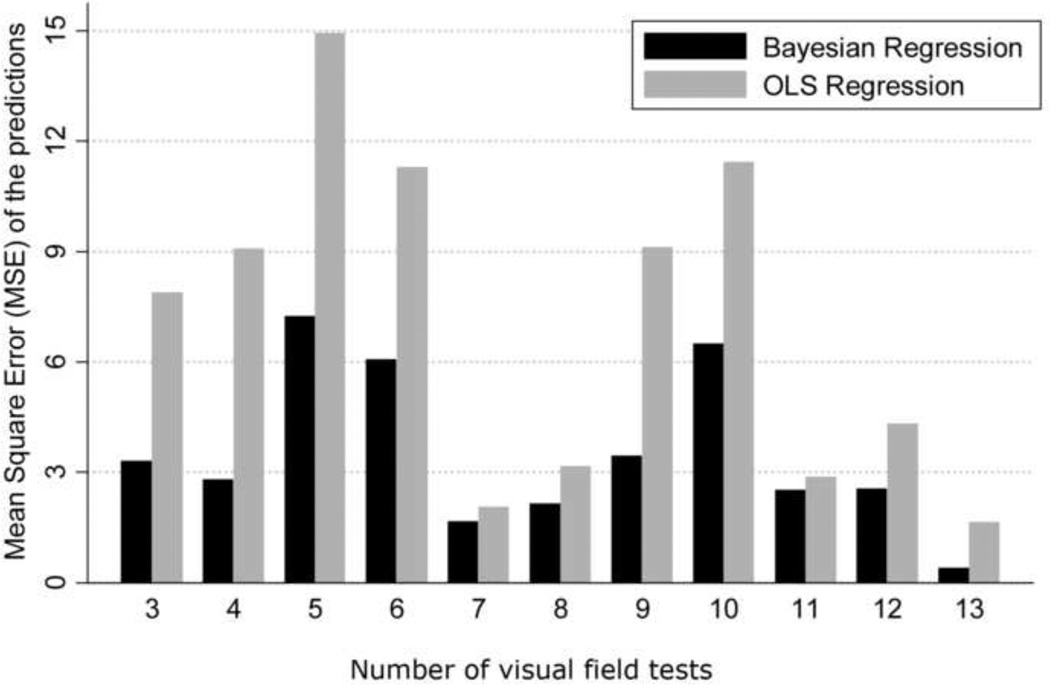
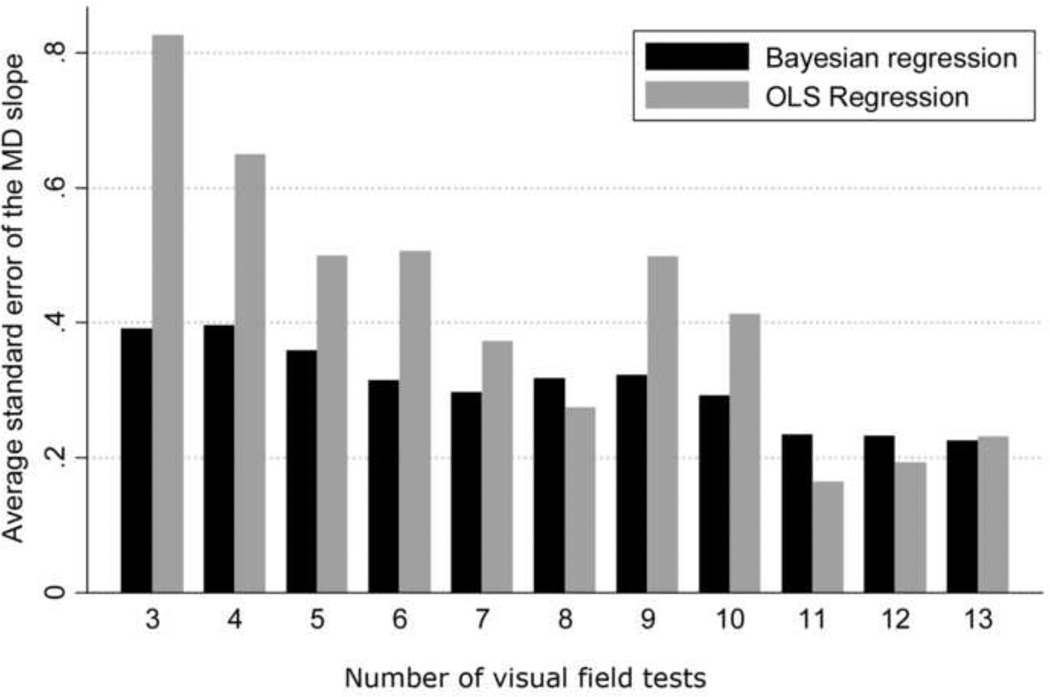
Figure 4 shows the relationship between the mean square error of the predictions for each method versus the number of visual fields available for calculation of the slopes of MD change. While there is a decrease in the difference between the two methods with an increase in the number of visual fields, the Bayesian method was superior to the ordinary least squares method even when a large number of visual fields were used for calculating the slopes. In addition, we also evaluated the precision of the MD slopes calculated with the Bayesian and ordinary least squares methods. The average standard error of the MD slopes calculated with the Bayesian method was significantly lower than that obtained by the ordinary least squares method (0.36dB vs. 0.53dB, respectively; P<0.001), indicating that Bayesian slopes were in general more precise than those obtained by ordinary least squares regression. Figure 5 shows a scatterplot of the standard errors of the MD slopes obtained by the Bayesian and ordinary least squares methods. Figure 6 shows the relationship between the average standard errors of the MD slopes calculated by the Bayesian and ordinary least squares methods and the number of visual fields available for calculation of the slopes.

Figure 4.

Bar plot illustrating the differences in mean square error of the predictions of mean deviation (MD) in glaucoma eyes between the Bayesian and ordinary least squares (OLS) methods. The horizontal axis shows the number of visual field tests used for calculating the slopes of change.

Figure 5.

Scatterplot of the relationship between standard errors of the slopes of mean deviation (MD) change in glaucomatous eyes over time obtained by the Bayesian and ordinary least squares (OLS) regression methods.

Figure 6.

Bar plot illustrating the differences between the Bayesian and ordinary least squares (OLS) regression methods in the average standard errors of the slopes of mean deviation (MD) change over time in glaucomatous eyes, according to the number of visual field tests used for calculating the slopes.

Predictions that underestimated the amount of visual field damage in future observations (i.e., predicted MD values were higher than observed values) are of particular concern due to the possibility of underestimating the risk of visual function loss. An underestimation of the actual MD value by more than 2dB was seen in 272 of the 916 (30%) visual fields with the ordinary least squares method, but only in 122 (13%) visual fields with the Bayesian model (P<0.01). Overestimation of functional losses (i.e., predicted MD values lower than observed values) by more than 2dB occurred in 168 of the 916 (18%) visual fields with the ordinary least squares method versus 111 (12%) with the Bayesian model (P<0.01).

We also evaluated whether estimates of rates of rim area change would also be more accurate than those obtained by the ordinary least squares method. A total of 751 HRT exams were available to evaluate the predictions of the Bayesian and ordinary least squares models, with a median number of 4 tests per eye. For the ordinary least squares method, the average difference between actual minus predicted rim area value was 0.024mm² (median: 0.006mm²; first quartile: −0.051mm²; third quartile: 0.061mm²). The mean square error of the ordinary least squares predictions was 0.027 (95% CI: 0.013 – 0.036). For the Bayesian method, the average difference between actual minus predicted rim area value was 0.022mm² (median: 0.012dB; first quartile: −0.022mm²; third quartile: 0.053mm²). The mean square error of the Bayesian predictions was 0.016 (95%CI: 0.01 – 0.022). The mean square error of the predictions was significantly lower for the Bayesian compared to the ordinary least squares model (P<0.01). Bayesian slopes of rim area change were in general more precise than those calculated from the ordinary least squares method, as indicated by the significantly lower average standard error (0.017mm² vs. 0.021mm²; P = 0.006).

DISCUSSION

In the current study, we showed that a Bayesian joint regression model combining longitudinal CSLO and SAP measurements resulted in improved accuracy and precision of estimates of rates of structural and functional glaucomatous progression compared to the conventional method of trend analysis based on ordinary least squares regression

In order to evaluate the accuracies of the calculated slopes of change from the Bayesian and ordinary least squares methods, we compared their predictive abilities when tested against future SAP and CSLO observations. The slopes of change were calculated from observations occurring during the first half of the follow-up interval and tested against observations from the subsequent follow-up period. Predictions obtained by extrapolating slopes of change calculated from the Bayesian model were closer to the actual MD values than those obtained by extrapolating ordinary least squares regression lines, as shown by differences in the mean square error of the predictions. This indicates that the Bayesian model had superior ability to estimate rates of visual field loss and, therefore, may be advantageous when monitoring progression and predicting the risk of functional impairment from the disease. In fact, rates of change estimated by ordinary least squares regression underestimated the amount of damage in future observations by more than 2dB in 30% of the visual fields compared to only 13% for the Bayesian model. Overestimation of future visual field losses could also have an adverse effect by increasing the cost and morbidity of treatment. Overestimation of functional losses by more than 2dB occurred in 18% of visual fields with the ordinary least squares method versus 12% with the Bayesian model. In addition to providing superior estimates of rates of functional loss, the Bayesian joint model also resulted in more accurate slopes of structural change assessed with the parameter rim area. It is known that some patients may show structural progression in the absence of statistically significant functional changes^3,7–14 and, therefore, detection of structural progression is also essential for adequate monitoring of the disease. By combining structural and functional measurements and improving the estimates of rates of change for both tests, the Bayesian methodology provides a potentially useful framework for the use of these tests in clinical practice.

The use of Bayesian statistics helps improve the estimates of slopes of change by incorporating “prior” information that contributes to their final estimation. In our methodology, the prior is composed of a multivariate distribution relating slopes and intercepts of structural and functional change. Therefore, the joint model allows for the correlation between structural and functional change over time and inferences on functional change are influenced by the presence of structural change and vice-versa.²⁵ This explains the stronger agreement between rates of structural and functional progression obtained from the Bayesian model compared to those from ordinary least squares regression, as indicated by the Spearman’s ρ coefficients (0.57 vs. 0.16, respectively). The stronger agreement seen with the combined Bayes method results from a better characterization of the true underlying relationship between the two tests, as it decreases the impact of measurement error by incorporating it in a joint model of the two longitudinal outcomes. ^30,33–36

Besides better accuracy, slopes of change obtained by Bayesian regression had also greater precision. The precision is a measure of how closely an estimator is expected to be to the true value of the parameter and can be measured by the standard error or confidence interval of the slopes. Large imprecision, i.e., large standard errors, will confound the interpretation of the clinical relevance of an estimated slope, as there will be great uncertainty about where the true slope of change is likely to be. Although rates of change in glaucoma have traditionally been estimated using ordinary least squares linear regression, the true rate of change is actually a latent or unobservable variable. The slope of change obtained from ordinary least squares is just an imprecise estimate of this latent variable, confounded by noise and influenced by the number and intervals of measurements during follow-up. In the presence of imprecise slopes, more tests will increase the precision of the estimate. Although an improvement in the predictions and standard error of the slopes was seen for both methods with an increase in the number of visual fields used for the calculation of the slopes, Bayesian predictions still outperformed ordinary least squares predictions for large number of tests, as indicated by Figure 4. It is known that as the number of measurements increases, the ordinary least squares estimate approaches the true underlying latent variable. However, in clinical practice, there is a cost associated with obtaining more measurements over time, including the expense of the test itself, the cost in patient time, and the cost related to delaying detection of change. By providing more precise estimates of rates of change with fewer tests, however, the Bayesian approach potentially allows more confident clinical decision making to be made earlier with regard to the clinical and statistical significance of the calculated slopes. It is important to emphasize, however, that when assessing the clinical relevance of an estimated slope, clinicians also need to consider other factors, such as life expectancy and the patient’s expectations with regard to treatment.

The current Humphrey Glaucoma Progression Analysis (GPA) software (Carl-Zeiss Meditec, Inc., Dublin, CA) shows a plot of changes of the visual field index (VFI) over time and calculates the rate of VFI loss using ordinary least squares regression. The slope of the line is based on the observed measurements for the eye under consideration and it is extrapolated to predict what the future measurements will be up to 3 to 5 years in the future, if the same rate of change persists over time. Evaluation of rates of functional loss in glaucoma eyes with the VFI has been suggested to be less susceptible than the mean deviation to the effects of cataract or diffuse media opacities.³⁷ In a previous study, we demonstrated that the use of Bayesian statistics may help improve the predictions obtained from slopes of VFI regression.³⁸ We also showed that a Bayesian joint model combining longitudinal scanning laser polarimetry RNFL thickness measurements and SAP VFI index values improves detection of glaucomatous progression with these instruments.²⁵ When we conducted similar analyses using the VFI instead of the MD index in our study, we obtained similar results (not shown), which is not surprising due to the very high correlation between VFI and MD values in our dataset (r = 0.96). Although we applied our methodology to optic disc topographic measurements and SAP data in the current study and to SLP data in another study,²⁵ it is likely that it will also perform well for combining other methods of evaluation of functional and structural loss, such as optical coherence tomography.

Our findings may have significant implications to the design of clinical trials measuring structural and functional changes in glaucoma. In clinical trials comparing the effect of different interventions on the rate of disease progression, the use of Bayesian joint regression models may allow more precise and accurate evaluation of rates of change, potentially decreasing the need to collect additional data and reducing the costs of the study. In addition, a combined evaluation of structural and functional information results in better identification of overall glaucomatous progression and is likely to increase the number of progression endpoints in a clinical trial, potentially decreasing sample size requirements. It is also important to emphasize that the proposed model provides individualized estimates of rates of change which could potentially be used in clinical practice for individual management. The estimation of parameters of the joint model depends on previously acquired data in order to evaluate the relationship between rates of structural and functional change in glaucoma. Accurate assessment of this relationship is essential in order to define how structural information will influence functional tests and vice-versa. However, once this information is available, the model can easily be used to estimate individualized slopes by taking into account the results of structural and functional tests performed in the eye under evaluation.

Our study has limitations. We assumed a linear rate of structural and functional change over time. Previous studies using cross-sectional data, however, suggest that functional changes over the whole course of the disease would probably not be linear. ^8,39–45 However, the assumption of linear change is probably a reasonable one when evaluating change in periods of short- to medium term follow-up, as performed in clinical practice. It should be noted, however, that extensions of our methodology to incorporate non-linear change are also possible, but their evaluation will likely require populations with longer follow-up times. It is important to note that the generalizability of our modeling approach will have to be tested under different clinical scenarios including patients followed in other geographic areas, with different degrees of disease severity, and followed under different clinical protocols. However, when we obtained model parameters based only on patients followed in San Diego and tested it in patients followed in Alabama and New York, we still found that the Bayesian model provided significantly more accurate visual field predictions than the ordinary least squares approach (MSE: 7.3 vs. 13.5, respectively; P<0.001).

In conclusion, a Bayesian joint regression model combining optic disc topographic measurements with visual field information resulted in more accurate and precise estimates of slopes of change compared to the conventional method of ordinary least squares regression. These findings may have significant implications for the use of these tests in clinical practice and in research trials evaluating glaucomatous progression.

Biography

Felipe A. Medeiros, M.D., Ph.D. is Professor of Ophthalmology at the University of California San Diego (UCSD). He is also Medical Director and Director of Visual Function Research of the Hamilton Glaucoma Center at UCSD. His research interests encompass many different areas in glaucoma, including identification of risk factors for development and progression of disease, methods and strategies for diagnosis, follow-up and management of glaucoma and evaluation of functional impairment from the disease.