Optimizing parameters in clinical trials with a randomized start or withdrawal design

Abstract

Disease-modifying (DM) trials on chronic diseases such as Alzheimer’s disease (AD) require a randomized start or withdrawal design. The analysis and optimization of such trials remain poorly understood, even for the simplest scenario in which only three repeated efficacy assessments are planned for each subject: one at the baseline, one at the end of the trial, and the other at the time when the treatments are switched. Under the assumption that the repeated measures across subjects follow a trivariate distribution whose mean and covariance matrix exist, the DM efficacy hypothesis is formulated by comparing the change of efficacy outcome between treatment arms with and without a treatment switch. Using a minimax criterion, a methodology is developed to optimally determine the sample size allocations to individual treatment arms as well as the optimum time when treatments are switched. The sensitivity of the optimum designs with respect to various model parameters is further assessed. An intersection-union test (IUT) is proposed to test the DM hypothesis, and determine the asymptotic size and the power of the IUT. Finally, the proposed methodology is demonstrated by using reported statistics on the placebo arms from several recently published symptomatic trials on AD to estimate necessary parameters and then deriving the optimum sample sizes and the time of treatment switch for future DM trials on AD.

1. Introduction

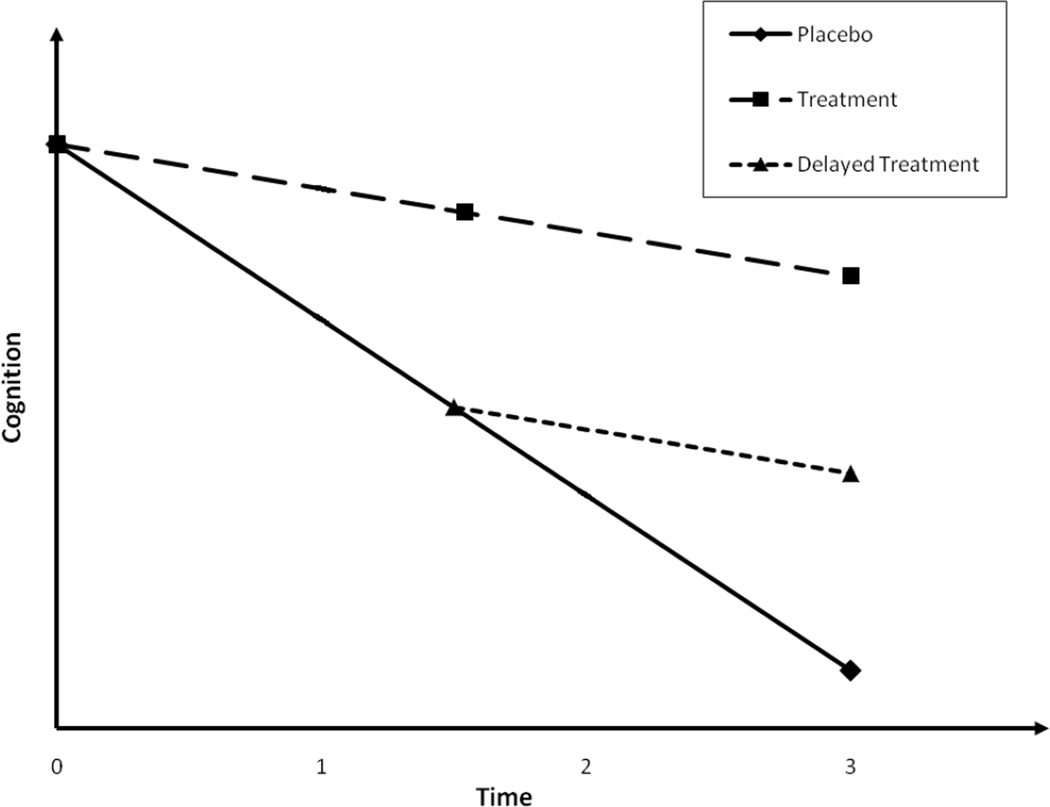
Many clinical trials require a switch of treatments in the middle of the studies, and yet are not conducted through a standard crossover design. Examples include disease-modifying (DM) trials on chronic diseases such as Alzheimer’s disease (AD) that strive not only to establish the symptomatic efficacy for novel treatments in improving cognition, function, and global measures or deferring decline over a relatively short period of time, but also to demonstrate that the course of AD has been altered and the rate of disease progression has been slowed (Cummings 2006, Aisen 2006, Citron 2004, Mani 2004) over a relatively long period of time. DM trials have been widely discussed in the AD research community (Leber 1997; Sampaio 2006; Whitehouse et al. 1998, Cummings et al. 2007). Clinicians have conceptualized designs of DM trials to allow a definite distinction from the symptomatic trials (Cummings 2006, Aisen 2006, Citron 2004). These designs in general require a switch of treatments in the middle of trials for at least a proportion of subjects originally randomized to either placebo or active treatment. One such design is the randomized start design (Mani 2004). All patients in the design eventually will receive the active treatment, but are randomized to two treatment groups that begin the active drug at different times. During the initial time period of the study one group receives active drug and the other placebo. After an interval of time sufficient to demonstrate the symptomatic efficacy for the active drug, the placebo group switches to the active drug. If the patients who begin active drug late ‘catch up’ with those who begin the active drug at baseline, the treatment effect is assumed to be symptomatic. If there is no ‘catch-up’, it is assumed that the effect of the drug is DM. Another DM design is the randomized withdrawal design (Mani 2004), which differs from the randomized start design only in that subjects initially on active drug are switched to placebo in the second phase. If the group withdrawn from the active drug maintains gains on the efficacy measure relative to the placebo group, it is assumed that the drug is DM. In both DM designs, in order to preserve the blinding, a second randomization must be performed to the initial placebo (or active drug) arm so that a proportion of patients will maintain on placebo (or active drug) throughout the trial. Figure 1 presents the expected longitudinal cognitive growth profiles of a randomized start design on AD. To date, all FDA-approved treatments to AD have been entirely based on their efficacy for treating symptoms (Kryscio et al. 2004, Ringman et al. 2009, Andrieu et al. 2006), partly because the design and analyses to establish the DM effectiveness of these treatments as well as many emerging ones (Salloway et al. 2008) have not been fully established.

Fig. 1.

Expected cognitive progression in a simple disease modifying trial on AD

This paper focus on the DM trial with a randomized start or withdrawal design for which only three repeated efficacy assessments are planned: one at the baseline, one at the end of the trial, and the other at the time when the treatments are switched. We formulate the DM hypothesis and propose a method to test the hypothesis, derive optimal sample size allocations to different treatment arms and the optimum time of treatment switch, and assess the sensitivity of these designs. Finally, we present optimum designs of future DM trials on AD using the reported statistics from recently published symptomatic trials.

2. A model for DM trials with a randomized start design

2.1. Estimating DM efficacy and testing the DM hypothesis

We will discuss our methodology by focusing on the DM trials on AD with a randomized start design, and point out that our proposed methods apply to many similar clinical trials on other diseases that require a switch of treatments in the middle of the trial (i.e., randomized withdrawal design). We use Y to denote the primary efficacy outcome in DM trials on AD (Cummings 2008). The Alzheimer’s Disease Assessment Scale-cognitive subscale (ADAS-cog, Rosen et al. 1984) has been the most commonly used primary cognitive outcome in symptomatic trials of AD. Recently, many modalities of biomarkers have now shown promising ability to track the disease progression, including magnetic resonance imaging-based brain volumes (Storandt et al. 2009), diffusion tensor imaging-based measures of white matter microstructure (Head et al. 2004), cerebrospinal fluid (Fagan et al. 2006), and molecular imaging of cerebral fibrillar amyloid with positron emission tomography using the [¹¹C] benzothiazole tracer, Pittsburgh Compound-B (Mintun et al. 2006).

We use u=tt and pp to represent the group of subjects who are in the treatment arm and placebo arm throughout the trial, respectively, and use u=pt to represent the group of subjects who initially receive the placebo and then switch to the active treatment. Assume that $y_j^u(t)$ is the observation of Y at time t for the j -th subject from treatment group u. Let t₁, t₂, t₃ be the three time points for repeated measures of Y in a DM trial with a randomized start design, where t₁ = 0 is the baseline, t₃ is the time of the final assessment, and t₂ is the time for the treatment switch. Let $y_{ji}^u=y_j^u(t_i)$,i = 1,2,3, and let $Y_j^u={(y_{j1}^u,y_{j2}^u,y_{j3}^u)}^t$ (superscript t means matrix transpose) be the vector of longitudinal measurements of the j -th subject from treatment group u. Because the DM design requires the establishment of both symptomatic efficacy prior to the treatment switch and the DM efficacy after the treatment switch, the first objective is to compare the change from the baseline between the treatment and the placebo before the treatment switch, and the second objective is to compare the change in efficacy outcome between subjects treated throughout the trial and those receiving the delayed treatment.

For subject j from treatment arm u, u=tt, pp, and pt, we assume a trivariate distribution for $Y_j^u={(y_{j1}^u,y_{j2}^u,y_{j3}^u)}^t$ whose first and second moments exist. Notice that here we do not assume a specific parametric family such as normal distributions for the joint distribution of $Y_j^u$. This more general assumption on the distributions is justified, especially in the future clinical trials on AD for which a wide range of cognitive and CSF and imaging biomarkers (Storandt et al. 2009, Head et al. 2004, Fagan et al. 2006, Mintun et al. 2006) with highly skewed distributions could potentially serve as efficacy endpoints. Let ${\mu }^u={({\mu }_1^u,{\mu }_2^u,{\mu }_3^u)}^t$ be the mean vector of $Y_j^u$ for group u. We assume that the duration of the trial, t₃, is pre-specified, but the time for the treatment switch, t₂, can be designed. Let

$$\mathrm{\Sigma }=\left(\begin{array}{ccc}\hfill {\sigma }_1^2\hfill & \hfill {\sigma }_{12}\hfill & \hfill {\sigma }_{13}\hfill \\ \hfill \hfill & \hfill {\sigma }_2^2\hfill & \hfill {\sigma }_{23}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill {\sigma }_3^2\hfill \end{array}\right)$$ (1)

be the shared covariance matrix of $Y_j^u$ for u=tt, pp, and pt. We point out that our proposed methods described below can also be generalized to the case when the variance and covariance parameters in Σ vary as a function of t₂. Because of the randomization at the baseline as well as the second randomization at the treatment switch time for those initially assigned to the placebo, we can assume that ${\mu }_1^{pp}={\mu }_1^{tt}={\mu }_1^{pt}$ and ${\mu }_2^{pp}={\mu }_2^{pt}$. Further, we assume that a linear trend adequately describes the longitudinal progression of the efficacy outcome for the treated group and the placebo group throughout the trial, and let

$${\beta }^u=\frac{{\mu }_2^u-{\mu }_1^u}{t_2-t_1}=\frac{{\mu }_3^u-{\mu }_2^u}{t_3-t_2}$$

be the mean slopes for u=tt and pp. Let

$${\beta }^{pt}=\frac{{\mu }_3^{pt}-{\mu }_2^{pt}}{t_3-t_2}$$

be the slope of efficacy outcome after the treatment switch. The comparative nature of ${\mu }^u={({\mu }_1^u,{\mu }_2^u,{\mu }_3^u)}^t$, u=tt, pp, and pt, determines whether the novel treatment is DM. More specifically, before the treatment switch, it is expected that the symptomatic efficacy for treating AD will be established. This implies that the mean decline since baseline for the treated and the placebo arms should be different, with the treated arm decline more slowly before the time when the placebo is switched to the active treatment. This implies that ${\mu }_2^{tt}-{\mu }_1^{tt}>{\mu }_2^{pp}-{\mu }_1^{pp}$, i.e., β^tt > β^pp. After the treatment switch, the efficacy for modifying the disease can only be established by the fact that the subjects whose treatment is delayed (i.e., u=pt) can never ‘catch up’ those whose treatment is not delayed if the trial continues indefinitely. Mathematically, this implies that, after the treatment switch, the rate of decline for the delayed treatment arm has to be equal to or faster than that for the treated arm throughout the trial, i.e., $({\mu }_3^{tt}-{\mu }_2^{tt})/(t_3-t_2)\ge ({\mu }_3^{pt}-{\mu }_2^{pt})/(t_3-t_2)$, or equivalently, β^tt ≥ β^pt. Therefore, an appropriate statistical hypothesis for establishing the DM efficacy of the novel treatment is β^tt ≥ β^pt > β^pp. In order to test this hypothesis, we have to estimate two differences on slopes: one is between the treated arm throughout the trial and the delayed treatment arm, i.e., δ = β^tt − β^pt, and the other is between the delayed treatment arm and the placebo arm throughout the trial, i.e., Δ = β^pt − β^pp.

Let n_u be the sample size within group u. Let n = n_tt + n_pp + n_pt be the total sample size. Let λ_u = n_u / n be the proportion (i.e., allocation) of the total sample size to each treatment group u=pp, tt, and pt. It is clear that λ_pp + λ_tt + λ_pt = 1. Let d₁ = t₂ − t₁, d₂ = t₃ − t₂, $s_1={\sigma }_1^2-2{\sigma }_{12},s_2={\sigma }_2^2-2{\sigma }_{23}$, s₃ = σ₁₃ − σ₁₂, $s_4={\sigma }_2^2+{\sigma }_3^2-2{\sigma }_{23}$. Let

$${\mathrm{\mu ̂}}_1^{tt}={\mathrm{\mu ̂}}_1^{pp}={\mathrm{\mu ̂}}_1^{pt}=\frac{\sum _{j=1}^{n_{tt}}{y}_{j1}^{tt}+\sum _{j=1}^{n_{pp}}{y}_{j1}^{pp}+\sum _{j=1}^{n_{pt}}{y}_{j1}^{pt}}{n}.$$

Because β^tt can be estimated by two unbiased estimators

$${\mathrm{\beta ̂}}_1^{tt}=\frac{\sum _{j=1}^{n_{tt}}{y}_{j2}^{tt}/n_{tt}-{\mathrm{\mu ̂}}_1^{tt}}{d_1},$$

and

$${\mathrm{\beta ̂}}_2^{tt}=\frac{\sum _{j=1}^{n_{tt}}(y_{j3}^{tt}-y_{j2}^{tt})}{d_2{n}_{tt}},$$

an optimum estimate to β^tt is

$${\mathrm{\beta ̂}}^{tt}=c{\mathrm{\beta ̂}}_1^{tt}+(1-c){\mathrm{\beta ̂}}_2^{tt},$$ (2)

for some constant c such that the variance of β̂^tt, ${\sigma }_{{\mathrm{\beta ̂}}^{tt}}^2$, as given in row 2 of Table 1, is minimized over the choice of c. A simple calculus reveals the optimum c as given by

$$c=\frac{s_4{d}_1^2/{\lambda }_{tt}-[({\sigma }_{23}-{\sigma }_2^2)/{\lambda }_{tt}-s_3]d_1{d}_2}{[{\sigma }_2^2/{\lambda }_{tt}+s_1]d_2^2+s_4{d}_1^2/{\lambda }_{tt}-2[({\sigma }_{23}-{\sigma }_2^2)/{\lambda }_{tt}-s_3]d_1{d}_2}.$$

Let

$${\mathrm{\mu ̂}}_2^{pp}={\mathrm{\mu ̂}}_2^{pt}=\frac{\sum _{j=1}^{n_{pp}}{y}_{j2}^{pp}+\sum _{j=1}^{n_{pt}}{y}_{j2}^{pt}}{n_{pp}+n_{pt}}.$$

β^pp can also be estimated by two unbiased estimators. One involves data from t₁ = 0 to t₂ for both the placebo arm throughout the trial and the delayed treatment arm,

$${\mathrm{\beta ̂}}_1^{pp}=\frac{{\mathrm{\mu ̂}}_2^{pp}-{\mathrm{\mu ̂}}_1^{pp}}{d_1}.$$

The other involves data from t₂ to t₃ for the placebo arm throughout the trial,

$${\mathrm{\beta ̂}}_2^{pp}=\frac{\sum _{j=1}^{n_{pp}}{y}_{j3}^{pp}/n_{pp}-{\mathrm{\mu ̂}}_2^{pp}}{d_2}.$$

An optimum estimate to β^pp is

$${\mathrm{\beta ̂}}^{pp}=f{\mathrm{\beta ̂}}_1^{pp}+(1-f){\mathrm{\beta ̂}}_2^{pp},$$ (3)

for some constant f such that the variance of β̂^pp, ${\sigma }_{{\mathrm{\beta ̂}}^{pp}}^2$, as given in row 3 of Table 1, is minimized over the choice of f. Another simple calculus reveals the optimum f as

$$f=\frac{[({\sigma }_3^2/{\lambda }_{pp}+s_2/({\lambda }_{pp}+{\lambda }_{pt})]d_1^2-[({\sigma }_{23}-{\sigma }_2^2)/({\lambda }_{pp}+{\lambda }_{pt})-s_3]d_1{d}_2}{[{\sigma }_2^2{d}_2^2+s_2{d}_1^2-2({\sigma }_{23}-{\sigma }_2^2)d_1{d}_2]/({\lambda }_{pt}+{\lambda }_{pp})+[s_1{d}_2^2+2s_3{d}_1{d}_2]+{\sigma }_3^2{d}_1^2/{\lambda }_{pp}}.$$

Next, the slope β^pt after the treatment switch can be estimated by

$${\mathrm{\beta ̂}}^{pt}=\frac{\sum _{j=1}^{n_{pt}}{y}_{j3}^{pt}/n_{pt}-{\mathrm{\mu ̂}}_2^{pt}}{d_2}.$$

The variance of β̂^pt, ${\sigma }_{{\mathrm{\beta ̂}}^{pt}}^2$, is given by row 5 of Table 1. Finally, based on the optimum estimator β̂^tt, δ = β^tt − β^pt can be estimated by δ̂ = β̂^tt − β̂^pt. The variance of δ̂, ${\sigma }_{\mathrm{\delta ̂}}^2$, is given by row 8 of Table 1, where the covariance of β̂^tt and β̂^pt, cov(β̂^tt, β̂^pt), is given by row 6 of Table 1. Likewise, based on the optimum estimator β̂^pp, Δ = β^pt − β^pp can be estimated by Δ̂ = β̂^pt − β̂^pp. The variance of Δ̂, ${\sigma }_{\mathrm{\Delta ̂}}^2$, is given by row 9 of Table 1, where cov(β̂^pt, β̂^pp) is given by row 7 of Table 1. It is clear that under standard regularity conditions required for the joint distribution of $Y_j^u$ in the Central Limit Theorem, the estimates, (δ̂,Δ̂), follow an asymptotic bivariate normal distribution with mean (δ,Δ) and covariance matrix

$$\mathrm{\Psi }=\left(\begin{array}{cc}{\sigma }_{\mathrm{\delta ̂}}^2\hfill & {\sigma }_{\mathrm{\delta ̂}\mathrm{\Delta ̂}}\hfill \\ \hfill & {\sigma }_{\mathrm{\Delta ̂}}^2\hfill \end{array}\right),$$

where the covariance of (δ̂,Δ̂), σ_δ̂Δ̂, is given by row 10 of Table 1 with the covariance of β̂^tt and β̂^pp, cov(β̂^tt, β̂^pp), given by row 4 of Table 1.

Table 1.

Variance and covariance of estimated parameters for testing DM efficacy (Notice that the covariance becomes variance when two estimates are the same)

Estimate 1	Estimate 2	Covariance between Estimate 1 and Estimator 2
β̂tt	β̂tt	$\frac{c^2}{d_1^2}(\frac{{\sigma }_2^2}{n_{tt}}+\frac{s_1}{n})+\frac{s_4{(1-c)}^2}{d_2^2{n}_{tt}}+\frac{2c(1-c)}{d_1{d}_2}(\frac{{\sigma }_{23}-{\sigma }_2^2}{n_{tt}}-\frac{s_3}{n})$
β̂pp	β̂pp	$\frac{f^2}{d_1^2}(\frac{{\sigma }_2^2}{n-n_{tt}}+\frac{s_1}{n})+\frac{{(1-f)}^2}{d_2^2}(\frac{{\sigma }_3^2}{n_{pp}}+\frac{s_2}{n-n_{tt}})+\frac{2f(1-f)}{d_1{d}_2}(\frac{{\sigma }_{23}-{\sigma }_2^2}{n_{pp}+n_{pt}}-\frac{s_3}{n})$
β̂tt	β̂pp	$\frac{cf{s}_1}{n{d}_1^2}-\frac{(c+f-2cf)s_3}{n{d}_1{d}_2}$
β̂pt	β̂pt	$\frac{1}{d_2^2}(\frac{{\sigma }_3^2}{n_{pt}}+\frac{s_2}{n_{pp}+n_{pt}})$
β̂tt	β̂pt	$\frac{-c{s}_3}{n{d}_1{d}_2}$
β̂pt	β̂pp	$\frac{f}{d_1{d}_2}(\frac{{\sigma }_{23}-{\sigma }_2^2}{n_{pp}+n_{pt}}-\frac{s_3}{n})+\frac{(1-f)s_2}{(n_{pp}+n_{pt})d_2^2}$
δ̂	δ̂	${\sigma }_{{\mathrm{\beta ̂}}^{tt}}^2+{\sigma }_{{\mathrm{\beta ̂}}^{pt}}^2-2\text{cov}({\mathrm{\beta ̂}}^{tt},{\mathrm{\beta ̂}}^{pt})$
Δ̂	Δ̂	${\sigma }_{{\mathrm{\beta ̂}}^{pt}}^2+{\sigma }_{{\mathrm{\beta ̂}}^{pp}}^2-2\text{cov}({\mathrm{\beta ̂}}^{pt},{\mathrm{\beta ̂}}^{pp})$
δ̂	Δ̂	$\text{cov}({\mathrm{\beta ̂}}^{tt},{\mathrm{\beta ̂}}^{pt})+\text{cov}({\mathrm{\beta ̂}}^{pt},{\mathrm{\beta ̂}}^{pp})-{\sigma }_{{\mathrm{\beta ̂}}^{pt}}^2-\text{cov}({\mathrm{\beta ̂}}^{tt},{\mathrm{\beta ̂}}^{pp})$

Table 1 summarizes the variance and covariance of all estimated parameters for testing DM efficacy as described above. Notice that the covariance in the third column of Table 1 becomes the variance when two estimates are the same.

To test the DM efficacy of the active treatment, we propose to test the null hypothesis H₀ : δ < 0 or Δ ≤ 0 against the alternative H₁ : δ ≥ 0 and Δ > 0. The null hypothesis is the union of two null hypotheses H_0δ : δ < 0 and H_0Δ : Δ ≤ 0, and the alternative is the intersection of two alternative hypotheses H_1δ : δ ≥ 0 and H_1Δ : Δ > 0. For each individual set of null and alternative hypotheses, let z^δ = δ̂ / σ_δ̂ and z^Δ = Δ̂ / σ_Δ̂ be the corresponding test statistic. If δ = 0 or Δ = 0, the corresponding test statistic follows an asymptotic standard normal distribution. To test the null hypothesis H₀ : δ < 0 or Δ ≤ 0 against the alternative H₁ : δ ≥ 0 or Δ > 0, an intersection-union test (IUT, Berger and Sinclair 1984, Berger 1989, Liu and Berger 1995) rejects the null hypothesis when both z^δ > M and z^Δ > M for some constant M. In order for the test to have a size of α (0 < α < 1), M has to be chosen such that

$${\text{sup}}_{H_0}{\text{lim}}_{{\text{min}}_u{n}_u\to \infty }\mathrm{P}\mathrm{r}(z^{\delta }>M,z^{\mathrm{\Delta }}>M)=\alpha .$$

Notice that

$$p(\delta ,\mathrm{\Delta },M)={\text{lim}}_{{\text{min}}_u{n}_u\to \infty }\mathrm{P}\mathrm{r}(z^{\delta }>M,z^{\mathrm{\Delta }}>M)={\text{lim}}_{{\text{min}}_u{n}_u\to \infty }{\int }_{m_{\delta }}^{\infty }{\int }_{m_{\mathrm{\Delta }}}^{\infty }\frac{{(2\pi )}^{-1}}{\sqrt{|{\mathrm{\Psi }}_1|}}\text{exp}[-0.5Z{\mathrm{\Psi }}_1^{-1}{Z}^t]d{z}^{\delta }d{z}^{\mathrm{\Delta }},$$ (4)

where Z = (z^δ,z^Δ), m_δ = M −δ / σ_δ̂ and m_Δ = M − Δ/σ_Δ̂, and

$${\mathrm{\Psi }}_1=\left(\begin{array}{cc}\hfill 1\hfill & \hfill {\sigma }_{\mathrm{\delta ̂}\mathrm{\Delta ̂}}/({\sigma }_{\mathrm{\delta ̂}}{\sigma }_{\mathrm{\Delta ̂}})\hfill \\ \hfill {\sigma }_{\mathrm{\delta ̂}\mathrm{\Delta ̂}}/({\sigma }_{\mathrm{\delta ̂}}{\sigma }_{\mathrm{\Delta ̂}})\hfill & \hfill 1\hfill \end{array}\right).$$

Because lim_δ→+∞ m_δ = −∞, it follows that if Δ = 0, i.e., still staying within H₀, then, as min_u n_u → ∞,

$$\alpha ={\text{sup}}_{H_0}\mathrm{P}\mathrm{r}(z^{\delta }>M,z^{\mathrm{\Delta }}>M)\ge {\text{lim}}_{\delta \to +\infty }P(\delta ,\mathrm{\Delta },M)=\mathrm{P}\mathrm{r}(z^{\mathrm{\Delta }}>M|\mathrm{\Delta }=0).$$

Therefore, when M = z_α, the 100α upper percentile of the standard normal distribution, the rejection region z^δ > M and z^Δ > M for the IUT provides asymptotic size α for testing H₀ : δ < 0 or Δ ≤ 0 against the alternative H₁ : δ ≥ 0 and Δ > 0. The corresponding approximate power function for the IUT is then given by

$$p(\delta ,\mathrm{\Delta })=\mathrm{P}\mathrm{r}(z^{\delta }>z_{\alpha },z^{\mathrm{\Delta }}>z_{\alpha }).$$ (5)

Thus, the sample sizes required to achieve an asymptotic statistical power of (1−η) (0 < η < 1) are the solutions to n_tt, n_pp, and n_pt such that P(δ,Δ) =1 − η.

If the total spacing t₃ has been determined, given the simple DM trial we consider here, an important design question is how the treatment switch time, t₂, should be chosen to give the best estimate to the efficacy parameters δ and Δ. Another important set of design parameters to be optimized is the sample size allocations λ_u, u = pp, tt, pt, subject to λ_u > 0,, and λ_pp + λ_tt + λ_pt = 1. Because the DM design requires simultaneous estimates to two parameters, (δ,Δ), an optimum design must simultaneously minimize the variances associated with both estimates, (δ̂,Δ̂). Hence, it is necessary to find the maximum possible variance from any linear combinations of the two estimates. Let L̂(τ₁, τ₂) = τ₁δ̂ + τ₂Δ̂ be a linear combination of the two estimators with weights (τ₁, τ₂) subject to τ₁² + τ₂². The variance of the linear combination is

$${\sigma }_{\mathrm{L̂}({\tau }_1,{\tau }_2)}^2=({\tau }_1,{\tau }_2)\mathrm{\Psi }{({\tau }_1,{\tau }_2)}^t.$$ (6)

The maximum variance from all possible linear combinations is the largest eigenvalue of Ψ (Noble and Daniel, 1977) as given by

$${\text{max}}_{{\tau }_1^2+{\tau }_2^2=1}{\sigma }_{\mathrm{L̂}({\tau }_1,{\tau }_2)}^2=0.5({\sigma }_{\mathrm{\delta ̂}}^2+{\sigma }_{\mathrm{\Delta ̂}}^2+\sqrt{{({\sigma }_{\mathrm{\delta ̂}}^2-{\sigma }_{\mathrm{\Delta ̂}}^2)}^2+4{\sigma }_{\mathrm{\delta ̂}\mathrm{\Delta ̂}}^2}).$$ (7)

Notice that ${\text{max}}_{{\tau }_1^2+{\tau }_2^2=1}{\sigma }_{\mathrm{L̂}({\tau }_1,{\tau }_2)}^2$ depends on both individual variances of (δ̂,Δ̂) and the covariance between them, σ_δ̂Δ̂. In the extreme case when two estimators are independent, i.e., σ_δ̂Δ̂ = 0, ${\text{max}}_{{\tau }_1^2+{\tau }_2^2=1}{\sigma }_{\mathrm{L̂}({\tau }_1,{\tau }_2)}^2$ is the maximum of the variances from (δ̂,Δ̂). To optimize the DM design, one criterion is to use the ‘minimax’ criterion, i.e., to choose all design parameters to minimize the maximum variance, ${\text{max}}_{{\tau }_1^2+{\tau }_2^2=1}{\sigma }_{\mathrm{L̂}({\tau }_1,{\tau }_2)}^2$, from all possible linear combinations of (δ̂,Δ̂). Notice that n ${\text{max}}_{{\tau }_1^2+{\tau }_2^2=1}{\sigma }_{\mathrm{L̂}({\tau }_1,{\tau }_2)}^2$ (n is the total sample size) is a function of λ_u, u = pp, tt, pt, and t₂. Assuming that the duration t₃ of the simple DM trial is pre-specified, we locate the optimum treatment switch time t₂ and the sample size allocations λ_u, u = pp, tt, pt, by minimizing n ${\text{max}}_{{\tau }_1^2+{\tau }_2^2=1}{\sigma }_{\mathrm{L̂}({\tau }_1,{\tau }_2)}^2$. Notice that the focus of the DM trial with a randomized start design is on the delayed and non-delayed treatment arms, i.e., data from these two arms alone already allow the test of the DM efficacy. Subjects randomized into the placebo again from the second randomization mainly serve to preserve the blinding of subjects and investigators to the active treatment, albeit they have to participate in the efficacy analyses based on the ‘intent-to-treat’ principle (Montori and Guyatt 2001, Heritier et al. 2003). Hence, it is practical for the investigators to pre-specify a small portion of subjects (denoted by λ₀) to be randomized to placebo from the second randomization, i.e., u=pp. The optimum treatment switch time t₂ and sample size allocations are then the solutions for minimizing n ${\text{max}}_{{\tau }_1^2+{\tau }_2^2=1}{\sigma }_{\mathrm{L̂}({\tau }_1,{\tau }_2)}^2$, subject to 0 = t₁ < t₂ < t₃ and 0 < λ_tt = 1 − λ₀ − λ_pt < 1. Mathematically, n ${\text{max}}_{{\tau }_1^2+{\tau }_2^2=1}{\sigma }_{\mathrm{L̂}({\tau }_1,{\tau }_2)}^2$, as a function of t₂ and λ_pt, is complicated. The minimization over t₂ and λ_pt has no closed form, and can be done by Newton–Raphson method (Bonnans et al. 2006) to solve the system of equations

$$\{\begin{array}{c}\frac{\partial (n{\text{max}}_{{\tau }_1^2+{\tau }_2^2=1}{\sigma }_{\mathrm{L̂}({\tau }_1,{\tau }_2)}^2)}{\partial t_2}=0\hfill \\ \frac{\partial (n{\text{max}}_{{\tau }_1^2+{\tau }_2^2=1}{\sigma }_{\mathrm{L̂}({\tau }_1,{\tau }_2)}^2)}{\partial {\lambda }_{pt}}=0\hfill \end{array}.$$ (8)

2.2. Specification of covariance matrix for the trivariate distribution

It is important to point out that the optimum design we proposed above does not assume a specific parametric family of trivariate distribution (e.g., normal distribution) for $Y_j^u$. However, the proposed methodology does require the existence of the mean vector ${\mu }^u={({\mu }_1^u,{\mu }_2^u,{\mu }_3^u)}^t$ and the covariance matrix for $Y_j^u$. The common covariance structure assumed for u=pp, pt, and tt has to be specified to derive the optimum design parameters for the DM trials. Because general linear mixed effects models have been very successful to fit the longitudinal data from many of the outcomes in AD studies (Johnson et al. 2009, Storandt et al. 2006), here we focus on the specific covariance structure that can be derived from the random intercept and random slope models (Laird and Ware 1982) on $y_j^u(t)$, 0 = t₁ ≤ t ≤ t₃, for group u=pp or tt. Assuming a linear trend over time for $y_j^u(t)$, a random intercept and slope model assumes that

$$y_j^u(t)={\beta }_{0j}^u+{\beta }_{1j}^{u}t+{\epsilon }_j^u(t),$$ (9)

where $({\beta }_{0j}^u,{\beta }_{1j}^u)$ is subject-specific vector of latent intercept and slope, and ${\epsilon }_j^u(t)$ is the within-subject random error over time. We further assume a bivariate (not necessarily normal) distribution for $({\beta }_{0j}^u,{\beta }_{1j}^u)$ across subjects with a 2 by 2 covariance matrix

$$\mathrm{\Omega }=\left[\begin{array}{cc}{\omega }_1^2\hfill & {\omega }_{12}\hfill \\ \hfill & {\omega }_2^2\hfill \end{array}\right],$$ (10)

and a stationary error process for ${\epsilon }_j^u(t)$, 0 = t₁ ≤ t ≤ t₃, with $E[{\epsilon }_j^u(t)]=0$ and the autocovariance function given by

$$\rho (h)=\text{cov}[{\epsilon }_j^u(t),{\epsilon }_j^u(t+h)],$$ (11)

for h ≥ 0. For example, if ρ(h) is a constant when h>0, it corresponds to the compound symmetry covariance structure in longitudinal models (Diggle et al., 2002). If

$$\rho (h)={\tau }^2{\rho }^h,$$ (12)

for h>0, it corresponds to the autoregressive covariance structure in longitudinal models (Diggle et al., 2002). Finally, with the standard assumption of independence between $({\beta }_{0j}^u,{\beta }_{1j}^u)$ and ${\epsilon }_j^u(t)$, 0 = t₁ < t₂ < t₃ in the linear mixed model, the covariance matrix for $Y_j^u={(y_j^u(t_1),y_j^u(t_2),y_j^u(t_3))}^t$ is given by

$$\mathrm{\Sigma }=\left(\begin{array}{ccc}\hfill {\omega }_1^2+\gamma (0)\hfill & \hfill {\omega }_1^2+t_2{\omega }_{12}+\gamma t_2\hfill & \hfill {\omega }_1^2+t_3{\omega }_{12}+\gamma t_3\hfill \\ \hfill \hfill & \hfill {\omega }_1^2+2t_2{\omega }_{12}+t_2^2{\omega }_2^2+\gamma (0)\hfill & \hfill {\omega }_1^2+(t_2+t_3){\omega }_{12}+t_2{t}_3{\omega }_2^2+\gamma (t_3-t_2)\hfill \\ \hfill \hfill & \hfill \hfill & \hfill {\omega }_1^2+2t_3{\omega }_{12}+t_3^2{\omega }_2^2+\gamma (0)\hfill \end{array}\right).$$ (13)

To assess how different parameters in the covariance structure affect the optimum choices for the treatment switch time and the sample size allocations to different treatment arms, we compute the optimum design parameters in a hypothetical DM trial with a duration of unit 1, i.e., t₁ = 0, t₃ = 1. We assume the following variance/covariance parameter for $({\beta }_{0j}^u,{\beta }_{1j}^u)$ in Equation (10): ${\omega }_1^2={\omega }_2^2=4$, ω₁₂ = 4γ, where γ is the correlation between the latent intercept and the slope across subjects. We also assume an autoregressive covariance structure for ${\epsilon }_j^u(t)$ in Equation (12) with τ² = 6 and ρ, the correlation between ${\epsilon }_j^u(t)$ and ${\epsilon }_j^u(t+1)$. For a wide range of γ and ρ, assuming 10% subjects are randomized to the placebo throughout the trial, Table 2 presents the optimum time of treatment switch (t₂) and optimum sample size allocations (λ_tt, λ_pt) to treatment groups. Results in Table 2 suggest that the optimum sample size allocations (λ_{tt, λpt}) are remarkably stable and robust as a function of the two correlations γ and ρ. Further, the correlation γ only minimally affects the optimum choice of treatment switch time t₂, whereas the correlation ρ in the autoregressive covariance structure for ${\epsilon }_j^u(t)$ seems to play a moderately bigger role in affecting the optimum treatment switch time, i.e., as ρ increases, the optimum treatment switch time t₂ increases moderately.

Table 2.

Optimum time of treatment switch (t₂) and sample size allocations (λ_tt, λ_pt) as a function of the correlation (γ) between the latent intercept and the slope and the correlation (ρ) in the autoregressive covariance structure for ${\epsilon }_j^u(t)$ in a hypothetical DM trial. A total trial duration of unit one assumed (i.e., t₁ = 0,t₃ = 1). 10% subjects assumed to receive the placebo throughout the trial.

γ	ρ	t2	λtt	λpt
0.1	0.1	0.25	0.17	0.73
0.1	0.3	0.30	0.18	0.72
0.1	0.5	0.33	0.20	0.70
0.1	0.7	0.34	0.20	0.70
0.1	0.9	0.35	0.19	0.71
0.3	0.1	0.26	0.17	0.73
0.3	0.3	0.30	0.19	0.71
0.3	0.5	0.33	0.20	0.70
0.3	0.7	0.34	0.20	0.70
0.3	0.9	0.35	0.19	0.71
0.5	0.1	0.27	0.18	0.72
0.5	0.3	0.30	0.19	0.71
0.5	0.5	0.32	0.20	0.70
0.5	0.7	0.33	0.20	0.70
0.5	0.9	0.34	0.19	0.71
0.7	0.1	0.27	0.18	0.72
0.7	0.3	0.31	0.20	0.70
0.7	0.5	0.31	0.20	0.70
0.7	0.7	0.32	0.20	0.70
0.7	0.9	0.33	0.18	0.72
0.9	0.1	0.27	0.18	0.72
0.9	0.3	0.30	0.20	0.70
0.9	0.5	0.31	0.20	0.70
0.9	0.7	0.32	0.20	0.70
0.9	0.9	0.32	0.17	0.73

The optimum allocation to group pt is from 59% to 67% in Table 2 if 20% subjects are assumed to receive the placebo throughout the trial.

3. Application: optimum DM trials on AD

We demonstrate the proposed methodology to design a future DM trial on AD using the latest available information from the literature. AD is characterized by an insidious onset of memory deterioration, progressive cognitive deterioration, emergence of neuropsychiatric symptoms and behavioral disturbances, impairment of activities of daily living, and loss of independent function. The looming public health crisis due to AD mandates a fast development of novel DM treatments for the disease. Currently, several compounds have been approved by the FDA to enhance cognition and global function of AD patients through symptomatic trials alone. On the other hand, recent advances in understanding AD pathogenesis have led to the development of numerous compounds that might modify the disease process. A wide array of antiamyloid and neuroprotective therapeutic approaches are under investigation on the basis of the hypothesis that amyloid beta (Abeta) protein plays a pivotal role in disease onset and progression and that secondary consequences of Abeta generation and deposition, including tau hyperphosphorylation and neurofibrillary tangle formation, oxidation, inflammation, and excitotoxicity, contribute to the disease process (Salloway et al. 2008). Interventions in these processes with agents that reduce amyloid production, limit aggregation, or increase removal might block the cascade of events comprising AD pathogenesis. Reducing tau hyperphosphorylation, limiting oxidation and excitotoxicity, and controlling inflammation might be beneficial disease-modifying strategies. Potentially neuroprotective and restorative treatments such as neurotrophins, neurotrophic factor enhancers, and stem cell-related approaches are also under investigation (Salloway et al. 2008). It is anticipated that these promising treatments will soon be tested for their ability to modify the disease process of AD through well designed DM clinical trials.

Unlike symptomatic trials for which a single randomization at baseline is generally implemented, DM trials require an initial randomization followed by a re-randomization of patients in either the placebo or treatment arm. Although the design and analysis of DM trials on AD have been extensively discussed in the AD literature (Cummings 2006, Aisen 2006, Citron 2004, Mani 2004), no DM trials on patients with AD have been reported to date. We therefore have to obtain necessary estimates to important model parameters through recently reported symptomatic trials on AD. These parameters include between and within subject variances and covariance ${\omega }_s^2$, s = 1,2, ω₁₂ in Equation (10) and τ² and ρ (in the autoregressive function of ${\epsilon }_j^u(t)$, t₁ ≤ t ≤ t₃). Using these estimates, here we provide optimum design parameters for future DM trials on AD by applying our proposed methodology to a variety of design scenarios. We assume a randomized start design in which 10% subjects will be randomized to receiving placebo throughout the trial and then optimize the sample size allocations to the treatment arm and the delayed treatment arm. We also optimize the time of treatment switch for the delayed treatment arm. The optimum weights c and f as given in Equations (2) and (3) are used to estimate β^tt and β^pp, as well as subsequently in the IUT of the DM efficacy.

More specifically, we conducted a comprehensive literature review on symptomatic clinical trials on AD. Most recently reported symptomatic trials on AD used ADAS-cog as the primary efficacy outcome measure. We therefore assumed that the future DM trials will also use the same cognitive outcome as the primary efficacy endpoint. Essentially all published symptomatic trials on AD reported the efficacy analyses using the change of ADAS-cog score from the baseline. These published symptomatic treatment trials on AD followed patients for a duration ranging from 4 weeks to 1.5 year (Qizilbash et al. 1998; Kaduszkiewicz et al. 2005, Sano et al. 2011), and therefore the reported variance for the change from baseline on ADAS-cog score also spanned a wide range. None of the published symptomatic trials on AD directly reported estimates to model parameters ${\omega }_s^2$, s = 1,2, ω₁₂, τ², and ρ as given in Equations (10) and (12). We hence combined the reported statistics from multiple published symptomatic trials on AD to obtain estimates necessary for optimizing DM trials with three outcome assessments. Three recently published trials (two published in 2011) that were reasonably large in sample size and long in follow-up duration were identified. These three trials specifically reported the variance associated with the change of ADAS-cog score from the baseline for the placebo arm (i.e., u=pp). Sano et al. (2011) reported the effect of simvastatin in treating mild to moderate AD for an 18 months trial from which 202 subjects were randomized to the placebo. Rafii et al. (2011) reported the effect of huperzine A in treating mild to moderate AD for a 16 weeks trial from which 73 subjects were randomized to the placebo. Rogers et al. (1998) reported the effects of Donepezil in treating AD for a 24-weeks trial from which 162 subjects were randomized to placebo. Because of variable length of longitudinal follow-up for these trials, the reported variance associated with the change of ADAS-cog score from the baseline is a function of the length of follow-up. However, if model (9) is appropriate for the placebo arm of the reported symptomatic trials, i.e., assuming a linear growth pattern of ADAS-cog over time, the annual rate of change on ADAS-cog (i.e., the slope) in the placebo arm can be estimated (sometimes through extrapolations with less than 1 year follow-up) by the reported mean difference from baseline divided by the length of follow-up (in years). Therefore, the standard deviation for the annual rate of change can be estimated by the reported standard deviation on the change from baseline divided by the number of years in follow-up. Let D be the duration of a reported symptomatic trial on AD. We linked the reported statistics on the change score of ADAS-cog from the baseline with our proposed covariance structure in Equation (13). Whereas these published trials did assess subjects at more than two time points, our approach is likely the only practical one because none of these trials reported relevant statistics on the efficacy at middle time points from the baseline to the final assessment. Specifically, the model given by Equation (9) implies

$$\frac{y_j^{pp}(D)-y_j^{pp}(0)}{D}={\beta }_{1j}^{pp}+\frac{{\epsilon }_j^{pp}(D)-{\epsilon }_j^{pp}(0)}{D}.$$

It then follows that

$$\frac{{\sigma }_d^2}{D^2}=\frac{2{\tau }^2(1-{\rho }^D)}{D^2}+{\omega }_2^2,$$ (14)

where ${\sigma }_d^2$ is the reported variance for the change score of ADAS-cog from the baseline in the placebo arm. In addition, all three published trials reported basic statistics of ADAS-cog at baseline for the placebo arm, which can be used to estimate the variance parameters in our covariance structure associated with the baseline outcome measure (Equation (13)). In fact, at baseline, i.e., t = t₁ = 0, ${\sigma }_b^2={\tau }^2+{\omega }_1^2$, where ${\sigma }_b^2$ is the reported variance for the baseline ADAS-cog. The reported statistics on the placebo arm from the three trials are given in Table 3.

Table 3.

Reported statistics from three recently published symptomatic trials on ADAS-Cog for the placebo arm

Study: author (year)	Sample size	Years of follow-up	Mean (SD) at baseline	Mean (SD) for the change from baseline
Rogers et al. 1998	162	0.46	27.28 (11.87)	1.82 (6.06)
Rafii et al. 2011	73	0.31	27.10 (10.58)	−0.34 (5.17)
Sano et al. 2011	202	1.50	23.90 (10.50)	8.18 (8.70)

From the reported statistics of the three trials (Rogers et al. 1998, Rafii et al. 2011, and Sano et al. 2011) along with Equation (14), we have the following system of equations:

$$\{\begin{array}{c}{6.06}^2/{0.46}^2=2{\tau }^2(1-{\rho }^{0.46})/{0.46}^2+{\omega }_2^2\hfill \\ {5.17}^2/{0.31}^2=2{\tau }^2(1-{\rho }^{0.31})/{0.31}^2+{\omega }_2^2\hfill \\ {8.70}^2/{1.50}^2=2{\tau }^2(1-{\rho }^{1.50})/{1.50}^2+{\omega }_2^2\hfill \end{array}.$$

Solving the system of equations revealed that ρ = 0.319, ${\omega }_2^2=1.125$, τ² = 44.627. Finally, using the baseline variance estimate from the largest trial in Table 3 (i.e., Sano et al. 2011), we estimated ${\omega }_1^2$ by ${10.5}^2={\tau }^2+{\omega }_1^2$, resulting ${\omega }_1^2=65.624$.

We have now obtained estimates to variance and covariance parameters ${\omega }_s^2$, s = 1,2, τ² and ρ in the covariance structure as given by Equation (13) except for ω₁₂, the covariance between the latent intercept and the slope across subjects in the random intercept and random slope model (Equation (9)). No information was directly reported in published symptomatic trials on AD that can be used to obtain an estimate to ω₁₂. Because ω₁₂ = γω₁ω₂, we therefore searched for the optimum design parameters for future DM trials on AD as a function of γ, the correlation between the latent intercept and the slope across subjects. For a range of γ, λ_pp = 10%, t₃ = 1.5 years or 2 years or 2.5 years, Table 4 reports the optimum sample size allocations to different arms as well as the optimum time of treatment switch for future simple DM trials on AD with three longitudinal assessments. Results in Table 4 confirm what has been found in Table 2, i.e., the optimum sample size allocations (λ_tt, λ_pt) and the optimum choice of treatment switch (t₂) are very stable and robust as a function of the correlation γ between the latent intercept and the slope.

Table 4.

Optimum time of treatment switch (t2) and sample size allocations (λ_tt, λ_pt)in a DM trial on AD with three repeated outcome assessments. γ = correlation between the latent intercept and the slope. 10% subjects assumed to the placebo throughout the trial

Trial duration (years)	γ	λtt	λpt	t2 (years)
1.5	0.1	0.15	0.75	0.45
1.5	0.3	0.15	0.75	0.45
1.5	0.5	0.15	0.75	0.45
1.5	0.7	0.15	0.75	0.45
1.5	0.9	0.15	0.75	0.45
2.0	0.1	0.14	0.76	0.54
2.0	0.3	0.15	0.75	0.57
2.0	0.5	0.15	0.75	0.57
2.0	0.7	0.15	0.75	0.57
2.0	0.9	0.15	0.75	0.57
2.5	0.1	0.14	0.76	0.65
2.5	0.3	0.15	0.75	0.68
2.5	0.5	0.15	0.75	0.69
2.5	0.7	0.15	0.75	0.70
2.5	0.9	0.16	0.74	0.73

The optimum allocation to group pt is from 62% to 64% in Table 4 if 20% subjects are assumed to receive the placebo throughout the trial.

Assuming a randomized start design with three efficacy assessments for a duration of 1.5 years, 2 years and 2.5 years, for a selected set of effect sizes typically reported in the AD literature, Table 5 presents the sample sizes for different treatment arms (i.e., u=pt and u=tt) required to detect the effect sizes with a statistical power of 80%. These individual sample sizes are based on the optimum sample size allocations (in %) to group u=pt and u=tt (i.e., λ_pt and λ_tt) and optimum treatment switch time as presented in Table 4. 10% subjects are assumed to be randomized into the placebo arm throughout the trial for preserving the blinding. Because the correlation (γ) between the latent intercept and the slope across subjects does not appreciably affect the optimum design parameters (i.e., sample size allocations λ_pt and λ_tt, and treatment switch time t₂) as evidenced in Table 4, we assumed that γ = 0.5 in Table 5. Power function in Equation (5) was evaluated by SAS function PROBBNRM (SAS Institute Inc., 1990) in Table 5.

Table 5.

Sample sizes (N) for individual treatment arms (u=tt or pt) in a future simple randomized start design required to detect a selected set of effect sizes (i.e., differences on the annual rate of decline in ADAS-cog (δ,Δ) = (β^tt − β^pt − β^pt − β^pp)) with a statistical power of 80% from the IUT. 10% subjects are randomized into placebo arm throughout the trial. A correlation of 0.5 (i.e., γ) between the latent intercept and the slope is assumed.

Trial duration (years)	δ = βtt − βpt	Δ = βpt − βpp	N for u=tt	N for u=pt	Total N
1.5	1.0	1.0	460	2301	3067
1.5	1.0	1.5	337	1689	2251
1.5	1.0	2.0	318	1593	2123
1.5	1.0	2.5	317	1589	2117
1.5	1.5	1.0	361	1805	2406
1.5	1.5	1.5	204	1023	1363
1.5	1.5	2.0	159	799	1064
1.5	1.5	2.5	145	725	966
1.5	2.0	1.0	351	1757	2342
1.5	2.0	1.5	167	836	1114
1.5	2.0	2.0	115	576	767
1.5	2.0	2.5	94	470	626
1.5	2.5	1.0	351	1756	2341
1.5	2.5	1.5	157	787	1049
1.5	2.5	2.0	97	486	647
1.5	2.5	2.5	73	368	490
2.0	1.0	1.0	294	1472	1962
2.0	1.0	1.5	213	1065	1420
2.0	1.0	2.0	199	996	1327
2.0	1.0	2.5	198	992	1322
2.0	1.5	1.0	234	1171	1561
2.0	1.5	1.5	130	654	871
2.0	1.5	2.0	101	506	674
2.0	1.5	2.5	91	455	606
2.0	2.0	1.0	229	1146	1527
2.0	2.0	1.5	108	540	720
2.0	2.0	2.0	73	368	490
2.0	2.0	2.5	59	298	396
2.0	2.5	1.0	229	1146	1527
2.0	2.5	1.5	102	513	683
2.0	2.5	2.0	62	313	416
2.0	2.5	2.5	47	235	313
2.5	1.0	1.0	207	1035	1380
2.5	1.0	1.5	148	744	991
2.5	1.0	2.0	138	693	923
2.5	1.0	2.5	138	690	920
2.5	1.5	1.0	165	828	1103
2.5	1.5	1.5	92	460	613
2.5	1.5	2.0	70	354	471
2.5	1.5	2.5	63	318	423
2.5	2.0	1.0	162	812	1082
2.5	2.0	1.5	76	381	507
2.5	2.0	2.0	51	258	343
2.5	2.0	2.5	41	209	277
2.5	2.5	1.0	162	812	1082
2.5	2.5	1.5	72	363	483
2.5	2.5	2.0	44	221	294
2.5	2.5	2.5	33	165	220

(some rows do not add precisely due to the rounding up in each sample size)

4. Discussion

In order to design optimum clinical trials for establishing the DM efficacy of potential novel treatments on chronic disease such as AD, we proposed a methodology to analyze the rate of change for efficacy outcome variable in a randomized start trial. We focused on the simplest longitudinal design with only three repeated outcome assessments from which the middle one serves as the time of treatment switch. We assumed a trivariate distribution without a specific parametric structure for the three repeated measures on the same subjects with a covariance matrix that was derived from a random intercept and random slope model (Laird and Ware 1982). Based on these assumptions, we first formulated the appropriate DM hypothesis by comparing the rate of change in efficacy outcome between the treated group throughout the trial and the delayed treatment group. Because of the second randomization to the subjects who are initially randomized to the placebo in a DM trial, a third treatment arm in which subjects are randomized to the placebo throughout the trial is available. The third treatment arm complicated the statistical test of DM efficacy due to the ‘intent-to-treat’ principle that requires that data from all randomized and treated subjects participate in the efficacy analysis. Because multiple unbiased estimators were available to the rate of change for the placebo and the treatment arms, we obtained optimum unbiased estimates to the rates of change by minimizing the variance of linear combinations of multiple estimators. With these optimum estimates, we developed a methodology to optimally determine the sample size allocations to different treatment arms as well as the time for treatment switch for subjects whose treatment was delayed. After the design parameters were optimally chosen, we proposed an intersection-union test to assess the efficacy of potential DM agents. We studied the size and the power of the IUT, and provided a method of determining the sample sizes to adequately power the test of DM efficacy.

The simple DM trials with a randomized start design we considered here differ from the standard crossover designs (Chi 1992) in the sense that the former allows some of the subjects receiving only placebo throughout the trials. Further, whereas most crossover trials are designed for testing the symptomatic efficacy of a novel treatment, the simple DM trials aim to establish DM efficacy which mandates the symptomatic efficacy as a prerequisite during the first phase of the trial. Therefore, the time of treatment switch becomes an important parameter in designing DM trials. Our proposed methodology provided an optimum choice of treatment switch time. Jarjoura (2003) considered the efficiency of a clinical trial design which did allow crossing control to treatment (i.e., similar to our designs), but optimal switching time for crossing controls to active treatment was only discussed under the assumption that the treatment effect is constant across time (please see page 311 of Jarjoura (2003)). Here, we have focused on the DM efficacy which requires not only a symptomatic treatment efficacy that is time-varying prior to treatment switching time but also a DM treatment efficacy that depends on whether the treatment is delayed or not. In addition, our analytic approaches also differed from those of other authors (Jarjoura 2003). The randomized start design we discussed here allowed the third arm of continued control throughout the trial (to protect the blinding after second randomization), which complicated the parameter estimations much more considerably than the two arm scenario that was discussed in Jarjoura (2003). We have assumed a trivariate distribution without a specific parametric structure for the three repeated measures on the same subjects whose mean vectors across different arms were used to define the DM hypothesis. The covariance structure of the trivariate distribution, however, was derived from a standard random intercept and random slope model (Laird and Ware 1982) which assumed a bivariate distribution for the latent intercept and slope and incorporated an autoregressive structure on the error process. We assumed a linear trend over time for subjects whose treatment was not switched in the middle of the trials. For individuals whose treatment was delayed, the simple DM trials we considered here forced a piecewise linear pattern. Our approach allowed potentially differential rate of change for subjects receiving delayed treatment as compared to those receiving the treatment throughout the trial, as well as a correlation on the rates of change before and after the treatment switch. Through a hypothetical DM trial, we found that the optimum sample size allocations were very stable and robust against different choices of the correlation (i.e., γ) between the latent intercept and the slope and the correlation (i.e., ρ) in the autoregressive covariance structure for ${\epsilon }_j^u(t)$ in model (11). We also found that the correlation ρ in the autoregressive covariance structure for ${\epsilon }_j^u(t)$ played a moderately bigger role in determining the optimum treatment switch time than the correlation γ.

The current definition of DM efficacy in clinical trials with a randomized start design requires two conditions to be met simultaneously: one is the symptomatic efficacy before the treatments are switched, and the other is the fact that the delayed treatment arm will never ‘catch up’ the continuously treated arm. It is therefore very intuitive to use some type of adaptive design in which the first condition (i.e., the symptomatic efficacy) is tested using data prior to the treatment switch, and then the second condition tested after the treatment switch. This type of adaptive design is called adaptive-hypotheses design (Chow and Chang 2008), and can be especially appealing for testing a novel treatment for which no symptomatic efficacy has ever been established, because the adaptive testing can prevent the trial from continuing (and thus saving cost) if the test of the first condition (symptomatic efficacy) is not even successful. On the other hand, even if the test of the first condition is successful, it can not establish the DM efficacy that requires both conditions simultaneously. Because our goal is to optimize design parameters such as treatment switch time and sample size allocations to different arms in a future DM trial and the cost of the clinical trial is not considered in the optimum design of the DM trials for the current work, we have hence chosen to use a randomized start design to test the DM efficacy by allowing a treatment switch in the middle of the trial. These are especially relevant to the companies whose drugs have already been approved by the FDA due to their successful symptomatic trials on the symptomatic efficacy. What they would like to do next is to prove that their drugs have additional DM efficacy. To achieve this, they would need to design a future DM trial involving a treatment switch. Our proposed methods provide them parameters to optimally design such trials.

We applied our proposed methodology to design future simple DM trials on AD. Because no DM trials on AD have been reported, we conducted a literature review on published symptomatic trials on AD, and located three recently reported symptomatic trials on AD that were relatively large in sample size and long in follow-up and also reported the variance associated with the change of ADAS-cog score from the baseline for the placebo arm (Rogers et al. 1998, Rafii et al. 2011, and Sano et al. 2011). Given that none of the three trials directly reported the estimates to parameters in the covariance structure in Equation (13), we proposed a novel approach to obtain pilot estimates to these important parameters by linking our proposed covariance structure with the reported statistics. More specifically, we solved a system of three equations that were derived from the reported variances associated with the change of ADAS-cog score from the baseline in the three trials. After obtaining estimates to these parameters, we computed the optimum design parameters (i.e., sample size allocations, and treatment switch time) for future simple DM trials on AD, and provided the sample sizes into different treatment arms required to detect a selected set of effect sizes with a statistical power of 80%. Our results indicate that clinical trials for DM treatments on AD can be adequately powered and optimized. Because a DM treatment, by definition, requires symptomatic efficacy, it is no surprise that a DM trial on AD requires a much larger sample size than symptomatic trials, as demonstrated by our findings. Another contributing factor to the relatively large sample sizes in future DM trials on AD is the relatively small effect sizes we have intentionally assumed in Table 5. This is based on the fact that, although ADAS-cog has shown a wide range of effect sizes in published symptomatic trials, smaller effect sizes are expected for future novel drugs on AD because any future clinical trials on AD will have to be conducted on the patients who have already been using approved drugs, i.e., the efficacy of future drugs on AD will have to be based on the incremental effect from the already approved AD drugs. Further, Table 5 suggests that, if the effect sizes are fixed, then the biggest effect on the required sample size is the trial duration. Whereas we have specifically considered the simplest longitudinal design of the DM trials with 3 observations per subject here, the issue of dropouts and missing data will play an important role in determining the final sample sizes of future DM trials. Given that a longer trial duration is in general associated with a higher likelihood of subject dropouts, further research is needed to fully understand the trade offs in final sample sizes between dropouts and the required three observations per subject. Finally, the relatively large sample size in Table 5 is also partly due to the fact that the rate of change on ADAS-cog is subject to a large variation as evidenced by Table 3 and therefore may not be an ideal efficacy outcome in future DM trials. More sensitive novel biomarkers will be needed to design future DM trials on AD with a much smaller sample size. For example, MRI-based brain volumes (Storandt et al. 2009), DTI-based measures of white matter microstructure (Head et al. 2004), CSF-based biomarkers (Fagan et al. 2006), and molecular imaging of cerebral fibrillar amyloid with PET using the [¹¹C] benzothiazole tracer, Pittsburgh Compound-B (PIB, Mintun et al. 2006), are all potential candidates of efficacy outcomes for future DM trials on AD. Our study has some limitations. First, we have assumed a linear growth or decline pattern over time for the efficacy outcome in group u=tt and u=pp and derived the optimum design parameters. Although our proposed method can be generalized to address a nonlinear pattern from time 1 to 2 to 3 in group u=tt and u=pp, the robustness of our optimum design parameters with respect to the potentially nonlinear growth patterns remained unknown. It is therefore important to carefully assess the linearity assumption before applying our proposed optimum designs. Second, we have focused on the simplest longitudinal design in which only three repeated efficacy assessments are planned for each subject: one at the baseline, one at the end of the trial, and the other at the time when the treatments are switched. More frequent observations per subject allow statistical assessment of the assumption of a linear response within each of the three groups, as well as appropriate analyses of missing data. Further, with reasonable statistical models, more frequent observations will also imply better statistical power for testing the DM efficacy. In addition, our proposed methodology has focused on one-sided tests to reflect the current definition of DM efficacy, i.e., the requirement of both the symptomatic efficacy before the treatments are switched and the additional efficacy demonstrating that the delayed treatment arm will never ‘catch up’ the continuously treated arm. The generalization to the efficacy tests with two-sided alternatives through the IUT is needed in real world applications when there is no guarantee that a novel treatment is always better than the placebo. Further, our proposed methodology only applies when the treatment will not have any serious side effect so that treatment can be given without stop and there is no alternative treatment besides the treatment in the trial. Finally, FDA typically requires two primary efficacy endpoints in clinical trials on AD (cognition and function). Although our proposed method can be applied to each efficacy endpoint in the DM trials of AD, the optimal design parameters for cognition is not necessarily optimal for function. Future research is needed to address these crucial questions.