Abstract
The radial mode matching (RMM) method has been used to calculate accurately the microwave field distribution of the TE0 1 1 mode in a spherical EPR cavity containing a linear aqueous sample, in order to understand in detail the factors affecting sensitivity in EPR measurements at X band. Specific details of the experiment were included in the calculations, such as the cavity geometry, the presence of a quartz dewar, the size of the aqueous sample, and the sample’s dielectric properties. From the field distribution, several key physical parameters were calculated, including cavity Q, filling factor, mean microwave magnetic field at the sample, and cavity efficiency parameter Λ. The dependence of EPR signal intensity on sample diameter for a cylindrical aqueous sample was calculated and measured experimentally for non-saturated and half-saturated samples. The optimal aqueous sample diameter was determined for both cases. The impact of sample temperature, conductivity, and cavity Q on sensitivity of EPR is discussed.
Keywords: EPR, Water, Sensitivity, Cavity, Field distribution
1. Introduction
The design of EPR experiments is often based on the approximation that sample size is negligible and the dielectric properties of the sample do not change the resonant conditions of the cavity. Indeed, when the complex permittivity of a sample at the microwave frequency is small or the sample is sufficiently small, this approach works well. However, for samples with large permittivity or size, the task of optimizing sample size and shape becomes important. This is the case for most biological applications, in which diluted aqueous samples are typical. The imaginary part of the complex permittivity of water is high at microwave frequencies and thus causes absorption, which can degrade the cavity’s quality factor (Q). The real part of the complex permittivity of water is also high and causes significant field redistribution within the cavity.
The sensitivity of EPR in biological studies at ambient temperature is an important problem. A typical biological EPR sample, such as a spin labeled protein in solution, has a spin concentration on the order of 10 μM and a volume of about 20 μl, giving about 1014 spins. This is only 10–100 times greater than the threshold of EPR detection, where S/N = 1. This is an especially difficult problem in the case of slow tumbling or restricted internal motion of a spin label, where the broad linewidth decreases S. Therefore, modern biological EPR usually works at the edge of sensitivity, which makes optimization an important issue.
According to Feher [1], EPR signal intensity is
| (1) |
where P is the incident power, η is the cavity filling factor, is the quality factor for the unloaded cavity with the sample, and χ″ is the sample’s magnetic susceptibility (proportional to the number of spins). Both filling factor and quality factor depend on the microwave field distribution within the cavity. The filling factor shows the fraction of the cavity’s microwave field energy that is concentrated at the sample [2],
| (2) |
where ϕ is the angle between the DC polarizing magnetic field and H1 (it is 90° for all experiments considered in this work, so the angle dependence is eliminated), Vs and Vc are the volumes of the sample and cavity and is the mean value of . The quality factor is the ratio of the energy U stored in the cavity to the energy P/ω dissipated in one cycle,
| (3) |
where and ω is angular frequency.
At sufficiently low microwave power, χ″ is constant, so S (Eq. (1)) is proportional to P1/2. However, at sufficiently high P, saturation occurs and χ″ depends on relaxation times T1 and T2, according to , where χ0 is the static susceptibility, and b depends on the homogeneity of broadening of the EPR line [3-6]. We consider two kinds of sample, one with short relaxation times, so that (non-saturated), and a sample with moderate relaxation times, so that (half-saturated).
To optimize the size of a non-saturated sample, where χ″ = χ0 and S is directly proportional to P1/2, it is sufficient to maximize , as shown by Feher [1] and Stoodley [7], who used perturbation approaches. In the first approach, the dielectric properties of the sample were completely neglected. In the second approach, the real part of the complex permittivity was taken into account, and the dependence of the signal intensity on sample size (tube radius) was analyzed theoretically for a sample of refractive index n = 8.0 (corresponding to a value of 64 for the real part of the water permittivity). It was predicted that the EPR signal intensity from an aqueous sample in a cylindrical tube in a cylindrical cavity with TE011 symmetry should have a maximal value when the internal diameter is 0.76 mm. There were no experiments done to test this hypothesis, and there was no investigation of other experimental conditions, such as sample temperature or conductivity. Wilmshurst [8] mentioned that the diameter of a saturated sample with severe dielectric loss should be as large as possible to maximize the EPR signal. This conclusion was made from a perturbation method analysis, and no experimental verification was made.
In subsequent studies, wave perturbation, wave-superposition, and finite-element methods were used to find η, Q, and EPR signal intensity for the case of a point sample placed inside a spherical bulb of varying dielectric liquid [9,10]. It was found that water decreases signal intensity due to degradation of cavity Q, but that it also redistributes (concentrates) the magnetic field due to the high real part of the complex permittivity.
In the present study, the distribution of the TE01 1 microwave field is calculated for the case of cylindrical aqueous samples in a spherical cavity, using a rigorous radial mode matching method. This permits the calculation of cavity Q, filling factor η, efficiency parameter Λ, and EPR signal intensity for cylindrical aqueous samples of varying diameter, including all relevant experimental details, including the temperature-control dewar, and the temperature and conductivity of the sample. The results of calculations are compared quantitatively with experimental results.
2. Methods
2.1. Theoretical
2.1.1. Radial mode matching method
The resonance frequency ν and the distribution of microwave magnetic and electric fields were calculated by the radial mode matching (RMM) method. The general idea of the RMM method [11] is to divide the inner space of a cavity into regions of different dielectric properties, construct a series of coupled equations describing the fields in each region, and solve these equations by requiring that the tangential fields must match at the boundaries of regions. The calculation is divided into three parts. First the resonance frequency is determined by matching the fields, then the field distribution is calculated, and this is used to calculate experimentally relevant EPR parameters such as the quality factor, filling factor, and EPR signal intensity.
We start with the Helmholtz vector equation, in cylindrical coordinates [11,12]:
| (4) |
where Ψ is the electromagnetic vector potential (representing the microwave electric and magnetic fields), k0 = 2πν/c, ν is the resonance frequency, c is the speed of light, and ε is the permittivity of the region. For the TE01 1 mode excited in a cylindrical or spherical cavity, m = 0 because of axial symmetry, and Eq. (4) is solved separately for each region (Fig. 1) by separation of variables
| (5) |
Fig. 1.
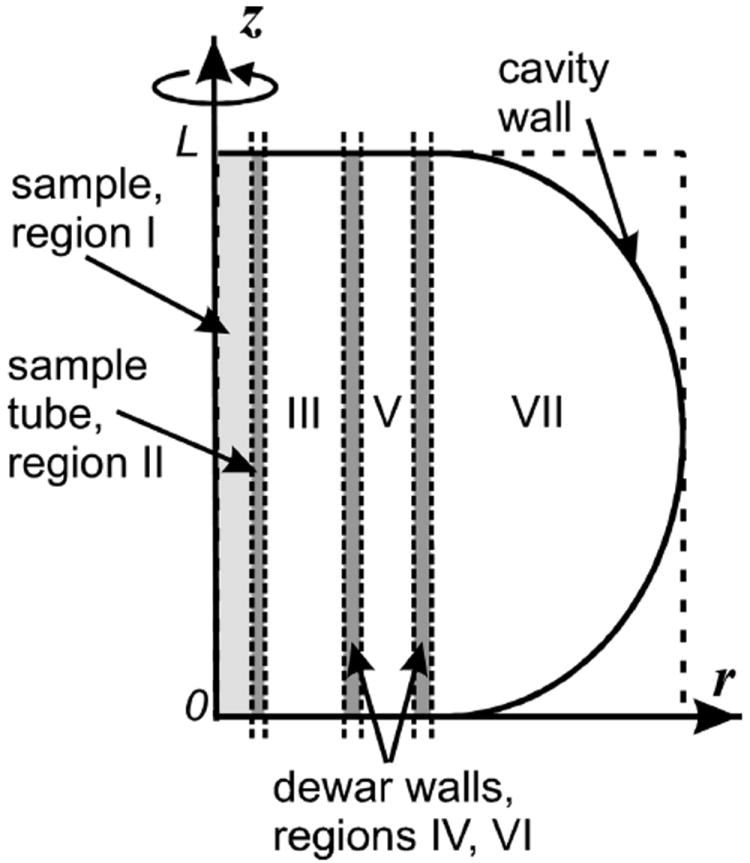
Half-cross-section of spherical (Bruker SHQ) cavity containing aqueous sample and dewar.
For each region i of Fig. 1,
| (6) |
| (7) |
where is an eigenvalue and
| (8) |
The general solution of Eq. (6) is a linear combination of Bessel functions
| (9) |
In the radial direction, the boundary condition of region I leaves the solution R1(r) = A1J0(p1r), because the term Y0(p1r) becomes infinite at r = 0. The general solution of Eq. (7) is a linear combination of trigonometric functions
| (10) |
Due to the boundary conditions Zi(z) = 0 at z = 0 and L, the solution is unaffected by canceling the term cos(κiz), and Zi(z) = Ci sin(κiz) in all regions. At z = 0 and L, Zi(z) = Ci sin(κiz) = 0, so κi = π/L for the first axial mode excited in a cavity.
For TE011 the tangential microwave fields can be expressed as
| (11) |
| (12) |
The key principle of the RMM method is that the tangential Hz and Eϕ fields must match at the boundaries ai between the regions:
| (13) |
| (14) |
For the boundary between regions 1 and 2 (r = a1),
| (15) |
and
| (16) |
Axial functions Zi(z) are the same for every region and are cancelled in Eqs. (15) and (16). Then, after eliminating coefficients,
| (17) |
and
| (18) |
For the boundary between regions 2 and 3 (r = a2),
| (19) |
| (20) |
| (21) |
and
| (22) |
Other boundaries are treated similarly. At r = aN (cavity wall), the boundary condition gives
| (23) |
2.1.2. Calculation of resonance frequency and field distribution
The first step is the determination of the resonance frequency (ν = k0c/2π). Starting with an initial estimate of the resonance frequency (the experimentally observed value for an empty cavity), the eigenvalue (Eq. (8)) and the coefficients Si and Ti (Eqs. (17), (18), (21), and 22)) are calculated. This procedure is continued iteratively, varying ν until Eq. (23) is fulfilled. Once this is achieved, the field distribution is calculated according to
| (24) |
| (25) |
| (26) |
For a cylindrical cavity, there is no dependence of cavity height L on cavity radius r (L(r) = const., Fig. 1, dashed line), so only 7 coaxial regions must be considered (Fig. 1). For a spherical cavity, L(r) ≠ const., leading to variation of eigenvalue (Eq. (8)), so the seventh region (between the dewar and cavity wall) was divided into coaxial regions. In order to achieve 1 MHz precision in the resonance frequency, it was necessary to use 2 × 104 regions. Each region’s height L was determined as L = 2[D2 − r2]1/2, where D is the radius of spherical cavity. The resonance frequency was calculated as a function of aqueous sample size, yielding results within 0.5% of experimental values.
The present study focuses on the Bruker SHQ spherical cavity, which has TE011 microwave field distribution (P. Hoefer, Bruker Biospin, private communication) and L = 4.25 cm. The inside radius D of the cavity was not known, so we calculated D of the empty spherical cavity using the method described above. The inside volume of spherical cavity was divided into 2 × 104 regions and for initially guessed D the resonant frequency was found by secant method. Then we change radius D until the calculated value of resonant frequency was equal to experimental resonant frequency for empty cavity with 1 MHz precision. We took initial guess for D from the radius of cylindrical cavity with the same height L and the same resonant frequency ν; which was calculated according to Eq. (26) with boundary condition Eϕ = 0 at a cavity wall. The solution for the radius of spherical cavity was D = 2.29 cm.
Calculations were carried out on a P4-2 GHz/512Mb PC computer usingMathematica 4 (Wolfram Research). Approximately 15 min was required to calculate the resonance frequency, field distribution, and all parameters (cavity Q, filling factor, etc.) for a particular sample diameter.
2.1.3. Determination of experimental EPR parameters
Once the field distributions have been determined, the calculation of EPR observables, the quality factor of the loaded cavity (QL) and signal intensity is straightforward. The experimentally measured QL at resonance can be expressed as a sum:
| (27) |
where QU is the value for the unloaded empty cavity (1/QU is proportional to loss in the cavity walls), 1/QE reflects nonresonant dielectric loss in the sample, 1/Qχ shows the effect of power absorption by the sample at resonance, 1/Qμ reflects the magnetic loss of the sample, and Qr is the radiation quality factor, reflecting energy lost through the cavity iris. Following previous work [9,13], Eq. (27) can be simplified to
| (28) |
because the terms 1/Qχ and 1/Qμ are negligible under typical experimental conditions, and because critical coupling implies that 1/Qr = 1/QU + 1/QE. QU′ is the quality factor of the unloaded cavity with dewar and sample.
1/QU is proportional to the intensity of the microwave magnetic field H1w at the cavity walls. Calculation of the microwave field distribution in a cavity with dewar and aqueous sample shows that H1w does not depend on the diameter of the aqueous sample, so we held QU constant. The loaded QL of a cavity with dewar and without the aqueous sample, measured with the Network Analyzer was QL = 14,050, then QU = 2QL = 28,100.
QE is due to dielectric loss in the sample,
| (29) |
where U is defined in Eq. (3), and PE is the mean power dissipated in the sample per cycle,
| (30) |
The signal intensity from a non-saturated aqueous sample is found from Eq. (1) to be
| (31) |
where χ″ and P are constants, and η and are defined in Eqs. (2) and (28).
The signal intensity of a half-saturated aqueous sample is found from (1) and expressions for η and Q (Eqs. (2), (3), (28)-(30)). If
| (32) |
then
| (33) |
at constant χ″ and .
The cavity efficiency parameter Λ [2] was found (using Eq. (32)) to be
| (34) |
or, for magnetic induction, B1 = μ0 H1:
| (35) |
All integrations were performed numerically with a step of 2 × 10−14 m3 , were calculated over the sample volume, and was calculated over the volume of the cavity, with boundaries marked by the solid line in Fig. 1.
There is one component of the microwave electric field in the cavity, Eϕ (since Ez and Er are 0), and there are two components of the microwave magnetic field, Hz and Hr (since Hϕ = 0). We used to determine the energy U stored in the cavity (Eq. (3)). In the calculation of , Hr can be neglected [14]; we found that under the conditions of this study, Hr is negligibly small and can be omitted.
The value of the complex permittivity of water was found from the Debye function [15]:
| (36) |
where ε(0) and ε(∞) are the low- and high-frequency permittivity, and τ is the relaxation time. Parameters ε(0), ε(∞), and τ depend on temperature and can be found elsewhere [15]. For T = 25 °C ε(0) = 78.36, ε(∞) = 5.16, and τ = 8.27 ps, which (for ν = 9.4 GHz) gives ε = 64.26 − i28.87. For T = 4 °C ε(0) = 85.98, ε(∞) = 4.63, and τ = 15.38 ps, which (for ν = 9.4 GHz) gives ε = 49.2 − i40.49.
Conductivity of a sample changes its complex permittivity [10,16],
| (37) |
where ε′ and ε″ are the real and imaginary parts of the complex permittivity of the sample, σ is the DC conductivity of the sample, and ε0 is the dielectric constant of free space.
3. Methods
3.1. Experimental
EPR experiments were performed with a Bruker EleXsys E500 spectrometer (Bruker Instruments, Billerica, MA), using the Bruker SHQ cavity with quartz dewar (Wilmad). The temperature was controlled using a nitrogen gas-flow temperature controller, and monitored with a digital thermometer using a Sensortek (Clifton, NJ) IT-21 thermocouple microprobe inserted into the top of the sample capillary, such that it did not affect the EPR signal. All measurements were done at critical coupling. The test sample was a solution of 100 μM aqueous TEMPO spin label, which provides a strong EPR signal intensity that is convenient for test measurements. Spectra were acquired using 100 kHz field modulation with 0.1 G peak-to-peak modulation amplitude. To determine the cavity efficiency parameter, Λ, PADS (peroxylamine disulfonate dianion) calibration was performed [17]. The power saturation curve of 0.6 mM PADS in 50 mM aqueous solution of K2CO3 was recorded at 0.03 G peak-to-peak modulation amplitude.
Samples were prepared with doubly distilled water (Millipore) with DC conductivity 2 μS/cm. A high-conductivity sample included 200 mM Na2HPO4. Conductivities of all solutions were determined using a CDM83 conductivity meter (Radiometer, Copenhagen, Denmark) at T = 25 °C. The meter was calibrated using a 0.005 M KCl (718 ± 1 μS/cm at T = 25 °C [18]). PADS, K2CO3, TEMPO, KCl, and Na2HPO4 were purchased from Aldrich (Milwaukee, WI). Samples were loaded into round fused quartz capillaries of different diameters (VitroCom, Mt. Lakes, NJ). EPR signal intensity of non-saturated samples was measured at constant incident power P = 20 μW. Signal intensity was also measured at half-saturation, as determined for each sample from the power saturation curve [5,12]. The quality factors QL of the cavity with dewar and aqueous samples were measured with an HP 8510C Network Analyzer at critical coupling [19].
4. Results
The resonance frequency of the cavity with inserted dewar and aqueous sample was calculated using the RMM method (Eqs. (8)-(23)) for different sample tube diameters, 0.2 mm ≤ ID ≤ 0.9 mm. The microwave electric and magnetic field distribution within the cavity were then calculated (Eqs. (24)-(26)). Then Q, η, and Λ were calculated from the distribution of fields (Eqs. (2), (3), (34), and (35)). Experiments were not performed when the aqueous sample inside diameter was greater than 0.9 mm, because critical coupling was not achievable.
Calculations and experiment show that the resonance frequency decreases with aqueous sample diameter. For a sample with ID = 0.9 mm, the frequency decrease was 2 MHz. The calculated resonance frequency was consistently in agreement with experiment, within 0.5%.
The experimentally observed dependence of signal intensity on sample tube diameter at constant, non-saturated incident power (P = 20 μW) is shown in Fig. 2, along with the theoretical values calculated according to Eq. (31). The permittivity of water at T = 4 and 25 °C and ν = 9.4 GHz was determined from the Debye equation (Eq. (36)): ε = 64.26 − i28.87 for T = 25 °C and ε = 49.2 − i40.49 for T = 4 °C.
Fig. 2.
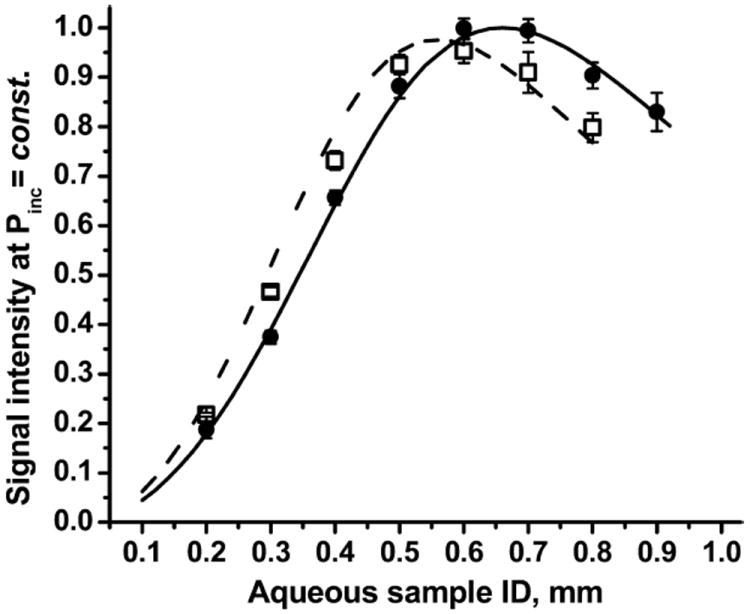
Signal intensity of non-saturated aqueous sample at 25 °C (solid line, theory; closed circles, experiment) and 4 °C (dashed line, theory; open squares, experiment).
The signal intensity of 100 μM aqueous TEMPO in a quartz tube of varying diameter at constant mean H1 at the sample is shown in Fig. 3. All experimental points were obtained at incident power corresponding to half-saturation (for a given sample, the half-saturation point corresponds to a specific mean H1 at the sample). Calculation of signal intensity dependence on tube diameter was made in accordance with Eq. (33).
Fig. 3.
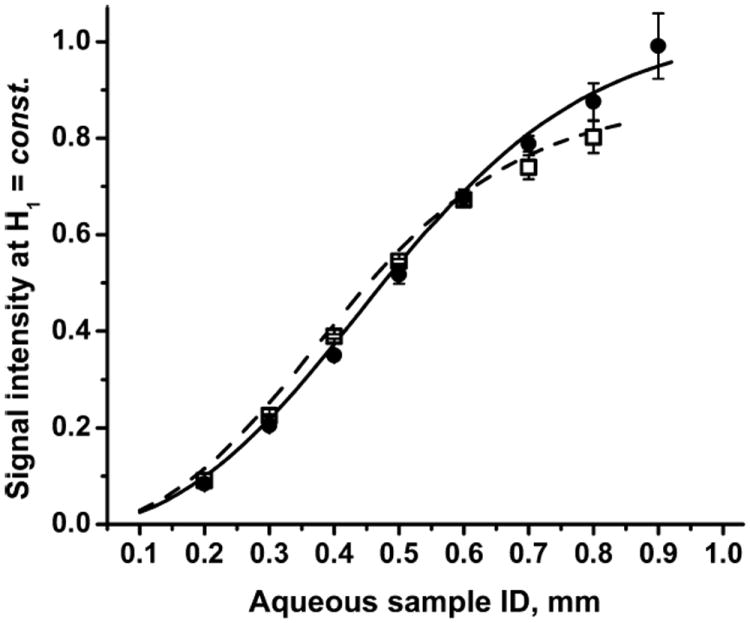
Signal intensity of half-saturated aqueous sample at 25 °C (solid line, theory; closed circles, experiment) and 4 °C (dashed line, theory; open squares, experiment).
The quality factor of the loaded cavity with dewar and aqueous sample in a quartz tube of varying diameter was calculated and measured at critical coupling (Fig. 4). The loaded cavity QL was calculated according to Eq. (28).
Fig. 4.
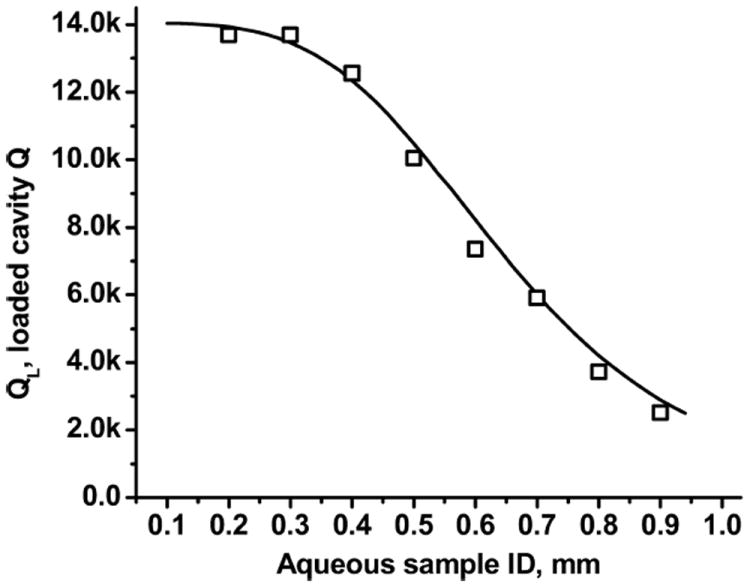
QL of a cavity with inserted dewar and aqueous sample at 25 °C. Critical coupling. Theory, solid line; experiment, open squares.
The dependence of cavity efficiency parameter Λ (Eqs. (34) and (35)) on sample diameter is shown in Fig. 5. To determine Λ experimentally, the power saturation curve of deoxygenated PADS solution was measured at T = 24 °C, where T1 = T2 = 4.1 × 10−7 s [17]. The sample was loaded into a Teflon tube with 0.3 mm ID and was held in nitrogen atmosphere for 30 min before the experiment and during the experiment. The measured derivative peak-to-peak linewidth was δ(M = 0) = 0.168 G, in agreement with previous results [17]. The microwave power at maximum signal intensity was P = 1.26 mW, where B1 is 0.098 G [17], giving a value of 2.76 G/Sqrt(W). Our calculated value for the same sample geometry is Λ = 3.82 G/Sqrt(W).
Fig. 5.
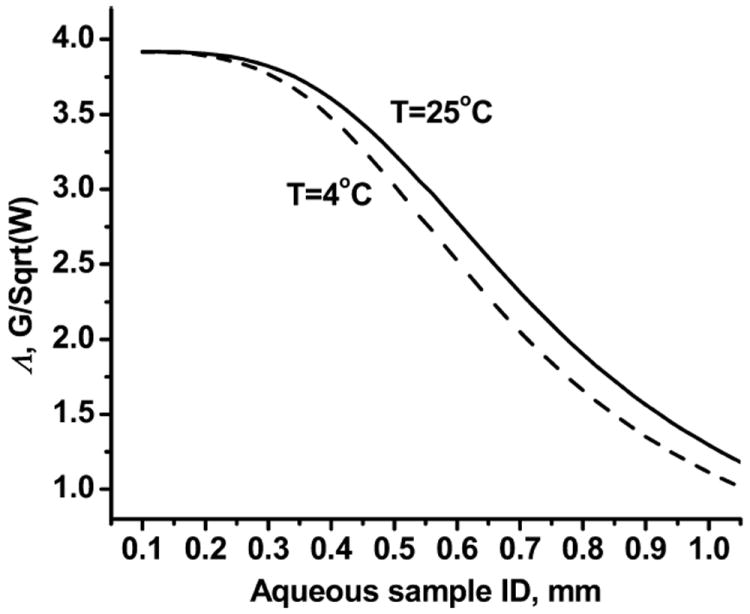
Calculated efficiency parameter H1 = ΛP1/2 for a cavity with dewar and aqueous sample. Sample temperature 25 °C, solid line; 4 °C, dashed line.
The calculated signal intensity of non-saturated and half-saturated aqueous samples at different cavity QU is shown in Fig. 6 (at constant P, Eq. (31)), and in Fig. 7 (at constant mean H1 at the sample, Eq. (33)).
Fig. 6.
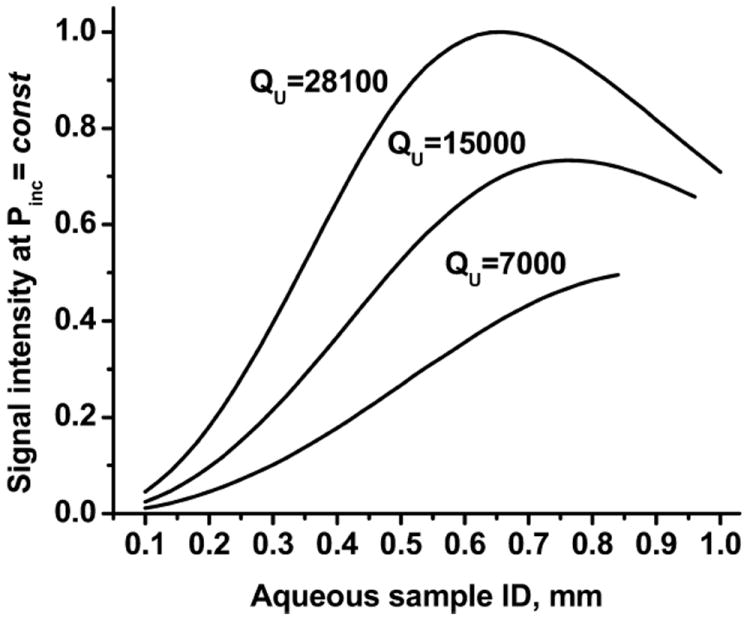
Normalized signal intensity of non-saturated aqueous sample at different cavity QU. T = 25 °C.
Fig. 7.
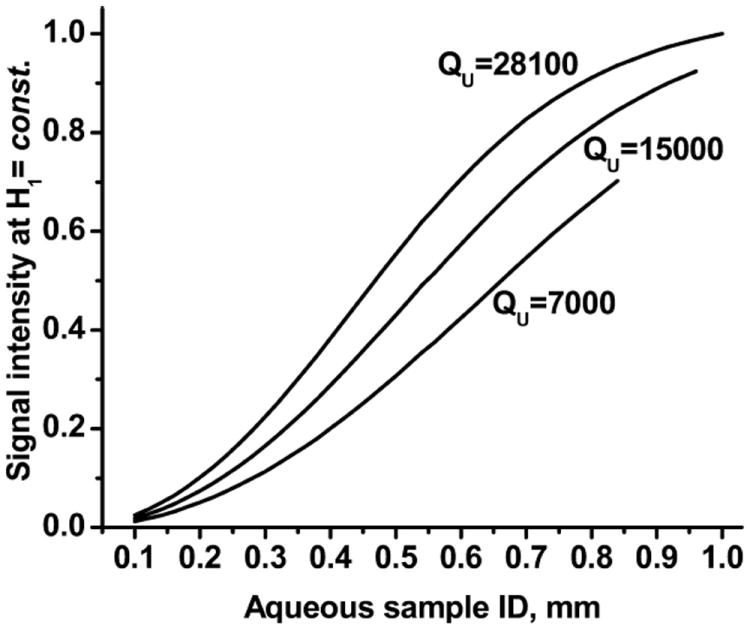
Normalized signal intensity of half-saturated aqueous sample at different cavity QU. T = 25 °C.
The signal intensity of 100 μM aqueous TEMPO samples with different DC conductivities (2 μS/cm, doubly distilled water; and 22 mS/cm, 200 mM solution of Na2HPO4) is shown in Fig. 8 (constant P) and Fig. 9 (constant mean H1 at the sample), with theoretical curves calculated according to Eqs. (31) and (33). Sample conductivity was taken into account according to Eq. (37).
Fig. 8.
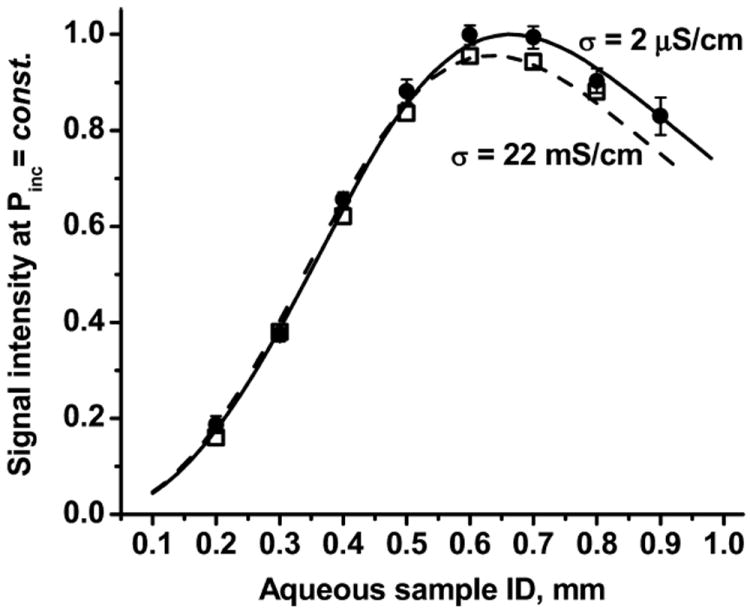
Normalized signal intensity of non-saturated aqueous sample at different sample conductivities. Water (solid line, theory; closed circles, experiment), 200 mM Na2HPO4 (dashed line, theory; open squares, experiment). T = 25 °C.
Fig. 9.
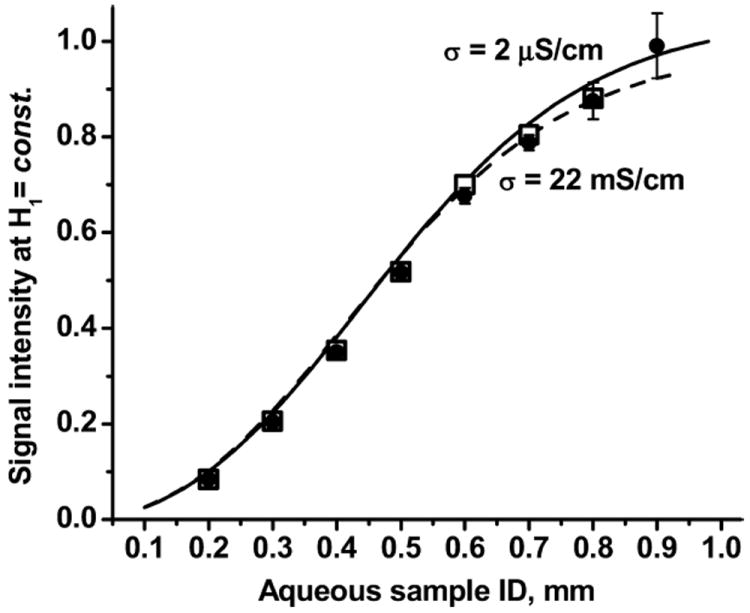
Normalized signal intensity at half-saturation, at two different sample conductivities. Water (solid line, theory; closed circles, experiment), 200 mM Na2HPO4 (dashed line, theory; open squares, experiment). T = 25 °C.
5. Discussion
5.1. Comparison with other computational methods
RMM is a rigorous method that has been developed to compute both the resonance frequency and the field distribution of resonators with cylindrical symmetry. Using the symmetry of a resonator, the analytical solution of Maxwell’s equations can be built, and accurate results can be obtained numerically. Hyde and Mett [20] used a comparable approach to analyze a rectangular cavity with an aqueous sample in a flat cell, again taking into account the symmetry of the system. An alternative approach that is frequently used is the commercially available Ansoft HFSS software [21]. However, that program does not take into account the symmetry of the resonator, making the calculation longer and more approximate.
5.2. Summary of results
The comparison of calculated and experimental data (Figs. 2-4, 8, and 9) shows that the RMM method is an accurate tool to analyze the distribution of microwave fields in a cavity with insertions, such as a dewar and a sample, to calculate the microwave field distribution over the sample, and to perform accurate calculations of EPR observables. This accuracy establishes the possibility to analyze the impact of experimental parameters (aqueous sample size, sample conductivity, and temperature) on EPR signal intensity of aqueous samples.
5.3. Non-saturated aqueous sample
Analysis of EPR signal intensity for non-saturated samples ( , P = const) shows that there is an optimal diameter for a linear aqueous sample, giving maximal sensitivity of EPR measurement (Fig. 2). At small tube diameter signal intensity depends mostly on sample size, because of the dependence of the filling factor η on sample volume Vs (Eq. (2)); signal intensity reflects the quadratic dependence of Vs on sample tube radius. Increased sample size leads to increased losses and decreased (Fig. 4, Eq. (28)) due to microwave absorption by water. At large tube diameter, losses govern the signal intensity. These competitive processes produce maximal signal intensity at a certain tube diameter. Decrease of QU decreases signal intensity and shifts the maximum of signal intensity to a larger sample tube diameter (Fig. 6). Increase of sample conductivity produces the opposite effect; it increases the imaginary part of aqueous sample permittivity and decreases QE then the maximum of signal intensity shifts to smaller sample tube diameter (Fig. 8). Increase of sample conductivity has a dramatic effect on NMR sensitivity, i.e., change of conductivity from σ = 2 μS/cm (doubly distilled water) to σ = 22 mS/cm (disodium phosphate aqueous solution, concentration 200 mM) decreases sensitivity by a factor of 4 [18]. In EPR, this change of non-saturated sample conductivity decreases the signal intensity by only 5% (Fig. 8).
Decrease of the sample temperature from 25 to 4 °C shifts the maximum signal to smaller sample tube diameters, with approximately the same value of signal intensity at the maximum. Change of sample temperature changes both the real and imaginary parts of complex permittivity of an aqueous sample; decrease of temperature decreases the real part and increases the imaginary part. Analysis shows that a decrease in the real part of sample permittivity shifts the maximum of signal intensity to smaller tube diameters and increases maximal signal intensity. An increase in the imaginary part also shifts the maximum to smaller tube diameters and decreases signal intensity. As a result, a decrease in sample temperature shifts the maximum of signal intensity to a smaller sample tube diameter without much change in signal intensity.
Calculation by the perturbation method [7] gave ID = 0.76 mm for maximum sensitivity of EPR measurement of an aqueous non-saturated sample in a cylindrical cavity; the calculation was made for n = 8.0, corresponding to ε′ = 64, close to ε′ = 64.26 for aqueous sample at T = 25 °C and ν = 9.4 GHz. Our calculation and experiment show that maximum sensitivity for a non-saturated aqueous sample at T = 25 °C can be reached when a sample is loaded in a tube with ID = 0.66 mm. As shown above, the optimal tube diameter does not change much with sample temperature or conductivity (Figs. 2 and 8). The signal intensity and optimal sample tube diameter are affected more with change of a cavity QU (Fig. 6), and the optimal aqueous sample diameter, therefore, depends on the particular cavity. The change of cavity dimensions will change the distribution of microwave fields and will affect the optimal sample size through the change of the cavity filling factor η.
5.4. Half-saturated aqueous sample
The dependence of signal intensity on sample diameter at constant mean H1 shows no maximum; the larger the sample, the greater the signal intensity (Fig. 3). According to Eq. (33), the signal intensity of a half-saturated sample is proportional to the sample volume Vs and the square root of the unloaded , which decreases with Vs. Due to this weak dependence of signal intensity on , the maximum signal intensity is shifted to large tube diameters, beyond the range where critical coupling is possible.
Decreased cavity QU and increased sample conductivity both decrease signal intensity (through their degradation of (Figs. 7 and 9). The decrease of temperature from 25 to 4 °C also decreases signal intensity at large tube diameters (Fig. 3). For example, from Figs. 3, 7, and 9, a fourfold decrease of cavity QU decreases the maximum signal intensity by 30%, and a change of sample conductivity from 2 μS/cm to 22 mS/cm decreases the maximum signal intensity by 7%, while a temperature decrease from 25 to 4 °C decreases signal intensity by 15% at large sample tube diameters.
5.5. Critical coupling
Changes of cavity QU, sample conductivity, and temperature affect the critical coupling conditions. The coupling is critical (coupling coefficient ), as long as Qr can compensate by iris adjustment; when becomes less than the minimal Qr, critical coupling fails. For the same cavity, depends on the dielectric properties of the sample, or on QE. In our particular case of the Bruker SHQ cavity with a dewar and aqueous sample, k = 1 until the tube ID = 0.9 mm, while k < 1 when ID ≥ 1.0 mm at T = 25 °C. For aqueous sample with ID = 0.9 mm, the calculated . Decreased sample temperature decreases QE, and for T = 4 °C, corresponds to ID = 0.88 mm, which means that critical coupling is not achievable for an aqueous sample with ID > 0.88 mm. Experiment shows that an aqueous sample with ID = 0.9 mm can be critically coupled at T = 25 °C (k = 1), but not at T = 4°C (k < 1). In Figs. 2-9, the calculated dependence of signal intensity on aqueous sample tube diameter is shown for critical coupling (k = 1).
5.6. Inhomogeneity of H1 at a sample
The distribution of H1 in a linear aqueous sample is quite inhomogeneous in the z-direction, due to the sinusoidal distribution of the microwave field in the cavity [11,22,23] and in the r-direction due to the redistribution of fields by the sample (“sucking in effect,” [7]). The major contribution to field inhomogeneity at the sample is inhomogeneity in the z-direction, where the field changes from zero at boundaries to a maximum value in the center of the cavity. Inhomogeneity in the r-direction depends on dielectric properties of the sample and sample diameter; in our case it changes from 0.5% at ID = 0.2 mm to 10% at ID = 0.9 mm for a linear aqueous sample at T = 25 °C. This inhomogeneity of the H1 field at a sample also has to be taken into account in saturation studies.
6. Conclusion
It is shown that the RMM is a convenient and an accurate computational method to calculate the microwave field distribution in a cylindrical/spherical EPR cavity. EPR parameters such as QL, the filling factor η, the dependence of signal intensity on aqueous sample dimensions, the mean microwave magnetic field at the sample, the distribution of microwave fields over the sample, and the cavity efficiency parameter can be determined accurately from the calculated field distribution. Specific experimental details such as dewar and aqueous sample; sample size, temperature, and conductivity can be included in the calculation, with results that agree quantitatively with experiment. This has allowed us to make specific recommendations to users of the SHQ cavity, indicating the optimal sample tube diameter (Fig. 2), and to point out that this is relatively insensitive to temperature (Figs. 2 and 3) and conductivity (Figs. 8 and 9). More importantly, the accuracy of this computational method establishes its potential in further applications, in which new resonators and sample geometries can be designed for the optimization of EPR experiments.
Acknowledgments
This work was supported by NIH Grants AR32961 (D.D.T.), AR48961 (Y.N.), and fellowship of University of Minnesota Supercomputing Institute (Y.N.).
References
- 1.Feher G. Sensitivity considerations in microwave paramagnetic resonance absorption techniques. Bell Syst Tech J. 1957;36:449–484. [Google Scholar]
- 2.Hyde JS, Froncisz W. Loop gap resonators. In: Hoff AJ, editor. Advanced EPR: Applications in Biology and Biochemistry. Elsevier; Amsterdam: 1989. pp. 277–306. [Google Scholar]
- 3.Sahlin M, Graeslund A, Ehrenberg A. Determination of relaxation times for a free radical from microwave saturation studies. J Magn Reson. 1986;67:135–137. [Google Scholar]
- 4.Altenbach C, Greenhalgh DA, Khorana HG, Hubbell WL. A collision gradient method to determine the immersion depth of nitroxides in lipid bilayers: application to spin-labeled mutants of bacteriorhodopsin. Proc Natl Acad Sci USA. 1994;91:1667–1671. doi: 10.1073/pnas.91.5.1667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Haas DA, Mailer C, Robinson BH. Using nitroxide spin labels. How to obtain T1e from continuous wave electron paramagnetic resonance spectra at all rotational rates. Biophys J. 1993;64:594–604. doi: 10.1016/S0006-3495(93)81418-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Castner TG., Jr Saturation of the paramagnetic resonance of a V center. Phys Rev. 1959;115:1506–1515. [Google Scholar]
- 7.Stoodley LG. The sensitivity of microwave electron spin resonance spectrometers for use with aqueous solutions. J Electron Contr. 1963;14:531–546. [Google Scholar]
- 8.Wilmshurst TH. Electron Spin Resonance Spectrometers. Adam Hilger; London: 1967. p. 130. [Google Scholar]
- 9.Dalal DP, Eaton SS, Eaton GR. The effect of lossy solvents on quantitative EPR studies. J Magn Reson. 1981;44:415–428. [Google Scholar]
- 10.Sueki M, Rinard GA, Eaton SS, Eaton GR. Impact of high-dielectric-loss materials on the microwave field in EPR experiments. J Magn Reson A. 1996;118:173–188. [Google Scholar]
- 11.Kaifez D, Guillon P. Dielectric Resonators. Noble; Atlanta, GA: 1998. [Google Scholar]
- 12.Nesmelov YuE, Surek JT, Thomas DD. Enhanced EPR sensitivity from a ferroelectric cavity insert. J Magn Reson. 2001;153:7–14. doi: 10.1006/jmre.2001.2415. [DOI] [PubMed] [Google Scholar]
- 13.Goldberg IB, Crowe HR. Effect of cavity loading on analytical electron spin resonance spectrometry. Anal Chem. 1977;49:1353–1357. [Google Scholar]
- 14.Poole CPJ. Electron Spin Resonance. Dover Publications; Mineola, NY: 1996. [Google Scholar]
- 15.Kaatze U, Uhlendorf V. The dielectric properties of water at microwave frequencies. Z Phys Chem. 1981;126:151–165. [Google Scholar]
- 16.Gabriel C, Gabriel S, Grant EH, Halstead BSJ, Mingos DMP. Dielectric parameters relevant to microwave dielectric heating. Chem Soc Rev. 1998;27:213–223. [Google Scholar]
- 17.Kooser RG, Volland WV, Freed JH. ESR relaxation studies on orbitally degenerate free radicals. I. Benzene anion and tropenyl. J Chem Phys. 1969;50:5243–5257. [Google Scholar]
- 18.Kelly AE, Ou HD, Withers R, Dotsch V. Low-conductivity buffers for high-sensitivity NMR measurements. J Am Chem Soc. 2002;124:12013–12019. doi: 10.1021/ja026121b. [DOI] [PubMed] [Google Scholar]
- 19.Kajfez D, Hwan EJ. Q-factor measurement with network analyzer. IEEE Trans MTT. 1984;32:666–670. [Google Scholar]
- 20.Mett RR, Hyde JS. Aqueous flat cells perpendicular to the electric field for use in electron paramagnetic resonance spectroscopy. J Magn Res. 2003;165:137–152. doi: 10.1016/s1090-7807(03)00275-1. [DOI] [PubMed] [Google Scholar]
- 21.Mett RR, Froncisz W, Hyde JS. Axially uniform resonant cavity modes for potential use in electron paramagnetic resonance spectroscopy. Rev Sci Instrum. 2001;72:4188. [Google Scholar]
- 22.Fajer P, Marsh D. Microwave and modulation field inhomogeneities and the effect of cavity Q in saturation transfer ESR spectra. Dependence on sample size. J Magn Reson. 1982;49:212–224. [Google Scholar]
- 23.Mailer C, Sarna T, Swartz HM, Hyde JS. Quantitative studies of free radicals in biology: corrections to ESR saturation data. J Magn Res. 1977;25:205–210. [Google Scholar]


