Abstract
Combining the approach of colloid transport with the generalized Higuchi theory of drug release and with the concept of minimum inhibitory concentration (MIC) known in microbiology, the theory of effective drug release from implants has been developed. Effective release of an antibiotic at a concentration above MIC is a necessary condition to achieve protection against infection from implants such as central catheters. The Higuchi theory in its present form is not predictive of the therapeutic effect from medical implants. The theory of effective release presented in this paper specifies two release modes, namely: one with therapeutic usefulness (effective release) and another without therapeutic effect. Therapeutic usefulness may be achieved when the antibiotic concentration, Cti, on the implant surface kills the organisms of interest and prevents the formation and propagation of biofilm when Cti exceeds the corresponding MIC of the released antibiotic compound. Currently, neither the Higuchi theory nor any other theory can provide such prediction. The present approach requires quantification of the antibiotic transport from the drug–polymer blend implant surface into the tissue and accounts for its coupling with drug diffusion inside the blend, a task that has not been developed in existing theories. Our solution to this task resulted in the derivation of an equation for the time of duration of effective release, Te, which depends on MIC, the Higuchi invariant and the characteristics of convective diffusion within the tissue. The latter characteristics include: diffusivity Dti and diffusion layer thickness δ which is controlled by the velocity of the interstitial fluid in tissue. A smaller Dti is favorable because transport from the catheter surface is weaker, while a thinner diffusion layer is harmful because this transport is stronger. The influence of the tangential component of interstitial velocity in the tissue is especially harmful because the diffusion within the incision exit site (IES) will be extremely enhanced such that it may decrease Cti to zero. The incorporation of convective diffusion into the theory of antibacterial protection by means of antibiotic release has revealed that physicochemical mechanisms predict the effectiveness of antibiotic-loaded catheters and defines the conditions necessary to achieve better protection by means of combining the level of catheter loading with antibiotics and the use of wound (IES) dressing.
Keywords: Effective drug release, Controlled drug release, Convective diffusion, Diffusivity within tissue, Diffusion layer thickness, MIC, Minimum inhibitory concentration, Antibiotic-loaded catheter, Incision exit site, IES, Monolithic nonporous polymer implant, Catheter, Physicochemical hydrodynamics
1. Introduction
Drug release kinetics and related pharmaceutical applications [1,2] are largely based on the principles of surface and colloid science. While drug delivery usually focuses on therapeutic applications to treat disease [2], drug release from implants to surrounding tissues has not so far received sufficient consideration. For example, antimicrobial protection of surgical sites after catheter placement is needed to prevent serious catheter-related infections [3,4]. In the cases of central catheters, once bacteria grows on the external surface of the catheter, biofilm develops and propagates until it reaches the bloodstream, which ultimately leads to serious catheter-related bloodstream infections (CRBSIs). Although antibiotic-impregnated catheters [3,4] are used in some instances, their effectiveness in preventing CRBSIs is still debatable. Effective release of antibiotics from the implants at levels above a critical concentration is necessary to prevent such infections. However, predictive models that define the above criteria are still lacking in the literature.
We have studied the “effective release” of antibiotics from a new class of tympanostomy tubes (ear tubes) used to treat chronic otitis media (OM), which is an infection of the middle ear. We have developed polymeric implant materials made by incorporating a special combination of antibiotics, and have demonstrated their long-term effectiveness, both in vitro and in vivo, in inhibiting bacterial attachment and biofilm growth [5]. Achieving effective release above the minimum inhibitory concentration (MIC) from the ear tubes was necessary to provide long-term protection against infection from organisms implicated in OM in the chinchilla animal model.
In order to prevent CRBSIs, long-term “effective release” of antimicrobial agents is required for up to about 8 weeks in some cases. In order to achieve these results, other conditions need to be satisfied beyond the optimization of the polymer–drug blend. During long-term release from implants, release rates may become rather low over time, and this leads to an important question: what is the minimal release rate that may be sufficient to effect robust antimicrobial protection against infection in the case of central venous catheters?
The MIC of antibiotic/antimicrobial compounds, the break point concentration at which microbial culture does not grow, is recognized as an important key parameter in microbiology. It is obvious that expressing the released drug concentration in the surrounding tissue from an implant in terms of MIC units would be helpful in addressing the above question. Surprisingly, this indispensable notion has been overlooked in the published theories of drug release. Accordingly, the current state of drug release theory does not permit optimization of polymer–drug blend formulations nor does it provide guidance regarding drug delivery from implanted medical devices. This optimization should allow achieving therapeutically effective long-term drug release despite the decrease in the release rate with time. Also, optimization of release kinetics will avoid risk from antibiotic overdose, which may cause irritation or inflammation of the surrounding tissues. The latter is especially important in long-term drug release situations around the implant site.
The objectives of this paper are: (1) to introduce MIC conditions into the theory of drug release, (2) to consider the variables that may affect effective therapeutic concentration from implants, and (3) to create the scientific basis for the optimization of the polymer–drug blend used as implants. Although special focus will be placed on central catheter-related infections, the developed theory should be applicable to other classes of drug therapies from implants, including anticancer, anti-inflammatory, etc. Therefore, the results of this work can be extended to cover other implant devices, other drug therapies and other surgical sites. Although the biological objectives of this study are clear, our approach will make use of the theories of colloid transport [6–9] and of physico-chemical hydrodynamics to develop the theory of effective release [14].
2. Controlled drug release and effective drug release
The notion of controlled drug release [2] is well known and has been covered in numerous papers. Here, we introduce the relevant notion of “effective release” for the first time to address the special topic of therapies from implanted medical devices. We selected the example of antibiotic release from central venous catheters to elaborate the theory of effective release in this paper.
It is now accepted that organisms in the form of biofilm develop on implant surfaces (e.g., catheters) [10] and then propagate along the surface of the device where they ultimately cause infections. Thus, antibiotic concentration at and near the surface of a device during implantation is important to ensure that no bacterial growth can occur. Drug release at the surface of an implant results in the distribution of the antimicrobial agent concentration in the adjacent tissue, Cti(x, t), where x is the distance to the implant surface and t is time. In particular, the drug concentration in the tissue at the implant surface is Cti(0, t), where the biofilm formation to be prevented must satisfy the following condition,
| (1) |
The true dependence of cumulative release M(t) and Cti(0, t) is schematically illustrated in Fig. 1, while their quantification will be described later. It is obvious that the decrease in the release rate with time causes Cti(0, t) to decrease. In general, as Cti(0, t) decreases, the entire release process may be divided into two portions where the requirement according to Eq. (1) is satisfied during the first portion of release, and is violated during the second. The “effective release” is defined as the portion of the release process where the condition according to Eq. (1) is satisfied. Accordingly, effective time Te is determined by the following conditions:
| (2) |
| (3) |
Te is the time duration of the effective release. This newly introduced notion has many practical applications. In fact, Te is an important characteristic of any polymer–drug blend and other forms of drug delivery vehicles used as implant devices. Such devices are useful only when the in-service use time is smaller than Te. When t > Te, the drug delivery device may become harmful in cases where excessive release of antibiotics/drugs may cause irritation or inflammation of the surrounding tissues. This leads to the need to define the optimal thickness of the drug delivery “slab” for the drug-polymer blend to be considered. Larger thickness may be harmful because a thickness increase above h0m does not prolong the effective release. Depending solely on the experimental approach to determine Te is not reliable or even possible because methods to measure the distribution of antibiotic concentration in tissue are unproven. Consequently, developing a theory for “effective release” is deemed necessary. This theory will provide equations for predicting an important set of practical characteristics: Te, h0m, etc. When the slab thickness is h0m or less, the release ceases spontaneously as soon as Cti becomes lower than the MIC. Since optimization of the materials is especially important in achieving long-term drug release, we restricted our focus to nonporous monolithic polymer implant systems [2]. The Higuchi theory [11,12] for drug release from monolithic dispersion has received wide recognition in drug delivery science and has become the accepted standard in assessing drug release. Further development of the “theory of effective release” will be useful in the design and in the safe use of drug-releasing implants.
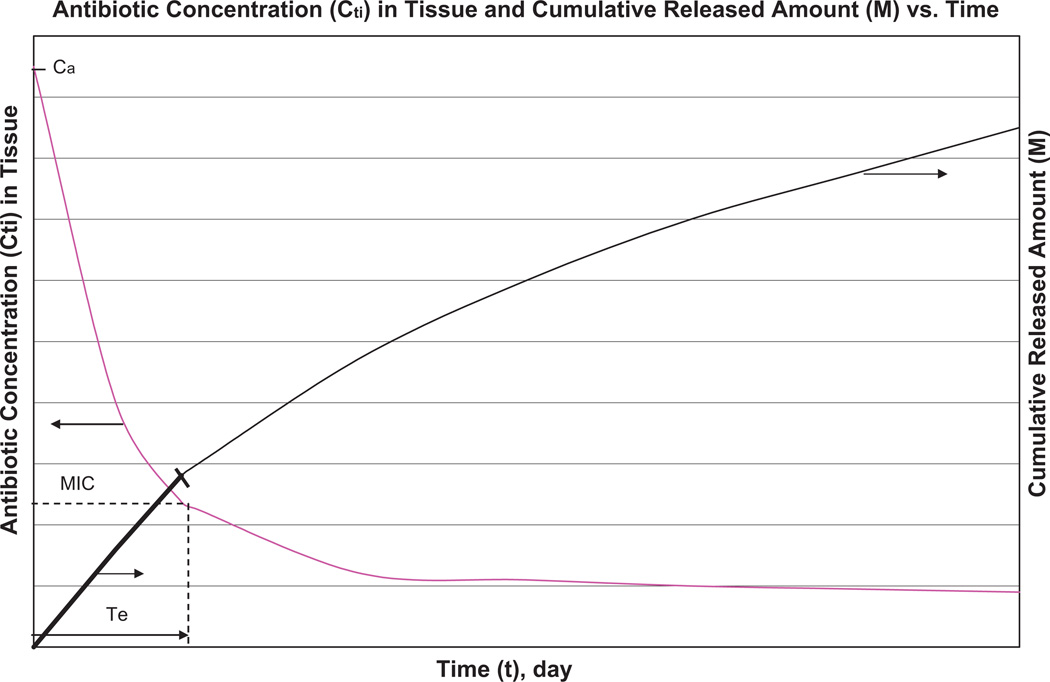
Fig. 1.
Qualitative illustration for the notion of effective release—M: cumulative amount released per unit area of catheter (implant) according to the Higuchi equation (Eq. (9b)); Cti: antibiotic concentration in tissue near polymer–drug blend surface according to Eq. (12); Ca: antibiotic solubility in water; MIC: minimum inhibitory concentration which provides bacterial inhibition; Te: duration of effective release during which Cti exceeds MIC. The release rate is maximal and Cti is almost equal to the maximum value Ca initially when the thickness h(t) of layer with dissolved drug particles remains small (Fig. 2) with concomitant rapid diffusion through this layer that provides high concentration Cti. As the drug dissolution proceeds and consequently the diffusion rate through this layer decreases, both the release rate and the concentration Cti decrease. The release remains therapeutically effective as long as Cti > MIC, in spite of Cti decrease. The duration of effective release corresponds to condition Cti(Te) = MIC. –: Effective release and –– useless portion of release.
3. The Higuchi theory
The Higuchi theory [11] may be generalized to derive an equation for , i.e., Cti(0, t). will exceed MIC at t < Te. It has now been recognized that the initial theory of Higuchi [11] is not sufficient to derive Eq. (1) because the so-called sink boundary condition for drug concentration in water near the polymer slab surface (Fig. 2):
| (4) |
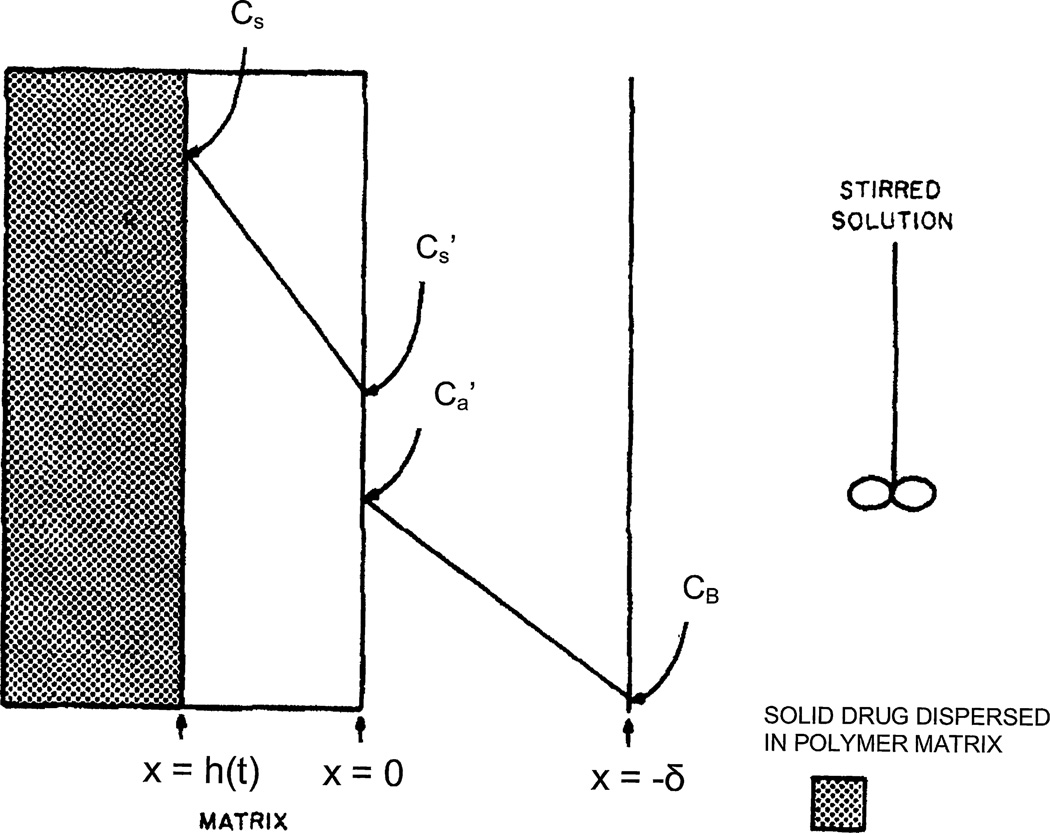
was used [11], where x = 0 corresponds to the slab surface. In the meantime, the antibiotic concentrations and (see Fig. 3) are interconnected by the condition of local equilibrium, i.e.,
| (5) |
where Ca is the antibiotic solubility in water.
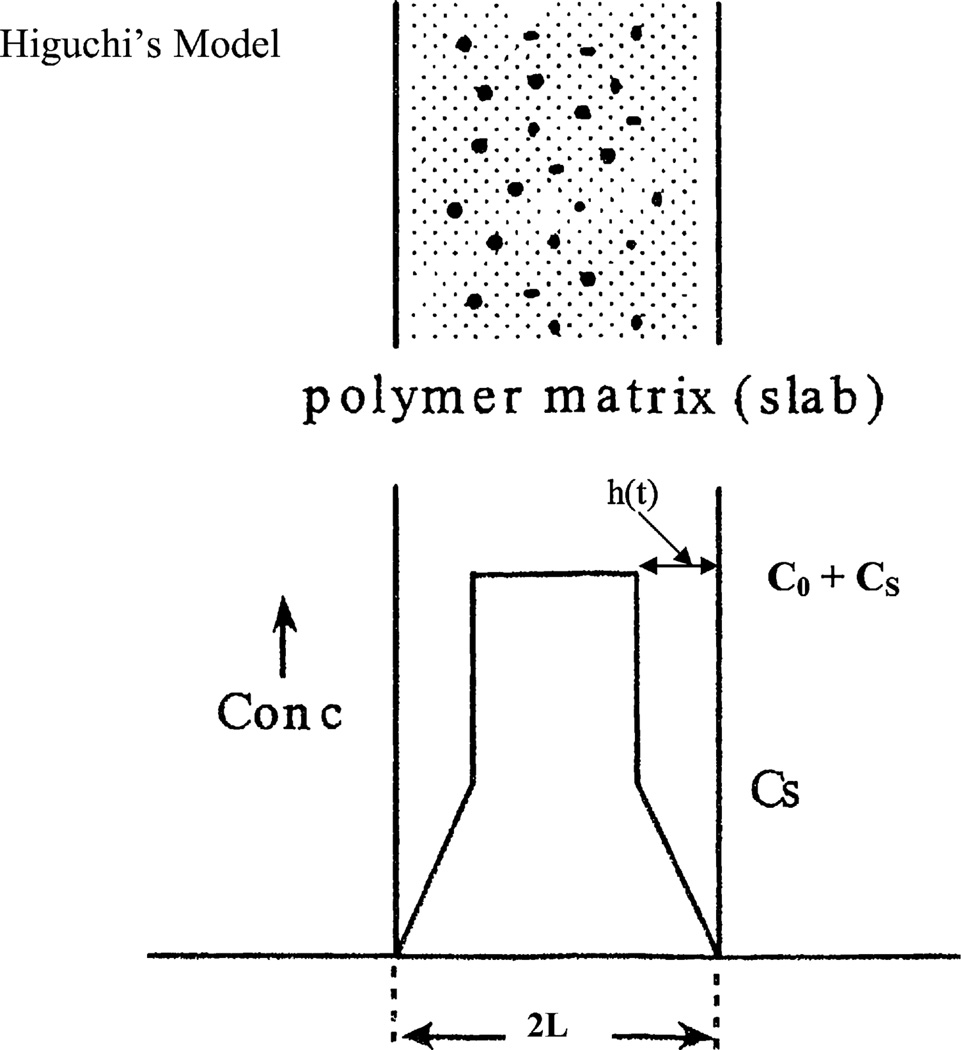
Fig. 2.
Higuchi’s model for drug release from a monolithic dispersion. The top figure shows the presence of dispersed drugs as well as dissolved drugs, and the bottom figure shows the concentration profile in the monolithic dispersion. C0 is the concentration of dispersed drug, and Cs is the solubility limit for the drug dissolved in the polymer.
Fig. 3.
Schematic diagram of the concentration profile in the polymer matrix containing dispersed drug and in the adjacent stirred solution in the receiving chamber.
, where Cs(t, x) is the non-steady antibiotic distribution within the polymer zone 0 < x < h where drug particles have already been dissolved. Both and decrease in time during antibiotic release, but their ratio is invariant and is the same, as in the experiment, when the antibiotic solubility in water Ca is measured after the equilibrium between the slab of the polymer–antibiotic blend and the water in the system as a whole is established (Fig. 3). The essential limitation of the Higuchi model follows from comparison of conditions (4) and (5), which leads to
| (6) |
instead of the necessary condition defined in Eq. (1).
If the solid drug is finely divided, uniformly suspended and rapidly dissolved, then a two-zone system will develop, as illustrated in Fig. 2. In the region closest to the receiving chamber [0 < x < h(t)], all the solid drug will have dissolved, and the drug will be present in a concentration below the solubility limit, Cs. Further away from the slab surface, the drug will still be present as a solid suspension at the original starting concentration in the slab, C0.
About 50 years ago, Higuchi [11,12] assumed a linear concentration in the dissolved zone, as illustrated in Fig. 3, which is a reasonable assumption when C0 ≫ Cs. He then required that the dissolution boundary h(t) be located so that the mass of drug left in the formulation would be equal to the amount of drug which diffused across the boundary at x = 0 into the receiving chamber. In Higuchi development
| (7) |
if Cs ≫ C0.
Interestingly, elimination of the sink condition from the Higuchi theory was made by Higuchi himself [13]. He clarified [13] that this approximation assumed that “the rate limiting step was the diffusion of drug from the matrix (matrix controlled),” while “the rate of diffusion from the surface of the matrix to the surrounding bulk solution will make a significant contribution to the total diffusion process” [13]. The notion of diffusion layer thickness δ [14], which accounts for possible spatial non-uniformity, was ignored in the initial Higuchi theory (Fig. 2). This enables one to describe the diffusion flux within the initial diffusion layer and at its boundary with the matrix as
| (8a) |
where Da is the drug diffusivity in water and M is the amount of released drug normalized per unit area of S of the slab.
A similar expression of the Higuchi approximation is valid within the quasi-steady diffusion layer of matrices
| (8b) |
An equation for h(t) which is valid during both release stages was derived by Higuchi [13] and in [5] with the use of Eqs. (8a) and (8b)
| (9a) |
where p = 2δDK/Da and q = 2DCs/(C0 − (Cs/2)).
It is clear that
| (9b) |
4. Theory of effective release for antimicrobial protection from an implant based on the Higuchi generalized model
Higuchi incorporated external convective diffusion into his model to interpret the kinetics of drug release under the conditions of the standard release experimental procedure, i.e., when a slab of polymer–drug blend is placed in a vial and the solution is stirred around it to provide a steady thickness of the diffusion layer, δ (Fig. 3). On the other hand, when drug release occurs within the tissue from an implant, the arising external diffusion transport of antibiotic is affected by convection as well; however, in this case, the transport will depend on the well-known movement of interstitial fluid in the surrounding tissue [15,16]. Interstitial fluid is the liquid which surrounds the cells in the body. Since the fluid velocity in the interstitium (interstitium is the space between cells in a tissue) is many orders of magnitude slower compared to the stirred experimental system used by Higuchi, δ is expected to be much thicker within the tissue adjacent to the implant. Nevertheless, δ may be much thinner than the catheter radius, a geometry which allows one to consider the local release from a curved surface of the catheter as a flat plate. This consideration permits us to apply the Higuchi model of one-dimensional diffusion.
The right-hand side in Eqs. (8a) and (8b) are equal, and interconnects three unknown functions of time , and h(t) (Fig. 3).
| (10) |
An additional interconnection is given by Eq. (5), which may be used in Eq. (10)
| (11) |
or may be found from this equation
| (12) |
Da in Eq. (11) is replaced by Dti because the diffusivity within the tissue is noticeably lower [15,16] than that in water (see Appendix A).
When t = 0, the dissolved zone (Fig. 2) is absent, i.e., h(t) = 0 and the adjacent water-tissue is in equilibrium with . Hence, the concentration has to be the same as that in water
| (13) |
This test for the derived Eq. (12) is satisfied because 1 in the denominator may be neglected in comparison with the very large second term in the denominator, when h(t) → 0. Afterwards, the right-hand side in Eq. (12) reduces to Cs/K which yields the qualitatively predicted result: .
This maximal value for preserves during times which satisfy the condition
| (14) |
At longer times, corresponding to the opposite condition
| (15) |
the denominator in Eq. (12) transforms into 1 and Eq. (12) takes the form:
| (16) |
i.e., the decrease in starts at condition (15) and continues to decrease approximately as t−1/2.
The onset of the second stage is inevitable for long-term release and the determination of the thickness of the wall h0m to provide effective release, i.e., release satisfying condition (Eq. (1)), must explore the asymptotics (16), i.e., [MIC] has to be substituted in the left-hand side of Eq. (16), while h0m in the right-hand side yields an estimate for the thickness of the cylindrical wall
| (17) |
The increase in the thickness of the cylindrical wall above h0m is senseless because the duration of effective release will not be longer than that at h0m.
The maximal duration of the effective release follows from Higuchi Eq. (7), i.e., by means of the substitution h0m, which yields
| (18) |
Te decreases with decreasing wall thickness h0
| (19) |
Measurements of the parameters which are present in Eq. (18) are necessary for the prediction of h0m and Tmax for a certain drug-blend.
Ca is known for many antibiotics or can be measured using standard experimental methods. Da is also known for these compounds. Measurement of the release rate at a sufficiently long period of time and its interpretation with the Higuchi Eq. (7) allow us to predict the product DCs.
5. Importance of convective diffusion in providing effective release of antibiotics
Convective diffusion plays a role only during the first drug release stage when it controls transport as a whole. In contrast, convective diffusion plays a cardinal role during the second stage of effective release when transport as a whole is controlled by diffusion within the polymer blend. This manifests itself in Eq. (16). The larger δ is, the higher will be. Expanding the diffusion layer (i.e., δ increase) is favorable for the transition from the non-effective mode of release to an effective one. A primitive explanation of this is based on the interrelationship between the concentration gradient and δ
| (20) |
At the same release rate (the same grad C), the increase in the denominator in Eq. (20) leads to an increase in the nominator, i.e., . This approach is useful with respect to the second stage of release, which is controlled by diffusion in the polymer matrix according to Eqs. (9a) and (9b), and correspondingly does not depend on convective diffusion. However, the rate of convective diffusion, expressed by Eq. (8a), is equal to dM/dt, expressed by Eq. (8b). Hence, combining Eqs. (8a) and (8b) yields
| (21) |
where dM/dt is determined by Eq. (8b), and Da has to be replaced by the diffusivity within the tissue, Dti, in our case.
during release from the portion of a coated catheter surrounded by tissue is affected by the flow of interstitial fluid [15]. Its velocity is estimated to be in the range of 5 × 10−4 to 5 × 10−3 cm/s [16] and the direction is parallel to the skin surface because the flow normal to skin is absent within the sub-epithelial layer.
To determine if convection affects diffusion transport may be predicted by estimation of the Peclet number (Pe) [14], which is an estimate for the ratio of convective flux to diffusion flux
| (22) |
where L is a characteristic length. L may be specified as the catheter radius R with respect to the radial component of velocity. As the angle between the catheter axis and the skin plane is small, this affects Vr, namely Vr ~ 0.1 V, which yields for
| (23) |
Peclet number in this range indicates that convection may be important.
Tissue swelling concomitant with inflammation leads to an increase in tissue diffusivity, Dti. In turn, this manifests itself as a decrease in according to Eq. (16). An important conclusion follows that inflammation may cause an essential decrease in . In this case, effective release may transition into a non-effective release during inflammation depending on the system under consideration.
6. Discussion
The concepts and fundamentals of drug release and their applications in controlled drug delivery systems are presented in monograph [2]. The following statement is provided in [2]: “It is the drug delivery module that will deliver a specific amount of a drug at the right time to the right place. The delivery of drugs using drug-delivery modules is collectively known as controlled drug delivery.” As to the determination of “specific amount of drug at the right time and right place,” this is a task of pharmacokinetics and pharmacodynamics, which requires comprehensive empirical testing in animal models and humans. The most difficult stage of this empirical testing process is when volunteers are involved in the safety and efficacy clinical studies.
With respect to medical implants like catheters, an easier and less expensive strategy is possible because site localization of biofilm formation is known and because the in vitro methodology for the determination of the MIC of antibiotics is well developed and is also reliable for further prediction of the in vivo effectiveness.
As soon as is incorporated into the theory of drug release for the case of an implant in a tissue, the theory for therapeutically effective release can be developed. One may suggest that controlled drug release according to its cited definition may be sufficient to determine the therapeutically effective conditions. However, this can only be achieved by performing expensive pharmacokinetic testing. The latter type of testing is not eliminated completely when the theory of effective release is used because regulatory approval of a drug delivery device mandates further in vivo and clinical testing. However, a higher level of success and less cost will be achieved with a new strategy based on the application of the theory of effective release presented in this paper.
Minimization of side effects of a drug-delivery system is emphasized in [1]. However, this task may only be achieved by a different form of pharmacokinetic testing. With respect to implanted catheters, such side effects may be manifested as irritation or inflammation of the surgical site, especially during long-term placement of the implant. In this case, the condition for infection suppression without irritation of tissue may also be defined in the framework of the theory of effective release. First, condition (Eq. (1)) should not be replaced with one with too high . Second, the slab thickness has to be optimized according to Eq. (17) in order to eliminate excessive drug release beyond what is needed to achieve the desired therapeutic effects.
Eq. (18) allows the prediction of the duration of effective release, Te, as well as its dependence on three factors. We specify these dependencies in Table 1 within accepted representative ranges for these factors. As to δ modeling, both the normal and tangential components of the interstitial velocity in adjacent tissue are important. This leads to two components of Peclet numbers, Pe∥ and Pe⊥. An estimate
| (24) |
is possible for δ controlled by the flow normal to the catheter axis according to Levich (Eqs. 72.12 and 72.13 in [14]). The interstitial velocity is parallel to the skin and almost parallel to the catheter surface because angle α (Fig. 4) is small. Hence
| (25) |
Table 1.
The duration of effective release, Te, for different MICs (day), two values of δ⊥, 0.04 and 0.007 cm, and (dM/dt)2t = 3 × 103 µg2/day cm2, Dti = 0.1 cm2/day.
| δ⊥ (cm) | MIC → (µg/ml) |
|||
|---|---|---|---|---|
| 1 | 2 | 4 | 10 | |
| 0.04 | > 60 | > 60 | 3 | 0.5 |
| 0.007 | 16 | 4 | 1 | 0.16 |
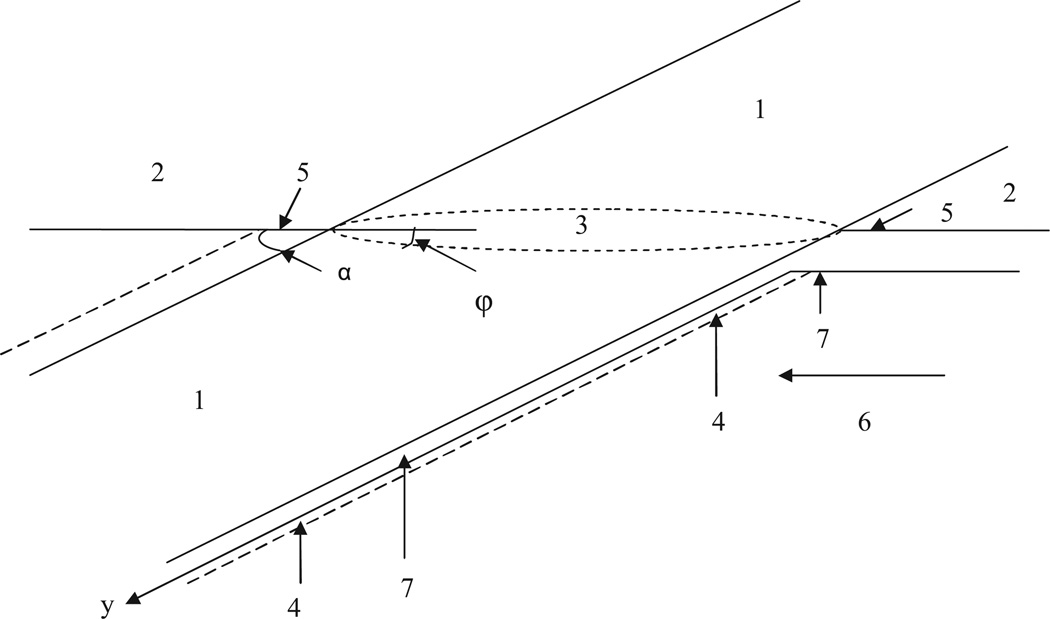
Fig. 4.
(1) Catheter; (2) skin; (3) elliptical crossing of catheter with skin; (4) incision in tissue formed by catheter; (5) incision exit site (IES); (6) direction of flow of interstitial liquid; (7) axial symmetrical streaming line (ASL); and α is the angle between catheter axis and skin plane.
The velocity 3 × 10−5 < u⊥ < 2 × 10−3 cm/s yields the range for Peclet number 6 < Pe⊥ < 200, when Dti ~ 10−6 cm2/s is accounted for. The substitution into Eq. (24) yields the range for δ ⊥ values
| (26) |
when R = 0.1 cm.
Since a rather high value of the Higuchi invariant (dM/dt)2t~3× 103 was achieved in our systematic experimental research of antibiotic release from a polymer blend, this value is acceptable. The Higuchi invariant value is calculated on the basis of the measurement of the rate of drug release for a period of time while it is time independent according to Higuchi Eq. (7). Te values calculated with Eq. (18) specified for Dti = 0.1 cm2/day for two values of δ⊥ and Higuchi invariant 2 × 103 µg2/day cm2 are presented in Table 1.
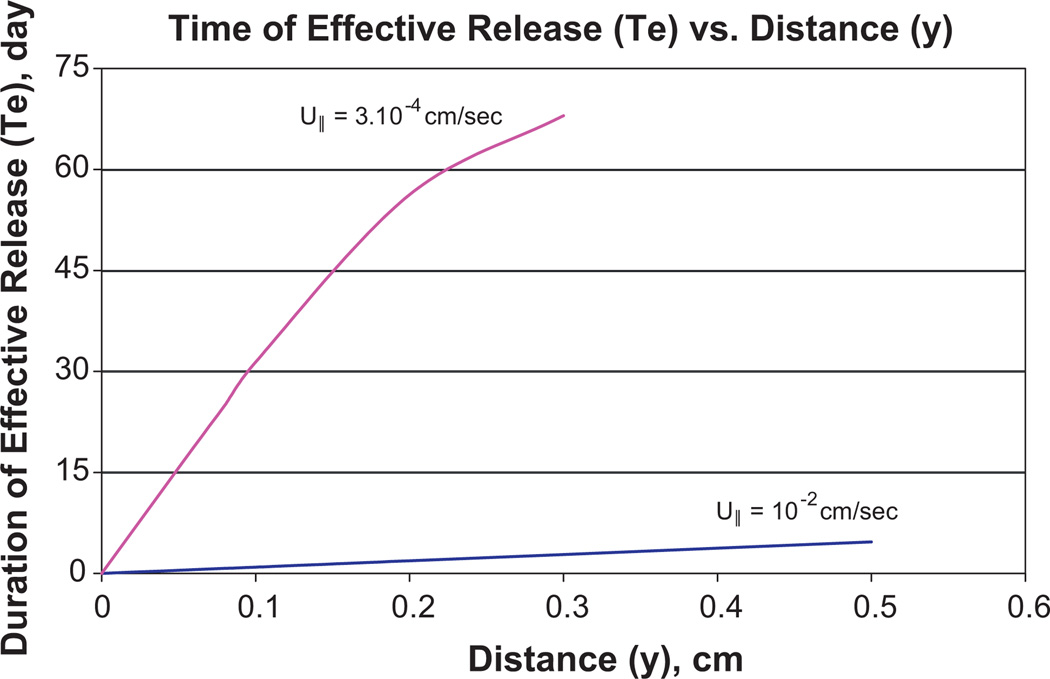
It can be seen that short-term effective release (Te < 4 days) is possible even at high interstitial velocity u∥ ~ 0.01 cm/s, if MIC is below 2. Long-range effective release is impossible even at MIC = 1 when the velocity is high. It is possible at low velocity u∥ ~ 3 µm/s, if MIC is about 3 or lower.
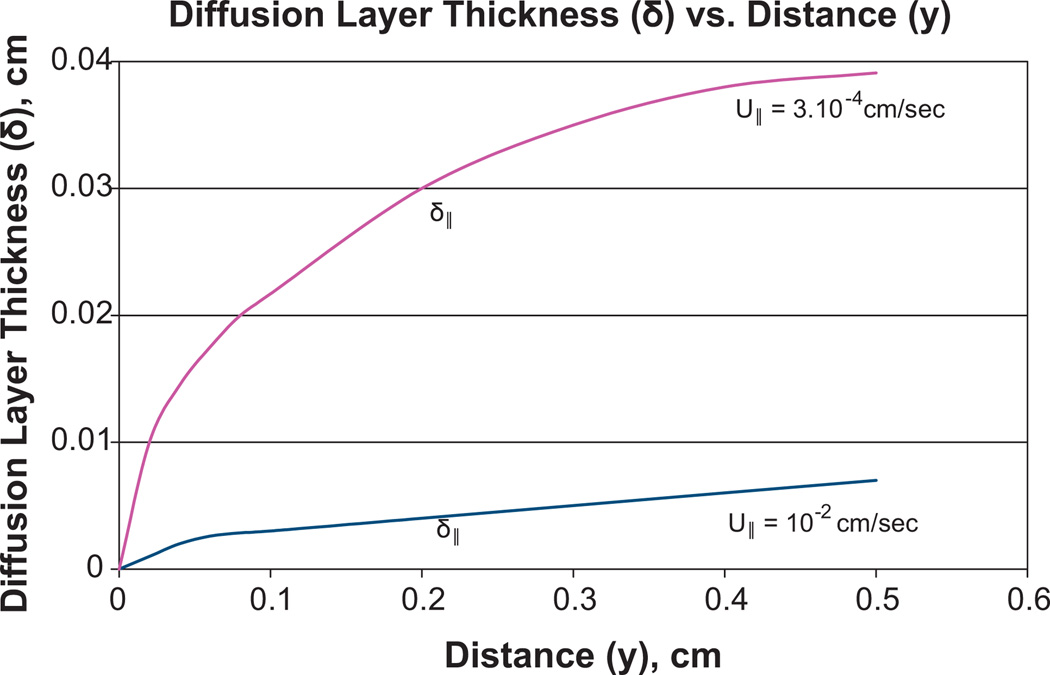
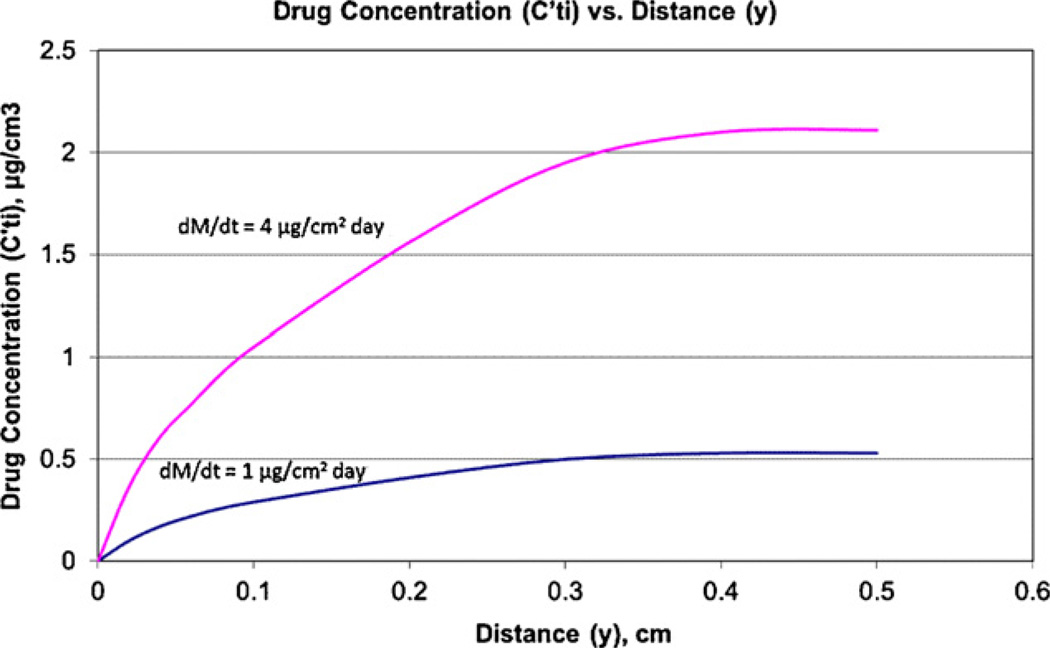
Unfortunately, the influence of u⊥ on diffusion layer formation predominates only at a large distance from the incision exit site (IES), while u∥ influence dominates at a small distance and causes much lower thickness δ∥, whose dependence on y is shown in Fig. 5 (Appendix B). The axial dependence of diffusion layer thickness causes the axial dependence of the antibiotic concentration on the catheter surface (Fig. 6). The data obtained in Table 1 characterizes the release efficiency only for a portion of the catheter with a distance longer than 4 mm from the IES. The shorter the distance y is to the IES, the lower is , which is calculated using Eq. (18). The data about δ(y) is presented in Fig. 5. The decrease with the approach to the IES causes a rapid decrease in Te, as shown in Fig. 7. Te(y) is calculated using Eq. (18) which is specified with the account for δ(y) dependence in Fig. 5.
Fig. 5.
The dependence of the diffusion layer thickness δ on distance y (along catheter) to incision exit site (y = 0) when Dti = 10−6 cm2/s and the velocities of interstitial liquids are 3 × 10−4 cm/s and 10−2 cm/s. The tangential velocity U∥ dominates in the formation of diffusion layer δ at smaller distance y. The perpendicular component of velocity U⊥ = U∥ sin α dominates at a larger distance in the formation of the diffusion layer with thickness δ⊥, sin α = 0.2.
Fig. 6.
The dependence of drug concentration Cti′ on the catheter surface on distance y to the incision exit site (y = 0) when Dti = 10−1 cm2/day and U∥= 3 × 10−4 cm/s and the release rates are 1 and 4 µg/cm2 day. The calculation is accomplished according to Eq. (B.14) where δ(y) is specified according to Fig. 5.
Fig. 7.
Dependence of effective release time Te on distance y to IES (y = 0) when Dti = 10−1 cm2/day and U∥ equals 3 × 10−4 cm/s and 10−2 cm/s. The value of Higuchi invariant (dM/dt)2t = 3 × 103 µg2/day and MIC = 2. Eq. (18) is used and δ(y) is presented in Fig. 5.
At high velocity u∥ ~ 0.01 cm/s, even a short time release is not efficient at a small distance to the IES, while this difficulty disappears at low velocity. At a very small distance to the IES, the release becomes inefficient even at a low velocity.
Assuming the worst possibility of biofilm formation in the vicinity of the IES, the therapeutic consequence of this event may not be dangerous if the higher antibiotic concentration downstream of the IES prevents the extension of biofilm towards the bloodstream, as was established in our experiment [10].
Catheter insertion leads to further exuding from the incision through the IES on the skin surface. The direction of the exudate stream is opposite to that of the interstitial flow, which existed before insertion. Initially, the exuding velocity is high and causes the reversal of the tangential velocity. While the flow before exuding displaces the released drug from the IES into deeper into the tissue, this causes to decrease, as illustrated in Fig. 6. The opposite direction of the tangential flow during exuding will cause an increase of at the approach to the IES. The exuding is the flow of interstitial fluid from tissue through the wound in the skin.
The exuding flow along the catheter surface to the IES is enriched by the released antibiotic, which will cause an increase in its concentration within the IES. This is an important topic for further modeling.
After catheter placement, exuding gradually weakens with time and its favorable influence on the release efficiency within the IES may terminate. This indicates the necessity of preventing bacteria transport towards the IES along the skin. Wound dressings such as the Biopatch are known to be effective in this situation. However, wound dressing with release duration much longer than that of the Biopatch will be necessary.
Further development of the Higuchi model by many groups [17–29] confirms its recognition in spite of the reporting of another kind of release kinetics in some experimental works. These discrepancies are possible for cases when the properties of polymer–drug blends do not satisfy the idealistic conditions inherent in the Higuchi model, including, for example, that a solid drug has to be finely divided, uniformly suspended and rapidly dissolved in a polymer. Control of the above properties is not easy in practical systems. Accordingly, publications with comments regarding the relationship between measured release kinetics and the Higuchi theory usually do not predict the control of the properties of the polymer–drug blends used. As soon as such control is absent, the possibility of deviation from the kinetics predicted by Higuchi is clear. Consequently, such publications cannot contribute to the estimates of the Higuchi theory.
The gradient of drug concentration within tissue arising due to drug release induces capillary osmotic flow [35–39] within the tissue, which in turn affects the antibiotic concentration on the implant surface. However, the influence is negligible when antibiotic molecules are uncharged because capillary osmosis is weak for uncharged solutes especially at low concentrations. The antibiotic concentration is usually about 1 µg/ml, i.e., it is very low. Although the capillary osmosis may be stronger for charged solute, it is weak as well when the solute concentration is low and simultaneously when the concentration of background electrolyte is high. This occurs during drug release within tissue because the physiological concentration of salt is in the centinormal range.
With respect to the influence of convective diffusion on , two portions of the coated catheter have to be considered separately, namely, that portion surrounded by the tissue and that portion submerged in the bloodstream. The blood velocity (about 20 cm/s) is orders of magnitude higher than the interstitial fluid velocity within the tissue. Correspondingly, diffusion layer thickness δle is approximately two orders of magnitude thinner in the portion submerged in the bloodstream. As δle is so small, it is doubtful that the condition similar to that of Eq. (1) may be satisfied for the bloodstream portion of the catheter, and consequently, the possibility of antimicrobial protection for this portion of the catheter with the use of a polymer antibiotic blend does not exist. On the other hand, positive results regarding the application of a coated catheter, when the placement time Tp is not long, is documented [3,4]. This contradiction will perhaps not exist if attention is paid to two factors. First, bacteria mainly penetrate through the IES from the skin. The conditions for biofilm growth are the most favorable near the IES. This is confirmed by our observations [10]. Second, bacteria in the bloodstream may be killed by immune cells which prevent biofilm formation on the catheter surface submerged in the bloodstream. Although there is a possibility of immune cells penetrating into the incision, their concentration under the skin is normally low. Taking this into account, we may conclude that bacteria suppression by means of antibiotic release is the most critical within the IES. Fortunately, conditions for protection by released antibiotics are more favorable within the incision where the harmful influence of convective diffusion is weaker. The positive results known for coated catheters (when the placement time is short) may be explained by antibiotic release into the tissue only. Whether antibiotic release from the portion of the catheter submerged in the bloodstream is useful remains uncertain.
7. Conclusions
Existing theories of drug release, including the generalized Higuchi theory, do not predict antibiotic concentration near an implant surface Cti which, in the case of catheters, has to exceed the MIC of the target organism to achieve antimicrobial protection. This shortcoming occurs because only the diffusion flux inside the polymer–drug blend towards the implant surface is considered in existing theories, while the flux from the surface into the tissue (or bloodstream), although critical, remains lacking. As the movement of interstitial liquid promotes drug transport, the convective diffusion within the tissue is a harmful factor which restricts the efficiency of released antibiotic. Methods of physico-chemical hydrodynamics are used for modeling the antibiotic transport from the catheter surface into the surrounding tissue.
Combining the Higuchi generalized theory with models of convective diffusion within tissue and by considering the microbiological approach known as MIC, we can derive the equation for antibiotic concentration near the catheter surface Cti as well as the equation for the duration of time Te of effective release. Derived Eq. (18) allows to predict the antimicrobial protection effectiveness of the catheter. In fact, this equation is the result of more complete modeling of the processes involved in catheter (implant) protection due to antibiotic release, although Eq. (18) and the Higuchi equation for drug release have to be analyzed in their combination. Eq. (18) may be called the equation of the efficiency of antimicrobial protection for catheters or implants. According to Eq. (18), Te depends on MIC, the Higuchi invariant, the characteristics of convective diffusion within tissue, diffusivity within tissue Dti and the diffusion layer thickness δ. The smaller Dti is favorable because the transport from the catheter surface is weaker. The thinner diffusion layer is harmful because the drug transport is stronger. The harmful enhancement of convective diffusion due to interstitial flow is quantified using methods of physico-chemical hydrodynamics taking into account the difference in the influence of the velocity components perpendicular and parallel to the catheter. The influence of the tangential component is especially harmful because the diffusion within the IES is extremely enhanced, which can decrease Cti to zero. This indicates the necessity of perfecting the suppression of bacteria transport along the skin towards the IES using proper wound dressing.
The release theory based on our models attains important new features. This theory is comprised of drug transport in the surrounding tissue, a process that is absent in the Higuchi theory. This predetermines the value of this new theory with respect to achieving therapeutic success from medical implants. Such progress becomes possible due to the application of colloid science principles, namely, colloid transport [6–9]. On the other hand, it must be recognized that rather crude estimations for Pe and δ were applied to the axial dependence for which occurs within the IES.
The incorporation of convective diffusion into the theory of antibacterial protection by means of antibiotic release has revealed physico-chemical mechanisms which can explain the limitations of antibiotic-loaded catheters, while at the same time define the conditions necessary to achieve better protection by means of combining catheter coating and wound dressing.
HIGHLIGHTS.
-
►
New theory of effective drug release from medical implants in surrounding tissues.
-
►
Theory allows quantification needed to achieve therapeutic effectiveness.
-
►
Role of convective diffusion in tissue using physicochemical hydrodynamics theory.
-
►
Theory predicts duration of effective release using theories of colloid transport.
-
►
Theory focuses on antibiotic release from implanted catheters.
Acknowledgments
The authors acknowledge funding for this research from the National Institute on Deafness and Other Communication Disorders, and the National Institutes of Health (Grant Numbers 1R43DC008907-01 and 2R44DC008907-02A1). We also express our sincere thanks to Omar Adam Labib and Anita Labib for editing this manuscript.
Appendix A. Decrease in macromolecular diffusion within tissue caused by the extracellular matrix
Complications arise when the diffusion within tissue is described but is not completely represented, as noted in the citation that follows [16]: “Plasma proteins are reported to have diffusion coefficients in the interstitium of 10–25% of that found in water (225), while the diffusion coefficient for hyaluronan in the umbilical cord interstitium is as low as 1% of its diffusion coefficient in water (304). Part of the low diffusion of hyaluronan is presumably due to entanglement between hyaluronan and collagen and between hyaluronan molecules. The diffusive properties of the interstitium have been described according to pore theory (225), giving pore radii of 120–200 Å for the normally hydrated umbilical cord or subcutaneous tissue as compared with molecular radii of 30–100 Å for plasma proteins.” The typical dimension of an antibiotic molecule is much smaller than that of proteins and its Dti has to be more than 25% of that found in water.
The influence of molecular convection in tissue has been fully investigated in the literature. The authors [16] state that the extracellular matrix does not decrease macromolecular convection if the molecular size is very small compared to the pore diameter. As this is valid for antibiotics, the above statement [16] is very helpful in better evaluating Dti because the extracellular matrix affects diffusivity depending on its hydrodynamic properties. The small change in macromolecular mobility according to [16] does not mean that Dti is about Da because there is another factor affecting the diffusion flux, namely: the cross-section for diffusion decreases within the tissue because this process takes place in the interstitium.
A similar problem arises when the influence of molecular chains on the electric current along an adsorbed polyelectrolyte layer is considered [31]. With respect to the problem of surface electric conductivity of adsorbed or grafted polyelectrolyte layers [31], it was proposed to use the equation derived in [32] for the description of the drop in conductivity of the macromolecular gel, KG, in comparison with the conductivity in the electrolyte KB, i.e., Eq. (5.1) in [31]
| (A.1) |
where Φ is the volume fraction of macromolecular chains, and B is the shape factor (5/2 for cylinder, 3/2 for sphere).
In the presence of large molecules, the resistance encountered by small molecules and by the ions moving between them is increased. Macromolecules distort the streamlines of the surface current and therefore lengthen the effective path of moving ions when considering conductance and diffusion.
The extracellular matrix (ECM) is an obstacle for macromolecular diffusion within the interstitium similar to the case when the fixed macromolecules of an adsorbed layer are an obstacle for the diffusion of small ions. This analogy allows to use Eq. (A.1), assuming that the geometry of ECM may be modeled as spherical or cylindrical particles of volume fraction, Φ, which is equal to the volume fraction of ECM, which is rather large, namely about 0.5 [30]. The substitution of Φ = 0.5 into Eq. (A.1) yields a negative value which shows that this equation is not valid for the case of large volume fraction. This possibility was discussed and cited in [31]: “The linear dependence of the conductivity on the volume fraction is possible, if Φ is sufficiently small. This dependence becomes nonlinear at a sufficiently large Φ [33]. The experimental analysis in [33] shows that the Bruggeman equation [33] is rather exact even at high volume fraction.”
As the Bruggeman equation was derived to calculate the averaged dielectric constant (ε) of a disperse system, i.e., a system with different values of dielectric constants of particles and media, it must be explained why this equation may be used to describe the diffusion in the disperse system. This is possible due to the principle of generalized conductivity, which has obtained large recognition and application. Its significance is explained, for example, in [33], Chapter 6, Paragraph 2.
Some problems pertaining to electrical conductivity, thermal conductivity and magnetic susceptibility and diffusion in disperse systems are analogous to the problem of calculating ε from data on the dielectric constants of constituents. This group of properties is combined under the common term “generalized conductivity,” which is due to the formal coincidence of the differential equations of the steady-state fluxes (j) of heat, electric current, electric and magnetic induction and diffusion fluxes (Table 5 in [33]). Each of the above steady-state fluxes satisfies the continuity equation
| (A.2) |
and is a linear function of the corresponding vector field X, which in the thermodynamics of irreversible processes is the thermodynamic force
| (A.3) |
where ε is phenomenological or kinetic coefficients.
In the case of a two-phase monodisperse system,
| (A.4) |
where ε is an unknown kinetic coefficient for a disperse system, ε0 and ε1 are known coefficients for dispersion medium and disperse phase (particles), respectively, and where the form of the functional relationship is determined by the geometric structure of the disperse system. The usefulness of the analogy, which is the essence of the principle of generalized conductivity, consists in the fact that each equation such as (A.4) can be employed to derive an expression for ε of a disperse system with a similar geometric construction
| (A.5) |
Or, in our case for diffusivity
| (A.6) |
where 0 means that the ECM is impermeable for macromolecular diffusion and F is the function derived by Bruggeman, namely Eq. (VI.29) in [33]. F is ~0.3 for volume fraction Φ = 0.5 according to the Bruggeman equation. This value is also given in Table 8 on page 189 in [33].
Appendix B. Influence of the axial component of interstitial velocity on the diffusion of released drug and on the formation of the diffusion boundary layer on the catheter surface
It will be demonstrated that the axial velocity which affects the diffusion of antibiotics released from a catheter is much stronger than the normal component, and this leads to a much smaller thickness of the diffusion layer
| (B.1) |
The cylindrical catheter (1), which crosses the skin (2) with the inclination angle α, is shown in Fig. 4. The skin and tissue are damaged during the insertion of the catheter into a blood vessel within a zone whose boundary is shown by the dashed line and is called the incision. A portion of this incision, which is the damaged skin, is usually called the incision exit site (IES). The axial symmetry is absent in the velocity distribution around the catheter. Consequently, the orbital angle φ is introduced in addition to the axial coordinate y.
The intersection of the skin with the catheter results in the elliptical shape of the IES (elliptical ring) due to the inclination angle α. The long axis of ellipse belongs to the plane perpendicular to the skin. An angular direction from this plane is characterized by angle φ, i.e., φ = 0 coincides with this plane of symmetry.
For the sake of simplicity, attention is paid to the case where the direction of the external interstitial flow coincides with the direction of the long axis of the ellipse. In other words, a streaming line is considered within plane φ = 0, which will be called the “axial streaming line” (ASL). The first portion of the ASL is located under the skin; the second one propagates along the cylinder wall. The y coordinate is introduced with its beginning at point y = 0, that is, the boundary between the cylinder and the IES. The diffusion of released drug is affected by the axial flow which causes y dependence of δ.
Many simplifications are necessary because the geometrical conditions of this system are extremely complicated. Their exact account is possible only with the application of numerical computation and huge efforts. This difficulty forces us to replace our task with a relevant one to reveal a clear physical regularity in somewhat simpler geometrical conditions, and afterwards to return back and show that this important regularity remains applicable in the more complicated realistic condition as well.
For the purposes of realizing this approach, we consider the situation where an imaginary cylinder has a very large radius which allows to disregard its curvature. In fact, with this idealization, we have a plane instead of a cylinder with angle α with respect to the skin, while the release for the plane is preserved. It is obvious that a value of the small angle α almost does not affect the processes initiated by the axial velocity. It allows to make the next and last simplification, namely, to choose α = 0. As a result, we obtain a task which has already been considered in physico-chemical hydrodynamics [14]. There is a tangential stream along a plane, along the y axis. The boundary conditions for the diffusion from the plane are:
| (B.2) |
| (B.3) |
This is equivalent to Eqs (20.12) and (20.13) in [14] with our nomination of y instead of x in [14].
These boundary conditions mean that there is no diffusion at y < h and that the diffusion layer starts to form after point y ~ h. The difference with our task is that dC/dx = J/D on the surface at y > h is given.
Let us compare Cti(x, y) slightly on the left and on the right from point y = h, i.e., at y = h − ε and y = h + ε, where ε is very small. This shows that Cti(h + ε, x) at any x has to be very small because Cti(h − ε, x) = 0 and because the concentration cannot increase in jump-wise mode between point (h − ε, x) and (h + ε, x). In other words, when the diffusion layer starts to form along the stream with increasing y, starting from y = h, δ(y) increases gradually starting from zero value δ(h) = 0, and δ(y) remains very small within the vicinity of point x = 0, y = h. This peculiarity of the onset of the diffusion layer formation downstream and its initial development because of tangential flow have fundamental significance for the antimicrobial protection of a catheter by release because δ(y) near zero means that is near zero within the incision exit site, i.e., IES is not protected in spite of , when y is large. Indeed, as , one obtains
| (B.4) |
and hence,
| (B.5) |
when
| (B.6) |
Now, when we return to the realistic and more complicated geometry, i.e., to the restoration of angle α and in consideration of the inclined cylinder with a finite radius, these geometrical conditions cannot affect the above discussed mechanism, which causes δ(h) = 0 and δ(y) to be small in the vicinity of point x = 0, y = h. Indeed, the onset of diffuse layer formation, when the liquid stream crosses the point x = 0, y = h and slowly moves downstream, depends only on the local conditions in the vicinity of this point and does not depend on the curvature of the cylinder and the angle α as long as α is sufficiently small.
Since the IES may not be protected by the antibiotic release, a question arises as to how thick the tissue layer adjacent to the IES is, which is unprotected because within this layer. The answer to this question may be obtained only by means of the solution of the equation for convective diffusion. Accounting for the influence of the cylinder curvature on the axial flow and for angle α would cause extreme difficulty in the modeling.
There is no reason which could cause a large difference in the convective diffusion along the axial streaming line (ASL) and in the model introduced above, which considers the case when α = 0 and disregards the cylinder curvature. This simplification allows to use the equation of convective diffusion in its cononical form [14].
| (B.7) |
where the x coordinate is perpendicular to the plane. x = 0 coincides with the plane (catheter surface). This is Eq. (15.1) in [14] for convective diffusion when the laminar liquid stream is parallel to a plane.
When a system is not porous, the normal velocity component Ux exists when the tangential velocity distribution is developed. A uniform hydrodynamic stream is retarded on the plane surface which causes Uy dependence on x and concomitantly leads to the arising of the Ux component. In our case, the extracellular surface causes hydrodynamic resistance which is uniform regarding the x coordinate which causes very weak dependence Uy(x). As Ux arises due to this dependence, it is very small and may be neglected. This allows to omit the first term on the left-hand side of Eq. (B.7) and presents Uy as invariant U, where U is the measured interstitial velocity averaged within the layer under the skin with a thickness of δ (about tens of hundreds microns).
| (B.8) |
There is a large similarity between this equation and the well-known equation for non-steady heat transport [34]
| (B.9) |
where T(x, t) is the temperature distribution and t is time. We will obtain the solution for Eq. (B.8) using the known solution of Eq. (B.9) and by means of the substitution of D/U instead of a and of y instead of t.
| (B.10) |
where
| (B.11) |
When the derivative is calculated on the basis of Eq. (B.10) and afterwards the obtained result is specified for x = 0, it turns out that
| (B.12) |
This confirms that the function (B.10) describes the diffusion layer formed due to release from a catheter under the condition of axial flow of the interstitial liquid.
The axial distribution of antibiotic concentration along a catheter surface follows from Eq. (B.10) after the substitution in it of x = 0. The second term disappears at this substitution, while exp(0) = 1 in the first term.
| (B.13) |
The comparison of this equation with one which defines δ(y)
| (B.14) |
Yields y dependence for δ
| (B.15) |
This increase in δ downstream is unlimited in the case of the plane. In our case of release from a cylindrical surface, the δ growth ceases when δ = R is achieved (in the absence of the normal component of velocity). As there is the normal component, δ growth ceases when δ ≈ R/Pe⊥0.5 is achieved.
References
- 1.Frontiers in Formulation Science. Colloids Surf. A; Selected Papers from 5th International Conference on Formulation Technology; November 2007; Potsdam, Germany. 2008. [Google Scholar]
- 2.Park K, Stowell JG. Controlled Drug-delivery Systems. Stipes Publishing, LLC; 2005. [Google Scholar]
- 3.Hetrick EM, Schoenfisch MH. Reducing implant-related infections: active release strategies. Chem. Soc. Rev. 2006;35(9):780–789. doi: 10.1039/b515219b. [DOI] [PubMed] [Google Scholar]
- 4.Noimark S, Dunnill CW, Wilson M, Parkin IP. The role of surfaces in catheter-associated infections. Chem. Soc. Rev. 2009;38(12):3435–3448. doi: 10.1039/b908260c. [DOI] [PubMed] [Google Scholar]
- 5.Labib M, Brumlik C, Stoodley P, Dukhin S, Davidson T, Tabani Y. Colloids Surf. A. 2010;354:331–337. doi: 10.1016/j.colsurfa.2009.10.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lyklema J. Fundamentals in Colloid and Interface Science. vol. 1. London, Toronto: Academic Press; 2000. Chapter 6. [Google Scholar]
- 7.Russel WB, Saville DA, Showalter WR. Colloidal Dispersions. Cambridge University Press; 1989. Chapters 2, 3, 7, 11, 13. [Google Scholar]
- 8.Elimelch M, Gregory J, Jia X, Williams RA. Particle Deposition and Aggregation. Butterworth Heinemann; Chapter 4. [Google Scholar]
- 9.Dukhin SS, Sjoblom J, Saether O. Chapter 1. In: Sjoblom J, editor. Emulsions and Emulsion Stability. Taylor and Frances; 2006. [Google Scholar]
- 10.Andes D, Nett J, Oschel P, Albrecht R, Marchillo K, Pitula A. Infect. Immun. 2004;72(10):6023–6031. doi: 10.1128/IAI.72.10.6023-6031.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Higuchi T. J. Soc. Cosmet. Chem. 1960;11:85–97. [Google Scholar]
- 12.Higuchi T. J. Pharm. Sci. 1961;50:874–875. doi: 10.1002/jps.2600501018. [DOI] [PubMed] [Google Scholar]
- 13.Roseman TJ, Higuchi W. J. Pharm. Sci. 1970;59:353–357. doi: 10.1002/jps.2600590317. [DOI] [PubMed] [Google Scholar]
- 14.Levich VG. Physico-chemical Hydrodynamics. Englewood Cliffs, NJ: Prentice Hall; 1962. [Google Scholar]
- 15.Swartz MA. Adv. Drug Delivery Res. 2001;50:3–30. doi: 10.1016/s0169-409x(01)00150-8. [DOI] [PubMed] [Google Scholar]
- 16.Reddy ST, Berk DA, Jain RK, Swartz A. J. Appl. Phys. 2005;101:1162–1169. doi: 10.1152/japplphysiol.00389.2006. [DOI] [PubMed] [Google Scholar]
- 17.Frenning G, Stromme M. Drug release modeled by dissolution, diffusion, and immobilization. Int. Int. J. Pharm. 2003;250:137–145. doi: 10.1016/s0378-5173(02)00539-2. [DOI] [PubMed] [Google Scholar]
- 18.Siepmann J, Peppas NA. Hydrophilic matrices for controlled drug delivery: an improved mathematical model to predict the resulting drug release kinetics (the “sequential layer” model) Pharm. Res. 2000;17:1290–1298. doi: 10.1023/a:1026455822595. [DOI] [PubMed] [Google Scholar]
- 19.Paul DC, McSpadden SK. J. Membr. Sci. 1976;1:33–48. [Google Scholar]
- 20.Lee PI. J. Membr. Sci. 1980;7:255–275. [Google Scholar]
- 21.Bunge AL. J. Control. Release. 1998;52:141–148. doi: 10.1016/s0168-3659(97)00211-3. [DOI] [PubMed] [Google Scholar]
- 22.Bunge ALR, Miller I. Chemical Engineering Education. 1997 Fall;:254–259. [Google Scholar]
- 23.Tojo K. J. Pharm. Sci. 1985;74:685–687. doi: 10.1002/jps.2600740622. [DOI] [PubMed] [Google Scholar]
- 24.Zhou Y, Wu XY. J. Control. Release. 2002;84:1–13. doi: 10.1016/s0168-3659(02)00263-8. [DOI] [PubMed] [Google Scholar]
- 25.Abdekhodale MJ, Cheng Y-L. J. Control. Release. 1997;43:175–182. [Google Scholar]
- 26.Zheng F. J. Control. Release. 1998;55:99. doi: 10.1016/s0168-3659(98)00007-8. [DOI] [PubMed] [Google Scholar]
- 27.Ayres JW, Lindstrom FT. J. Pharm. Sci. 1977;66:654–664. doi: 10.1002/jps.2600660513. [DOI] [PubMed] [Google Scholar]
- 28.Lindstrom FT, Ayres JW. Pharm. Sci. 1977;66:662–668. doi: 10.1002/jps.2600660514. [DOI] [PubMed] [Google Scholar]
- 29.Frenning C. J. Control. Release. 2003;92:331–339. doi: 10.1016/s0168-3659(03)00338-9. [DOI] [PubMed] [Google Scholar]
- 30.Aukland K, Reed RK. Physiol. Rev. 1993;73:1–77. doi: 10.1152/physrev.1993.73.1.1. [DOI] [PubMed] [Google Scholar]
- 31.Duval JFI, Zimmermann R, Cordeiro AI, Rein N, Werner C. Langmuir. 2009;25:10691. doi: 10.1021/la9011907. [DOI] [PubMed] [Google Scholar]
- 32.Elworthy PH, Florence AT, Rahman A. J. Phys. Chem. 1972;76:1763. [Google Scholar]
- 33.Dukhin SS, Shilov VN. Dielectric Phenomena and the Double Layer in Disperse Systems and Polyelectrolytes. New York: Wiley; 1974. [Google Scholar]
- 34.Likov AV. Chapter 4, p. 149, Eq. 12. Theory of Heat Transport, High School, Moscow. 1987 (in Russian) [Google Scholar]
- 35.Dukhin SS, Derjaguin BV. In: Surface and Colloid Science. Matijevic E, editor. vol. 7. New York: John Wiley and Sons; 1972. p. 174. [Google Scholar]
- 36.Prieve DC. Adv. Colloid Interface Sci. 1982;16:321. [Google Scholar]
- 37.Kylstra JA, Longmuir IS, Grace M. Science. 1968;161(3838):289. doi: 10.1126/science.161.3838.289. [DOI] [PubMed] [Google Scholar]
- 38.Hills B. Med. Hypotheses. 1999;53:259–263. doi: 10.1054/mehy.1997.0640. [DOI] [PubMed] [Google Scholar]
- 39.Babchin A, Levich E, Melamed Y, Sivashinsky G. Osmotic phenomena in application for hyperbaric oxygen treatment. Colloids Surf. B: Biointerfaces. 2011;83:128–132. doi: 10.1016/j.colsurfb.2010.11.019. [DOI] [PubMed] [Google Scholar]