Abstract
Successful implementation of homogeneous slice-selective RF excitation in the human brain at 9.4T using 16-channel parallel transmission (pTX) is demonstrated. A novel three-step pulse design method incorporating fast real-time measurement of eddy current induced B0 variations as well as correction of resulting phase errors during excitation is described. To demonstrate the utility of the proposed method, phantom and in-vivo experiments targeting a uniform excitation in an axial slice were conducted using two-spoke pTX pulses. Even with the pre-emphasis activated, eddy current induced B0 variations with peak-to-peak values greater than 4 kHz were observed on our system during the rapid switches of slice selective gradients. This large B0 variation, when not corrected, resulted in drastically degraded excitation fidelity with the coefficient of variation (CV) of the flip angle calculated for the region of interest being large (∼12% in the phantom and ∼35% in the brain). By comparison, excitation fidelity was effectively restored, and satisfactory flip angle uniformity was achieved when using the proposed method, with the CV value reduced to ∼3% in the phantom and ∼8% in the brain. Additionally, experimental results were in good agreement with the numerical predictions obtained from Bloch simulations. Slice-selective flip angle homogenization in the human brain at 9.4T using 16-channel 3D spoke pTX pulses is achievable despite of large eddy current induced excitation phase errors; correcting for the latter was critical in this success.
Introduction
Parallel transmission (pTX) in the context of magnetic resonance imaging [1]–[4] consists of simultaneously playing different RF pulse shapes on independent transmit (Tx) channels. It is known that by designing multidimensional (multi-D) spatially selective pTX RF pulses, in concert with time varying encoding gradients, one can mitigate the impact of Tx B1 (B1+) nonuniformities [5]–[7] as well as achieve arbitrarily shaped RF excitation profiles [3], [8], [9]. Such techniques are especially relevant at ultra-high magnetic fields (i.e., 7T and beyond) where B1+ profiles in human anatomical targets are notoriously heterogeneous. However, multi-D RF pulses are highly sensitive to deviations in excitation k-space trajectory arising from system imperfections such as gradient amplifier nonlinearities, time delays or residual eddy currents [10], [11].
We have demonstrated in-vivo on a 9.4 T human system large improvement in 2D pTX excitation fidelity by including susceptibility induced main field inhomogeneities (ΔB0) maps and actual k-space trajectories, measured on the fly, in pTX RF pulse design involving encoding gradients along x- and y-axes [10]. However, when expanding this approach towards slice-selective 3D spoke pTX RF pulse design to achieve homogeneous excitation within axial slices on the same scanner, significant residual excitation errors were observed, even though in this case measured and nominal k-space trajectories were virtually identical [12], [13]. We hypothesized that this was due to eddy current induced zero-order B0 modulations, resulting from slice-selective z-axis encoding gradient switches, that are not described in a conventional k-space trajectory representation limited to linear spatially encoding gradients [13]. In the current work we detail the successful implementation of 3D pTX in the human brain at 9.4T with drastically improved excitation fidelity when correcting for eddy current induced B0 variations. A three-step pulse design is proposed:
In-vivo measurement of eddy current induced B0 modulation, B1+ and ΔB0 maps.
Initial 3D pTX pulse design based on B1+ and static ΔB0 maps.
Final 3D pTX pulse design with correction of eddy current induced B0 modulation.
Materials and Methods
Ethics Statement
The human experiments performed in the present study were approved by the local institutional review board of the University of Minnesota. Healthy volunteers who signed a written consent form were recruited and received compensation for their participation.
General setting and hardware
All experiments were conducted on a 9.4T, 65-cm-diameter inner bore MR human scanner (Magnex, Oxford, UK) driven by a DirectDrive console (Agilent, Santa Clara, CA). The scanner was equipped with a head gradient coil (Magnex, Oxford, UK) with an inner diameter of 40 cm, powered by a Siemens gradient amplifier (Siemens, Erlangen, Germany) allowing a maximum gradient strength of 48 mT/m and a maximum slew rate of 240 T/m/s. Prior to the current study, the calibration of pre-emphasis currents to counteract gradient induced eddy currents had been performed on the system following standard manufacturer procedures [14]. Note that the compensation of eddy current induced B0 variations is obtained by applying a time varying current on a physical B0 coil (capable of generating a frequency modulation up to about 4 kHz) rather than by modulating in real time the carrier RF frequency. The DirectDrive console was equipped with 16 independent Tx channels, each powered by a 500W RF amplifier (CPC, NY, USA). As previously described [10], [15], [16], a home-built multi-channel RF power monitoring unit continuously measured the output power of each RF amplifier to ensure compliance with safety guidelines on maximum specific absorption rate. A 16-channel Transmit/Receive open-faced head array [17], consisting of separable upper and lower coil formers each with eight resonance elements, was used for both RF transmission and reception. When combined, the upper and lower formers resulted in an elliptical shape in the transverse plane (20 and 24 cm long in the left-right and anterior-posterior directions, respectively). Each array element was built using a 12 mm wide copper strip conductor and a 42 mm wide RF ground plane, with 12 mm thick Teflon dielectric in between. All MR signals were simultaneously acquired on 16 independent receive channels. Phantom studies were performed prior to the in-vivo experiments to test and optimize the imaging protocols, using a spherical saline phantom (99 mM NaCl, 16 cm in diameter) doped with copper sulfate (T1 ∼ 200 ms) as in Ref. [10] where the relatively short T1 value allowed for fast acquisition without having to use a long repetition time to attain sufficient longitudinal magnetization relaxation. In-vivo experiments were obtained in three human subjects using the same acquisition protocol.
Gradient and Eddy Current Characterization
The present study is focused on pTX pulse design aiming at achieving homogeneous excitation within axial slices using multiple slice-selective RF sub-pulses with spatially encoding gradient blips along the x and y axes inserted between the sub-pulses. Slice-selective spoke gradients were always applied along the Z direction, and the eddy current induced B0 modulations were measured using a gradient characterization approach previously described [18]. The pulse sequence developed for data acquisition comprised a conventional slice-selective RF excitation along the Z direction, immediately followed by the application of the spoke gradient during which MR signals are sampled (with neither phase encoding nor readout gradients). The phase evolution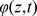
of the signal due to the spoke gradient within a slice positioned at a distance z from the gradient isocenter can be described as:
 |
(1) |
with
 |
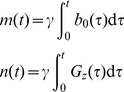Here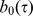
is the eddy current induced B0 variations (i.e., zero order eddy current which is spatially invariant),
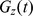the linear gradient including corresponding first order eddy current terms, and
the proton gyromagnetic ratio.
Similar to Ref. [18],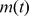 
and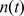
were first obtained by fitting
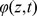of a multi-slice dataset to the linear model of Eq. 1 with respect to the varying slice positions z for each time point t, and were then used to calculate
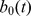and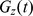
, respectively. Phase accumulations arising from other sources such as main field inhomogeneities (ΔB0) and slice selective gradient used for slice excitation (not the measured spoke gradient) were also obtained with the spoke gradient turned off and were removed from the signal phases so as to obtain phase evolutions purely due to the spoke gradient. In both phantom and human experiments, the slice selective RF excitation was achieved using a low-bandwidth RF pulse (8 ms in length), and MR signals, sampled at a temporal resolution of 4 μs, were obtained in an interleaved manner in three slices (slice thickness = 1.5 mm) positioned at z = –10, 0 and 10 mm, respectively. To improve SNR, a multi-slice dataset averaged over 32 acquisitions was taken to calculate the eddy current induced B0 shifts. The total acquisition was obtained within 15.4 s with TR/TE = 240/10.8 ms.
B1 and ΔB0 Field Mapping
Transmit and receive complex B1 maps as well as ΔB0 maps were obtained as previously described [10]. Briefly, complex-valued B1+ maps for all 16 channels were obtained with a fast hybrid multi-channel B1+ mapping technique where one absolute flip angle map is merged with 16 relative B1+ maps to generate 16 absolute |B1k+| maps (k = 1,2,…,16), exploiting the knowledge of complex interferences between channels derived from the relative B1+ maps [19]. The 16 relative B1+ maps were derived from a series of small tip angle gradient echo (GRE) images with one channel transmitting at a time, acquired with TR/TE = 100/2.3 ms, slice thickness = 5 mm, matrix size =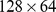 
, acquisition time = 115 s, and FOV = 
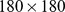mm2 for the phantom and 
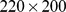mm2 for the human head. The absolute B1+ magnitude map was obtained, with all channels transmitting together, using the actual flip angle imaging (AFI) method [20] with TR1/TR2/TE = 25/125/2.6 ms, slice thickness = 9 mm, matrix size = 
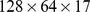, acquisition time = 165 s, and FOV = 
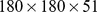mm3 for the phantom and FOV = 
mm3 for the human head. Fig. 1 displays the 16 complex B1+ maps measured in the phantom and in the human brain. An additional small tip angle GRE image was obtained using the same RF pulse as in the AFI and was divided by the sine of the AFI flip angle map to estimate the receive B1 magnitude (|B1-|) multiplied by proton density (ρ). Note that in such estimation one would expect residual T1-related signal variations in the brain since a relatively short TR (100 ms) was used. ΔB0 maps were derived from two GRE images (TE1/TE2 = 5/5.5 ms) and were incorporated into the pulse design to avoid distortions of excitation pattern due to susceptibility induced off-resonance. All field maps were down-sampled to match the spatial resolution used in the subsequent pulse design.
Figure 1. Transmit B1 maps measured for the 16-channel transceiver in the phantom (a) and in the human brain (b).
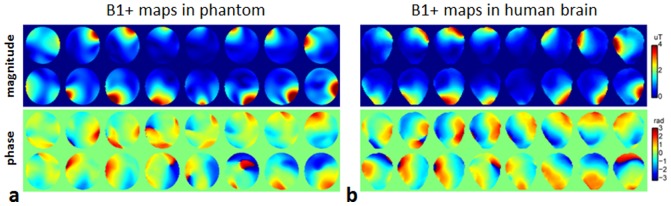
The B1+ magnitude and relative phase maps are shown in the top and bottom panels, respectively.
Initial RF Pulse Design
3D pTX RF pulses were designed to achieve uniform excitation within an axial slice, using the nominal two-spoke excitation k-space trajectories. These RF pulses consisted of two Gaussian-shaped sub-pulses (1 ms in length, time-bandwidth-product = 2), each applied during the plateau of a trapezoidal slice-selective spoke gradient (G z) with maximum amplitude of 16.5 mT/m and maximum slew rate of 150 T/m/s, in order to obtain a slice thickness of 5 mm.
Complex coefficients (i.e., RF magnitude and phase) for individual channels and individual sub-pulses were calculated with the magnitude least squares optimization [21]:
 |
(2) |
where
is a 32-element (16 × 2 = 32) vector of complex-valued coefficients, A is a complex-valued matrix incorporating the B1+ sensitivities of individual channels, modulated by the Fourier kernel corresponding to spoke placements in k-space as well as by the measured static ΔB0 maps, and
is a real-valued regularization parameter used to determine a tradeoff between excitation error and total RF power.
A uniform 10° excitation target was defined on a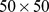 
grid with in-plane isotropic spatial resolution of 3.6 mm for the phantom and of 4.4 mm for the human brain. Similar to Ref. [6], the spoke placement in the transverse k-space was constrained to be symmetric about the origin and was optimized over a grid defined by an array of rotation angles (from 0° to 170° with 10° increments) and an array of spatial frequencies (from 8 to 18 cm−1 with 2 cm−1 increments). After the spoke placement was determined, the regularization parameter 
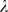used for pulse calculation was chosen based on the L-curve criterion [3]. Only pixels inside the region of interest (ROI), i.e. within the phantom or brain tissues, were considered in the pulse design. All waveforms were defined with a dwell time of 4 μs, and the total pulse duration including the slice-selective gradient rewinder lobe was 3 ms.
Corrected RF Pulse Design
In order to achieve satisfactory excitation quality, RF pulses were corrected for eddy current induced B0 variations arising from the application of the spoke gradient. The corrected pulse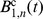 
for the n-th channel was obtained by applying a phase modulation to the initially calculated pulse 
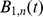based on the eddy current measurement:
 |
(3) |
In practice, this spatially invariant phase modulation is equivalent to a time-varying modulation of the carrier RF frequency. Note that no trajectory correction (i.e. no linear term Gx, Gy or Gz) was incorporated in the proposed pulse design since we found no difference in excitation patterns when comparing the use of nominal and measured transverse gradient blips for pulse calculation in our initial investigation.
Experimental verification
The excitation patterns for the initial and corrected pTX pulses were measured using 3D AFI, with TR1/TR2/TE = 25/125/3.6 ms, matrix size =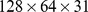 
, FOV = 
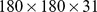mm3 for the phantom and FOV = 
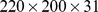mm3 for the human head, nominal flip angle = 50° in the phantom and 40° in the human brain. The coefficient of variation (CV), defined as the std/mean of flip angle values within the ROI, was calculated for quantitative comparison between different pulses. Additional GRE images were obtained, using a modified 3D GRE pulse sequence where the RF excitation module was replaced by the initial or the corrected pTX pulse, with nominal flip angle = 10°, TR/TE = 100/4 ms, matrix size = 
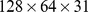, FOV = 
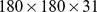mm3 for the phantom and 
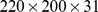mm3 for the human head, acquisition time = 199 s. These GRE images were further normalized by the estimated product
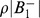as described earlier in order to compare the excitation patterns.
Simulations
Bloch simulations were conducted to calculate excitation patterns with initial and corrected pTX RF pulses. To reproduce as closely as possible the experimental conditions, these simulations included the measured eddy current induced B0 variations as well as the measured gradient, B1+ and ▵B0 maps. Excitation patterns were defined, as for the experimental settings, on a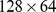 
grid with a field of excitation of 
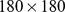mm2 for the phantom and of 
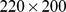mm2 for the human head. All simulations assumed uniform longitudinal magnetization at equilibrium and ignored relaxation and diffusion effects. All computations, including RF pulse design and Bloch simulations, were performed in Matlab (MathWorks, Natick, MA, USA).
Results
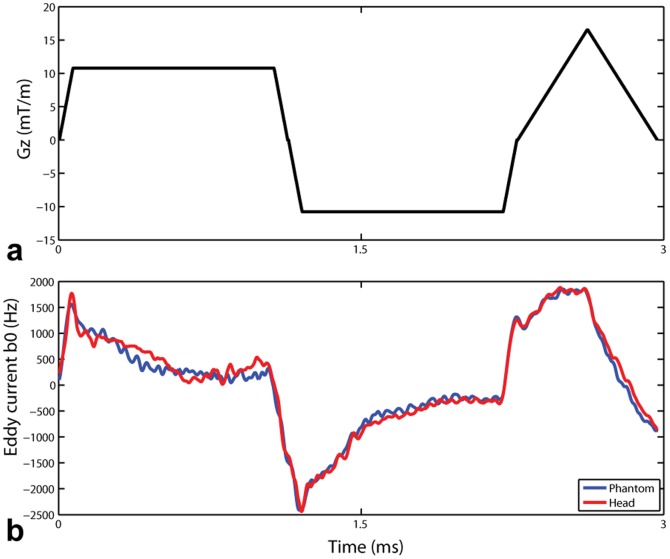
Large eddy current induced B0 variations were observed on our system, with peak-to-peak values greater than 4 kHz and with fairly short time constants (<1 ms) during the rapid switches of the 2-spoke slice selective gradients (Fig. 2). A comparison between the blue and red curves in Fig. 2b indicates a high consistency between phantom and human brain based measurements.
Figure 2. The 2-spoke slice selective gradient waveform (a) used in the pulse design and the resulting eddy current induced B0 shifts (b) measured in the phantom (blue curve) and in the human brain (red curve).
Note that large eddy current induced B0 variations with about 4-emphasis eddy current compensation.
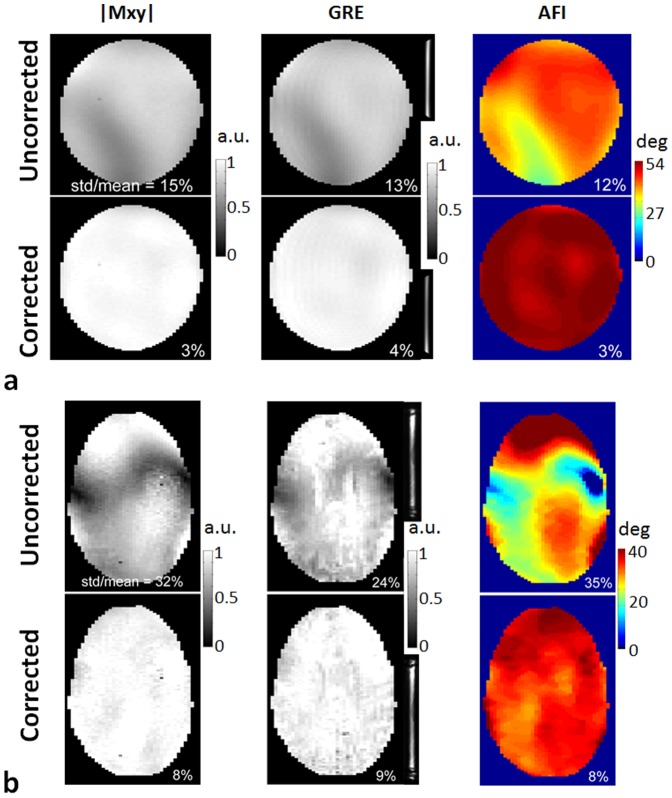
When these B0 temporal modulations were not accounted for in the pulse design, the excitation pattern |Mxy|, as predicted by Bloch simulations, was drastically degraded for both phantom and human brain data, and the corresponding experimental data very closely reproduced these predicted distortions both in small flip angle GRE images and in measured flip angle maps (Fig. 3). By contrast, excitation homogeneity dramatically improved when eddy current induced B0 temporal modulations were corrected in pTX RF pulse design (Fig. 3). The slice selectivity remains unchanged between uncorrected and corrected pulses as seen in a mid-sagittal slice of the 3D GRE acquisition (Fig. 3, middle column). CV values in phantom data as measured by |Mxy| (via Bloch simulations), GRE image signal intensities, and flip angle maps decreased from 15%, 13% and 12% without correction for eddy current induced B0 shifts, down to 3%, 4% and 3% with correction, respectively. Corresponding CV values in the brain dropped from 32%, 24% and 35% down to 8%, 9% and 8%, respectively.
Figure 3. Uncorrected vs corrected 2-spoke pTX RF pulses in terms of excitation fidelity evaluated in the phantom (a) and in the human brain (b) at 9.4 T.
The coefficient variation values (i.e., std/mean) for both uncorrected and corrected pulses quantifying the flip angle inhomogeneities were calculated based on the corresponding Bloch simulations (left column), 3D GRE images normalized with respect to receive B1 (middle column) and actual flip angle imaging (right column). A mid-sagittal slice of the original 3D GRE acquisition is also shown on the right of each normalized GRE image, to appreciate the intact slice selectivity of both the uncorrected and corrected RF pulses. A nominal flip angle of 10° was used in both Bloch simulation and 3D GRE acquisition, and a higher nominal flip angle of 50° for the phantom and 40° for the brain was employed in the flip angle mapping. Note that in both the phantom and the human brain signal voids due to eddy current induced B0 shifts observed with the uncorrected RF pulses were effectively restored with significantly improved excitation homogenization when using the corrected pulses. Additionally, good agreement was seen between numerical predictions and experiments.
Figure 4 displays the predicted excitation patterns |Mxy|, GRE acquisition and actual flip angle mapping in the human brain when using eddy current corrected single-spoke pTX pulses (i.e., static B1 shimming), obtained with imaging parameters similar to those for the 2-spoke pulse design. As can be seen, the CV numbers achieved with B1 shimming were larger than those with 2-spoke pulses, showing that B1 shimming is not as effective as the 2-spoke pulse design in B1+ homogenization.
Figure 4. Excitation fidelity of static B1 shimming (i.e., single-spoke pTX pulse design) in the human brain at 9.4 T using eddy current B0 corrected single-spoke pTX pulses.
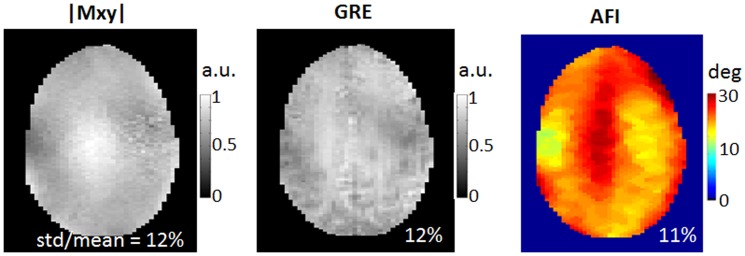
The coefficient variation values (i.e., std/mean) were calculated based on the corresponding Bloch simulations (left column), 3D GRE images normalized with respect to receive B1 (middle column) and actual flip angle imaging (right column). A nominal flip angle of 10° was used in both Bloch simulation and 3D GRE acquisition, and a higher nominal flip angle of 23° was employed in the flip angle mapping. Note that B1 shimming was not as effective as 2-spoke pTX pulse design in creating uniform excitation.
Discussion
In this study, we have demonstrated the successful implementation of 16-channel 3D slice-selective pTX RF excitation in the human brain at 9.4 T, counteracting large eddy current induced excitation errors in the pulse design. Importantly, our results show that very fast eddy current calibration can be obtained in-vivo, providing reliable results for excitation RF pulse design, suitable as a routine step in MR protocols. In the proposed approach an initial version of the pTX pulses is first calculated without eddy current compensation, based on the B1+ maps and taking into account the measured static ΔB0 maps. Eddy current induced temporal B0 modulations associated with the multi-spoke slice selective gradients, measured on the fly, were then used to correct the RF pulse by incorporating the corresponding phase variations. Experimental results acquired both in a phantom and in the human brain demonstrated that this compensation effectively mitigated signal loss and pattern distortion observed with the initial uncorrected RF pulses, resulting in satisfactory in-plane excitation homogeneity despite of severe eddy currents induced by the slice selective gradients.
Although pre-emphasis settings used to counteract gradient induced eddy currents were always active during this study, large amplitudes of B0 variations were still present during multi-spoke gradient waveforms with slice selection set along the z axis, possibly corresponding to the limits of the pre-emphasis hardware resources on our system to address high amplitude, short time constant B0 eddy currents. It is remarkable that transient B0 variations as large as 4 kHz could be addressed by correcting the pTX RF pulse, yielding satisfactory excitation fidelity. Recently, Schneider et al. [11] proposed an MRI based technique to map local phase accumulations of the transverse magnetization as a result of gradient applications and susceptibility effects during spatially selective RF excitations; this technique, however, is complex to implement and requires a relatively long calibration. By contrast, the calibration method used in the current study is easy to implement and requires very short acquisition time while providing reliable results.
It is interesting to note that here we did not observe any significant impact of eddy current induced gradient distortions (in Gx, Gy or Gz) on the excitation quality, whereas we had reported in a previous study, on the same system, major deteriorating impact of k-space deviations when using 2D Transmit SENSE RF pulses [10]. This can be explained by the fact that the two gradient blips used for the 2-spoke pulse design in the present study are very small in amplitude (not exceeding 4 mT/m) and very short in time (∼ 350 µs), yielding negligible excitation phase errors due to gradient imperfection. By contrast, the 2D spiral gradients that were applied during 2D Transmit SENSE pulses in the former study were 5-fold stronger in maximum amplitude and 7-fold longer in duration, yielding large k-space errors due to gradient distortions that could not be ignored. On the other hand, we observed in the present study large residual eddy current induced B0 shifts after switching the z-gradient coil, even with system pre-emphasis activated, whereas we did not observe such large B0 variations when using 2D Transmit SENSE pulses where the x- and y-gradient coils were highly solicited. We hypothesize that these differences in response between, on the one hand, the x-gradient and y-gradient coils, and, on the other hand, the z-gradient coil, are the result of inherent hardware characteristics of the gradient coil and of its interaction with the magnet.
Note that although demonstrated at the high field strength of 9.4 T, the proposed technique would also be applicable at lower field strengths (such as 3 T), whenever residual eddy current induced B0 shifts would be large enough to not be ignored during multi-spoke RF pulse design. Likewise, the proposed technique aims at providing satisfactory excitation pattern by addressing eddy current induced B0 modulations during the RF excitation and therefore can be used for the excitation module (up to 90° flip angles) in any conventional sequence when such correction is necessary. Further investigations, however, will be needed to see how such phase errors could be overcome when large flip angles are used, such as in pTx RF refocusing pulses in diffusion weighted imaging where residual eddy current induced B0 shifts may also be present following the application of diffusion gradients.
Although the focus of the current study is not on comparing different pTX pulse design strategies, it can be noticed that using only two spokes with 16 Tx channels already provides fairly homogeneous excitation profile through a 2D slice in the human brain, outperforming static B1 shimming results (Fig. 4). Two-spoke pTX RF pulses can still be fairly short, with limited sensitivity to T 2 effects during RF excitation while preserving reasonably TE values, and therefore are expected to be suitable for a large array of imaging applications at 9.4T.
Conclusion
We have demonstrated the successful implementation of 16-channel 3D parallel transmission in the human brain at 9.4T, with a multi-step RF pulse design strategy involving fast real-time calibration, capable of correcting for large eddy current induced excitation phase errors in addition to compensating for susceptibility induced off-resonance effects.
Acknowledgments
The authors would like to acknowledge Lance DelaBarre for his help with setting up the 9.4 T multi-transmit system, Dinesh Deelchand and Pierre-Gilles Henry for their assistance with 3D AFI sequence development, and Sebastian Schmitter, Julien Sein and Federico De Martino for their help with preparation of in-vivo experiments.
Funding Statement
This work was supported by the W.M. Keck Foundation, NIH NIBIB P41 EB015894 (previously NIH NCRR P41 RR008079), and NIH R01 EB006835, R01 EB007327, S10 RR25437, R21 EB009133. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Katscher U, Bornert P, Leussler C, van den Brink JS (2003) Transmit SENSE. Magn Reson Med 49: 144–150. [DOI] [PubMed] [Google Scholar]
- 2. Zhu Y (2004) Parallel excitation with an array of transmit coils. Magnetic Resonance in Medicine 51: 775–784. [DOI] [PubMed] [Google Scholar]
- 3. Ullmann P, Junge S, Wick M, Seifert F, Ruhm W, et al. (2005) Experimental analysis of parallel excitation using dedicated coil setups and simultaneous RF transmission on multiple channels. Magn Reson Med 54: 994–1001. [DOI] [PubMed] [Google Scholar]
- 4. Grissom W, Yip CY, Zhang Z, Stenger VA, Fessler JA, et al. (2006) Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magnetic Resonance in Medicine 56: 620–629. [DOI] [PubMed] [Google Scholar]
- 5. Zhang Z, Yip CY, Grissom W, Noll DC, Boada FE, et al. (2007) Reduction of transmitter B1 inhomogeneity with transmit SENSE slice-select pulses. Magn Reson Med 57: 842–847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Setsompop K, Alagappan V, Gagoski B, Witzel T, Polimeni J, et al. (2008) Slice-selective RF pulses for in vivo B1+ inhomogeneity mitigation at 7 tesla using parallel RF excitation with a 16-element coil. Magn Reson Med 60: 1422–1432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Cloos MA, Boulant N, Luong M, Ferrand G, Giacomini E, et al. (2012) kT -points: short three-dimensional tailored RF pulses for flip-angle homogenization over an extended volume. Magn Reson Med 67: 72–80. [DOI] [PubMed] [Google Scholar]
- 8. Setsompop K, Wald LL, Alagappan V, Gagoski B, Hebrank F, et al. (2006) Parallel RF transmission with eight channels at 3 Tesla. Magn Reson Med 56: 1163–1171. [DOI] [PubMed] [Google Scholar]
- 9. Sbrizzi A, Hoogduin H, Lagendijk JJ, Luijten P, Sleijpen GL, et al. (2012) Fast design of local N-gram-specific absorption rate-optimized radiofrequency pulses for parallel transmit systems. Magn Reson Med 67: 824–834. [DOI] [PubMed] [Google Scholar]
- 10. Wu X, Vaughan JT, Ugurbil K, Van de Moortele PF (2010) Parallel excitation in the human brain at 9.4 T counteracting k-space errors with RF pulse design. Magn Reson Med 63: 524–529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Schneider JT, Haas M, Ruhm W, Hennig J, Ullmann P (2011) Robust spatially selective excitation using radiofrequency pulses adapted to the effective spatially encoding magnetic fields. Magnetic resonance in medicine 65: 409–421. [DOI] [PubMed] [Google Scholar]
- 12.Wu X, Vaughan JT, Ugurbil K, van De Moortele PF (2010). 16-Channel Parallel Transmission in the Human Brain at 9.4 Tesla: Initial Results. In: Proc Intl Soc Mag Reson Med 18; Stockholm, Sweden. pp. 107.
- 13.Wu X, Adriany G, Ugurbil K, van De Moortele PF (2011). Parallel Transmission in Human Brain at 9.4T Counteracting Eddy Current Induced Excitation Errors in RF Pulse Design.In: Proc Intl Soc Mag Reson Med 19; Montreal, Quebec, Canada. pp. 4441.
- 14. Wysong RE, Lowe IJ (1993) A simple method of measuring gradient induced eddy currents to set compensation networks. Magn Reson Med 29: 119–121. [DOI] [PubMed] [Google Scholar]
- 15. Deelchand DK, Van de Moortele PF, Adriany G, Iltis I, Andersen P, et al. (2010) In vivo 1H NMR spectroscopy of the human brain at 9.4 T: initial results. J Magn Reson 206: 74–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Wu X, Akgun C, Vaughan JT, Andersen P, Strupp J, et al. (2010) Adapted RF pulse design for SAR reduction in parallel excitation with experimental verification at 9.4 T. J Magn Reson. 205: 161–170. [PMC free article] [PubMed] [Google Scholar]
- 17.Adriany G, Deelchand D, Henry PG, Tian J, Vaughan JT, et al.. (2009) A 16 channel T/R Open-Faced Head Array for Humans at 9.4T. In: Proc Intl Soc Mag Reson Med 17; Honolulu, Hawaii, USA. pp. 3005.
- 18. Papadakis NG, Martin KM, Pickard JD, Hall LD, Carpenter TA, et al. (2000) Gradient preemphasis calibration in diffusion-weighted echo-planar imaging. Magn Reson Med 44: 616–624. [DOI] [PubMed] [Google Scholar]
- 19.Van de Moortele PF, Snyder C, DelaBarre L, Adriany G, Vaughan JT, et al.. (2007) Calibration Tools for RF Shim at Very High Field with Multiple Element RF Coils: from Ultra Fast Local Relative Phase to Absolute Magnitude B1+ Mapping. In: Proc Intl Soc Mag Reson Med 15; Berlin, Germany. pp. 1676.
- 20. Yarnykh VL (2007) Actual flip-angle imaging in the pulsed steady state: a method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magnetic Resonance in Medicine 57: 192–200. [DOI] [PubMed] [Google Scholar]
- 21. Setsompop K, Wald LL, Alagappan V, Gagoski BA, Adalsteinsson E (2008) Magnitude least squares optimization for parallel radio frequency excitation design demonstrated at 7 Tesla with eight channels. Magn Reson Med 59: 908–915. [DOI] [PMC free article] [PubMed] [Google Scholar]