Abstract
We report here new computational tools and strategies to efficiently generate three-dimensional models for oligomeric biomolecular complexes in cases where there is limited experimental restraint data to guide the docking calculations. Our computational tools are designed to rapidly and exhaustively enumerate all geometrically possible docking poses for an oligomeric complex, rather than generate detailed, atomic-resolution models. Experimental data, such as inter-atomic distance measurements, are then used to select and refine docking poses that are consistent with the experimental restraints. Our computational toolkit is designed for use with sparse datasets to generate intermediate-resolution docking models, and utilizes distance difference matrix analysis to identify further restraint measurements that will provide maximum additional structural refinement. Thus, these tools can be used to help plan optimal residue positions for probe incorporation in labor-intensive biophysical experiments such as chemical crosslinking, EPR, or FRET spectroscopy studies. We present benchmark results for docking the collection of all 176 heterodimer protein complexes from the ZDOCK database, as well as a protein homodimer with recently collected experimental distance restraints, to illustrate the toolkit’s capabilities and performance, and to demonstrate how distance difference matrix analysis can automatically identify and prioritize additional restraint measurements that allow us to rapidly optimize docking poses.
Introduction
Oligomeric complex formation by proteins and other biomolecules is crucial for many biological processes, including signal transduction, gene transcription, enzyme activation, etc., and detailed structural information for these oligomeric assemblies is highly desirable. X-ray crystallography and multi-dimensional NMR spectroscopy are primary tools used to obtain high-resolution structures. However, oligomeric complexes may often form only relatively weak and/or transient interactions, which can make it difficult to obtain diffraction-quality crystals. These complexes are also generally quite large, a challenge for standard multi-dimensional NMR structural methods.
There are a variety of other experimental techniques that can be used to obtain structural information for large biomolecular complexes that do not suffer from challenges posed by system size or crystallization difficulties, such as EPR double electron-electron resonance (DEER) spectroscopy, fluorescence resonance energy transfer (FRET) spectroscopy, many solid-state NMR techniques, and various chemical crosslinking methods, to name a few. However, the datasets obtained with these methods are usually quite “sparse”, when compared to x-ray or solution-phase NMR datasets, i.e., the dataset is normally a relatively small number of interatomic distances that may provide only one geometric restraint per 5–10 residues, so that structures are often severely underdetermined. As a result, it can be quite challenging to use conventional structure refinement methods (1–3) to generate physically plausible three-dimensional structural models, since these methods typically perform quite poorly with severely underdetermined datasets (4).
Therefore, we need an alternate computational strategy to generate 3D models for dimeric/oligomeric complexes based on sparse distance datasets. There are a variety of software tools available for protein-protein docking applications (5–27), some with the ability to utilize distance restraints to restrict the solution search. However, these tools generally have as a primary objective the prediction of an atomic-resolution docking model, and emphasize chemical and physical details of the docking interface during the model generation. For reasons discussed below, we have chosen to develop a new docking toolkit that emphasizes sampling speed (ability to rapidly explore large numbers of diverse docking poses) and reliance on experimental data at the expense of more sophisticated scoring criteria utilized in many existing docking programs. We report here the development of a suite of tools and strategies to use sparse distance datasets, such as those obtained in EPR DEER or FRET experiments, to rapidly generate plausible 3D structures for oligomeric protein complexes. One important feature of our toolkit is a data assessment feedback option that can be used to plan the most effective additional experiments. This assessment is based on the variability of inter-residue distances observed in the ensemble of models constructed using the current dataset, and aids identification of one or more additional inter-residue distance measurements that would reduce solution degeneracy most dramatically, i.e., eliminate the maximum number of unique 3D model candidates from the previous model generation step. The toolkit is designed for tight integration with experimental measurements, in an iterative process of measurement and subsequent 3D model generation, rather than as a “post-processing” tool to refine atomic-resolution structures after data collection is completed. Therefore, we have emphasized ease of use and computational efficiency in development of this toolkit, and optimized the methods for effective performance with sparse datasets. We present here details of our toolkit, including novel algorithms we have developed, as well as integration of existing computational techniques into our model generation protocol. We present results from test calculations for a large dataset of structurally well-characterized heterodimeric protein complexes to illustrate the toolkit capabilities and performance. We also present docking results for a protein homodimer complex, using distance restraint data collected recently with EPR DEER measurements, and compare our toolkit performance for this homodimer complex with two state-of-the-art protein docking programs, HADDOCK (20) and RosettaDock (27). Finally, we discuss briefly how TagDock can be used to generate models for trimers and higher-order oligomeric assemblies.
Methods
Docking Algorithim Overview
TagDock is a toolkit, comprised of a collection of programs and scripts, that produces structures for macromolecular complexes by generating randomly posed docked pairs (decoys) starting from rigid structures for each monomer, and scores each decoy with a penalty function that determines its agreement with a set of experimentally derived inter-monomer distance restraints. In order to maximize the number of unique docking poses, we do not utilize the distance restraints directly in the initial pose generation process. Instead, we perform a completely unrestrained and uniform sampling of pose space, subsequently examining regions of this space that yield good agreement with the restraints. TagDock is written in NAB, a C-like “molecular manipulation” programming language, which is provided in the AmberTools program suite (28). The TagDock algorithm is quite efficient, and can generate more than 25,000 poses per minute on a single CPU core in a typical Linux desktop workstation.
The TagDock algorithm has two phases. In phase 1, the second molecule in a dimer pair is repeatedly, and randomly, rotated and translated onto the surface of a large virtual sphere that is centered on the first molecule. The molecules are then brought into physical contact without changing their relative orientation. Between 1×104 and 1×106 such candidate structures are typically generated, and ~1×102 decoys that best satisfy the experimental restraints are automatically selected for a second, higher resolution docking phase. During phase 2, the second molecule in each selected decoy is subjected to progressively smaller rotations and translation changes, creating a finer resolution search via a Monte Carlo focusing algorithm that minimizes the restraint penalty. The final docking candidates are sorted automatically, with the model complex that best satisfies the experimental distance restraints ranked first.
Phase 1: Low-resolution docking details
In Phase 1, TagDock initially places molecule 1 and molecule 2 in a “reference pose” at the origin, where molecule 1 (M1) remains fixed. Each decoy is created using a standard randomized 4×4 rotation/translation matrix; molecule 2 (M2) coordinates are multiplied by this random matrix to generate new M2 coordinates, distal from M1. The distance from M1 to M2 geometric centers is constant for all the decoys, and creates a virtual sampling sphere of sufficient radius to ensure that no interatomic overlaps exist between the two monomers at the outset.
Next, the shortest inter-monomer C-beta distance is calculated, and M2 is translated toward the origin (where M1 is centered) by this distance so that M1-M2 are now in contact, but with no regard for physically unreasonable monomer overlaps. A transformation matrix representing this complex structure is stored, along with its restraint penalty score, and this process is repeated to generate ~1×106 decoy poses.
Scoring
A penalty score, based on agreement with experimental distance restraints, is computed for each decoy during each phase of the docking algorithm. Given N experimental restraints, the score is simply the sum of the individual distance restraint violations:
with individual restraint violations vi computed as
where riexp is an experimental distance, ridecoy is the corresponding distance for the decoy being scored, and σi is the experimental error and/or distribution inherent to riexp.
Phase 2: High-resolution docking
TagDock ranks the low-resolution decoys from lowest to highest penalty score. In Phase 2 of the algorithm, TagDock selects a user-defined subset (default 200) of the best (lowest) scoring decoys from Phase 1 and performs more focused high-resolution docking, via a user-tunable, multi-stage Monte Carlo optimization algorithm (29). For each selected decoy, the focusing algorithm aggressively samples nearby poses via cycles of random moves constrained by narrowing intervals of translation and rotation. Each decoy is replaced as lower scoring poses are encountered. This process is accelerated by early exit of the sampling cycles, when progress is deemed insufficient. As a default, the initial focusing cycle samples 100,000 moves, with a random translation from the range [0.0 – 3.0] Å along each axis and random rotation from the range [0.0 – 15.0] degrees about each axis. This initial sampling cycle exits early if the score fails to improve by 0.5 in any of 20,000 consecutive steps. A second, higher resolution sampling cycle of 50,000 steps explores random translations from 0.0 – 1.5Å and random rotations from 0.0 – 5.0 degrees, exiting early if score improvements of 0.1 are not observed in 10,000 steps. In the final, highest resolution cycle, 10,000 steps with a 1.0Å maximum random translation and 1.0 degree maximum random rotation are sampled, exiting early if no score improvements are seen in 2,000 steps. The user can customize the Phase 2 focusing algorithm by specifying the total number of focusing cycles, the total number of steps and intervals of translation and rotation sampled in each cycle, and the early termination thresholds. After the top-ranked decoys have been focused, TagDock re-ranks them, outputs a final score report, and writes sequentially numbered PDB files for each decoy.
Distance difference matrix analysis
When sparse experimental datasets are used for filtering, TagDock may produce competing populations of models that all satisfy the distance restraints equally well. While it is clear that additional experimental restraints will reduce degeneracy in these populations, it is not immediately clear which additional restraint measurements are likely to be most discriminating. We use distance difference matrix (DDM) analysis to suggest the additional distance measurements that will enable maximal model discrimination.
Ensemble-averaged DDM analysis (30) is the inverse of distance geometry (31). Distance geometry uses a matrix of self-consistent inter-atomic distance bounds to compute the ensemble of Cartesian coordinate sets that is consistent with the bounds matrix. DDM analysis works in reverse, converting the Cartesian coordinates of an ensemble of structures into a set of distance “bounds”. These bounds are obtained by computing the difference of each inter-atomic distance over all unique pairs of structures in the ensemble. Averaging the pairwise distance differences reveals quantitatively the intrinsic variability of each distance over the ensemble. A distance that is essentially invariant over the full ensemble of structures will yield an ensemble-averaged distance difference of approximately zero. Distances that exhibit larger variation over the full ensemble of structures correspond to regions of increasing structural variability. This analysis thus identifies and quantifies specific regions that have the most structural variability across the ensemble. It is important to emphasize that DDM analysis does not rely on structural superposition, which is required for standard RMSD analysis. Superposition is an inherently biased, global procedure that has a tendency to hide localized structural differences. In particular, the specific atoms that are selected to drive the superposition process can significantly influence conclusions if one attempts to quantify localized structural fluctuations with an RMSD calculation. Performing the structural comparison in distance space rather than Cartesian space removes this bias entirely.
For each model in the TagDock-generated ensemble, our distance difference matrix (DDM) analysis tool first computes a rectangular matrix containing all intermolecular inter-residue distances. Then, the tool calculates the variability (distance differences) for each matrix element, across the entire set of matrices. This yields the ensemble-averaged distance difference for each inter-residue distance, considered across all models. The largest distance difference elements indicate those inter-residue distances that vary most dramatically between candidate docking poses; thus, additional experiments to measure these specific inter-residues distances will provide maximal discrimination between the candidate docking poses, eliminating many poses from further consideration. As final output, our tool lists all residue pairs, ordered by decreasing ensemble-averaged distance differences. A complete ensemble of structures – one that samples all poses compatible with the existing sparse dataset - is guaranteed to contain the information required to prioritize the most strategic placements of the next label, at least from a purely geometric standpoint. The exhaustive Monte Carlo search algorithm employed by TagDock is specifically designed to rapidly produce such complete ensembles. DDM analysis for this ensemble then automatically, objectively, and unambiguously identifies the additional measurements that will resolve the largest sources of ambiguity, i.e., degeneracy, in the current candidate pose ensemble.
Test set restraint generation
We used all 176 protein heterodimer complex structures contained in the ZDOCK database (32) for our benchmarking calculations. To extract a small number of atom pair distances from each complex to serve as a proxy for a sparse experimental distance restraint set, we developed an automated, heuristics-based protocol to derive these distance restraints from the parent crystal structures, in order to avoid potential biases that might arise if we selected restraint distances manually. The protocol was implemented as a simple C++ program and scans the PDB file for all HELIX and SHEET records in each monomer, selecting the penultimate residue in each helix or sheet. From this set of candidate residue positions, the algorithm selects the set of three residues that define the largest triangle area in the protein monomer, i.e., the three residues that collectively have the greatest spatial separation from each other. In a few ZDOCK entries (E.g., 4CPA), one monomer of the complex has little or no helix or sheet secondary structural elements; in these cases, all but the first and last five residues in the polypeptide chain were considered. In many ZDOCK database entries, segments of polypeptide chain are missing for one or both monomer crystal structures relative to the heterodimer complex structure. We restricted residue position selection to only those residues resolved in both the isolated monomer structures as well as the complex, since our docking protocol uses the isolated monomer structures to initiate the docking search.
This protocol provides three “label” sites in each protein, producing nine possible inter-monomer distance restraints. Since many practical docking exercises will often begin with fewer than nine distance restraints, we arbitrarily removed one “label” site from one monomer of each complex, generating a six-restraint dataset to begin each docking calculation.
Results
Heterodimeric test structures
We performed docking calculations for all 176 entries in the ZDOCK protein-protein docking benchmarking database (32). For each entry in this database, there is an x-ray crystal structure of the protein complex and separate x-ray or NMR structures of each individual protein. We can divide the complex structures into two categories: rigid-body complexes where the monomer structures are essentially unchanged when the complex forms (the RMSD100 of the free versus docked partners is < 3 Å; RMSD100 is a normalized RMSD calculation that eliminates the influence of variable sequence length on computed results (33) and docking examples where one or both proteins undergo significant conformational changes when the complex forms (the RMSD100 of the free versus docked partners is > 3 Å). We ran three sequential TagDock calculations for each ZDOCK complex. For the first TagDock calculation, we used the six-distance restraint sets generated by our heuristic method described above. Then, we performed DDM analysis for the docking poses generated in the first TagDock calculation to identify additional distance measurements that would most effectively reduce solution degeneracy, as discussed in the Methods section. Based on this DDM analysis, one additional “label” site was selected in the monomer containing two residue sites, yielding a nine-distance restraint set for each complex. TagDock calculations were repeated with the nine-distance restraint sets, and DDM analysis was used once again to process the docking pose solutions and select additional distance measurements for pose discrimination. A fourth “label” site was added for one monomer in this final iteration, producing a twelve-distance restraint set for each complex, and the TagDock calculations were repeated. Each separate TagDock calculation required 15 to 90 minutes and DDM analysis only requires a few seconds, so the entire ZDOCK database can be processed in ~5 days on a single-processor workstation.
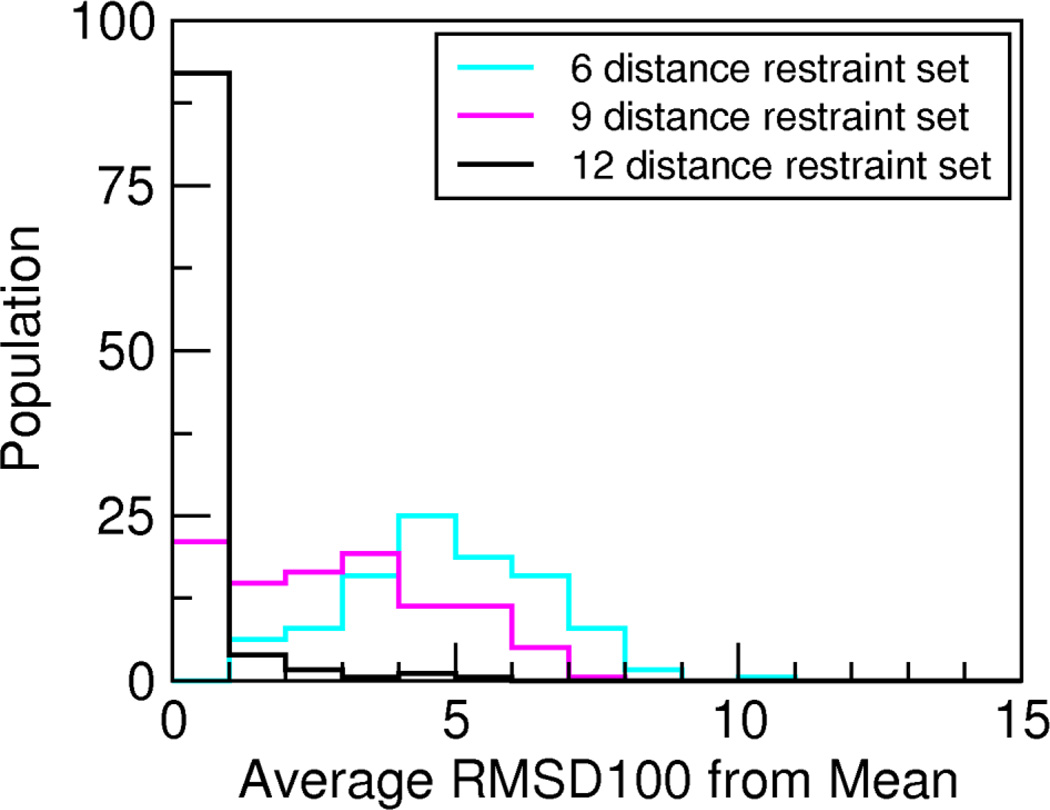
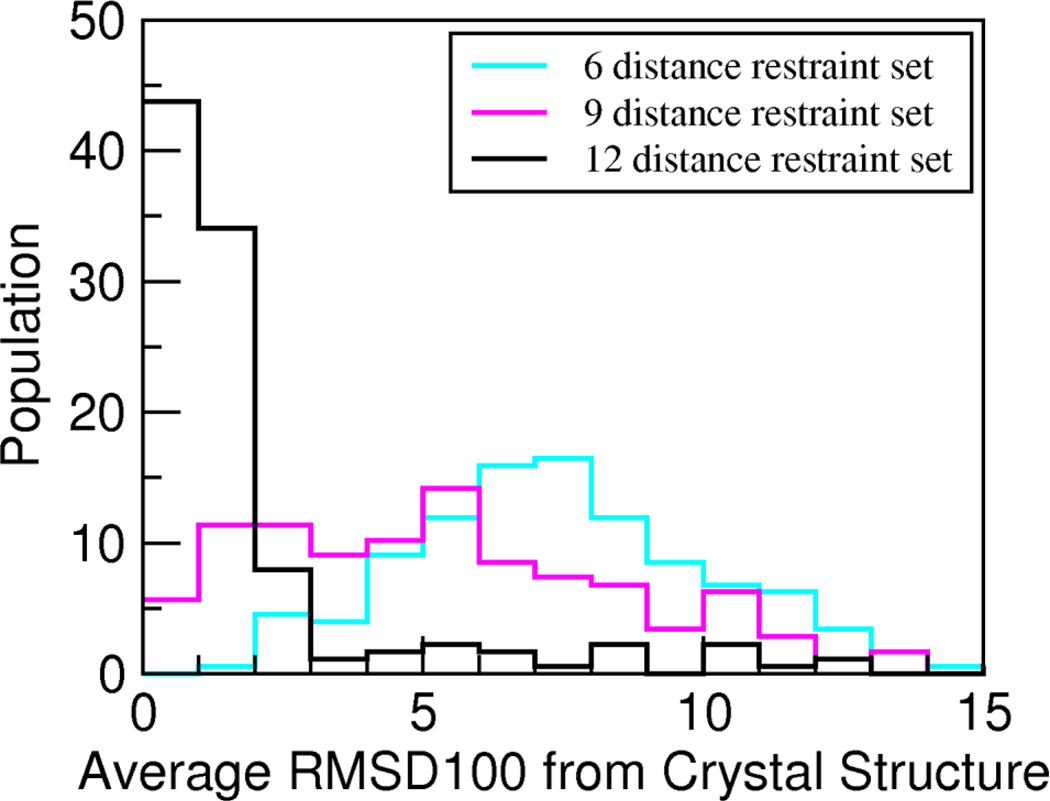
TagDock automatically filters the resulting docking poses using the penalty score described above in Methods. To retain only models that best fit the experimental data, we performed one additional statistical filter to select all structures whose penalty score was within one standard deviation of the lowest penalty score structure. For the ZDOCK database entries, we have the luxury of a crystal structure for each complex that allows us to document and quantify “convergence” of our calculations. In real applications for unknown structures, we need practical metrics to assess solution convergence. The convergence of the structural ensemble can be quantified by calculating the average RMSD to the mean structure for all accepted poses. Figure 1 shows these results for the six-, nine-, and twelve-distance restraint sets for all 176 ZDOCK structures, and the trend is quite clear. The accepted poses converge to more tightly defined docking pose clusters as the number of distance restraints increases from six to twelve. In most cases, the pose ensembles cluster closely around a mean structure, and also have small RMSD100 values relative to the reference x-ray complex structures, as shown in Figure 2. As can be seen in this figure, only two additional restraint distances suggested by DDM analysis yield a final TagDock pose <3Å RMSD from the crystal structure for 86% of the test cases (151/176 ZDOCK entries); in 44% of the test cases (77/176 ZDOCK entries) the TagDock solution has ~1Å RMSD relative to the reference crystal structure.
Figure 1. TagDock convergence facilitated by distance difference matrix analysis.
The histogram depicts the average RMSD100 relative to the mean structure for all 176 ZDOCK benchmark protein-protein complexes, demonstrating how often TagDock produced ensembles that converged to a cluster of closely-related models. For each complex, the mean structure was computed from all TagDock poses that scored within one standard deviation of the best-scoring pose. The average RMSD100 between this mean structure and each TagDock pose was then computed for each of the 176 TagDock ensembles and sorted into 1Å bins. The number of structures in each 1Å bin is displayed as a percentage of the total solution set.
Figure 2. Benchmark of TagDock accuracy guided by distance difference matrix analysis.
The histogram depicts the average RMSD100 relative to the complex crystal structure for all 176 ZDOCK benchmark protein-protein complexes, demonstrating how often TagDock produced ensembles that converged to the experimentally-determined structure. The average RMSD100 between the complex crystal structure and each TagDock pose was computed for each of the 176 test case ensembles and sorted into 1Å bins. The number of structures in each 1Å bin is displayed as a percentage of the total solution set.
For all cases in the true rigid body class, we successfully reproduce the crystal structure within 3Å RMSD using the crystal or NMR structures of the free partners. In only 14% (25/176) of cases do we not reproduce the crystal structure of the docked pair starting from the free monomers. In all of these cases the experimental structure for one or both of the isolated protein monomers deviates significantly (> 3Å RMSD) from the corresponding monomer structure in the heterodimer complex. Neither TagDock, nor any other rigid docking program, can handle cases like these easily, and a docking method that explicitly incorporates extensive backbone conformational sampling will be necessary to generate reasonable docking poses for these complexes.
Docking with Real Experimental Restraints
Our benchmark results with the ZDOCK dataset clearly show that TagDock can rapidly determine the correct docking pose for the vast majority of examples using only 6–12 inter-monomer distances for solution set filtering. However, real experimental data may not be so well-conditioned as our synthetic distance datasets for the ZDOCK database entries. We therefore used TagDock to generate poses for the CDB3 homodimer (PDB: 1HYN), using a set of 18 previously published DEER distance restraints shown in Table 1 (34). The CDB3 homodimer is not an ideal test case because there is no CDB3 monomer structure. However, the CDB3 homodimer is the only system for which we have access to both an atomic-resolution structure of the complex and a reliable, published set of experimentally determined, long-range intermolecular distance restraints. While our toolkit is not intended to compete with protein docking programs that incorporate chemical or knowledge-based scoring functions to generate atomic-resolution models, we felt it would be instructive nonetheless to compare TagDock's performance to two of the most widely-distributed and well-known protein docking packages, HADDOCK 2.1 (20) and RosettaDock (27) as distributed with Rosetta 3.5.
Table 1.
Eighteen DEER-measured inter-molecular distances for the CDB3 homodimer (34) stated in TagDock input restraint format. Each atom is listed as a chain identifier, residue number, and atom name. Experimentally derived distance distributions are listed in the final column. These restraint distances were also used for HADDOCK and Rosetta-Dock calculations.
| Atom 1 | Atom 2 | Distance (Å) | Distribution (Å) |
|---|---|---|---|
| P:84:CB | Q:84:CB | 27.20 | 2.50 |
| P:96:CB | Q:96:CB | 32.60 | 5.00 |
| P:105:CB | Q:105:CB | 15.40 | 3.70 |
| P:108:CB | Q:108:CB | 6.20 | 4.40 |
| P:112:CB | Q:112:CB | 18.00 | 6.90 |
| P:116:CB | Q:116:CB | 17.40 | 3.10 |
| P:142:CB | Q:142:CB | 32.10 | 3.10 |
| P:199:CB | Q:199:CB | 36.20 | 5.00 |
| P:208:CB | Q:208:CB | 47.70 | 13.20 |
| P:277:CB | Q:277:CB | 29.80 | 3.40 |
| P:290:CB | Q:290:CB | 38.40 | 0.50 |
| P:339:CB | Q:339:CB | 14.70 | 0.40 |
| P:340:CB | Q:340:CB | 34.60 | 0.80 |
| P:341:CB | Q:341:CB | 31.90 | 3.60 |
| P:342:CB | Q:342:CB | 24.90 | 1.10 |
| P:343:CB | Q:343:CB | 34.00 | 2.30 |
| P:344:CB | Q:344:CB | 37.00 | 4.20 |
| P:345:CB | Q:345:CB | 35.50 | 6.60 |
The individual monomer chains in the CDB3 homodimer crystal structure display similar, but unique, 3D conformations designated as chains P and Q. Any docking calculation initiated with the unique P and Q conformations is clearly biased and would not provide a critical assessment of our toolkit capabilities. Therefore, we performed a 10ns molecular dynamics simulation for each monomer using a Generalized Born continuum solvation model in AMBER (28). The P and Q monomer backbone conformations were restrained at the crystallographic positions, but side chains were unrestrained. The final snapshots from these two simulations were used as the input monomer structures for all of the docking results reported below.
The general protocols we used to dock the CDB3 dimer with TagDock, HADDOCK, and RosettaDock were similar to one another, so that the results can be compared directly. Individual program defaults or previously recommended/published options were used for all calculations. The restraints were implemented as Cβ-Cβ distances, with error bars equal to the experimentally determined distance distributions (Table 1). We generated 10,000 decoys with each program utilizing the experimental restraints, and selected the 200 docking poses that best satisfied the restraints for analysis. We discarded all poses with a restraint penalty greater than one standard deviation above the mean penalty value. This statistical filter is less restrictive than the one we used in the ZDOCK benchmark results described above. This less restrictive filter was necessary in order to retain the best (closest to experiment) models produced by HADDOCK and RosettaDock. This filter cutoff change did not impact TagDock results, as both filters produced the same selection of TagDock decoys. The restraint penalty scores from each program were normalized to the range [0–1], and plotted versus the Cα RMSD to the 1HYN crystal structure. Results for all three docking programs are shown in Figure 3.
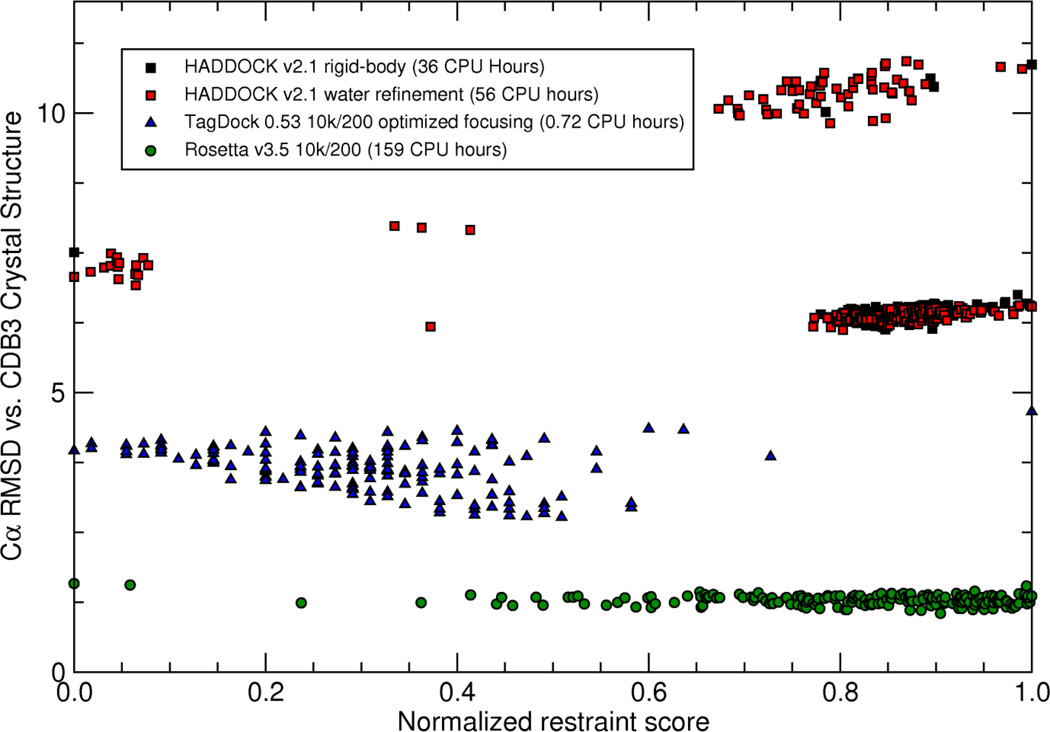
Figure 3. CDB3 Homodimer Docking from 18 experimentally measured (DEER) distance restraints using HADDOCK 2.1, RosettaDock 3.5, and TagDock.
10,000 decoys were computed with each program, and the 200 models that best satisfy the experimental restraints were selected for analysis. RosettaDock (green circles) produces atomic-resolution structures with this restraint set, with the best model just 1.1Å Cα RMSD from chains P and Q of the 1HYN crystal structure. TagDock (blue triangles) produces intermediate-resolution structures with Cα RMSD as small as 2.8Å from the crystal structure. HADDOCK (red and black squares) had trouble assembling the interdigitating dimer arms of CDB3 (best Cα RMSD of 6.1Å). We suspect this is due to a more limited search of pose space during its rigid-body phase (black squares), which we observed to produce a large number of degenerate structures. For example, the best-scoring rigid-body HADDOCK pose depicted at the far left of the graph was replicated 16 times in the 10,000 output poses. These degenerate structures resolved into unique structures only after the high-resolution refinement stage (red squares).
RosettaDock produced the closest pose to the target crystal structure, but was also the most computationally expensive option (159 CPU hours on a standard Linux workstation with an Intel W3570 CPU). The RosettaDock decoys that best satisfy the experimental restraints have 1.05–1.58Å Cα RMSD from the crystal structure. TagDock produced decoys between 2.77 and 4.66Å Cα RMSD from the crystal structure (Figure 4) but required only 43 CPU minutes. The CDB3 homodimer presented a special challenge for HADDOCK, and the best-scoring poses have 6.12 –10.93Å Cα RMSD from the crystal structure. We suspect this is due to the nature of the interlocking dimer “arms” in the CDB3 structure (residues ~316–348). To find the correct pose, the docking algorithm must be able to interdigitate the monomer structures by moving them in a specific direction. This requires a significant amount of sampling during the rigid-body stage of the calculation. Close inspection of the HADDOCK output from the rigid-body phase (Figure 3 – filled black squares) reveals a significant amount of degeneracy in the structures, suggesting that although the algorithm output 10,000 structure files, it did not adequately sample all regions of pose space prior to switching to high-resolution mode. For example, the HADDOCK rigid-body result displayed as the black square in Figure 3 with Score=0, RMSD = 7.5 Å is actually 16 degenerate structures that become differentiated from each other only after HADDOCK refines them further (see the adjacent filled red circles in the refined dataset). The HADDOCK algorithms required 56 CPU hours, with 36 hours of that attributed to the rigid-body phase.
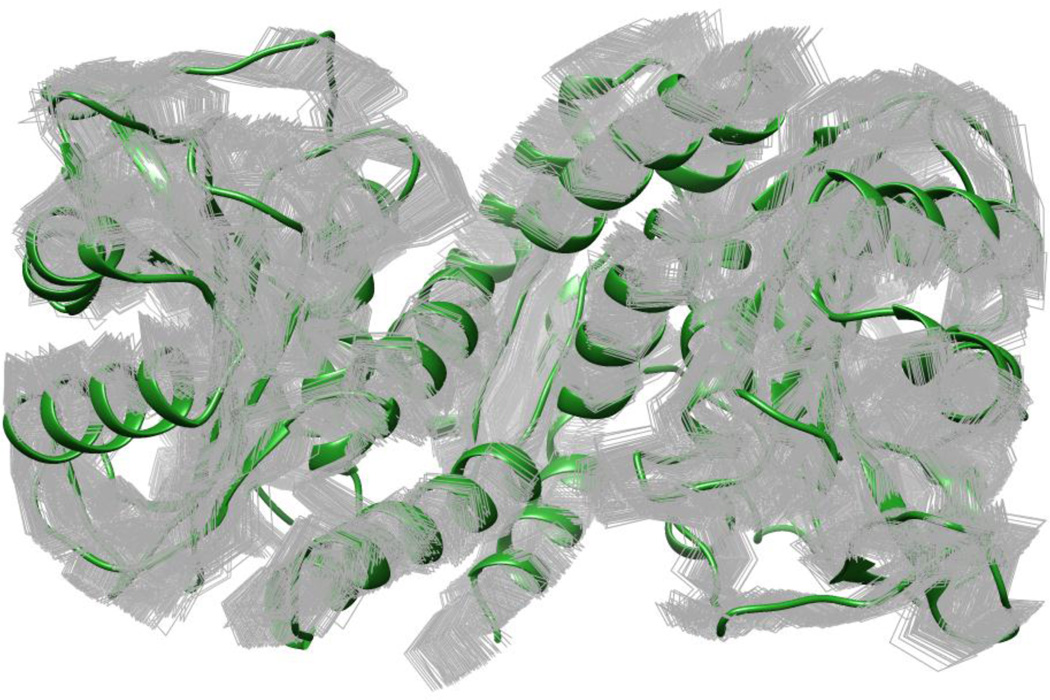
Figure 4. Top-scoring cluster of CDB3 structures produced by TagDock using the published set of 18 EPR DEER distance restraints (33) superimposed onto the P and Q chains of the 1HYN PDB entry for CDB3.
The 153 TagDock decoys are rendered as gray wireframe Ca traces, while the 1HYN PDB structure is rendered as a green ribbon. The Ca RMSDs of these 153 structures to the crystal structure range between 2.77Å and 4.66Å.
Discussion
Previous studies have shown that conventional structure refinement methods cannot be used routinely to generate sensible three-dimensional models when only limited structural restraint data is available. Unfortunately, it is often the case that only limited structural information is available for large, oligomeric biomolecular complexes. To address this situation, we present here a computational strategy and protocols to rapidly generate moderate-resolution 3D models for oligomeric protein complexes, using sparse intermolecular distance datasets to identify the most reasonable solution candidates. We have developed a rigid-body docking algorithm that can rapidly generate all geometrically feasible docking orientations for a complex, using an exhaustive Monte Carlo search strategy. Our method does not utilize the restraint data to explicitly guide the initial docking process, nor does it consider any chemical features or properties to bias results in favor of chemically sensible models, i.e., we sacrifice the information that these data might provide in docking calculations in favor of computational speed and an exhaustive geometric search that will produce a complete solution ensemble. As a result, many of the preliminary models generated will be chemically and/or structurally unreasonable. We then use the available restraint data to filter all docking decoys, excluding all models that do not satisfy available experimental data. This process can be iterated repeatedly, using solutions from the previous cycle as starting points in docking calculations that use progressively finer resolution grids, our “focusing” procedure. As additional focusing iterations are employed, docking solutions generally converge on a small number of candidate decoys that best satisfy the experimental restraint data. TagDock generated optimal docking poses within 3Å RMSD of the crystal structure for 86% of the ZDOCK database entries, and for most of the rigid-body class entries, the optimal TagDock solution was within 1Å RMSD of the reference crystal structure. These final candidate structures could be further “refined” with energy minimization and limited molecular dynamics simulation, or used as high quality starting structures for atomic-resolution docking programs like HADDOCK or RosettaDock.
Our results indicate that TagDock is able to produce intermediate-resolution docking results with minimal computational resources when compared to programs designed for atomic-resolution protein docking applications. RosettaDock did provide an atomic-resolution solution for CDB3 homodimer, due primarily to the refinement process driven by its sophisticated scoring function. We should note that the CDB3 homodimer crystal structure was part of the training set used to derive the RosettaDock scoring function, which may influence its performance relative to the HADDOCK results. TagDock does not use a traditional, parameterized scoring function to select the “best” docking poses. It only considers the experimental distance restraints, and thus produces the full ensemble of structures that best satisfy the experimental data. This ensemble can then be used as input for DDM analysis to objectively and unambiguously prioritize additional experiments. Most traditional docking algorithms utilize a parameterized scoring function that dutifully produces clusters of models that minimize the target function. However, this can be a problem in cases where the best-scoring poses deviate significantly from the correct structure, perhaps because the scoring function places excessive emphasis on certain terms. In these cases, the candidate docking poses provide little useful guidance to plan additional experimental measurements, and could possibly even misdirect the process.
We should emphasize that with real (i.e., imperfect) distance restraint data, the TagDock structure with the lowest penalty score may not be the structure closest to the correct structure. This is clearly seen in Figure 3, where the TagDock structures with the lowest RMSD to the crystal structure are actually in the middle of the observed penalty score range. This is due to a combination of imperfect restraint data and the simple nature of TagDock’s target function. As a result, one must consider all poses in the lowest-scoring cluster generated by TagDock. More sophisticated, atomic-resolution modeling methods could be used to distinguish candidates in the lowest-scoring cluster, if necessary.
Since we typically work with severely under-determined restraint data sets, we normally obtain degenerate solutions, i.e., multiple, distinct models that all satisfy the experimental constraints equally well. We then use distance difference matrix (DDM) analysis to rapidly identify, in a completely automated and unbiased way, additional distance measurements that will enable us to most effectively differentiate competing models. This data can be used to plan subsequent experiments, suggesting which new measurements are likely to provide the greatest “information content”. The test calculations presented above provide strong evidence that our protocols and strategy are effective. The docking calculations are optimized so that large numbers of unique docking decoys are generated rapidly, and the DDM analysis has allowed us to identify additional “measurements” that enable us to quickly and efficiently converge to an optimal solution.
While much effort has been invested to ensure ease of use and effective default parameters, our algorithm design and protocol workflow also allow for considerable user control and great flexibility in choice of restraint data used. We have focused primarily on intermolecular distance restraints in the examples presented here but the user is not restricted to literal experimental distance measurements. For example, it would be straightforward to extend the restraint input to include surface contact areas (which can be viewed as a set of distributed, short-range distances). Almost any sort of restraint data could be used in our filtering procedure, provided it can be represented as some type of quantitative geometrical information. We are currently developing extensions to our program that will allow us to utilize the rich information contained in EPR spectroscopic measurements for protein complexes, and many other specialized capabilities can be implemented in the future.
We emphasize that our toolkit is not intended to perform atomic-resolution molecular docking calculations. As discussed above, there are many software packages available to perform this task, and any of those programs would be more appropriate if the goal is generation of a specific, atomic-resolution model. As reported above, our toolkit can yield high-quality structures for true rigid-body docking complexes when there are sufficient distance restraints, so it can be used effectively as a “stand-alone” molecular docking program in these situations.
All the examples presented here focused on hetero- or homodimeric protein complexes, simply because these are the only practical benchmark examples we have presently, i.e, these are the only systems for which we have reference crystal structures for the complex, and independent experimental distance measurements (in the case of the CDB3 homodimer). However, the current version of TagDock can also be used to generate models for trimers or higher oligomeric assemblies via a simple iterative procedure: TagDock is first used to generate dimer poses for two monomers in the oligomer assembly, an additional monomer is then docked with the dimer candidate poses to generate a collection of trimer poses, etc. Future versions of TagDock will permit direct oligomer assembly with no need for this iterative process.
Our toolkit is designed to perform an efficient, exhaustive search of docking pose space for an oligomeric complex, with the primary goal being to help plan “optimal” experiments. Since we focus on systems that have limited available experimental data at the outset, it is clear that additional measurements will be needed to more completely and accurately characterize the complex. Given that many of these experiments will likely involve additional site-directed mutagenesis, chemical labeling, or other labor-intensive molecular modifications, it would be advantageous to have some idea which new experiments are most likely to yield additional, useful information. The primary purpose of our toolkit is to help maximize the “return on investment” for experimental studies, and we believe the test calculations presented here suggest that the toolkit will make this goal possible.
Supplementary Material
Acknowledgments
Funding Sources
This work was supported by National Institutes of Health grant P01 GM080513 (T.P.L.).
Abbreviations
- DDM
Distance Difference Matrix
- DEER
Double Electron-Electron Resonance
- EPR
Electron Paramagnetic Resonance
- FRET
Fluorescence Resonance Energy Transfer
- NMR
Nuclear Magnetic Resonance
- NOE
Nuclear Overhauser Effect
- RMSD
Root Mean Square Deviation
Footnotes
Supporting Information
The supporting information includes the following tables: complete data for all 176 ZDOCK database docking calculations and complete restraint sets for all 176 docking cases. This material is available free of charge via the Internet at http://pubs.acs.org.
The TagDock software, user’s manual and scripts necessary to run docking calculations are available from the authors upon request.
Works Cited
- 1.Güntert P, Mumenthaler C, Wüthrich K. Torsion angle dynamics for NMR structure calculation with the new program DYANA. Journal of Molecular Biology. 1997;273:283–298. doi: 10.1006/jmbi.1997.1284. [DOI] [PubMed] [Google Scholar]
- 2.Brünger a. T, Adams PD, Clore GM, DeLano WL, Gros P, Grosse-Kunstleve RW, Jiang JS, Kuszewski J, Nilges M, Pannu NS, Read RJ, Rice LM, Simonson T, Warren GL. Crystallography & NMR System: A new software suite for macromolecular structure determination. Acta Crystallographica Section D Biological Crystallography. 1998;54:905–921. doi: 10.1107/s0907444998003254. [DOI] [PubMed] [Google Scholar]
- 3.Pearlman DA, Case DA, Caldwell JW, Ross WS, Cheatham TE, DeBolt S, Ferguson D, Kollman P. AMBER, A package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structural and energetic properties of molecules. Computer Physics Communications. 1995;91:1–41. [Google Scholar]
- 4.Chen J, Won H-S, Im W, Dyson HJ, Brooks CL. Generation of native-like protein structures from limited NMR data, modern force fields and advanced conformational sampling. Journal of Biomolecular NMR. 2005;31:59–64. doi: 10.1007/s10858-004-6056-z. [DOI] [PubMed] [Google Scholar]
- 5.Katchalski-Katzir E, Shariv I, Eisenstein M, Friesem AA, Aflalo C, Vakser IA. Molecular surface recognition: Determination of geometric fit between proteins and their ligands by correlation techniques. Proceedings of the National Academy of Sciences of the United States of America. 1992;89:2195–2199. doi: 10.1073/pnas.89.6.2195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gabb HA, Jackson RM, Sternberg MJ. Modelling protein docking using shape complementarity, electrostatics and biochemical information. Journal of Molecular Biology. 1997;272:106–120. doi: 10.1006/jmbi.1997.1203. [DOI] [PubMed] [Google Scholar]
- 7.Aloy P, Moont G, Gabb HA, Querol E, Aviles FX, Sternberg MJ. Modelling repressor proteins docking to DNA. Proteins: Structure, Function, and Genetics. 1998;33:535–549. [PubMed] [Google Scholar]
- 8.Moont G, Gabb HA, Sternberg MJ. Use of pair potentials across protein interfaces in screening predicted docked complexes. Proteins: Structure, Function, and Genetics. 1999;35:364–373. [PubMed] [Google Scholar]
- 9.Dixon JS. Evaluation of the CASP2 docking section. Proteins: Structure, Function, and Genetics Suppl. 1997;1:198–204. doi: 10.1002/(sici)1097-0134(1997)1+<198::aid-prot26>3.3.co;2-d. [DOI] [PubMed] [Google Scholar]
- 10.Jackson RM, Gabb HA, Sternberg MJ. Rapid refinement of protein interfaces incorporating solvation: Application to the docking problem. Journal of Molecular Biology. 1998;276:265–285. doi: 10.1006/jmbi.1997.1519. [DOI] [PubMed] [Google Scholar]
- 11.Koehl P, Delarue M. Application of a self-consistent mean field theory to predict protein side- chains conformation and estimate their conformational entropy. Journal of Molecular Biology. 1994;239:249–275. doi: 10.1006/jmbi.1994.1366. [DOI] [PubMed] [Google Scholar]
- 12.Lesk VI, Sternberg MJE. 3D-Garden: A system for modelling protein-protein complexes based on conformational refinement of ensembles generated with the marching cubes algorithm. Bioinformatics. 2008;24:1137–1144. doi: 10.1093/bioinformatics/btn093. [DOI] [PubMed] [Google Scholar]
- 13.Ackermann F, Herrmann G, Posch S, Sagerer G. Estimation and filtering of potential protein- protein docking positions. Bioinformatics. 1998;14:196–205. doi: 10.1093/bioinformatics/14.2.196. [DOI] [PubMed] [Google Scholar]
- 14.Palma PN, Krippahl L, Wampler JE, Moura JJ. BiGGER: a new (soft) docking algorithm for predicting protein interactions. Proteins: Structure, Function, and Genetics. 2000;39:372–384. [PubMed] [Google Scholar]
- 15.Comeau SR, Gatchell DW, Vajda S, Camacho CJ. ClusPro: An automated docking and discrimination method for the prediction of protein complexes. Bioinformatics. 2003;20:45–50. doi: 10.1093/bioinformatics/btg371. [DOI] [PubMed] [Google Scholar]
- 16.Mandell JG, Roberts VA, Pique ME, Kotlovyi V, Mitchell JC, Nelson E, Tsigelny I, TenEyck LF. Protein docking using continuum electrostatics and geometric fit. Protein Engineering. 2001;14:105–113. doi: 10.1093/protein/14.2.105. [DOI] [PubMed] [Google Scholar]
- 17.TenEyck LF, Mandell J, Roberts VA, Pique ME. Surveying Molecular Interactions With DOT. Proceedings of the 1995 ACM/IEEE Supercomputing Conference. 1995 [Google Scholar]
- 18.Ausiello G, Cesareni G, Helmer-Citterich M. ESCHER: A new docking procedure applied to the reconstruction of protein tertiary structure. Proteins: Structure, Function, and Genetics. 1997;28:556–567. [PubMed] [Google Scholar]
- 19.Andrusier N, Nussinov R, Wolfson HJ. FireDock: Fast interaction refinement in molecular docking. Proteins: Structure, Function, and Bioinformatics. 2007;69:139–159. doi: 10.1002/prot.21495. [DOI] [PubMed] [Google Scholar]
- 20.Dominguez C, Boelens R, Bonvin AMJJ. HADDOCK: A protein-protein docking approach based on biochemical or biophysical information. Journal of the American Chemical Society. 2003;125:1731–1737. doi: 10.1021/ja026939x. [DOI] [PubMed] [Google Scholar]
- 21.Macindoe G, Mavridis L, Venkatraman V, Devignes M-D, Ritchie DW. HexServer: An FFT-based protein docking server powered by graphics processors. Nucleic Acids Research. 2010;38:W445–W449. doi: 10.1093/nar/gkq311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ghoorah AW, Devignes M-D, Smaïl-Tabbone M, Ritchie DW. Spatial clustering of protein binding sites for template based protein docking. Bioinformatics. 2011;27:2820–2827. doi: 10.1093/bioinformatics/btr493. [DOI] [PubMed] [Google Scholar]
- 23.Alexander N, Bortolus M, Al-Mestarihi A, Mchaourab H, Meiler J. De novo high-resolution protein structure determination from sparse spin-labeling EPR data. Structure. 2008;16:181–195. doi: 10.1016/j.str.2007.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hirst SJ, Alexander N, McHaourab HS, Meiler J. RosettaEPR: an integrated tool for protein structure determination from sparse EPR data. Structure. 2011;173:506–514. doi: 10.1016/j.jsb.2010.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pierce BG, Hourai Y, Weng Z. Accelerating protein docking in ZDOCK using an advanced 3D convolution library. PloS One 6. e24657 doi: 10.1371/journal.pone.0024657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mintseris J, Pierce B, Wiehe K, Anderson R, Chen R, Weng Z. Integrating statistical pair potentials into protein complex prediction. Proteins: Structure, Function, and Bioinformatics. 2007;69:511–520. doi: 10.1002/prot.21502. [DOI] [PubMed] [Google Scholar]
- 27.Gray JJ, Moughon S, Wang C, Schueler-Furman O, Kuhlman B, Rohl Ca, Baker D. Protein-protein docking with simultaneous optimization of rigid-body displacement and side-chain conformations. Journal of Molecular Biology. 2003;331:281–299. doi: 10.1016/s0022-2836(03)00670-3. [DOI] [PubMed] [Google Scholar]
- 28.Case DA, Darden TA, Cheatham TE, III, Simmerling CL, Wang J, Duke RE, Luo R, Walker RC, Zhang W, Merz KM, Roberts B, Hayik S, Roitberg A, Seabra G, Swails J, Götz AW, Kolossváry I, Wong KF, Paesani F, Vanicek J, Wolf RM, Liu J, Wu X, Brozell SR, Steinbrecher T, Gohlke H, Cai Q, Ye X, Hsieh M-J, Cui G, Roe DR, Mathews DH, Seetin MG, Salomon-Ferrer R, Sagui C, Babin V, Luchko T, Gusarov S, Kovalenko A, Kollman PA. AMBER 12. San Francisco: University of California; 2012. [Google Scholar]
- 29.Dickman BH, Gilman MJ. Monte Carlo optimization. Journal of Optimization Theory and Applications. 1989;60:149–157. [Google Scholar]
- 30.Akke M, Forsén S, Chazin WJ. Solution structure of (Cd2+)1-calbindin D9k reveals details of the stepwise structural changes along the Apo-->(Ca2+)II1-->(Ca2+)I,II2 binding pathway. Journal of Molecular Biology. 1995;252:102–121. doi: 10.1006/jmbi.1995.0478. [DOI] [PubMed] [Google Scholar]
- 31.Havel TF, Kuntz ID, Crippen GM. The theory and practice of distance geometry. Bulletin of Mathematical Biology. 1983;45:665–720. [Google Scholar]
- 32.Hwang H, Vreven T, Janin J, Weng Z. Protein-protein docking benchmark version 4.0. Proteins. 2010;78:3111–3114. doi: 10.1002/prot.22830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Carugo O, Pongor S. A normalized root-mean-square distance for comparing protein three- dimensional structures. Protein Sci. 2001;10:1470–1473. doi: 10.1110/ps.690101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhou Z, DeSensi SC, Stein Ra, Brandon S, Dixit M, McArdle EJ, Warren EM, Kroh HK, Song L, Cobb CE, Hustedt EJ, Beth AH. Solution structure of the cytoplasmic domain of erythrocyte membrane band 3 determined by site-directed spin labeling. Biochemistry. 2005;44:15115–15128. doi: 10.1021/bi050931t. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.