Abstract
A microfluidic device was utilized to measure the viscosity gradients formed in carbohydrate solutions of biological significance during desiccation and skin formation. A complementary numerical model employed the free volume theory to predict the concentration-dependent diffusion coefficients and viscosity gradients in concentrated solutions. It was established that the glassy skin formation at the gas-liquid interface played a key role in water entrapment and the formation and persistence of very steep concentration and viscosity gradients in the desiccating solutions. The results of this study highlighted an important phenomenon that should be accounted for during isothermal drying of glass-forming solutions: solutions with high glass transition temperatures, inevitably, dry heterogeneously. In the final product, there are significant spatial variations in water and solute content affecting the storage stability.
I. INTRODUCTION
Certain carbohydrates protect organisms against drought and freeze-thaw damage. Upon exposure to environmental extremes Escherichia Coli,1 yeast,2 and nematodes3 synthesize the disaccharide trehalose and transition into a state of “suspended animation” (anhydrobiosis), a response which was shown to be crucial for their survival.4 The mechanism of action of trehalose has been attributed to its bonding affinity to cellular proteins and lipids in the absence of liquid water, therefore stabilizing their native structures (the water replacement hypothesis5). A complementary hypothesis proposed to explain the mechanism of suspended animation is based on the glass-forming capacity of trehalose. A glass is a metastable liquid with very high viscosity (1013 Pa s), in which low frequency relaxational motions (such as translational diffusion) of large molecules practically stop (in the experimental time scales considered). It has been shown in certain plant seeds6 that the cytoplasmic glasses are formed by rapid cooling and/or desiccation and the diffusion-limited biochemical reactions can be slowed down.
Extensive research efforts were channeled to utilize certain carbohydrates (trehalose, sucrose, mannitol, raffinose, dextran, etc.) and polymers (such as polyvinyl pyrrolidone) in the biopreservation solution formulations to stabilize and store mammalian cells in a frozen (cryopreserved), freeze-dried (lyophilized), or desiccated (anhydrobiotic) state. For many mammalian cells the effectiveness of the carbohydrate-based biopreservation solutions were established in cryo-preservation (for a recent, detailed review, see Fuller et al.7). However, a similar level of success cannot yet be claimed for lyophilization or desiccated state preservation.
In nature, drought, and freezing progress slowly, either by a slow decrease in the environmental temperature or by gradual dehydration. Sensing environmental change, the anhydrobiotic organisms trigger carbohydrate synthesis and slowly transition into suspended animation.8 In the laboratory experiments performed for the desiccated state preservation of biological materials on the other hand, usually fast desiccation protocols are applied in order to minimize osmotic damage.9 However, drying kinetics of concentrated solutions is inherently different during slow and fast desiccation. During slow drying, the limiting factor is the diffusion of water in the surrounding air. On the contrary, during fast drying, the drying kinetics is limited by the diffusion of water in the solution. With increasing solute concentration, the diffusion coefficient of water in the solution decreases and steep concentration gradients are formed in the drying solution; sometimes to such an extent that a thin glassy layer is formed at the liquid-gas interface10 even though, on the average, the solution has high water content.
Additional complications arise due to the interactions of the drying carbohydrate solution with the surrounding solid surfaces. For example, the presence of a solid surface causes secondary flows11 and structural instability in a drying droplet causing compartmentalization in the dried product.10,12 This complicates the experimental determination of the desiccation and vitrification kinetics of glass-forming carbohydrate solutions. It also makes it impossible to determine the exact history and the microenvironmental conditions around the biological material suspended in the biopreservation solution.
In order to circumvent these complications, a microfluidic device designed to enable controlled desiccation and one-dimensional modeling of the concentration and viscosity gradients formed in desiccating aqueous carbohydrate and glycerol solutions was developed. A molecular rotor, whose fluorescence emission intensity was correlated to local viscosity enabled verification of the model predictions.
II. MATERIALS AND METHODS
The experiments involved controlled desiccation of aqueous glycerol, fructose, sucrose, and trehalose solutions in microchannels. The initial concentration of the chemicals in the solution was 30% w/w. High purity trehalose dihydrate was purchased from Pfanstiehl (Ferro Pfanstiehl Laboratories Inc., Waukegan, IL). Other chemicals were purchased from Sigma (Sigma-Aldrich Corp., St. Louis, MO). Prior to the preparation of the solutions, all of the powder chemicals were kept in an 85 °C atmospheric oven for 24 h to remove residual water. The solutions were prepared on a microbalance using ultrapure water. For the real-time viscosity measurement in desiccating solutions, a molecular rotor [9-(2-carboxy-2-cyanovinyl)julolidine (CCVJ) Helix Research Inc., Springfield, OR] at a concentration of 40 nM was added to all of the experimental solutions. CCVJ, when excited at 440 nm, has two mechanisms of relaxing back to its ground state: (a) by mechanical rotation of its sidegroup, or (b) by photon emission at 475 nm. Increased local viscosity hinders the preferred mechanical relaxation mode and therefore, the intensity of fluorescence emission at 475 nm increases with increasing local viscosity. The size of the CCVJ molecule (268 Da) is comparable to that of trehalose and sucrose and larger than fructose and glycerol molecules.
A. The microfluidic device
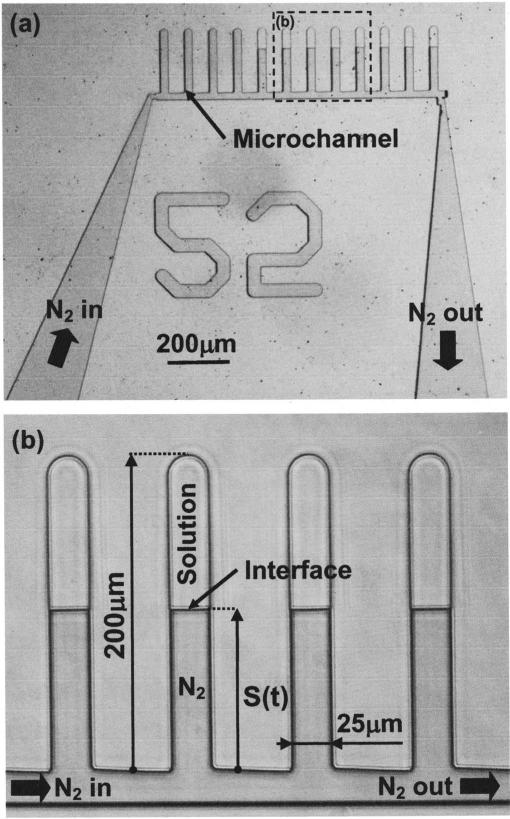
The polydimethylsiloxane (PDMS)(Sylgard 184, Dow Corning, Corning, NY) microchannels had rectangular cross-sectional areas, measuring 25×25 μm2 in width and thickness, and 200 μm in length [Fig. 1(a)]. An array of micro-channels were connected at their open ends to a common channel through which nitrogen gas can be circulated in a controlled manner. The device was transparent to enable the transmitted light and fluorescence analysis. The walls of the microchannels and the common channel were uniformly hydrophobic. This eliminated the sticking, ensured nearly flat meniscus geometry, and facilitated flow control. The microfluidic device was fabricated in PDMS by irreversibly bonding two PDMS pieces together: one flat and one containing the microfluidic network [Fig. 1(b)]. The flat PDMS piece was produced by curing a layer of PDMS on a flat silicon wafer. The second piece was produced by rapid prototyping techniques and involved SU8 (Microlithography Corp., Newton, MA) photopatterning on a silicon wafer using a glass-chrome mask (Advanced Reproduction, Andover, MA). Following the developing step, the negative of the microfluidic network was created on the silicon wafer, which in turn was used to cast the PDMS piece. The inlet and outlet access holes for the experimental solutions and the nitrogen gas were drilled with a beveled 25-gauge needle, and the two PDMS pieces were bonded together after exposure to oxygen plasma (150 mTorr, 50 W, and 20 s) in a plasma asher (March Inc., Concord, CA). The device was then bonded on a glass microscope slide. Microfluidic devices were stored for at least 24 h before use to allow the recovery of the characteristic natural hydrophobicity of the PDMS surfaces.
FIG. 1.
(a) The microfluidic device and (b) zoom view of the microchannels.
B. Experimental setup
The microfluidic device was placed on a fully automated inverted optical microscope (Zeiss Axiovert 200, Zeiss Co., Germany) with fluorescence capability. After the microelectromechanical system (MEMS) device was primed with the experimental solution, a nitrogen gas tank with two pressure regulators connected in series was connected to the inlet port and ultradry nitrogen gas was purged at a predefined pressure of 2.0 psi. The initial temperature of the solution varied with the room temperature in the range of 22.5-25.5 °C. Time-lapse phase contrast and fluorescence images were taken during desiccation at every 10 s up to the point when the movement of the interface practically stopped (approximately at 1200 s). An image analysis software (IMAQ Vision Builder, National Instruments Corp., Austin, TX) was used to analyze (a) the phase contrast images in order to determine the location of the gas-liquid interface as a function of desiccation time and, (b) the fluorescent images to quantify the viscosity gradients within the desiccating liquid. Each experiment was repeated three to four times with identical conditions.
III. MATHEMATICAL MODEL
The drying of the carbohydrate solutions in the micro-channels were modeled as a one-dimensional, coupled heat, and mass transfer problem. The high length to width ratio of the microchannels allowed one-dimensional modeling. For each experimental solution, the interface movement during desiccation was simulated and the respective water concentration distribution (as well as the viscosity gradients) within the drying microchannel were predicted. The governing partial differential equations and the boundary conditions for a moving reference frame [with the transformation ζ = z/S(t)] are
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where c is the concentration, D is the mutual diffusion coefficient of the binary solution, t is time, hV is the convective heat transfer coefficient in the liquid-gas interface, hm is the convective mass transfer coefficient, δ is the thickness of the microchannel, S(t) is the location of the interface, Pw is the partial pressure, r is the latent heat of water evaporation, and T, ρ, cp, and k are the temperature, mass density, specific heat, and thermal conductivity of the solution, respectively. The subscripts 1, 2, and A represent the solvent, the solute and the gas, respectively, while 0 represents the initial condition and s represents the saturation water pressure at the experimental temperature. Note that in the model the heat transfer between the surrounding air and the solution through the channel wall was also included. Conservation of the solute mass defined the location of the liquid-gas interface position through
| (7) |
where L is the channel length. The water vapor pressure in the ultradry nitrogen gas was taken as zero. The saturated water vapor pressure above the interface was calculated from13,14
| (8) |
where P0 is the vapor pressure of the pure solvent, ϕ is its volume fraction, χ is the Flory-Huggins solute-vapor interaction constant, σ is the ratio of the molecular volume of solute to the solvent, and f = 0 when the solution temperature is higher than the glass transition temperature, Tg, of the solution. For temperatures lower than the glass transition temperature, f is given by15
| (9) |
where M is the molecular weight, ω is the weight fraction, R is the universal gas constant, and Δcp,g is the change in specific heat during glass transition. For the binary solutions used, the glass transition temperature was calculated using the Gordon-Taylor equation as follows:
| (10) |
where κ is an empirically determined parameter. According to Crank,16 the mutual diffusion coefficient, D, is related to the self-diffusion coefficient of water in the solution, D1, and the thermodynamic properties by
| (11) |
where μ1 is the chemical potential of the solvent. Since the water concentration, c1 is the product of the water volume fraction, ϕ1, and the density of pure water, Eqn. (11) can be rewritten as
| (12) |
The chemical potential of water is related to its volume fraction by the Flory-Huggins theory as given by
| (13) |
The self-diffusion coefficient was then calculated using the following equation based on the free volume theory,17,18
| (14) |
where D0 is a preexponential factor, ΔE is the activation energy for the diffusion of water molecules in the solution, γ is an overlap factor which is introduced since the same free volume is available to more than one molecule, V̂* is the specific hole free volume of the component i required for a diffusion jump, ξ is the ratio of the molar volume of the jumping unit of the solvent to that of the solute, K11 and K21 are the free volume parameters for the solvent, and K12 and K22 are those for the solute. Although there are 13 independent parameters in the above equation, some of them can be grouped together reducing the total number of parameters to be determined to 10. These are: , , K12/γ, K22–Tg2, K11/γ, K21–Tg1, D0, ΔE, X, and ξ.
The William-Landel-Ferry (WLF) viscosity model19 was used to predict the viscosity change during drying
| (15) |
where η is viscosity and C1 and C2 are the two model parameters, which can be calculated from the free volume parameters as follows:20
| (16) |
| (17) |
Viscosity of the glass was calculated using the following equation:21
| (18) |
where Vm is the solution molar volume, and A, B are the two model parameters.
The thermal and physical properties and the free volume parameters of the binary aqueous solutions of glycerol, fructose, sucrose, and trehalose used in this study were determined in a separate communication22 and are summarized in Table I. The heat transfer coefficient between the surrounding air and the channel wall, hA, was taken as 10 W/m2 K, which is typical for natural convective heat transfer. The heat transfer coefficient above the interface, hV, was set to decrease from 20 to 10 W/m2 K in a linear fashion [determined by two-dimensional (2D) numerical analysis of the flow field, data not shown] from the top to the bottom of the channel (as the interface moved) so as to account for the effect of the change in the nitrogen gas speed above the interface. Similarly, mass transfer coefficient, hm, decreased from 2.6×10−7 to 1.3×10−7 s/m from the top to the bottom of the channel. The typical mass transfer coefficient for natural convection is approximately 1.8×10−7 s/m,23 which is within the values used in this study. The surrounding air temperature varied from 22.5 to 25.5 °C. The vapor pressure of pure water, P0, was determined by fitting a fourth order polynomial to the data in the temperature range of 0-100 °C reported in the literature.24
TABLE I.
Thermal and physical properties used in the numerical model.
| Parameters | Water | Glycerol | Fructose | Sucrose | Trehalose | |
|---|---|---|---|---|---|---|
| D 0 | m2 s–1 | 1.39 × 10–7 | · · · | · · · | · · · | · · · |
| Δ E | J mol–1 | 1982.97 | · · · | · · · | · · · | · · · |
| ml g–1 | 0.91 | · · · | · · · | · · · | · · · | |
| ml g–1 | · · · | 0.716 | 0.6 | 0.59 | 0.587 | |
| K 11 /γ | ml g–1 K–1 | 1.945 × 10–3 | · · · | · · · | · · · | · · · |
| K 12 /γ | ml g–1 K–1 | · · · | 7.36 × 10–4 | 5.22 × 10–4 | 3.36 × 10–4 | 2.16 × 10–4 |
| K 21 | K | –19.73 | · · · | · · · | · · · | · · · |
| K 22 | K | · · · | 4.26 | 23.9 | 69.2 | 89.9 |
| T g1 | K | 136 | · · · | · · · | · · · | · · · |
| T g2 | K | · · · | 193.15 | 289.15 | 347.15 | 387.15 |
| κ | · · · | 0.53 | 0.289 | 0.2721 | 0.17 | |
| χ | · · · | 0.26 | 0.43 | 0.52 | 0.22 | |
| ξ | · · · | 0.93 | 0.7 | 0.79 | 0.75 | |
| k | Wm–1 K–1 | 0.6 | 0.29 | 0.29 | 0.29 | 0.29 |
| ρ | kg m–3 | 1000 | 1.26 | 1.6 | 1.587 | 1.58 |
| cp | J kg–1 K–1 | 4200 | 2380 | 560 | 560 | 560 |
| x | 1.0 | 4.07 | 6.26 | 11.78 | 11.72 | |
| Δ cp,g | J kg–1 K–1 | · · · | 0.5 | 0.544 | 0.544 | 0.534 |
| r | J g–1 | 4.18(598.34–0.585 T) | · · · | · · · | · · · | · · · |
| A | · · · | 214.5 | 32.87 | 9.27 | 10.03 | |
| B | mol l1 | · · · | 65.41 | 98.13 | 80.74 | 131.24 |
The governing equations for the heat and mass transfer subjected to the given boundary conditions [Eqs. (1)-(6)] were solved numerically using a commercially available finite element-based partial differential equation solver package FEMLAB (v3.0, COMSOL, Inc., Burlington, MA) in the transformed one-dimensional domain. A total of 120 Lagrange-quadratic elements with 482 degrees of freedom were used to discretize the computational domain for both the heat and mass transfer analyses. The actual element size decreased with time (although it remained constant in the transformed domain) since the actual total computational domain shrank during drying. Further refinement of the mesh did not change the modeling results significantly (less than 0.5%). Relative and absolute tolerances for the convergence of the solution algorithm were 1% and 0.001, respectively. The time increments were adjusted automatically to ensure convergence.
IV. RESULTS
A. Interface location
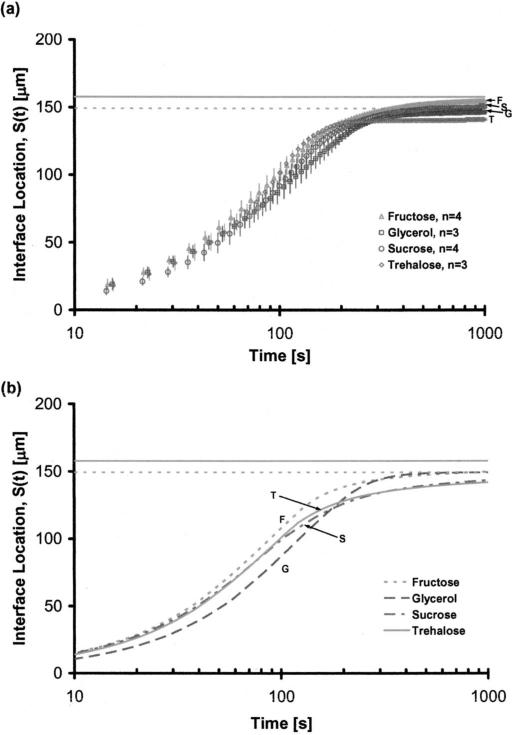
Applying a constant pressure flow of ultradry nitrogen gas, the solutions in the microchannels were dried and time-lapse phase contrast and fluorescence images were taken at 10 s increments until the movement of the liquid-gas interface practically stopped. The experiments were performed at room temperature (22.5-25.5 °C). Each experiment was repeated three to four times and the results were plotted as a function of time [Fig. 2(a)]. In Fig. 2 the horizontal solid gray line shows the location of the interface at 0% water content for the three sugars, which have similar density values (ρ ~ 1.6 kg/m3 at room temperature). The horizontal dashed gray line on the other hand, shows the interface location for glycerol at 0% water content. Note that the density of pure glycerol is 1.26 kg/m3 at room temperature. The standard deviations of the experiments within each group, especially after 200 s of drying, were very low. The final interface locations (measured at t=1200 s) for the sugars indicated that the most water was entrapped in trehalose, followed by sucrose and fructose solutions. As such the final average water contents of the glycerol, fructose, sucrose, and trehalose solutions were 3.91%, 8.86%, 9.09%, and 19.18% by mass, respectively. Note that these values are the gross averages calculated based on the interface location (and therefore are based on the overall volume) and they do not imply that the water concentration gradients within each group are uniform. All of the solutions tested had an initial linear rapid evaporation regime (0<t<75 s) followed by gradual slowing. The shape of the gas-liquid interface, at all times during drying, was flat in glycerol and fructose. Since the glass transition temperatures for these chemicals are approximately –80 and –16 °C (at zero water content) there was no skin formation at the interface. For sucrose and trehalose on the other hand, the interface was initially flat, turning into an arc with increased drying. For the interface location measurements this was taken into consideration by taking the average of the leading and the trailing meniscus locations. Note that the glass transition temperatures of sucrose and trehalose at zero water content are approximately 74 and 114 °C, respectively.
FIG. 2.
Interface location, S(t), as a function of drying time, (a) experimental, (b) simulation results for ΔP=2.0 psi, constant pressure flow.
The predictions of the one-dimensional model for the interface location were considerably close to the experimental measurements [Fig. 2(b)]. The predicted final average water contents of the glycerol, fructose, sucrose and trehalose solutions were 1.73%, 10.12%, 16.89%, and 18.41%, respectively. With the exception of sucrose, the difference between the predicted and measured values was less than 2.18%. For, sucrose, however, the difference was approximately 7.8% with the model overestimating the trapped water volume. For trehalose, a difference between the predicted and measured interface locations appeared at 120 s, reaching a peak of approximately 7.25% of the measured value at 215 s (corresponding to skin formation, as discussed in the next section), where the simulation consistently underestimated the interface location. The difference between the measurements and the predictions dropped down to less than 1% of the measured value after t=240 s. Optical analysis showed that at around t=180 s the interface shape started to change from flat to an arc (introducing a multidimensional instability). This is assumed to be the main reason for the discrepancy between the experimental measurements and the one-dimensional model predictions. For the glycerol solution, at all times during drying, the difference between the predictions and experimental values was less than 2.18%. For fructose, the model predictions matched the experimental measurement of the interface location precisely in the rapid and transitional drying regimes but underestimated the equilibrium location of the interface by 1.26% of the experimental value. For all of the experimental groups, at all times during drying the difference between the predictions and measurements were consistently less than 7.8% and therefore the one-dimensional model was deemed sufficiently precise for the purpose of this study. For certain cases, a two-dimensional model was also employed (results not shown) and it was noted that the difference between the one-dimensional and the two-dimensional predictions was less than 2%.
B. Viscosity gradients
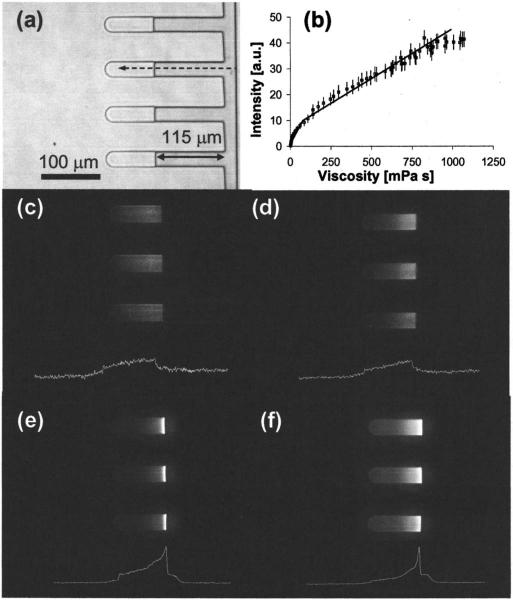
An objective of this study was to examine the formation of viscosity gradients during desiccation of sugar solutions in microchannels and to examine the effects of interface skin formation on the desiccation kinetics. A fluorescent molecular rotor (CCVJ) was utilized to measure the spatial variation of viscosity in the drying sugar solutions in real time. In Fig. 3(a) phase image of drying glycerol solution at S(t)=115 μm is shown. In Fig. 3(b) the calibration curve for CCVJ constructed by measuring the fluorescence intensity corresponding to known viscosity values of glycerol solutions is presented. The calibration measurements indicated that for the given concentration of the probe, following an exponential response (1<η <100 mPa s) the correlation between viscosity and fluorescence intensity was fairly linear up to 1150 mPa s (R2=0.97). In Figs. 3(c)-3(f), the fluorescence images taken for all of the experimental groups are presented at S(t)=115 μm. The white curve below each image shows the CCVJ intensity change as a function of location in the respective solution. At the same S(t), the viscosity gradients across the solution for fructose and glycerol were fairly linear [Figs. 3(d) and 3(e)]. For the sucrose and treha-lose samples [Figs. 3(f) and 3(g)], the viscosity values at respective locations were higher and the gradients within the solutions were steeper, more significantly in trehalose than in sucrose. For both cases, at close proximity to the gas-liquid interface, the viscosity increased exponentially. The exact location of the interface was not easily detectable in the fluo rescence images due to the light scattering (as observed by the halo to the right of the interface). The fluorescence images mainly supplied qualitative information for comparing the steepness of the concentration gradients formed in the solutions drying in the microchannels.
FIG. 3.
(a) 200× phase image of microchannels loaded with glycerol, (b) calibration curve for CCVJ, 200× fluorescence image of the microchannels with (c) glycerol solution (texposure=1000 ms), (d) fructose solution (texposure=55 ms), (e) sucrose solution (texposure=55 ms), and (f) trehalose solution (texposure=1000 ms).
The prediction capability of the one-dimensional model was confirmed by comparing the viscosity profiles predicted by the mathematical model at different time points inside the drying glycerol solution to those obtained by fluorescence analysis. Figure 4 shows for the glycerol solution the normalized viscosity profiles predicted by the model and measured experimentally by CCVJ fluorescence. Note that the gas-liquid interface is located at S(t)*=1. S(t)*=0 corresponds to S(t)=200 μm and η*=η/ηmax. For the glycerol solution, at all time points during drying the predictions were in very good agreement with the measurements. The evaporation rate at the interface was initially limited by the diffusion of water in the circulating nitrogen gas (0<t<100 s). With increasing glycerol concentration close to the interface, however, the diffusion of water in the solution started to play a major role, resulting in steeper gradients of concentration and therefore viscosity (t~180 s). Later on, with diminishing water content the viscosity profile started to flatten and at t=1200 s it was completely flat as predicted by the model and measured experimentally.
FIG. 4.
The measured (symbols) and predicted (solid lines) viscosity profiles in a glycerol solution drying in a microchannel.
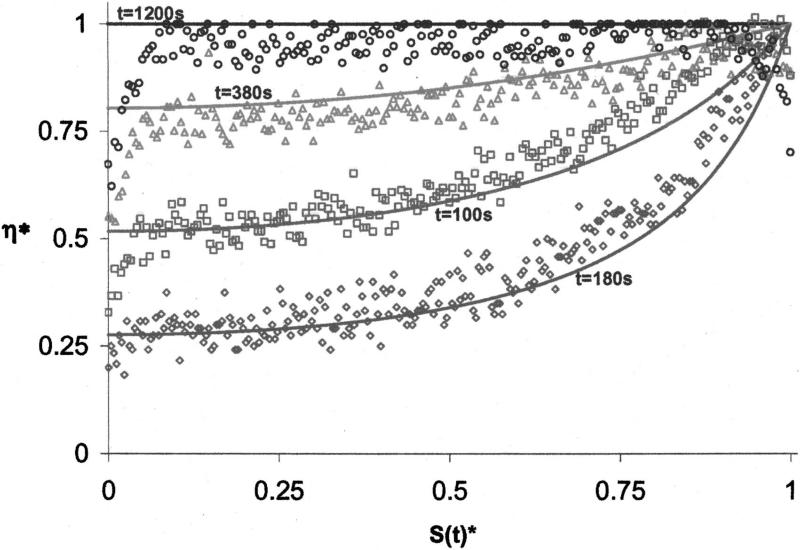
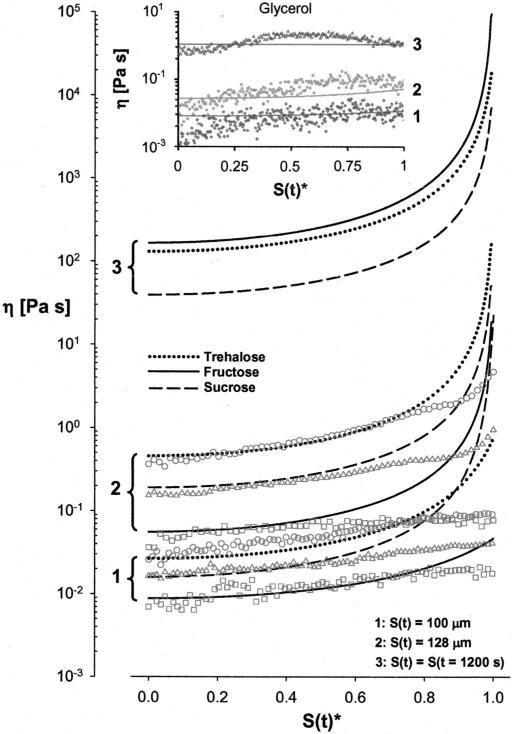
After confirming the predictive capacity of the one-dimensional model, simulations were performed to determine the formation of viscosity gradients in desiccating sucrose, trehalose and fructose solutions (Fig. 5). The symbols in the figure show the measured values of viscosity (CCVJ fluorescence analysis) and the lines show the predictions of the numerical model. The model predicted that for S(t) = 100 μm and S(t)=128 μm, far from the interface [S(t)* <0.9] the viscosity of trehalose solution at any point in the microchannel was the highest, followed by sucrose and fructose. For S(t)=100 μm, and S(t)*>0.9 sucrose viscosity was higher than trehalose owing to higher predicted water diffusivity and lower water content close to the interface. The model also predicted that at t=1200 s the viscosity of the fructose solution exceeded trehalose and sucrose at any point in the microchannel except for a very narrow region at the interface. Note that data corresponding to S(t)*>0.995 were omitted from Fig. 5 for clarity due to extremely high viscosity values predicted by the model (η >1013 Pa s).
FIG. 5.
Predicted and measured values of viscosity in the experimental solutions.
For the trehalose solutions, the predictions and the measurements matched well for S(t)*<0.8. Closer to the interface, S(t)*>0.8, the measured viscosity gradients were not as steep as those predicted by the model. For the sucrose solutions, the predictions and the measurements matched well for S(t)*<0.5 but the predictions consistently overestimated viscosity in the rest of the region. A similar observation was also made for the fructose solutions except for the case of S(t)=100 μm, where the agreement between the model and the predictions was valid up to S(t)*=0.8. For the glycerol solutions (Fig. 5, insert) there was close to perfect agreement between the predicted and the measured values for all interface locations.
V. DISCUSSION
One-dimensional desiccation experiments were performed with biologically important aqueous carbohydrate and glycerol solutions using a microfluidic device. A fluores-cent molecular rotor was added to the solutions to obtain real-time viscosity information during desiccation. A one-dimensional numerical model based on the free volume theory was also utilized to predict the location of the gas-liquid interface and the viscosity fields in the desiccating solutions. For all three carbohydrate solutions and the glycerol solution, the experimental measurements, and the model predictions agreed well for the interface movement and the average water content remaining in the solution. After drying for 1200 s, a significant amount of water was still trapped in the trehalose (19.18% w/w measured, 18.41% w/w predicted) and the sucrose solutions (9.09% w/w measured, 16.89% w/w predicted) due to the vitrified skin formation at the liquid-gas interface. The interface of the fructose solution, on the other hand, has never vitrified and therefore the overall solution reached a significantly lower water content (8.86% w/w measured, 10.12% w/w predicted) during the same period of time.
The model and the measurements indicated that steep viscosity gradients formed and persisted within the desiccating solutions. The model, however, persistently overestimated the viscosity values close to the interface location. After extensive drying, viscosity within the fructose solution (anywhere along the length of the microchannel, with the exception of a very narrow region at the interface) was higher than sucrose and trehalose solutions, even though vitrification did never occur. In the glycerol solution, the gradients diminished after 1200 s, and the water entrapped in the solution was uniformly distributed.
These results indicated that even though the glass transition temperatures of the sucrose and trehalose are significantly higher than fructose, due to glassy skin formation at the interface a significantly higher amount of water is entrapped in the solution. This resulted in lower viscosity, especially at regions far away from the gas-liquid interface. Therefore, it can be stated that in terms of attaining a higher viscosity and lower mobility, carbohydrates with lower glass transition temperatures are more efficient during rapid iso-thermal drying.
The desiccation kinetics of a glass-forming solution depends on the initial concentration of the solute in the solution,10 the environmental conditions and the interaction of the solution with the surrounding surfaces (the container its dried in or the surface it is dried on). In order to have a fairly uniform concentration gradient in a desiccating solution, the diffusion rate of the solvent within the solution should be comparable to that in the surrounding air. With increasing solute concentration, however, the solvent diffusion in the solution decreases. For high glass transition temperature carbohydrates, at the gas-liquid interface a glassy skin is formed slowing down (if not completely halting) the solvent mobility even further. The skin is of very small thickness and has been thought not to present a major barrier against desiccation. This may be true for the binary solutions when the solvent size is significantly smaller than the molecular free volume of the vitrified matrix (for example, in the case of aqueous dextran solutions). However, as shown here, even though trehalose and sucrose have significantly higher glass transition temperatures than fructose, the overall viscosity of the fructose solution, at the end of drying, was higher, due to the reduced (or maybe even halted) water diffusion through the skin formed in the trehalose and sucrose solutions.
It has been proposed that the superior protective capability of trehalose is a combination of its high bonding affinity to (or high exclusion capacity from) the protein and lipid surfaces (especially when liquid water is scarce) and its high glass transition temperature enabling high viscosity and reduced mobility in the preserved state. Results of this study suggest that as far as the postdesiccation viscosity is concerned (which is related to the glass transition temperature), fructose has a distinct advantage over sucrose and trehalose (even though their glass transition temperatures are 90 and 130 K higher than fructose, respectively). The viscosity within the fructose solution homogeneously [S(t)*<0.99] reached higher values than sucrose and trehalose after 20 min of drying. This is due to very low diffusivity at the glassy skin [S(t)*>0.99] formed during drying of the treha-lose and sucrose solutions, which upon reaching certain thickness, practically stopped further evaporation of water, entrapping it within the solution and therefore causing the sucrose and the trehalose solutions to have higher average water contents.
An equally widely utilized protectant glycerol, has been shown to be more efficient than trehalose in terms of dampening the protein conformational fluctuations25 even though its glass transition temperature is approximately 200 K lower. This is attributed to the glycerol's ability to suppress structural vibrations much better than trehalose.26 The results of this study show that one other major factor to be considered is the homogeneity of the desiccated solutions, which ensures that the product present in the solution has a spatially (and probably temporally) uniform history. For example, if a model protein was incorporated in the solutions used in this research and its activity was quantified as a function of desiccation time and storage conditions, deceptive results could be obtained since only in the glycerol solution the overall protein population would have the same desiccation history. In the carbohydrate solutions, however, depending on the distance from the interface, the subpopulations would have experienced significantly different desiccation histories and microenvironmental conditions. Therefore, it may be suggested that one of the main factors contributing to the high preservation efficiency of certain chemicals (such as glycerol) may be the homogeneity of the viscosity and water activity gradients formed in the desiccated product. This issue requires further investigation. Note that this effect would only be an issue in applications that do not involve freeze drying.
In the biopreservation media formulation development for the desiccated/vitrified state preservation of biological materials, the tendency of the biopreservation media to form a glassy skin at the interface causing water entrapment and nonuniform concentration gradients should be taken into consideration. The solutions with high glass transition temperatures, inevitably, will yield to nonuniform drying resulting in very steep concentration gradients within the desiccated/vitrified product. Especially in the biopreservation field, the nonhomogeneities formed within the desiccated/vitrified/cryopreserved products have never been accounted for and the calorimetric glass transition temperature (which is a gross measure) has been used as the sole indicator of stability. In light of the observations presented here, future work is warranted to determine the effects of various methods and preservation agents on the homogeneity of the preserved product.
VI. SUMMARY
A microfluidic device enabling one-dimensional desiccation of aqueous solutions was manufactured and the desiccation kinetics of biologically important carbohydrate and glycerol solutions were characterized. The viscosity gradients formed in aqueous solutions during desiccation were compared experimentally and numerically. Most of the previous work focused either on numerical prediction of the concentration gradients formed in thin films during desiccation of binary solutions or experimentation with the desiccating droplets to determine secondary flows, instabilities, and nonhomogeneities. The microfluidic channels designed for this study enabled direct comparison of the desiccation kinetics of the preservation solutions and the viscosity gradients formed within the dried solution by completely isolating the secondary effects introduced during the experimentation with droplets. The microfluidic device manufactured in this study is currently being used for the real-time measurement of intra/extracellular molecular mobility during carbohydrate loading and desiccation of live mammalian cells.
ACKNOWLEDGMENT
This research is funded by a National Institutes of Health (NIH EB 002349) grant.
Contributor Information
Alptekin Aksan, Department of Mechanical Engineering, University of Minnesota, Minneapolis, Minnesota 55455.
Daniel Irimia, Center for Engineering in Medicine and Surgical Services, Massachusetts General Hospital, Harvard Medical School, and Shriners Hospital for Children, Boston, Massachusetts 02114.
Xiaoming He, Center for Engineering in Medicine and Surgical Services, Massachusetts General Hospital, Harvard Medical School, and Shriners Hospital for Children, Boston, Massachusetts 02114.
Mehmet Toner, Center for Engineering in Medicine and Surgical Services, Massachusetts General Hospital, Harvard Medical School, and Shriners Hospital for Children, Boston, Massachusetts 02114.
References
- 1.Kandror O, DeLeon A, Goldberg AL. Proc. Natl. Acad. Sci. U.S.A. 2002;99:9727. doi: 10.1073/pnas.142314099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Attfield PV. FEBS Lett. 1987;225:259. doi: 10.1016/0014-5793(87)81170-5. [DOI] [PubMed] [Google Scholar]
- 3.Madin KAC, Crowe JH. J. Exp. Zool. 1975;193:335. [Google Scholar]
- 4.Crowe JH, Hoekstra FA, Crowe LM. Annu. Rev. Physiol. 1992;54:579. doi: 10.1146/annurev.ph.54.030192.003051. [DOI] [PubMed] [Google Scholar]
- 5.Webb SJ. Bound Water in Biological Activity. Charles C. Thomas; Springfield, IL: 1965. [Google Scholar]
- 6.Sun WQ, Irving TC, Leopold AC. Physiol. Plant. 1994;90:621. [Google Scholar]
- 7.Fuller BJ, Lane AN, Benson EE. Life in the Frozen State. CRC Press; Boca Raton, FL: 2004. [Google Scholar]
- 8.Sun WQ, Leopold AC. Comp. Biochem. Physiol. A. 1997;A117:327. [Google Scholar]
- 9.Mazur P, Leibo S, Chu EHY. Exp. Cell Res. 1972;71:345. doi: 10.1016/0014-4827(72)90303-5. [DOI] [PubMed] [Google Scholar]
- 10.Aksan A, Morris SC, Toner M. Langmuir. 2005;21:2847. doi: 10.1021/la047760y. [DOI] [PubMed] [Google Scholar]
- 11.Hu H, Larson RG. Langmuir. 2005;21:3963. doi: 10.1021/la047528s. [DOI] [PubMed] [Google Scholar]
- 12.Aksan A, Toner M. Langmuir. 2004;20:5521. doi: 10.1021/la0355186. [DOI] [PubMed] [Google Scholar]
- 13.Hancock BC, Zografi G. Pharm. Res. 1993;10:1262. doi: 10.1023/a:1018901325842. [DOI] [PubMed] [Google Scholar]
- 14.Zhang J, Zografi G. J. Pharm. Sci. 2000;89:1063. doi: 10.1002/1520-6017(200008)89:8<1063::aid-jps11>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- 15.Vrentas JS, Vrentas CM. Macromolecules. 1991;24:2404. [Google Scholar]
- 16.Crank J. The Mathematics of Diffusion. Clarendon; Oxford: 1975. [Google Scholar]
- 17.Vrentas JS, Duda JL. J. Polym. Sci., Polym. Phys. Ed. 1977;15:403. [Google Scholar]
- 18.Vrentas JS, Duda JL. J. Polym. Sci., Polym. Phys. Ed. 1977;15:417. [Google Scholar]
- 19.Williams ML, Landel RF, Ferry JD. J. Am. Chem. Soc. 1955;77:3701. [Google Scholar]
- 20.Duda JL, Vrentas JS, Ju ST, Liu HT. AIChE J. 1982;28:279. [Google Scholar]
- 21.Soesanto T, Williams MC. J. Phys. Chem. 1981;85:3338. [Google Scholar]
- 22.He X, Irimia D, Aksan A, Toner M. J. Phys. Chem. (in preparation) [Google Scholar]
- 23.Alsoy S, Duda JL. AIChE J. 1999;45:896. [Google Scholar]
- 24.Lide DR. Handbook of Chemistry and Physics. Vol. 83. CRC Press; Boca Raton, FL: 2003. [Google Scholar]
- 25.Sastry GM, Agmon N. Biochemistry. 1997;36:7097. doi: 10.1021/bi9626057. [DOI] [PubMed] [Google Scholar]
- 26.Caliskan G, et al. J. Chem. Phys. 2004;121:1978. doi: 10.1063/1.1764491. [DOI] [PubMed] [Google Scholar]