Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1996 Oct 29;93(22):12648–12653. doi: 10.1073/pnas.93.22.12648

Impact of vaccination on the spatial correlation and persistence of measles dynamics.

B M Bolker 1, B T Grenfell 1
PMCID: PMC38047  PMID: 8901637

Abstract

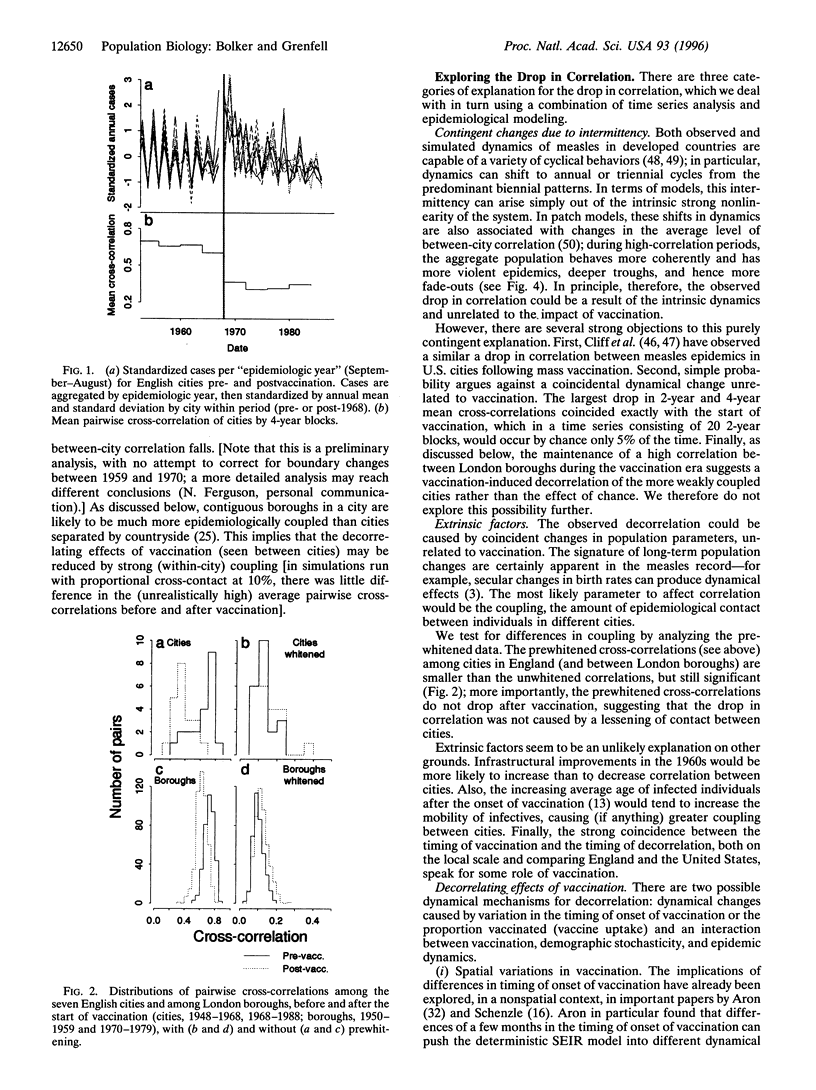
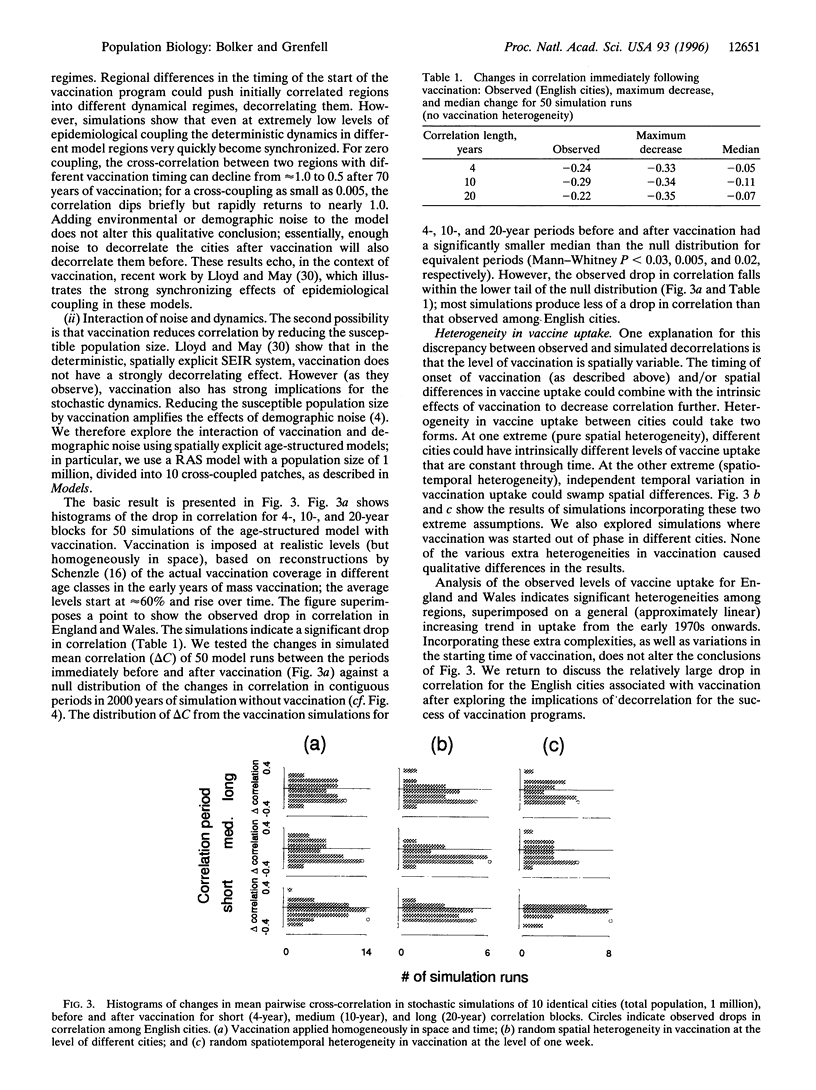
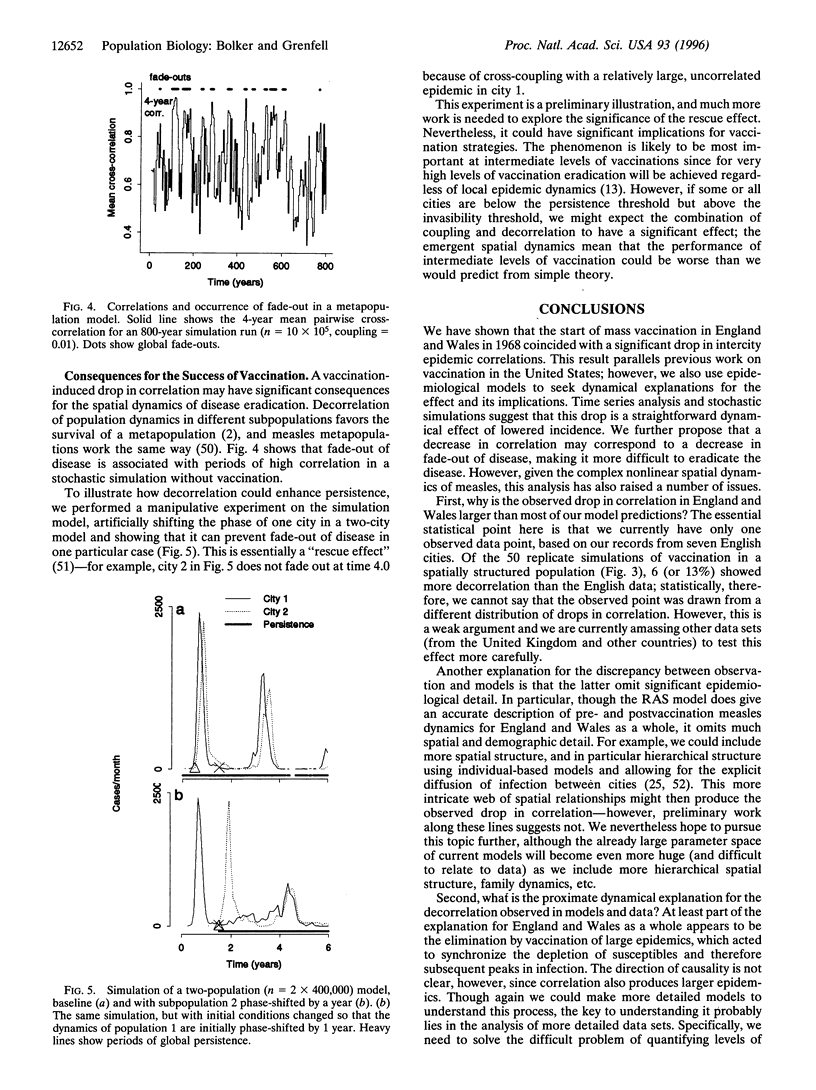
The onset of measles vaccination in England and Wales in 1968 coincided with a marked drop in the temporal correlation of epidemic patterns between major cities. We analyze a variety of hypotheses for the mechanisms driving this change. Straightforward stochastic models suggest that the interaction between a lowered susceptible population (and hence increased demographic noise) and nonlinear dynamics is sufficient to cause the observed drop in correlation. The decorrelation of epidemics could potentially lessen the chance of global extinction and so inhibit attempts at measles eradication.

Full text

PDF
12648

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Allen J. C., Schaffer W. M., Rosko D. Chaos reduces species extinction by amplifying local population noise. Nature. 1993 Jul 15;364(6434):229–232. doi: 10.1038/364229a0. [DOI] [PubMed] [Google Scholar]
  2. Anderson R. M., Grenfell B. T., May R. M. Oscillatory fluctuations in the incidence of infectious disease and the impact of vaccination: time series analysis. J Hyg (Lond) 1984 Dec;93(3):587–608. doi: 10.1017/s0022172400065177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Anderson R. M., May R. M. Age-related changes in the rate of disease transmission: implications for the design of vaccination programmes. J Hyg (Lond) 1985 Jun;94(3):365–436. doi: 10.1017/s002217240006160x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Anderson R. M., May R. M. Spatial, temporal, and genetic heterogeneity in host populations and the design of immunization programmes. IMA J Math Appl Med Biol. 1984;1(3):233–266. doi: 10.1093/imammb/1.3.233. [DOI] [PubMed] [Google Scholar]
  5. Anderson R. M., May R. M. Vaccination and herd immunity to infectious diseases. 1985 Nov 28-Dec 4Nature. 318(6044):323–329. doi: 10.1038/318323a0. [DOI] [PubMed] [Google Scholar]
  6. Aron J. L. Multiple attractors in the response to a vaccination program. Theor Popul Biol. 1990 Aug;38(1):58–67. doi: 10.1016/0040-5809(90)90003-e. [DOI] [PubMed] [Google Scholar]
  7. Aron J. L., Schwartz I. B. Seasonality and period-doubling bifurcations in an epidemic model. J Theor Biol. 1984 Oct 21;110(4):665–679. doi: 10.1016/s0022-5193(84)80150-2. [DOI] [PubMed] [Google Scholar]
  8. Black F. L. Measles endemicity in insular populations: critical community size and its evolutionary implication. J Theor Biol. 1966 Jul;11(2):207–211. doi: 10.1016/0022-5193(66)90161-5. [DOI] [PubMed] [Google Scholar]
  9. Bolker B. M., Grenfell B. T. Chaos and biological complexity in measles dynamics. Proc Biol Sci. 1993 Jan 22;251(1330):75–81. doi: 10.1098/rspb.1993.0011. [DOI] [PubMed] [Google Scholar]
  10. Bolker B. Chaos and complexity in measles models: a comparative numerical study. IMA J Math Appl Med Biol. 1993;10(2):83–95. doi: 10.1093/imammb/10.2.83. [DOI] [PubMed] [Google Scholar]
  11. Bolker B., Grenfell B. Space, persistence and dynamics of measles epidemics. Philos Trans R Soc Lond B Biol Sci. 1995 May 30;348(1325):309–320. doi: 10.1098/rstb.1995.0070. [DOI] [PubMed] [Google Scholar]
  12. Cliff A. D., Haggett P. Changes in the seasonal incidence of measles in Iceland, 1896--1974. J Hyg (Lond) 1980 Dec;85(3):451–457. doi: 10.1017/s002217240006352x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Cliff A. D., Haggett P., Stroup D. F., Cheney E. The changing geographical coherence of measles morbidity in the United States, 1962-88. Stat Med. 1992 Aug;11(11):1409–1424. doi: 10.1002/sim.4780111102. [DOI] [PubMed] [Google Scholar]
  14. Cliff A. D., Haggett P., Stroup D. F. The geographic structure of measles epidemics in the northeastern United States. Am J Epidemiol. 1992 Sep 1;136(5):592–602. doi: 10.1093/oxfordjournals.aje.a116537. [DOI] [PubMed] [Google Scholar]
  15. Fine P. E., Clarkson J. A. Measles in England and Wales--I: An analysis of factors underlying seasonal patterns. Int J Epidemiol. 1982 Mar;11(1):5–14. doi: 10.1093/ije/11.1.5. [DOI] [PubMed] [Google Scholar]
  16. Fine P. E., Clarkson J. A. Measles in England and Wales--III: Assessing published predictions of the impact of vaccination on incidence. Int J Epidemiol. 1983 Sep;12(3):332–339. doi: 10.1093/ije/12.3.332. [DOI] [PubMed] [Google Scholar]
  17. Grenfell B. T., Anderson R. M. The estimation of age-related rates of infection from case notifications and serological data. J Hyg (Lond) 1985 Oct;95(2):419–436. doi: 10.1017/s0022172400062859. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Grenfell B. T., Kleczkowski A., Gilligan C. A., Bolker B. M. Spatial heterogeneity, nonlinear dynamics and chaos in infectious diseases. Stat Methods Med Res. 1995 Jun;4(2):160–183. doi: 10.1177/096228029500400205. [DOI] [PubMed] [Google Scholar]
  19. Lloyd A. L., May R. M. Spatial heterogeneity in epidemic models. J Theor Biol. 1996 Mar 7;179(1):1–11. doi: 10.1006/jtbi.1996.0042. [DOI] [PubMed] [Google Scholar]
  20. London W. P., Yorke J. A. Recurrent outbreaks of measles, chickenpox and mumps. I. Seasonal variation in contact rates. Am J Epidemiol. 1973 Dec;98(6):453–468. doi: 10.1093/oxfordjournals.aje.a121575. [DOI] [PubMed] [Google Scholar]
  21. Olsen L. F., Schaffer W. M. Chaos versus noisy periodicity: alternative hypotheses for childhood epidemics. Science. 1990 Aug 3;249(4968):499–504. doi: 10.1126/science.2382131. [DOI] [PubMed] [Google Scholar]
  22. Olsen L. F., Truty G. L., Schaffer W. M. Oscillations and chaos in epidemics: a nonlinear dynamic study of six childhood diseases in Copenhagen, Denmark. Theor Popul Biol. 1988 Jun;33(3):344–370. doi: 10.1016/0040-5809(88)90019-6. [DOI] [PubMed] [Google Scholar]
  23. Rand D. A., Wilson H. B. Chaotic stochasticity: a ubiquitous source of unpredictability in epidemics. Proc Biol Sci. 1991 Nov 22;246(1316):179–184. doi: 10.1098/rspb.1991.0142. [DOI] [PubMed] [Google Scholar]
  24. Sattenspiel L., Dietz K. A structured epidemic model incorporating geographic mobility among regions. Math Biosci. 1995 Jul-Aug;128(1-2):71–91. doi: 10.1016/0025-5564(94)00068-b. [DOI] [PubMed] [Google Scholar]
  25. Schaffer W. M., Kendall B. E., Tidd C. W., Olsen L. F. Transient periodicity and episodic predictability in biological dynamics. IMA J Math Appl Med Biol. 1993;10(4):227–247. doi: 10.1093/imammb/10.4.227. [DOI] [PubMed] [Google Scholar]
  26. Schenzle D. An age-structured model of pre- and post-vaccination measles transmission. IMA J Math Appl Med Biol. 1984;1(2):169–191. doi: 10.1093/imammb/1.2.169. [DOI] [PubMed] [Google Scholar]
  27. Schwartz I. B. Multiple stable recurrent outbreaks and predictability in seasonally forced nonlinear epidemic models. J Math Biol. 1985;21(3):347–361. doi: 10.1007/BF00276232. [DOI] [PubMed] [Google Scholar]
  28. Schwartz I. B. Small amplitude, long period outbreaks in seasonally driven epidemics. J Math Biol. 1992;30(5):473–491. doi: 10.1007/BF00160532. [DOI] [PubMed] [Google Scholar]
  29. Smith H. L. Subharmonic bifurcation in an S-I-R epidemic model. J Math Biol. 1983;17(2):163–177. doi: 10.1007/BF00305757. [DOI] [PubMed] [Google Scholar]
  30. Sugihara G., Grenfell B., May R. M. Distinguishing error from chaos in ecological time series. Philos Trans R Soc Lond B Biol Sci. 1990 Nov 29;330(1257):235–251. doi: 10.1098/rstb.1990.0195. [DOI] [PubMed] [Google Scholar]
  31. Yorke J. A., Nathanson N., Pianigiani G., Martin J. Seasonality and the requirements for perpetuation and eradication of viruses in populations. Am J Epidemiol. 1979 Feb;109(2):103–123. doi: 10.1093/oxfordjournals.aje.a112666. [DOI] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES