Middle-ear velocity transfer function, cochlear input immittance, and middle-ear efficiency in chinchilla

Abstract

The transfer function H_V between stapes velocity V_S and sound pressure near the tympanic membrane P_TM is a descriptor of sound transmission through the middle ear (ME). The ME power transmission efficiency (MEE), the ratio of sound power entering the cochlea to power entering the middle ear, was computed from H_V measured in seven chinchilla ears and previously reported measurements of ME input admittance Y_TM and ME pressure gain G_MEP [Ravicz and Rosowski, J. Acoust. Soc. Am. 132, 2437–2454 (2012); J. Acoust. Soc. Am. 133, 2208–2223 (2013)] in the same ears. The ME was open, and a pressure sensor was inserted into the cochlear vestibule for most measurements. The cochlear input admittance Y_C computed from H_V and G_MEP is controlled by a combination of mass and resistance and is consistent with a minimum-phase system up to 27 kHz. The real part Re{Y_C}, which relates cochlear sound power to inner-ear sound pressure, decreased gradually with frequency up to 25 kHz and more rapidly above that. MEE was about 0.5 between 0.1 and 8 kHz, higher than previous estimates in this species, and decreased sharply at higher frequencies.

INTRODUCTION

This paper continues our studies of the transmission of sound power through the external and middle ear to the sensory cells of the cochlea (Ravicz and Rosowski, 2012b, 2013). Specifically, we examine the transformation of ear canal sound pressure to stapes velocity through the middle ear of chinchilla and use these data and concurrent measurements of other middle- and inner-ear acoustical quantities in the same ears to compute (1) the input admittance of the cochlea and (2) the middle-ear efficiency, the ratio of sound power absorbed by the inner ear at the oval window (OW) to the power absorbed at the tympanic membrane (TM), the entrance of the middle ear (Rosowski et al., 1986; Rosowski, 1991, 1994). (A table of nomenclature is provided at the end of this paper.)

We focus on inner-ear sound power absorption because hearing sensitivity has been hypothesized to be directly related to the power absorbed by the inner ear (e.g., von Waetzmann and Keibs, 1936; Khanna and Tonndorf, 1969); therefore, according to this hypothesis, the effect of the middle ear on sound power transmission to the cochlea could influence the frequency range of hearing (Rosowski et al. 1986; Rosowski, 1991). Furthermore, the frequency dependence of noise-induced hearing loss produced by broadband impulse noise has been related to the frequency dependence of sound power absorption by the inner ear (Tonndorf, 1976; Rosowski, 1991; Patterson et al., 1993). If so, the absorption of harmful levels of sound power might be reduced by protecting the ear from sound in the frequency range where middle-ear power transfer is most efficient. In this study we ignore those processes that relate the sound pressure of a free-field stimulus and the amount of sound power absorbed at the entrance to the middle ear and focus on power transmission and absorption within the middle ear.

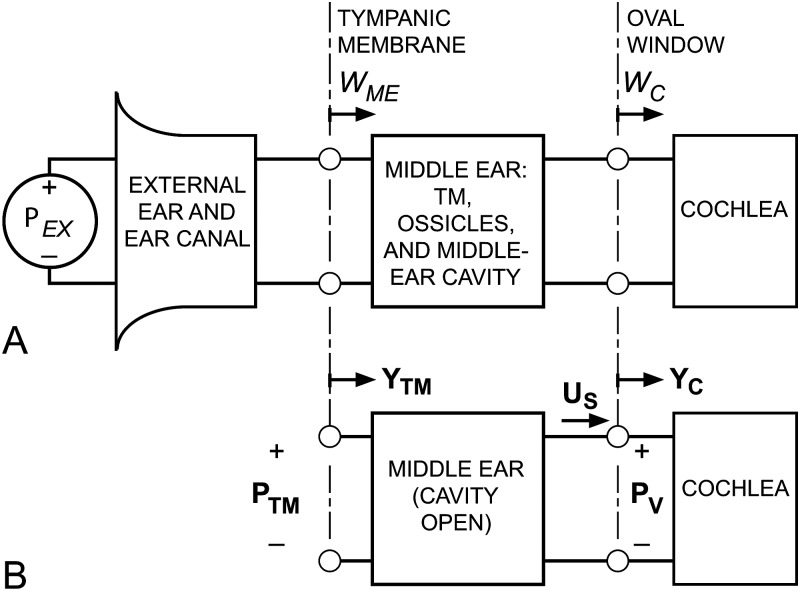
The theoretical framework we use to quantify sound power flow through the middle ear is outlined in Fig. 1, a block diagram of the mammalian auditory periphery that defines the significant acoustic input and output variables of the external, middle, and inner ears (adapted from Rosowski et al., 1986 and Rosowski, 1991). The transfer of sound power from the external environment to the cochlea (left to right in Fig. 1) is governed by sound transmission through each block and sound power delivery from one block to the next. In panel (A), sound pressure just outside the entrance to the external ear P_ex produces a sound power that is incident on the tympanic membrane (TM), which we consider to be the entrance of the middle ear. As mentioned above, we ignore the processes that lead to the generation of this incident sound power (e.g., Kuhn, 1979; Shaw, 1988) and the fraction of the power incident at the TM that is reflected back down the ear canal (Rosowski et al., 1986, 1988; Rosowski, 1991; Keefe et al., 1994); instead, we concentrate on the sound power that enters the ME at the TM (W_ME). Some fraction of this power (W_C) passes through the middle ear and is absorbed at the oval window (OW), the entrance to the cochlea and inner ear (IE). The remaining fraction (W_ME – W_C) is lost within the middle ear through losses in the motion of the TM and/or ossicular chain or through losses associated with the compression and rarefaction of the air within the middle-ear cavity.

Figure 1.

A block diagram of the auditory periphery to quantify acoustic power flow through the external and middle ear into the inner ear. (A) The interaction of the sound pressure in the outside world P_ex and the head, body, and the external and middle ear results in sound power incident on the TM. Some of this sound power enters the middle ear (W_ME), and some fraction of that is transmitted to the cochlea (W_C). The MEE = W_C/W_ME. (B) The acoustics of our preparation and sound power calculations. The cochlear input admittance Y_C, the ratio of stapes volume velocity U_S to sound pressure in the cochlear vestibule P_V, was computed from measurements of stapes velocity in each of seven ears resulting from a sound pressure at the TM P_TM in the truncated ear canal and the previously reported sound pressure in the cochlear vestibule P_V (Ravicz and Rosowski, 2013) measured in the same ears. MEE was computed from P_V, P_TM, Y_C, and previously reported middle-ear input admittance Y_TM (Ravicz and Rosowski, 2012b) also measured in the same ears.

The middle-ear efficiency (MEE) is defined as the ratio of the sound power that enters the cochlea W_C to the sound power that enters the middle ear W_ME (Rosowski et al., 1986, 1988):

$$\text{MEE}=W_C/W_{\mathit{M}\mathit{E}}.$$ (1)

Computation of MEE generally requires three measurements: The input immittances (impedance or admittance) of the middle ear and the inner ear (defined below), and a transfer function between a middle-ear input variable (typically, sound pressure or volume velocity) and an inner-ear input variable—see Fig. 1B. The sound pressure at the TM (P_TM) and the mean volume velocity of the TM (U_TM) are related by the middle-ear input admittance Y_TM = U_TM/P_TM.1 The sound pressure within the inner ear vestibule P_V and the stapes footplate volume velocity U_S are related by the cochlear input admittance Y_C = U_S/P_V. A complication in these computations is that some of these quantities must be estimated from measurements at nearby locations or with procedures that may modify their normal value; for instance, we were constrained to measure the sound pressure P_near-TM 1–1.5 mm from the TM and estimate P_TM from P_near-TM using an ear-canal model.

A previous investigation computed MEE in chinchilla from the data available at the time: means of measurements of Y_TM and the transfer functions between stapes velocity or scala vestibuli sound pressure and P_TM, each performed in different subject animals in different laboratories (Rosowski, 1991, 1994). The MEE computed from those data differed substantially from estimates in other species, but it was impossible to evaluate the statistical significance of these differences: The various sound pressures and velocities were measured in different populations, hence, any interdependence between the variances of these variables in each species could not be quantified. In this study, we compute MEE in individual ears from measurements of the necessary acoustical and mechanical quantities made in each ear; thus, we can assess directly the variance in MEE within the test population.

In this paper we present measurements of V_S as the stapes velocity transfer function H_V, the ratio of V_S to ear canal sound pressure near the TM. We also use a previously developed model of the ear canal (Ravicz and Rosowski, 2012b, 2013) to provide better estimates of P_TM and therefore H_V at frequencies above 10 kHz. We use H_V, simultaneous measurements of the middle-ear pressure gain G_MEP = P_V/P_TM (Ravicz and Rosowski, 2013), and other measurements of stapes footplate area (Vrettakos et al., 1988) to compute cochlear input admittance for power computations, as described in Sec. 3B below. We compute MEE from these data and concurrent measurements of Y_TM in these same ears (Ravicz and Rosowski, 2012b) over the frequency range 0.1–17 kHz. We use a simple ear-canal model (Ravicz and Rosowski, 2012b, 2013) to extend our estimates of MEE to 27 kHz.

METHODS

Preparation

These experiments were performed in accordance with guidelines published by the U.S. Public Health Service and were approved by the Massachusetts Eye & Ear Infirmary Institutional Animal Care and Use Committee. Seven chinchilla ears were used in this study and in the companion papers (Ravicz and Rosowski, 2012b, 2013). Animals remained alive throughout the experiment and were euthanized after completion of the experiments. The preparation and anesthesia2 have been described in detail previously (Slama et al., 2010; Ravicz and Rosowski, 2012b). The bony ear canal was greatly shortened in order to expose the TM to view, and a short brass tube (5 mm inner diameter, 9 mm long) was glued to the skull around the bony ear canal to allow the sound source (see next section) to be coupled repeatably to the ear. A stainless steel sleeve (1.3 mm outer diameter, 19 mm long) was glued under the brass coupler to position the tip of a probe tube microphone to measure sound pressure P_near-TM within 1–1.5 mm of the umbo in the center of the TM. A hole was made in the superior middle-ear cavity (bulla) wall to cut the tensor tympani tendon and immobilize the stapedius muscle by sectioning the tympanic segment of the facial nerve (Rosowski et al., 2006). A second hole was made in the bulla wall posterior to the ear canal and TM to view the cochlear windows and stapes. A thin bony ridge that obscured the view of the stapes and the OW and round-window (RW) niches was carefully removed. Additional bony ridges posterior and medial to the RW were removed to provide access to the bony wall of the vestibule just posterior to the OW. Several small glass beads were dropped onto the stapes and oval window to be used as reflective targets for stapes velocity measurements (Songer and Rosowski, 2006). See Fig. 1 of Slama et al. (2010) for a diagram of the preparation.

After initial measurements of V_S, a small hole (170–340 μm diameter) was drilled through the vestibular wall, and a pressure sensor was inserted into the inner ear. Later, a similar small hole was made in the base of the cochlear capsule approximately 1 mm inferior to the RW (the “hook” region), and a second pressure sensor was introduced into scala tympani (ST).

Stimuli, responses, and equipment

Stimulus generation and presentation were the same as described previously (Ravicz and Rosowski, 2012b, 2013). Three sound stimuli were used: A broadband chirp with uniform component magnitude from 49 Hz to 49 kHz, a tone sequence that ranged from 98 Hz to 49 kHz at 6 points/octave (as permitted by a 49-Hz frequency spacing) or a high-frequency sequence from 14–49 kHz at 12 points/octave.3 The chirp stimulus was repeated over a period of 30–60 s. Each tone in the sequences was played for 1–2 s. Tone stimulus levels were determined by the response of the sound source to a constant-level input and were generally 95–110 dB sound pressure level over the frequency range.

Three types of responses were measured: (1) sound pressure in the ear canal near the TM (P_near-TM), (2) velocity of the target on the stapes and of other points on nearby bone, and (3) sound pressures within the inner ear. The inner-ear sound pressure measurements were described in a previous publication (Ravicz and Rosowski, 2013) and will not be discussed here. Ear canal sound pressure was measured with a small microphone (FG23652, Knowles, Itasca, IL) attached to a thin probe tube. Sound-induced velocities were measured on the medial or posterior stapes footplate (if visible) or the posterior crus and on the petrous bone near the OW and also 2–3 mm away with a laser vibrometer (CLV-1000 with an M050 Decoder set to 2 mms⁻¹ V⁻¹ and an MOO2 filter module with the low-pass filter cutoff set at 100 kHz; Polytec, Waldbronn, Germany). Velocity response phases were corrected for the 44-μs delay of the filter module. Ear-canal microphone responses were amplified with a gain of 10 (P5, detuned; Grass, Warwick, RI). The amplified microphone and vibrometer signals were digitized at 400 kHz by a data acquisition board (PCI6122 or PXI6122, National Instruments, Austin, TX) and saved on a computer. Up to four response channels could be saved at a time.

The P_near-TM microphone, including the probe tube, was calibrated against 1/4 and 1/8 in. reference microphones as described previously (Ravicz and Rosowski, 2012b). Repeated calibrations showed variations of less than 2 dB and 0.01 cycles in phase.

Noise floor, artifact, and measurement limitations

Measurements were limited at high frequencies by noise and artifact. We define sensor noise floor (microphones or vibrometer) as the smallest discriminable stimulus-related change in sensor response, usually determined practically by a comparison of the sensor outputs with and without a stimulus present. Our noise floors were generally defined from spectra of the responses to tonal stimuli, where the noise floor was estimated from the RMS average of responses at nearby frequencies. The high-frequency limit for P_near-TM was generally around 44 kHz, and for V_S, 30–40 kHz (lower for ears ch18 and ch19; see below).

An “artifact” is defined as a sensor response to stimulus-linked mechanical or acoustical signals secondary to those of interest. For instance, a potential artifact in our velocity measurements was stimulus-induced motion of the entire head. This velocity artifact was assessed by measuring motion of the petrous bone within a few mm of the footplate as described in Sec. 2B. Generally, our data were limited by the noise floor, with significant artifact only at isolated frequencies. Data in which the responses were within a factor of 3 of noise or artifact levels have been omitted.

Access to the stapes head and footplate was via the open middle ear and was limited by the tympanic ring [see Fig. 1 of Slama et al. (2010)]. V_S was assessed from the velocity of a single point, along a line approximately 40° to the direction of piston-like motion. We made no attempt to correct for the angle between the measurement direction and the piston direction.

Course of experiment

Stapes velocity was measured with the inner ear intact; after making a hole into the cochlear vestibule; after inserting a pressure sensor in the hole; after making a hole into scala tympani; and after inserting a second sensor into the scala tympani hole. In all or most of these conditions, ME input admittance (Ravicz and Rosowski, 2012b) and sound pressures in the vestibule and scala tympani near the RW (Ravicz and Rosowski, 2013) were also measured.

RESULTS

Stapes velocity V_S

All quantities described in this section were measured with the ME opened and are normalized by P_near-TM.

Inner ear intact

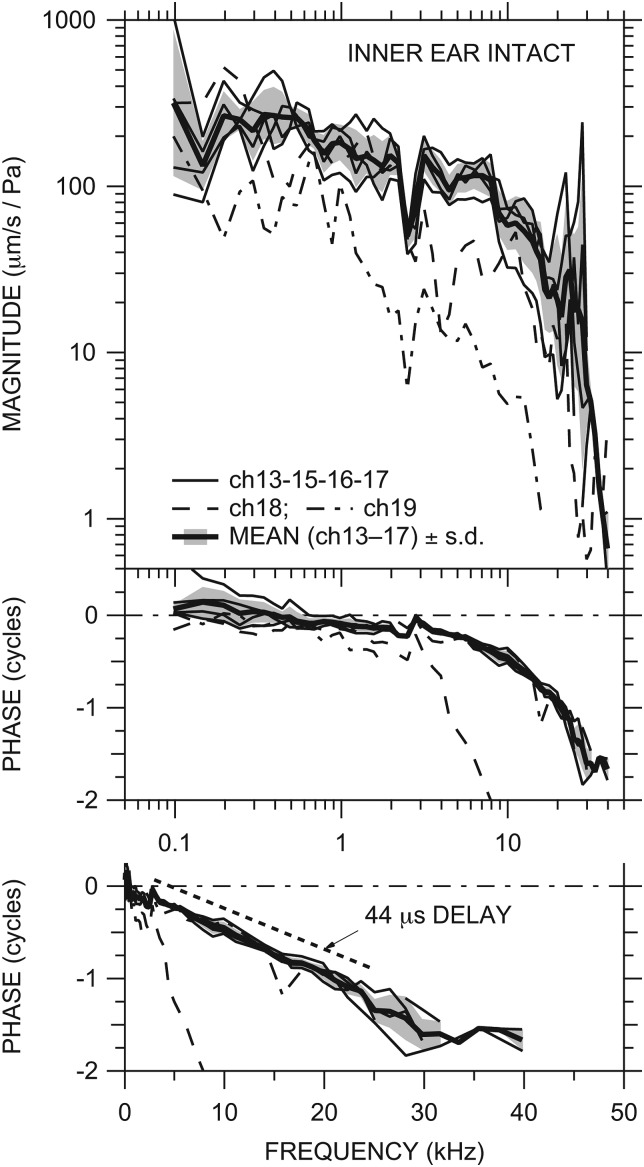
Stapes velocity V_S was measured in 6 of the 7 ears (not ch11) with the inner ear intact. Middle-ear velocity transfer functions H_V (V_S normalized by P_near-TM) measured with tone sequences in each ear are illustrated in Fig. 2. The thin lines represent a single measurement in one ear or the logarithmic mean of two measurements made in the same ear under similar stimulus conditions; several measurements with similar normalized results were taken at lower stimulus levels. Variation between these measurements was generally less than a factor of 1.5. Hints of a stimulus-level-dependent nonlinearity at low frequencies (below 400 Hz; Rosowski et al., 2006) were seen in two ears but not investigated further4 as it was not the focus of this study.

Figure 2.

Middle-ear velocity transfer function H_V (stapes velocity V_S normalized by P_near-TM) in six ears with the IE intact: ch18 and ch19 (dashed and dot-dashed lines, respectively) and others (thin solid lines). Also shown is the mean H_V (thick solid line) of all ears except ch18 and ch19 ± 1 standard deviation (s.d.—shaded area; see text). Top: magnitude; middle: phase; bottom: phase on a linear frequency scale. ∠H_V in ear ch18 reaches −4.5 cycles by 30 kHz. The phase slope corresponding to a constant delay of 44 μs is shown between 3 and 25 kHz by the dotted line.

Between 100 Hz and about 10 kHz the magnitude of H_V (|H_V|) was between 30 and 500 μm s⁻¹ Pa⁻¹ in nearly all ears. |H_V| in all ears decreased slowly with frequency over this range and the phrase angle of H_V (∠H_V) was slightly negative (except in ear ch18 above 3 kHz), which implies that H_V is controlled primarily by resistance with some influence of mass. In all ears H_V showed a sharp decrease in magnitude of ∼30% coupled with a 0.25 cycle phase step around 2.5 kHz, presumably due to a resonance between the middle-ear cavity and the bulla hole (Ravicz et al., 1992; Rosowski et al., 2006; see Sec. 4A2 below). Above 10 kHz |H_V| decreased more rapidly with frequency and ∠H_V continued to accumulate. Above about 18 kHz |H_V| showed a peak in most ears. The frequency dependence of ∠H_V between 3 and 25 kHz is well fit by a delay of 44 μs (bottom panel of Fig. 2).

Above about 25 kHz |H_V| decreased rapidly, falling by a factor of 10–30 by 35 kHz in all ears. ∠H_V also decreased sharply around 25–30 kHz before flattening out at the highest measurable frequencies. Data obtained with chirp stimuli with a finer frequency spacing (see Sec. 2B above) helped define this rapid phase change at high frequencies but were contaminated by noise at the highest frequencies; hence, the phase accumulation above 25 kHz could be 1 cycle greater than what is shown.

H_V was similar in four of the six ears; the exceptions were ears ch18 and ch19 (dashed and dot-dashed lines, respectively). In these ears, |H_V| decreased more rapidly with frequency above 2.5 kHz than in the other ears, and ∠H_V was generally more negative. We have reason to believe that we damaged the ossicular chain in ear ch18;5 and since H_V in ch19 shows similar behavior, we suspect ossicular chain damage in that ear as well.

Figure 2 also shows the logarithmic mean of stapes velocity in ears ch13, ch15, ch16, and ch17 (thick line) ±1 standard deviation (s.d.; shading). The mean H_V is representative of H_V in most ears.

The contribution of noise and stimulus artifacts to the measured H_V was checked in all ears by measuring the stimulus-linked velocity of points near the OW that were not expected to respond to sound (Sec. 2C). Motion of the petrous bone was generally a factor of 100 or more lower than |V_S|, which indicates that motion of the whole head was negligible. Interestingly, in some ears, motion of the bone near the OW was sometimes only a factor of 5 lower than |V_S|, suggesting a compliant vestibular wall that provides a shunt path for volume velocity around the cochlear input immittance which should lead to an increase in stapes velocity (though we saw no correlation between |H_V| or |Y_C| and vestibular wall velocity; see Sec. 3C below).

Sensor in vestibule

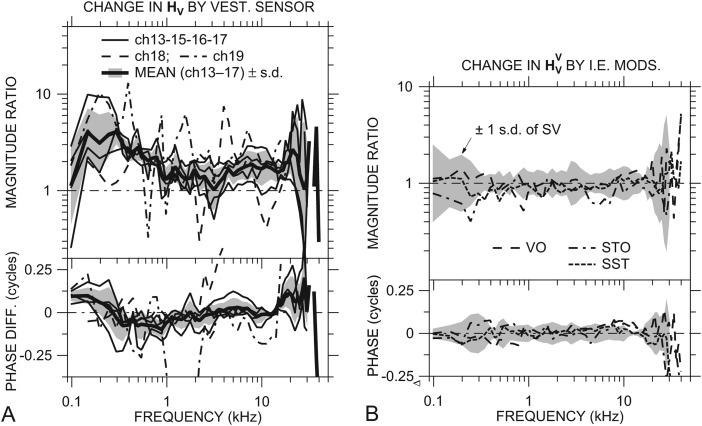
Middle-ear velocity transfer functions were also computed from stapes velocity measured in all 7 ears after a pressure sensor was inserted into the vestibule (${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$). As for H_V, one or two V_S measurements were made in each ear under similar stimulus conditions, these measurements generally varied by less than a factor of 1.5, and only hints of low-frequency stimulus level dependence nonlinearity were seen.4 The ratio rH_V = ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$/H_V, which describes the effect of opening the IE hole and placing the sensor on H_V, is shown for six ears in Fig. 3A.

Figure 3.

(A) Effect of a sensor in the vestibule on H_V in individual ears: rH_V = ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$/H_V. Data for ch18 and ch19 are shown by dashed and dot-dashed lines, respectively; others by thin solid lines. Mean effects ±1 s.d. shown by thick solid lines and shading. (B) Ratio of normalized stapes velocity with various other inner-ear manipulations to ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ with a sensor in the vestibule: the vestibule hole open but no sensor in place (VO), a sensor in the vestibule hole and a hole in scala tympani (STO), and sensors in both the vestibule and ST holes (SST). The gray regions are ±1 s.d. of |${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$| about 1 and of $\mathrm{\angle }{\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ about 0. The result that the plotted ratios are generally within ±1 s.d. of ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ suggests that the other manipulations had little additional effect on ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$. Both panels—top: magnitude; bottom: phase.

Opening the small hole in the vestibule and inserting the sensor caused an increase in |${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$| relative to |H_V| in all six ears at nearly all frequencies measured. The |rH_V| was 2 or higher between 150 and 600 Hz (400–600 Hz in ear ch18) and near 20 kHz. There was a weak correlation between the open hole area (the area between the sensor and the surrounding bone) and |rH_V| between 150 and 300 Hz. The sensor caused a substantial phase increase in ∠H_V (∠rH_V ≈ +0.1 cycle) in most ears at the lowest frequencies (below 250 Hz) and near 20 kHz and a slight phase decrease between 0.3 and 1 kHz. The changes in H_V at the lowest frequencies resulting from opening a hole in the vestibule and inserting the sensor are consistent with a decrease in cochlear resistance allowing middle-ear compliance to become more important in determining stapes response (Slama et al., 2010).

The mean rH_V (in all ears except ch18 and ch19; thick solid line) is descriptive of the effect of the vestibule hole with the sensor in place in ears ch13–ch17. In both ears ch18 and ch19, rH_V shows spectral peaks and notches not seen in the other ears. The increase in | ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$| relative to |H_V| in ears ch13–ch17 was statistically significant6 at nearly all frequencies except 100 Hz, near 3 kHz, and above 20 kHz. The differences between $\mathrm{\angle }{\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ and ∠H_V were statistically significant below 200 Hz and from about 0.5 to 1 kHz.

In other conditions vs sensor in vestibule

Once a hole was made in the vestibule and a sensor was inserted, other IE modifications had much smaller effects. Figure 3B shows the mean ratios of normalized stapes velocity to ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ under several other conditions: with the vestibule hole open but no sensor in place (VO), with a sensor in the vestibule hole and a hole in scala tympani (STO), and with a sensor in both the vestibule and ST holes (SST). The shaded area is ±1 s.d. of ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$. The normalized stapes velocity measured in the other conditions was statistically indistinguishable from ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$.

High-frequency correction to H_V

In a previous paper we developed a correction factor $\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{T}\mathbf{M}}$ to estimate ear canal sound pressure very close to the TM at high frequencies from P_near-TM in each of the individual animals [see Ravicz and Rosowski, 2013, Fig. 5(A)] based on a simple uniform-tube acoustical model of the brass coupler and the chinchilla ear canal remnant (Ravicz and Rosowski, 2012b). Due to limitations in our analysis (Ravicz and Rosowski, 2012b), $\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{T}\mathbf{M}}$ in individual ears is well-defined only at frequencies below 30 kHz. The estimated ME velocity transfer functions ${\widehat{\mathbf{H}}}_{\mathbf{V}}$ (with intact IE) and ${\widehat{\mathbf{H}}}_{\mathbf{V}}^{\mathbf{V}}$ (with a sensor in the vestibule), defined as stapes velocity normalized by sound pressure at the TM, are computed from H_V and ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ measured in each ear:

$${\widehat{\mathbf{H}}}_{\mathbf{V}}={\mathbf{H}}_{\mathbf{V}}\hspace{0.17em}\hspace{0.17em}\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{T}\mathbf{M}}\hspace{1em}\text{and}\hspace{1em}{\widehat{\mathbf{H}}}_{\mathbf{V}}^{\mathbf{V}}={\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}\hspace{0.17em}\hspace{0.17em}\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{T}\mathbf{M}}.$$ (2)

The predicted mean ${\widehat{\mathbf{H}}}_{\mathbf{V}}$ and ${\widehat{\mathbf{H}}}_{\mathbf{V}}^{\mathbf{V}}$ are shown in Figs. 4A, 4B (solid line and shaded area in each panel). Also shown are the mean uncorrected H_V (from Fig. 2) and ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ (dashed lines). The effects of the $\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{T}\mathbf{M}}$ correction are to (a) reduce |H_V| and |${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$| in a frequency band around the peak near 21–28 kHz in transfer functions in individual ears (see Fig. 2), which reduces the mean |H_V| and |${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$| by as much as a factor of 2–4 between 10 kHz and 30 kHz and removes the peak near 23 kHz; (b) increase ∠H_V and ∠${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ in individual ears in the 21–28 kHz range; and (c) omit data above about 30 kHz. The predicted ${\widehat{\mathbf{H}}}_{\mathbf{V}}$ and ${\widehat{\mathbf{H}}}_{\mathbf{V}}^{\mathbf{V}}$ represent our best estimates of H_V and ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ at frequencies up to 30 kHz.

Figure 4.

Mean ME velocity transfer functions estimated using a correction for P_TM derived from an ear-canal model. (A) Mean ${\widehat{\mathbf{H}}}_{\mathbf{V}}$ in six ears (thick solid line) ±1 s.d. (shading) estimated from H_V (Fig. 2; dashed line) with the $\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{T}\mathbf{M}}$ correction. (B) Mean ${\widehat{\mathbf{H}}}_{\mathbf{V}}^{\mathbf{V}}$ in seven ears (thick solid line) ±1 s.d. (shading) estimated from ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ (dashed line) with the $\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{T}\mathbf{M}}$ correction. Top: magnitude; bottom: phase.

Cochlear input admittance Y_C

Cochlear input admittance (sensor in vestibule)

The cochlear input admittance Y_C is the acoustical load that the IE presents to the ME and is an important component of inner-ear power computations (see Sec. 1). We computed Y_C with a sensor in the vestibule from P_V and V_S measured simultaneously by

$${\mathbf{Y}}_{\mathbf{C}}={\mathbf{V}}_{\mathbf{S}}\hspace{0.17em}\hspace{0.17em}{A}_{\mathit{F}\mathit{P}}/{\mathbf{P}}_{\mathbf{V}}={\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}\hspace{0.17em}\hspace{0.17em}{A}_{\mathit{F}\mathit{P}}/{\mathbf{G}}_{\mathbf{M}\mathbf{E}\mathbf{P}},$$ (3)

using the previously presented G_MEP (Ravicz and Rosowski, 2013) and a stapes footplate area A_FP of 2.0 mm² (Vrettakos et al., 1988). We assume that stapes motion is basically piston-like so that the stapes volume velocity in the piston direction is the simple product of V_S and A_FP. (We test that assumption in Sec. 3C2 below.) Note that, because V_S and P_V were measured simultaneously in each ear, the normalization of both by either P_near-TM or P_TM is superfluous, and the Y_C computation is independent of any uncertainties in ear canal sound pressure. We used both ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ and G_MEP before applying the P_TM correction factor discussed in Sec. 3B.

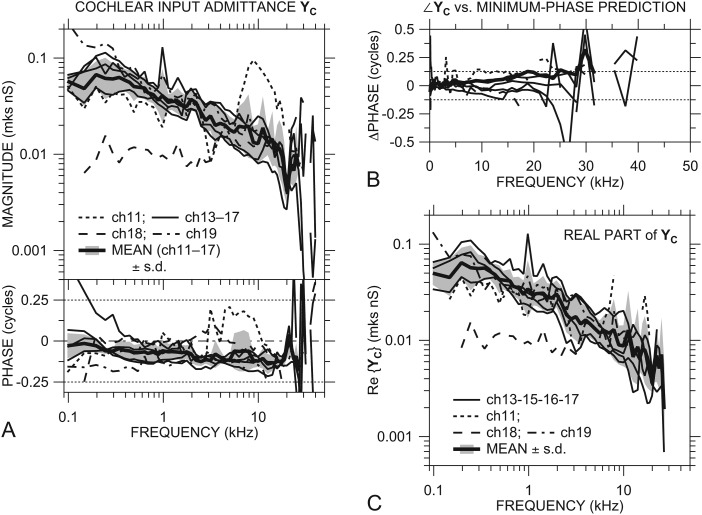
Y_C in the seven ears is shown in Fig. 5A. Both |Y_C| and ∠Y_C were similar among most ears over the entire frequency range of measurement: |Y_C| decreased slowly with frequency from 0.03–0.08 mks nS (nanosiemens = 10⁻⁹ m³ s⁻¹ Pa⁻¹) at 500 Hz to 0.003–0.015 nS at 20 kHz. Below 500 Hz |Y_C| was approximately flat with frequency and decreased at the lowest frequencies. Y_C in most ears showed a magnitude notch and phase peak near 20 kHz. ∠Y_C was generally between 0 and −0.125 cycles below 20 kHz. The |Y_C| slope and ∠Y_C in this frequency range are consistent with the admittance of a system dominated by a mixture of mass and resistance.

Figure 5.

(A) Cochlear input admittance Y_C with an IE sensor in all ears, computed from ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ and G_MEP [Rosowski and Ravicz, 2013, Fig. 2(A)] in the same ears. Y_C in ch11, ch18, and ch19 shown by dotted, dashed, and dot-dashed lines, respectively, others by thin solid lines. Also shown is the mean Y_C ± 1 s.d. (thick solid line and shaded area) of all ears except ch18 and ch19 (see text). Points where ∠Y_C was inconsistent with a passive system or differed from a minimum-phase estimate by more than 0.125 cycle are omitted from the computation of the mean. Top: magnitude; bottom: phase. (B) Deviation of ∠Y_C in each ear from a minimum-phase estimate based on |Y_C| in that ear. Line types as for panel A. (C) Real part of cochlear input admittance Re{Y_C}, omitting points based on the passive-system and minimum-phase criteria described above. Line types as for panel (A). Mean Re{Y_C} ± 1 s.d. is shown by the thick solid line and shading.

In several ears Eq. 3 produced outlier values in Y_C over part of the frequency range. |Y_C| in ear ch18 was a factor of 3–10 lower than in other ears at frequencies below 3 kHz and flat with frequency, and ∠Y_C in ch18 was generally closer to 0 than ∠Y_C in the other ears, consistent with Y_C being almost purely resistive. |Y_C| in ear ch11 showed shallow notches near 0.25, 0.5, 1, and 3 kHz and a broad peak at 9 kHz that were not present in the other ears, and ∠Y_C in ch11 was much higher (∼+0.2 cycles) between 3 and 10 kHz, consistent with an additional stiffness-mass resonance. |Y_C| in ch19 was higher below 300 Hz than in the other ears, and ∠Y_C in ch17 was higher below 350 Hz than in the other ears.

Y_C in ch19 was similar to Y_C in other ears above 300 Hz, even though |V_S| and |G_MEP| in this ear were lower than in other ears. This similarity is consistent with any ME damage in this ear being lateral to the stapes footplate and annular ligament.

Although we saw measurable motion of the vestibular wall near the OW in most ears (see Sec. 3A2 above), there was no correlation between this motion and |Y_C|: For instance, we would expect that higher vestibular wall motion would lead to a higher |Y_C| and higher |V_S|, yet the vestibular wall velocity was highest in ears ch18, which had the lowest |V_S| and lowest |Y_C| at frequencies less than 3 kHz.

Application of physical constraints

Y_C in all ears below 22 kHz (where not contaminated by artifact or noise) is generally consistent with physical constraints. Because we used high stimulus levels, measured P_V far from the cochlear partition, and saw no signs of level-dependent nonlinearity in P_V (Ravicz and Rosowski, 2013) or V_S, the cochlea input immittance should appear passive. ∠Y_C in all ears (except ear ch17 below 200 Hz) is consistent with a driving-point admittance of a passive system: ∠Y_C is between −0.25 and +0.25 cycles.

Furthermore, the relationship between |Y_C| slope with frequency and ∠Y_C in all ears is consistent with the input admittance of a minimum-phase system7 in this frequency range, as seen in Fig. 5B: The discrepancy between the measured ∠Y_C and its minimum-phase value predicted from |Y_C| is generally less than 0.125 cycles below 22 kHz except at a few isolated frequencies. These observations support the validity of our H_V and G_MEP data and suggest that possible complications such as non-piston-like stapes motion do not affect our measurements substantially below 22 kHz.

At higher frequencies (>22 kHz), ∠Y_C in several ears was outside ±0.25 cycles, and |Y_C| was quite variable and increased sharply in some ears [Fig. 5A]. At these frequencies ∠Y_C differed substantially from the minimum-phase prediction [Fig. 5B]. This result suggests that our assumption that the measured V_S is representative of piston-like stapes motion breaks down above 22 kHz, which can lead to errors in V_S and therefore Y_C. Studies in other species have shown that the nature of stapes motion can deviate substantially from that of a simple piston [e.g., in gerbil (Decraemer et al., 2007; Ravicz et al., 2008) and human (Hato et al., 2003)], so it is not surprising to see evidence of such non-piston-like stapes motion at high frequencies in chinchilla as well.

Figure 5A also includes the (logarithmic) mean of Y_C ± 1 s.d., where those points in individual ears where ∠Y_C was inconsistent with a passive system or deviated from the minimum-phase estimate by more than 0.125 cycles were omitted from the mean. Data from ears ch18 and ch19 were also omitted, even though Y_C in ch19 was similar to Y_C in the other ears. The mean Y_C includes ear ch11, which has a Y_C unlike other ears above 3 kHz but which is included in the means of H_V and G_MEP. The mean Y_C captures the important features of Y_C in most individual ears below 24 kHz. The phase of the mean Y_C deviates from a minimum-phase estimate by less than 0.05 cycles below 12 kHz and by less than 0.125 cycles below 27 kHz [Fig. 5B], the high-frequency limit by the passive and minimum-phase criteria above.

Real part of cochlear input admittance Re{Y_C}

The real part of Y_C (also called the cochlear conductance) is an essential component of our sound power and efficiency calculations [see Eq. 5 below]. Figure 5C shows Re{Y_C}=|Y_C| cos ∠Y_C in all ears (trimmed as described above). Re{Y_C} generally increased slightly between 50 Hz and 250 Hz and decreased from about 0.05 nS at 500 Hz to 0.01 nS at 10 kHz and more sharply to about 0.005 nS at 20 kHz. Above about 8 kHz Re{Y_C} generally varies with the inverse of frequency f, consistent with a slope of −1 on a log-log scale. Above 20 kHz Re{Y_C} generally increased sharply, then decreased more at higher frequencies. Consistent with Y_C described above, Re{Y_C} in ear ch18 was lower below 4 kHz than Re{Y_C} in other ears. The logarithmic mean and s.d. of Re{Y_C} (omitting ch18 and ch19) are representative of Re{Y_C} in most individual ears.

Middle-ear efficiency MEE

The MEE, the ratio of sound power entering the cochlea to sound power entering the middle ear [Eq. 1], is an important descriptor of the role of the ME in sound transmission from the external environment to the sensory cells of the cochlea. Sound power (time-averaged) entering the cochlea W_C is given by

$$W_C=\frac{1}{2}{\mathbf{P}}_{\mathbf{V}\hspace{0.17em}}\hspace{0.17em}{\mathbf{U}}_{\mathbf{S}}^{*}=\frac{1}{2}\left|{\mathbf{P}}_{\mathbf{V}}\right|\hspace{0.17em}\left|{\mathbf{U}}_{\mathbf{S}}\right|\hspace{0.17em}\cos \left(\mathrm{\angle }{\mathbf{P}}_{\mathbf{V}}-\mathrm{\angle }{\mathbf{U}}_{\mathbf{S}}\right)=\frac{1}{2}\left|{\mathbf{P}}_{\mathbf{V}}\right|\hspace{0.17em}\left|{\mathbf{U}}_{\mathbf{S}}\right|\hspace{0.17em}\cos \left(\mathrm{\angle }{\mathbf{Z}}_{\mathbf{C}}\right),$$ (4a)

where U_S* is the complex conjugate of U_S, and the cochlear input impedance Z_C = Y_C^–1. W_C can also be computed from the square of the magnitude of either P_V or U_S and the real part of the immittance by

$$W_C=\frac{1}{2}{\left|{\mathbf{U}}_{\mathbf{S}}\right|}^2\hspace{0.17em}\hspace{0.17em}\mathrm{Re}\left\{{\mathbf{Z}}_{\mathbf{C}}\right\}=\frac{1}{2}{\left|{\mathbf{P}}_{\mathbf{V}}\right|}^2\hspace{0.17em}\hspace{0.17em}\mathrm{Re}\left\{{\mathbf{Y}}_{\mathbf{C}}\right\}.$$ (4b)

Similarly, the time-averaged power entering the ME is given by

$$W_{\mathit{M}\mathit{E}}=\hspace{0.17em}\frac{1}{2}{\left|{\mathbf{U}}_{\mathbf{T}\mathbf{M}}\right|}^2\text{Re}\left\{{\mathbf{Z}}_{\mathbf{T}\mathbf{M}}\right\}\hspace{1em}\text{or}\hspace{1em}{W}_{\mathit{M}\mathit{E}}=\frac{1}{2}{\left|{\mathbf{P}}_{\mathbf{T}\mathbf{M}}\right|}^2\text{Re}\left\{{\mathbf{Y}}_{\mathbf{T}\mathbf{M}}\right\},$$ (4c)

where U_TM is the volume velocity at the TM, Z_TM = Y_TM⁻¹, and Re{Y_TM} is the real part of Y_TM as above.

We computed MEE for individual chinchillas using our measurements of Re{Y_C} [Fig. 5C], G_MEP with the P_TM correction [Ravicz and Rosowski, 2013, Fig. 5(B)], and Re{Y_TM} [Ravicz and Rosowski, 2012b, Fig. 5(D)] in the same ears

$$\text{MEE}=\frac{W_C}{W_{\mathit{M}\mathit{E}}} =\frac{{\left|{\mathbf{P}}_{\mathbf{V}}\right|}^2\mathrm{Re}\left\{{\mathbf{Y}}_{\mathbf{C}}\right\}}{{\left|{\mathbf{P}}_{\mathbf{T}\mathbf{M}}\right|}^2\mathrm{Re}\left\{{\mathbf{Y}}_{\mathbf{T}\mathbf{M}}\right\}} ={\left|{\mathbf{G}}_{\mathbf{M}\mathbf{E}\mathbf{P}}\right|}^2\frac{\mathrm{Re}\left\{{\mathbf{Y}}_{\mathbf{C}}\right\}}{\mathrm{Re}\left\{{\mathbf{Y}}_{\mathbf{T}\mathbf{M}}\right\}}.$$ (5)

Because MEE is a power transfer function and the middle ear is considered passive, MEE can never exceed 1. If no power enters the cochlea, MEE = 0.

An advantage of our choice of |G_MEP| and Y_C for MEE computations is that these parameters are relatively unaffected by experimental limitations: (a) P_V is a scalar quantity, and the measured G_MEP is independent of measurement direction (unlike V_S). (b) Y_C is computed from simultaneous measurements of P_V and V_S and is unaffected by P_TM measurement errors. (c) Y_C is governed by physical constraints, so frequencies at which Y_C is inconsistent with these physical constraints (such as might result from non-piston components of stapes motion) can be identified and these suspect data can be omitted from further analysis (see Sec. 3C2 above). We showed previously that Re{Y_TM} varies little with small variations in measurement location at frequencies up to 17 kHz (Ravicz and Rosowski, 2012b).

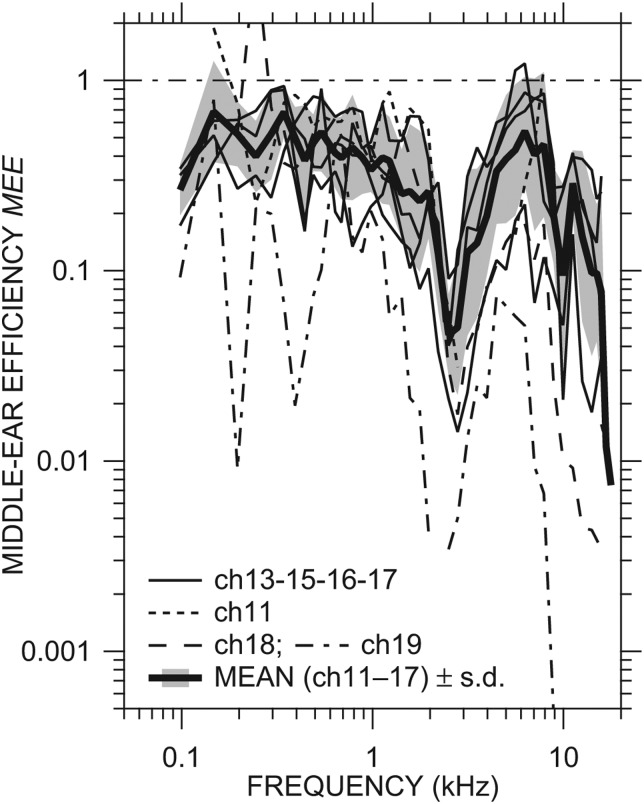
The MEE computed in individual ears with the ME open and a sensor in the vestibule is shown in Fig. 6. Our estimates of MEE are limited to frequencies below 17 kHz, the upper frequency of valid Re{Y_TM} measurement (Ravicz and Rosowski 2012b). In ears ch11–ch17, MEE was generally between 0.2 and 1 below 2 kHz and from 3.5 to 8 kHz and decreased at higher frequencies. Ears ch11, ch17, and ch18 had MEE > 1 at 2–3 isolated frequencies; in all other ears, MEE < 1 at all frequencies measured. All ears showed a sharp drop in MEE between 2 and 3.5 kHz, presumably due to the bulla hole resonance near 2.5 kHz (see Sec. 4A5 below for more discussion). In the two ears in which ossicular chain damage was suspected (ch18 and ch19), MEE was more variable at low frequencies than in the other ears. MEE in ear ch18 was comparable to ears ch11–ch17 below 2 kHz and lower than in most of those ears but still within their range of variation up to 10 kHz. MEE in ear ch19 was much lower than in other ears across the frequency range, consistent with other indications of poor ME transmission [H_V (Fig. 3A] and G_MEP (Ravicz and Rosowski, 2013)].

Figure 6.

MEE in all ears, computed from Re{Y_C} [Fig. 5C] and previously presented Re{Y_TM} and |G_MEP| in the same ears. MEE in ch11, ch18, and ch19 are shown by dotted, dashed, and dot-dashed lines, respectively, others by thin solid lines. MEE = 1 indicates perfect efficiency. Also shown is the mean MEE ± 1 s.d. (thick solid line and shaded area) of all ears except ch18 and ch19.

Figure 6 also includes the (logarithmic) mean MEE from ears ch11, ch13, ch15, ch16, and ch17 ± 1 s.d. (thick line and shading). The mean MEE decreases from 0.7 at 150 and 350 Hz to 0.3 at 2 kHz, has a sharp deep notch between 2 and 3.5 kHz, is between 0.1 and 0.6 between 3 and 14 kHz, and decreases sharply between 15 and 17 kHz. The mean + 1 s.d. is slightly greater than 1 below 150 Hz and between 6 and 8 kHz, and less than 1 at all other frequencies. With the exception of the frequency region around the bulla hole resonance (2.5 kHz), MEE is approximately 0.5 over a wide frequency range, 0.1–8 kHz.

DISCUSSION

We have presented measurements of stapes velocity V_S with a bulla hole open and the inner ear intact or with a sensor in the cochlear vestibule, and we have computed the ME velocity transfer function H_V from V_S and estimates of sound pressure at the TM. We have used simultaneous measurements of the ME pressure gain measured in the same ears (Ravicz and Rosowski, 2013) and published values of the stapes footplate area (Vrettakos et al., 1988) to compute cochlear input admittance Y_C and its real part Re{Y_C} in individual ears, and we have used concurrent measurements of ME input admittance Y_TM in the same ears (Ravicz and Rosowski, 2012b) to compute ME efficiency in individual ears. In this section we examine the effects of experimental conditions on our measurements and computed values. We also compare our H_V and Y_C data and estimates of MEE to those from previous studies.

Effects of experimental conditions on H_V, Y_C, and MEE

In these experiments we (1) made two large (∼5 mm diameter) holes in the auditory bulla for access to the stapes, OW, RW, tensor tympani tendon, and facial nerve and (2) made a 0.2-mm diameter hole into the cochlear vestibule and inserted a sensor to measure sound pressure. Our manipulations of the middle-ear cavities and the introduction of holes and sensors into the inner ear are expected to cause significant but fairly-well-defined changes in ME transfer functions, Y_C, and MEE.

Effect of EC sound pressure measurement location on H_V and Y_C

In computing the stapes velocity transfer function, we initially normalized the measured V_S by P_near-TM (the sound pressure measured within 1–1.5 mm of the center of the TM). We used a correction computed from an ear canal model (Ravicz and Rosowski, 2012b, 2013) to compute a better estimate of P_TM and therefore H_V (Fig. 4), as we did previously for G_MEP [Ravicz and Rosowski, 2013, Fig. 5(B)]. The correction from P_near-TM to P_TM has a small but significant effect on our estimates of H_V at frequencies above 10 kHz as it did for G_MEP.

Because we compute Y_C directly from the ratio of simultaneous measurements of V_S and P_V, P_TM does not enter into the computation of Y_C, and the ear canal sound pressure measurements have no effect on our Y_C estimates.

Effect of opening the middle ear on H_V and Y_C

Consistent with previous measurements of cochlear microphonic (Dallos, 1970), umbo velocity (Ruggero et al., 1990), and middle-ear input admittance (Rosowski et al., 2006), we expect that the effect of opening the ME cavity on middle-ear sound transfer is significant only at low and moderate frequencies. Based on these previous data we estimate that the open ME caused an increase in |H_V| of about a factor of 5 at 100 Hz and a phase shift of as much as +0.25 cycle below 1 kHz relative to the intact state (Ravicz and Rosowski, 2013). Furthermore, the data of Rosowski et al. (2006) suggest that the magnitude notch and phase step in H_V (and G_MEP; Ravicz and Rosowski, 2013) near 2.5 kHz result from a resonance between the acoustic stiffness of the air in the ME cavity and the acoustic mass of the air associated with transmission through and radiation from the bulla hole.

The “series model” of the middle ear (Zwislocki, 1962; Møller, 1965; Huang et al., 1997; Voss et al., 2000) suggests that the ME cavity acts to restrict the motion of the TM by coupling the sound pressures produced in the middle-ear cavity to the inward and outward motions of the TM. While some have suggested that the resultant middle-ear pressures can also directly stimulate the inner ear, the magnitudes of these effects are estimated to be quite small (Peake et al., 1992; Shera and Zweig, 1992); therefore, opening the ME should have a negligible effect on Y_C. The cancellation of the cavity-hole-induced notches and phase steps near 2.5 kHz in G_MEP and H_V in the computation of Y_C is consistent with this view.

Effect of the angle between the V_S measurement direction and piston-like stapes motion

Measurements of V_S were made at an angle roughly 40° to the “piston-like” direction of stapes motion (where the piston-like direction is roughly perpendicular to the plane of the stapes footplate). This angle was necessary because the footplate is behind the TM and is at best only partly observable through the bulla holes. Measurements of stapes motion in other species (Decraemer et al., 2007 and Ravicz et al., 2008 in gerbil; Hato et al., 2003 and Chien et al., 2006 in human temporal bones) have shown that stapes motion is mostly piston-like at low and moderately high frequencies and deviates considerably from piston-like at high frequencies. Such a deviation can cause Y_C computed from V_S measured at a single location on the stapes to appear non-minimum-phase or even non-passive (e.g., Decraemer et al., 2007).

At low frequencies, where the primary mode of motion of the stapes is simple and piston-like, motion in the piston direction can be estimated fairly accurately from measurements along another direction using the cosine of the angle between the two directions (40°), which would increase V_S by a factor of (cos 40°)^–1 = 1.3 at all frequencies. At higher frequencies, where other modes of motion could become significant, the relationship between stapes motion and measurements in a non-piston-like direction could be more complicated (Chien et al., 2006). Because of these uncertainties, the V_S measurements we present are not corrected for the angle of measurement. Instead, we use physical constraints on the input immittance to establish limits on valid V_S measurements. The observation that Y_C is well fit by a minimum-phase estimate at frequencies below 22 kHz (see Sec. 3C2) suggests that V_S is a reasonably good description of the piston component of stapes motion to at least 22 kHz.

Effect of the vestibule hole and sensor on H_V and Y_C

The observed changes (small increases in magnitude and phase angle) in H_V caused by opening the inner ear and inserting a sensor [Fig. 3A] are qualitatively similar to the changes observed in a previous study [Slama et al., 2010, Fig. 4(B)]. However, the increases we see in |H_V| below 4 kHz and in ∠H_V below 250 Hz are larger than in the previous study8 and statistically significant. These increases may be the result of a larger sensor hole. We did not see the distinct peak in effect near 6 kHz seen by Slama et al. The effects we saw were virtually identical to the effect of a superior semicircular canal dehiscence (SCD) seen by Songer and Rosowski (2006, Fig. 10), including the double-humped increase in |H_V| at about 150 and 300 Hz. We did not observe any diminution of effect below 150 Hz.

Because it was necessary to open the inner ear to measure P_V, and we were unable to seal the hole around the sensor, we were unable to determine the effect of the IE hole and vestibule sensor directly on P_V or Y_C. Since the impedance of the sensor is sufficiently high to have negligible effect on Y_C (Ravicz and Rosowski, 2013), we assume that the admittance of the hole around the sensor Y_H acts in parallel with ${\mathbf{Y}}_{\mathbf{C}}^{\mathbf{I}}$, the cochlear input admittance in the intact ear [see model in Slama et al., 2010, Fig. 7(A)]. We also expect that, with an IE hole, the magnitude of the measured admittance Y_C = |Y_H| + |${\mathbf{Y}}_{\mathbf{C}}^{\mathbf{I}}$| is greater than |${\mathbf{Y}}_{\mathbf{C}}^{\mathbf{I}}$| alone. The computed9|Y_H| for hole diameters between 200 and 400 μm is comparable to our measured |Y_C| below 1–2 kHz and substantially smaller at higher frequencies, which suggests that the effect of the hole is significant only below 1–2 kHz. Therefore, we expect that |${\mathbf{Y}}_{\mathbf{C}}^{\mathbf{I}}$| is lower than the measured |Y_C| shown in Fig. 5A below 1–2 kHz, as predicted by a mathematical analysis (Ravicz and Rosowski, 2012a); and estimates of Y_C from P_V measured with a sensor sealed in a hole through the braincase into the vestibule show a roughly constant magnitude with frequency below 1–2 kHz (D.C. Chhan and J.J. Rosowski, private communication, 2011).

Effect of opening the middle ear on MEE

At frequencies less than 1 kHz: The decrease in middle-ear stiffness.

The air in the intact middle-ear cavity acts as a nearly ideal acoustical stiffness K_MEC in series with the stiffness of the TM and ossicles K_TOC, where the total stiffness K_TM = K_MEC + K_TOC dominates the middle-ear input impedance (that governs TM and ossicular motion) at low frequencies (Zwislocki, 1962; Rosowski, 1994; Rosowski et al., 2006). If the only effect of opening the ME cavity is to remove the contribution of K_MEC (Zwislocki, 1962; Møller, 1965; Ravicz et al., 1992; Rosowski, 1994), we would expect this manipulation to have a significant effect on H_V, G_MEP, and Y_TM only at frequencies below 1 kHz and very little effect on Y_C and MEE (see below).

The removal of the contribution of K_MEC by the open bulla hole is responsible for the increase in middle-ear sound transfer and |Y_TM| at frequencies below 1 kHz that has been observed after opening the ME cavities in chinchilla (Dallos, 1970; Ruggero et al., 1990; Rosowski et al., 2006). A comparison of the effects of the open ME on stapes motion (Ruggero et al., 1990, Fig. 10) and Re{Y_TM} [Ravicz and Rosowski, 2012b, Fig. 6(B)] shows that, in the computation of MEE, the increase in the |G_MEP|² term in Eq. 5 by the open ME (Ravicz and Rosowski, 2013) is balanced by a proportionate increase in Re{Y_TM}. This conclusion is consistent with the removal of an ideal stiffness, which by definition is purely reactive and does not absorb power. (Deviations from a pure stiffness effect due to viscous and thermal losses to the bulla walls are expected to be small and significant only at very low frequencies.) Therefore, the reduction of middle-ear stiffness due to the open bulla hole should have very little effect on MEE.

At frequencies near 2.5 kHz: The introduction of a bulla-hole resonance.

While removing the contribution of the middle-ear air stiffness K_MEC has little effect on Re{Y_TM}, the introduction of a hole in the bulla has a substantial effect. This occurs because the bulla holes also introduce (a) a “cavity-hole” antiresonance10 between K_TM and the acoustic mass of the holes and (b) losses via the radiation of sound from the hole. This antiresonance produces a narrow deep notch in |Y_TM| (Rosowski et al., 2006, Fig. 3; Ravicz and Rosowski, 2012b, Fig. 6) that is associated with the narrow notches and phase steps observed in G_MEP [Ravicz and Rosowski, 2013, Fig. 2(A)] and our H_V (Fig. 2) near 2.5 kHz. Because the notch appears in both |G_MEP| and |H_V|, it does not appear in |Y_C| or Re{Y_C} (Fig. 5), consistent with the assertion in Sec. 4A2 above that |Y_C| is not affected by the state of the middle ear. The shape and size of the notch are comparable in |G_MEP| and Re{Y_TM}, so the net effect on MEE (due to the |G_MEP|² term) is a notch about a factor of 3 in depth. The |Y_TM| notch is present only in the open-hole condition [Rosowski et al., 2006, Fig. 3(B) vs 3(A)], and therefore we expect that closing the cavity hole would remove the MEE notch near 2.5 kHz and have little effect at other frequencies.

Summary of effects of experimental methods

We have chosen the variables used in MEE computations to minimize the effects of experimental conditions and measurement errors. The openings in the vestibule should affect MEE only at low frequencies (below 1 kHz), while the opening in the ME wall should affect MEE only near the bulla hole antiresonance near 2.5 kHz. If the low-frequency effect of the vestibule hole is not large, MEE computed from measurements with an open ME and a vestibule sensor should be fairly representative of MEE in the intact ear except near the bulla antiresonance frequency.

Comparison of H_V and Y_C to previous studies

H_V

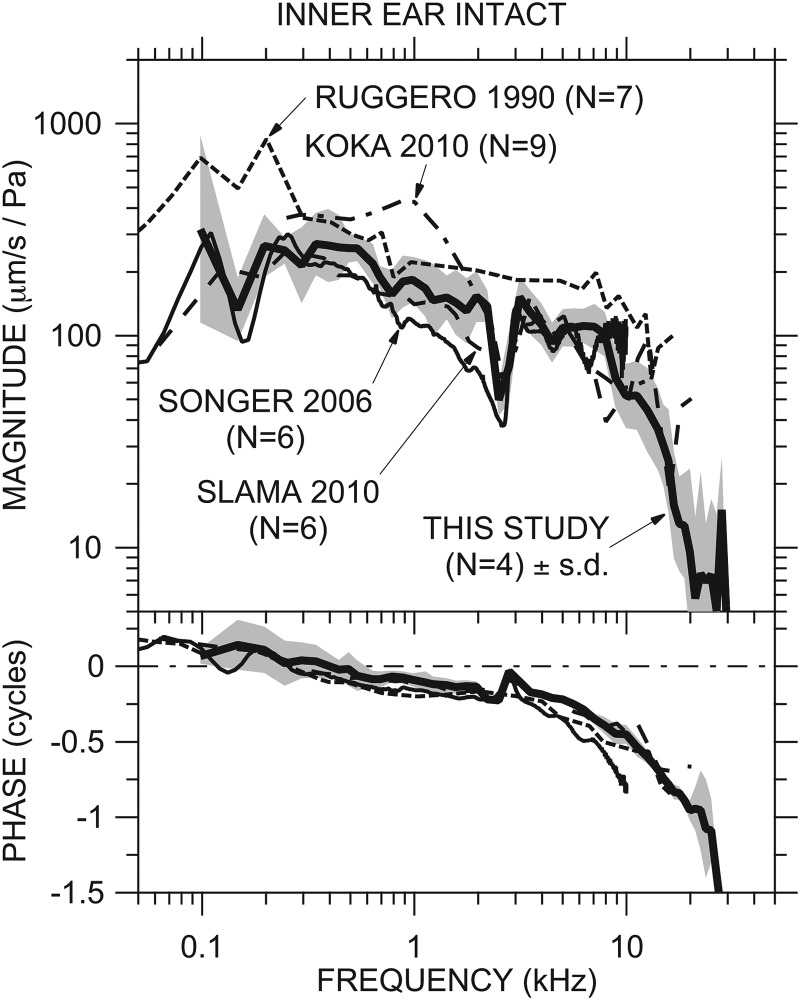
Our mean H_V with the ME open and IE intact [Fig. 4A] is quite similar to that measured in other studies from our laboratory (Songer and Rosowski, 2006; Slama et al., 2010) and elsewhere (Ruggero et al., 1990, Figs. 8 and 9, adjusted for stimulus level; Koka et al., 2010) in which the IE was intact and extends to higher frequencies; see Fig. 7. Our H_V phase accumulates more slowly than Songer's normalized phase. As mentioned in Sec. 4A4 above, the effect of the IE sensor on H_V is virtually identical to the effect of a SCD on normalized stapes velocity seen by Songer and Rosowski (2006).

Figure 7.

Comparison of our mean H_V with the IE intact ± 1 s.d. [Fig. 5A; thick solid line and shading] to the mean normalized stapes velocity from Ruggero et al. (1990, Figs. 5 and 6; dotted line), Songer and Rosowski (2006, Fig. 7; thin solid line), Slama et al. (2010, Fig. 5, dashed line), and Koka et al. (2010, Fig. 6, dot-dashed line; magnitude only). Top: magnitude; bottom: phase.

Y_C and Re{Y_C}

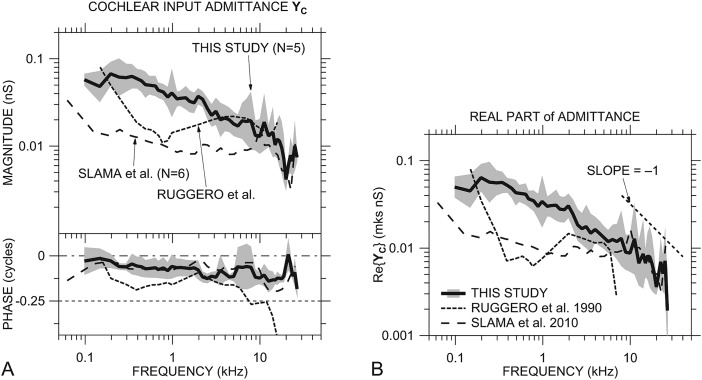
Figure 8A shows similarities and differences between our mean Y_C [from Fig. 5A] and previous cochlear immittance estimates (originally presented as impedance; converted to Y_C here). Our mean |Y_C| estimate is considerably higher than those computed from Slama et al. (2010, Fig. 10) and Ruggero et al. (1990, Figs. 15 and 17): by a factor of 3–4 below 2 kHz, less at higher frequencies. Our |Y_C| has a similar frequency dependence to that from Slama below 5 kHz, though our |Y_C| continues to decrease with frequency above 1.5 kHz while that from Slama flattens. Our ∠Y_C is similar to that from Slama across the entire frequency range. The frequency dependence of our Y_C is much different from that from Ruggero below 3 kHz.

Figure 8.

(A) Comparison of our mean Y_C ± 1 s.d. with a sensor in the vestibule [Fig. 5A; thick solid line and shading] to the cochlear admittance computed from previous measurements by Slama et al. (2010, Fig. 10; dot-dashed line) and an estimate from Ruggero et al. (1990, Figs. 15 and 17; dashed line). Top: Magnitude; bottom: phase. (B) Comparison of our mean Re{Y_C} ± 1 s.d. with an IE sensor [Fig. 5C; thick solid line and shading] to Re{Y_C} computed from the previous studies shown in panel (A). Line code as for panel (A). The thin dotted line shows an inverse relationship with frequency.

Y_C computed from Slama et al. (2010) supports our finding of a cochlear admittance characterizable as a combination of mass and resistance (see Sec. 3C1). This combination admittance is consistent with the Dallos (1970, p. 495) conjecture that Z_C in cat and chinchilla has a significant low-frequency reactive component due to an inertance introduced by the helicotrema. Unlike Dallos' prediction of a substantial |Z_C| rolloff and phase shift below 1 kHz, our results suggest a gentle |Z_C| increase with frequency above 200 Hz and very little phase difference from a purely resistive cochlea.

Between 3 and 15 kHz our |Y_C| data are similar to those from Ruggero, and our ∠Y_C data are similar to those from Slama. Generally, our Y_C and that from Slama are approximately minimum-phase (see Sec. 3C2) over the entire frequency range. The relationship between |Y_C| and ∠Y_C computed from Ruggero's estimate (which used Ruggero's stapes velocity measurements and scala vestibuli sound pressure from Décory et al., 1990) deviates from a minimum-phase system by more than 0.1 cycle above 800 Hz and by more than 0.15 cycle above 3 kHz.

In Fig. 8B, our mean Re{Y_C} [from Fig. 5C] is compared to Re{Y_C} computed from the previous cochlear impedance estimates. Consistent with Y_C, our Re{Y_C} is higher than others below 5 kHz but shows some similarities at higher frequencies to that computed from Slama. Our Re{Y_C} decreases approximately as 1/f above 8 kHz (as mentioned in Sec. 3C3 above; compare to thin dotted line), whereas that from Slama is more variable. The frequency response of our Re{Y_C} is quite different from that from Ruggero et al. but similar to that computed from the Slama data. The Re{Y_C} computed from Ruggero is much lower than ours below 2 kHz and negative above 7 kHz. The consistency of our high-frequency data with those from Slama and the consistency of both these data sets with physical constraints suggest that our data and Slama's are more accurate representations of cochlear immittance at high frequencies.

MEE and power flow to the cochlea

Comparison to previous studies

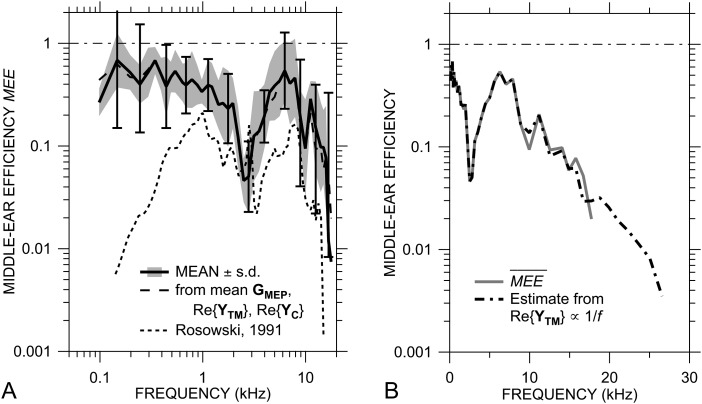
Our computed mean MEE (±s.d.; shaded area) is higher than a previous estimate of MEE in chinchilla, as seen in Fig. 9A, especially at frequencies below 1 kHz. The previous estimate (Rosowski, 1991, Fig. 7; thin dotted line) used previously published means of stapes velocity, SV sound pressure, and A_FP and unpublished measurements of middle-ear input impedance, all from different laboratories.11 The previous estimate of MEE was also lower than MEE estimates in cat and guinea pig (Rosowski, 1991, 1994). Our new estimate of MEE from individuals is significantly higher than the earlier estimate, by a factor of 2 to 3 between 1 and 8 kHz, by as much as a factor of 30 below 1 kHz, and by a factor of 5 to 10 above 8 kHz. Our new estimate is more similar to MEE estimates in cat: about half of the sound power entering the middle ear is transmitted to the cochlea.

Figure 9.

(A) Comparison of the mean MEE ± 1 s.d. with the middle ear and inner ear opened (from Fig. 6; solid line and shaded area) and $\overline{\text{MEE}}$ computed from the mean |G_MEP|, Re{Y_C}, and Re{Y_TM} (dashed line; error bars show ± 1 s.d.) to a previous MEE estimate (Rosowski, 1991, Fig. 7; dotted line). (B) $\overline{\text{MEE}}$ (solid gray line) and an estimate of high-frequency MEE using Re{Y_TM} = 13 nS at 9 kHz and extrapolated to 27 kHz assuming an inverse variation with frequency (as for Re{Y_C}; dot-dashed line).

Variance and validity of MEE estimates

One of the motivations for this study was to obtain an estimate of the variance in MEE to check the validity of our computed MEE. The standard deviation of MEE computed in the logarithmic domain from the five individuals is a factor of 1.5–3 over the entire frequency range of 0.1 to 17 kHz. As mentioned in Sec. 3D above, the mean MEE + s.d. exceeds 1 at only a few isolated frequencies, consistent with a passive middle ear, which supports the validity of our computed MEE.

Figure 9A also compares the mean of the individual MEE measurements to an estimate $\overline{\text{MEE}}$ (dashed line) computed from the mean G_MEP [Ravicz and Rosowski, 2013, Fig. 5(B)], mean Re{Y_TM} [Ravicz and Rosowski, 2012b, Fig. 5(D)], and mean Re{Y_C} [Fig. 5C]. $\overline{\text{MEE}}$ is quite similar to the mean MEE, being slightly lower above 12 kHz but well within 1 s.d. of the mean of the individuals. The standard deviation we compute for $\overline{\text{MEE}}$ from the variances of the individual components12 (assuming independent variances; error bars) is comparable to the s.d. of MEE between 250 Hz and 7 kHz and is about twice the s.d. of MEE (a factor of 4–5) below 250 Hz and above 8 kHz. In contrast, estimates of the variance of the previous MEE estimate (Rosowski, 1991, assuming independent variation of the measurements made in the different laboratories) were so large that they suggested that the efficiency varied at most frequencies beyond the 0 to +1 range. By measuring all quantities in individual animals, we reduce the variance of our computed MEE considerably and increase confidence in our computations.

Our new estimate appears to be robust to experimental conditions: for example, the counterbalancing effects of the open ME on |G_MEP|² and Re{Y_TM} demonstrate that MEE is independent of whether the middle ear is open or closed. The previous underestimate of chinchilla MEE (Rosowski, 1991, 1994) is primarily due to differences in the data used in the calculations: primarily in the estimate of Y_TM and Y_C at low frequencies (see Fig. 5 of Rosowski, 1991).

MEE estimates at high frequencies

The similarity between $\overline{\text{MEE}}$ and the mean MEE from individuals indicates that $\overline{\text{MEE}}$ can be used to estimate the effects of measurement corrections or ME or IE modifications on MEE. For example, our mean data suggest a rapid rolloff in $\overline{\text{MEE}}$ above about 17 kHz; however, this conclusion is limited by the lack of Re{Y_TM} data at higher frequencies. Re{Y_C} decreases as 1/f above 10 kHz [Fig. 8B], and the decrease in Re{Y_TM} above 9 kHz [Ravicz and Rosowski, 2012b, Fig. 5(D)] can also be described fairly well as varying inversely with frequency. Examination of Eq. 5 shows that, if Re{Y_C} and Re{Y_TM} covary, the high-frequency rolloff in MEE is due to the rolloff in |G_MEP|. Using the mean data, we can easily extrapolate MEE to higher frequencies by assuming that Re{Y_TM} continues to vary as 1/f above 9 kHz. The $\overline{\text{MEE}}$ estimated using this extrapolation above 9 kHz [Fig. 9B] shows a rapid high-frequency rolloff that continues to the high-frequency limit of Re{Y_C} at 27 kHz.

SUMMARY AND CONCLUSIONS

• (1)Stapes velocity V_S and sound pressure in the ear canal close to the TM P_near-TM were measured in seven live chinchillas in which the ME was opened and the IE was intact (Fig. 2). The ME velocity transfer function H_V (Fig. 4) was computed from those measurements in these individual animals using an estimate of TM sound pressure derived from P_near-TM and an ear-canal model. H_V was generally similar to previous measurements from other studies (Fig. 7).
• (2)Small but significant changes in H_V were produced by the introduction of a hole in the vestibule and the insertion of a pressure sensor (${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$); but once the sensor was in place in the vestibule hole, further IE modifications had little effect on ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ (Fig. 3).
• (3)The cochlear input admittance Y_C (Fig. 5) computed from ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ and G_MEP had a higher magnitude than that computed from some previously presented cochlear input impedance data (Fig. 8). Our mean Y_C was consistent with the input admittance of a passive minimum-phase system at frequencies up to 27 kHz (in all individual ears, up to 22 kHz), which suggests that potential errors due to non-piston-like stapes motions are small below 22 kHz.
• (4)The MEE (Fig. 6) computed from Re{Y_C}, |G_MEP|, and Re{Y_TM} in the same ears is substantially higher than a previous estimate in chinchilla (Rosowski, 1991), especially at low and high frequencies [Fig. 9A]. The relatively small variance of MEE due to the use of complete data sets in individual animals establishes the validity of our estimate.
• (5)While our estimates of MEE are limited to 17 kHz, a sharp rolloff in MEE is observed just at that limit. Examination of the factors of MEE suggests that, because Re{Y_C} and Re{Y_TM} decrease proportionally with frequency between 10 and 17 kHz, this MEE rolloff is due to the rolloff in |G_MEP| at 17 kHz rather than to a change in Re{Y_TM}. An extrapolation of the 1/f frequency dependence of Re{Y_TM} predicts a sharp decrease in MEE up to 27 kHz [Fig. 9B].

Nomenclature

A_FP

Stapes footplate area

$\mathbf{c}{\widehat{\mathbf{P}}}_{\mathbf{T}\mathbf{M}}$

Correction factor to estimate P_TM from P_near-TM

f

Frequency (Hz)

G_MEP

Middle-ear pressure gain

H_V

Middle-ear velocity transfer function = V_S/P_TM

${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$

 with a pressure sensor in the vestibule

IE

Inner ear

K_MEC

Stiffness of air in ME cavity

K_TM

Stiffness associated with Y_TM

K_TOC

Stiffness of TM, ME ossicles, and cochlea

ME

Middle ear

MEE

Middle-ear efficiency

$\overline{\text{MEE}}$

 computed from mean factors

OW

Oval window

P

Sound pressure

P_ex

 external to the EC

P_near-TM

 measured near the TM

P_TM

 measured at the TM

P_V

 measured in the cochlear vestibule

rH_V

Ratio of ${\mathbf{H}}_{\mathbf{V}}^{\mathbf{V}}$ to H_V

Re{Y}

Real part of admittance

RW

Round window

s.d.

Standard deviation of the mean

ST

Scala tympani

TM

Tympanic membrane

U_TM

Volume velocity entering the ME

V_S

Stapes velocity (evaluated from single-point measurement)

W_C

Sound power entering the cochlea

W_ME

Sound power entering the ME

Y_BH

Admittance of bulla holes

Y_C

Cochlear input admittance with a vestibule sensor = V_SA_FP/G_MEP

${\mathbf{Y}}_{\mathbf{C}}^{\mathbf{I}}$

Cochlear input admittance with the IE intact

Y_H

Admittance of vestibule hole

Y_TM

Middle-ear input admittance

Z_C

Cochlear input impedance = Y_C⁻¹

Z_TM

Middle-ear input impedance = Y_TM⁻¹

σ

Standard deviation = variance^1/2

Superscript ^V refers to sound pressure measured with a sensor in the vestibule. The circumflex (^) denotes quantities estimated from an EC model (Ravicz and Rosowski, 2012b, 2013).