Optimized Nonlinear Gradients for Reversed-Phase Liquid Chromatography in Shotgun Proteomics

Abstract

Reversed-phase liquid chromatography has become the preferred method for separating peptides in most of the mass spectrometry-based proteomics workflows of today. In the way the technique is typically applied, the peptides are released from the chromatography column by the gradual addition of an organic buffer according to a linear function. However, when applied to complex peptide mixtures, this approach leads to unequal spreads of the peptides over the chromatography time. To address this, we investigated the use of nonlinear gradients, customized for each setup at hand. We developed an algorithm to generate optimized gradient functions for shotgun proteomics experiments and evaluated it for two data sets consisting each of four replicate runs of a human complex sample. Our results show that the optimized gradients produce a more even spread of the peptides over the chromatography run, while leading to increased numbers of confident peptide identifications. In addition, the list of peptides identified using nonlinear gradients differed considerably from those found with the linear ones, suggesting that such gradients can be a valuable tool for increasing the proteome coverage of mass spectrometry-based experiments.

Shotgun proteomics, also referred to as bottom-up proteomics, has become an essential tool in biological research.¹ Tremendous developments in sample preparation,² instrumentation,³ and data analysis software⁴ have enabled the identification and quantification of thousands of proteins in a single run.⁵ In its most widespread workflows, the technique involves the digestion of the proteins of interest into peptides, the separation of the resultant peptide mixture into one or several fractions, followed by mass spectrometry (MS) analysis of the peptides in each fraction. The generated fragmentation spectra are subsequently matched to peptide sequences and assigned statistical confidence, and a list of proteins likely to be present in the initial sample is inferred.

Within these advancements, a major role has been played by fractionation techniques, in particular reversed-phase liquid chromatographic (RPLC), which despite other options remains the almost exclusive method for separating peptides prior to electrospray ionization.⁶ In the way the technique is typically applied, the peptides are separated on a liquid chromatography (LC) column under gradient conditions, by the progressive addition of an increasing percentage of organic solvent according to a linear function.⁷ In the past decade, several studies have shown that alterations in column length, inner diameter, packing material or temperature may dramatically increase the yield of a shotgun proteomics experiment.⁸⁻¹⁰ Furthermore, it has been shown that modern LC-systems combined with ultralong gradients are a powerful technology, with great potential in the context of clinical samples where often limited amounts of biological material are available.^11,12 However, whereas a number of studies have examined the effects of extending the gradient time,^13,14 little is known about the consequences of changing the shape of the gradient function when analyzing complex peptide mixtures.

Currently, a limiting factor for the number of proteins that can be identified in a shotgun experiment is the rate at which the mass spectrometer fragments peptides.¹⁵ As an example, without considering miscleavages, post-translational modifications, or sequence variations, a theoretical digest of the human Swissprot 2012_09 database contains more than 3.7 × 10⁵ unique tryptic peptides. Assuming a four hours experiment, this translates to a total of 1500 peptides that the mass spectrometer would need to sequence every minute, which is beyond the capabilities of even the fastest instruments presently available. This problem is further augmented by the unequal spread of the peptides over the gradient time, with a majority of the peptides eluting in only a short portion of the chromatography run.¹⁶ While in theory one could calculate different gradient functions producing even distributions of the peptides, little is known about the use of such functions in the context of shotgun proteomics experiments of complex mixtures.

Following these observations, we herein investigate the use of nonlinear gradients for the RPLC separation of complex peptide mixtures. We implemented an algorithm that calculates two such gradients, one designed to produce an even distribution for the theoretical peptides from an in silico digest, and one that evens the distribution of the high-intensity MS1 ions. We evaluated the nonlinear gradients for two data sets consisting of four replicate runs of a complex sample, and found that they produced both more equally spread peptides throughout the run, and increased numbers of confident peptide identifications. In addition, the list of peptides identified using nonlinear gradients differed considerably from the one found with the linear ones, suggesting that such gradients can facilitate the identification of novel peptide species. The algorithm to calculate nonlinear gradients is straightforward to apply, and a python implementation can be downloaded under MIT license at http://code.google.com/p/nonlinear-gradients/.

Experimental Section

Sample Preparation

A tryptic digest of HeLa protein extracts was prepared as previously described.^12,14 Briefly, nocodazole arrested HeLa Kyoto cells were harvested and protein was purified by acetone precipitation. After resuspension in 8 M urea in 0.5 M ammonium bicarbonate (ABC), disulfide bridges were reduced using 0.05 μg of dithiothreiotol (DTT) per μg of protein, and alkylated with 0.25 μg of iodoacetamide per μg of protein. The sample was subsequently diluted with 50 mM ABC, first to 6 M urea, followed by 2 h digestion with LysC (1:50 w/w), and then to 0.8 M urea followed by o/n digestion with trypsin (1:30 w/w).

Reversed-Phase Liquid Chromatography

Four Hour Gradient Experiments

HeLa digest peptide mixture (0.5 μg per injection) was separated on an UltiMate 3000 RSLCnano system (Dionex) using a 50 cm × 75 μm i.d. column (AcclaimPepMap C18, 2 μm, 100 Å, Dionex).¹² The sample was first loaded onto a trapping column (2 cm × 100 μm i.d.; Acclaim PepMap C18, 5 μm, 100 Å) for 10 min using 0.1% TFA as a loading solution and a loading pump flow rate of 25 μL/minutes. Subsequently, the trapping column was switched in-line with the analytical column and the linear gradient was started using a pump flow rate of 230 nL/min. Solvent solutions were solvent A (0.1% FA) and solvent B (0.08% FA and 80% acetonitrile).

For the linear gradient experiments, the analytical column was first equilibrated in 98% A and 2% B, followed by a linear gradient starting with 2% B at 10 min (the time-point of valve switching) and increasing to 40% B at 250 min. To clear the system from hydrophobic peptides, the linear gradient was followed by an increase to 50% B at 255 min and to 90% B at 260 min, which was held constant for further 10 min. Subsequently, the concentration of solvent B was decreased to 2% within 2 min, which was maintained for 33 min to prepare the system for the next injection. The mass spectrometer was started by a contact closure signal from the RSLC at 10 min.

For the nonlinear gradients, all settings were kept identical, including the settings of 2% B at 10 min and 40% B at 250 min. However, for each minute between the time points 11 and 249 min, the calculated concentration of solvent solution B for the respective optimized nonlinear gradient was rounded at one decimal place and inserted into the LC method (248 additional data points). Of note, the time intervals were interpreted by the LC system as a series of linear gradients of 1 min duration. The LC system therefore did not deliver a step-gradient but rather approximated the concentration of solvent B during each of the 1 min intervals. This strategy permitted a simple yet flexible design as well as an adequate representation of the nonlinear nature of the optimized gradients within the framework of the standard LC control software (Chromeleon, version 6.80 SR11).

Two blank runs were programmed on the LC before each of the individual linear or nonlinear sample analyses. Solvent solutions for blanks were identical to samples, and the gradient was: 2% B for 10 min, followed by a linear gradient from 2% B to 40% B from 10 to 40 min, increased to 90% B at 45 min, which was maintained for 5 min, then 2% B at 52 min continued for 23 min for column equilibration.

The time difference between the LC method and the MS raw file was estimated experimentally using an LC method identical to the linear gradients described above, except for the fact that 98% A and 2% B were maintained for 30.00 min, followed by a sharp increase to 30% B at 30.01 min. This permitted an observation of the well-defined time-point in the MS raw file at which peptides eluting from the analytical column due to the abrupt increase in organic solvent concentration were detected in the MS. Only 50 ng of the peptides were injected for this purpose. For further details, refer to the Design of Optimized Gradients section.

Two Hour Gradient Experiments

An Ultimate 3000 LC system (Dionex) was employed for the 2 h gradient experiments. 0.5 μg HeLa digest peptide mixture was injected and separated on a 15 cm × 75 μm i.d. column (Acclaim PepMap C18, 2 μm, 100 Å, Dionex). After the sample was loaded onto a trapping column (5 mm × 300 μm i.d.; Acclaim PepMap C18, 5 μm, 100 Å) for 10 min using 0.1% TFA as a loading solution and a loading pump flow rate of 25 μL/min, the trapping column was switched in-line with the analytical column and the linear gradient was started using a pump flow rate of 230 nL/min. Solvent solutions were solvent A (0.1% FA) and solvent B (0.08% FA and 80% acetonitrile).

The analytical column was first equilibrated in 98% A and 2% B. The linear gradient started with 2% B at 10 min (the time-point of valve switching), increasing to 40% B at 130 min, followed by 90% B from 135 min until 140 min, then 2% B from 142 to 165 min to prepare the system for the next injection. The mass spectrometer was started by a contact closure signal from the LC at 20 min.

The nonlinear gradients were developed in an analogous way as described above for the 4 h gradients except for the different linear gradient time. The time delay between the LC and the MS was estimated with an LC method that included a step gradient which led to a sharp increase in the concentration of organic solvent (%B) at 30.01 min LC time.

Mass Spectrometry Analysis

Four Hour Gradient Experiments

For the long gradient experiments, the LC was connected to a Q Exactive mass spectrometer (Thermo Scientific) via a nanoelectrospray ion source (Proxeon). The mass spectrometry method duration was 290 min, and the mass spectrometer was operated in positive ionization mode. The source voltage was 1.9 kV, and the capillary temperature was 275 °C. One MS1 scan (m/z 350–2000, AGC target 3 × 10⁶ ions, maximum ion injection time 60 ms) acquired at a resolution of 70 000 (at 200 m/z) was followed by up to 10 tandem MS scans (resolution 17 500 at 200 m/z) of the most intense ions fulfilling the defined selection criteria (peptide match on, exclude isotopes on, exclusion of singly charged precursors, AGC target 1 × 10⁵ ions, underfill ratio 20%, maximum ion injection time 120 ms, isolation window 2 Da, dynamic exclusion time 90 s). The HCD collision energy was set to 30% NCE and the polydimethylcyclosiloxane background ions at 445.120025 were used for internal calibration (lock mass).

Two Hour Gradient Experiments

An LTQ-Orbitrap XL/ETD mass spectrometer (Thermo Scientific) was connected to the LC via a nanoelectrospray ion source (Proxeon) and operated in positive ionization mode with a source voltage of 1.5 kV and a capillary temperature of 200 °C. Method duration was 140 min. One MS1 scan (m/z 400–1800, AGC target 1 × 10⁶ ions, maximum ion injection time 500 ms) acquired at a resolution of 60 000 at 400 m/z was followed by up to 10 collision-induced dissociation scans (normalized collision energy 35, activation time 30 ms, activation Q 0.25) of the most intense ions (monoisotopic precursor selection enabled, exclusion of singly charged precursor ions, AGC target 5 × 10⁴ ions, maximum ion injection time 100 ms, dynamic exclusion time 30 s with an exclusion window of ±5 ppm). The minimal signal threshold was 5 × 10⁴, isolation width was 3 Da. FT preview mode was enabled and polydimethylcyclosiloxane background ions at 445.120025 were used for internal calibration (lock mass).

Data Processing

The tool msconvert from the ProteoWizard software suite¹⁷ was used to convert all the raw data to the .mzML and .ms2 file formats. We used Hardklör version 2.03¹⁸ for deconvolution and mass and charge calculations, and Bullseye version 1.30¹⁹ to assign to each peptide the apex retention time of its corresponding feature. The fragmentation spectra were searched with Crux version 1.37,²⁰ using the sequest–search command and the following parameter values: precursor mass window of 10 ppm, the enzyme set to trypsin, and the missed-cleavages option switched on. The only fixed modification searched was the carbamidomethylation of cysteine (57.021464 Da to all cysteines). The data sets were searched against both the human Swissprot 2012_09 database, and a decoy database obtained by reversing the sequences from the human database. The resulting peptide-spectrum matches were postprocessed using Percolator version 2.04,²¹ which improved the rate of confidently identified spectra, and provided statistical significance measures such as false discovery rates (FDR) and posterior error probabilities (PEP) at peptide level.

The full lists of peptide identifications obtained following these procedures and parameters used to run each software tool are available online at http://www.nada.kth.se/lumi/datasets/nonlinear_gradient/nonlinear_gradient.html.

Design of Optimized Gradients

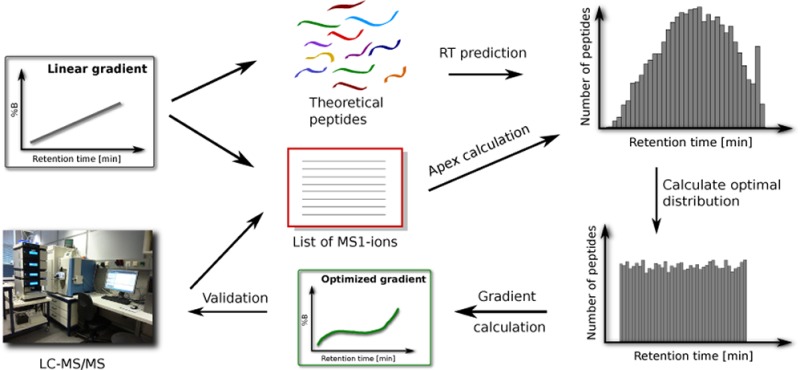
We designed two nonlinear gradients, denoted in silico-optimized and MS1-optimized, tailored to give even distributions across the chromatographic run for the theoretical peptides from an in silico digest of the human proteome, and for the high-intensity MS1 ions detected using a linear gradient, respectively. Each new gradient was defined by a function giving the percentage of solvent B at every minute during the chromatographic run.

To design these gradients, we first needed to estimate the correspondence between the times t_LC in which the gradient was given to the LC-system, and the times t_MS when the effects of these instructions were reported in the output file from the mass spectrometer. This correspondence can be expressed by

1

where t_lag is a constant characteristic for the respective LC-MS system. We determined the value of t_lag for our data experimentally, using the following procedure: we modified the linear LC gradient so that 98% solvent A and 2% solvent B were delivered until 30.00 min, followed by an abrupt rise to 30% solvent B at 30.01 min (LC method time). This led to a surge of peptides eluting from the analytical column at a well-defined time-point (t_{peptide_surge}) which was observable in the MS raw file, permitting the calculation of the time difference between the LC and the MS as t_lag = t_{peptide_surge}–30. For the 4 h runs we obtained t_lag = 6.2 min, and for the 2 h runs t_lag = −6.87 min.

In silico-Optimized Gradient

The in silico-optimized gradient is designed to give an even spread for all the predicted peptides of the analyzed proteome. The procedure consists of two steps: the prediction of the peptides’ retention times, and the calculation of an altered gradient giving a theoretical constant elution rate for these peptides. Both steps are described in more details below.

To predict peptide retention times, we randomly selected 1500 peptides confidently identified (FDR < 1%) in one of the runs based on the linear gradient, and used these together with their observed retention times to train a retention time model using the software package Elude.^16,22 The observed retention time of each confident peptide was assigned by first considering the best scoring spectrum for that particular peptide, and then use Bullseye version 1.30¹⁹ to find for each such spectrum the apex retention time of its corresponding feature.

Next, we performed an in silico digest of the proteins in the Swissprot 2012_09 database, and retained only the peptides with masses between 600 and 8000 Da and between 8 and 50 amino acids long. We estimated the retention times of these peptides using the previously trained retention model and excluded the peptides predicted to elute outside the gradient time. The remaining set included 378 058 unique peptide sequences. Here we emphasize that, since the retention model was trained on data generated using a linear gradient, the retention time distribution obtained for the theoretical peptides was the one expected when such a gradient is used.

In the next step we calculated an optimal theoretical peptide elution rate, Q = N/T_Δ, where N is the number of theoretical peptides and T_Δ is the gradient time. For the 4 h runs conditions, we used N = 378 058 and T_Δ = 240 min, which resulted in an optimal elution rate of Q = 1575.2 theoretical peptides per minute. For the 2 h runs, T_Δ = 120 min, and thus Q = 3150.5. We translated the predicted retention time of each peptide to the corresponding volume fraction of solvent B (ϕ^%B), taking the time translation of eq 1 into account. We sorted the peptides according to their assigned volume fraction, ϕ_i^%B, so that ϕ_i ≤ ϕ_i+1^%B for each pair of peptides, i and i + 1. We then defined the in silico-optimized gradient by assigning to each time point t_MS the volume fraction ϕ^%B corresponding to a linear interpolation between the peptides with indices closest to t_MSQ. More formally, the gradient was defined by the function given below:

2

Here we use the notation ⌊t_MSQ⌋ for the closest integer smaller than t_MSQ, and ⌈t_MSQ⌉ for the closest larger integer. Out of practical reasons we selected to calculate ϕ^%B(t_MS) in steps of one minute from the beginning to the end of the gradient time. We subsequently converted the time values to LC-times using eq 1.

MS1-Optimized Gradient

The first step in calculating the MS1-optimized gradient was to compile an accurate list of MS1 ions using Krönik version 2.02.²³ We chose to retain only those features that persisted over at least four consecutive scans, with a gap tolerance of one scan. Furthermore, if we assume a fragmentation speed of 300 peptides/min for the Q Exactive mass spectrometer, this would result in a maximum of 72 000 MS1-features that could get fragmented during a 4 h experiment. Following this reasoning, we considered in our calculations only the 72 000 MS1-features with the highest intensity. Thus, the MS1-optimized gradient aimed at producing an even distribution of the highest abundant features that could get fragmented during a shotgun proteomics experiment. For the 2 h runs, we considered the 17 000 most abundant MS1-features.

The procedure to derive the gradient function was identical to the one described for the in silico case, with the theoretical peptides being replaced by the abundant MS1-features, and the predicted retention times with the observed retention time apexes of these features.

Estimation of Chromatography Peak Widths

We fitted a Gaussian to the chromatography profile of each MS1-feature by applying a logarithm transformation of the data, followed by a parabolic line of best fit. To minimize the tailing effects, we computed the best fit using only the points within 25% from the maximum intensity, and computed the coefficient of determination R² for this subset. Further, we retained only the 50% MS1-features with the highest intensity that fulfilled R² > 0.95. We divided the gradient time in windows of 10 min, and computed the median peak width of the features eluting in each such window. The peak widths were expressed in terms of the full width at half-maximum (FWHM), which gives the width of a Gaussian peak at 50% of the maximum peak height.

Experimental Design

For both the 4 and 2 h gradients, we carried out twelve shotgun runs (a total of 24 runs): four identical runs based on a linear gradient, four identical runs based on an in silico-optimized gradient, and four runs based on slightly different MS1-optimized gradients. Each of the MS1-optimized gradients was calculated using each of the runs based on a linear gradient, while the in silico-optimized gradient was calculated using only one of the linear runs. The reason why we chose to calculate only one in silico-optimized gradient is related to the low resolution of the current retention time prediction algorithms. While such predictors are useful for estimating the general distribution of the peptides across the run, they are often not able to capture subtle changes in retention times, such as the ones observed across replicate runs. Since the overall spread of the peptides is highly similar across all the replicates based on a linear gradient, training the predictor on one of these runs is sufficient to learn this distribution.

In each case the four runs based on linear gradients were carried out first, followed by the runs based on the nonlinear gradients. All the experimental conditions were kept identical, except for the gradient functions.

Results and Discussion

Nonlinear Gradient Functions

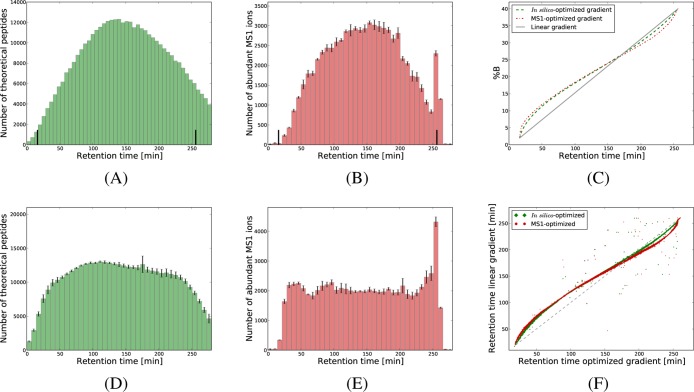
For complex peptide mixtures, the conventional linear gradients used in liquid chromatography produce an unequal spread of the peptides over time.¹⁶ To illustrate this, we first examined the retention times of the analytes when using a 4 h linear gradient and a Q Exactive mass spectrometer. We illustrated the distributions across the run of the peptides identified at a 1% FDR (Figure 1), of the theoretical peptides from an in silico digest of the human proteome (Figure 2A), and of the abundant MS1-features (Figure 2B). Clearly, all three distributions deviate considerably from uniformity, with larger numbers of peptides eluting in the middle of the run, and relatively few peptides eluting in the beginning and toward the end of the gradient time.

Figure 1.

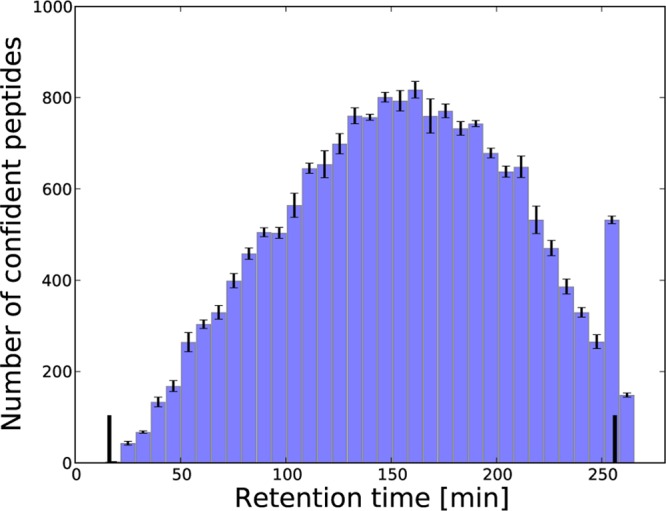
Uneven distribution of confident peptide identifications. We display the average number of confident peptide identifications (FDR 1%) across the replicates based on a 4 h linear gradient as a function of retention time. The small segments on each bin indicate the standard deviation, while the two vertical black lines illustrate the start and end of the linear gradient. Supporting Information Figure S-1 gives a similar representation for the replicates based on 2 h gradients.

Figure 2.

Nonlinear gradient functions. In panel A, we display the distribution of the predicted retention times for the theoretical peptides from an in silico digest of the human proteome when a linear gradient is used. Panel B gives the average number of high-intensity MS1-features for the four replicates based on a linear gradient. In panel C, we illustrate the in silico-optimized gradient designed to uniformize the distribution in panel A, and one of the four MS1-optimized gradients calculated to even one of the distributions summarized in panel B. Panel D displays the average number of theoretical peptides as a function of predicted retention time when the in silico-optimized gradient was used. Similarly, panel E gives the average number of highly abundant MS1-features yielded by the four replicates based on MS1-optimized gradients. The small segments on top of each bin give the standard deviation over the four replicates. In panel F, we considered all the peptides identified at 1% FDR in both a run based on the linear gradient, and the corresponding runs based on the nonlinear gradients. We show for each such peptide the retention time obtained with the linear gradient against the retention times in the runs based on the optimized gradients. All figures correspond to 4 h gradients, while representations for the 2 h runs are given in Supporting Informatin Figure S-2.

In typical shotgun proteomics experiments, the mass spectrometers are able to fragment only a fraction of the peptides eluting at any given time point, most often selecting for the highest-intensity ions.²⁴ This implies that, assuming the distributions displayed in Figure 2, the peptides eluting in the middle of the run get a lower probability to be selected for fragmentation, and thus identified. A preferred scenario would include an even spread of the peptides throughout the run, ensuring that the instrument has access to equal numbers of analytes at any time point. However, this cannot be achieved using the linear gradients typically employed in such experiments, but would require the design of more sophisticated nonlinear gradient functions.

To address this, we implemented an algorithm that calculates two such nonlinear gradients, denoted in silico-optimized and MS1-optimized. The in silico-optimized gradient is tailored to give an even distribution of the theoretical peptides from an in silico digest, while the MS1-optimized gradient aims at uniformizing the abundant MS1 ions. As an example, Figure 2C illustrates the nonlinear gradients designed to uniformize the distributions in Figure 2A and B, with each gradient described as a function giving the percentage of solvent B at every minute of the gradient run. As expected, the two nonlinear gradients are steeper than the linear one in the areas where few peptides are eluting, and more gradual in the regions where the bulk of the peptides elute. Note that the distributions displayed in Figure 2A and B vary with the chromatography system. Hence, the optimized gradient functions for other systems may be significantly different from the ones displayed in Figure 2C.

Our procedure to calculate nonlinear gradients depends only on the following parameters: (i) start and end of the gradient, (ii) correspondence between LC and MS times (see Experimental Section), and (iii) the retention time distribution to optimize. This makes the algorithm straightforward to apply for optimizing other retention time distributions or chromatography systems of interest. In addition, only changes in the chromatography setup that alter substantially these parameters would require the recalculation of the gradient. Furthermore, we draw the attention to an interesting difference in the workflows to calculate the two nonlinear gradients. To design an MS1-optimized gradient, we need to prerun our samples with a linear gradient, since in the design process we require a list of MS1 intensities from a linear gradient. This is not the case for the in silico-optimized gradient, where it suffices to have access to a representative retention time model of linear gradients.

Also, it is worth pointing out that the view described here is a highly simplified one. A multitude of additional factors such as differences in ionization efficiencies of the peptides, ion suppression, or variations in chromatographic efficiencies can greatly affect the peptide identification rate achieved in a shotgun experiment. While we do not address such factors in the current work, the complexity they entail makes it impossible to predict the exact effect that a new gradient will have on the number of confidently identified peptides.

Retention Time Distributions

The two types of nonlinear gradients were first evaluated on a data set consisting of four replicate runs using 4 h gradients as described in the Experimental Section. To start with, we assessed the performance of the new gradients by examining whether each of them produced the expected behavior in terms of retention time distributions. Figure 2D and E summarize the retention time distributions obtained when the two optimized gradients were used. Clearly, these data demonstrate that both nonlinear gradients produced significantly more even retention time distributions compared to when using a linear gradient. This translated to a nearly constant number of fragmentation events triggered by the mass spectrometer throughout the run (Figure 3).

Figure 3.

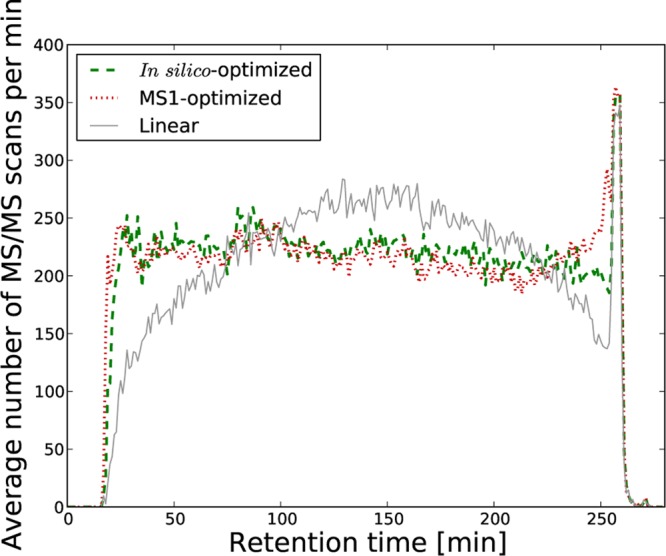
Fragmentation rate across run. For one replicate based on a 4 h gradient, we display the number of MS/MS fragmentation events per minute for each of the three types of gradients.

Further, for the peptides confidently identified with both the linear and one of the corresponding nonlinear gradients, we plotted the retention time observed in the linear run as a function of the retention time in the optimized runs (Figure 2F). The resulting representations closely reproduced the nonlinear gradient functions given in Figure 2C, indicating that our calculations matched the experimental results, and that our procedure preserved the relative order of elution of the peptides. More generally, these results suggest that the nonlinear gradients are as predictable as the linear ones.

The nonlinear gradients were also assessed for shorter runs of 2 h. In coherence with the 4 h runs, the optimized gradients produced more evenly distributed peptides for this data as well, as compared to a linear gradient (Supporting Information Figure S-2). However, for these runs the distribution of the abundant MS1-features produced by the MS1-optimized gradient was slightly more skewed compared to the 4 h runs (Supporting Information Figure S-2E). This effect may be due to the fact that the initial distribution to be optimized (Supporting Information Figure S-2B) was significantly more skewed as well.

Peptide Identifications

Next, we evaluated the optimized gradients in terms of unique peptides confidently identified in each of the runs (Table 1). All of the optimized gradients led to statistically significant increases in numbers of peptide identifications for both gradient lengths (two sample t test, one-tailed p < 0.01). Notably, the increases were larger for the shorter gradients, where the MS1-optimized gradient led to an average of 10% more peptide identifications compared to the linear gradient. Also, while for the 4 h runs the in silico-optimized gradient seem to perform better, the MS1-optimized gradient gave better results for the shorter runs. This suggests that although the optimized gradients gave improved identification rates for all the data sets we investigated, the extent of these improvements vary with the chromatography system and instrument settings employed.

Table 1. Number of confident peptide identifications^a.

	gradient type
gradient length	linear	in silico-optimized	MS1-optimized
4 h	17 433	18 079	17 759
	17 228	17 843	17 449
	17 363	17 978	17 804
	17 210	17 590	17 576
average	17 308.5	17 872.5	17 647.0
2 h	6176	6478	6700
	6030	6298	6583
	5980	6239	6713
	5965	6412	6578
average	6037.8	6356.8	6643.5

^aWe give the number of peptides identified at 1% FDR for all the data sets investigated throughout the study.

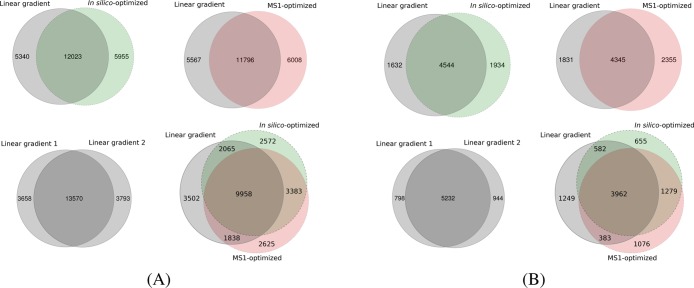
Interestingly, the list of confident peptide identifications obtained using optimized gradients differed considerably from the peptides generated by the linear gradients. For example, for the 4 h runs the overlap between the peptides identified using a linear gradient, and the ones found using an optimized one, ranged between 66% and 70% across the four replicates, compared to 74–82% when comparing any two replicates based on linear gradients (Figure 4A). A similar trend was observed for the 2 h runs (Figure 4B), where between 69% and 78% of the peptides identified with a linear gradient were also found with an optimized gradient, compared to 81–87% when comparing two runs based on a linear gradient. Hence, the optimized gradients did not only lead to more identifications but also allowed us to identify different peptide species than the typical linear gradients.

Figure 4.

Peptide identifications for optimized gradients. The overlap between the peptides identified with each of type of gradient is displayed. Panel A corresponds to one replicate using 4 h gradients, while panel B corresponds to 2 h gradients.

This latter observation is particularly important in connection to shotgun studies of complex mixtures, where a great deal of efforts have been directed toward increasing the proteome coverage.²⁵ In this context, some common strategies include the use of enzymes with different specificity,²⁶ the use of long gradients,^11,12 and the analysis of the same sample various times.²⁷ In our data we found that by pooling the peptide identifications obtained in one 4 h run based on a linear gradient, and one based on an optimized gradient, we gain an average 10% more peptide identifications compared to pooling the identifications from any two runs based on a linear gradient. This effect was even more pronounced for the 2 h runs, where we obtained an average of 18% more peptide identifications. Following this observation, we can speculate that this effect would be even larger for gradients deviating more from linearity than the ones used throughout this study. This suggests that carefully designed nonlinear gradients could be used to improve the comprehensiveness of proteomics studies.

When inspecting the peptides identified only with a nonlinear gradient, we found across the replicates based on 4 h gradients that between 89% and 91% of these peptides mapped to proteins identified with at least one confident peptide (1% FDR) in the corresponding run based on a linear gradient. This was similar to comparing any two runs based on a linear gradient, where between 88% and 91% of the peptides identified in only one of the runs mapped to proteins that were identified with at least one confident peptide in the other run. The same observation was valid for the 2 h runs, although these numbers were somewhat lower: between 81% and 86% of the peptides identified only with a nonlinear gradient belonged to a protein identified with the corresponding linear gradient, compared to 81–85% when comparing two runs based on a linear gradient. These results indicate that the nonlinear gradients did not favor a different class of proteins, but rather facilitated the identification of different peptides for the same proteins as the ones identified using a linear gradient.

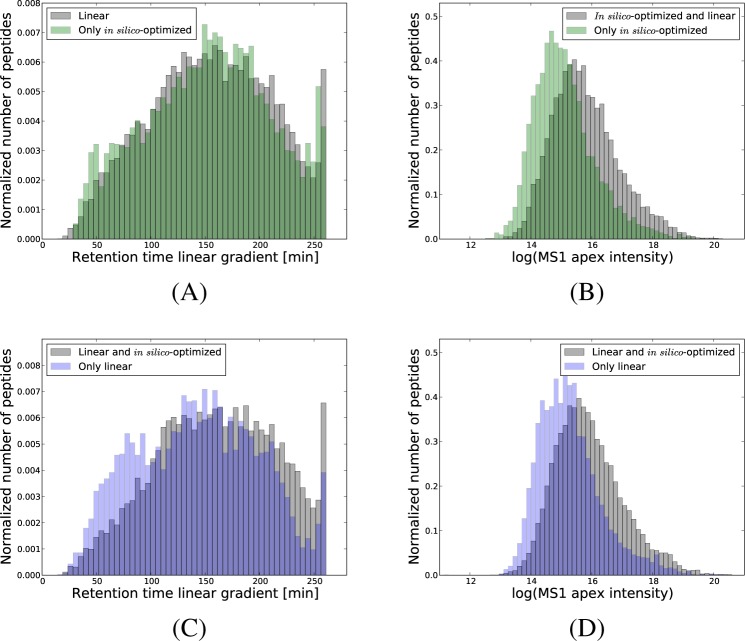
Further, we checked the retention times of the peptides identified only with a nonlinear gradient, and found an enrichment of peptides predicted to elute in the most crowded areas of the linear run (Figure 5A and Supporting Information Figure S-3A). This, despite the fact that the nonlinear gradients produced nearly uniform distributions of the confident peptide identifications (Supporting Information Figure S-4A and B). When examining the intensity of the MS1 precursor ions, we found that the peptides identified only with the nonlinear gradients corresponded to lower intensity precursors compared to the common peptide identifications (Figure 5B and Supporting Information Figure S-3B).

Figure 5.

Peptides identified with only one type of gradient. For one of the replicates based on 4 h gradients, we considered the peptides identified at 1% FDR using the in silico-optimized gradient, but that were not identified with the linear gradient. In panel A, we calculated the corresponding retention times that these peptides would have had if a linear gradient was used, and plotted the obtained distribution in green color. In gray, we give the distribution of the confident peptides identified with the linear gradient. For the same peptides, panel B gives in green color the apex intensity of their precursor ions. In gray, we display the precursor intensity of the common peptide identifications between the in silico-optimized and linear run. Panels C and D give similar representations for the peptides confidently identified with the linear gradient, but that were not present among the peptide identifications obtained with the in silico-optimized gradient. Note that for facilitating the comparison of the distributions, all the histograms were normalized. In absolute numbers, the green and blue distributions are much smaller than the gray ones.

In addition, we inspected the retention times and precursor intensities of the peptides that were identified at 1% FDR with the linear gradient, but missed at the same FDR threshold with the corresponding nonlinear gradients. Figure 5C and D give the results of these analyses when comparing a run based on a linear gradient with one based on the in silico-optimized gradient, and Supporting Information Figure S3-C and D give similar representations for the MS1-optimized gradient. These results indicate that (i) there was an enrichment of peptides identified only with the linear gradient in the areas where this gradient was shallower than the in silico-optimized one; (ii) the peptides identified only with the linear gradient corresponded to lower abundance precursor ions than the common peptide identifications. The same observations were valid for the 2 h gradients (Supporting Information Figures S-5 and S-6).

To summarize, the nonlinear gradients missed some of the confident identifications eluting in parts of the run where the linear gradient was shallower, but compensated for them by facilitating the identification of more peptides in the crowded areas of the linear run. Both the missed and the additional peptides corresponded to lower intensity precursors compared to the common identifications.

Chromatographic Peak Widths

Previous research has shown that shallower gradients lead to peak broadening.¹³ Since the nonlinear gradients often displayed gentler slopes compared to the linear ones (Figure 2C), we examined the extent of this effect in our data. Figure 6 displays the median peak width as a function of the retention time for one of the 4 h runs. Indeed, the two nonlinear gradients generated wider peaks in the middle of the run, corresponding to the regions where they increased slower than the linear gradient. However, they produced sharper peaks in the beginning and at the end of the gradient time.

Figure 6.

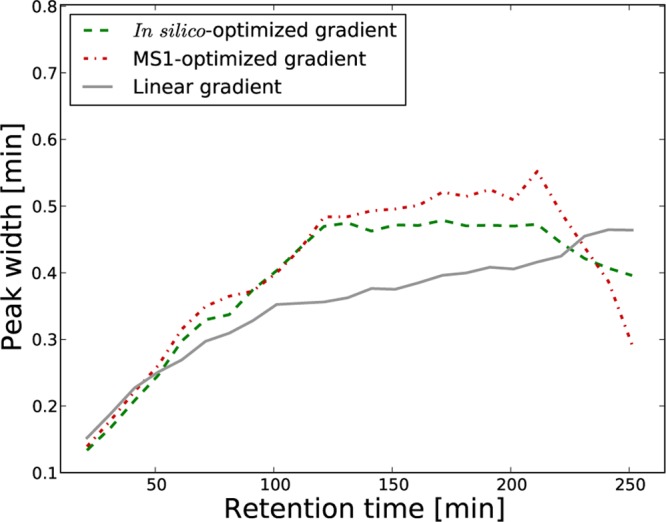
Chromatographic peak widths. For each type of gradient, we display the estimated peak width as a function of the retention time. The graphs corresponds to one of the 4 h runs, while Supporting Information Figure S-7 gives a similar representation for the 2 h runs.

In general, broader peaks translate to a decrease in the signal reaching the mass spectrometer, which in turn is associated to a drop in number of peptide identifications.¹⁴ However, with our optimized nonlinear gradients, the negative impact of the wider peaks was surpassed by the advantage of having a more even distribution of the peptides throughout the run. Nevertheless, one can imagine that the use of nonlinear gradients for very long runs may be hampered by such an effect. A straightforward solution to this would be to limit the allowed slope at any time of the optimized gradient. While this implies that the resulted nonlinear gradient may not correspond to a perfectly even distribution of the peptides throughout the run, it would still give an improved spread of the peptides, while controlling for the allowed peak broadening.

Reproducibility of the Nonlinear Gradients

Further, as our data comprised of replicates for each of the three gradients, we investigated the reproducibility of the gradients in terms of confident peptide identifications (Table 2). Our results showed that the two nonlinear gradients yielded similar numbers of peptide identifications common to more replicates as the linear gradients. As an example, for the 4 h runs 78% and 80% of the peptides found using the MS1-optimized and in silico-optimized gradients, respectively, were identified in at least two out of the four replicates run with each of these gradients. The same figure was 77% for the replicates based on a linear gradient. Thus, in terms of reproducibility, the optimized gradients yielded comparable results to the linear ones.

Table 2. Reproducibility of the Confident Peptide Identifications^a.

		gradient type
gradient length	number of replicates	linear	in silico-optimized	MS1-optimized
4 h	1/4	5645 (23%)	4875 (20%)	5655 (22%)
	2/4	3741 (15%)	3681 (15%)	4221 (17%)
	3/4	4457 (18%)	4107 (17%)	4741 (19%)
	4/4	10 684 (44%)	11 733 (48%)	10 567 (42%)
2 h	1/4	1384 (18%)	1488 (18%)	1705 (19%)
	2/4	944 (12%)	1111 (13%)	1143 (13%)
	3/4	965 (12%)	1103 (13%)	1193 (14%)
	4/4	4496 (58%)	4602 (55%)	4751 (54%)

^aFor each of the three gradient types, we investigated how many peptides were identified at 1% FDR in one (1/4), two (2/4), three (3/4), or all (4/4) of the four replicates run with that gradient. The results are given in both number of peptide identifications and percentages.

Availability

The python script to calculate nonlinear gradients can be downloaded under MIT license at http://code.google.com/p/nonlinear-gradients/.

Conclusions

Despite extensive efforts to improve peptide separation in RPLC,⁶ little is known about the effects of changing the shape of the linear gradient functions typically employed in such experiments. Here, we have implemented an algorithm that calculates two nonlinear gradient functions, designed to produce even spreads over the chromatography time for the peptides of a complex mixture. Our results showed that the nonlinear gradients produced more even retention time distributions, while yielding increased numbers of confident peptide identifications. Furthermore, they led to a considerable number of distinct peptide identifications eluting in the crowded areas of the linear runs, suggesting the potential of using such gradients for improving the proteome coverage attained by shotgun experiments. The new gradients produced reproducible results, were straightforward to implement, and can be easily extended to optimize other distributions of interest.

Supporting Information Available

Additional material as described in the text. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.