Sample Size Determination for Clustered Count Data

Abstract

We consider the problem of sample size determination for count data. Such data arise naturally in the context of multi-center (or cluster) randomized clinical trials, where patients are nested within research centers. We consider cluster-specific and population-average estimators (maximum likelihood based on generalized mixed-effects regression and generalized estimating equations respectively) for subject-level and cluster-level randomized designs respectively. We provide simple expressions for calculating number of clusters when comparing event rates of two groups in cross-sectional studies. The expressions we derive have closed form solutions and are based on either between-cluster variation or inter-cluster correlation for cross-sectional studies. We provide both theoretical and numerical comparisons of our methods with other existing methods. We specifically show that the performance of the proposed method is better for subject-level randomized designs, whereas the comparative performance depends on the rate ratio for the cluster-level randomized designs. We also provide a versatile method for longitudinal studies. Results are illustrated by three real data examples.

1. Introduction

Randomized clinical trials involving multiple centers are used extensively in large-scale studies to evaluate effects of medical interventions on health outcomes. These studies involve both cross-sectional and longitudinal designs. Most studies that are submitted to the Food and Drug Administration involve clinical trials of a drug relative to an appropriate placebo control in multiple centers. In such studies, the convention is to randomly assign experimental conditions to subjects nested within centers or sites. This kind of randomization is termed as subject-level randomization and the studies are called multi-center studies. Hence in multi-center studies each center receives both treatment and control regimen. In many cases, subject-level randomization is not practical and randomization is implemented at the center (schools, hospitals, counties etc.) level, i.e. all subjects belonging to a center receive the same intervention (e.g. drug or placebo). This randomization scheme is called the cluster-level randomization and the studies are called cluster randomized studies. Merits of both randomization scheme are discussed extensively in [1].

The clustered count (e.g. number of infections, exacerbations, hospital visits etc.,) data are generally analyzed by using Cluster-Specific (CS) or Population-Averaged (PA) Poisson regression models [2]. The choice of analysis method depends on whether the covariate of interest varies within or between the clusters [3]. If the primary focus is on the cluster specific responses, then CS models also known as mixed models are preferred. Some form of the Maximum Likelihood (ML) method is frequently used to estimate the parameters [4]. On the other hand, the generalized estimating equation (GEE) approach is commonly used to estimate the parameters in PA models. Although, for log linear models, the estimated treatment effect has been shown to be unbiased even when clustering (due to omitted covariates) is not accounted in the analyses [2, 5], the precision of the estimates do depend on the analyses. Therefore, a sample size calculation which ignores clustering risks yielding biased estimate of required sample size.

Observations within each cluster are usually positively correlated. An appropriate sample size determination method for such data must consider the dependencies among cluster members [6]. Sample size determination methods for clustered data are well developed for linear models [7],[8]. In recent years, focus has shifted towards non-linear models. Several authors have proposed complex iterative solutions for longitudinal designs in the generic framework of population averaged models using GEE approach [9], [10], [11]. On the other hand, a methodology for cluster specific models using mixed-effects models (MM) has been developed specifically for a repeated-count measurements [12]. These methods are based on the first order Taylor series approximation of the non-linear functions.

Sample size formula for cross-sectional designs can be derived either from methods developed for longitudinal studies or can be derived independently. Simple independently derived expressions of sample size for cluster randomized studies for a two group comparison of various non-Gaussian data are found in [13],[14]. Their expressions are based on the coefficient of variation (CV) which is not as commonly reported as intraclass correlation (ICC) in the literature. Thus, simple expression to calculate sample size which directly utilizes ICC is necessary. On the other hand, for multi-center studies independently derived formula for count data are not commonly available. Although longitudinal methods can be simplified to obtain expression for cross-sectional design, the expression so derived are based on the approximation. We independently derive an alternative expression utilizing properties of a Poisson distribution that provides significant improvement over the approximated methods.

In cross-sectional studies the parameter of interest is the regression coefficient corresponding to the treatment group indicator. Whereas, in longitudinal studies, the interest is on the time by treatment interaction. The notion of sample size determination arises in testing of these corresponding parameters. In this paper we (i) provide an exact sample size expression for multi-center cross-sectional studies and show that it provides better estimate compared to the expression derived from the longitudinal method, (ii) provide simple sample size expressions based on the ICC for cluster randomized cross-sectional studies and derive conditions in which it is favorable compared to the alternative, and (iii) provide a very flexible sample size expression for longitudinal designs which accommodates differential allocation of subjects across groups along with differential attrition rates over the follow up time points.

The rest of the paper is organized as follows. In Section 2, we provide a generic expression of sample size formula for a two group comparison. In section 3, we consider both multi-center and cluster randomized cross-sectional designs; and derive expressions for calculating the required number of centers/clusters in each design. In section 4, we consider longitudinal studies. In Section 5, we illustrate our results with three real data examples. The article is concluded with a discussion in section 6. All derivations are presented in the Appendix in Section 7.

2. General sample size determination

Let β be a model parameter related to the treatment effect. In this section we provide a generic expression to determine the required number of clusters N for testing the null hypothesis H₀ : β ≤ 0 against the alternative hypothesis H₁ : β = $\tilde{\beta }(>0)$, at a significance level α in order to achieve at least (1 – η)100% power. Let $\widehat{\beta }$ be a consistent estimator of β. Let z_α denote the (1 – α)th percentile point of a standard normal distribution. We denote the variance of $\widehat{\beta }$ under the null and alternative hypotheses by $\frac{\varphi \left(0\right)}{N}$ and $\frac{\varphi \left(\tilde{\beta }\right)}{N}$ respectively, thus $V(\widehat{\beta }\mid H_0)=\frac{\varphi \left(0\right)}{N}$ and $V(\widehat{\beta }\mid H_a)=\frac{\varphi \left(\tilde{\beta }\right)}{N}$. Let $z=\frac{\widehat{\beta }-\beta }{\sqrt{V\left(\widehat{\beta }\right)}}$. We propose z as a test statistic for H₀. Note that z follows a standard normal distribution asymptotically. Our decision rule is to reject H₀ if $\widehat{\beta }$ > c. The threshold value c is determined under the following two conditions.

$$P(\widehat{\beta }>c\mid H_0)=\alpha ,$$ (1)

$$P(\widehat{\beta }>c\mid H_a)=1-\eta .$$ (2)

Solving (1) and (2) we obtain

$$c=z_{\alpha }\sqrt{\frac{\varphi \left(0\right)}{N}}=\tilde{\beta }-z_{\eta }\sqrt{\frac{\varphi \left(\tilde{\beta }\right)}{N}},$$

which gives

$$N\ge \frac{{\left[z_{\alpha }\sqrt{\varphi \left(0\right)}+z_{\eta }\sqrt{\varphi \left(\tilde{\beta }\right)}\right]}^2}{{\tilde{\beta }}^2}.$$ (3)

The expression in the right side of (3) provides the lower bound for the number of clusters required to achieve at least (1 – η)100% power. For two-sided hypothesis, z_α is replaced by z_α/2 in equation (3). One may also choose to compute variances of $\widehat{\beta }$ based entirely on alternative hypothesis value of β. In that case ϕ(0) is replace by ϕ($\tilde{\beta }$) in equation (3).

3. Cross-sectional studies

3.1. Subject-randomized/Multi-center Designs

In this section we discuss cross-sectional subject-level randomized designs and provide formulae for determining number of clusters using the MM method. Multi-center randomized clinical trials with subject-level randomization are often used in medical research. It is the most frequently used design for evaluating the efficacy and safety of a therapy allowing for between-site variation. In such trials, participants are recruited from multiple centers (N), and within each center n/2 subjects are randomly assigned to treatment and n/2 subjects are randomly assigned to control conditions. Let y_ij be the count of events for the j^th subject in the i^th center with an associated 1 × 2 covariate vector z_ij = (1, x_ij) with corresponding coefficients γ = (β₀, β₁). The x_ij is 1 for a subject assigned to treatment condition and it is 0 for a subject assigned to the control condition. Hence, the structure of the design matrix for the ith cluster is as follows:

$$Z_i=\left(\begin{array}{cc}\hfill 1_{n∕2}\hfill & \hfill 1_{n∕2}\hfill \\ \hfill 1_{n∕2}\hfill & \hfill 0_{n∕2}\hfill \end{array}\right),$$ (4)

where 1_k is a vector of 1’s of dimension k. We assume n is an even number. Here, we have assumed equal cluster sizes for convenience. Towards the end of this subsection, we discuss an alternative when number of subjects are different across the clusters.

Whittemore provided an approximate closed-form solution for sample size determination for the fixed-effecs multiple logistic regression model [15]. He assumed a distribution on covariates and utilized its moment generating function to obtain a closed-form estimate of the asymptotic covariance matrix of the maximum likelihood estimate. The approximation is valid when a probability of response is small. Signorini applied a similar approach to obtain the exact solution for the sample size required for a fixed-effect Poisson regression model [16]. However, for clustered count data, fixed-effect Poisson regression based estimates are inefficient. We extend this approach from fixed-effect to the mixed-effect Poisson regression models.

For mixed-models, a cluster-specific intercept u is assumed to be randomly distributed with a probability distribution. A normal distribution with mean 0 and variance σ² is a common choice for the distribution of u. We denote this normal density function by g(u). Then the mixed-effects Poisson regression model incorporating the correlation of subjects(j) nested within the same center (i) is specified as follows:

$$\begin{array}{cc}\hfill y_{\mathit{ij}}& \sim \text{Poisson}\left({\lambda }_{\mathit{ij}}\right),\hfill \\ \hfill \mathit{log}({\lambda }_{\mathit{ij}}\mid u_i)& ={\beta }_0+{\beta }_1{x}_{\mathit{ij}}+u_i,\hfill \\ \hfill \text{where}{u}_i& \sim g_u\left(u_i\right).\hfill \end{array}$$ (5)

Under the normal distribution assumption of u_i, λ_ij follows a log-normal distribution with the following mean and variance.

$$E\left({\lambda }_{\mathit{ij}}\right)=e^{{\beta }_0+{\beta }_1{x}_{\mathit{ij}}+{\sigma }^2∕2},$$ (6)

and

$$\text{and}V\left({\lambda }_{\mathit{ij}}\right)=\left(e^{2{\beta }_0+2{\beta }_1{x}_{\mathit{ij}}+{\sigma }^2}\right)(e^{{\sigma }^2}-1),$$ (7)

where σ² is the inter-cluster variance parameter on the log-lambda scale and (e^{2β₀+2β₁x_ij+σ2})(e^σ2 – 1) is the corresponding inter-cluster variance on the original scale. In model (5), β₀ and β₁ are fixed parameters. β₀ and β₀ + β₁ represent event rates in control and treatment groups respectively on the logarithmic scale. The correlation of the subjects nested within the same cluster is accounted for by the presence of the cluster effect u_i. We assume that x ~ Bernoulli(1, p) and denote it by f_x(x_ij). The parameter p determines the proportion of subjects allocated to each treatment groups within a cluster. The likelihood function for the joint distribution of Y, x and u is

$$L({\beta }_0,{\beta }_1)=\prod _{\mathit{ij}}{g}_u\left(u_i\right)f_x\left(x_{\mathit{ij}}\right){\lambda }_{\mathit{ij}\mid u_i}^{y_{\mathit{ij}}}e(-{\lambda }_{\mathit{ij}\mid u_i})∕y_{\mathit{ij}}!.$$

A vector of maximum likelihood estimators of regression parameters converges asymptotically to a multivariate normal distribution with mean vector (β₀, β₁)’ and covariance matrix ${\left[I({\widehat{\beta }}_0,{\widehat{\beta }}_1)\right]}^{-1}$, where $I({\widehat{\beta }}_0,{\widehat{\beta }}_1)$ is the Fisher Information matrix which has the following expression.

$$\begin{array}{cc}\hfill I({\widehat{\beta }}_0,{\widehat{\beta }}_1)& =-E_u{E}_x\left[\frac{d^2\mathit{log}L({\beta }_0,{\beta }_1)}{d\gamma {\gamma }^T}\right]\hfill \\ \hfill & =e^{({\beta }_0+{\sigma }^2∕2)}{E}_x\left[\sum _{\mathit{ij}}\left(\begin{array}{cc}\hfill 1\hfill & \hfill x_{\mathit{ij}}\hfill \\ \hfill x_{\mathit{ij}}\hfill & \hfill x_{\mathit{ij}}^2\hfill \end{array}\right)e^{{\beta }_1{x}_{\mathit{ij}}}\right]\hfill \\ \hfill & =N_n{e}^{({\beta }_0+{\sigma }^2∕2)}\left(\begin{array}{cc}\hfill (1-p)+p{e}^{{\beta }_1}\hfill & \hfill p{e}^{{\beta }_1}\hfill \\ \hfill p{e}^{{\beta }_1}\hfill & \hfill p{e}^{{\beta }_1}\hfill \end{array}\right).\hfill \end{array}$$ (8)

The variance of ${\widehat{\beta }}_1$ is given by the second diagonal element of ${\left[I({\widehat{\beta }}_0,{\widehat{\beta }}_1)\right]}^{-1}$. Thus

$$\begin{array}{cc}\hfill V\left({\widehat{\beta }}_1\right)& =\frac{1}{\mathit{Nn}{e}^{({\beta }_0+{\sigma }^2∕2)}}\left[\frac{1}{p{e}^{{\beta }_1}}+\frac{1}{1-p}\right]=\frac{\varphi \left({\beta }_1\right)}{N},\hfill \\ \hfill \text{where}\varphi \left({\beta }_1\right)& =\frac{1}{n{e}^{({\beta }_0+{\sigma }^2∕2)}}\left[\frac{1}{p{e}^{{\beta }_1}}+\frac{1}{1-p}\right].\hfill \end{array}$$ (9)

The details of the derivation of $V\left({\widehat{\beta }}_1\right)$ are provided in Appendix 7.1. We calculate the required number of clusters by substituting the expression of $\varphi \left(\widehat{\beta }\right)$ from (9) into the sample size formula in (3). Hence the expression of the proposed number of clusters (N_p) is:

$$N_p\ge \frac{{\left[z_{\alpha }\sqrt{\frac{1}{e^{({\beta }_0+{\sigma }^2∕2)}}\left[\frac{1}{p}+\frac{1}{1-p}\right]}+z_{\eta }\sqrt{\frac{1}{e^{({\beta }_0+{\sigma }^2∕2)}}\left[\frac{1}{p{e}^{\tilde{\beta }}}+\frac{1}{1-p}\right]}\right]}^2}{n{\tilde{\beta }}^2}.$$ (10)

The Fisher Information matrix in (8) is exponentially proportional to σ². The term e^{(β₀+σ2/2)} in the Fisher Information matrix comes from the mean of a log-normal distribution (see equation (6)). The addition of σ²/2 to β₀ implies the inflation of the background incidence rate. It is well known in epidemiological studies when the disease is prevalent, smaller sample sizes are sufficient to detect the treatment effect. The expression in (10) implies that the background incidence rate effectively increases with larger values of σ² and as a result, we need less number of clusters. For linear models, Roy et al. [17], and Heo and Leon [18] observed that determination of sample size does not depend on the inter-cluster variance parameter when randomization is performed at the subject level. On the contrary, for the current model, the variance parameter plays an important role in sample size determination due to the lognormal nature of the distribution which brings the variance parameter to the regression parameters to determine the mean efficacy.

It is not always practical to assume that the number of subjects n across all the clusters are the same. However, certain minimal information on the cluster sizes must be available to calculate N. In practice, investigators can usually make informative assumption about number of subjects expected in the largest ($\stackrel{‒}{n}$) and the smallest ($\underset{¯}{n}$) cluster. We may impose uniform($\stackrel{‒}{n}$, $\underset{¯}{n}$) distribution on n and replace it with $E\left(n\right)=\frac{\stackrel{‒}{n}+\underset{¯}{n}}{2}$ in equation (8). With such assumption, equation (10) is modified as follows:

$$N_{p_M}\ge \frac{{\left[z_{\alpha }\sqrt{\frac{1}{e^{({\beta }_0+{\sigma }^2∕2)}}\left[\frac{1}{p}+\frac{1}{1-p}\right]}+z_{\eta }\sqrt{\frac{1}{e^{({\beta }_0+{\sigma }^2∕2)}}\left[\frac{1}{p{e}^{\tilde{\beta }}}+\frac{1}{1-p}\right]}\right]}^2}{\frac{\stackrel{‒}{n}+\underset{¯}{n}}{2}{\tilde{\beta }}^2}.$$ (11)

To study the impact of unequal cluster size, let $\stackrel{‒}{n}=a\times \underset{¯}{n}$. Further, letting $\stackrel{‒}{n}=n$, it is easy to show that N_pM is larger than N_p by a factor of $\frac{2a}{a+1}$. For example, if the largest cluster is 4 times larger than the smallest cluster, i.e. a = 4, then N_pM is 1.6 time larger than N_p. That is, a consequence of specified discrepancy in cluster sizes is an increase in required number of clusters by 60% to achieve the same power.

3.2. Comparision with corrected Ogungbenro and Aarons method

Ogungbenro and Aarons developed a sample size calculation method for repeated measures based on an approximate inference in the generalized linear mixed models [12],[19]. When this method is applied to cross-sectional designs, we obtain following variance expression for ${\widehat{\beta }}_1$ (see Appendix).

$$V_{\mathit{OA}}\left({\widehat{\beta }}_1\right)=\frac{2}{\mathit{Nn}}[2{\sigma }^2+e^{-{\beta }_0}(1+e^{-{\beta }_1}\left)\right].$$ (12)

Using the general expression of N in (3), number of clusters required by the Ogungbenro and Aarons’ method (N_OA) is as follows.

$$N_{\mathit{OA}}\ge \frac{2{\left[z_{\alpha }\sqrt{2{\sigma }^2+2e^{-{\beta }_0}}+z_{\eta }\sqrt{2{\sigma }^2+e^{-{\beta }_0}(1+e^{-\tilde{\beta }})}\right]}^2}{n{\tilde{\beta }}^2}.$$ (13)

Now, we analytically prove that N_OA > N_P for all possible combinations of σ², β₀, and $\tilde{\beta }$. Let us assume the balanced sample sizes, i.e. p = 0.5 in N_p, A = 1 + $e^{-\tilde{\beta }}$ and B = e^−β₀.

$$\begin{array}{cc}\hfill & N_{\mathit{OA}}>N_p\hfill \\ \hfill \mathit{if}& \frac{{\left[z_{\alpha }\sqrt{2{\sigma }^2+2e^{-{\beta }_0}}+z_{\eta }\sqrt{2{\sigma }^2+e^{{\beta }_0}(1+e^{-\tilde{\beta }})}\right]}^2}{{\tilde{\beta }}^{2}n}>\frac{2{\left[z_{\alpha }\sqrt{\left[\frac{1}{p}+\frac{1}{1-p}\right]}+z_{\eta }\sqrt{\left[\frac{1}{p{e}^{\beta }}+\frac{1}{1-p}\right]}\right]}^2}{n{e}^{({\beta }_0+{\sigma }^2∕2)}{\tilde{\beta }}^2}.\hfill \\ \hfill \mathit{if}& \frac{2{[z_{\alpha }\sqrt{2{\sigma }^2+2B}+z_{\eta }\sqrt{2{\sigma }^2+\mathit{BA}}]}^2}{{\tilde{\beta }}^{2}n}>\frac{{[2z_{\alpha }+z_{\eta }\sqrt{2A}]}^2}{n{e}^{({\beta }_0+{\sigma }^2∕2)}{\tilde{\beta }}^2}\hfill \\ \hfill \mathit{if}& \sqrt{e^{({\beta }_0+{\sigma }^2∕2)}}\left[z_{\alpha }\sqrt{2{\sigma }^2+2B}+z_{\eta }\sqrt{2{\sigma }^2+\mathit{BA}}\right]>\left[\sqrt{2z_{\alpha }}+z_{\eta }\sqrt{A}\right]\hfill \\ \hfill \mathit{if}& z_{\alpha }\left[\sqrt{e^{({\beta }_0+{\sigma }^2∕2)}}\sqrt{2{\sigma }^2+2B}-\sqrt{2}\right]+z_{\eta }\left[\sqrt{e^{({\beta }_0+{\sigma }^2∕2)}}\sqrt{2{\sigma }^2+\mathit{BA}}-\sqrt{A}\right]>0.\hfill \end{array}$$ (14)

It is easy to show that $\sqrt{e^{({\beta }_0+{\sigma }^2∕2)}}\sqrt{2{\sigma }^2+2B}-\sqrt{2}>0$, and $\sqrt{e^{({\beta }_0+{\sigma }^2∕2)}}\sqrt{2{\sigma }^2+\mathit{BA}}-\sqrt{A}>0$. Also for α = 0.05, and η = 0.20 both z_α and z_η are positive. Hence (14) holds and thus N_OA > N_p, i.e., the exact method we derived requires less clusters compared to the Ogungbenro and Arrons approximated method. In the following section, for some parametric combinations, we numerically show how our method performs better than the method proposed by Ogunbenro and Aarons.

3.3. Simulation Study for Subject-Level Randomization

We conduct a limited simulation study to investigate the performance of our method proposed for clustered count data in the previous section. For simplicity we consider a balanced design with n subjects nested within each of N clusters. The observed event count y_ij for an individual j (= 1⋯n) in cluster i (= 1⋯N) is assumed to follow a Poisson distribution with rate λ_ij along with x_ij = 1 for a treated subject and x_ij = 0 for a control subject. We fix the Type 1 error rate at 5% and determine the number of clusters required to achieve 80% power.

We generate data from a Poisson distribution with mean λ_ij. The event rate λ_ij is assumed to follow the model in equation (5) i.e. λ_ij|u_i = exp (β₀ + β₁x_ij + u_i), where u_i is a cluster-specific random effect that follows N(0, σ²). We evaluate regression parameters β₀ and β₁ for a wide range of values representing different background rates and varying rate ratios respectively. To induce a moderate intra-cluster correlation among the subjects nested within the same cluster we set σ² to 0.5. We generate 10,000 independent simulation runs of y_ij for each combination of parameters.

Tables 1a-1b report the required number of clusters obtained by using formula (10) and (13) for various combinations of pre-specified parameters. In addition we compute the corresponding power via simulation (provided in the parenthesis). In Table 1a we fix the background rate at 0.20 (i.e. β₀ = −1.6), between-cluster variance parameter at 0.5, n = 20, 50, and 200. We compute N for various values of the treatment effect β₁. For each value of β₁, we provide (in parenthesis) the corresponding effect size (i.e. percent increment of the incidence rate in the treatment group compared to that in the control group). Results in Table 1a show that the required number of clusters monotonically decreases with the increasing magnitude of the treatment effect.

Table 1.

Required number of centers N and corresponding power for multicenter trials using a random effect Poisson regression model: ln(λ_i) = β₀ + β₁x + ν_i.

(a) Required number centers for varying number of subjects n and β1, while β0 = −1.6 and σ2 = 0.5 were fixed.
		0.18 (20%)	0.22 (25%)	0.26(30%)	0.3(35%)	0.34(40%)	0.38 (46%)	0.42 (52%)	0.46 (58%)
20	Np NOA	179 (0.81) 258	122 (0.82) 172	87 ( 0.82) 123	65 ( 0.81) 92	51 ( 0.83) 71	40 (0.82) 57	33 (0.85) 47	27 (0.83) 39
50	Np NOA	72 (0.84) 104	49 ( 0.84) 69	35 ( 0.82) 49	26 ( 0.84) 37	21 ( 0.83) 29	16 (0.83) 23	14 (0.86) 19	11 (0.86) 16
200	Np NOA	18 ( 0.83) 26	13 ( 0.84) 18	9 ( 0.83 ) 13	7 ( 0.82) 10	6 ( 0.87) 8	4 (0.80) 6	4 (0.86) 5	3 (0.86) 4

(b) Required number of centers N for varying number of within center subjects n and baseline rate β0, while β1 = 0.18 and σ2 = 0.5 were fixed.
		−1.6 (0.20)	−1.2 (0.30)	−0.8 (0.45)	−0.4 (0.67)	0 (1.0)	0.4 (1.49)	0.8 (2.23)	1.2 (3.32)	1.6 (4.95)
20	Np NOA	179 (0.82) 258	120 (0.82) 181	81 (0.82) 130	54 (0.84) 95	36 (0.83) 72	25 (0.80) 56	17 (0.82) 46	11 (0.80) 39	8 (0.83) 34
50	Np NOA	72 (0.82) 104	48 (0.81) 73	33 (0.82) 52	22 (0.83) 38	15 (0.81) 29	10 (0.81) 23	7 (0.79) 19	5 (0.85) 16	3 (0.76) 14
200	Np NOA	18 (0.82) 26	12 (0.82) 19	9 (0.85) 13	6 (0.82) 10	4 (0.81) 8	3 (0.84) 6

In Table 1b, the inter-cluster variance parameter is again set at a moderate value of 0.5 and the treatment effect is assumed to be 20% higher than that of the control. The background rate is varied from 0.20 to 4.9. Table 1b reveals that when the background incidence rate (i.e. the rate in control group) becomes more prevalent, we need fewer clusters (N) in order to detect the same magnitude of the treatment effect. This table also shows that the OA method requires two to four times more clusters compared to the proposed method depending on the values of control effect and within center sample sizes.

In addition, Table 1c reveal that for larger inter-cluster variances fewer clusters are required to estimate and detect the specified effect size by the proposed method. This counter intuitive result is a consequence of inflation of background incidence rate by the inter-cluster variance parameter. The simulated power provided in these tables is between 80 and 84 percent. Similar gain in power allowing a reduction in sample size for the higher inter-cluster variance have been reported for continuous data [8] and for binary data [10].

(c) Required number of centers N for varying number of within center subjects n and between center variance σ2, while β0 = −1.6 and β1 = 0.18 were fixed.
		0.1	0.3	0.5	0.7	0.9	1.1	1.3	1.5
20	Np NOA	223 (0.83) 251	202 (0.79) 286	183 (0.81) 324	165 (0.80) 366	150 (0.79) 410	135 (0.80) 458	123 (0.82) 511	111(0.81) 567
50	Np NOA	90 (0.83) 100	81 (0.81) 114	73 (0.84) 130	66 (0.81) 146	60 (0.81) 164	54 (0.80) 183	49 (0.81) 204	45 (0.77) 227
200	Np NOA	23 (0.83) 25	21 (0.82) 29	19 (0.83) 32	17 (0.83) 37	15 (0.81) 41	14 (0.77) 46	13 (0.79) 51	12 (0.81) 57

3.4. Cluster Randomized Designs

In a cluster-randomized study, research sites are randomly assigned to different intervention regimens, and all subjects within a cluster receive the same treatment. The treatment effect in these studies is now exclusively a between-center effect, since each center or site has only one treatment. Analyses of data from this type of study should invariably involve use of PA regression models (center, subject, occasion). A positive intra-class correlation (ICC) between outcomes of individuals nested within the same cluster is expected due to the differences in characteristics between clusters, the interaction between individuals within the same cluster, or to commonalities of the intervention experienced by the entire cluster.

In this section we provide a simple expression of number of clusters in cluster randomized cross-sectional studies. The expression we present here is essentially a Rochon’s method simplified for a comparison of two groups in cross-sectional cluster randomized design. However, in addition to providing an expression that utilizes ICC, the purpose of this section is to analytically compare the derived method with the equally compelling alternative method and show the conditions when each approach has its advantage over the alternative.

We assume that there are N clusters and n participants are nested within each cluster. One half of the N clusters are randomized to the treatment and the other half are randomized to the control. The design matrices are $Z_{\mathit{ic}}=\left(1_n{0}_n\right)$ for the ith cluster assigned to the control and $Z_{i^{\prime }t}=\left(1_n{1}_n\right)$ for the i’th cluster assigned to the treatment.

3.4.1. Generalized Estimating Equation

PA models are often used to model clustered count data and are analyzed using the GEE approach. The model for the i^th cluster with n × 1 vector of counts y_i, and n × m matrix of covariates is

$$\begin{array}{cc}\hfill \mathit{ln}\left({\lambda }_{\mathit{ij}}\right)& ={\beta }_0+{\beta }_1{z}_{\mathit{ij}}={\gamma }^T{\mathrm{z}}_{\mathrm{ij}},\hfill \\ \hfill \text{with}\mathit{V}\left(y_i\right)& ={\mathit{V}}_i.\hfill \end{array}$$

Then, the estimating equation for N clusters is given by:

$$\sum _{i=1}^N{Z}_i^T{\mathit{E}}_i{\mathit{V}}_i^{-1}(y_i-e_i)=0,$$ (15)

where ${\mathrm{e}}_{\mathrm{i}}={({\mathrm{e}}^{{\gamma }^{\mathrm{T}}{\mathrm{z}}_{\mathrm{i}1}},\dots ,{\mathrm{e}}^{{\gamma }^{\mathrm{T}}{\mathrm{z}}_{\mathrm{in}}})}^{\mathrm{T}},{\mathrm{E}}_{\mathrm{i}}=\text{diag}\left({\mathrm{e}}_{\mathrm{i}}\right),{\mathrm{V}}_{\mathrm{i}}={\mathrm{E}}_{\mathrm{i}}^{1∕2}\mathrm{R}\left(\rho \right){\mathrm{E}}_{\mathrm{i}}^{1∕2}$ and R(ρ) is an assumed working correlation matrix of y_i. The GEE estimator $\widehat{\gamma }$ is the solution to equation (15). Under certain regularity conditions, as the number of clusters N increases, $\widehat{\gamma }$ is consistent and asymptotically normally distributed [20]. Hence to $\sqrt{N}(\widehat{\gamma }-\gamma )\stackrel{d}{\to }N(0,{\mathit{V}}_{\mathit{G}})$, where V_G = lim_N→∞V_G,N with

$${\mathrm{V}}_{\mathrm{G},\mathrm{N}}=N{\left[\sum _{\mathrm{i}}{\mathrm{Z}}_{\mathrm{i}}^{\mathrm{T}}{\mathrm{E}}_{\mathrm{i}}{\mathrm{V}}_{\mathrm{i}}^{-1}{\mathrm{E}}_{\mathrm{i}}{\mathrm{Z}}_{\mathrm{i}}\right]}^{-1}\left[\sum _{\mathrm{i}}{\mathrm{Z}}_{\mathrm{i}}^{\mathrm{T}}{\mathrm{E}}_{\mathrm{i}}{\mathrm{V}}_{\mathrm{i}}^{-1}\mathrm{Cov}\left({\mathrm{y}}_{\mathrm{i}}\right){\mathrm{V}}_{\mathrm{i}}^{-1}{\mathrm{E}}_{\mathrm{i}}{\mathrm{Z}}_{\mathrm{i}}\right]{\left[\sum _{\mathrm{i}}{\mathrm{Z}}_{\mathrm{i}}^{\mathrm{T}}{\mathrm{E}}_{\mathrm{i}}{\mathrm{V}}_{\mathrm{i}}^{-1}{\mathrm{E}}_{\mathrm{i}}{\mathrm{Z}}_{\mathrm{i}}\right]}^{-1}.$$ (16)

For clustered data, the exchangeable working correlation matrix with elements corr(y_ij, y_ij’)=ρ is usually used. For the purpose of sample size calculation we assume that this working correlation structure is the true one and Cov(y_i) = V_i. Then the asymptotic covariance matrix of $\widehat{\gamma }={\mathit{V}}_{G,N}∕N$ simplifies to ${\left[{\sum }_i{\mathit{Z}}_i^{\mathit{T}}{\mathit{E}}_i{\mathit{V}}_i^{-1}{\mathit{E}}_i{\mathit{Z}}_i\right]}^{-1}$ with ${\mathit{V}}_i^{-1}={\mathit{E}}_i^{1∕2}\mathit{R}{\left(\rho \right)}^{-1}{\mathit{E}}_i^{-1∕2}$. Hence,

$$\mathrm{Cov}\left(\widehat{\gamma }\right)=(1-\rho ){\left[\sum _{i=1}^N\left(Z_i^T{E}_i{Z}_i-\frac{\rho }{1+(n-1)\rho }{Z}_i^T{E}_i^{1∕2}{1}_i{1}_i^T{\mathrm{E}}_i^{1∕2}{\mathrm{Z}}_i\right)\right]}^{-1}.$$ (17)

We use the expressions of Z_ic and Z_i’t for clusters assigned to control and treatment respectively and derive the following expression for Cov($\widehat{\gamma }$):

$$\begin{array}{cc}\hfill \mathrm{Cov}\left(\widehat{\gamma }\right)& =\frac{2(1-\rho )}{N}{\left[\begin{array}{cc}\hfill (e_c+e_t)\left(n-\frac{n^2\rho }{1+[n-1]\rho }\right)\hfill & \hfill e_t\left(n-\frac{n^2\rho }{1+[n-1]\rho }\right)\hfill \\ \hfill e_t\left(n-\frac{n^2\rho }{1+[n-1]\rho }\right)\hfill & \hfill e_t\left(n-\frac{n^2\rho }{1+[n-1]\rho }\right)\hfill \end{array}\right]}^{-1}\hfill \\ \hfill & =\frac{2[1+(n-1\left)\rho \right]}{\mathit{Nn}{e}^{{\beta }_0}}{\left(\begin{array}{cc}\hfill 1+e^{{\beta }_1}\hfill & \hfill e^{{\beta }_1}\hfill \\ \hfill e^{{\beta }_1}\hfill & \hfill e^{{\beta }_1}\hfill \end{array}\right)}^{-1}.\hfill \end{array}$$ (18)

Using the expression of Cov($\widehat{\gamma }$) in (18) we compute the following asymptotic variance of ${\widehat{\beta }}_1$.

$$\begin{array}{cc}\hfill V\left({\widehat{\beta }}_1\right)& =\frac{\varphi \left({\beta }_1\right)}{N},\hfill \\ \hfill \text{where},\varphi \left({\beta }_1\right)& =\frac{2[1+(n-1\left)\rho \right][1+e^{-{\beta }_1}]}{n{e}^{{\beta }_0}}.\hfill \end{array}$$

We use the expression of N in (3) and obtain the required number of clusters for the cluster-level randomization for GEE.

$$N_{P1}\ge \frac{2[1+(n-1\left)\rho \right]{\left[z_{\alpha ∕2}\sqrt{2}+z_{\eta }\sqrt{[1+e^{-\tilde{\beta }}]}\right]}^2}{n{e}^{{\beta }_0}{\tilde{\beta }}^2}.$$ (19)

As mentioned earlier, the expression in (19) is essentially a simplification of Rochon’s method for a comparison of two groups in cross-sectional cluster randomized design. This result reveals, as for the continuous data, the sample size required for the cluster randomized design of count data is a simple multiplication of sample size required for ordinary Poisson regression by the design effect. In the following section, we discuss an alternative method which we will use as a comparator for our method.

3.4.2. Hayes-Donner method

In this context, Hayes and Bennett [13] compute the sample size based on the coefficient of variation (CV). They assume that the ith cluster nested within the sth group has an event rate (λ_i) that follows a normal distribution with mean λ_s and variance σ². They provide the following expression for the number of clusters N_HD.

$$N_{\mathit{HD}}=2\left[1+\frac{{(z_{\alpha ∕2}+z_{\eta })}^2\left\{\right({\lambda }_1+{\lambda }_2)∕n+{\mathit{CV}}^2({\lambda }_1^2+{\lambda }_2^2\left)\right\}}{{({\lambda }_1-{\lambda }_2)}^2}\right]$$ (20)

$$=\left[2\frac{{(z_{\alpha ∕2}+z_{\eta })}^2({\lambda }_1+{\lambda }_2)}{n{({\lambda }_1-{\lambda }_2)}^2}\right]\mathit{IF},$$ (21)

where

$$\mathit{IF}=\left[1+\frac{{\mathit{CV}}^2({\lambda }_1^2+{\lambda }_2^2)}{{\lambda }_1+{\lambda }_2}\right].$$

The expression in (21) is derived by [14]. The first factor in the equation (21) is the sample size required for comparing two group rates when CV=0. They observed that in the presence of inter-cluster variation it requires more clusters. The factor denoted by IF is known as the inflation factor which is a quadratic function of CV. The CV is not as commonly reported as the ICC in cluster randomized studies. Therefore, the expression in (21) needs to be modified in order to utilize the ICC to calculate sample size for our comparison. As there is no direct relationship between CV and ICC, we use a heuristic approach by equating the inflation factor from (21) and (19) to approximate CV from the ICC as follows.

$$\begin{array}{cc}\hfill 1+(n-1)\rho & =1+\frac{{\mathit{CV}}^2({\lambda }_1^2+{\lambda }_2^2)}{{\lambda }_1+{\lambda }_2}\hfill \\ \hfill \Rightarrow {\mathit{CV}}^2& =\frac{\rho (n-1)({\lambda }_1+{\lambda }_2)}{{\lambda }_1^2+{\lambda }_2^2}.\hfill \end{array}$$ (22)

The number of clusters (N_HD) in equation (21) can be expressed in terms of ICC by substituting the expression of CV² in equation (22).

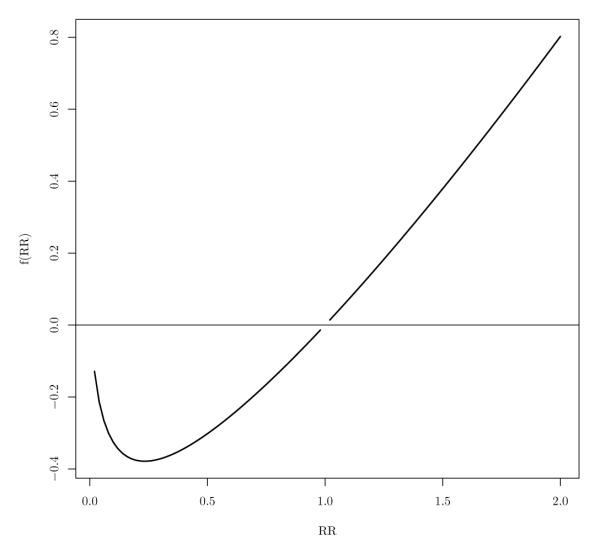
Denote the rate ratio (i.e $\frac{{\lambda }_2}{{\lambda }_1}$) by RR. In Appendix 7.2 we define a function f(RR) using the difference of the expressions of N_P1 and N_HD. In Figure 1, we observe that for RR less than 1, f(RR) is less than 0, which implies that our method requires less number of clusters compared to the Hayes-Donner method when RR < 1. This Figure also shows that Hayes-Donner method performs better than the proposed method for RR between 1 and 3. We do not consider values of RR more than 3 as they are hardly observed in practice.

Figure 1.

The plot of the difference between number of centers calculated by the proposed method N_p and Ogungbenro-Aaron method N_OA as a function of Rate Ratio (RR). Note that the functional value is not a magnitude of difference, it only demonstrates conditions based on RR where the N_p or the N_OA perform better.

3.5. Simulation Results for Cluster-Level Randomization

We have conducted a limited simulation study to investigate the performance of our proposed methodology for analyzing cluster-randomized count data. For simplicity we again consider a balanced design with n subjects nested in each of the N clusters. In this design N/2 clusters are randomized to the treatment group and the remaining N/2 clusters are randomized to the control group. The observed event count y_ij for an individual j (= 1⋯n) in cluster i (= 1⋯N) is assumed to follow a Poisson distribution with rate λ_ij along with x_ij = 1 and x_ij = 0 for subjects in treated and control clusters respectively.

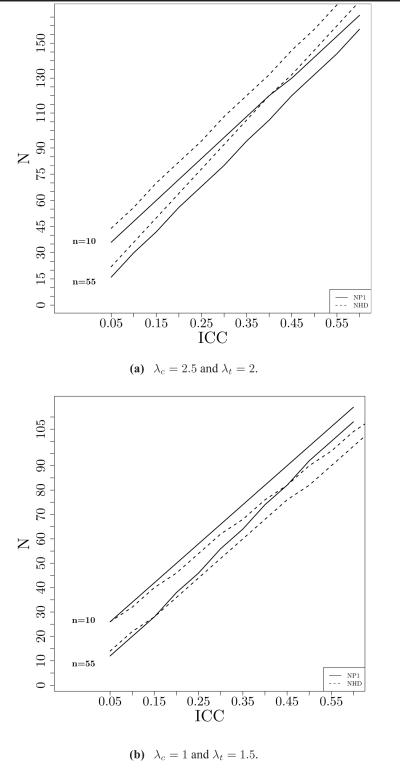
Figures 2 (a)-(b) show the effect of the ICC on the number of clusters required to obtain a power of 80% for testing β₁. These figures reveal that for a larger ICC we need significantly more clusters. We also notice in these figures that for the same ICC, we require fewer clusters when the corresponding cluster sizes (n) are increased. For larger cluster sizes (n > 55), however, there is a minimal impact of further increment of n on the reduction of N. We fix RR < 1 for 2 (a). In this Figure we observe that for .05 ≤ ρ ≤ .55 the proposed method requires less number of clusters compared to the Hayes-Donner method for both cluster sizes n = 10 (compaaring first two lines from the top) and n = 55 (compaaring first two lines from the bottom). Figure 2 (b) depicts the opposite picture when RR > 1. In this Figure we see that for very small values of ρ the difference between the number of clusters determined by these two method is indistinguishable. However, for larger values of ρ Hayes-Donner method performs better. These findings match with our expectation discussed in the previous section.

Figure 2.

Required number of clusters (N) as a function intra-cluster correlation ICC when number of subjects nested within each cluster is n. Control group rate λ_c and treatmemt group rate λ_t are fixed for cluster randomized designs.

4. Longitudinal studies

In this Section we consider longitudinal studies and provide a formula for determining number of subjects required to achieve a desired power. The derivation closely follows Ogungbenro and Arrons approach but with one important correction. Let p proportion of total N subjects are randomly assigned to treatment (x_is = 1) and the remaining 1 – p proportion are randomly assigned to control conditions (x_is = 0). Let y_ist and λ_ist denote outcome count variable and the conditional mean, respectively, of the ith subject belonging to the sth group at the tth time point. For such a design, we consider the following two-level mixed-effects Poisson regression model.

$$\mathit{ln}\left({\lambda }_{\mathit{ist}}\right)={\beta }_0+{\beta }_{1}g\left(t\right)+{\beta }_2{x}_{\mathit{is}}+{\beta }_3{x}_{\mathit{is}}g\left(t\right)+v_{0i}+v_{1i}g\left(t\right).$$ (23)

In (23), β₀ + β_1g(t) is the fixed linear trend (of a continuous time function g(t)) for the control group, and β₀ + β₂ + (β₁ + β₃)g(t) is the linear trend for the intervention group on the log scale. ν_0i + ν_1ig(t) is the random linear trend for the ith subject and it takes into account of the correlation that exists between multiple observations nested within the same subject. We assume that the random-effects follow a bivariate normal distribution given by

$$\left(\begin{array}{c}\hfill v_{i0}\hfill \\ \hfill v_{i1}\hfill \end{array}\right)\sim N\left[\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{cc}\hfill {\sigma }_{v_0}^2\hfill & \hfill {\sigma }_{v_{01}}\hfill \\ \hfill {\sigma }_{v_{01}}\hfill & \hfill {\sigma }_{v_1}^2\hfill \end{array}\right)\right].$$ (24)

We denote the variance-covariance matrix of the above random-effects by Σ_ν. Here we point out that as oppose to unstructured covariance matrix used here, OA uses diagonal matrix which limits its use only to the uncorrelated random effects.

The statistical significance of the treatment effect is determined by the significance of group by time interaction parameter β₃. The function g(t) can be any function of t such as sqrt(t), log(t), (t – c)^r etc. which allows investigators to model non-linear mean response over time. The main interest is in testing the following hypotheses

$$H_0:{\beta }_3=0\mathit{vs}{H}_1:{\beta }_3\ne 0.$$ (25)

Let T be a number of outcome assessment occasions, β be the vector of fixed-effects parameters and ν_i be the vector containing the random-effects parameters for the ith subject, i.e., β = [β₀, β₁, β₂, β₃] and ν_i = [ν_0i, ν_1i] . Further, let m_ist be a vector consisting of partial derivatives of the mean λ_ist with respect to random-effects ν_i computed at ν_i = 0, i.e., ${\mathrm{m}}_{\mathit{ist}}={\left(\frac{\partial {\lambda }_{\mathit{ist}}}{\partial v_{0i}}\frac{\partial {\lambda }_{\mathit{ist}}}{\partial v_{1i}}\right)}_{v_i=0}$. Let M_is denote the matrix containing the row vectors m_ist for all the time points t = 1, …, T, and J_is denote the Jacobian of the transformation from the mean space to the parametric space (see Appendix for details). Hence the dimensions of M_is and J_is are T × 2. The first order approximation of the variance-covariance matrix of the pseudo-observation for the ith subject (see [12] and [19]) can be written as,

$$\begin{array}{cc}\hfill {\mathrm{V}}_{\mathit{is}}& ={\mathrm{M}}_{\mathit{is}}{\Sigma }_v{\mathrm{M}}_{\mathit{is}}^T+{\mathrm{W}}_{\mathit{is}},\hfill \\ \hfill {\mathrm{W}}_{\mathit{is}}& =\mathit{diag}\{{\lambda }_{\mathit{is}1},\cdots ,{\lambda }_{\mathit{isT}}\mid v_i=0\}.\hfill \end{array}$$ (26)

where

$${\mathrm{W}}_{\mathit{is}}=\mathit{diag}\{{\lambda }_{\mathit{is}1},\cdots ,{\lambda }_{\mathit{isT}}\mid v_i=0\}.$$

Ogungbenro and Aarons erroneously referred V_is as a covariance matrix of the parameters. It actually is the covariance matrix of the linearized dependent variable. The matrix W_is is a T × T diagonal matrix containing the conditional variance of the ith subject at each time-point. The first term on the right hand side of the equation (26) is the variance of random-effects transformed to the mean space by the Jacobian matrix M_is. Therefore, the contribution of the ith subject from the sth group to the Fisher information matrix is

$${\mathrm{I}}_{\mathit{is}}\left(\widehat{\beta }\right)={\mathrm{J}}_{\mathit{is}}^T{\mathrm{V}}_{\mathit{is}}^{-1}{\mathrm{J}}_{\mathit{is}}.$$ (27)

A critical error in the Ogungbenro and Aarons’ original paper is the use of V_is as oppose to ${\mathrm{V}}_{\mathit{is}}^{-1}$ in the current derivation. We do not see theoretical basis for using V_is in equation (27). Hence, the corrected approximate Fisher Information matrix based on all the subjects in both the groups is,

$$\mathrm{I}\left(\widehat{\beta }\right)=\sum _{s=0}^1\sum _{i=1}^N{\mathrm{J}}_{\mathit{is}}^T{\mathrm{V}}_{\mathit{is}}^{-1}{\mathrm{J}}_{\mathit{is}}.$$ (28)

Note that I($\widehat{\beta }$) depends on the conditional variance W_is. We can estimate the conditional variance when observations are available. However, for sample size determination when observations are not provided in advance, we replace the diagonal elements of the conditional variance by their respective values evaluated at ν = 0. By doing so, the dependence of W_is on ith subscript disappears. In addition, both M_is and J_is do not depend on the ith subscript. Hence the overall Fisher information matrix for all subjects can be written approximately by dropping the ith subscript,

$$\mathrm{I}\left(\widehat{\beta }\right)=N\left(\right(1-p){\mathrm{J}}_0^{\prime }{\mathrm{V}}_0^{-1}{\mathrm{J}}_0+p{\mathrm{J}}_1^{\prime }{\mathrm{V}}_1^{-1}{\mathrm{J}}_1)=N\Phi ,$$ (29)

where $\Phi =\left(\right(1-p){\mathrm{J}}_0^{\prime }{\mathrm{V}}_0^{-1}{\mathrm{J}}_0+p{\mathrm{J}}_1^{\prime }{\mathrm{V}}_1^{-1}{\mathrm{J}}_1)$ and p is the proportion of total subjects assigned to the treatment group. The 4-th diagonal element $I_{44}^{-1}$ of the inverse of the Fisher information matrix I($\widehat{\beta }$) is the estimated variance of ${\widehat{\beta }}_3$. Thus, a number of subjects required in each group can now be calculated by using (3) with $\varphi \left(\beta \right)={\Phi }_{44}^{-1}$. Final sample size in the treatment group is obtained by multiplying calculated N by the p.

In longitudinal study, large proportion of recruited subjects do not complete the study. The anticipated attrition in sample size must be accounted for in sample size calculation to compensate a loss in the effective power of the study. In order to incorporate the attrition rates, let us us denote π_st as the fraction of subjects nested within the s-th group measured at only the first t time points. We denote this vector of fractions by π_s = (π_s1,⋯, π_sT)’ and call it the attrition vector. Therefore, (1 – p)Nπ_0t is the number of subjects in the control group participated up to t-time points and then dropped from the study. Similarly, pNπ_1t is the number of subjects in the treatment group who would have participated up to t-time points and then dropped from the study. Let us also define a matrix W_st containing first t-diagonal elements of W_s and the remaining (T – t) diagonal elements as 0s. In addition let M_st be a T × 2 matrix consisting of first t rows of M_s and the remaining (T – t) elements as 0s. Similarly let J_st be defined as the first t rows of J_s and the remaining (T – t) elements as 0s. Thus, the contribution of the fraction of subject from t-time point to the information matrix for the treatment and the control group are,

$${\mathrm{I}}_{0t}\left(\widehat{\beta }\right)=N(1-p){\pi }_{0t}{\mathrm{J}}_{0t}^{\prime }{\mathrm{V}}_{0t}^{-1}{\mathrm{J}}_{0t}\text{and}{\mathrm{I}}_{1t}\left(\widehat{\beta }\right)=N_{p{\pi }_{1t}}{\mathrm{J}}_{1t}^{\prime }{\mathrm{V}}_{1t}^{-1}{\mathrm{J}}_{1t}$$ (30)

where,

$${\mathrm{V}}_{\mathit{st}}={\mathrm{M}}_{\mathit{st}}{\Sigma }_v{\mathrm{M}}_{\mathit{st}}^T+{\mathrm{W}}_{\mathit{st}}.$$ (31)

Therefore, the overall Fisher information matrix for all subjects accommodating for attrition vectors can be written as

$$\mathrm{I}\left(\widehat{\beta }\right)=N\sum _{t=1}^T\left[\right(1-p){\pi }_{0t}{\mathrm{J}}_{0t}^{\prime }{\mathrm{V}}_{0t}^{-1}{\mathrm{J}}_{0t}+p{\pi }_{1t}{\mathrm{J}}_{1t}^{\prime }{\mathrm{V}}_{1t}^{-1}{\mathrm{J}}_{1t}].$$ (32)

Thus the method presented here is versatile as it accommodates differential allocations across groups and also differential attritions over follow up time points. This method can also be extended for multiple groups and composite hypothesis testing. Performance of this approach in the simplest situation is evaluated via simulation in the next section.

4.1. Simulation study

We present results of a small scale simulation study in Table 2. Results are based on data generated using the model in equation (23) with varying values of group by time interaction parameter β₃ and variance component associated with the slope parameter ${\sigma }_{v_1}^2$. Other three regression coefficients β₀, β₁ and β₂ in the model (23) were fixed at 0.10, 0.25 and 0.20 respectively. Similarly, remaining two variance components ${\sigma }_{v_0}^2$ and σ_ν0ν1 in the covariance matrix of random effect distribution (24) were fixed at 0.5 and 0.20 respectively. Two sets of simulations were performed, first for three time point (T = 3) follow up and the second for five time point (T = 5) follow up. The sample size N is assumed equal across the two treatment groups. The sample size N for each group was calculated using expression (3) with variance of ${\widehat{\beta }}_3$ obtained from the 4-th diagonal element of the inverse of the Fisher information matrix (32). Power for each combination of parameters is a proportion of p-values associated with ${\widehat{\beta }}_3$ that are less than 0.05 in corresponding 1000 simulations.

Table 2.

The required number of centers N and corresponding power calculated for longitudinal designs. The treatment by time interaction parameter β₃ and variance component ${\sigma }_{v1}^2$ associated with the slope parameter varied and other regression coefficients β₀, β₁ and β₂ in the model (23) were fixed at 0.10, 0.25 and 0.20 respectively.

	T=3				T=5
	${\sigma }_{v1}^2$ = 0.25		${\sigma }_{v1}^2$ = 0.75		${\sigma }_{v1}^2$ = 0.25		${\sigma }_{v1}^2$ = 0.75
β 3	N	power	N	power	N	power	N	power
0.2	190	0.843	387	0.831	113	0.795	309	0.762
0.3	82	0.863	170	0.815	50	0.814	137	0.771
0.4	46	0.886	95	0.821	28	0.831	77	0.813
0.5	29	0.864	60	0.806	18	0.817	49	0.813
0.6	20	0.887	42	0.833	13	0.834	34	0.779
0.7	14	0.878	30	0.829	9	0.831	25	0.804
0.8	11	0.880	23	0.819	7	0.832	20	0.824
0.9	9	0.879	18	0.820	6	0.876	16	0.820

Table 2 shows that a desired 80% power is achieved based on the sample size calculated using proposed method. There is a tendency of achieving more power than required, especially, at the lower end of the table where sample sizes are small. It is partly due to the bigger impact of rounding on the small sample sizes. For example, adding one extra subject in a small but adequate sample size, say 8, is much greater than in adequately large sample, say 189.

5. Illustration

5.1. Cross-sectional Studies

To illustrate sample size computation in subject-level randomized studies, we consider a study of combination therapy for chronic obstructive pulmonary disease. The chronic obstructive pulmonary disease (COPD) is a leading cause of morbidity worldwide. It is characterized by chronic progressive symptoms, airflow obstruction, and impaired health status. The symptoms are worse in those who have frequent, acute episodes of symptom exacerbation. A combination of inhaled long-acting β₂-agonists and inhaled corticosteroids may improve airflow obstruction, control of symptoms, and health status in patients with COPD. In order to study a combination therapy, Calverley et al. [21] conducted a randomized, double-blind, placebo-controlled, parallel-group trial of combined salmeterol and fluticasone in the treatment of COPD. A total of 1465 outpatients patients with COPD were recruited from 196 hospitals from 25 countries, which is about 8 patients per hospitals in average. They participated in a 2-week run-in to the trial, a 52-week treatment period with clinic visits at weeks 0, 2, 4, 8, 16, 24, 32, 40, and 52, and a 2-week post-treatment follow-up. Every participating center was supplied with a list of patient numbers (assigned to patients at their first visit) and a list of treatment numbers. Patients who satisfied the eligibility criteria were assigned the next sequential treatment number from the list. The occurrence of acute exacerbations was investigated at every clinic visit. At the end of the of follow-up period the estimated exacerbation rate was 1.30 (i.e. β₀ = 0.26) for patients randomized to placebo and 1.0 for patients randomized to the combination therapy, thus RR = 0.769 and β₁ = −0.26. The authors did not account for the between center variance in the exacerbation rate in their analysis. For this illustration we consider following three values of between center variances: 0.1, 0.3 and 0.5. Using expressions in (10) for each parameter combination, we find that 46, 42 and 38 hospitals are required respectively to detect exacerbation risk reduction of 0.769 attributed to the combination therapy while maintaining 80% power. We also verify via simulation that the computed number of hospitals provide about 78% power for the parameter values considered for this example.

To illustrate sample size computation in cluster-level randomized studies, we consider the data example presented in [22]. The study evaluated an educational intervention aimed at improving the management of lung disease in adults attending South African primary-care clinics. Forty clusters were randomized to either intervention or the control arm. In each clinic 50 patients were interviewed at baseline and 3 months later. The outcome of interest was the number of clinic visits from baseline until follow up. The analysis found β₀ = 1.47, $\tilde{\beta }$ = −0.18 and ρ = 0.32. Using these parameter values in equation (19) we calculate number of cluster required to maintain 80% power in similar future studies to be 72. With the same values of parameter Hayes-Donner method would require 78 clusters. The result we obtained in this example is not surprising as the RR < 1.

5.2. Longitudinal Studies

To illustrate sample size computation in a longitudinal studies, we apply sample size calculation formula to one of the examples presented in [19]. This data set is collected from a clinical trial of 59 epileptics who were randomized to a new drug (Trt = 1) or a placebo (Trt = 0) as an adjuvant to the standard chemotherapy. A multivariate response variable at five time points consisted of the counts of seizures at baseline and during the 2-weeks before each of four clinic visits. We fit log-linear mixed-effect model in (23) to this data and obtain following estimates of the parameters: β₀ = 3.34, β₁ = 0.20, β₂ = −0.43, β₃ = −0.14, ${\sigma }_{v_0}^2$ = 0.53, σ_ν0ν1 = −0.03 and ${\sigma }_{v_1}^2$ = 0.04. If the same parametric values are expected in future studies, 44 subjects will be required in each group based on the propose method to achieve 80% power.

6. Discussion

Randomized clinical trials are the gold standard for demonstrating efficacy and safety of a new intervention. These trials are often conducted in multiple sites. Although the protocols are strictly followed, there remains variation among the participating sites. In some cases, randomization by subject is not possible and the intervention must be randomly assigned to the participating sites. For a trial with event count as an outcome, Poisson regression models are routinely used. The number of clusters required in such trials depends on the background event rate, inter-cluster variability, cluster size and the expected effect size. We provide closed form solutions to determine the required number of clusters for both subject-level and cluster-level randomizations. These solutions provide an easy way to compute the number of clusters needed to conduct such trials successfully with adequate power to detect the hypothesized effect.

The proposed method for cross-sectional studies requires less number of clusters compared to Ogungbenro and Aarons method. For cluster-level randomization, a comparison of our method with that of Rochon indicates that though the former is a special case, but the advantage for considering a cross-sectional design provides us a closed form solution as opposed to an iterative solution by Rochon. In addition, we compare our method (thereby Rochon’s method) with another simple method proposed by Hayes and Donner. The proposed method has a clear edge over the method by Hayes and Donner when the rate ratio is less than one.

For cluster-level randomized designs using GEE, the variance of the regression coefficient is inflated by a multiplicative factor of (1 – (n – 1)ρ) when it is compared to the variance of regression coefficient for an ordinary Poisson regression. The variance of the estimate converges to the variance of an ordinary Poisson regression when the intra-cluster correlation goes to 0. In subject-level randomization, number of clusters can be substantially reduced when cluster sizes (n) are increased. In contrast, for cluster-level randomization, the impact of cluster size on the number of clusters is minimal when that number crosses a certain threshold value. For both subject and cluster randomized designs, we need a significantly larger number of clusters for rare events.

Our simulation results sometimes produce more power to detect the corresponding effect size. This is due to the rounding of the computed sample size to the next integer. This effect is more severe for cluster randomized designs as it require two additional clusters in the experiment. In light of potential imbalance, model violations and loss of a few clusters, this type of overestimation protects against potentially under-powered studies.

For longitudinal designs using mixed-effect models, we presented a corrected version of the Ogundbenro and Aarons’ method. The method presented here is versatile in the sense that it allows differential group allocations with differential attrition rates. This method can also be easily extended for composite hypotheses testings. For GEE approach, an alternative procedure is available due to Rochon.

7. Appendix.

7.1. Derivation of Variance of ${\widehat{\beta }}_1$ for Mixed-Effects Poisson Regression Models

We assume

$$\begin{array}{cc}\hfill \text{We assume}{y}_{\mathit{ij}}& \sim \text{Poisson}\left({\lambda }_{\mathit{ij}}\right),\hfill \\ \hfill \mathit{log}({\lambda }_{\mathit{ij}}\mid u_i)& ={\beta }_0+{\beta }_1{x}_{\mathit{ij}}+u_i,\hfill \\ \hfill u_i& \sim f_u\left(u_i\right)=N(0,{\sigma }_{u_i}^2).\hfill \end{array}$$ (33)

Then assuming x ~ f_x(x_ij) =binomial(1,p), the likelihood function from the joint distribution of Y, x and u, will be

$$\begin{array}{cc}\hfill L({\beta }_0,{\beta }_1)& =\prod _{\mathit{ij}}{f}_u\left(u_i\right)f_x\left(x_{\mathit{ij}}\right){\lambda }_{\mathit{ij}\mid u_i}^{y_{\mathit{ij}}}{e}^{-{\lambda }_{\mathit{ij}\mid u_i}}∕y_{\mathit{ij}}!\hfill \\ \hfill \mathit{logL}({\beta }_0,{\beta }_1)& =\sum _{\mathit{ij}}\mathit{log}{f}_u\left(u_i\right)+\mathit{log}{f}_x\left(x_{\mathit{ij}}\right)+y_{\mathit{ij}}\mathit{log}\left({\lambda }_{\mathit{ij}\mid u_i}\right)-{\lambda }_{\mathit{ij}\mid u_i}-\mathit{log}(y_{\mathit{ij}}!)\hfill \\ \hfill \frac{\mathit{dlogL}({\beta }_0,{\beta }_1)}{d\gamma }& =\sum _{\mathit{ij}}(y_{\mathit{ij}}-{\lambda }_{\mathit{ij}\mid u_i}){\mathrm{z}}_{\mathit{ij}}\hfill \\ \hfill \frac{\mathit{dlogL}({\beta }_0,{\beta }_1)}{d\gamma {\gamma }^T}& =\sum _{\mathit{ij}}-{\lambda }_{\mathit{ij}\mid u_i}{\mathrm{z}}_{\mathit{ij}}{\mathrm{z}}_{\mathit{ij}}^T.\hfill \end{array}$$

The maximum likelihood estimator converges asymptotically in distribution to a multivariate normal distribution with mean (β₀, β₁) and covariance matrix ${\left[I({\widehat{\beta }}_0,{\widehat{\beta }}_1)\right]}^{-1}$, where $I({\widehat{\beta }}_0,{\widehat{\beta }}_1)$ is the Fisher information matrix given by

$$\begin{array}{cc}\hfill I({\widehat{\beta }}_0,{\widehat{\beta }}_1)& =-E_u{E}_x\left[\frac{\mathit{dlogL}({\beta }_0,{\beta }_1)}{d\gamma {\gamma }^T}\right]\hfill \\ \hfill & =-E_u{E}_x\left[\sum _{\mathit{ij}}-{\lambda }_{\mathit{ij}\mid u_i}{\mathrm{z}}_{\mathit{ij}}{\mathrm{z}}_{\mathit{ij}}^T\right]\hfill \\ \hfill & =-E_u{E}_x\left[\sum _{\mathit{ij}}-e^{({\beta }_0+{\beta }_1{x}_{\mathit{ij}}+u_i)}{\mathrm{z}}_{\mathit{ij}}{\mathrm{z}}_{\mathit{ij}}^T\right]\hfill \\ \hfill & =e^{({\beta }_0+{\sigma }^2∕2)}{E}_x\left[\sum _{\mathit{ij}}{e}^{{\beta }_1{x}_{\mathit{ij}}}{\mathrm{z}}_{\mathit{ij}}{\mathrm{z}}_{\mathit{ij}}^T\right]\hfill \\ \hfill & =e^{({\beta }_0+{\sigma }^2∕2)}{E}_x\left[\sum _{\mathit{ij}}\left(\begin{array}{cc}\hfill 1\hfill & \hfill x_{\mathit{ij}}\hfill \\ \hfill x_{\mathit{ij}}\hfill & \hfill x_{\mathit{ij}}^2\hfill \end{array}\right)e^{{\beta }_1{x}_{\mathit{ij}}}\right]\hfill \\ \hfill =& e^{({\beta }_0+{\sigma }^2∕2)}\left[\sum _{\mathit{ij}}\left(\begin{array}{cc}\hfill (1-p)+p{e}^{{\beta }_1}\hfill & \hfill p{e}^{{\beta }_1}\hfill \\ \hfill p{e}^{{\beta }_1}\hfill & \hfill p{e}^{{\beta }_1}\hfill \end{array}\right)\right]\hfill \\ \hfill =& \mathit{Nn}{e}^{({\beta }_0+{\sigma }^2∕2)}\left(\begin{array}{cc}\hfill (1-p)+p{e}^{{\beta }_1}\hfill & \hfill p{e}^{{\beta }_1}\hfill \\ \hfill p{e}^{{\beta }_1}\hfill & \hfill p{e}^{{\beta }_1}\hfill \end{array}\right).\hfill \end{array}$$

The covariance matrix of $\widehat{\gamma }$ is

$${\left[I({\widehat{\beta }}_0,{\widehat{\beta }}_1)\right]}^{-1}=\mathrm{Cov}\left(\widehat{\gamma }\right)=\frac{1}{\mathit{Nn}{e}^{({\beta }_0+{\sigma }^2∕2)}(1-p)p{e}^{{\beta }_1}}\left(\begin{array}{cc}\hfill p{e}^{{\beta }_1}\hfill & \hfill -p{e}^{{\beta }_1}\hfill \\ \hfill -p{e}^{{\beta }_1}\hfill & \hfill (1-p)+p{e}^{{\beta }_1}\hfill \end{array}\right).$$

Thus the variance of ${\widehat{\beta }}_1$ is

$$V\left({\widehat{\beta }}_1\right)=\frac{1}{\mathit{Nn}{e}^{({\beta }_0+{\sigma }^2∕2)}}\left[\frac{1}{p{e}^{{\beta }_1}}+\frac{1}{1-p}\right].$$ (34)

7.2. Comparison of N_p1 and NHD for Cluster-level Randomized Designs

Let $\frac{{\lambda }_2}{{\lambda }_1}=\mathit{RR},{\lambda }_1=e^{{\beta }_0},\frac{{\lambda }_2}{{\lambda }_1}=e^{\stackrel{\sim }{\mathit{beta}}}$. Hence

$$\begin{array}{cc}\hfill & N_{p1}-N_{\mathit{HD}}\hfill \\ \hfill =& \frac{{\left[z_{\alpha ∕2}\sqrt{2}+z_{\eta }\sqrt{[1+e^{-\tilde{\beta }}]}\right]}^2}{n{e}^{{\beta }_0}{\tilde{\beta }}^2}-\frac{{(z_{\alpha ∕2}+z_{\eta })}^2({\lambda }_1+{\lambda }_2)}{n{({\lambda }_1-{\lambda }_2)}^2}.\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill & N_{p1}<N_{\mathit{HD}}\hfill \\ \hfill \mathit{if}& \frac{{\left[z_{\alpha ∕2}\sqrt{2}+z_{\eta }\sqrt{[1+e^{-\tilde{\beta }}]}\right]}^2}{{(z_{\alpha ∕2}+z_{\eta })}^2}<\frac{e^{{\beta }_0}{\tilde{\beta }}^2({\lambda }_1+{\lambda }_2)}{{({\lambda }_1-{\lambda }_2)}^2}.\hfill \\ \hfill =& \frac{{[z_{\alpha ∕2}\sqrt{2{\lambda }_2}+z_{\eta }\sqrt{{\lambda }_1+{\lambda }_2}]}^2}{{(z_{\alpha ∕2}+z_{\eta })}^2}<\frac{({\lambda }_1+{\lambda }_2){\lambda }_1{\lambda }_2{\left[\mathit{ln}\frac{{\lambda }_2}{{\lambda }_1}\right]}^2}{{({\lambda }_1-{\lambda }_2)}^2}\hfill \\ \hfill \mathit{if}& \frac{{[z_{\alpha ∕2}\sqrt{2\mathit{RR}}+z_{\eta }\sqrt{1+\mathit{RR}}]}^2}{{(z_{\alpha ∕2}+z_{\eta })}^2}<\frac{\mathit{RR}(1+\mathit{RR}){\left(\mathit{lnRR}\right)}^2}{{(1-\mathit{RR})}^2}\hfill \\ \hfill \mathit{if}& \frac{{[z_{\alpha ∕2}\sqrt{2\mathit{RR}}+z_{\eta }\sqrt{1+\mathit{RR}}]}^2}{{(z_{\alpha ∕2}+z_{\eta })}^2}-\frac{\mathit{RR}(1+\mathit{RR}){\left(\mathit{lnRR}\right)}^2}{{(1-\mathit{RR})}^2}<0\hfill \\ \hfill =& f\left(\mathit{RR}\right),\text{where}f\left(\mathit{RR}\right)=\frac{{[z_{\alpha ∕2}\sqrt{2\mathit{RR}}+z_{\eta }\sqrt{1+\mathit{RR}}]}^2}{{(z_{\alpha ∕2}+z_{\eta })}^2}-\frac{\mathit{RR}(1+\mathit{RR}){\left(\mathit{lnRR}\right)}^2}{{(1-\mathit{RR})}^2}.\hfill \end{array}$$

7.3. Computation of M_is and J_is

Denote the right hand side of the model (23) the function f_ist(β, ν_i) for ith subject from sth group at tth time-point. Hence, f_ist(β, ν_i) is the linear expression of the ln(λ_ist) at the tth time point specific to the ith subject nested within the sth group. Then respective row elements for the matrix M_is can be computed by applying the chain rule as follow $\frac{\partial {\lambda }_{\mathit{ist}}}{\partial {\mathit{v}}_i}=\frac{\partial {\lambda }_{\mathit{ist}}}{\partial f_{\mathit{ist}}(\beta ,{\mathit{v}}_i)}\frac{\partial f_{\mathit{ist}}(\beta ,{\mathit{v}}_i)}{\partial {\mathit{v}}_i}$. By noting that, $\frac{\partial {\lambda }_{\mathit{ist}}}{\partial f_{\mathit{ist}}(\beta ,{\mathit{v}}_i)}{\mid }_{v_i=0}=e^{f_{\mathit{ist}}(\beta ,0)},\frac{\partial f_{\mathit{ist}}(\beta ,{\mathit{v}}_i)}{\partial {\mathit{v}}_{0i}}{\mid }_{{\mathit{v}}_i=0}=1$ and $\frac{\partial f_{\mathit{ist}}(\beta ,{\mathit{v}}_i)}{\partial {\mathit{v}}_{1i}}{\mid }_{{\mathit{v}}_i=0}=g\left(t\right)$ we obtain

$${\mathrm{M}}_{\mathit{ist}}=\left(e^{f_{\mathit{ist}}(\beta ,0)}{e}^{f_{\mathit{ist}}(\beta ,0)}g\left(t\right)\right).$$ (35)

Each row of J_is denoted by j_ist is given as,

$${\mathrm{j}}_{\mathit{ist}}=\left(\frac{\partial {\lambda }_{\mathit{ist}}}{\partial {\beta }_0}\frac{\partial {\lambda }_{\mathit{ist}}}{\partial {\beta }_1}\frac{\partial {\lambda }_{\mathit{ist}}}{\partial {\beta }_2}\frac{\partial {\lambda }_{\mathit{ist}}}{\partial {\beta }_3}\right).$$ (36)

Applying the chain rule again, we obtain $\frac{\partial {\lambda }_{\mathit{ist}}}{\partial \beta }=\frac{\partial {\lambda }_{\mathit{ist}}}{\partial f_{\mathit{ist}}(\beta ,{\mathit{v}}_i)}\frac{\partial f_{\mathit{ist}}(\beta ,{\mathit{v}}_i)}{\partial \beta }$. Hence, for each group the corresponding row vectors of J_is are given as,

$$\begin{array}{cc}\hfill {\mathrm{j}}_{i0t}& =\left(e^{Q_0(\beta ,0)}{e}^{Q_0(\beta ,0)}g\left(t\right)00\right),\hfill \\ \hfill {\mathrm{j}}_{i1t}& =\left(e^{Q_1(\beta ,0)}{e}^{Q_1(\beta ,0)}g\left(t\right)e^{Q_1(\beta ,0)}{e}^{Q_1(\beta ,0)}g\left(t\right)\right).\hfill \end{array}$$ (37)

7.4. Derivation of V_OA $\left({\widehat{\beta }}_1\right)$

In what follows we assume that for s = 1, x = 0, and for s = 2, x = 1. It means that x is an indicator variable that takes value 0 for control group and 1 for the treatment group. In the model (5)

$$\begin{array}{cc}\hfill {\lambda }_{\mathit{sij}}& =e^{({\beta }_0+{\beta }_{1}x+u_i)}\hfill \\ \hfill M_{\mathit{sn}}& =\frac{\partial {\lambda }_{\mathit{sij}}}{\partial u_i}{\mid }_{u_i=0}=e^{({\beta }_0+{\beta }_{1}x)}\hfill \\ \hfill {\mathit{J}}_{\mathit{sn}}^{\mathit{T}}& =\frac{\partial {\lambda }_{\mathit{sij}}}{\partial \beta }{\mid }_{u_i=0}=\left(e^{({\beta }_0+{\beta }_{1}x)}{\mathit{xe}}^{({\beta }_0+{\beta }_{1}x)}\right)\hfill \\ \hfill V_{\mathit{sn}}& =e^{({\beta }_0+{\beta }_{1}x)}\left[{\sigma }^2{e}^{({\beta }_0+{\beta }_{1}x)}+1\right].\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill F\left(\beta \right)=& \frac{n}{2}\sum _{s=1}^2\sum _{i=1}^N{\mathit{J}}_{\mathit{sn}}^{\mathit{T}}{\mathit{V}}_{\mathit{sn}}^{-1}{\mathit{J}}_{\mathit{sn}}\hfill \\ \hfill =& \frac{\mathit{Nn}}{2}[\left(\begin{array}{c}\hfill e^{{\beta }_0}\hfill \\ \hfill 0\hfill \end{array}\right)\left(e^{{\beta }_0}0\right){\left[e^{{\beta }_0}\right({\sigma }^2{e}^{{\beta }_0}+1\left)\right]}^{-1}\phantom{]}\hfill \\ \hfill & +\phantom{[}\left(\begin{array}{c}\hfill e^{({\beta }_0+{\beta }_1)}\hfill \\ \hfill e^{({\beta }_0+{\beta }_1)}\hfill \end{array}\right)\left(e^{({\beta }_0+{\beta }_1)}{e}^{({\beta }_0+{\beta }_1)}\right){\left[e^{({\beta }_0+{\beta }_1)}\left({\sigma }^2{e}^{({\beta }_0+{\beta }_1)}+1\right)\right]}^{-1}]\hfill \\ \hfill & F\left(\beta \right)=\left(\begin{array}{cc}\hfill A_1+A_2\hfill & \hfill A_2\hfill \\ \hfill A_2\hfill & \hfill A_2\hfill \end{array}\right),\hfill \end{array}$$ (38)

where $A_1=\frac{\mathit{Nn}}{2}{e}^{{\beta }_0}{({\sigma }^2{e}^{{\beta }_0}+1)}^{-1}$ and $A_2=\frac{\mathit{Nn}}{2}{e}^{({\beta }_0+{\beta }_1)}{({\sigma }^2{e}^{({\beta }_0+{\beta }_1)}+1)}^{-1}$. Hence, the second diagonal element of ${\left[F\right(\beta \left)\right]}^{-1}$ is

$$\begin{array}{cc}\hfill V_{\mathit{OA}}\left({\widehat{\beta }}_1\right)& =\frac{1}{A_1}+\frac{1}{A_2}\hfill \\ \hfill & =\frac{2}{\mathit{Nn}}\left[2{\sigma }^2+\left(e^{-{\beta }_0}+e^{(-{\beta }_0-{\beta }_1)}\right)\right].\hfill \end{array}$$ (39)