Abstract
Objective
EEG source localization is demonstrated in three cases of acute traumatic brain injury (TBI) with progressive lesion loads using anatomically faithful models of the head which account for pathology.
Methods
Multimodal magnetic resonance imaging (MRI) volumes were used to generate head models via the finite element method (FEM). A total of 25 tissue types—including 6 types accounting for pathology— were included. To determine the effects of TBI upon source localization accuracy, a minimum-norm operator was used to perform inverse localization and to determine the accuracy of the latter.
Results
The importance of using a more comprehensive number of tissue types is confirmed in both health and in TBI. Pathology omission is found to cause substantial inaccuracies in EEG forward matrix calculations, with lead field sensitivity being underestimated by as much as ~200% in (peri-) contusional regions when TBI-related changes are ignored. Failing to account for such conductivity changes is found to misestimate substantial localization error by up to 35 mm.
Conclusions
Changes in head conductivity profiles should be accounted for when performing EEG modeling in acute TBI.
Significance
Given the challenges of inverse localization in TBI, this framework can benefit neurotrauma patients by providing useful insights on pathophysiology.
Keywords: Electroencephalography, Traumatic brain injury, finite element method, Magnetic resonance imaging
1. Introduction
The study of cortical electrical activity using electroencephalography (EEG) has useful applications to the diagnosis, monitoring, and therapeutic evaluation of traumatic brain injury (TBI) patients (Friedman et al., 2009). Specifically, EEG can provide a variety of insights on how brain function is affected by acute TBI, and the ability to localize the electrical activity of the brain in patients by means of this technique can enhance the benefit of using EEG recordings in a clinical setting.
An excellent example of a potentially serious condition for which source localization would be useful is post-traumatic epilepsy (PTE). Though it is known that non-convulsive seizures after TBI are associated with hippocampal atrophy in the chronic phase (Vespa et al., 2010), the detailed mechanisms of this association remain poorly understood. Additionally, although PTE accounts for about 5% of all cases of epilepsy and for over 20% of cases of symptomatic epilepsy, the current understanding of trauma-induced seizure pathophysiology remains very rudimentary (Garga and Lowenstein, 2006). The incidence of seizures after acute TBI can range from 2% to 25%, and seizure frequency as measured via EEG has been found to be directly proportional to injury severity (Angeleri et al., 1999). In military personnel, the combined incidence of early and late PTE has been shown to range from 33% to 53% and is highest with penetrating head injuries (Salazar et al., 1985). Because antiepileptic agents eliminate seizures in only about 35% of PTE cases, many patients can benefit from surgery for epileptogenic focus removal (Lee et al., 2008). Such statistics reveal that accurate source localization is of considerable relevance in PTE because the surgical removal of an epileptic focus cannot be accurately accomplished without accurate knowledge of its spatial location. Though examination of EEG recordings from acute TBI patients is frequently performed, this is primarily done as a means to detect pathophysiological activity and not necessarily in order to identify its sources. Thus, the prospect of performing inverse localization of EEG activity in acute TBI patients is appealing from the standpoint of acquiring useful information on TBI-related clinical conditions such as PTE.
The process of computing the electric potentials produced at the scalp due to current sources in the brain is known as the forward problem of bioelectricity, whereas the process of localizing brain activity based on scalp EEG measurements is referred to as the inverse problem (Irimia et al., 2009; Lima et al., 2006). Despite the potential clinical usefulness of EEG source localization in acute TBI, there is a disappointing paucity of studies which have explored this topic. This may partly be due to the difficulty of accounting for TBI-related structural pathology within EEG forward models, including phenomena such as (1) the absence of skin and skull parts due to open head injuries or craniotomies, or (2) local conductivity profile alterations due to brain hemorrhage and edema.
In this paper, we explore the effects of acute TBI-related changes in tissue conductivities upon EEG forward and inverse solutions using finite element method (FEM) models of the head extracted from magnetic resonance imaging (MRI). One advantage of such models is that they allow the head to be represented as a volume conductor (Gencer and Acar, 2004) with a variable number of tissues which have distinct conductivities. Whereas 10 or fewer tissue types have typically been used in previous studies of FEM-based EEG source localization (Gencer and Acar, 2004), we characterize and employ 25 distinct material types including the effects of brain hemorrhage and edema upon the forward and inverse solutions. We additionally compare our detailed model to a more typical FEM model with four tissue types. Three-dimensional (3D) finite-element meshes are generated from MRI volumes to account for the geometric and electric properties of tissues and the effects of TBI-related pathology upon EEG source localization accuracy is investigated in three selected cases of acute TBI. Anatomically-faithful, high-resolution FEM models of the head are generated and the interface between white matter (WM) and gray matter (GM) is populated with current dipole sources spaced approximately 1 mm apart. A minimum-norm, noise-normalized linear operator (Liu et al., 2002) is used for inverse localization, and the widely-used crosstalk metric (Haufe et al., 2010, Liu, 2002, Sazonov et al., 2009) is employed to evaluate localization accuracy for each simulated brain source in a systematic fashion. The effect of TBI pathology upon EEG localization is then quantified as a percentage difference in crosstalk between the pathologyinclusive and the pathology-naïve models. Although our study does not demonstrate improved accuracy in localizing epileptic foci noninvasively via EEG, our study remains very relevant to the PTE neurosurgery community because such improvements cannot be accomplished without detailed understanding of the issues explored in this paper.
2. Methods
2.1. Image acquisition and processing
Approval for this study was obtained from the Institutional Review Board of the School of Medicine at the University of California, Los Angeles (approval #10-000929), and signed informed consent was obtained either from the patients or from their legally authorized representatives before the performance of any procedure. The TBI cases used in this study included three male subjects. For patient 1 (age 25), the Glasgow Coma Score (GCS) at admission to the Neurointensive Care Unit (NICU) was 14, the Glasgow Outcome Score-Extended (GOS-E) at discharge from the NICU was 3, and the GOS-E at 6 months was 8. For patient 2 (age 31), the GCS was 9, the GOS at discharge was 3, and the GOS-E at 6 months was 3. For patient 3 (age 45), the GCS at admission was 14, the GOS-E at discharge was 3, and the GOS-E at 6 months was 8. From each patient, MRI volumes (1 mm3 voxel size) were acquired at 3.0 T (Siemens Trio TIM scanner, Erlangen, Germany) within 72 h post-injury. The MRI protocol consisted of magnetization prepared rapid acquisition gradient echo (MP-RAGE) T1-weighted imaging, fluid attenuated inversion recovery (FLAIR), turbo spin echo (TSE) T2-weighted imaging, gradient-recalled echo (GRE) T2-weighted imaging, and susceptibility weighted imaging (SWI). Conventional computed tomography (CT) scans were also acquired for each patient. In addition to these three acute TBI patients, a healthy adult male (age 28) was included in the study for the purpose of reference and comparison. From this subject, the imaging protocol consisted of T1- and T2-weighted MRI volumes acquired using the same sequences as in the TBI patients. EEG measurements were acquired from each patient after the electrodes had been placed upon the skin according to the standard 10–10 monopolar EEG montage. Co-registration of electrodes to the scalp was accomplished within the NFT toolbox, as described elsewhere (Acar and Makeig, 2010).
The LONI (Laboratory of Neuro Imaging) Pipeline (http://pipeline.loni.ucla.edu) was used to carry out image processing steps such as image alignment, bias field correction and skull stripping. Automatic segmentation of WM, GM, cerebrospinal fluid (CSF), cerebellar WM/GM and subcortical structures was performed using FreeSurfer (FS) (Dale et al., 1999), followed by manual correction of tissue labeling errors by three experienced users with training in neuroanatomy. TBI-related lesions were segmented from GRE/SWI/FLAIR volumes as discussed elsewhere (Irimia et al., 2011; Irimia et al., 2012a), skin was segmented from T1 MRI, and hard bone was segmented either from CT (in the case of TBI patients) or from T1- and T2-weighted MRI (in the case of the healthy patient, where CT had not been acquired for safety reasons). Eyes, muscle, cartilage, mucus, nerves, teeth, and ventriculostomy shunts were segmented from T1/T2 MRI. 3D models for each tissue type were generated in 3D Slicer (slicer.org). Execution of the complete protocol for user-guided segmentation and FEM model generation required ~3 h per subject.
2.2. Forward modeling
Because the primary sources of scalp EEG potentials are thought to be currents within the apical dendrites of cortical pyramidal cells (Dale and Sereno, 1993a), EEG generators were modeled as dipolar currents oriented perpendicular with respect to the cortical surface (Irimia et al., 2012b). A regular grid-based mesh with an average edge length of approximately 2 mm, with ~400,000 nodes and ~450,000 linear elements was constructed for the head of each subject by discretizing the head volume into linear hexahedral isoparametric elements based on the MRI-derived segmentation. The presence of 60 referential electrodes arranged on the scalp surface in the standard 10–10 montage was assumed. In the second patient, electrode positioning was affected by the presence of a craniotomy above the right hemisphere. In this case, sensor locations reflected careful placement of electrodes by clinicians after the skin had been sutured in place subsequent to the craniotomy. A total of 25 material types with distinct conductivity values σ were modeled. It should be noted that the symbol σ is used here to denote conductivity (as is customary in physics), rather than standard deviation (as in statistics). Tissue conductivity values were taken from the available literature, as summarized in Table 1.
Table 1.
Electrical conductivities (σ, in units of Siemens per meter, S/m) for the material types used in each model.
| Material | σ [S/m] | Source |
|---|---|---|
| Healthy-appearing skin | 0.33 | Gabriel et al. (1996a) and Gabriel et al. (1996b) |
| Edematous skin | 0.45 | Gabriel (1996a,b) |
| Fat | 0.036 | Gabriel (1996a,b) |
| Hard bone | 0.015 | Akhtari et al. (2002) |
| Soft bone | 0.04 | Akhtari (2002) |
| CSF | 1.79 | Baumann et al. (1997) |
| Healthy-appearing GM | 0.352 | Gabriel (1996a,b) |
| Edematous GM | 0.482 | Gabriel (1996a,b) |
| Hemorrhaging GM | 1.0 | Gabriel (1996a,b) |
| Healthy-appearing WM | 0.147 | Gabriel (1996a,b) |
| Edematous WM | 0.2 | Gabriel (1996a,b) |
| Hemorrhaging WM | 0.417 | Gabriel (1996a,b) |
| Cerebellum | 0.157 | Gabriel (1996a,b) and Ramon et al. (2006) |
| Spinal cord | 0.571 | Gabriel, (1996a,b) and Ramon (2006) |
| Subcortex | 0.25 | Foster and Schwan (1989) |
| Epidural hemorrhage | 1.0 | Gabriel (1996a,b) |
| Connective tissue | 0.4 | (Trakic et al. (2010) |
| Muscle | 0.1 | Gabriel (1996a,b) |
| Eyes | 1.57 | Lindenblatt and Silny (2001) |
| Cartilage | 0.88 | Binette et al. (2004) |
| Mucus | 1.4 | Trakic (2010) |
| Nerve | 0.13 | Jacquir et al. (2007) and Rijkhoff et al. (1994) |
| Teeth | 0.02 | Reyes-Gasca et al. (1999) |
| Polyurethane shunt | 0.001 | Haynes (2011) |
| Sinus air | 10−17 | Haynes (2011) |
FEM models were created after co-registration of the head and sensor locations, and existing methodologies (Acar and Gencer, 2004; Acar and Makeig, 2010) were used to calculate the forward matrix A of dimensions m × n, where m and n are the number of sensors and sources, respectively. The entire head volume was discretized into volume elements in which the electric potential was defined via linear interpolation functions (Acar and Gencer, 2004). For some given sensor i and cortical source j, the matrix element aij of A specifies the electric potential recorded by sensor i due to a current dipole of unit strength active at the location of source j. Row ai of A represents the lead field (LF) of sensor i, i.e., it specifies how each current dipole contributes to the signal recorded by sensor i. Let Jp denote the primary density of electric current sources in the brain. To provide the solution to the forward problem of electrical source imaging, the potential Φ must be solved for, subject to
| (1) |
| (2) |
where V and S denote the head volume and surface, respectively, n is the unit normal on S, and σ is the local conductivity. To calculate the forward matrix within the FEM formalism used here, a point source model described elsewhere (Yan et al., 1991) was employed to place dipoles at desired locations inside the head. An equivalent discretized model was constructed for each finite element (FE) using Galerkin’s weighted residuals method, and all element contributions were subsequently assembled to form a system of equations whose solution yields the values of the electric potential (Acar and Gencer, 2004).
2.3. Forward solution accuracy
Our FEM models account for at least 19 tissue types, i.e., considerably more than the typical EEG forward model with 4 compartments (scalp, bone, gray matter and white matter). Thus, it is useful to quantify the effects of accounting for the 16 tissue types which are not usually included in EEG localization studies. We therefore first compare two distinct FEM model types, i.e. M4 and M19. Model M4 includes 4 tissue types (healthy-appearing skin, hard bone, healthy-appearing WM and GM), whereas M19 additionally accounts for the presence of fat, soft bone, CSF, healthyappearing GM, cerebellum, spinal cord, subcortex, connective tissue, muscle, eyes, cartilage, mucus, nerves, teeth and sinus air. Thus, M4 is similar to a typical EEG FEM model with four material types (scalp, bone, WM and GM), whereas M19 is a more sophisticated model with 19 tissue types. In the case of M4, the conductivity of each tissue represented in M19 but not in M4 is replaced by one of four values. Specifically, all extracranial tissue structures are replaced by skin, all intracranial non-cerebral structures are replaced by healthy-appearing WM, and soft bone is replaced by hard bone. This set of substitutions aims to partially mimic the typical geometry of an EEG model with four tissue types.
One measure which can be used to quantify the effect upon the forward solution due to including the 16 tissue types accounted for in M19 but not in M4 is the sensor sensitivity area β(x), defined as the percentage of cortical dipoles projecting to a given sensor with a strength which is at least x% as strong as that of the dipole with the strongest projection onto that sensor. For example, if β(70%) = 1/4, then one fourth of all cortical dipoles project to the sensor with at least 70% of the strength associated with the strongest-projecting dipole. It should be noted that β(x) can be expressed as a percentage of the total cortical area; thus, β(0) = 1 and β(1) = 0. Alternatively, β(x) can be defined as the cortical area populated with dipoles j whose projected signal strengths |aij| at sensor i are greater than or equal to x% of the maximum projected signal of any dipole j on the cortex. Incidentally, it can be shown based on these definitions that the function β(x) is identically equal to one minus the cumulative distribution function of the lead field magnitude. Yet another useful definition of β(x) is the proportion of entries |aij| in the lead field magnitude vector |ai| which satisfy the relationship,
| (3) |
For some sensor i, the difference in sensor sensitivity area between two models Mc and Mr (where c, r are non-negative integers) can be quantified using the metric,
| (4) |
To simplify notation, the dependence of Δβ upon i and x is implicit. The subscripts c and r stand for ‘comparison’ and ‘reference’, respectively, which indicates that the comparison model Mc is being evaluated with respect to the reference model Mr. If one aims to evaluate the model with four tissue types with respect to the model with 19 tissue types, then Mc = M4 and Mr = M19, and the arguments to Δβ denote the models for which Δβ is calculated. The quantity Δβ (Mc,Mr) is thus the absolute value of the difference in β between the two models for sensor i, computed as a percentage of the electrode sensitivity area in the reference model Mr, which is equal to M19 in this case.
In analogy with the analysis described above, one can investigate the effects of ignoring conductivity changes due to TBI-related pathology. Specifically, let M25 denote the pathology-inclusive TBI model with 25 tissue types, including 6 types accounting for pathology. In this context, M19 denotes a ‘pathology-naïve’ TBI model which ignores the effects of pathology because it contains only 19 tissue types. Thus, for M19, the conductivity of each pathology-affected tissue is replaced by the conductivity of the corresponding healthy-appearing tissue. By means of this substitution, M25 can be compared to M19 in the context of TBI and the effect of TBI-related conductivity changes upon the forward solution accuracy can be determined. In analogy with the case described previously, the difference in sensor sensitivity area between M25 and M19 can be quantified using the quantity Δβ (M19, M25). Note that Mc = M19 and Mr = M25 here, i.e. the reference model Mr is set to M25 because M25 captures TBI anatomy more closely from a geometric standpoint.
2.4. Inverse modeling
The framework for source localization employed here involves a minimum-norm inverse linear operator previously described and widely used (Liu, 2002). Briefly, let,
| (5) |
where x is the vector of EEG measurements, A is the forward EEG matrix, s is a vector containing the strengths of each source, and n is the sensor noise vector. To solve the problem of identifying s from the measurements x using a linear inverse operator approach, the inverse operator W must be found such that the expected difference 〈‖Wx − s‖2〉 between the estimated and true inverse solutions is minimized. If n and s are normally distributed with zero mean, it can be shown (Liu, 2002) that W is of the form,
| (6) |
where C and R are the sensor noise and source covariance matrices, respectively. For simplicity, Gaussian white noise can be assumed for sources and sensors such that R and C are multiples of the identity matrix. As detailed elsewhere (Dale and Sereno, 1993b, Liu, 2002), we weigh the sensor covariance matrix C by a regularization parameter r defined as
| (7) |
where SNR is the root mean square signal-to-noise ratio and ‘tr’ is the matrix trace operator, such that
| (8) |
A conservative SNR value of 10 is assumed. Because one is primarily interested in the estimation of cortical activity whose magnitude is appreciably larger than that of the noise, it is often useful to normalize each row of the inverse operator matrix based on the noise sensitivity of the latter at each location (Liu, 2002). By means of this, activity at locations with comparably low noise sensitivity is assigned a larger weight than activity at locations with higher sensitivity. The noise normalization approach adopted here has been described previously (Liu, 2002) and involves estimating noise sensitivity by projecting the noise covariance estimate into the inverse operator. The noise sensitivity-adjusted inverse operator is then pre-multiplied by a diagonal noise sensitivity matrix T whose matrix elements are given by
| (9) |
such that the noise sensitivity-normalized inverse is now
| (10) |
2.5. Inverse localization accuracy
To quantify the accuracy of the inverse localization, we compute the localization error (LE) and the average crosstalk metric ξ2 (Liu, 2002). The LE is most useful in the context of active focal sources, and is defined as the Euclidian distance between (1) the true location of the electric source, and (2) the point on the cortex which the localization method estimates as the most likely location of that source, in a statistical sense. Crosstalk, on the other hand, is more useful in distributed source models because it accounts for the spatial aspect of extended source distributions (Liu, 2002). For each cortical location j, let ΔLE (Mc, Mr) be the absolute value of the difference in LE between two models Mc and Mr being compared:
| (11) |
To simplify notation, the dependence of ΔLE upon j is implicit. For any model Many, the average crosstalk for some source j may be defined as
| (12) |
where w̃j(Many) is the j-th row of W̃(Many)—the noise-normalized inverse operator for model Many—and ak(Many) is the k-th column of A (Many)—the forward matrix for the same model. As defined above, the crosstalk metric quantifies the sensitivity of the source estimate at location j to activity at all other locations k = 1,⋯,n, where j ≠ k. The lower the crosstalk for some location i, the less biased the activity at that location is to activity at other locations, and therefore the more accurate the estimate of the activity at that location (Liu, 2002). The presence of w̃jak in the denominator of the term being summed over indicates that the sensitivity of the estimate at location j to activity at location k is normalized with respect to the sensitivity of the activity estimate at location j. For example, a crosstalk value of 0 indicates that the estimated activity at j is completely unaffected by electrical activity at other locations.
To compare the difference in localization accuracy between one model Mc and a reference model Mr, one can compute the quantity,
| (13) |
which quantifies the absolute difference in localization accuracy between the two models as a percentage of ξ2(Mr), the latter being the crosstalk to be expected in the context of the reference (i.e., more anatomically faithful) of the two models. To simplify notation as before, the dependence of Dξ upon j is implicit. If Dξ(Mc, Mr) = 0, the two models have equal expected localization accuracy at location j; if, however, Dξ(Mc, Mr) > 0, the two models have different localization accuracies and Dξ(Mc, Mr) quantifies the amount of mis-localization due to the difference between the modeled conductivity profiles of the head. In this study, we quantify both Dξ(M4, M19) as well as Dξ(M19, M25). The former of these quantifies the amount of mis-localization due to the omission of 16 tissue types which exist both in the presence and in the absence of TBI (e.g., fat, connective tissue, etc.), whereas the latter quantity measures the mislocalization due to the omission of TBI-related changes in conductivity. In the first case, the reference model is M19 because accounting for more tissue types is more anatomically faithful in both health and TBI; in the second case, the reference model is M25 because it is more anatomically faithful to account for TBI-related tissue types.
2.6. Effect of conductivity measurement uncertainties upon localization accuracy in TBI
In addition to investigating localization accuracy differences between pathology-naïve and pathology-inclusive models, we sought to determine the dependence of localization accuracy upon the conductivity of pathology-affected tissues. To this end, all 6 TBI-related tissues were first simultaneously assigned a single conductivity value σP, within a resulting model M20 with 20 tissue types (19 tissues encountered in all heads as well as one TBI-related tissue). The value of σP in units of Siemens per meter (S/m) was then varied from 5 × 10−2 S/m to 5 S/m in increments of 1 S/m to investigate the dependence of localization accuracy upon conductivity. This was done for each conductivity value in this range by calculating the value of the crosstalk metric for each cortical source. The metric used to quantify and to compare localization accuracy as a function of σP was the expected relative localization error R, defined as,
| (14) |
Above, denotes the crosstalk value computed at each cortical location j within the model M20, whereas represents the crosstalk value calculated within the reference model M25 previously described. Averaging over j indicates that the quantity R is an average of over cortical sources j = 1,⋯,n. The crosstalk is explicitly dependent upon the pathology-related conductivity parameter σP being varied and is normalized by the crosstalk of the reference model M25, i.e., by the crosstalk value for the model with reference conductivity values reported in the literature. The purpose of this normalization is to investigate conveniently the dependence of upon σP by relating this former quantity to a reference value—namely to —which facilitates comparison by serving as a convenient unit. Thus, each ratio is the crosstalk value for M20(σP) expressed in units of the reference crosstalk . Thus, R < 1 indicates that the expected crosstalk over the entire cortex is smaller than that in the reference model M25, whereas R > 1 indicates that the expected crosstalk is larger than in the reference model.
3. Results
3.1. FEM models
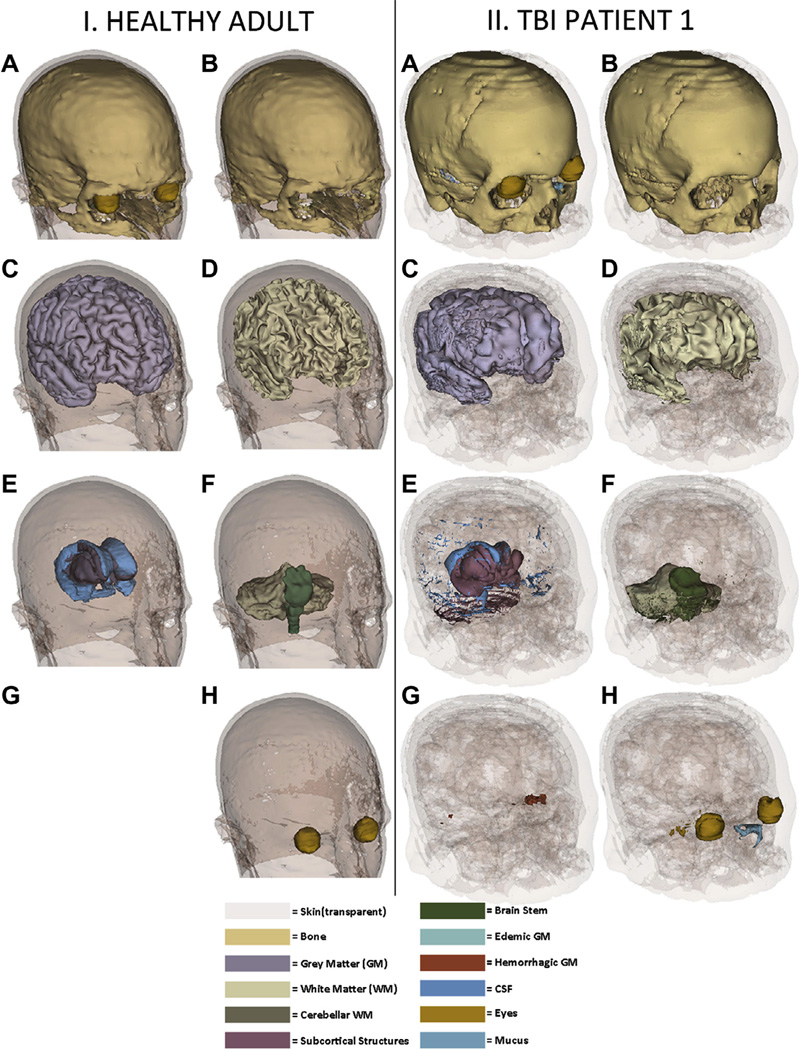
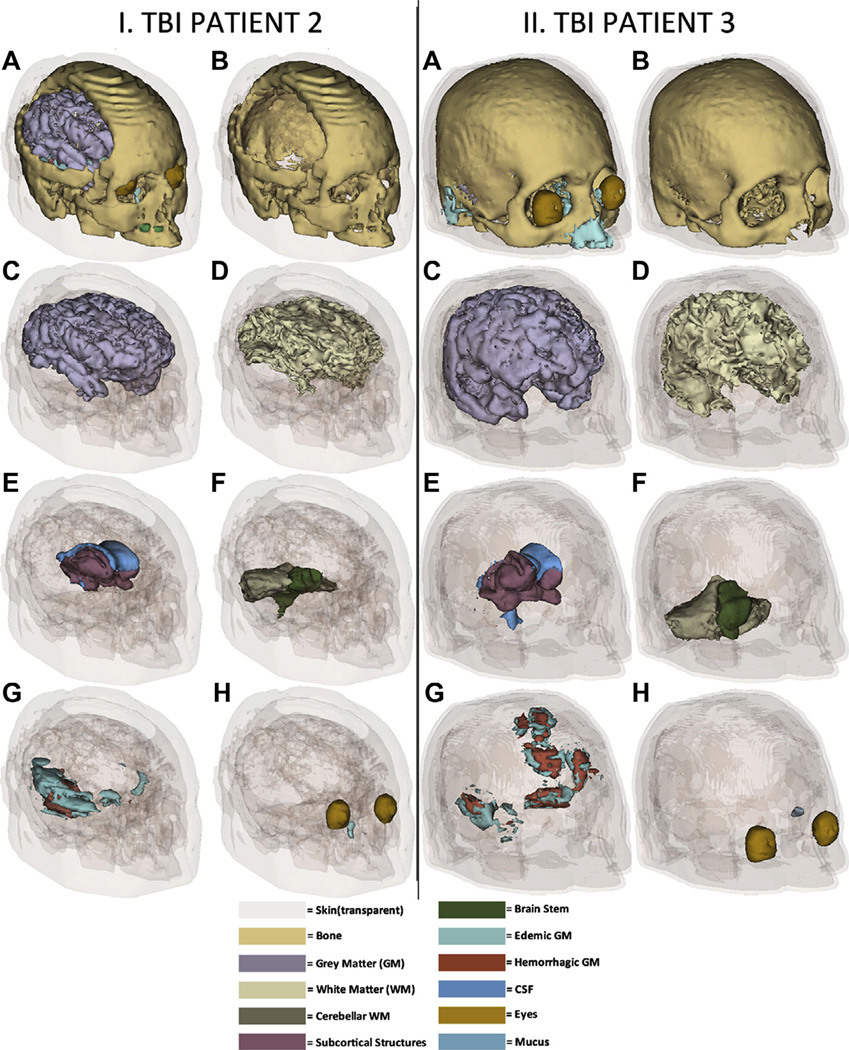
It is useful to visualize various tissue types so as to capture the essential geometric features of our models. Figs. 1 and 2 show 3D models of the head for each subject included in the study. In Fig. 1, inset I shows the healthy subject and inset II shows TBI patient 1; in Fig. 2, insets I and II show TBI patients 2 and 3, respectively. Whereas gyri and sulci have a normal appearance in Fig. 1 (insets I.C and I.D) (as one might expect for a healthy subject), various degrees of abnormality due to non-uniform swelling and increased intracranial pressure are visible in each of the three TBI patients (Fig. 1, insets II.C, II.D, and Fig. 2, insets I.C, I.D, II.C, and II.D). Additionally, skin appearance and thickness are more uniform in the healthy adult compared to each of the three TBI patients, partly due to the presence of appreciable scalp bruising in TBI (which alters scalp geometry and thickness) and possibly due to the fewer number of MRI sequences available in the healthy adult subject compared to the TBI patients (namely two vs. five, see Methods), leading to somewhat different segmentation results. In Fig. 2, insets I.A and I.B reveal the presence of a large craniotomy above the left hemisphere in TBI patient 2. By contrast, in Fig. 1, inset I.G does not reveal the presence of any pathology-related structures, as expected from a healthy adult subject. In Figs. 1 and 2, insets showcasing brain pathology (insets I.G and II.G in each figure) reflect our intent to order the TBI subjects according to their apparent structural severity. This is summarized in Table 2, which shows the brain volume, lesion load (LL), total skin area (TSA), edematous skin area (ESA) and ratios involving these four quantities for each subject. Whereas TBI patient 1 has relatively modest brain pathology, TBI patients 2 and 3 exhibit appreciably more edema and hemorrhage. Additionally, in TBI patient 2, the pathology is observed to cover primarily regions in the frontal and temporal lobes of the right hemisphere (Fig. 2, inset II.G), while in TBI patient 3 lesions can be observed to extend over both frontal regions (bilaterally) as well as over temporal cortex (right hemisphere).
Fig. 1.
3D models of the head and tissues for the health adult subject (insets I.A–I.H) and for TBI patient 1 (insets II.A–II.H). In addition to the full model which includes all tissue types, other tissues are also represented for illustration. Skin is shown transparent for convenience so as not to obscure the view of underlying tissues. For brevity, only some of the most representative tissues are displayed (e.g., fat, muscles and connective tissues are not shown). Both hemorrhagic and non-hemorrhagic GM is visible, as segmented from GRE T2 and SWI imaging.
Fig. 2.
As in Fig. 1, for TBI patient 2 (insets I.A–I.H) and TBI patient 3 (insets II.A–II.H).
Table 2.
Brain volume (BV), lesion load (LL), total skin area (TSA), edematous skin area (ESA) and ratios involving these four quantities for each subject in the study. Note: values for the TSA represent the total area of the skin made available for segmentation in the anatomical MRI volume. Because each subject’s head is positioned differently within the MR volume, the total amount of skin available for segmentation varies from subject to subject. For this reason, the expected direct scaling relationship between BV and TSA may not be readily apparent based on the results above.
| Subject | Brain volume (BV, cm3) | Lesion load (LL, cm3) | LL/BV [%] | Total skin area (TSA, cm2) | Edematous skin area (ESA, cm2) | ESA/TSA [%] |
|---|---|---|---|---|---|---|
| Healthy adult | 1,087.56 | 0.00 | 0.00 | 1,308.28 | 0.00 | 0.00 |
| TBI patient 1 | 1,133.26 | 2.46 | 0.02 | 1,273.23 | 56.21 | 4.41 |
| TBI patient 2 | 1,055.66 | 62.38 | 5.91 | 1,052.56 | 182.35 | 17.32 |
| TBI patient 3 | 1,136.50 | 43.82 | 3.86 | 1,188.89 | 280.27 | 23.57 |
3.2. Forward modeling
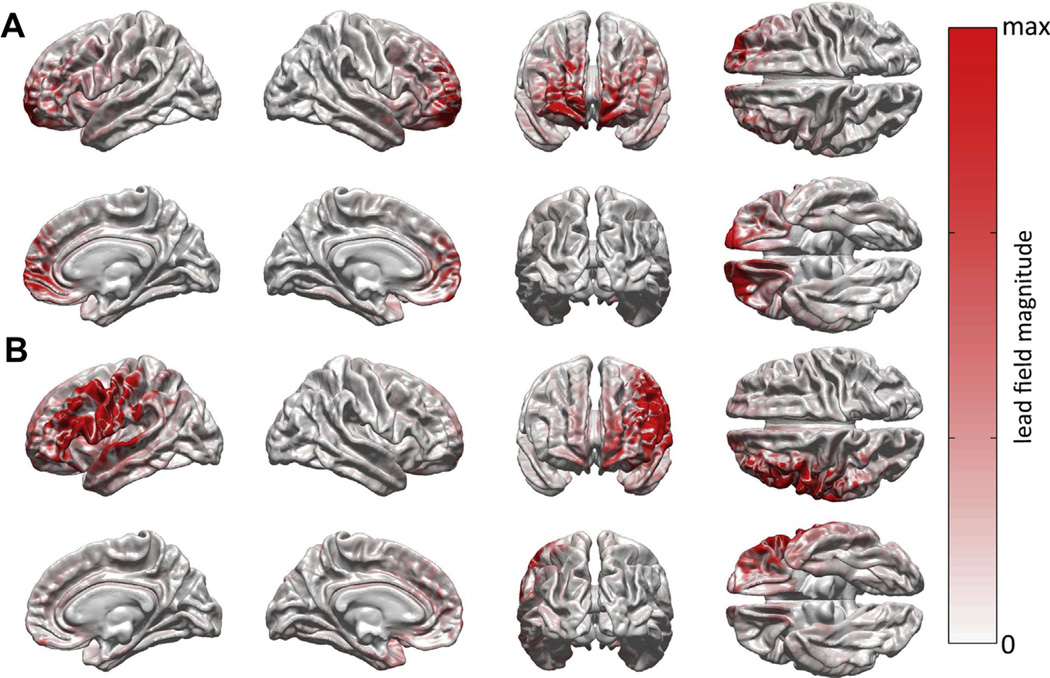
Cortical mapping of forward model metrics can be useful for the purpose of revealing the ability of individual sensors to record from underlying brain regions. For example, Fig. 3 provides visual insight on the physical meaning of the sensor sensitivity area measure β(x). This figure displays the normalized magnitude of the cortical LF for two sample electrodes in TBI patient 3. The LFs shown in parts A and B of Fig. 3 are for EEG electrodes Fp2 and C3, respectively. As a reminder, β(x) can be defined as the cortical area populated with dipoles whose projected signal strengths at some sensor are greater than or equal to x% of the maximum projected signal of any cortical dipole. Thus, the brain area painted in a hue above some color brightness threshold x roughly corresponds to the value of β(x) for that brightness threshold. For example, when x = 0%, one can see that the mapped value of β(0) corresponds to the area painted in a hue of any brightness (i.e., to the entire cortical surface). By contrast, when x = 50%, the hue brightness desired is indicated by the mid-range hue value in the color bar, and thus β(0.5) corresponds to all areas of the brain painted in a hue whose brightness is equal to or greater than the brightness of that hue. In the case of the Fp2 sensor, the electrode is sensitive to right hemisphere frontopolar areas, to medial bilateral frontal cortex as well as to frontal regions contralateral to the hemisphere above which the sensor is located. In the second case, the measuring electrode is observed to be sensitive not only to left dorsolateral prefrontal cortex, but also to portions of the left parietal and temporal lobes.
Fig. 3.
Cortical map of LF magnitudes for EEG electrodes Fp2 (A) and C3 (B). Plotted is the quantity |ai|/max(|ai|), i.e. the magnitude |ai| of the cortical LF ai normalized by the maximum LF magnitude max(|ai|).
3.3. Forward solution accuracy
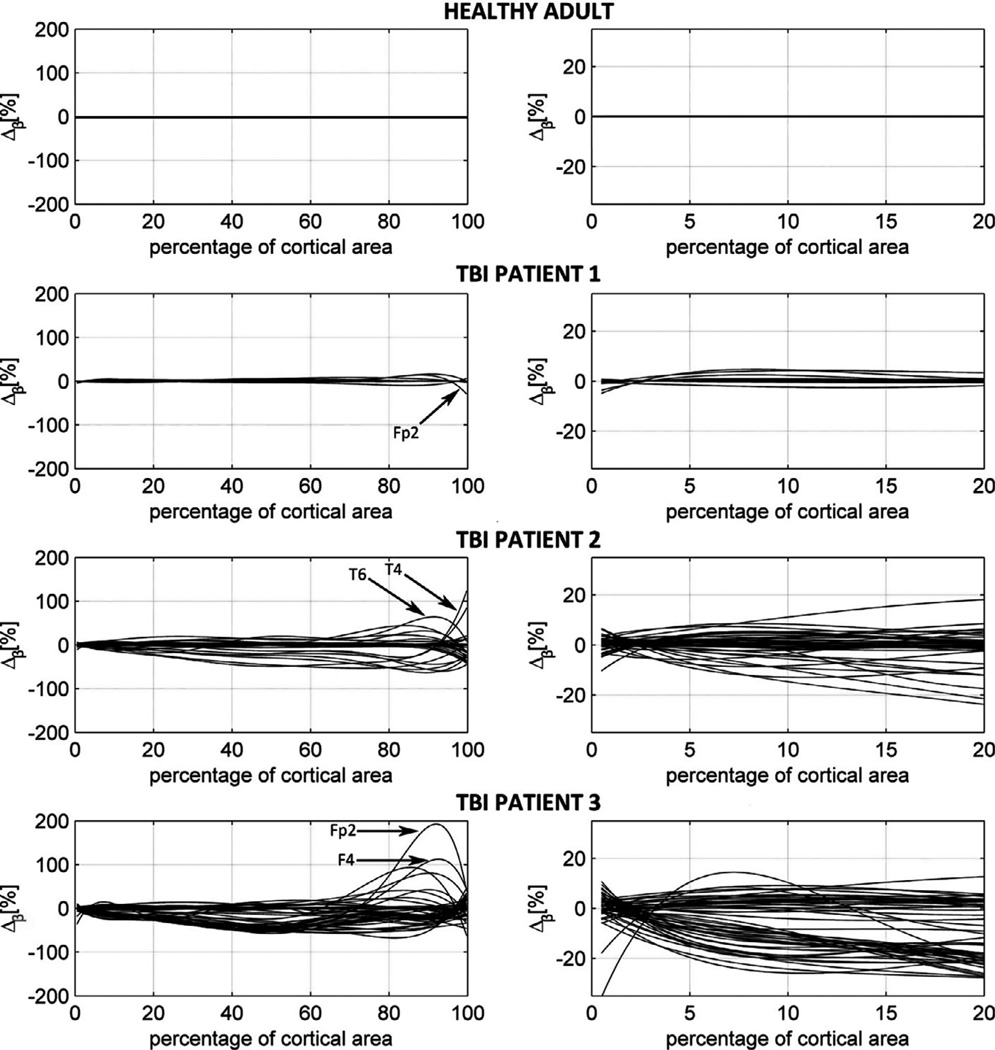
The effects of varying the number of tissues are explored in Fig. 4, which shows Δβ (M19, M25), i.e., the amount of sensitivity area misestimation between M19 and M25. This figure illustrates the amount of sensitivity area misestimation due to the omission of 6 TBI-related tissue types, as a function of the argument x in β(x), i.e., as a function of cortical area percentage. Whereas the first column shows the full profile of Δβ for 0% ≤ Δβ ≤ 100%, the second column focuses upon the interval 0% ≤ Δβ ≤ 20%, thus highlighting how the omission of TBI-related tissue conductivity changes in the forward model leads to the misestimation of LF values for those dipoles which project to each sensor most strongly (i.e., with a strength greater than or equal to 20% of the maximum dipole strength). One way to interpret Fig. 4 involves first selecting a value of x, say 90%. Because Δβ (x = 90%) = 190% for one sensor in TBI patient 3, Fig. 4 indicates the amount by which the simpler model M19 underestimates the sensor sensitivity area β. In the case of the healthy adult, this is always 0% because that subject has no pathology, whereas for TBI patients this can be as high as ~190%. In other words, if the effect of TBI pathology is omitted from the forward model by assuming normal tissue conductivities for TBI-affected regions, the fraction of the cortical area with sources projecting to the sensor with a strength greater than or equal to (100 – 90)% = 10% of the maximum dipole strength is underestimated by as much as ~190% for the sensor in question. If the pathology-naïve and pathology-inclusive models were to estimate the forward solution (and thus the LF profile) identically in each TBI patient, the trace for each electrode would be a horizontal line at Δβ = 0 for each of them, as in the healthy adult. Deviations from this line therefore indicate the amount by which the omission of pathology leads to underestimation (Δβ < 0) or overestimation (Δβ > 0) of LF values. This analysis provides quantitative insight on the accuracy of our forward solution results.
Fig. 4.
Dependence of Δβ(M19, M25), the amount of sensitivity area misestimation due to pathology omission, a function of the percentage x of total cortical area for each patient. In each subject, sensor names are indicated for two electrodes whose LFs are highly dependent upon the inclusion of pathology in the model. Whereas the first column shows the full profile of Δβ(M19, M25) for 0% ≤ x ≤ 100%, the second column focuses upon the interval 0% ≤ x ≤ 20%, thus highlighting how the omission of TBI-related conductivity changes from the forward model leads to the misestimation of LF values for those dipoles which project to each sensor most strongly (i.e., with a strength greater than or equal to 20% of the maximum dipole strength). Each trace corresponds to an electrode. Deviations from the line Δβ = 0 indicate the amount by which the omission of pathology leads to underestimation (Δβ < 0) or overestimation (Δβ > 0) of LF values. In the healthy adult, Δβ = 0 for all sensors and all values of x because no pathology is present.
Fig. 4 indicates that:
forward solution potentials can be misestimated appreciably when TBI pathology is omitted from the FEM model;
the percentage of misestimation varies nonlinearly as the percentage of cortex from which an EEG sensor records increases from 0% to 100%;
a relationship of proportionality exists between the amount of misestimation and the amount of pathology present in each subject.
With regard to the last statement above, comparison of the LL/VB and ESA/TSA ratios for each subject in Table 2 to the results in Fig. 4 indicates that, for the three TBI patients of our study, the extent of forward solution misestimation is directly related to the amount of pathology, as expected. For example, TBI patient 1 has an LL/VB ratio of 0.02%, an ESA/TSA ratio of 4.41%, and a maximum value of |Δβ| equal to 30%. By contrast, TBI patient 3 has an LL/VB ratio of 3.86%, an ESA/TSA ratio of 23.57% and a maximum value of |Δβ| equal to almost 200%. Given that the ESA/TSA ratio appears to have an appreciable effect upon the amount of forward solution inaccuracy in the few subjects analyzed here, it may be useful for future studies to explore this causative relationship in the context of a larger sample of TBI patients. Nevertheless, these results provide useful insight into the importance of accurately modeling shallow head layers in the context of the EEG forward and inverse problems.
3.4. Localization error analysis
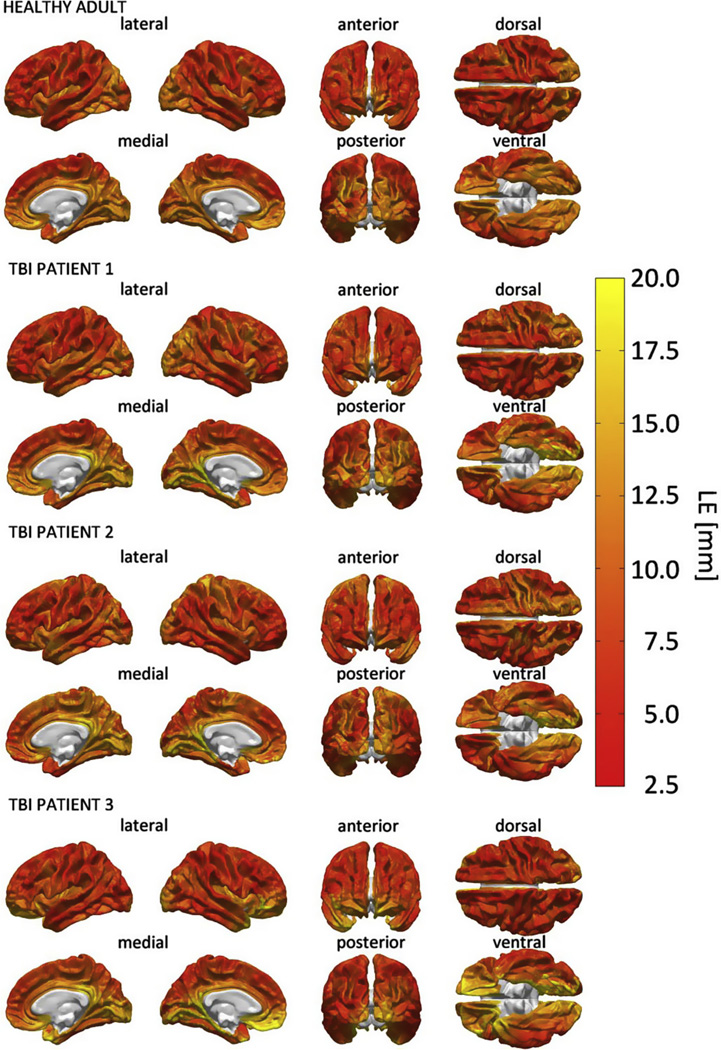
It is important to quantify LE in order to understand the localization abilities of each model. Fig. 5 displays the LE of M19 for each cortical location in both the healthy adult as well as in the TBI patients. This figure allows one to evaluate the localization accuracy of the FEM model with 19 tissue types without the confounding factor of conductivity changes due to TBI-related pathology. One convenient feature of M19 is that it can be used as a reference model to investigate the effect of either decreasing or increasing the number of tissue types. A common feature shared by all four LE maps over the cortical surface in Fig. 5 is their indication that EEG localization accuracy decreases with source depth in the brain. Additional—though typically more limited—variability in LE is observed in various areas of dorsolateral cortex in each subject, possibly due to differences in physical features such as skull thickness and fat layer thickness across the head.
Fig. 5.
Cortical map of LE in M19. For each point on the cortical surface, the LE associated with inverse localizing a source positioned there is displayed.
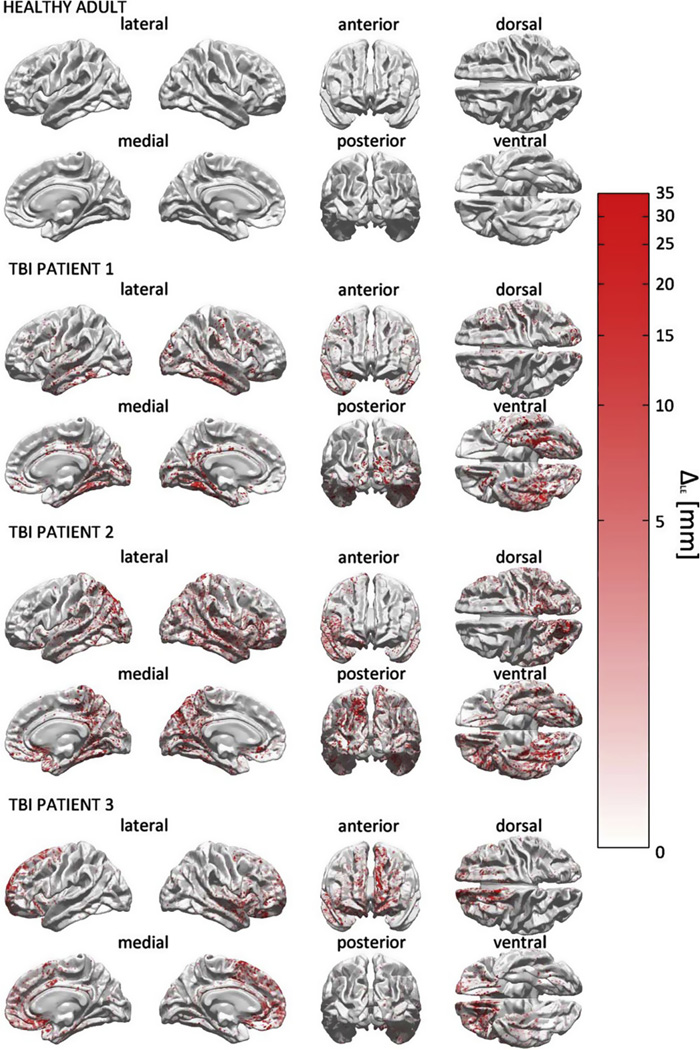
Differences between the highly simplified model M4 and the more complex model M19 are shown in Fig. 6, which explores LE differences between these models, i.e., the effect upon localization of reducing the number of FEM model tissues types from 19 to 4. This effect is observed to vary across the brain, with various regions exhibiting greater changes in LE compared to others. The quantity mapped over the cortex is ΔLE (M4, M19), i.e., the absolute difference in LE between these two models. The extent and spatial distribution of these differences are found to vary appreciably from subject to subject, with no obvious pattern which holds across all subjects.
Fig. 6.
Localization accuracy comparison between M4 and M19 using the LE metric. For each activation source on the cortical mesh, the quantity ΔLE(M4, M19), i.e., the absolute value of the difference in localization error between M4 and M19, is displayed.
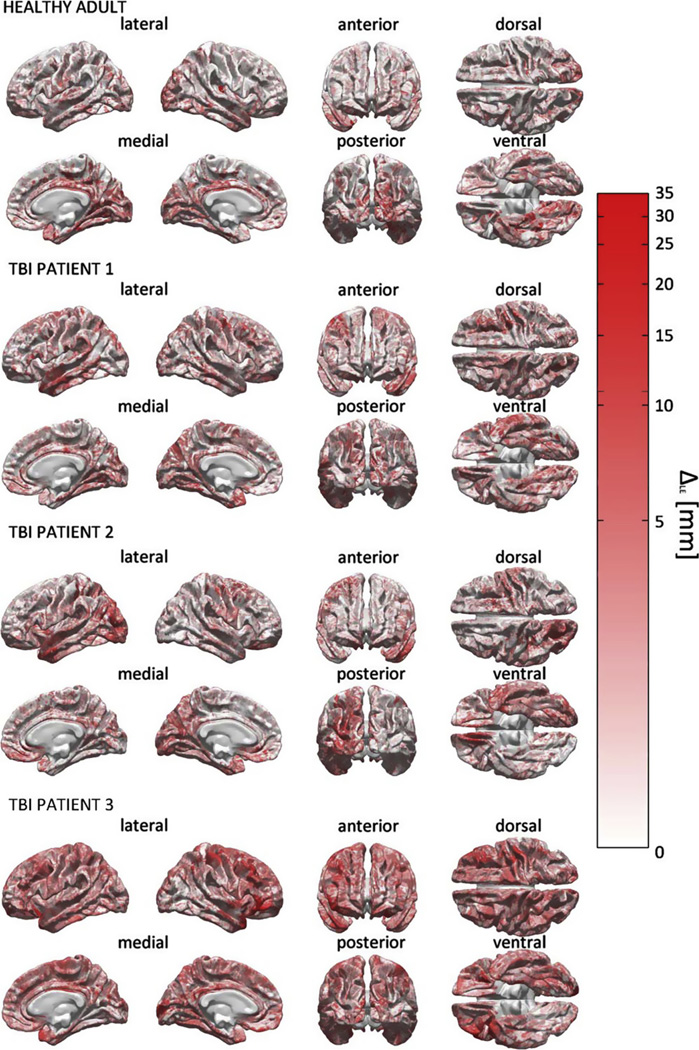
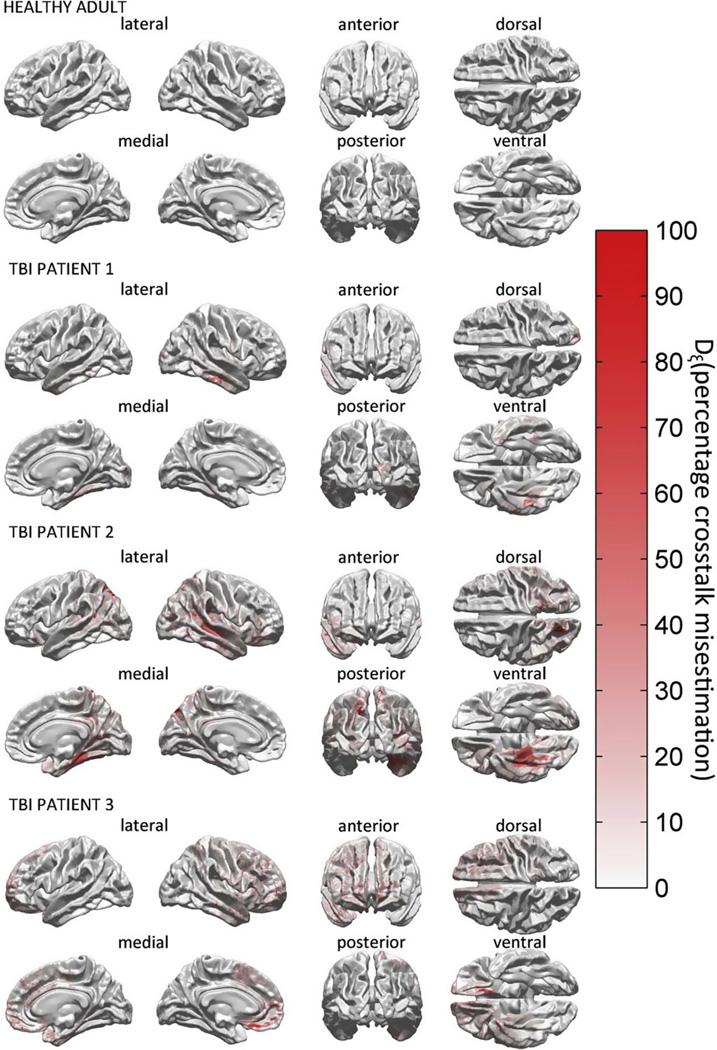
The effect of including pathology-related tissue types is explored in Fig. 7, where the metric ΔLE (M19, M25) is used to perform a comparison between the pathology-inclusive model M25 and the pathology-naïve model M19 in terms of localization accuracy. Specifically, for each activation source on the cortical mesh, the quantity ΔLE (M19, M25), i.e., the absolute value of the difference in localization error between M19 and M25, is displayed. Since ΔLE (M19, M25) is the amount of LE due to ignoring the effect of pathology, Fig. 7 reveals the effect of this omission upon inverse solution accuracy as quantified using the LE metric. We emphasize that Fig. 7 displays ΔLE (M19, M25) (the absolute difference in LE between M19 and M25, see Eq. 11), rather than the LE itself. Thus, the upper bound value of 35 mm in the legend to Fig. 7 is the maximum difference in LE between the two models, not the LE of either model. In other words, when pathology effects are omitted, the LE is seen to change by as much as 35 mm in TBI patients. By contrast, no changes are seen in the healthy adult because no pathology is present in this subject. An important observation to be made is that qualitative agreement exists between the locations of pathology-affected areas (see Figs. 1 and 2) and the locations of cortical areas with large ΔLE (Fig. 7, in red). The fact that large portions of the cortex are drawn in white for each TBI patient indicates that, as expected, the two models M25 (pathology-inclusive) and M19 (pathology-naïve) do not typically differ in their abilities to localize sources which are located relatively ‘far’ from the locations of pathology. By contrast, for those sources located within a contusion or peri-contusionally, the amount of LE which is due solely to the omission of pathology in M25 compared to M19 is found to be substantial. It should be noted that differences in LE between the two models are due not solely to the presence of brain lesions, but also to the inclusion of edematous skin and epidural hemorrhage as separate tissue types. In TBI patient 2, for example, some differences in LE are found between the two models for sources in the occipital lobe, though no gross brain injury is found in those regions (see Fig. 2). This is due to the fact that, in this particular subject, the skin in the back of the head is substantially affected by swelling, whose presence alters the source localization of the pathology-inclusive model.
Fig. 7.
Localization accuracy comparison between M19 and M25 using the LE metric. For each activation source on the cortical mesh, the quantity ΔLE(M19, M25), i.e., the absolute value of the difference in localization error between M19 and M25, is displayed.
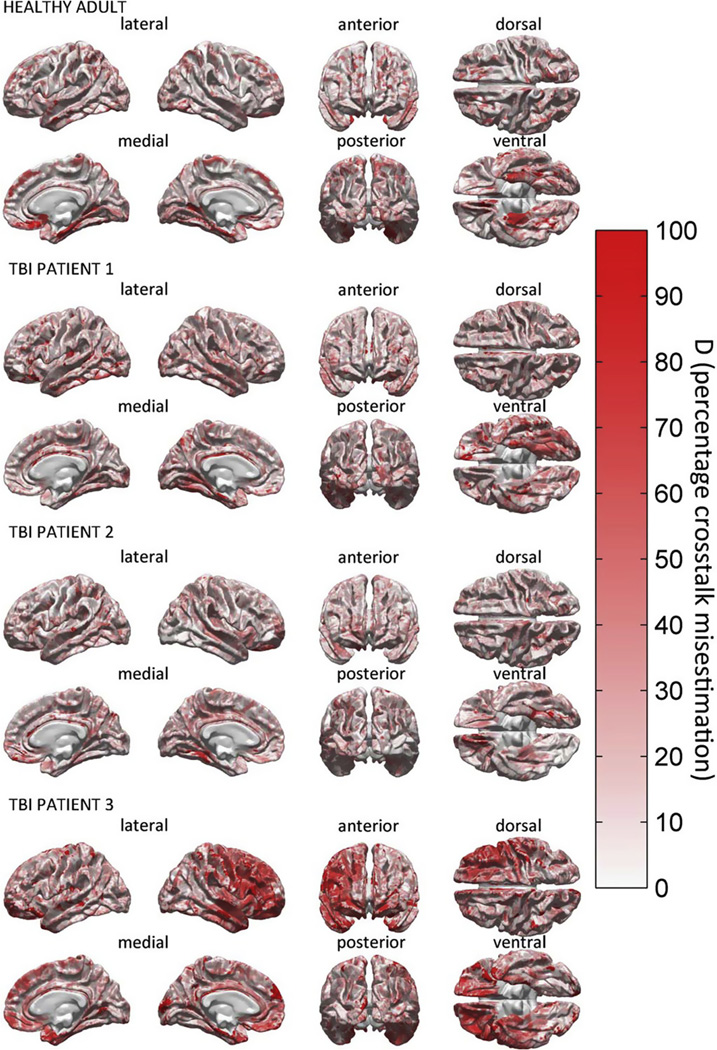
3.5. Crosstalk calculation analysis
Aside from studying the LE, it is also useful to investigate crosstalk in order to pinpoint the effects of tissue conductivity alterations. Figs. 8 and 9 are similar to Figs. 6 and 7, respectively, in that Figs. 8 and 9 also illustrates the results of comparing two different models, namely M4 to M19 (Fig. 8) and M19 to M25 (Fig. 9) in terms of differences in localization accuracy. However, whereas the metric of choice in Figs. 6 and 7 was the difference in localization error ΔLE, the metric used in Figs. 8 and 9 is Dξ, i.e., the percentage difference in crosstalk. As previously stated, the LE is more useful in the context of active focal sources, whereas crosstalk provides more insight into localization accuracy in the context of distributed source models (Liu, 2002). The quantity Dξ plotted in Figs. 8 and 9 quantifies the difference in localization accuracy due to pathology omission, expressed in units of how much crosstalk should be expected in the reference model (see the denominator of Eq. 13). The reference model is M19 in Fig. 8 and M25 in Fig. 9. Fig. 8 confirms the findings in Fig. 6, according to which the collective omission of various tissue types encountered in both health and pathology (e.g., fat, soft bone, etc.) is associated with substantial changes in localization accuracy. Similarly, Fig. 9 suggests that the omission of pathology can lead to substantial and undesirable increases in crosstalk. In both cases, the amount of mis-localized electrical activity can be twice as large in the simplified model as in the more complex model being compared.
Fig. 8.
Localization accuracy comparison between M4 and M9 using the crosstalk metric. For each activation source on the cortical mesh, the quantity Dξ(M4, M19), i.e., the absolute value of the difference in crosstalk between M4 and M19, is displayed.
Fig. 9.
Localization accuracy comparison between M19 and M25 using the crosstalk metric. For each activation source on the cortical mesh, the quantity Dξ(M4, M19), i.e., the absolute value of the difference in crosstalk between M19 and M25, is displayed.
3.6. Conductivity effects upon localization accuracy
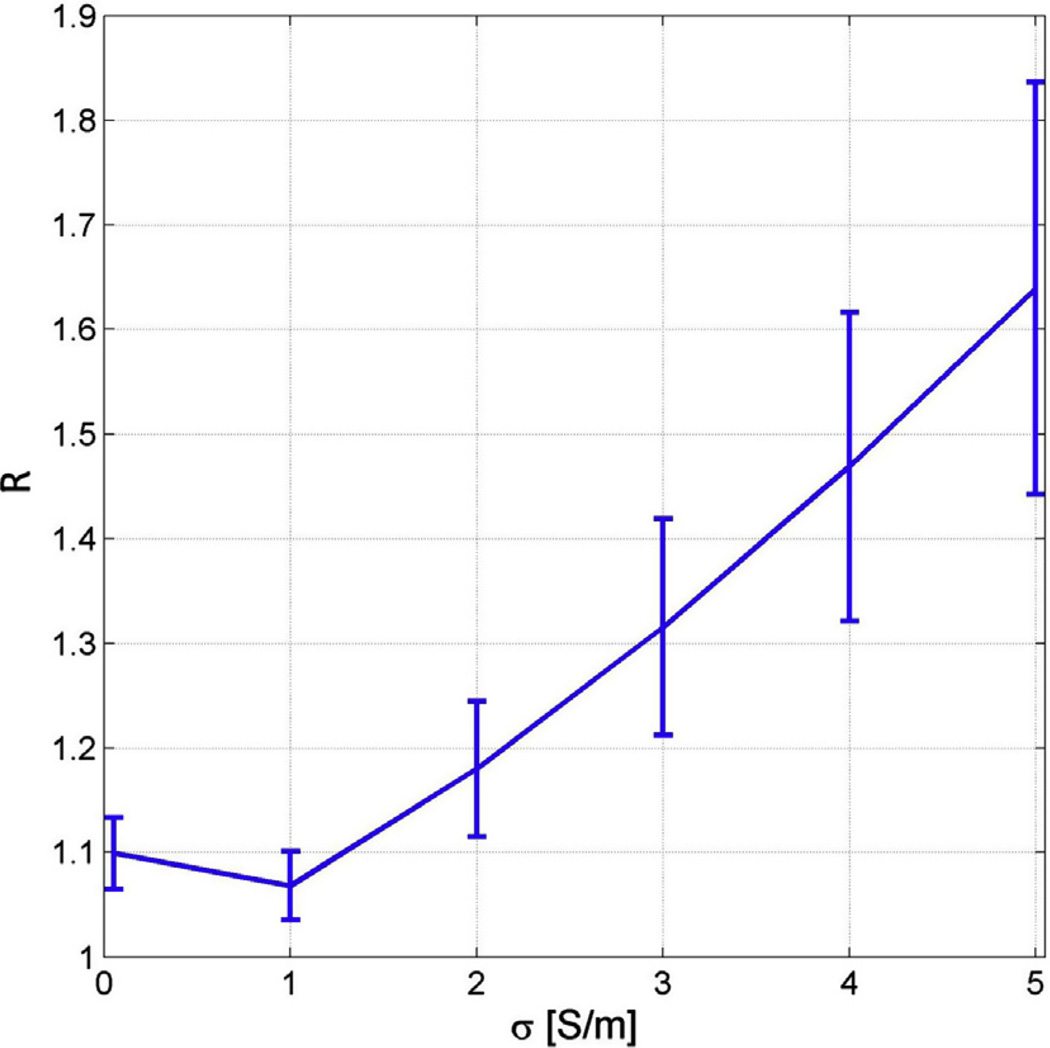
Whereas Figs. 6–9 summarize the effect of pathology upon localization accuracy, Fig. 10 investigates the dependence of cortical localization accuracy upon the conductivity value assigned to pathology. The quantity plotted on the horizontal axis is the value of the conductivity parameter σP, whereas the quantity plotted on the vertical axis is the relative expected localization error R. Fig. 10 illustrates that uncertainties in the conductivity of pathology-related tissues have a nonlinear effect upon crosstalk and upon localization accuracy. Specifically, values of σP between 0.05 and ~1 S/m are associated with average crosstalk values which are smaller than for the reference model M25, whereas the opposite is the case for values of σ between ~1 and 5 S/m. The implication is that, as the value of σP increases from 0.05 to ~1 S/m, the average source estimate sensitivity to activity from other locations decreases, as does the average localization error. By contrast, as conductivity increases again from ~1 to 5 S/m, the sensitivity of the source estimate to other activity increases as well and the expected localization accuracy decreases. What Fig. 10 suggests is that there is relatively low variation in localization accuracy associated with pathology-related changes in conductivity in the interval 0–~1.3 S/m. In other words, as long as the effective conductivity of pathology-affected tissues falls within the interval [0, ~1.3] S/m, the localization accuracy of our method is not expected to change very much compared to the scenario in which the conductivity of pathology-affected tissues is larger than ~1.3 S/m.
Fig. 10.
Dependence of cortical localization accuracy upon the conductivity value assigned to pathology. The quantity plotted on the horizontal axis is the value of the conductivity parameter σP, whereas the quantity plotted on the vertical axis is the relative expected localization error R.
4. Discussion
4.1. Clinical potential of EEG localization in acute TBI
The acquisition and examination of EEG recordings in acute TBI patients has been undervalued, yet offers unique opportunities to inform patient treatment and to affect recovery. For example, localization of EEG potentials recorded following acute TBI may be useful for prospectively evaluating the usefulness of EEG in the preoperative planning of epileptogenic focus removal (Ebersole, 1999; Ebersole and Wade, 1990, 1991). Similarly, continuous EEG (cEEG) has proven to be very important in the treatment of TBI patients with status epilepticus (SE), where this technique has allowed clinicians to evaluate treatment effectiveness in patients who are treated continuously using infusions of antiepileptic drugs (Brophy et al., 2012). Localization of cortical potentials beginning in acute TBI patients may also be useful for longitudinal studies, where clinically relevant hypotheses on brain tissue fate and on the long-term effects of pharmacological agents upon the TBI brain may benefit from the insights provided by electrophysiological recordings.
In the period following acute brain injury, it can be particularly difficult to localize pathophysiological brain activity due to the complexity of structural brain changes prompted by TBI, and this difficulty is currently seen as deterrent to certain clinical interventions, such as surgery to remove epileptic foci (Mani and Barry, 2006). Though such invasive clinical interventions are not performed acutely due to the inherently chronic nature of this condition, the task of pathophysiological activity localization remains of interest at all stages post-injury. This is because,
the relationship between the spatial patterns of acute, subacute and chronic pathophysiological activity remains insufficiently understood,
EEG source localization allows one to study resting state functional connectivity patterns in TBI patients
functional connectivity inferred via EEG localization can be combined with functional magnetic resonance imaging (fMRI) for improved insight into TBI-related brain dynamics (Holmes et al., 2013; Yang et al., 2010).
Thus, the putative clinical relevance of improving the accuracy of currently available source localization methods for TBI is appreciable for both acute and chronic TBI.
4.2. Importance of TBI-related tissue conductivity changes
The accumulation of blood and other fluids at the site of a concussion leads to increases in local tissue conductivity, which presumably affects how electric currents propagate from the sites of brain activity to those of scalp EEG sensors. In turn, such physical changes affect the preferential sensitivity of EEG electrodes to certain electric sources in the brain, and how this occurs is highly dependent upon the anatomy and physical properties of the head and injuries. Thus, aside from addressing the challenges associated with modeling closed- and open-head TBI, another important strength of our study is that it sheds light upon how the presence of pathology can influence the accuracy of inverse source localization via EEG recordings.
In this examination, we establish that the presence of TBI-induced pathology can lead to marked mis-localization of cortical activity, particularly in contusional and peri-contusional brain regions. In the three acute TBI cases presented, the effect of TBI-related anatomic changes upon forward and inverse solution accuracy appear to be predicated not only upon lesion load, but also upon how much scalp was affected by trauma. This observation is unsurprising given the sensitivity of EEG signals to the conductivity of head tissues surrounding the sensor, and our study provides novel evidence in support of the widely held view that accurate modeling of superficial head layers is very important for the purpose of EEG forward and inverse solution accuracy (Hallez et al., 2007; von Ellenrieder et al., 2006).
The accurate localization of noninvasively recorded cortical activity depends on a number of factors, one of which is the realism of the head model used in the forward calculation of electric potentials (Gencer and Acar, 2004). Anatomically faithful head models account for head anatomy and tissue conductivity, both of which are of particular significance in TBI forward modeling due to the presence of pathology. On the one hand, open head injuries can pose appreciable modeling challenges in the context of boundary element method (BEM) models with closed shells, which makes accounting for such injuries more amenable for the FEM instead. Thus, for TBI models involving open head injuries, the FEM formalism adopted here and applied to the modeling of different tissue classes is a principal strength of this approach over BEM-based methods; naturally, this is not to imply that the FEM is generally superior to BEM, only that the FEM is more convenient when accounting for open head pathology. For example, previous investigations involving models which account for the presence of brain lesions and cavities have shown that the latter can have a significant qualitative and quantitative effect upon the computed electric potentials (He et al., 1987). Because EEG source localization accuracy depends highly upon forward model accuracy, the ability demonstrated here to generate EEG forward solutions based on models which capture the underlying anatomy with high fidelity is very important to the task of source localization. In addition, our study addresses the challenge of identifying the spatial extent of TBI-related pathology through the use of multimodal neuroimaging methods including computed tomography (CT) and MRI sequences which are tailored for the accurate detection of edematous and hemorrhagic tissues.
4.3. Consequences of tissue conductivity measurement uncertainties
One factor which has been widely acknowledged as limiting the accuracy of forward-inverse EEG models is the variability of tissue conductivities across subjects and measurement location (Awada et al., 1998; Yitembe et al., 2011, 2012). Importantly for the problem at hand, the effects of TBI pathology upon tissue conductivity has not been explored. The investigation of such effects upon inverse solution accuracy is useful because (1) the precise conductivities of pathology-affected tissues are difficult to obtain from TBI patients, (2) errors in the estimation of conductivity for such tissues has a yet unknown effect upon localization accuracy, and because (3) knowledge of such errors is important when assessing the feasibility and accuracy of TBI source localization.
In the present study, the effects of acute TBI upon inverse localization were first discussed in the context of TBI-related conductivity values which had been assigned to pathology-affected tissues based on previous experimental studies. Nevertheless, one can expect that the conductivities of hemorrhagic and edematous GM/WM can vary depending on various factors which affect tissue composition such as proteinaceous content, state of CSF perfusion (particularly in the case of edematous regions), as well as blood content (especially in the case of hemorrhaging tissues). Determining the effects of these factors upon inverse solution accuracy can be challenging because different combinations of pathology types may lead to widely different values of effective tissue conductivity. In addition, because the gold standard for localization accuracy typically requires in vivo measurements which can be methodologically and ethically challenging to obtain, the subject of localization accuracy and validation remains a topic open for discussion even in the context of anatomically faithful head models.
Because the effects of varying conductivities for common tissue types such as bone, scalp, GM and WM have been widely explored elsewhere (Chen et al., 2010; Ferree et al., 2000; Pohlmeier et al., 1997; Zhang et al., 2006) and are relatively better understood than the effect of pathology, this type of analysis is not reproduced here. In the case of pathology, Fig. 10 suggests that the most substantial changes in localization accuracy relative to our reference model can be expected to occur when TBI-affected tissue conductivity is larger than ~1.3 S/m, as may occur in cases where TBI-related accumulation of CSF, blood and other fluids is substantial. Thus, although the individual effect of variations in the conductivity of blood, edematous WM/GM and other pathology-related tissue types is not explored here, our study does provide useful initial information in the assessment of how conductivity measurement uncertainties may affect localization accuracy.
4.4. Model complexity considerations
This study is among the very few to illustrate the calculation of the EEG forward matrix in TBI patients while also accounting for the effects of hemorrhage and edema upon the conductivity profile of WM, GM and scalp in the context of a FEM model which is anatomically faithful. An additional innovation is that our model takes into account 25 tissue types when calculating the EEG forward matrix. This is in contrast to previous FEM studies, which have typically modeled the head using 12 or fewer tissue types (Gencer and Acar, 2004). As our results suggest, the modeling of pathology is important for capturing lead field focality, as quantified using the percentage difference in sensor sensitivity area between M19 and M25.
Because our EEG modeling approach involves substantially more tissues than in typical inverse localization studies, it is of interest to determine whether all tissues included are equally important, and whether fewer tissue types can be used with minimal reductions in accuracy. When attempting to answer these questions in the context of FEM models, it is important to note that the number of tissue types accounted for in a model is effectively equal to the number of distinct conductivities included. Consequently, from this standpoint, FEM model complexity is intimately related to conductivity profile complexity. For example, an anatomically faithful FEM model with N + 1 tissue types (where N is a positive integer) can be reduced to a model with N tissue types by assigning one of the N + 1 tissues the conductivity of another tissue. Thus, one way to study the effect of ignoring the conductivity-related effects of a certain tissue type involves assigning that tissue the conductivity of another tissue in the model. For example, ignoring the effect of subcutaneous fat could be studied in our context by assigning the conductivity of skin to FEs accounting for fat, and similar changes can be effected in order to investigate the consequences of failing to account for other tissue types. This is, in fact, the approach adopted to study the effect of pathology, and the same method is used to determine the effect of ignoring conductivity effects due to other tissue types. Because Fig. 6 indicates the presence of substantial differences in localization accuracy due to the omission of various tissue types encountered in both health and in TBI (e.g., fat, subcortex, etc.), it is useful to comment on these findings. In the case of dorsal cortical sources, the most important effects upon ΔLE (M4, M19) are probably due to the omission of subcutaneous fat, soft bone, CSF and connective tissue (e.g., dura mater) from M4. This is because these four tissue types are positioned directly between sensors and dorsolateral cortex, and variations in their thickness over the head are therefore most likely to affect localization accuracy. By contrast, ΔLE(M4, M19) over ventral cortex is most likely affected by the omission of conductivity effects due to other tissue types such as cerebellum, subcortex and brain stem. By comparison, the omission of the eyes as a separate tissue type is likely to cause a more moderate effect upon localization accuracy because the brain is separated from the eye sockets by the skull, and the latter probably takes precedence as the most substantial factor influencing localization accuracy in frontoventral areas. Similarly, it is likely that optic nerves have a rather limited effect upon localization accuracy, and that their inclusion as a separate tissue type modestly affects localization to structures such as the orbital gyrus. In any case, the results presented in Fig. 5 indicate that appreciable changes in localization accuracy are brought about by the exclusion of certain tissue types from the model, and future studies should explore further how inclusion of each tissue type individually contributes to localization accuracy in the FEM approach.
In addition to the effects of tissue conductivity upon localization accuracy, the effects of tissue geometry are also of interest. When discussing such effects, however, it is important to distinguish between anatomically- and ideally-shaped models because each of these is based on a different set of assumptions which can complicate direct comparison. Here we restrict our discussion to anatomically faithful models because the various differences between anatomically- and ideally-shaped models have been reviewed elsewhere (Hallez, 2007). In the restricted context of our own anatomically faithful model, it can be challenging to explore tissue geometry effects without simultaneously ignoring at least some of the geometry-related information provided by structural imaging. In other words, as long as detailed tissue geometry data are available (as in our case), it is more principled to investigate tissue type effects while also taking such information into consideration. For this reason, a surrogate and potentially insightful strategy for exploring the effect of geometry alterations in our own context involves starting from the most geometrically complex model and altering the conductivity values of individual FEs in that model. Because each model has a relatively large number of FEs and thus high anatomical resolution, this type of alteration can be expected to reflect geometry changes to some extent. For example, our comparison of pathology-naïve and pathology-inclusive models can be said to involve the exploration of geometry differences between models in this fashion. Beyond the exploration of geometry changes related solely to pathology, however, one can also investigate geometry changes from the standpoint of alterations in the number and spatial configuration of tissues which are present in both pathology-naïve and pathology-inclusive models (e.g., fat, skin, bone, etc.). However, given that we aim to restrict our framework to anatomically-shaped models which do not dismiss available structural information, changes in the spatial configurations of such tissues can also be modeled as changes in the conductivity profiles of their constitutive FEs. This particular type of investigation is conducted here by comparing the 19-material model to a simplified 4-material model, with the conclusion that such geometry simplifications are associated with localization accuracy decreases which are most pronounced around locations where the geometry and conductivity simplifications in question are effected.
4.5. Effects of varying the scalp density of EEG sensors
In this study, EEG localization accuracy was investigated in the context of a standard montage consisting of 60 scalp electrodes. In the case of healthy subjects, the spatial sampling profile of EEG as a measurement technique is dependent upon both the location as well as number of scalp electrodes (Lantz et al., 2003), with higher-density montages commonly being seen as beneficial to the accuracy of inverse localization. Whereas some studies (Odabaee et al., 2013) have suggested that hundreds of sensors are needed to sample scalp potentials at their true spatial frequency resolution, others (Lau et al., 2012) have suggested that using more than ~40 electrodes is only marginally useful. In addition, the issue of optimal spatial sampling is complicated by the possibility that the surface density of sensors required for accurate localization may differ from case to case based on considerations such as source focality, spatial configuration and signal cancellation (Irimia, 2012b). In the case of source localization for acute TBI, local conductivity increases related to swelling and hemorrhage are expected to increase the source blurring effect of the EEG spatial filter, which would decrease the spatial frequency of EEG. This, in turn, may counteract the beneficial effect of increasing sensor density in scalp regions affected by pathology because the spatial frequency of EEG in such regions is lower than in unaffected areas. Consequently, because the local spatial frequency of EEG at and around pathology locations may decrease due to local conductivity changes caused by injury, higher electrode densities over such regions are not expected to improve localization accuracy as much as over unaffected regions.
4.6. Limitations and caveats
One criticism of this work is that in vivo tissue conductivities vary across subjects and anatomical locations. Such ambiguities remain problematic because the electrical conductivity distribution of the human head cannot be measured in vivo in human subjects, so that average conductivity values reported in the literature must be used instead. This introduces inherent inaccuracies when considering the variation of conductivity in individuals relative to mean values. In addition, conductivity may vary as a function of position and time, which adds to the difficulties of realistically capturing the effects of variability in tissue conductivity values. To address these limitations, we varied the conductivity of tissues associated with pathology within a wide range, and computed the resulting changes in source localization accuracy. In this context, Fig. 10 points to the importance of accurately modeling how tissue conductivities are modified by trauma and highlights the need for improved methods to estimate tissue conductivity in TBI-affected patients. These results can safely be assumed to provide upper and lower bounds on the effect of TBI-related conductivity variations upon inverse localization accuracy. This is because (1) conductivity was varied here across two orders of magnitude within the bounds which can be expected for the conductivity of biological tissues, and also because (2) the true effect of pathology-related conductivity variations upon localization accuracy is likely smaller than the most extreme effects described in Fig. 10.
Another limitation of this exploration is the fact that the models do not account for spatial anisotropies in tissue conductivity. Such anisotropies are believed to have some effect upon source localization according to previous studies (Cook and Koles, 2008; Marin et al., 1998), and the inclusion of WM conductivity anisotropies based on spatial information provided by diffusion tensor imaging (DTI) has been proposed as a useful way to reduce source localization errors (Lee et al., 2009). In addition to WM, bone conductivity is also known to be spatially anisotropic and values for both its radial and angular components have been reported in the literature (Chauveau et al., 2004). Thus, inclusion of tissue anisotropy would be beneficial in the context of this modeling framework.
5. Conclusions
We employed an anatomically constrained FEM model of the head to quantify the effects of TBI-related tissue conductivity changes upon EEG forward and inverse solution accuracy. Results suggest that modeling TBI pathology is important for the purpose of faithfully capturing lead field properties and parameters, including spatial focality. Furthermore, because crosstalk quantifies how biased the activity at some location can be to activity at other locations, our results indicate that ignoring the effects of TBI upon the conductivity profile of the head results in misestimating source localization bias by an amount which can be as large as the amount of bias to be expected from the inverse localization procedure when pathology is taken into account. These findings are the first to quantify the importance of realistic TBI contusion modeling for the purpose of EEG source localization in the acute phase of brain injury. Future work will focus on the application of this methodological approach to the localization of healthy and epileptogenic sources in acute TBI patients (Irimia et al., in preparation).
HIGHLIGHTS.
Omission of pathology can produce substantial inaccuracies in EEG forward models of acute TBI.
Ignoring TBI-related conductivity changes affects localization accuracy in (peri-) contusion areas.
Head conductivity changes should be accounted for in forward/inverse models of acute TBI.
Acknowledgments
We acknowledge Zeynep Akalin Akar, Eric Halgren, Eran Mukamel, Paul M. Vespa, and the staff in the Laboratory of Neuro Imaging at UCLA for assistance and useful discussions. 3D Slicer is a multi-platform, free and open source software package for visualization and medical image computing available from www.slicer.org. This work was supported by the National Alliance for Medical Image Computing (NA-MIC; www.na-mic.org), under NIH Roadmap Initiative Grant 2U54EB005149 (to R. K., sub-award to J. D. V. H.), and by the NINDS, Grants R41NS081792 (to Stephen R. Aylward and J. D. V. H.) and P01NS058489 (to Paul M. Vespa).
Footnotes
The authors report no conflict of interest.
References
- Acar Z, Gencer N. An advanced BEM implementation for the forward problem of electro-magnetic source Imaging. Phys Med Biol. 2004;49:5011–5028. doi: 10.1088/0031-9155/49/21/012. [DOI] [PubMed] [Google Scholar]
- Acar Z, Makeig S. Neuroelectromagnetic forward head modeling toolbox. J Neurosci Methods. 2010;190:258–270. doi: 10.1016/j.jneumeth.2010.04.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akhtari M, Bryant HC, Mamelak AN, Flynn ER, Heller L, Shih JJ, et al. Conductivities of three-layer live human skull. Brain Topogr. 2002;14:151–167. doi: 10.1023/a:1014590923185. [DOI] [PubMed] [Google Scholar]
- Angeleri F, Majkowski J, Cacchio G, Sobieszek A, D’Acunto S, Gesuita R, et al. Posttraumatic epilepsy risk factors: one-year prospective study after head injury. Epilepsia. 1999;40:1222–1230. doi: 10.1111/j.1528-1157.1999.tb00850.x. [DOI] [PubMed] [Google Scholar]
- Awada KA, Jackson DR, Baumann SB, Williams JT, Wilton DR, Fink PW, et al. Effect of conductivity uncertainties and modeling errors on EEG source localization using a 2-D model. IEEE Trans Biomed Eng. 1998;45:1135–1145. doi: 10.1109/10.709557. [DOI] [PubMed] [Google Scholar]
- Baumann SB, Wozny DR, Kelly SK, Meno FM. The electrical conductivity of human cerebrospinal fluid at body temperature. IEEE Trans Biomed Eng. 1997;44:220–223. doi: 10.1109/10.554770. [DOI] [PubMed] [Google Scholar]
- Binette JS, Garon M, Savard P, McKee MD, Buschmann MD. Tetrapolar measurement of electrical conductivity and thickness of articular cartilage. J Biomech Eng. 2004;126:475–484. doi: 10.1115/1.1785805. [DOI] [PubMed] [Google Scholar]
- Brophy GM, Bell R, Claassen J, Alldredge B, Bleck TP, Glauser T, et al. Guidelines for the evaluation and management of status epilepticus. Neurocrit Care. 2012;17:3–23. doi: 10.1007/s12028-012-9695-z. [DOI] [PubMed] [Google Scholar]
- Chauveau N, Franceries X, Doyon B, Rigaud B, Morucci JP, Celsis P. Effects of skull thickness, anisotropy, and inhomogeneity on forward EEG/ERP computations using a spherical three-dimensional resistor mesh model. Hum Brain Mapp. 2004;21:86–97. doi: 10.1002/hbm.10152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen F, Hallez H, Staelens S. Influence of skull conductivity perturbations on EEG dipole source analysis. Med Phys. 2010;37:4475–4484. doi: 10.1118/1.3466831. [DOI] [PubMed] [Google Scholar]
- Cook MJ, Koles ZJ. The effect of tissue anisotropy on the EEG inverse problem. Conf Proc IEEE Eng Med Biol Soc. 2008;2008:4563–4566. doi: 10.1109/IEMBS.2008.4650228. [DOI] [PubMed] [Google Scholar]
- Dale A, Fischl B, Sereno M. Cortical surface-based analysis – I. Segmentation and surface reconstruction. Neuroimage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Dale A, Sereno M. Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction: a linear approach. J Cogn Neurosci. 1993a;5:162–176. doi: 10.1162/jocn.1993.5.2.162. [DOI] [PubMed] [Google Scholar]
- Dale AM, Sereno MI. Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction – a linear-approach. J Cogn Neurosci. 1993b;5:162–176. doi: 10.1162/jocn.1993.5.2.162. [DOI] [PubMed] [Google Scholar]
- Ebersole JS. Non-invasive pre-surgical evaluation with EEG/MEG source analysis. Electroencephalogr Clin Neurophysiol Suppl. 1999;50:167–174. [PubMed] [Google Scholar]
- Ebersole JS, Wade PB. Spike voltage topography and equivalent dipole localization in complex partial epilepsy. Brain Topogr. 1990;3:21–34. doi: 10.1007/BF01128858. [DOI] [PubMed] [Google Scholar]
- Ebersole JS, Wade PB. Spike voltage topography identifies two types of frontotemporal epileptic foci. Neurology. 1991;41:1425–1433. doi: 10.1212/wnl.41.9.1425. [DOI] [PubMed] [Google Scholar]
- Ferree TC, Eriksen KJ, Tucker DM. Regional head tissue conductivity estimation for improved EEG analysis. IEEE Trans Biomed Eng. 2000;47:1584–1592. doi: 10.1109/10.887939. [DOI] [PubMed] [Google Scholar]
- Foster KR, Schwan HP. Dielectric properties of tissues and biological materials: a critical review. Crit Rev Biomed Eng. 1989;17:25–104. [PubMed] [Google Scholar]
- Friedman D, Claassen J, Hirsch LJ. Continuous electroencephalogram monitoring in the intensive care unit. Anesth Analg. 2009;109:506–523. doi: 10.1213/ane.0b013e3181a9d8b5. [DOI] [PubMed] [Google Scholar]
- Gabriel C, Gabriel S, Corthout E. The dielectric properties of biological tissues: I. Literature survey. Phys Med Biol. 1996a;41:2231–2249. doi: 10.1088/0031-9155/41/11/001. [DOI] [PubMed] [Google Scholar]
- Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz–20 GHz. Phys Med Biol. 1996b;41:2251–2269. doi: 10.1088/0031-9155/41/11/002. [DOI] [PubMed] [Google Scholar]
- Garga N, Lowenstein DH. Posttraumatic epilepsy: a major problem in desperate need of major advances. Epilepsy Curr. 2006;6:1–5. doi: 10.1111/j.1535-7511.2005.00083.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gencer N, Acar C. Sensitivity of EEG and MEG measurements to tissue conductivity. Phys Med Biol. 2004;49:701–717. doi: 10.1088/0031-9155/49/5/004. [DOI] [PubMed] [Google Scholar]
- Hallez H, Vanrumste B, Grech R, Muscat J, De Clercq W, Vergult A, et al. Review on solving the forward problem in EEG source analysis. J Neuroeng Rehabil. 2007;4:46. doi: 10.1186/1743-0003-4-46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haufe S, Tomioka R, Nolte G, Muller KR, Kawanabe M. Modeling sparse connectivity between underlying brain sources for EEG/MEG. IEEE Trans Biomed Eng. 2010;57:1954–1963. doi: 10.1109/TBME.2010.2046325. [DOI] [PubMed] [Google Scholar]
- Haynes WM. CRC Handbook of Chemistry and Physics. CRC Press; 2011. [Google Scholar]
- He B, Musha T, Okamoto Y, Homma S, Nakajima Y, Sato T. Electric dipole tracing in the brain by means of the boundary element method and its accuracy. IEEE Trans Med Imaging. 1987;34:406–413. doi: 10.1109/tbme.1987.326056. [DOI] [PubMed] [Google Scholar]
- Holmes MJ, Yang X, Landman BA, Ding Z, Kang H, Abou-Khalil B, et al. Functional networks in temporal-lobe epilepsy: a voxel-wise study of resting-state functional connectivity and gray-matter concentration. Brain Connect. 2013;3:22–30. doi: 10.1089/brain.2012.0103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irimia A, Chambers MC, Alger JR, Filippou M, Prastawa MW, Wang B, et al. Comparison of acute and chronic traumatic brain injury using semi-automatic multimodal segmentation of MR volumes. J Neurotrauma. 2011;28:2287–2306. doi: 10.1089/neu.2011.1920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irimia A, Chambers MC, Torgerson CM, Filippou M, Hovda DA, Alger JR, et al. Patient-tailored connectomics visualization for the assessment of white matter atrophy in traumatic brain injury. Front Neurol. 2012a;3:10. doi: 10.3389/fneur.2012.00010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irimia A, Swinney KR, Wikswo JP. Partial independence of bioelectric and biomagnetic fields and its implications for encephalography and cardiography. Phys Rev E Stat Nonlin Soft Matter Phys. 2009;79:051908. doi: 10.1103/PhysRevE.79.051908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irimia A, Van Horn JD, Halgren E. Source cancellation profiles of electroencephalography and magnetoencephalography. Neuroimage. 2012b;59:2464–2474. doi: 10.1016/j.neuroimage.2011.08.104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacquir S, Fruitet J, Guiraud D, Clerc M. Computation of the electrical potential inside the nerve induced by an electrical stimulus. Conf Proc IEEE Eng Med Biol Soc. 2007;2007:1711–1774. doi: 10.1109/IEMBS.2007.4352639. [DOI] [PubMed] [Google Scholar]
- Lantz G, Grave de Peralta R, Spinelli L, Seeck M, Michel CM. Epileptic source localization with high density EEG: how many electrodes are needed? Clin Neurophysiol. 2003;114:63–69. doi: 10.1016/s1388-2457(02)00337-1. [DOI] [PubMed] [Google Scholar]
- Lau TM, Gwin JT, Ferris DP. How many electrodes are really needed for EEG-based mobile brain imaging? J Behav Brain Sci. 2012;2:387–393. [Google Scholar]
- Lee HO, Koh EJ, Oh YM, Park SS, Kwon KH, Choi HY. Effect of vagus nerve stimulation in post-traumatic epilepsy and failed epilepsy surgery: preliminary report. J Korean Neurosurg Soc. 2008;44:196–198. doi: 10.3340/jkns.2008.44.4.196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee WH, Liu Z, Mueller BA, Lim K, He B. Influence of white matter anisotropic conductivity on EEG source localization: comparison to fMRI in human primary visual cortex. Clin Neurophysiol. 2009;120:2071–2081. doi: 10.1016/j.clinph.2009.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lima EA, Irimia A, Wikswo JP. The magnetic inverse problem. In: Clarke J, Braginski AI, editors. The SQUID handbook: Applications of SQUIDs and SQUID systems. Weinheim, Germany: Wiley-VCH; 2006. [Google Scholar]
- Lindenblatt G, Silny J. A model of the electrical volume conductor in the region of the eye in the ELF range. Phys Med Biol. 2001;46:3051–3059. doi: 10.1088/0031-9155/46/11/319. [DOI] [PubMed] [Google Scholar]
- Liu AK, Dale AM, Belliveau JW. Monte Carlo simulation studies of EEG and MEG localization accuracy. Hum Brain Mapp. 2002;16:47–62. doi: 10.1002/hbm.10024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mani J, Barry E. Posttraumatic epilepsy. Hagerstown, MD, Lippincott: Williams & Wilkins; 2006. [Google Scholar]
- Marin G, Guerin C, Baillet S, Garnero L, Meunier G. Influence of skull anisotropy for the forward and inverse problem in EEG: simulation studies using FEM on realistic head models. Hum Brain Mapp. 1998;6:250–269. doi: 10.1002/(SICI)1097-0193(1998)6:4<250::AID-HBM5>3.0.CO;2-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Odabaee M, Freeman WJ, Colditz PB, Ramon C, Vanhatalo S. Spatial patterning of the neonatal EEG suggests a need for a high number of electrodes. Neuroimage. 2013;68:229–235. doi: 10.1016/j.neuroimage.2012.11.062. [DOI] [PubMed] [Google Scholar]
- Pohlmeier R, Buchner H, Knoll G, Rienacker A, Beckmann R, Pesch J. The influence of skull-conductivity misspecification on inverse source localization in realistically shaped finite element head models. Brain Topogr. 1997;9:157–162. doi: 10.1007/BF01190384. [DOI] [PubMed] [Google Scholar]
- Ramon C, Schimpf PH, Haueisen J. Influence of head models on EEG simulations and inverse source localizations. Biomed Eng Online. 2006;5:10. doi: 10.1186/1475-925X-5-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reyes-Gasca J, Garcia R, Alvarez-Fregoso O, Chavez-Carvayar JA, Vargas-Ulloa LE. Conductivity in human tooth enamel. J Mater Sci. 1999;34:2183–2188. [Google Scholar]
- Rijkhoff NJ, Holsheimer J, Koldewijn EL, Struijk JJ, van Kerrebroeck PE, Debruyne FM, et al. Selective stimulation of sacral nerve roots for bladder control: a study by computer modeling. IEEE Trans Biomed Eng. 1994;41:413–424. doi: 10.1109/10.293215. [DOI] [PubMed] [Google Scholar]
- Salazar AM, Jabbari B, Vance SC, Grafman J, Amin D, Dillon JD. Epilepsy after penetrating head injury. I. Clinical correlates: a report of the Vietnam Head Injury Study. Neurology. 1985;35:1406–1414. doi: 10.1212/wnl.35.10.1406. [DOI] [PubMed] [Google Scholar]
- Sazonov AV, Ho CK, Bergmans JW, Arends JB, Griep PA, Verbitskiy EA, et al. An investigation of the phase locking index for measuring of interdependency of cortical source signals recorded in the EEG. Biol Cybern. 2009;100:129–146. doi: 10.1007/s00422-008-0283-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trakic A, Akhand M, Wang H, Mason D, Liu F, Wilson S, et al. Computational modelling of blood-flow-induced changes in blood electrical conductivity and its contribution to the impedance cardiogram. Physiol Meas. 2010;31:13–33. doi: 10.1088/0967-3334/31/1/002. [DOI] [PubMed] [Google Scholar]
- Vespa PM, McArthur DL, Xu Y, Eliseo M, Etchepare M, Dinov I, et al. Nonconvulsive seizures after traumatic brain injury are associated with hippocampal atrophy. Neurology. 2010;75:792–798. doi: 10.1212/WNL.0b013e3181f07334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Ellenrieder N, Muravchik CH, Nehorai A. Effects of geometric head model perturbations on the EEG forward and inverse problems. IEEE Trans Biomed Eng. 2006;53:421–429. doi: 10.1109/TBME.2005.869769. [DOI] [PubMed] [Google Scholar]
- Yan Y, Nunez PL, Hart RT. Finite-element model of the human head: scalp potentials due to dipole sources. Med Biol Eng Comput. 1991;29:475–481. doi: 10.1007/BF02442317. [DOI] [PubMed] [Google Scholar]
- Yang L, Liu Z, He B. EEG-fMRI reciprocal functional neuroimaging. Clin Neurophysiol. 2010;121:1240–1250. doi: 10.1016/j.clinph.2010.02.153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yitembe BR, Crevecoeur G, Van Keer R, Dupre L. Reduced conductivity dependence method for increase of dipole localization accuracy in the EEG inverse problem. IEEE Trans Biomed Eng. 2011;58:1430–1440. doi: 10.1109/TBME.2011.2107740. [DOI] [PubMed] [Google Scholar]
- Yitembe BR, Crevecoeur G, Van Keer R, Dupre L. Reduction of the impact of multiple uncertain conductivity values on EEG dipole source analysis. Int J Numer Methods Biomed Eng. 2012;29:363–379. doi: 10.1002/cnm.2510. [DOI] [PubMed] [Google Scholar]
- Zhang Y, van Drongelen W, He B. Estimation of in vivo brain-to-skull conductivity ratio in humans. Appl Phys Lett. 2006;89:223903–2239033. doi: 10.1063/1.2398883. [DOI] [PMC free article] [PubMed] [Google Scholar]