Abstract
Electron-phonon coupling (EPC) plays an important role in solid state physics. Here, we demonstrate an experimental method that enables investigation of the elemental processes of the indirect transition, in which EPC participates in photoexcitation in solids, by resolving the energy and momentum of phonons and electrons simultaneously. For graphite, we used angle-resolved photoelectron spectroscopy to observe electron emission at the Γ-point being scattered from the K-point by a phonon. Energy conservation during phonon emission implies that the step-like structure in the spectrum is near the Fermi level, and angle-resolved measurements revealed phonon dispersions that contribute to EPC because of parallel momentum conservation. The observed phonon branch depends on the photon energy, i.e., the final photoexcitation state; this dependency is partly explained by the selection rule, which is determined by the electron state symmetry for the initial, intermediate, and final states and the phonon.
An electron in a solid interacts with the motion of the lattice and can be scattered into a different state. This “electron-phonon coupling” (EPC) phenomenon is an important issue in solid state physics that has been studied extensively for many years because it governs many of the critical properties of solids, such as electronic and thermal conductance, and plays a major role in many important phenomena, such as superconductivity1. The main spectroscopic methods that have been used to investigate EPC in solids to date have been optical spectroscopy2, including Raman spectroscopy3, and angle-resolved photoelectron spectroscopy (ARPES)4. Through optical spectroscopy, the phonon energy can be accurately determined; however, the momentum of the phonon and the energy and momentum of the electron cannot in principle be resolved. By using an ARPES spectrum, the energy and parallel momentum of the electron can be well resolved; however, the elemental process of EPC has not been determined in previous work. In ARPES, the EPC is analysed via the self-energy 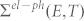 in the quasiparticle spectral function, the real and imaginary parts of which determine the kink structure and width, respectively, of the electronic bands near the Fermi level in the ARPES spectrum4. The self-energy is determined as
in the quasiparticle spectral function, the real and imaginary parts of which determine the kink structure and width, respectively, of the electronic bands near the Fermi level in the ARPES spectrum4. The self-energy is determined as
where 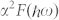 denotes the Eliashberg function, which is averaged over the phonon momentum q, and
denotes the Eliashberg function, which is averaged over the phonon momentum q, and 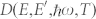 is a distribution function derived from the Fermi-Dirac and Bose-Einstein functions of electrons and phonons, respectively4. Thus, in previous studies, electron-phonon scattering could only be investigated in an integrated manner over the branches and momentum values of the phonons. In this study, however, we investigated the elemental process of EPC with ARPES to resolve both the energy and the momentum of both the phonon and electron during the indirect transition that accompanies EPC. The experimental method used is simple. The energy and momentum of the system, which consists of electrons and phonons, are conserved during scattering. Thus, if the same quantities are known before the scattering process, then the measurements of the scattered electrons allow us to determine the energy and momentum of the phonons that scattered the electrons. Here, for the first time, we observe the electrons after the scattering process caused by EPC in graphite and probe the phonon dispersion using the ARPES technique. Furthermore, by varying the photon energy, the final state of the photoexcitation that accompanies EPC is experimentally defined. The photon energy, i.e., the final state, determines the phonon branch that is involved in the EPC process. By applying the selection rule, the symmetries of all the electronic and phonon states that participate in the indirect transition, i.e., the photoexcitation that accompanies EPC, can be discussed.
is a distribution function derived from the Fermi-Dirac and Bose-Einstein functions of electrons and phonons, respectively4. Thus, in previous studies, electron-phonon scattering could only be investigated in an integrated manner over the branches and momentum values of the phonons. In this study, however, we investigated the elemental process of EPC with ARPES to resolve both the energy and the momentum of both the phonon and electron during the indirect transition that accompanies EPC. The experimental method used is simple. The energy and momentum of the system, which consists of electrons and phonons, are conserved during scattering. Thus, if the same quantities are known before the scattering process, then the measurements of the scattered electrons allow us to determine the energy and momentum of the phonons that scattered the electrons. Here, for the first time, we observe the electrons after the scattering process caused by EPC in graphite and probe the phonon dispersion using the ARPES technique. Furthermore, by varying the photon energy, the final state of the photoexcitation that accompanies EPC is experimentally defined. The photon energy, i.e., the final state, determines the phonon branch that is involved in the EPC process. By applying the selection rule, the symmetries of all the electronic and phonon states that participate in the indirect transition, i.e., the photoexcitation that accompanies EPC, can be discussed.
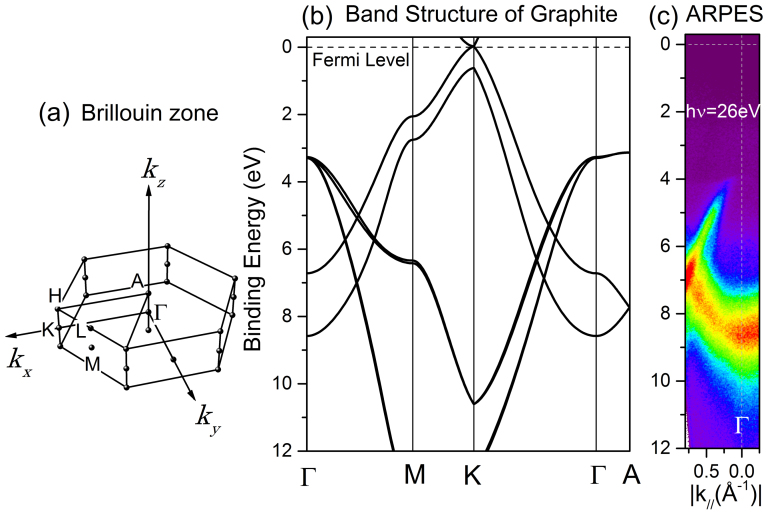
For the study of EPC, we selected graphite (highly oriented pyrolytic graphite; HOPG) as the target material. The advantages of graphite are as follows. 1) The EPC in graphite is very important for understanding the properties of carbon-based materials, such as graphene, fullerenes, and carbon nanotubes (CNT), that have been the focus of research for many years3,5. 2) The electronic properties of graphite are highly suitable for the detection of scattered electrons. Figures 1(a) and (b) present the Brillouin zone and part of the band structure of graphite, respectively, calculated from the density functional theory-local density approximation (DFT-LDA) using Hamada's all-electron band-structure calculation package (ABCAP)6. Because graphite consists of graphene layers and the interlayer interaction is weaker than the intralayer interaction, the band dispersion along the plane parallel to the layer (the kx-ky plane) is greater than that along the axis normal to the layer (the kz-axis). The band crosses the Fermi level along the K-H line, which is along the kz axis and located at the zone boundary. The highest occupied band at the Γ-point (or A-point) lies ~4 eV below the Fermi level. The calculated band structure is confirmed by the results of our ARPES measurements, as demonstrated in Fig. 1(c). Note that the azimuthal orientation is random and that the observed dispersion curves around the Γ-point are averaged in the HOPG7. There is considerable correspondence between the DFT calculations and the ARPES results, although the absolute binding energy has an error of approximately 20%7. The electronic properties of graphite provide two advantages when we investigate scattering from the electron that occupies the band just below the Fermi level: a) we can observe the electrons that are scattered into the Γ-A line without disturbing the photoelectron emission from the occupied band, and b) the parallel momentum k// of the electron before the transition is precisely determined because it is located at the K(A) point in the two-dimensional Brillouin zone along the kx-ky plane. 3) Finally, Liu et al. recently used photoelectron spectroscopy to observe electron scattering from the K-point to the Γ-point caused by a 67-meV phonon in graphite8. Although the authors were unable to resolve the momentum of the electron, their ground-breaking research provided a foundation for the direct observation of EPC. From an experimental viewpoint, the use of photons with lower energies significantly distinguishes this study from that of Liu et al. When photon energies less than ~20 eV are used, the final photoexcitation state is not far from the vacuum level and therefore cannot be treated as a free-electron-like band, which is assumed in ordinal photoelectron spectroscopy. Instead, the state should be treated as an unoccupied band of the graphite. Thus, by tuning the photon energy to act as the excitation energy from the occupied band to the unoccupied band, we can explicitly define the final excitation state for both the photons and phonons, and specific states may be observed with higher efficiency than in the higher-photon-energy case, which we recently demonstrated9.
Figure 1. Electronic structure of graphite.
(a) Brillouin zone of graphite. (b) Band dispersion of graphite calculated using ABCAP. (c) ARPES spectra of the HOPG sample at 35 K.
Results
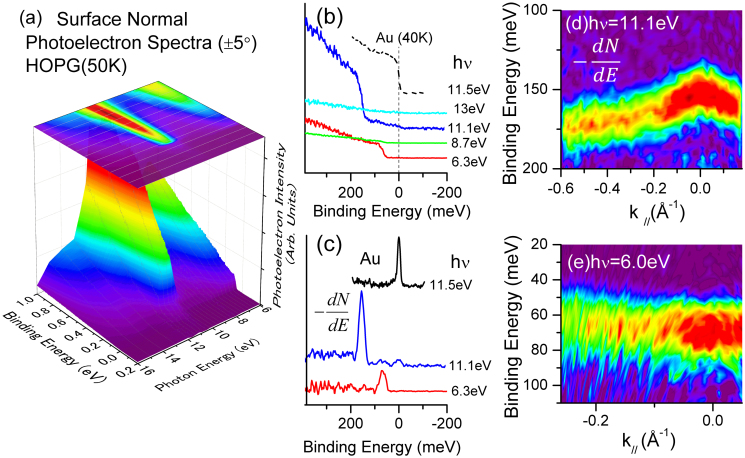
Figure 2(a) presents a series of surface-normal (±5°) photoelectron spectra for HOPG at 50 K in the region near the Fermi level with photon energies (hν) varying from 6 to 16 eV. Note that the temperature is greater than the critical temperature at the point where the strong peak is observed in this energy region of the surface-normal photoelectron spectra because of a superstructure formation at the graphite surface9. The spectral shapes and intensities can change dramatically, depending on the photon energy. The feature that we focus on here is the step-like edges that provide the step-like structure located at either 154 meV or 67 meV with respect to the Fermi level. Typical spectra at hν = 13, 11.1, 8.7, and 6.3 eV are shown in detail in Fig. 2(b) along with the spectrum from a gold film at 40 K taken at hν = 11.5 eV, where the Fermi edge observed at the binding energy (EB) is zero. In Fig. 2(c), the differentials of the photoelectron intensity with the binding energy are displayed to convert the edge to a peak for convenience. The peaks are clearly visible at EB = 154 meV (for hν = 11.1 eV) and 67 meV (for hν = 6.3 eV). Step-like edges are also observed in the spectra taken at off-angles from the surface normal. Figures 2(d) and (e) present the results of angle-resolved measurements, where the colours (from violet to red) represent the intensity of the differential of the photoelectron intensity with the binding energy and the horizontal axis represents the electron momentum k//, which is parallel to the surface. Figure 2 (d) presents the results taken at hν = 11.1 eV, and Fig. 2(e) presents the results for hν = 6.0 eV. These figures, particularly in the case for which hν = 11.1 eV, clearly demonstrate that the energy of the step edge varies as a function of the electron momentum.
Figure 2. Photoelectron spectra of graphite.
(a) Surface-normal photoelectron spectra of HOPG at 50 K taken at 6 eV ≤ hν ≤ 16 eV. (b) Typical spectra of HOPG taken at several photon energies along with that of the Au film at 40 K. (c) Differentials of the photoelectron intensity with respect to the binding energy. (d,e) Differentials of the photoelectrons as a function of the parallel momentum of the electron.
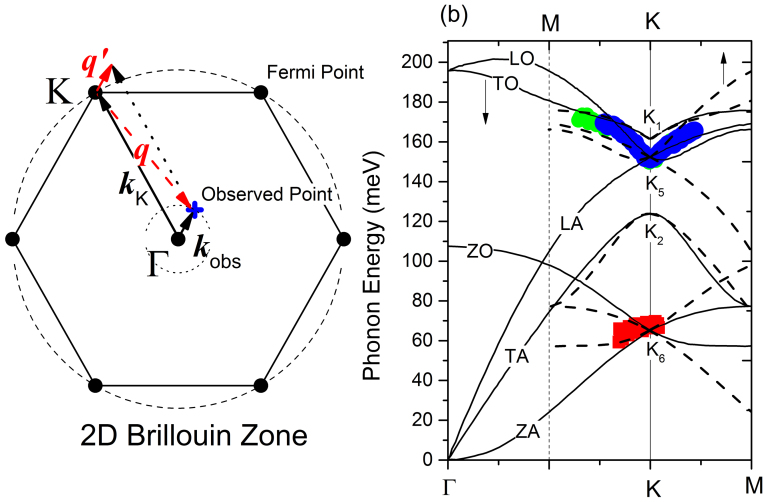
The π-band of the graphite crosses the Fermi level at the K(H) point, and no electronic states are located near the Fermi level at the Γ(A) point. Therefore, the observed surface-normal photoelectron emission (Fig. 2) cannot be ascribed to the ordinal photoexcitation process but is instead ascribed to the scattering of the electrons from the K(H) point to the Γ(A) point or to the defect states. However, emission from the defect states or scattering by impurities cannot explain the step-like feature. Furthermore, according to energy conservation, the electron loses as much energy as the phonon energy when the phonon is emitted. We therefore conclude that the observed electron emission is due to EPC and that the energy of the step matches the energy of the phonon that is involved, similar to the findings of Liu et al8. The phonon absorption process can be neglected at low temperatures8. Furthermore, according to momentum conservation, the momentum of the observed electron in the ARPES (kobs) equals the momentum of the phonon that is measured with respect to the K(H) point in the Brillouin zone, as illustrated schematically in Fig. 3(a). We cannot determine the exact direction of the phonon vector because there are six equivalent K(H) points in the Brillouin zone of the graphite from which the electron may be scattered into the Γ(A) point. Regardless, for HOPG, the phonon dispersion is averaged around the K(H) point because HOPG is azimuthally randomised layer by layer. Figure 3(b) shows the observed energies of the step-like structure as a function of electron momentum for hν = 11.1 eV and hν = 6.0 eV. These energies must be compared with the phonon dispersion curves around the K(H) point. Figure 3(c) presents the DFT calculation results for the dispersion curves of the graphite along the K-Γ and K-M lines according to the process of ref. 10. The results of the experiments and calculations agree and clearly confirm the interpretation that the step-like structure is caused by the phonon emission in the EPC process, although detailed comparisons for the dispersion are difficult because of the ambiguity in the phonon vector direction. At the K(H) point, the 154- and 67-meV gaps are ascribed to the longitudinal optical LO- and/or the longitudinal acoustic LA-phonon (K5) and the out-of-plane acoustic ZA- and/or out-of-plane optical ZO-phonon (K6) of graphite, respectively5,10,11.
Figure 3. Description of phonon-dispersion measurement using ARPES.
(a) Schematic of electron-phonon scattering in the two-dimensional Brillouin zone. The electron at the K-point (kK) is scattered by the phonon (q) and then observed at kobs. Here, kobs = q′ = q + kK. (b) The pseudo-gap energy as a function of the parallel momentum of the electron (the green and blue dots represent the results of independent measurements at hν = 11.1 eV, and the red dots represent the results at hν = 6.0 eV). The solid and dotted lines represent the results of the phonon dispersion on the K-Γ and K-M lines, respectively. Irreducible representations of the phonon symmetry at the K-point are shown in the figure.
For the first time, phonon dispersion has been measured using the ARPES technique, although energy loss due to phonon emission in the photoelectron spectroscopy process has been observed by other researchers. In addition to Liu et al., who studied graphite8, Arafune et al.12 observed coupling with the vibration of an adsorbed molecule on a metal surface, and Ishizaka et al.13 observed coupling with the localised optical phonon in diamond. However, neither of these researchers was able to observe the angular or photon-energy dependence of the photoelectron, as this study has demonstrated.
Discussion
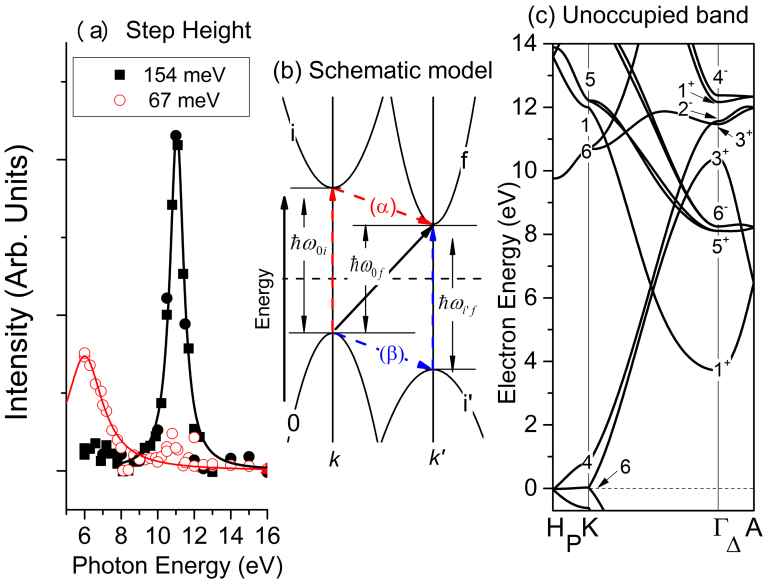
We now seek a reasonable explanation for why different photon energies lead to different phonon emissions. Figure 4(a) plots the intensities of the steps at 154 and 67 meV in the surface-normal photoelectron spectra as a function of the photon energy. These intensities represent the electron-scattering intensities from K(H) to Γ(A) by the phonons at the K(H) point in the Brillouin zone. The black (red) solid line is the Lorentzian curve, where the centre and width energies are 11.05 and 0.92 eV (6.0 and 1.2 eV), respectively. Note that the true photon energy that corresponds with the maximum step height for the 67 meV edge may be less than 6.0 eV, which is the lower limit of the experiments. This hν-dependence indicates that the final photoexcitation state is definitely defined by the photon energy and that this state determines the phonon branch that can scatter the electron. Note that this photon-energy dependence clearly demonstrates that we are observing EPC among the electrons in bands of the solid. The photoexcitation process that accompanies electron-phonon scattering is widely known as the “indirect transition” that is often observed in semiconductor materials14,15. According to standard textbooks14,15, the transition probabilities of the indirect transition can be formulated as follows. When the electron at momentum k of band 0 (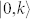 ) is indirectly (i.e., with the help of a phonon with energy
) is indirectly (i.e., with the help of a phonon with energy 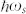 ) excited into momentum k′ of the band f (
) excited into momentum k′ of the band f (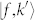 ) by a photon with energy
) by a photon with energy 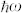 , the transition probability
, the transition probability 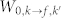 can be written as
can be written as
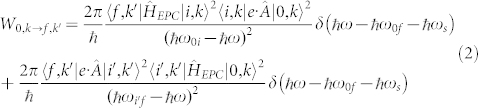 |
for the phonon emission, where 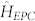 and
and 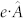 denote the Hamiltonian operator for the EPC and the optical excitation, respectively, and
denote the Hamiltonian operator for the EPC and the optical excitation, respectively, and 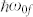 ,
, 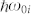 , and
, and 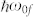 denote the energy differences between
denote the energy differences between 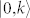 and
and 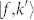 ,
, 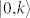 and
and 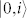 , and
, and 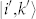 and
and 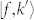 , respectively, as indicated in Fig. 4(b). The first term on the right side of equation (2) denotes the passage through a virtual intermediate state
, respectively, as indicated in Fig. 4(b). The first term on the right side of equation (2) denotes the passage through a virtual intermediate state 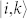 [(α) in Fig. 4(b)], where EPC occurs between the unoccupied states, whereas the second term denotes passage through the intermediate state
[(α) in Fig. 4(b)], where EPC occurs between the unoccupied states, whereas the second term denotes passage through the intermediate state 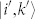 [(β) in Fig. 4(b)], where EPC occurs between the occupied states. Equation (2) indicates the following: 1) when the matrix elements for the optical excitation, such as
[(β) in Fig. 4(b)], where EPC occurs between the occupied states. Equation (2) indicates the following: 1) when the matrix elements for the optical excitation, such as 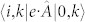 , or those for the electron-phonon scattering, such as
, or those for the electron-phonon scattering, such as 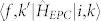 , vanish, no observable photoexcitation is expected; thus, the dipole selection rules for these matrix elements are valid. 2) When the photon energy equals the energy difference between the intermediate state and the initial or final state, the probability is resonantly enhanced by the denominator term. 3) The delta function determines the energy of the final photoexcitation state.
, vanish, no observable photoexcitation is expected; thus, the dipole selection rules for these matrix elements are valid. 2) When the photon energy equals the energy difference between the intermediate state and the initial or final state, the probability is resonantly enhanced by the denominator term. 3) The delta function determines the energy of the final photoexcitation state.
Figure 4. Description of the ‘direct' observation of the indirect transition.
(a) The step-height intensity of the two gaps as a function of the phonon energy (solid square: 154 meV; red open circles: 67 meV), together with the Lorentzian peaks (black solid line: 11.05 eV of the peak and 0.92 eV of the width; solid red line: 6.0 eV of the peak and 1.2 eV of the width). (b) Schematic model of the indirect transition. See equation (2) for details. (c) Band dispersion for the unoccupied state of graphite from the DFT-LDA calculations. Irreducible representations of the band symmetry at the K- and Γ-points are shown in the figure.
The dipole selection rule for the optical transition in graphite was derived based on group theory16,17,18. Hereafter, we first discuss the indirect transition from the K-point to the Γ-point at kz = 0 because it has the highest symmetry and provides the most basic standpoint for the EPC selection rule. The following notation for the irreducible character in graphite follows that of Herring17. Table 1 lists the possible final state of photoexcitation from the K6 band, which is the initial state for the two cases of the electric field vector of the photon, together with a possible intermediate state, from which photoexcitation occurs into the Γ1 band18. We will also justify why only the Γ1 band is considered. For EPC, the selection rule is derived using the products between the irreducible characters at different points in the Brillouin zone according to the method of Lax et al19. The possible final states after electron-phonon scattering from the K-point are listed in Table 2.
Table 1. Selection rules for optical transition in graphite. Possible initial/final states of the optical transitions from/to the K6/Γ1+ bands for polarizations that are perpendicular (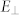 ) and parallel (
) and parallel (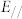 ) to the (0001) surface.
) to the (0001) surface.
| Initial/final states | K6 | Γ1+ | |
|---|---|---|---|
| Allowed States | 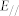 |
K2,K4,K6 | Γ6− |
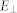 |
K5 | Γ2− | |
Table 2. Selection rules for phonon scattering in graphite. Possible final states at the Γ point for phonon scattering from the K point.
| Initial State | K1 | K2 | K3 | K4 | K5 | K6 | |
|---|---|---|---|---|---|---|---|
| Allowed States | K1(TO) | Γ1+, Γ3− | Γ3+, Γ1− | Γ2+, Γ4− | Γ4+, Γ2− | Γ6+, Γ5− | Γ5+, Γ6− |
| K2(TA) | Γ3+, Γ1− | Γ1+, Γ3− | Γ4+, Γ2− | Γ2+, Γ4− | Γ5+, Γ6− | Γ6+, Γ5− | |
| K5(LA,LO) | Γ6+, Γ5− | Γ5+, Γ6− | Γ6+, Γ5− | Γ5+, Γ6− | Γ1+, Γ3−, Γ2+ | Γ3+, Γ1−, Γ4+ | |
| Γ4−, Γ5+, Γ6− | Γ2−, Γ6+, Γ5− | ||||||
| K6(ZA,ZO) | Γ5+, Γ6− | Γ6+, Γ5− | Γ5+, Γ6− | Γ6+, Γ5− | Γ3+, Γ1−, Γ4+ | Γ1+, Γ3−, Γ2+ | |
| Γ2−, Γ6+, Γ5− | Γ4−, Γ5+, Γ6− | ||||||
The photon-energy dependence is due to the final photoexcitation state. Figure 4(c) shows the unoccupied band of the graphite from the LDA-DFT calculation, similar to that presented in Fig. 1(b). Note that the absolute electron energy in the LDA calculation may be inaccurate7; therefore, direct interpretation by comparison of the electron energies is difficult. The final states at the Γ-point in the energy region that must be considered are Γ1+ (3.7 eV), Γ5+ (8.0 eV), Γ6− (8.2 eV), Γ3+ (10.4 eV), Γ3+ (11.4 eV), Γ2− (11.5 eV), Γ1+ (12.1 eV), and Γ4− (12.3 eV). The intermediate states that may be able to satisfy the resonant conditions of 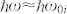 or
or 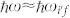 are K6 (10.7 eV), K1 (12.0 eV), and K5 (12.2 eV). Among these states, there are two transition passes for which the selection rules are satisfied for both the optical transitions and EPC, and the resonant condition is nearly satisfied; these passes are 1) K6 (EF) → K6 (10.7 eV) → Γ3+ (10.4 eV), which occurs with s-polarized (
are K6 (10.7 eV), K1 (12.0 eV), and K5 (12.2 eV). Among these states, there are two transition passes for which the selection rules are satisfied for both the optical transitions and EPC, and the resonant condition is nearly satisfied; these passes are 1) K6 (EF) → K6 (10.7 eV) → Γ3+ (10.4 eV), which occurs with s-polarized (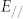 ) light and EPC by the K5 phonon, and 2) K6 (EF) → K5 (12.2 eV) → Γ4− (12.3 eV) or Γ1+ (12.1 eV), which occurs with p-polarized (
) light and EPC by the K5 phonon, and 2) K6 (EF) → K5 (12.2 eV) → Γ4− (12.3 eV) or Γ1+ (12.1 eV), which occurs with p-polarized (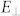 ) light and EPC by the K5 phonon. In both cases, only EPC by the K5 phonon can be observed. Because the momentum along the surface normal is ambiguous, excitation from the state on the line along the K-P-H direction into the state on the line along the Γ-Δ-A direction must be considered. In this case, both K5 and K6 are converted to P3. Thus, the transition with EPC by the ZA and ZO phonons is also allowed. The small peak for the 67-meV edge at ~11 eV may be caused by this contribution. At this stage, it is difficult to determine which of the contributions are responsible for the peak at hν = 11.05 eV because of the error in the absolute energy in the DFT-LDA calculations. Experiments using the polarisation of the photon may help clarify the interpretation. The peak at hν = 11.05 eV for the K5 phonon is therefore understood in terms of the selection rules and the resonant condition. However, the reason why a single rather than double peak was observed remains unclear.
) light and EPC by the K5 phonon. In both cases, only EPC by the K5 phonon can be observed. Because the momentum along the surface normal is ambiguous, excitation from the state on the line along the K-P-H direction into the state on the line along the Γ-Δ-A direction must be considered. In this case, both K5 and K6 are converted to P3. Thus, the transition with EPC by the ZA and ZO phonons is also allowed. The small peak for the 67-meV edge at ~11 eV may be caused by this contribution. At this stage, it is difficult to determine which of the contributions are responsible for the peak at hν = 11.05 eV because of the error in the absolute energy in the DFT-LDA calculations. Experiments using the polarisation of the photon may help clarify the interpretation. The peak at hν = 11.05 eV for the K5 phonon is therefore understood in terms of the selection rules and the resonant condition. However, the reason why a single rather than double peak was observed remains unclear.
For the K6 phonon (67 meV), however, the simple interpretation that is valid for the K5 phonon is not possible. The final state of this photoexcitation is located above the Fermi level by 6 eV or less (Fig. 4(a)); thus, it should be Γ1+ (3.7 eV) or, more likely, the state on the Γ-Δ-A line connected to Γ1+. In this case, we must use the intermediate state that does not satisfy the resonant condition. The unoccupied states at the K-point with energies that are near Γ1+ are K4 (0.8 eV) and K6 (10.7 eV), and the occupied states at the Γ-point with energies that are near Γ1+ are Γ5+ and Γ6−, which are located 3.3 eV below the Fermi level (not shown in Fig. 4(c)). Among them, the allowed transitions are K6 (EF) → K6 (10.7 eV) → Γ1+ (3.7 eV), which occurs with s-polarised (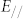 ) light and EPC by the K6-phonon, and K6 (EF) → Γ6− (−3.3 eV) → Γ1+ (3.7 eV), which occurs with s-polarized (
) light and EPC by the K6-phonon, and K6 (EF) → Γ6− (−3.3 eV) → Γ1+ (3.7 eV), which occurs with s-polarized (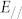 ) light and EPC by any of the K1, K2, K5, or K6 phonons. The excitation pass via the intermediate state of K6 (10.7 eV) potentially explains why only the step-like feature of the K6 phonon is observed at hν ~ 6 eV. However, this pass of the indirect transition does not satisfy the resonant condition, and the probability is expected to be significantly less than the case for which hν ~ 11 eV if the matrix elements for both photon energies are similar. Thus, the intensities of the matrix elements may be considerably different in two different passes of the indirect transition. Another possibility is that the defect or step-edge state, which may be located at ~0 eV at the Γ-(A-) point or at ~6 eV at the K-(H-) point, could most likely be the intermediate state.
) light and EPC by any of the K1, K2, K5, or K6 phonons. The excitation pass via the intermediate state of K6 (10.7 eV) potentially explains why only the step-like feature of the K6 phonon is observed at hν ~ 6 eV. However, this pass of the indirect transition does not satisfy the resonant condition, and the probability is expected to be significantly less than the case for which hν ~ 11 eV if the matrix elements for both photon energies are similar. Thus, the intensities of the matrix elements may be considerably different in two different passes of the indirect transition. Another possibility is that the defect or step-edge state, which may be located at ~0 eV at the Γ-(A-) point or at ~6 eV at the K-(H-) point, could most likely be the intermediate state.
Liu et al. observed the step-like structure at 67 meV in a surface-normal photoelectron spectrum of graphite taken at hν = 23 eV8. We confirmed this step-like structure in the spectrum at hν = 23 eV and observed that the intensity of the step height is approximately 1/50 of that at hν = 6.0 eV (not shown). Because Γ1+ is the irreducible character of the nearly free electron state that is expected to be the final state after photoexcitation by a 23 eV phonon, a similar mechanism of photoexcitation accompanying the EPC may work in both cases. Further work is required to clarify the mechanism in detail.
In this study, we observe photoelectron emission that is indirectly excited via EPC. We maintain that it is possible to map the dispersions of the phonons that are involved in EPC thanks to the conservation rules of energy and momentum. This study is the first to observe phonon dispersion based on ARPES measurements. However, we do not insist that this experimental method is superior for measuring the phonon dispersion compared with other methods, such as the inelastic x-ray scattering11 and high-resolution electron-energy-loss spectroscopy (HREELS)20. In fact, energy loss of the electron due to scattering by the phonon has been detected using HREELS and is not new. The advantage of the present study is that the electron-phonon scattering occurs within the band of the solid, unlike in HREELS, for which the scattering occurs within the plane wave of free electrons. Thus, additional insights about electron-phonon scattering in the solid will be gained from further research using this method. A comparison with the results of theoretical calculations of the intensity of the electron-phonon interaction while resolving the energy and momentum of all the contributing electronic states and phonons will lead to deeper insight into EPC in solids. Note that the dispersion of the phonons was not discussed in detail in this paper because the dispersion direction cannot be defined for HOPG. A detailed study of phonon dispersion in a single crystal has the potential to provide important insights into the dependence of EPC on the momentum of the phonons. Furthermore, the validity of this method may not be limited simply to graphite or other carbon nanomaterials. The Fermi surface of metals spreads widely in the Brillouin zone; thus, the step-like structure detected in the photoelectron spectra at a particular electron momentum is constructed by convolution of the phonons to spread in the Brillouin zone. This fact indicates that this method will not work for metals. However, in some materials, such as Dirac-cone-related materials21, the momentum at the Fermi surface in the Brillouin zone is limited; thus, this method may reveal EPC by deconvolution of the ARPES results.
Methods
All the ARPES studies were performed at the BL7U SAMURAI beamline of the UVSOR-II synchrotron radiation facility at the Institute for Molecular Science22. A normal-incidence monochromator combined with a 3-m-long APPLE-II type undulator provided p-polarised highly monochromatized photons. The MgF2 filter was used when the photon energy was less than 10.9 eV to reduce the higher-order light. The photon intensity was calibrated with a silicon photodiode. The ARPES apparatus consists of a hemispherical photoelectron-energy analyser with a wide-angle electron lens (A-1 Analyser, MB Scientific, Sweden) located at 50° from the incident photons and a liquid helium-flow cryostat with a six-axis manipulation system (i-GONIO virtual-shaft-type, A-VC, R-DEC Co., Japan). The typical instrumental resolution was 10 meV at hν = 11.1 eV. The basic angular resolution was 0.18°; however, the resolution was changed to 10° and 0.9° when the hν-dependent surface-normal photoelectron spectra and the ARPES spectra, respectively, were measured to obtain better signal-to-noise ratios. To analyse the step-edge in the photoelectron spectrum caused by electron-phonon scattering, an error function multiplied by a linear function was used to fit the experimental results. The HOPG sample was freshly cleaved with adhesive tape in an ultra-high vacuum system at ~7 × 10−9 Pa, where the ARPES measurements were taken. The sample temperature was controlled by varying the flow rate of the liquid He in the cryostat.
Author Contributions
S.K. and M.M. constructed and maintained all the experimental devices. S.T. performed the experiments with assistance from M.M. and S.K. S.T. was responsible for the data analysis, theoretical calculations, and writing of the paper. All the authors discussed the results and commented on the manuscript.
Acknowledgments
This work was partly supported by Grants-in-Aid for Scientific Research from the Ministry of Education, Culture, Sports, Science, and Technology of Japan (Grant Nos. 23540366 and 25400326). The work was partially performed at the UVSOR facility under the Joint Studies Programme of the Institute for Molecular Science. The authors would like to thank N. Hamada at Tokyo University of Science, who constructed and distributed ABCAP and who kindly assisted S.T. with the calculations performed using the package. The authors would also like to thank J. Charlebois for carefully reading the manuscript.
References
- Ashcroft N. W. & Mermin N. D. Solid State Physics (Holt, Reinhart & Winston, Philadelphia, 1976). [Google Scholar]
- Toyozawa H. Optical Processes in Solids (Cambridge Univ. Press, Cambridge, 2003). [Google Scholar]
- Reich S. & Thomsen C. Raman spectroscopy of graphite. Phil. Trans. R. Soc. Lond. A 362, 2271–2288 (2004). [DOI] [PubMed] [Google Scholar]
- Hüfner S. Very High Resolution Photoelectron Spectroscopy (Springer, Berlin, 2007). [Google Scholar]
- Saito R., Hofmann M., Dresselhaus G., Jorio A. & Dresselhaus M. S. Raman spectroscopy of graphene and carbon nanotubes. Adv. Phys. 60, 413–550 (2011). [Google Scholar]
- Hamada N., Imai T. & Funashima H. Thermoelectric power calculation by the Boltzmann equation: NaxCoO2. J. Phys. Condens. Matter. 19, 365221 (2007). [DOI] [PubMed] [Google Scholar]
- Zhou S. Y. et al. Coexistence of sharp quasiparticle dispersions and disorder features in graphite. Phys. Rev. B 71, 161403 (2005). [Google Scholar]
- Liu Y. et al. Phonon-induced gaps in graphene and graphite observed by angle-resolved photoemission. Phys. Rev. Lett. 105, 136804 (2010). [DOI] [PubMed] [Google Scholar]
- Tanaka S., Matsunami M. & Kimura S. Observation of anomalous peaks in the photoelectron spectra of highly oriented pyrolytic graphite: Folding of the band due to the surface charge density wave transition. Phys. Rev. B 84, 121411(R) (2011). [Google Scholar]
- Lazzeri M., Attaccalite C., Wirtz L. & Mauri F. Impact of the electron-electron correlation on phonon dispersion: Failure of LDA and GGA DFT functionals in graphene and graphite. Phys. Rev. B 78, 081406 (R) (2008). [Google Scholar]
- Mohr M. et al. Phonon dispersion of graphite by inelastic x-ray scattering. Phys. Rev. B 76, 035439 (2007). [Google Scholar]
- Arafune R., Hayashi K., Ueda S., Uehara Y. & Ushioda S. Inelastic photoemission due to scattering by surface adsorbate vibrations. Phys. Rev. Lett. 95, 207601 (2005). [DOI] [PubMed] [Google Scholar]
- Ishisaka K. et al. Temperature-dependent localized excitations of doped carriers in superconducting diamond. Phys. Rev. Lett. 100, 166402 (2008). [DOI] [PubMed] [Google Scholar]
- Riddley B. K. Quantum Processes in Semiconductors Ch. 5 (Oxford Science Publ., New York, 1993). [Google Scholar]
- Yu Y. & Cardona M. Fundamentals of Semiconductors Ch. 6 & 7 (Springer-Verlag Berlin, 1996). [Google Scholar]
- Dresselhaus M. S., Dresselhaus G. & Jiro A. Group Theory (Springer-Verlag Berlin, 2008). [Google Scholar]
- Herring C. Character Tables for Two Space Groups. J. Franklin Inst. 233, 525 (1942). [Google Scholar]
- Benhow R. L. Dipole selection rules for hexagonal-closed-packed lattice. Phys. Rev. B 22, 3775 (1980). [Google Scholar]
- Lax M. & Hoppmld J. J. Selection Rules Connecting Different Points in the Brillouin Zone. Phys. Rev. 124, 115 (1961). [Google Scholar]
- Oshima C. et al. Surface Phonon Distribution Curves of Graphite (000l) over the Entire Energy Region. Solid State Commun. 65, 1601 (1988). [Google Scholar]
- Moore J. E. The birth of topological insulators. Nature 464, 194 (2010). [DOI] [PubMed] [Google Scholar]
- Kimura S. et al. SAMRAI: A novel variably polarized angle-resolved photoemission beamline in the VUV region at UVSOR-II. Rev. Sci. Instrum. 81, 053104 (2010). [DOI] [PubMed] [Google Scholar]