Skip to main content
PMC home page
The ISME Journal logoLink to The ISME Journal
. 2013 Jun 6;7(11):2069–2079. doi: 10.1038/ismej.2013.93

Quantifying community assembly processes and identifying features that impose them

James C Stegen 1,*, Xueju Lin 1,2, Jim K Fredrickson 1, Xingyuan Chen 3, David W Kennedy 1, Christopher J Murray 4, Mark L Rockhold 3, Allan Konopka 1
PMCID: PMC3806266  PMID: 23739053

Abstract

Spatial turnover in the composition of biological communities is governed by (ecological) Drift, Selection and Dispersal. Commonly applied statistical tools cannot quantitatively estimate these processes, nor identify abiotic features that impose these processes. For interrogation of subsurface microbial communities distributed across two geologically distinct formations of the unconfined aquifer underlying the Hanford Site in southeastern Washington State, we developed an analytical framework that advances ecological understanding in two primary ways. First, we quantitatively estimate influences of Drift, Selection and Dispersal. Second, ecological patterns are used to characterize measured and unmeasured abiotic variables that impose Selection or that result in low levels of Dispersal. We find that (i) Drift alone consistently governs ∼25% of spatial turnover in community composition; (ii) in deeper, finer-grained sediments, Selection is strong (governing ∼60% of turnover), being imposed by an unmeasured but spatially structured environmental variable; (iii) in shallower, coarser-grained sediments, Selection is weaker (governing ∼30% of turnover), being imposed by vertically and horizontally structured hydrological factors;(iv) low levels of Dispersal can govern nearly 30% of turnover and be caused primarily by spatial isolation resulting from limited exchange between finer and coarser-grain sediments; and (v) highly permeable sediments are associated with high levels of Dispersal that homogenize community composition and govern over 20% of turnover. We further show that our framework provides inferences that cannot be achieved using preexisting approaches, and suggest that their broad application will facilitate a unified understanding of microbial communities.

Keywords: metacommunity assembly, Hanford Site, neutral theory, niche theory, null models, phylogenetic beta diversity

Introduction

‘Actual ecological communities are undoubtedly governed by both niche-assembly and dispersal-assembly rules, along with ecological drift, but the important question is: what is their relative quantitative importance?' (Hubbell, 2001)

Across microbial community ecology, there are many examples of niche-based processes strongly influencing community composition (for example, Gilbert et al., 2012), whereas other studies support neutral or stochastic community assembly (for example, Ofiteru et al., 2010). Clearly, knowledge gained from these and many conceptually similar studies is vital for understanding each interrogated system. Less clear is how to build from this body of work to achieve a more unified understanding of processes that govern the composition of microbial communities.

We suggest one path forward is to work towards realizing Hubbell's (2001) vision, as summarized above, such that relative process influences can be quantified and compared across microbial systems. To do so, we work within Vellend's (2010) conceptual framework, which is focused on the influences of Selection, Dispersal, Drift and Speciation. Selection is the result of biotic and abiotic pressures causing variation in reproductive success across individuals and species; Dispersal governs the degree to which individuals move among communities; Drift results from population sizes fluctuating due to chance events; and Speciation can cause differences in species richness among sets of communities that do not exchange individuals through dispersal. On the other hand, Speciation should have little influence within a set of communities where individuals disperse among local communities, known as a ‘metacommunity' (Leibold et al., 2004). Turnover in community composition within a metacommunity is therefore governed by a combination of Selection, Dispersal and Drift.

Within a metacommunity, the magnitude of Dispersal can range from very limited to very high levels of exchange between communities. Low levels of Dispersal constrain the exchange of organisms among local communities, which can lead to spatial turnover in composition; we refer to this scenario as ‘Dispersal Limitation.' Dispersal Limitation alone, however, is not enough to cause spatial turnover in composition. Limited exchange of organisms among local communities allows the composition of ecological communities to diverge through stochastic changes in local population sizes. That is, Dispersal Limitation allows Drift to cause much greater spatial turnover in community composition than when Drift acts alone (Hubbell, 2001). On the other hand, high levels of Dispersal can homogenize community composition, thereby causing little turnover in composition (Mouquet and Loreau, 2003; Leibold et al., 2004); we refer to this scenario as ‘Homogenizing Dispersal.' We note that our concept of Homogenizing Dispersal is similar to ‘mass effects' and ‘source-sink dynamics', but we avoid these terms as they invoke additional assumptions and processes (see Leibold et al., 2004); Homogenizing Dispersal simply indicates that dispersal is high enough to cause low turnover by overwhelming other processes.

Quantitatively estimating the influences of Selection, Dispersal Limitation acting in concert with Drift, Drift acting alone and Homogenizing Dispersal is fundamental to our understanding of ecological systems. Such estimates have not, however, been achieved. Instead, recent studies have made progress towards characterizing gradients in the influence of Selection (Chase, 2010; Kraft et al., 2011) and testing ecological neutral theory (Ofiteru et al., 2010; Ricklefs and Renner, 2012). These studies provide important insights, but continued progress requires that we characterize how multiple processes simultaneously govern ecological systems (Gravel et al., 2006; Adler et al., 2007; Vellend, 2010; Stegen and Hurlbert, 2011).

Previous work attempts to characterize the simultaneous influences of ecological processes by partitioning variation in community composition into a fraction explained by environmental variables and a fraction explained by spatial variables (Tuomisto et al., 2003; Cottenie, 2005; Legendre et al., 2009). However, this technique cannot be used to infer the influences of Selection, Dispersal or Drift (Legendre et al., 2009; Gilbert and Bennett, 2010; Jacobson and Peres-Neto, 2010; Smith and Lundholm, 2010; Anderson et al., 2011; Stegen and Hurlbert, 2011).

One limitation of standard analyses that relate ecological community composition to environmental and/or spatial variables is that one must decide a priori which variables are potentially associated with Selection and which potentially result in Dispersal Limitation. For example, we may assume that environmental changes associated with increasing subsurface depth impose Selection on microbial communities. However, there may be unknown hydrological barriers that strongly influence composition by spatially isolating communities. The framework developed here distinguishes between such scenarios by reversing the standard direction of inference. Instead of making a priori decisions, we use ecological patterns to identify which environmental and spatial aspects of our study system impose Selection and which impose Dispersal Limitation.

Our framework relies in part on null models (that is, randomizations) (for example, Chase et al., 2011; Stegen et al., 2012) to identify features that impose Selection or Dispersal Limitation and to quantitatively estimate the influences of Selection, Dispersal Limitation acting alongside Drift, Drift acting alone and Homogenizing Dispersal. Our framework characterizes the spatial structure of both measured and unmeasured environmental variables that impose Selection. In turn, abiotic features that impose Selection can be rigorously distinguished from those that impose Dispersal Limitation. This is true even if key features have not been measured in the field and even if measured environmental variables are related to unknown dispersal barriers, as in the example above.

We apply our analytical framework to subsurface sediments collected from both the Hanford and Ringold geological formations within an unconfined aquifer in southeastern Washington State. These two formations have distinct physical structure, mineralogical composition and geological history (Figure 1; Bjornstad et al., 2009). By comparing inferences across formations and spatial scales, we link ecological processes to geological processes that govern the structure of physical environments.

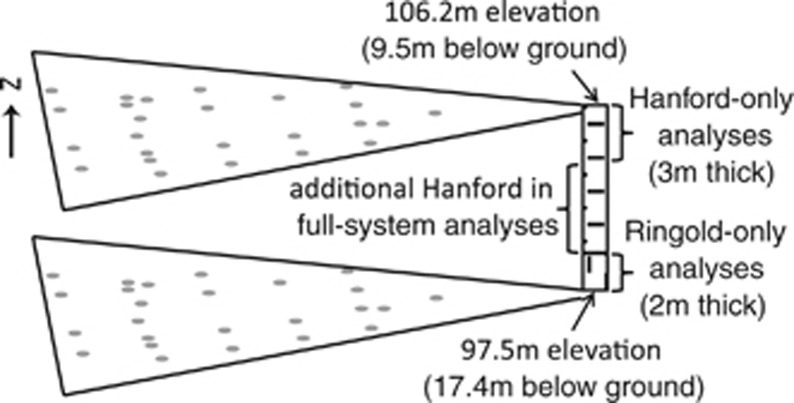
Figure 1.

Figure 1

Open in a new tab

Sampling sites within the Hanford Integrated Field-Scale Research Challenge field site, located ∼250 m from the Columbia River in the Hanford Site 300 area. Gray circles show two-dimensional distribution of sampling locations; the maximum horizontal distance between any two communities is ∼53 m. The two geological formations (Hanford and Ringold) are shown with horizontal and vertical dashes, respectively. Our formation-specific analyses examine communities across the specific vertical ranges shown, whereas the ‘full-system' analyses include additional communities in the middle section of the Hanford.

Materials and methods

We study a bacterial metacommunity associated with subsurface sediments within the unconfined aquifer ∼250 m from the Columbia River in the 300 Area of the Hanford Site in Richland, WA (Figure 1). Our system is characterized by two geological formations; the saturated zone of the coarse-grained Hanford formation ranges from approximately 10 m to 17 m below ground surface and below is the Ringold with finer-grained sediments (Bjornstad et al., 2009). DNA was extracted from sediments as in Lin et al. (2012a), and the V1–V2 region of the 16S rRNA gene was PCR amplified with primers 27F and 338R before pyrosequencing as in Lin et al. (2012b), and processed using QIIME (Caporaso et al., 2010) whereby sequences were clustered as operational taxonomic units (OTUs) defined by 97% sequence similarity (see Supplementary Material). All statistical analyses were carried out in R (R-Core-Team, 2012). Environmental data included a sample's elevation, horizontal distance from the Columbia River, the elevation of the top of the Ringold formation at its geographic location (Bjornstad et al., 2009) and its percent mud (see Supplementary Material).

Analytical framework development

Turnover in phylogenetic community composition

To infer ecological processes, our analytical framework relies, in part, on phylogenetic turnover, which is the evolutionary distance separating OTUs found in one community from OTUs found in a second community (Graham and Fine, 2008; Stegen et al., 2012). Using phylogenetic turnover to infer ecological processes requires ‘phylogenetic signal' in OTUs' optimal habitat conditions (Kraft et al., 2007; Cavender-Bares et al., 2009; Fine and Kembel, 2011), whereby habitat preferences of closely related taxa are more similar to each other than to the habitat preferences of distant relatives (Losos, 2008). We tested for phylogenetic signal to determine whether we could use phylogenetic turnover to make ecological inferences in our system, and to determine the most appropriate metric of phylogenetic turnover.

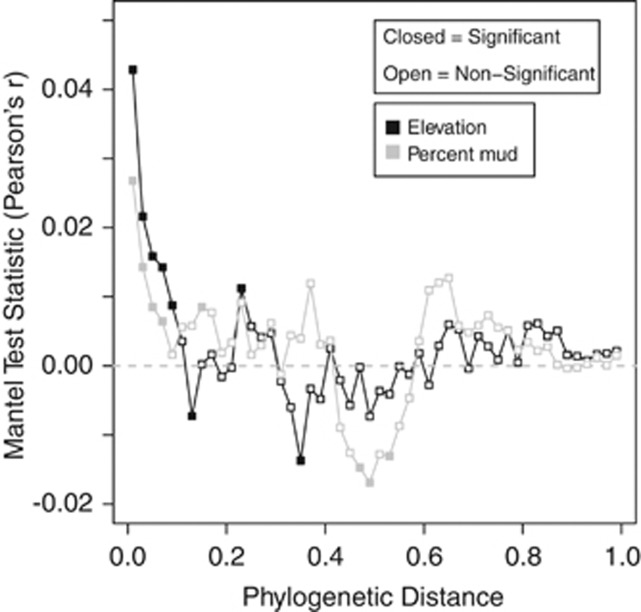
We found significant phylogenetic signal, but only across relatively short phylogenetic distances (Figure 2), consistent with previous work (Andersson et al., 2010; Diniz-Filho et al., 2010; Hardy et al., 2012; Stegen et al., 2012). It is therefore most appropriate to quantify phylogenetic turnover among closest relatives (Stegen et al., 2012). For this reason, we use the between-community version of the (abundance-weighted) β-mean-nearest taxon distance (βMNTD) (Fine and Kembel, 2011; Webb et al., 2011). βMNTD quantifies the phylogenetic distance between each OTU in one community (k) and its closest relative in a second community (m):

Figure 2.

Figure 2

Open in a new tab

Phylogenetic Mantel correlogram showing significant phylogenetic signal across short phylogenetic distances. Solid and open symbols denote significant and nonsignificant correlations, respectively, relating between-OTU niche differences to between-OTU phylogenetic distances across a given phylogenetic distance. An optimal elevation and an optimal percent mud were estimated for each species; these values were taken to be estimates of OTU environmental niches across both abiotic axes. Significantly positive correlations indicate that ecological niche distance between OTUs increases with their phylogenetic distance, but only across the phylogenetic distance class being evaluated (that is, there is phylogenetic signal in OTU environmental niches).

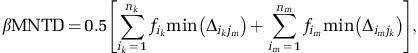graphic file with name ismej201393e1.jpg

where 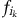Inline graphic is the relative abundance of OTU i in community k, nk is the number of OTUs in k and 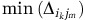Inline graphic is the minimum phylogenetic distance between OTU i in community k and all OTUs j in community m. βMNTD was calculated using R function ‘comdistnt' (abundance.weighted=TRUE; package ‘picante').

βMNTD can be less than, greater than or equal to the degree of turnover expected when Selection does not influence turnover in community composition. Lower than expected βMNTD should result from environmental conditions constraining community composition by imposing Selection on OTUs. Greater than expected βMNTD should be due to divergent environmental conditions causing each community to be composed of an ecologically distinct set of OTUs.

These expectations assume at least a minor degree of organismal exchange among local communities through deep evolutionary time so that individual communities do not evolve evolutionarily distinct assemblages in situ. This assumption is likely upheld in our system, which is within a single unconfined aquifer (maximum of 54 m separating any two communities) through which groundwater continuously flows and into which the Columbia River annually intrudes (Peterson et al., 2008; Lin et al., 2012b). The degree to which βMNTD deviates from a null model expectation therefore measures the degree to which community composition is limited by Selection on OTU ecological niches.

To quantify the degree to which βMNTD deviates from a null model expectation, we used a randomization that shuffled species names and abundances across the tips of the phylogeny (see Supplementary Material for phylogeny inference methods). After shuffling, βMNTD was recalculated to provide a null value, and repeating the randomization 999 times provided a null distribution. The difference between observed βMNTD and the mean of the null distribution was measured in units of s.d. (of the null distribution) and is referred to as the β-nearest taxon index (βNTI). βNTI values <−2 or >+2 indicate significantly less than or greater than expected phylogenetic turnover, respectively (see also Stegen et al., 2012).

Turnover in OTU composition

Most metrics of turnover in OTU composition provide no information on whether the observed degree of turnover deviates from that expected if community assembly was governed primarily by Drift. One exception is Raup–Crick (Chase et al., 2011). Raup–Crick does not account for OTU relative abundances, however, which carry information useful for understanding ecological processes (Anderson et al., 2011). Here we extend Raup–Crick to consider OTU relative abundances by modifying the procedure of Chase et al. (2011). In short, local communities were assembled probabilistically, where the probability of observing an individual of a given OTU was related to the number of communities occupied by the OTU and the OTU's relative abundance across all sampled communities. Observed OTU richness and number of individuals were maintained for each community (see Supplementary Material). For a given pair of communities, each was probabilistically assembled 999 times. For each iteration Bray–Curtis dissimilarity was used to quantify compositional turnover, thereby generating a null distribution of Bray–Curtis values. Similar to Chase et al. (2011), we standardize the deviation between empirically observed Bray–Curtis and the null distribution to vary between −1 and +1, and refer to the resulting metric as RCbray.

We interpret RCbray values >+0.95 or <−0.95 as significant departures from the degree of turnover expected when Drift acts alone (Chase et al., 2011). In turn, |RCbray|>0.95 indicates that turnover in community composition is governed primarily by Selection, Dispersal Limitation acting in concert with Drift or Homogenizing Dispersal; RCbray values between −0.95 and +0.95 are consistent with Drift acting alone (Chase et al., 2011).

We suggest that Dispersal Limitation acting alone should not lead to a significant RCbray value. For example, consider one homogenous community that is split into two communities with no dispersal between them. For compositional differences to emerge, OTU-specific birth and death rates must differ between the communities such that OTU population sizes differ between the communities. In this case, it is unclear how Dispersal Limitation alone could cause between-community differences in OTU birth and death rates. Drift, however, results from stochastic differences in birth and death rates. If one allows for Drift to occur alongside Dispersal Limitation, pairwise difference in community composition should grow through time and eventually lead to RCbray>+0.95.

On the other hand, Homogenizing Dispersal may cause less than expected turnover in OTU composition. The expected degree of turnover results from stochastic assembly of local communities by drawing individuals from the regional pool of OTUs (see above). When dispersal between a pair of communities is very high, however, local community assembly is not governed by the composition of the regional pool. For example, take a community that continuously sends large numbers of individuals to a second community. If Selection is relatively weak, the composition of the second community will be determined by the composition of the first community, instead of being determined by the regional pool. Such a scenario should lead to less turnover than when both communities are assembled from the regional pool; that is, RCbray<−0.95.

Estimating influences of ecological processes

We aim to quantitatively estimate the degree to which spatial turnover in community composition is influenced by Selection, Drift acting alone, Dispersal Limitation acting in concert with Drift and Homogenizing Dispersal. To do so, we take advantageof (i) assuming some dispersal among communities across evolutionary time, non-random phylogenetic turnover arises from Selection (Hardy, 2008) and(ii) non-random turnover in OTU compositioncan result from Selection or Dispersal Limitation (Chase et al., 2011), or as discussed above,from Homogenizing Dispersal. We note thatour framework assumes that all sources of error have a roughly equivalent influence over the quantitative estimates of each process, whereby our estimates should be reasonably close to the true values.

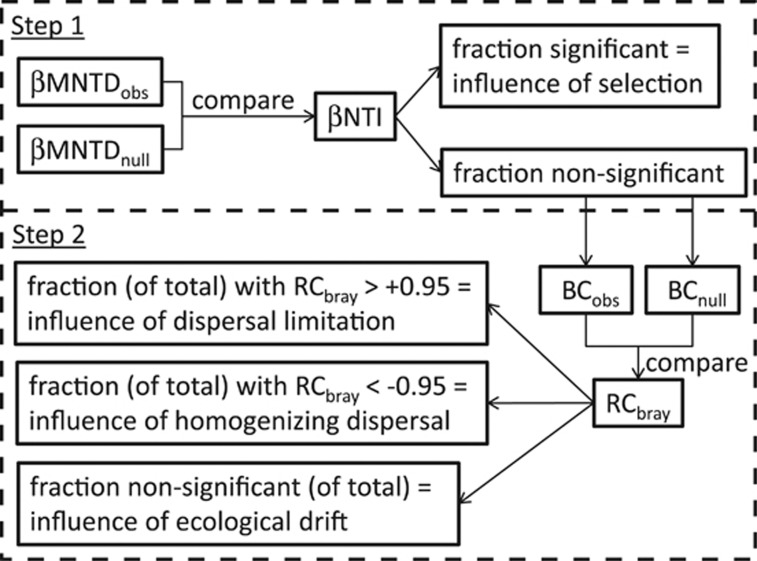
To estimate process influences, we follow a two-step procedure (Figure 3). First, we quantified βNTI for all pairwise community comparisons. As discussed above, a value of |βNTI|>2 indicates that observed turnover between a pair of communities is governed primarily by Selection. In turn, the influence of Selection across a set of local communities was estimated as the fraction of pairwise community comparisons with |βNTI|>2. As a corollary, pairwise comparisons with |βNTI|<2 should be governed by Drift acting alone, Dispersal Limitation acting alongside Drift or Homogenizing Dispersal.

Figure 3.

Figure 3

Open in a new tab

Flowchart summarizing procedure for estimating influences of ecological processes, broken into two major steps discussed in the section ‘Estimating influences of ecological processes.' First, the observed degree of phylogenetic turnover for each pairwise community comparison was quantified (βMNTDobs). A randomization was then used to generate a null distribution of phylogenetic turnover (βMNTDnull). The value of βNTI characterizes the magnitude of deviation between βMNTDobs and βMNTDnull. The fraction of pairwise comparisons with significant βNTI values (|βNTI|>2) is the estimated influence of Selection. As part of the second major step in our procedure, pairwise comparisons with nonsignificant βNTI values were further evaluated by comparing observed Bray–Curtis (BCobs) to Bray–Curtis expected under the randomization (BCnull). The value of Bray–Curtis-based Raup–Crick (RCbray) characterizes the magnitude of deviation between BCobs and BCnull; a value of |RCbray|>0.95 was considered significant. The number of pairwise comparisons with RCbray>+0.95, the number with RCbray<−0.95 and the number with |RCbray|<0.95 were each divided by the total number of all pairwise comparisons; the resulting fractions estimate the influence of Dispersal Limitation combined with Drift, Homogenizing Dispersal and Drift acting alone, respectively.

The second step in our procedure quantified RCbray for pairwise community comparisons that were not governed by Selection (that is, those with |βNTI|<2). Within this set, Dispersal Limitation coupled with Drift should lead to greater than expected turnover (RCbray>+0.95), whereas Homogenizing Dispersal should lead to less than expected turnover (RCbray<−0.95). As such, we divided the number of pairwise comparisons with |βNTI|<2 and RCbray>+0.95 by the total number of all pairwise comparisons. The resulting fraction estimates the influence of Dispersal Limitation acting in concert with Drift. The fraction of all pairwise comparisons with |βNTI|<2 and RCbray<−0.95 was taken as an estimate for the influence of Homogenizing Dispersal. The fraction of all pairwise comparisons with |βNTI|<2 and |RCbray|<0.95 estimates the influence of Drift acting alone.

Combining spatial eigenvectors and measured abiotic variables with model selection

In addition to estimating influences of ecological processes, we aim to characterize system features that impose Selection and Dispersal Limitation. To this end, we described spatial and environmental relationships among local communities by combining spatial eigenvector analysis with measured abiotic variables. Spatial eigenvectors describe spatial relationships among communities across a range of spatial scales; the first eigenvector breaks sampling locations into broadly distributed clusters, and subsequent eigenvectors characterize spatial relationships at increasingly fine scales (Borcard and Legendre, 2002; Borcard et al., 2011; Heino et al., 2011).

For spatial eigenvector analyses, we used the R function ‘pcnm' within package ‘vegan'. The ‘pcnm' function takes a spatial distance matrix as input. For analyses within the Ringold and Hanford formations, we used geographical locations (Eastings and Northings, Supplementary Table S1) of each well to build the distance matrix, thereby describing spatial relationships in two dimensions. For analyses across both formations (the ‘full system'), we described spatial distances in three dimensions due to increased vertical distances among communities. These three-dimensional Euclidean distances were used to define spatial eigenvectors. Note that spatial eigenvector analysis is robust in one, two or three dimensions (Borcard and Legendre, 2002).

Spatial eigenvectors only describe spatial relationships among sampling locations. As such, some eigenvectors may describe the spatial scales at which dispersal operates, whereas others may be related to the spatial structure of environmental variables (Legendre et al., 2009). In addition to spatial relationships we measured four abiotic variables. However, these measured variables may also simply describe spatial relationships among communities. For example, horizontal distance from the Columbia River may reflect spatial relationships or may reflect different environmental conditions related to spatially structured river water intrusion (Lin et al., 2012b; Stegen et al., 2012). In addition, measured abiotic variables may co-vary with each other and/or with spatial eigenvectors.

To combine all variables and minimize co-variation, we combined measured abiotic variables with spatial eigenvectors using principal components analysis (PCA). The resulting PCA axes (Supplementary Tables S2–S4) were used as independent variables in a model-selection procedure with either βNTI or RCbray as the dependent variable. Note that three separate sets of PCA axes were characterized: one for the Hanford formation, one for the Ringold formation and one for the full system (Hanford and Ringold formations combined). Labels associated with Hanford formation PCA axes have no relationship to, for example, labels of Ringold formation axes.

To identify features of the system that impose Selection or Dispersal Limitation, we fit statistical models to βNTI and RCbray using distance-based redundancy analysis (Legendre and Anderson, 1999) (R function ‘capscale' within package ‘vegan') combined with a model-selection procedure.Distance-based redundancy analysis takes positive, pairwise community distances as input such that βNTI and RCbray were each normalized to vary between 0 and 1 before model selection; for each, the absolute magnitude of the minimum (negative) value was added to all values (making all ⩾0), and the resulting values were then divided by their maximum (making all ⩾0 and ⩽1). We used forward model selection (Blanchet et al., 2008) where independent variable significance (α=0.05) was evaluated stepwise and the order of variable evaluation was based on improvement in the model's adjusted R2. Model selection proceeded until the next independent variable was nonsignificant as determined by 1000 permutations (R function ‘ordiR2step' within package ‘vegan'). Separate model-selection procedures were carried out for the Hanford, the Ringold and the full system, and βNTI and RCbray were evaluated separately.

The magnitude of βNTI is governed by the influence of Selection relative to the influences of Dispersal Limitation and Drift. Any PCA axes that explain a significant fraction of variation in βNTI should therefore reflect one or more environmental variables that impose Selection. This is true even if a significant PCA axis is unrelated to measured abiotic variables.

If a given PCA axis is significant for βNTI but measured abiotic variables do not load onto it, we consider this PCA axis to be an unmeasured, spatially structured environmental variable that imposes Selection. If measured abiotic variables load heavily onto a significant PCA axis, we consider the axis to be a measured environmental variable that imposes Selection. Furthermore, all PCA axes nonsignificant for βNTI were considered to primarily characterize spatial relationships among communities. This is true even if measured abiotic variables load heavily; measuring a given abiotic variable does not indicate that the variable imposes Selection.

Before RCbray model selection, we used the βNTI model-selection results to characterize each PCA axis as an unmeasured environmental variable, a measured environmental variable or a spatial variable. Following RCbray model selection, these variable designations were used (in conjunction with PCA loadings) to interpret the factors imposing Selection or Dispersal Limitation. For example, if a given variable (that is, PCA axis) was not related to βNTI, it was concluded that this variable characterized spatial relationships among local communities. If this same variable was significantly related to RCbray values, it was identified as characterizing features of the system that impose Dispersal Limitation. To determine if any measured features impose Dispersal Limitation, the PCA loadings on the selected variable were examined.

Comparison of inferences with those from preexisting approaches

We compared insights derived from our analytical framework with those derived from a preexisting approach (similar to, for example, Legendre et al., 2009; Heino et al., 2011). To achieve a direct comparison with our approach, we used the same PCA axes with the same model-selection procedure described above, but with Bray–Curtis dissimilarity as the dependent variable.

Results and Discussion

Quantitative process estimates

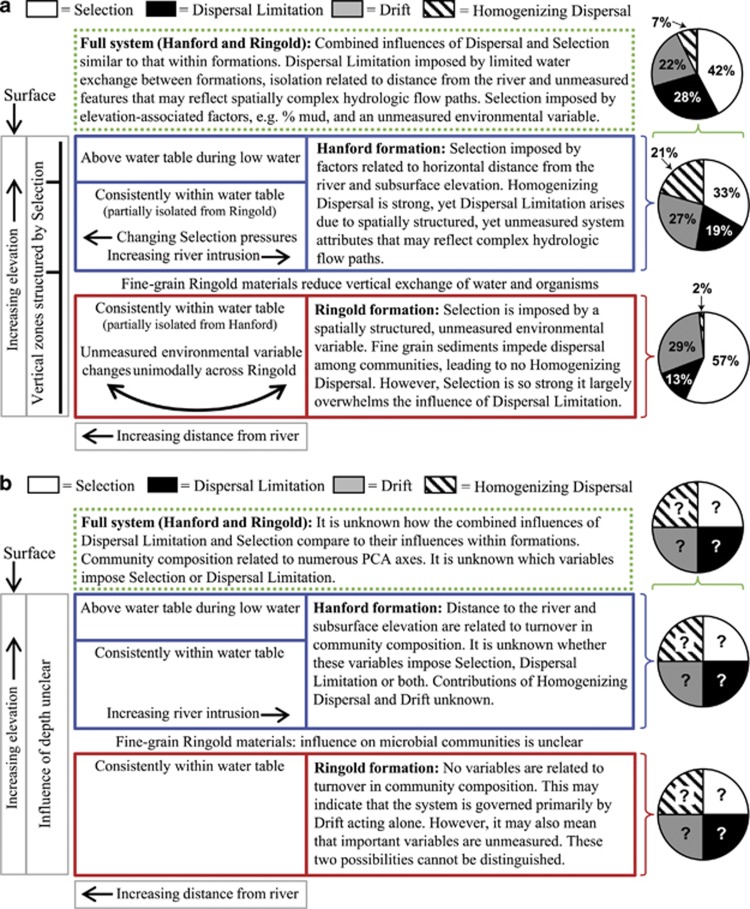
Here we provide the first quantitative parsing of ecological processes that influence community assembly (Figure 4a). Across formations and spatial scales, we find that ∼33–57% of turnover in community composition is primarily due to Selection, ∼13–28% of turnover is primarily due to Dispersal Limitation acting in concert with Drift, ∼0–21% of turnover is primarily due to Homogenizing Dispersal and ∼22–29% of turnover is primarily due to Drift acting alone (see Figure 4a for specifics). Preexisting approaches provide no process estimates (Figure 4b).

Figure 4.

Figure 4

Open in a new tab

Summary of key insights and results for the three systems analyzed: Hanford (blue) and Ringold (red) formations and across the full system (green dashed box). For comparison, panels provide inferences based on (a) the framework developed here and (b) a preexisting framework. Pie charts give the percent of turnover in community composition governed primarily by Selection acting alone (white fill), Dispersal Limitation acting in concert with Drift (black fill), Drift acting alone (gray fill) and Homogenizing Dispersal (line fill).

Our quantitative results are consistent with qualitative conclusions from previous work showing that Selection often has some detectable influence over microbial communities (Andersson et al., 2010; Ofiteru et al., 2010; Stegen et al., 2012). However, we also find that Dispersal Limitation acting in concert with Drift can have a substantial influence over community composition, in contrast to the classic paradigm that ‘all microbes are everywhere' (see de Wit and Bouvier, 2006; Martiny et al., 2006). This result adds to a growing literature showing an important influence of Dispersal Limitation in microbial systems (for example, Dumbrell et al., 2010; Martiny et al., 2011).

At the other end of the dispersal continuum, Homogenizing Dispersal has a strong influence on community structure in the Hanford formation, but effectively no influence in the Ringold. These contrasting influences of Homogenizing Dispersal make conceptual sense, given the hydrological characteristics of the two formations; in the highly permeable Hanford formation, between-community Dispersal appears to be so high that community composition is often determined primarily by immigration; Dispersal is sufficiently low in the Ringold formation, such that community composition is not strongly influenced by immigration.

We expected to observe a decreased influence of Drift acting alone when considering both formations simultaneously; the larger spatial extent of the system as a whole may increase Dispersal Limitation, and the greater range in environmental conditions may increase the influence of Selection.In contrast to this expectation, Drift alone consistently accounted for ∼25% of turnover in community composition (Figure 4a). It is difficult to compare this result to prior work; to the best of our knowledge, the influence of Drift has neverbeen quantitatively estimated, although Drift is known to have some detectable influence over community assembly in microbial (for example, Ofiteru et al., 2010) and macroorganism (for example, Chase, 2010) systems.

Factors that impose Selection

In addition to quantifying ecological processes, it has long been a goal in ecology to characterize factors that impose Selection (for example, Whittaker, 1967). Previous work, however, has been plagued by the impossibility of measuring all influential environmental variables (Anderson et al., 2011). We overcame this obstacle by running model selection on βNTI, which showed that unmeasured and measured environmental variables impose Selection and that the identity of influential variables changes across formations and spatial scales (Table 1).

Table 1. Summary of model selection results across formations using βNTI and RCbray.

Formation Turnover metric Environmental variables Spatial variables
Ringold βNTI 7 NA
Ringold RCbray None None
Ringold BCobs None None
Hanford βNTI 1, 3 NA
Hanford RCbray 1, 3 7
Hanford BCobs 1, 3 None
Full βNTI 1, 19, 32 NA
Full RCbray 1, 32 2, 4, 5, 6, 14, 16, 18, 20, 27, 26, 33
Full BCobs 1, 2, 4, 32, 34 5, 6, 12, 14, 16, 20, 26
Open in a new tab

Abbreviations: βNTI, β-nearest taxon index; BCobs, observed Bray–Curtis; NA, not applicable; RCbray, Bray–Curtis-based Raup–Crick.

We identified spatially structured, influential environmental variables as those PCA axes significant for βNTI. PCA axes significant for βNTI are never considered spatial variables (hence, ‘NA'). For RCbray, significant PCA axes are identified as environmental or spatial based on the results of βNTI model selection. Numerical values indicate PCA axis numbers and map to PCA loadings in Supplementary Tables S2–S4. Note that PCA axis numbers are formation-specific and that each axis is a combination of measured abiotic variables and spatial eigenvectors. For comparison, results from a preexisting approach using empirically BCobs are provided, where PCA axes are characterized as environmental or spatial based only on PCA loadings of measured abiotic variables (see Supplementary Tables S2–S4).

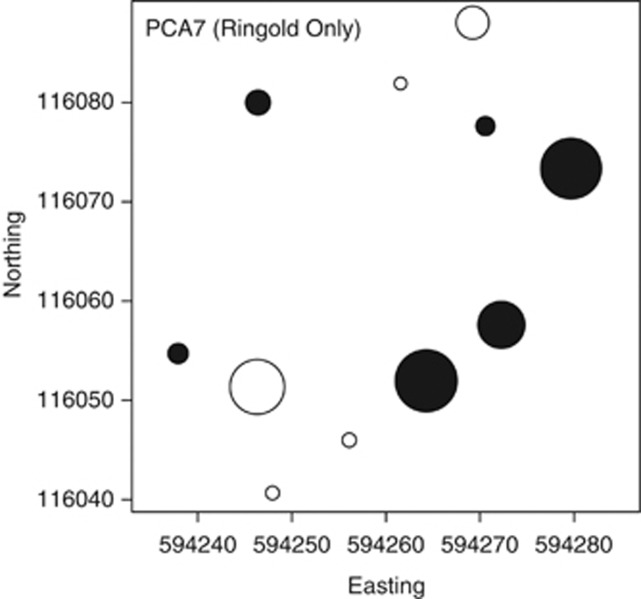
In the Ringold formation, βNTI model selection identified one significant PCA axis (PCA7). No measured abiotic variables loaded onto PCA7 (Supplementary Table S2). PCA7 is therefore an unmeasured, spatially structured environmental variable that imposes Selection. The spatial structure of this unmeasured variable is shown in Figure 5. Importantly, model selection for Bray–Curtis identified no significant PCA axes. Relying on preexisting approaches would have therefore provided essentially no information on ecological processes even though the system is heavily governed by Selection (Figure 4).

Figure 5.

Figure 5

Open in a new tab

Spatial variation in PCA axis 7 within the Ringold formation. PCA7 was identified as an influential, yet unmeasured, environmental variable using model selection for βNTI. The spatial configuration of PCA7 suggests that a key environmental variable changes unimodally along an axis running northwest to southeast. Axis (absolute) magnitude increases with circle diameter, with negative and positive values represented as open and closed circles, respectively.

In the shallower Hanford formation, βNTI model selection identified PCA1 and PCA3 as significant axes. The strongest loadings on PCA1 and PCA3 were distance-from-the-river and subsurface elevation, respectively (Supplementary Table S3). The hydrology of the Hanford formation is strongly influenced by elevation fluctuations of the Columbia River, and the strong loadings of distance-from-the-river and subsurface elevation on PCA1 and PCA3 suggest an important influence of river elevation fluctuations. In particular, the spring runoff-associated river-elevation increase causes water-table rise and intrusion of river water into the subsurface at our site (Peterson et al., 2008; Lin et al., 2012b). Microbial communities near the top of the aquifer may therefore experience saturated or unsaturated hydrological conditions depending on the time of year, and communities further from the river likely experience decreased and less-frequent river intrusion (Lin et al., 2012b). In turn, we hypothesize that in the Hanford formation, Selection causes turnover in community composition due to (i) vertically structured differences in the temporal dynamics of saturation states and (ii) horizontally structured differences in river intrusion. We note that a preexisting approach also selected PCA1 and PCA3 as significant variables, but given the strong spatial structure of these variables, such approaches cannot evaluate whether they impose Selection or Dispersal Limitation.

From analysis of the two formations together (‘full system'), model selection identified three PCA axes associated with βNTI. Examining the loadings of measured abiotic variables on these PCA axes (Supplementary Table S4) suggests that Selection is imposed by factors associated with elevation, such as the percent mud within sediments (Table 1, Supplementary Table S4) and (potentially) between-formation differences in mineralogical composition, age, cementation and vertical layering. In particular, the Ringold is far older (∼ 8.5–3.4 million years old) than the Hanford formation (∼0.015 million years old) with greater cementation and vertical layering (Bjornstad et al., 2009). In addition, measured abiotic variables did not load onto one selected PCA axis, PCA19, suggesting that this axis represents an unmeasured environmental variable that imposes Selection across the full system.

Coupling quantitative process estimates with the βNTI model selection contributes to a system-level conceptual model that contrasts sharply with that derived using a preexisting approach (Figure 4). Our framework suggests that (i) low-energy deposition of fine-grained sediments (as in the Ringold (Bjornstad et al., 2009)) leads to very strong Selection (governing ∼60% of turnover) imposed by an unmeasured, spatially structured environmental variable (Table 1, Supplementary Table S2, Figure 5); (ii) high-energy deposition of coarse-grained sediments (as in the Hanford (Bjornstad et al., 2009)) partially homogenizes abiotic conditions leading to weaker Selection (governing ∼30% of turnover) imposed by spatially structured, hydrology-related environmental factors (Table 1, Supplementary Table S3); and (iii) differences in the physical energy of geological depositional processes can result in between-formation environmental differences that cause turnover due to Selection (governing ∼40% of turnover) (Table 1, Supplementary Table S4). In the case of our particular system, the primary between-habitat environmental differences are related to sediment composition and the degree of vertical layering (Bjornstad et al., 2009); Ringold and Hanford sediments are ∼90% and ∼4% mud, respectively (Supplementary Table S1), and the Ringold has more vertical layering (Bjornstad et al., 2009).

Factors imposing Dispersal Limitation

Fundamental to our understanding of ecological communities is knowledge of the factors that impose Dispersal Limitation. In non-microbial systems, Dispersal Limitation is common, but further inferences are usually limited to the spatial scales across which Dispersal Limitation operates (for example, Legendre et al., 2009). In contrast, we couple model selection for RCbray with βNTI-basedcharacterization of PCA axes to enable characterization of abiotic features that impose Dispersal Limitation. Key to our approach is that variation in RCbray can be driven by variation in the strength of Selection or by variation in the magnitude of Dispersal (Chase et al., 2011). PCA axes retained in RCbray model selection that were not retained in βNTI model selection therefore represent among-community spatial relationships across which dispersal varies (that is, across which Dispersal Limitation is imposed). Inferences drawn from this approach contribute critical elements to our conceptual model (Figure 4a).

At the ‘full-system' scale, model selection for RCbray suggests that Dispersal Limitation is imposed, in part, by vertical separation among communities (Table 1, Supplementary Table S4). This is consistent with previous hydrological characterization, suggesting that the fine-grained composition of the Ringold restricts vertical exchange of water between the Ringold and upper Hanford formations (Bjornstad et al., 2009). The disparate geological history of the two formations is therefore indirectly responsible for strong Dispersal Limitation and Selection at the ‘full-system' scale. Model-selection results further suggest that Dispersal Limitation is also related to horizontal distance from the Columbia River (Table 1, Supplementary Table S4); decreased and less-frequent river intrusion into communities further from the river (Lin et al., 2012b) may therefore cause additional isolation. There also appears to be a number of important unmeasured factors (Table 1, Supplementary Table S4), suggesting that spatially complex hydrological flow paths may strongly influence patterns of organismal exchange among local communities across the ‘full system.'

Within the Hanford formation, RCbray model selection identified one PCA axis that was not related to βNTI and onto which no measured abiotic variables loaded (Table 1, Supplementary Table S3). This suggests that an unmeasured feature of the Hanford formation imposes Dispersal Limitation. From the available data, it is impossible to know the identity of this unmeasured feature, but as for the ‘full system,' we hypothesize that spatially structured hydrological flow paths influence the degree to which local communities exchange organisms.

Conclusions

Inferences drawn across our analytical framework provide a unique conceptual model (Figure 4a) linking quantitative estimates of Selection, Dispersal Limitation and Drift to the measured andunmeasured abiotic factors that impose these processes. Our analyses provide a fundamentally deeper understanding of ecological communities and provide inferences that are qualitatively distinct from those derived through traditional analyses (Figure 4).

For a direct comparison with our analyses, we employed an approach similar to that used in previous work. This approach identified PCA axes that are significantly related to Bray–Curtis, but provides no means to determine the processes imposed by significant variables. Previous studies that use approaches similar to this ‘preexisting approach' appear to assign processes to significant variables (for example, Tuomisto et al., 2003; Cottenie, 2005; Legendre et al., 2009; Heino et al., 2011). Doing so requires one to decide a priori which variables are associated with which ecological process. Identifying the features of a system that impose Selection and those that impose Dispersal Limitation is an empirical question, however, that requires an answer informed by ecological patterns of a given system. Further, preexisting approaches cannot estimate the relative influences of ecological processes or identify unmeasured environmental variables. All these limitations would remain if other preexisting approaches were used, such as using redundancy analysis on raw community composition data (for example, Legendre et al., 2009).

Although we suggest that our framework provides novel insights, it is important to recognize that there are limitations and, as with any new approach, these limitations can be vetted through additional use and simulation-based studies. One limitation, for example, is that the current framework does not parse out sub-classes of Selection, such as competition and trophic interactions. In addition, the framework could be sensitive to factors such as phylogenetic uncertainty and alpha diversity underestimation. These particular factors are partially controlled by confirming phylogenetic signal upfront and using null models that hold observed alpha diversity constant, respectively. Simulation studies are nonetheless needed for a full evaluation.

More generally, the knowledge we seek builds from a revolution in ecological thought that has largely taken place across the last decade. Although often rebuked and rejected (for example, Ricklefs and Renner, 2012), Hubbell's (2001) neutral theory encouraged broader recognition of Drift and Dispersal. As a consequence, it is now broadly recognized that Selection works alongside Drift and Dispersal (Cottenie, 2005; Gravel et al., 2006; Adler et al., 2007; Legendre et al., 2009; Dumbrell et al., 2010; Chase and Myers, 2011). This is the conceptual foundation from which we work and out of which a unification of community ecology can emerge (Vellend, 2010).

Acknowledgments

JCS was supported by a Linus Pauling Distinguished Postdoctoral Fellowship at Pacific Northwest National Laboratory. We thank AH Hurlbert, NJB Kraft and M Vellend for their helpful discussions related to this work. This research was supported by the US Department of Energy (DOE), Office of Biological and Environmental Research (BER), as part of Subsurface Biogeochemistry Research Program's Scientific Focus Area (SFA) and Integrated Field-Scale Research Challenge (IFRC) at the Pacific Northwest National Laboratory (PNNL). PNNL is operated for DOE by Battelle under contract DE-AC06-76RLO 1830.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on The ISME Journal website (http://www.nature.com/ismej)

Supplementary Material

Supplementary Information
Click here for additional data file. (3.1MB, doc)

References

  1. Adler PB, HilleRisLambers J, Levine JM. A niche for neutrality. Ecol Lett. 2007;10:95–104. doi: 10.1111/j.1461-0248.2006.00996.x. [DOI] [PubMed] [Google Scholar]
  2. Anderson MJ, Crist TO, Chase JM, Vellend M, Inouye BD, Freestone AL, et al. Navigating the multiple meanings of β diversity: a roadmap for the practicing ecologist. Ecol Lett. 2011;14:19–28. doi: 10.1111/j.1461-0248.2010.01552.x. [DOI] [PubMed] [Google Scholar]
  3. Andersson AF, Riemann L, Bertilsson S. Pyrosequencing reveals contrasting seasonal dynamics of taxa within Baltic Sea bacterioplankton communities. ISME J. 2010;4:171–181. doi: 10.1038/ismej.2009.108. [DOI] [PubMed] [Google Scholar]
  4. Bjornstad BN, Horner JA, Vermeul VR, Lanigan DC, Thorne PD. Borehole Completion and Conceptual Hydrogeologic Model for the IFRC Well Field, 300 Area, Hanford Site. PNNL-18340. Pacific Northwest National Laboratory: Richland, WA; 2009. [Google Scholar]
  5. Blanchet FG, Legendre P, Borcard D. Forward selection of explanatory variables. Ecology. 2008;89:2623–2632. doi: 10.1890/07-0986.1. [DOI] [PubMed] [Google Scholar]
  6. Borcard D, Legendre P. All-scale spatial analysis of ecological data by means of principal coordinates of neighbour matrices. Ecol Model. 2002;153:51–68. [Google Scholar]
  7. Borcard D, Gillet F, Legendre L. Numerical Ecology with R. Springer: New York, NY; 2011. [Google Scholar]
  8. Caporaso JG, Kuczynski J, Stombaugh J, Bittinger K, Bushman FD, Costello EK, et al. QIIME allows analysis of high-throughput community sequencing data. Nat Methods. 2010;7:335–336. doi: 10.1038/nmeth.f.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cavender-Bares J, Kozak KH, Fine PVA, Kembel SW. The merging of community ecology and phylogenetic biology. Ecol Lett. 2009;12:693–715. doi: 10.1111/j.1461-0248.2009.01314.x. [DOI] [PubMed] [Google Scholar]
  10. Chase JM. Stochastic community assembly causes higher biodiversity in more productive environments. Science. 2010;328:1388–1391. doi: 10.1126/science.1187820. [DOI] [PubMed] [Google Scholar]
  11. Chase JM, Kraft NJB, Smith KG, Vellend M, Inouye BD. Using null models to disentangle variation in community dissimilarity from variation in α-diversity. Ecosphere. 2011;2:art24. [Google Scholar]
  12. Chase JM, Myers JA. Disentangling the importance of ecological niches from stochastic processes across scales. Philos Transact Royal Soc B Biol Sci. 2011;366:2351–2363. doi: 10.1098/rstb.2011.0063. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Cottenie K. Integrating environmental and spatial processes in ecological community dynamics. Ecol Lett. 2005;8:1175–1182. doi: 10.1111/j.1461-0248.2005.00820.x. [DOI] [PubMed] [Google Scholar]
  14. de Wit R, Bouvier T. ‘Everything is everywhere, but, the environment selects' what did Baas Becking and Beijerinck really say. Environ Microbiol. 2006;8:755–758. doi: 10.1111/j.1462-2920.2006.01017.x. [DOI] [PubMed] [Google Scholar]
  15. Diniz-Filho JAF, Terribile LC, da Cruz MJR, Vieira LCG. Hidden patterns of phylogenetic non-stationarity overwhelm comparative analyses of niche conservatism and divergence. Global Ecol Biogeogr. 2010;19:916–926. [Google Scholar]
  16. Dumbrell AJ, Nelson M, Helgason T, Dytham C, Fitter AH. Relative roles of niche and neutral processes in structuring a soil microbial community. ISME J. 2010;4:337–345. doi: 10.1038/ismej.2009.122. [DOI] [PubMed] [Google Scholar]
  17. Fine PVA, Kembel SW. Phylogenetic community structure and phylogenetic turnover across space and edaphic gradients in western Amazonian tree communities. Ecography. 2011;34:552–565. [Google Scholar]
  18. Gilbert B, Bennett JR. Partitioning variation in ecological communities: do the numbers add up. J Appl Ecol. 2010;47:1071–1082. [Google Scholar]
  19. Gilbert JA, Steele JA, Caporaso JG, Steinbruck L, Reeder J, Temperton B, et al. Defining seasonal marine microbial community dynamics. ISME J. 2012;6:298–308. doi: 10.1038/ismej.2011.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Graham CH, Fine PVA. Phylogenetic beta diversity: linking ecological and evolutionary processes across space in time. Ecol Lett. 2008;11:1265–1277. doi: 10.1111/j.1461-0248.2008.01256.x. [DOI] [PubMed] [Google Scholar]
  21. Gravel D, Canham CD, Beaudet M, Messier C. Reconciling niche and neutrality: the continuum hypothesis. Ecol Lett. 2006;9:399–409. doi: 10.1111/j.1461-0248.2006.00884.x. [DOI] [PubMed] [Google Scholar]
  22. Hardy OJ. Testing the spatial phylogenetic structure of local communities: statistical performances of different null models and test statistics on a locally neutral community. J Ecol. 2008;96:914–926. [Google Scholar]
  23. Hardy OJ, Couteron P, Munoz F, Ramesh BR, Pélissier R. Phylogenetic turnover in tropical tree communities: impact of environmental filtering, biogeography and mesoclimatic niche conservatism. Global Ecol Biogeogr. 2012;21:1007–1016. [Google Scholar]
  24. Heino J, Grönroos M, Soininen J, Virtanen R, Muotka T. Context dependency and metacommunity structuring in boreal headwater streams. Oikos. 2011;121:537–544. [Google Scholar]
  25. Hubbell SP. The Unified Neutral Theory of Biodiversity and Biogeography. Princeton University Press: Princeton, NJ; 2001. [Google Scholar]
  26. Jacobson B, Peres-Neto PR. Quantifying and disentangling dispersal in metacommunities: how close have we come? How far is there to go. Landscape Ecol. 2010;25:495–507. [Google Scholar]
  27. Kraft NJB, Cornwell WK, Webb CO, Ackerly DD. Trait evolution, community assembly, and the phylogenetic structure of ecological communities. Am Nat. 2007;170:271–283. doi: 10.1086/519400. [DOI] [PubMed] [Google Scholar]
  28. Kraft NJB, Comita LS, Chase JM, Sanders NJ, Swenson NG, Crist TO, et al. Disentangling the drivers of β diversity along latitudinal and elevational gradients. Science. 2011;333:1755–1758. doi: 10.1126/science.1208584. [DOI] [PubMed] [Google Scholar]
  29. Legendre P, Anderson MJ. Distance-based redundancy analysis: testing multispecies responses in multifactorial ecological experiments. Ecol Monogr. 1999;69:1–24. [Google Scholar]
  30. Legendre P, Mi XC, Ren HB, Ma KP, Yu MJ, Sun IF, et al. Partitioning beta diversity in a subtropical broad-leaved forest of China. Ecology. 2009;90:663–674. doi: 10.1890/07-1880.1. [DOI] [PubMed] [Google Scholar]
  31. Leibold MA, Holyoak M, Mouquet N, Amarasekare P, Chase JM, Hoopes MF, et al. The metacommunity concept: a framework for multi-scale community ecology. Ecol Lett. 2004;7:601–613. [Google Scholar]
  32. Lin X, Kennedy D, Peacock A, McKinley J, Resch CT, Fredrickson J, et al. Distribution of microbial biomass and potential for anaerobic respiration in Hanford Site 300 Area subsurface sediment. Appl Environ Microb. 2012a;78:759–767. doi: 10.1128/AEM.07404-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Lin X, Mckinley J, Resch CT, Lauber C, Fredrickson J, Konopka AE. Spatial and temporal dynamics of microbial community in the Hanford unconfined aquifer. ISME J. 2012b;6:1665–1676. doi: 10.1038/ismej.2012.26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Losos JB. Phylogenetic niche conservatism, phylogenetic signal and the relationship between phylogenetic relatedness and ecological similarity among species. Ecol Lett. 2008;11:995–1003. doi: 10.1111/j.1461-0248.2008.01229.x. [DOI] [PubMed] [Google Scholar]
  35. Martiny JBH, Bohannan BJM, Brown JH, Colwell RK, Fuhrman JA, Green JL, et al. Microbial biogeography: putting microorganisms on the map. Nat Rev Micro. 2006;4:102–112. doi: 10.1038/nrmicro1341. [DOI] [PubMed] [Google Scholar]
  36. Martiny JBH, Eisen JA, Penn K, Allison SD, Horner-Devine MC. Drivers of bacterial β-diversity depend on spatial scale. Proc Natl Acad Sci USA. 2011;108:7850–7854. doi: 10.1073/pnas.1016308108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Mouquet N, Loreau M. Community patterns in source-sink metacommunities. Am Nat. 2003;162:544–557. doi: 10.1086/378857. [DOI] [PubMed] [Google Scholar]
  38. Ofiteru ID, Lunn M, Curtis TP, Wells GF, Criddle CS, Francis CA, et al. Combined niche and neutral effects in a microbial wastewater treatment community. Proc Natl Acad Sci USA. 2010;107:15345–15350. doi: 10.1073/pnas.1000604107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Peterson RE, Rockhold ML, Serne RJ, Thorne PD, Williams MD. Uranium Contamination in the Subsurface Beneath the 300 Area, Hanford site, Washington. PNNL-17034. Pacific Northwest National Laboratory: Richland, WA; 2008. [Google Scholar]
  40. R-Core-Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing: Vienna, Austria; 2012. [Google Scholar]
  41. Ricklefs RE, Renner SS. Global correlations in tropical tree species richness and abundance reject neutrality. Science. 2012;335:464–467. doi: 10.1126/science.1215182. [DOI] [PubMed] [Google Scholar]
  42. Smith TW, Lundholm JT. Variation partitioning as a tool to distinguish between niche and neutral processes. Ecography. 2010;33:648–655. [Google Scholar]
  43. Stegen JC, Hurlbert AH. Inferring ecological processes from taxonomic, phylogenetic and functional trait β-diversity. PLoS One. 2011;6:e20906. doi: 10.1371/journal.pone.0020906. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Stegen JC, Lin X, Konopka AE, Fredrickson JK. Stochastic and deterministic assembly processes in subsurface microbial communities. ISME J. 2012;6:1653–1664. doi: 10.1038/ismej.2012.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Tuomisto H, Ruokolainen K, Yli-Halla M. Dispersal, environment, and floristic variation of western amazonian forests. Science. 2003;299:241–244. doi: 10.1126/science.1078037. [DOI] [PubMed] [Google Scholar]
  46. Vellend M. Conceptual synthesis in community ecology. Q Rev Biol. 2010;85:183–206. doi: 10.1086/652373. [DOI] [PubMed] [Google Scholar]
  47. Webb CO, Ackerly DD, Kembel S.2011Phylocom: software for the analysis of phylogenetic community structure and character evolution (with phylomatic and ecoevolve) User's Manualversion 4.2. http://www.phylodiversity.net/phylocom/ .
  48. Whittaker RH. Gradient analysis of vegetation. Biol Rev. 1967;42:207–264. doi: 10.1111/j.1469-185x.1967.tb01419.x. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (3.1MB, doc)

Articles from The ISME Journal are provided here courtesy of Oxford University Press

RESOURCES