Chronic Disease Burden and the Interaction of Education, Fertility, and Growth

Abstract

This study considers the eradication of hookworm disease from the American South as a test of the quantity-quality (Q-Q) framework of fertility. Eradication was principally a shock to the price of quality because of three factors: hookworm (i) depresses the return to human-capital investment, (ii) had a very low case-fatality rate, and (iii) had negligible prevalence among adults. Consistent with the Q-Q model, we find a significant decline in fertility associated with eradication. Relative sizes of fertility and human-capital responses to hookworm indicate that the Q-Q mechanism is of a similar magnitude to secular co-movements in these same variables.

1. Introduction

Virtually all economies that experienced sustained increases in school attainment and per capita incomes have also experienced substantial declines in fertility rates. This stylized fact has motivated the emergence of a diverse theoretical and empirical literature linking economic development and fertility. A significant number of researchers, most notably the participants of the European Fertility Project¹ (hereafter EFP), emphasize the spread of both new moral and cultural norms as well as birth-control technologies. Others stress the importance of factors affecting the direct costs of children, such as female wages, child mortality, and urbanization. Still others examine the link between parental investment into the ‘quality’ of their children (through investments into education or health) and the fertility (‘quantity’) decision.

The existing empirical literature on the demographic transition relies heavily on cross-country panel-data on fertility, education, and other socioeconomic and cultural variables. It has proved difficult to distinguish between alternative theories of the fertility transition using such data. The observed correlations between variables measuring economic development and fertility are consistent with a variety of different models. While the empirical literature has shown a number of interesting patterns in the time-series, it has provided little basis for discriminating among the different theories.

We present new empirical evidence on the mechanisms driving the fertility transition. The policy intervention we examine (and describe in detail below) effectively increased the return to human capital or, in the language of the theoretical literature, reduced the price of child “quality”. We know of no other study in the fertility-transition literature that examines similar variation. We find support for models that link the fertility decision to the economic prospects of children. Our results therefore support the literature emphasizing economic incentives, and more specifically models connecting children's economic welfare to parental fertility decisions through intergenerational altruism.

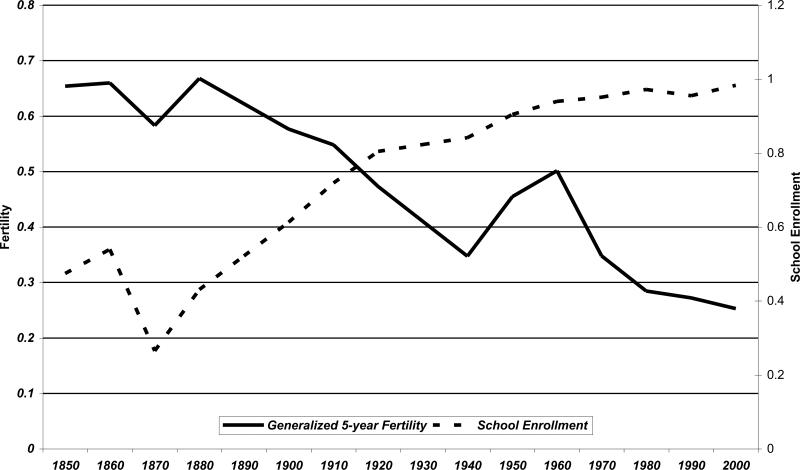
The analysis is based on an important episode in the economic history of the southern United States. Figure 1 documents how, at the beginning of the 20th century, the American South was transitioning from a high fertility, low education society to one characterized by high levels of education and low fertility rates. We consider an improvement in the health environment during this period that raised the return to schooling, and whether this affected fertility. Specifically, we examine the consequences of a particular policy intervention—the eradication of hookworm disease—in the American South during the 1910s.²

Figure 1.

Fertility and Schooling in the American South.

Notes: This figure plots averages by census year of the indicated variables. The base sample consists of natives living in the Southern United States in the IPUMS data, 1850-2000. The fertility measure is the number of own children in the household for females aged 15-49. The school enrollment data are computed for children aged 8-16.

The sudden and external origins of the eradication campaign combine with cross-area differences in pre-treatment infection rates to form our identification strategy. In spite of infecting approximately 40% of children in the South, hookworm was not recognized as a public health problem until the turn of the century. Shortly afterward a large-scale eradication program was mounted through the efforts of the Rockefeller Sanitary Commission. This intervention originated in developments outside the region (through innovations to knowledge and funding). The substantial regional variation in hookworm infection rates allows us to define treatment and comparison areas for the analysis.

The interpretation of our results hinges on the nature of the disease eradicated. Three facts about hookworm disease are especially important. First, this intestinal parasite was common among children aged 6-14 throughout the region, but rarely affected adults. Second, hookworm infection caused anemia and listlessness in affected children. Third, the disease was rarely lethal. Together, these three facts allow us to discard effects on fertility that operated via parental wages or child mortality. Instead we interpret the eradication as affecting the ability of school-aged children to acquire human capital.

Forward-looking models of the demographic transition predict that an increase in the returns to schooling will reduce contemporaneous fertility rates. We find robust evidence in favor of this prediction: after hookworm eradication, fertility decreased markedly in areas that had previously had high rates of hookworm infection. The abrupt onset of the hookworm eradication campaign is clearly reflected in the changing fertility rates of the “treatment” areas relative to the “control” areas during the same time period. In contrast, we find essentially no difference in fertility trends both before the hookworm eradication campaign and after its completion.

We consider and reject several alternative hypotheses for this result. The finding is robust to controlling for a variety of additional factors, including crop mixes and production technologies, racial differences, child mortality, variation in moral norms correlated with religious denominations, and pre-existing differences in fertility and human capital. We also consider the non-fertility outcomes of adults as a falsification exercise, and find no evidence that hookworm eradication was spuriously proxying for migration, income, or sectoral shocks. Furthermore, the fact that changes in schooling and fertility were abrupt and coincident with the eradication campaign is useful to our argument, especially in comparison with slowly moving variables like cultural norms.

Our results suggest that forward-looking models of the fertility transition based on intergenerational altruism can potentially explain the entire reduction in fertility observed during the demographic transition. We estimate a response of fertility and of education due to the eradication of hookworm. The ratio of these estimates delivers a decline in fertility per unit of increase in education associated with hookworm eradication. A similar decline in fertility per unit of increase in education can be obtained from the time-series data during this period. Both estimates are of similar magnitude. This suggests that forward-looking behavior (though not specifically hookworm eradication) can explain most if not all of the decline in fertility during the demographic transition.

We proceed as follows. Section 2 reviews the existing literature on the fertility transition. Section 3 describes hookworm disease, the historical processes that led to its eradication in the South, and the research design used in the present study. Section 4 presents the empirical results and addresses a number of alternative explanations for our findings. Section 5 describes the quantitative exercise that supports a large role for the quantity-quality trade-off in explaining this region's fertility decline during its human-capital take-off. Section 6 concludes.

2. The Literature on the Demographic Transition

The Malthusian model of economic development provides a gloom outlook on the evolution of human societies. Malthus (1798) argued that population growth inevitably followed technological progress, and thus negates any gains in income that might come from the advance of knowledge. In the Malthusian world, only temporary episodes of economic prosperity are possible. However, the experience of the past 200 years has not borne out this pessimistic scenario. Instead, a growing number of nations have experienced a transition to permanently lower birth rates and sustained per capita income growth. How could this fertility transition come about?

One approach to understanding the fertility transition focuses on the spread of new birth control technologies and the differential impact of these technologies depending on social norms and cultural circumstances. This approach has become known as the Innovation hypothesis. It received support from the European Fertility Project (EFP) (Coale and Watkins, 1986), a large collaborative effort of social scientists from all backgrounds. The EFP analysed the fertility transition in several hundred European regions and could not find systematic correlations of socioeconomic variables with the onset of the fertility transition. Instead, they observed that the beginning of the fertility transition correlated across provinces with religious, cultural, or linguistic ties. They concluded that cultural norms restricted the adoption of techniques for the effective regulation of fertility in the pre-transition stage. Changing norms and technological advances then represent an increasing adoption of birth control techniques. The fertility transition is the response to this shift.

The economic literature, in contrast, has linked the fertility transition with time-variation in economic variables such as the returns to investing into education or the opportunity costs of fertility. Becker (1960), Mincer (1963), and Becker and Lewis (1973) explored fertility choices as the outcome of individual utility maximization subject to economic constraints. In a simple consumer choice model, the opportunity costs of the number of children (hereafter: the “price” of children) can reasonably be assumed to be affected by variables such as female wages or infant mortality rates.³ Secular variation in such variables — for instance because modern economies provide women with expanded labor market opportunities — can then potentially explain the fertility transition.

Becker (1960) and Becker and Lewis (1973) developed the idea that increasing expenditures on the quality of individual children raise the costs of fertility. Variation in the prices of quality or quantity therefore generate a negative relation between the quantity and quality of children. This interaction has become known as the quantity-quality, or Q-Q, interaction. This literature explains the secular decline in fertility as due to exogenous (Becker, Murphy, and Tamura, 1990) or endogenous (Galor and Weil, 2000; Doepke, 2004; Hazan and Berdugo, 2002; and Moav, 2005) increases in the returns to education.⁴

There is indeed considerable evidence (Leibowitz, 1974; Hanushek, 1992; and many others) for a negative association between the size of families and the quality of children. We refer the reader to Schultz (2007)⁵ for a recent review of this and also a more recent literature using the incidence of twinning or the sibling sex composition as instruments for family size.⁶

The exogenous variation in our study differs from the variation exploited in the twinning (and sibling-sex) studies in an important aspect. Our study exploits variation in the constraints for investing into children – the price of quality investments. Twin studies by contrast identify the effect of rationing parents away from their optimal fertility choice. In the Q-Q model however both the quantity and quality of children are endogenous variables. It is therefore not possible to speak of a causal effect of family size on the quality of children. Ideally, the model is tested by examining variation in fertility and investment into children as incomes and (shadow) prices for quantity and quality are varied. Of course, the problem is that it is hard to measure the prices of having larger families and of investing in children. We interpret the disease burden associated with hookworm as affecting the ease with which families can invest in their children. The differential burden of the disease coupled with the eradication therefore provides variation in the costs of educating children. In this sense, our study is more closely linked to a test of the Q-Q model than the existing studies based on twinning and the sibling sex composition.

3. Background and Research Design

3.1. Hookworm and the Rockefeller Commission

Hookworm is an intestinal parasite that infects humans. The main symptoms of hookworm infection are lethargy and anemia. Death from hookworm disease is rare. The parasite's lifespan is relatively short (on the order of a year or two), and so continual reinfection is required to generate a sustained worm load. Preventive measures include limiting skin contact with polluted soil (through the use of shoes, for example) and dealing with excrement in ways that minimize soil pollution (e.g., the use of sanitary latrines). An infected person can also be treated with de-worming medication, but this might only provide temporary benefits if the reinfection problem is not solved.

The Rockefeller Sanitary Commission for the Eradication of Hookworm Disease (abbreviated below as the “RSC”) was formed in 1910 with the donation of $1 million by John D. Rockefeller. (See Ettling (1981) for a thorough history of the campaign.) Because hookworm was not commonly recognized as a problem at the time, the RSC began by conducting surveys of hookworm-infection rates among children across the region. The RSC surveyed over 600 counties in the South and found hookworm infection to be over 40% in the coastal plain. The RSC also mounted a treatment campaign, which consisted of both free de-worming medications and a public education campaign. Followup surveys conducted immediately afterward as well as in the subsequent decade showed a substantial decline in hookworm infection. Although the stated goal of full eradication was not achieved, the hookworm-infection rate of the region did drop by more than half, and fewer cases of the disease went unnoticed and untreated.

3.2. Identification Strategy

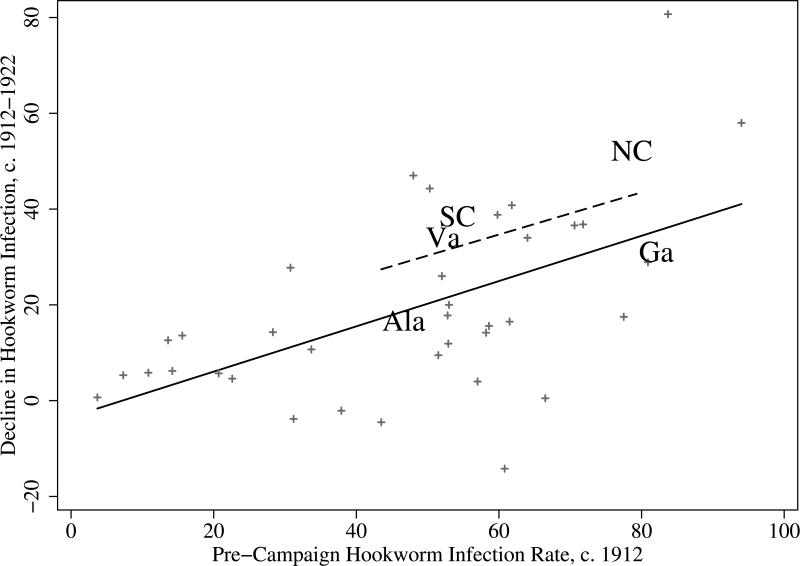
There are two ingredients for identifying the impact of the anti-hookworm campaign on fertility. First, the initiation of the RSC campaign was largely a function of factors external to the Southern states. The eradication campaign was made possible by critical innovations to funding (Rockefeller's philanthropy) and to knowledge (understanding how the disease worked and recognizing its presence). Second, prevalence of the disease varied across the South, largely because of soil type and climate. As a result, populations in areas with higher pre-campaign infection rates stood to benefit more from the RSC's efforts, while areas with low prevalence did not. The data shown in Figure 2, which plots the post-RSC decline in hookworm infection as a function of the pre-campaign infection rates, confirms the latter proposition: areas that had greater hookworm burdens saw greater progress against the disease.

Figure 2.

Highly Infected Areas Saw Greater Declines in Hookworm

Notes: The y axis displays the decrease in hookworm infection post-intervention, as measured by follow-up surveys. The x axis is the pre-treatment hookworm infection rate, as measured by the Rockefeller Sanitary Commission. State abbrevations denote data at the state level, as reported by Jacocks (1924). Plus signs display data for counties in Alabama, as reported by Havens and Castles (1930). Both resurveys are from the early 1920s. Dashed and solid lines represent OLS predictions for the state and county data, respectively.

Areas with higher pre-eradication infection rates received a greater intensity of treatment during the RSC's campaign, which motivates the central variable of the present study:

$$Z_{jt}\equiv H_j^{pre}\times Pos{t}_t,$$

where j indexes the geographic area and t indicates the year. The variable $H_j^{pre}$ denotes the level of hookworm infection among school-aged children in area j at the time of the RSC's initial survey, and Post_t is a dummy variable indicating whether year t is later than the active years of the RSC campaign (1910–1915). We put this variable in a reduced-form equation (estimated below using OLS) to measure the contribution of the eradication campaign to the observed changes in some outcome Y_ijt for person i in area j at time t:

$$Y_{ijt}=\beta Z_{jt}+{\delta }_t+{\delta }_j+X_{ijt}\Gamma +{\epsilon }_{ijt}$$ (1)

in which the δ_t are time dummies, the δ_j are geographic fixed effects, and X_ijt is some vector of individual-level controls. Note that equation 1 has the flavor of a difference-in-difference model. (See Bleakley, 2007, for more on the derivation of this specification.)

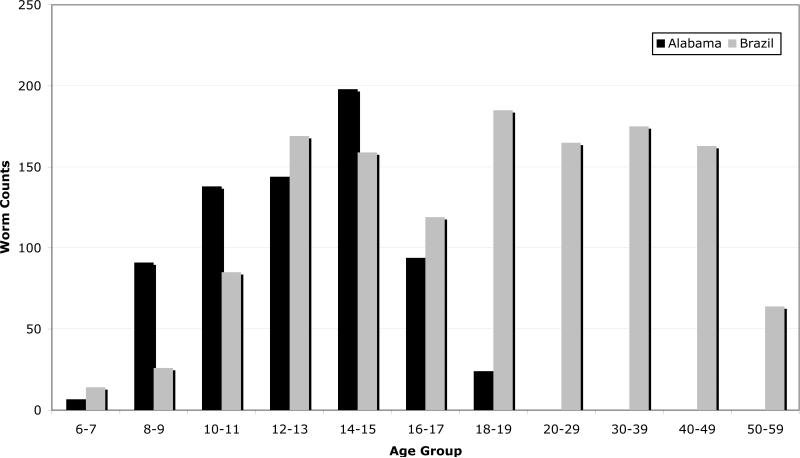
Two additional ingredients help us interpret our results in the quantity-quality framework. First, mortality from hookworm infection was extremely rare in the American South, and so we are able to consider the effects on fertility through morbidity and its effect on the return to schooling. In other words, we argue that hookworm brought about a change in the price of quality, without a change in the price of quantity. Secondly, in the American South, hookworm disease affected almost exclusively children, and not the adult population. This assumption is supported by the infection surveys of region from that period, as seen in Figure 3.⁷ The decline in hookworm infection after age 14 for the Southern U.S. is commonly linked to the age at which children started wearing shoes and the relatively dry forms of agriculture practiced in the region. The fact that hookworm was basically a childhood disease means that we can rule out direct effects of hookworm eradication on adults, and therefore analyze the fertility decision as a function of childhood factors.

Figure 3.

Average Worm Counts, by Age Group, in Alabama and Brazil

Notes: This figure plots the age profile of hookworm counts reported by Smillie and Augustine (1926) for Alabama (black bars) and Brazil (graybars). Smillie and Augustine report counts for ages above 19 as “very light” in Alabama.

4. Empirical Results

4.1. Data and Descriptive Statistics

This study links county-level data on hookworm infection with individual-level data on schooling and fertility. Because county boundaries changed during the period, we use aggregated county groupings, the so-called “State Economic Areas”(referred to below as SEAs or county groups) as the geographic unit. For a detailed description of the sources and definitions of the variables employed in this study, see the data appendix.

Summary statistics for various outcomes at the SEA level are presented in Table I. The first column of numbers shows statistics for the whole sample, while the next two columns present results decomposed by pre-campaign hookworm intensity. The aggregated data show a region with high levels of hookworm infection circa 1910. The infection rates were computed from surveys of school-aged children conducted by RSC in 550+ counties across the South. Also of note is that the RSC directed more resources toward areas with greater hookworm infection, as seen in the data on treatments issued and individuals treated.

Table I.

Summary Statistics: Aggregate Data by County Groups, c. 1910.

	Whole Sample	By Hookworm Infection		Source
		> 40%	<40%
Hookworm-Infection Rate	0.328 (0.234)	0.560 (0.136)	0.161 (0.117)	RSC Annual Reports
Treatments Issued by the RSC, Per Capita	0.059 (0.067)	0.096 (0.068)	0.031 (0.052)	RSC Annual Reports
Individuals Treated at Least Once by the RSC, Per Capita1	0.029 (0.029)	0.048 (0.027)	0.015 (0.022)	RSC Annual Reports
School Enrollment, 1910	0.721 (0.104)	0.711 (0.099)	0.729 (0.108)	IPUMS, author's calculations
Δ Schooling Enrollment, 1910-20	0.089 (0.080)	0.103 (0.090)	0.078 (0.072)	IPUMS, author's calculations
Generalized 5-year Fertility Rate	0.558 (0.130)	0.599 (0.127)	0.529 (0.125)	IPUMS, author's calculations
Δ Generalized Fertility Rate, 1910-1920	−0.060 (0.091)	−0.080 (0.102)	−0.046 (0.080)	IPUMS, author's calculations
Age-adjusted 5-year Fertility Rate	0.545 (0.139)	0.585 (0.134)	0.517 (0.136)	IPUMS, author's calculations
Δ Age-adjusted Fertility Rate, 1910-1920	−0.054 (0.089)	−0.076 (0.097)	−0.038 (0.080)	IPUMS, author's calculations
Sample Size	115	48	67

Notes: Displayed are means and (in brackets) standard deviations, averaged at the level of State Economic Area (county group). The underlying sample of children includes native born blacks and whites age 8-16 in IPUMS from RSC surveyed units in the indicated years. The adult sample includes native born black and white females aged 15-49 in IPUMS from RSC surveyed units in the indicated years. School enrollment is calculated using all native born black and whites in the RSC surveyed units between the ages 8 and 16. The Generalized Fertility Rate is the average number of children less than 5 years per female aged 15-49. The age-adjusted fertility is adjusted for the age composition of the population using a regression of fertility on age dummies in the 1910

¹The treatment intensity variables are only available for 114 (rather than 115) SEAs.

The micro-level data employed in the present study come from the Integrated Public Use Micro Sample (IPUMS), the output of a project to harmonize the coding of historical U.S. Census microdata (Ruggles and Sobek, 1997). The sample consists of native-born whites and blacks in the age range [8,16] in the case of school-age children and in the age range [15,49] for female adults in the study of fertility. The generalized fertility rate reported in Table I is a measure of fertility only available for the aggregate level data. It is calculated as the ratio of children less than 5 years old to females aged 15-49. We also report an age-adjusted fertility rate (adjusted using regression estimates of the age effects of fertility in the 1910 sample), and obtain similar numbers. Note that 1910 fertility rates throughout the South were high, but declining, and school enrollment rates were increasing. Both these trends continue over the period 1910-1920.

The summary statistics are consistent with the prediction of the Q-Q model. The low school enrollment rates in areas with high pre-RSC hookworm infection rates and the post-RSC increase in enrollment in these same areas suggest that hookworm was an impediment to childhood investments, and that the eradication of the disease raised the returns to education. The Q-Q model predicts that fertility would decline following a drop in price of quality, and, indeed, declines in fertility are seen in the two aggregate measures, both in the whole sample, and differentially so in the areas with higher infection rates.

4.2. Main Results

4.2.1. Human Capital

We first estimate the effect of hookworm eradication on school enrollment using equation (1) and the 1910 and 1920 censuses. As described above, the variable of interest, Z_jt; is the interaction of pre-period hookworm infection, $H_j^{pre}$, with a dummy, Post_t, indicating whether the year comes after the RSC. The results reported here are similar to those presented by Bleakley (2007), who describes in greater detail the effect of hookworm eradication on schooling and literacy.⁸

We find that living in areas with high levels of hookworm infection in 1910 is associated with a substantial additional increase in human-capital investments during 1910-1920. We show estimates of pre-period hookworm×post for three different binary dependent variables measuring human-capital investments: school enrollment, regular school attendance, and literacy.⁹ Our finding is the same for all three of these measures: areas with higher levels of hookworm infection saw greater increases in human-capital investment following the anti-hookworm intervention.¹⁰

The human capital investment findings are significant for our study as they allow us to determine the sign of the hookworm eradication effect on the returns to education. (It makes no particular difference for our analysis whether we interpret the disease burden as affecting the effort cost of learning or the labor-market return to human-capital investment.) The sizable excess increase in human-capital investments observed during this period in areas with high pre-period infection rates indicate a positive effect of hookworm eradication on the returns to schooling.

4.2.2. Fertility

Table II, Panel B reports the results of a regression analysis of fertility, again using equation 1. We consider five different measures of fertility: the number of children less than 5 years old, an indicator variable for whether the woman has a child less than 5 years old, an indicator variable for whether the woman has a child less than 1 year old, the total number of children, and an indicator variable for whether the woman has any children. The results are qualitatively similar across outcomes: fertility declines faster in SEAs with high rates of hookworm infection in 1910. The estimates imply that an additional standard deviation in 1910 hookworm infection rates is associated with an additional decline in the number of children younger than 5 years old per fertile woman of about 0.025 per women between 1910 and 1920. The aggregate decline in this fertility measure during this time period amounts to about 0.05. It is also possible to roughly translate these numbers into total fertility rates (TFR), a more familiar measure of fertility. The TFR in the entire sample declined from about 4 to about 3.65 between 1910 and 1920, a decline of about 0.35. This compares with a predicted decline in the TFR of about 0.5 for an SEA with an additional standard deviation in hookworm infection rates between 1910 and 1920. The direct effects of the hookworm eradication campaign on fertility are therefore substantial.

Table II.

Main Results

	Estimates on 1910 Hookworm * Post
Dependent Variables:
Panel A: Quality (Human Capital)
School enrollment	0.0827 (0.0220)
Regular school attendance	0.1565 (0.0254)
Literacy	0.0500 (0.0200)
Panel B: Quantity (Fertility)
Children less than five years old	−0.1023 (0.0239)
At least one child less than five years old	−0.0529 (0.0127)
At least one child less than one year old	−0.0330 (0.0110)
Total number of children	−0.1554 (0.0542)
At least one child	−0.0381 (0.0135)

Notes: Each cell reports estimated coefficients on the interaction pre-campaign hookworm infection rate with the post-period indicator (year=1920) for various fertility and human capital measures as dependent variables. The specification corresponds to equation (1) described in the text. The reported specifications include county-group (SEA) fixed effects as well as fully interacted sets of Age, Race, Region, and Post-period indicators. Standard errors (clustered on SEA) are reported in parentheses. All coefficients are statistically significant at the 1% level. Sample consists of females in the IPUMS between the ages of 15 and 49 in the RSC-surveyed geographic units for 1910 and 1920.

4.2.3. Timing of the Effects

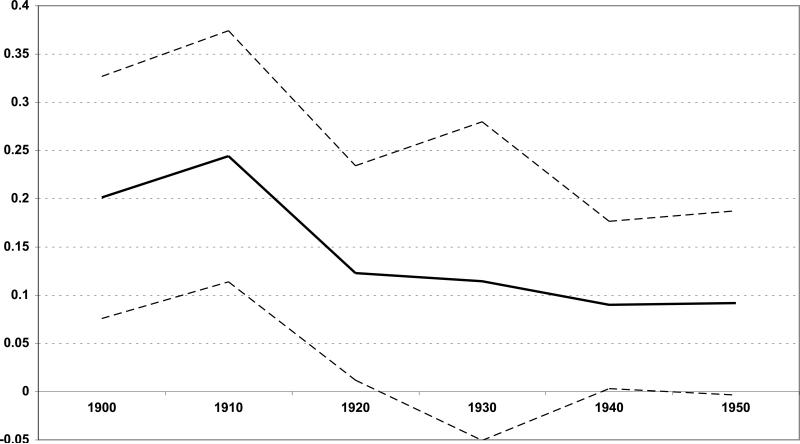
We next show that the changes in fertility and human-capital investment coincide with the Rockefeller campaign rather than with some pre-existing trend. To do this, we expand the analysis to include each decennial census from 1900 to 1950. We estimate pooled regressions on the 1900-1950 data and interact the pre-eradication hookworm-infection rate with year dummies for all years. Figure 4 displays these year-specific coefficients for school and fertility outcomes. (Rather than choose a base year, we omit the SEA fixed effects so as to estimate the interaction between the infection rate and year dummies for all census years between 1900 and 1950. Figure 4 shows that the decline in the relation between hookworm and fertility was indeed concentrated in the period 1910-1920.¹¹

Figure 4.

Impact of 1910 Hookworm Infection Rate on Fertility.

Notes: The y axis plots the year-specific coefficients on the circa 1913 hookworm-infection rate (solid line), plus the 95%-confidence intervals (dashed lines). The x axis is the Census year. The sample consists of all native-born white and black females in the IPUMS between the ages of 8 and 16 in the RSC-surveyed geographic units for 1900, 1910, 1920, 1930, 1940, and 1950. For each year, the coefficients are estimated in a regression of fertility (the number of own children under 5 years old in the household) on pre-intervention hookworm infection and demographic controls. Standard errors are clustered on SEA.

The period of eradication is associated with a major change in the relation between school enrollment and fertility and the 1910 local hookworm infection rate. Also relevant in this context is that, in the period preceding the eradication campaign, the relation between fertility and infection rates is essentially stable. The excess decline in fertility rates in high-infection areas is therefore not the continuation of a pre-existing trend. Moreover, we find that the vast majority of the decline in fertility associated with the hookworm infection rates is observed between 1910 and 1920.

4.3. Sensitivity Analysis

4.3.1. Additional Control Variables

In this subsection, we evaluate the robustness of our finding to controlling for a variety of alternative explanations. The results from this sensitivity analysis on the 1910 and 1920 sample are provided in Table III. Each row in Panel A shows the coefficients on the main variable of interest (hookworm interacted with post) for several different specifications. These additional control variables appear in the regression specification interacted with Post_t, while the main effects of these variables are absorbed by area-level fixed effects. Each row reports the F-statistics related to the interaction of these additional controls with Post_t. These regressions allow for a variety of alternative explanations of why areas with high hookworm infection rates might have experienced disproportional declines in fertility during the period considered here. In row 1, we reproduce the results from Table II, Panel B to facilitate comparison.

Table III.

The Effect of Hookworm Eradication on Fertility: Sensitivity Analysis.

Dependent Variables:	Children less than five years old	At least one child less than five years old	At least one child less than one year old	Total number of children	At least one child
Panel A: Alternative Sets of Control Variables
Additional controls:
None (baseline specification)	−0.1023*** (0.0239)	−0.0529*** (0.0127)	−0.0330*** (0.0110)	−0.1554*** (0.0542)	−0.0381*** (0.0135)
Health and health policy	−0.0691** (0.0276) {4.58}	−0.0531*** (0.0154) {7.50}	−0.0127 (0.0136) {3.23}	−0.1415*** (0.0577) {6.43}	−0.0385** (0.0179) {7.56}
Education and race	−0.0990*** (0.0254) {4.85}	−0.0481*** (0.0139) {3.06}	−0.0302*** (0.0099) {4.91}	−0.1186** (0.0565) {4.66}	−0.0401*** (0.0136) {2.12}
Agriculture	−0.1020*** (0.0300) {5.26}	−0.0487*** (0.0181) {4.02}	−0.0317** (0.0138) {4.91}	−0.2380*** (0.0670) {6.21}	−0.0494** (0.0190) {4.65}
Religion	−0.0888*** (0.0270) {5.50}	−0.0496*** (0.0145) {2.49}	−0.0301** (0.0119) {5.54}	−0.1736*** (0.0612) {1.67}	−0.0505*** (0.0152) {0.50}
All of the above	−0.1008*** (0.0330) {11.55}	−0.0456** (0.0175) {9.03}	−0.0090 (0.0134) {11.22}	−0.2501*** (0.0596) {14.29}	−0.0404* (0.0215) {9.44}
Panel B: Results by Maternal Age
Age range of subsample:
[15,20)	−0.0694*** (0.0238) [0.116]	−0.0479*** (0.0180) [0.095]	−0.0456*** (0.0106) [0.049]	−0.0705*** (0.0269) [0.135]	−0.0466** (0.0185) [0.102]
[20,25)	−0.0634 (0.0537) [0.668]	−0.0339 (0.0298) [0.414]	−0.021 (0.0234) [0.170]	−0.0429 (0.0673) [0.889]	−0.0118 (0.0332) [0.458]
[25,30)	−0.1566** (0.0679) [0.922]	−0.0682** (0.0324) [0.536]	−0.0441 (0.0273) [0.182]	−0.1939 (0.1279) [1.899]	−0.0952*** (0.0314) [0.670]
[30,35)	−0.2119*** (0.0781) [0.836]	−0.0798** (0.0357) [0.516]	−0.0456* (0.0265) [0.151]	−0.1723 (0.1750) [2.661]	−0.0398 (0.0314) [0.744]
[35,40)	−0.1439** (0.0700) [0.723]	−0.1048*** (0.0401) [0.455]	−0.0267 (0.0248) [0.130]	−0.5465** (0.2145) [3.284]	0.0352 (0.0352) [0.793]
[40,50)	−0.0073 (0.0412) [0.305]	−0.0033 (0.0274) [0.223]	−0.0061 (0.0131) [0.043]	−0.2286 (0.1462) [3.116]	−0.0451 (0.0322) [0.781]

Notes: Each cell reports results from a separate regression. Reported are the estimated coefficients on the interactions of pre-eradication hookworm (c. 1910) with the post-period indicator (year=1920). The dependent variables are as indicated in the column headings. The row headings describe additional controls. All specifications include S.E.A. fixed effects as well as fully interacted sets of Age, Race, Region, and Year dummies. For Panel A, F-statistics for the added control sets are reported in curly brackets. For Panel B, the 1910 dependent-variable mean is provided in square brackets. Description of controls are provided in the data appendix. Standard errors (clustered on SEA) are reported in parentheses. Single asterisk denotes statistical significance at the 90% level of confidence, double 95%, triple 99%. Base sample consists of females in the IPUMS between the ages of 15 and 49 in the RSC-surveyed geographic units in 1910-1920.

First, we consider in row 2 the possibility that health and sanitary conditions in 1910 might have correlated with hookworm disease infection rates and might have had an independent effect on subsequent fertility. We control for measures of local health and sanitary conditions collected both by the RSC and other sources. These variables are described in more detail in the data appendix. Of particular interest is the measure of child mortality that we constructed using the 1900 and 1910 census questions on the number of children ever born and the number of surviving children.¹² We also control for fertility in the pre-period directly, as well as for pre-existing fertility trends. Because the Federal government cleaned up unsanitary conditions in and around camps, we control for World War I camp population per resident population. We also include malaria mortality due to the importance of this disease in the development of the American South.

The F-statistic on these health controls clearly indicates that these controls help explain the relative fertility patterns across geographic areas during this period. But, for us the most important finding is that the coefficient on the main variables of interest is robust to the inclusion of these variables. This finding will be similar in all the subsequent rows of Table III, Panel A: the additional controls tend to explain parts of the geographic variation in the fertility decline, but the coefficient on the interaction between 1910 hookworm infection rates with the post-period indicator is not sensitive to the inclusion of these controls.

For row 3 of Panel A, we control for a variety of changes in education systems over this time-period and also for the variation in racial composition and racial conflict across locations during this time. The education controls capture changes in the inputs (pupil-teacher ratios, school density, value of school buildings and equipment, teacher salaries, Rosenwald classrooms, county spending on schools), variation in the returns to literacy across areas, and changes in literacy rates among adults and among children. The racial variables are the fraction of black individuals in 1910 and also the number of lynchings per capita recorded during this time. Again, we see that the coefficient estimate on the main variable of interest is very similar to the baseline estimates in row 1.

Table III, A - 4 is motivated by the link between soil and climate conditions and hookworm infection. The worm favors sandy soil and a warm, humid climate. It is possible that there is a spurious correlation between hookworm infection rates and agricultural factors during this period. We collected data on both the importance of agriculture in the local economy (fraction of population living in urban centers), the value and amount of land available per capita and the sharecropping acreage, and the amounts (per capita) of land used to grow cotton and tobacco. These latter two crops represent the major cash crops grown in the American South during this time. Again, we find that all of these variables jointly contribute to explain fertility trends, but they do not affect the coefficient estimates on hookworm infection in any substantial manner.

Table III, A - 5 directly addresses the Innovation Hypothesis (see Section 2) promoted by the Princeton Project. Here we control for the share of the population that was either Baptist, Methodist, Catholic, or non-churchgoing during this time. (The total of all other religions is the omitted category.) We do indeed find a role for these variables, especially for the share of Catholics. However, estimates of the hookworm coefficient are not materially different from the baseline.

Table III, A - 6 presents the results of controlling for all of these controls simultaneously, and again we find that hookworm eradication leads to an excess decline in fertility rates. All in all, the coefficient estimate on hookworm is quite insensitive to the inclusion of the various control sets.

Table III, Panel B then considers a different mechanism that could have given rise to the observed patterns. The eradication campaign took place between 1910 and 1914. This implies that some of the women in our 1920 data were directly affected as children by the eradication. They thus acquired more human-capital as a result of the eradication campaign, which could directly affect their fertility behavior because schooling competes with child rearing and improves labor market opportunities. If this was indeed the mechanism for the observed decline in fertility rates, then our results cannot be interpreted as supporting a forward-looking, altruism-based model of the fertility transition.

To examine this alternative hypothesis, we estimate the fertility regressions separately by age-group and report these results in Table III, Panel B. The campaign will only have affected school enrollment for women 25 or younger in 1920. There is no evidence that the decline in fertility might be due to different opportunities available to these young women. Indeed, the estimates indicate that the eradication of hookworm reduced fertility across the entire age range.

4.3.2. Labor-market outcomes of adults

We now consider how hookworm eradication affected labor-market outcomes of adults. These should not have been directly affected by eradication, given the neglible prevalence of hookworm among adults. Therefore, examining outcomes related to adults can serve as a falsification exercise. The goal is to search for evidence of shocks to income or sectoral demand that affected fertility and were spuriously correlated with the hookworm measure.

We examine the effect of hookworm eradication on labor-force participation, the choice of occupation¹³, on the probability of living on a farm, and finally the probability of having been born in a different state. The latter variable can serve as a composite index indicating changes in the attractiveness of particular locales for adults. It also helps rule out directly any contamination of the data due to selective migration.

We see little evidence that hookworm eradication directly affected the labor market opportunities of adults during this period. These results are found in Table IV. We examine all of the above outcomes for males and females of different ages. In no instance do we find evidence of an impact of hookworm eradication on adult outcomes if we pool the data within gender across ages. If we look at each age group separately, only in the case of males aged 50-55 do we observe a significant impact of hookworm eradication. It is not surprising that we found one significant coefficient estimate given that we now have six demographic (gender age group) subsamples and seven outcome variables. In summary, there is little evidence of a direct effect of hookworm eradication on adult outcomes.

Table IV.

Falsification Tests: Hookworm Eradication on Adult Occupational Outcomes.

	Samples:
	Females:				Males:
Dependent variables:	All Ages	Ages [25,35)	Ages [35,50)	Ages [50,55]	All Ages	Ages [25,35)	Ages [35,50)	Ages [50,55]
Labor-force participation	−0.0056 (0.0284) [0.3238]	0.0207 (0.0349) [0.3277]	−0.0264 (0.0331) [0.3237]	−0.0382 (0.0501) [0.3091]	−0.0069 (0.0065) [0.9790]	0.0051 (0.0084) [0.9766]	−0.0048 (0.0094) [0.9824]	−0.0492 ** (0.0234) [0.9760]
Occupational income score	0.0581 (0.4163) [3.3444]	0.2195 (0.5295) [3.4879]	−0.1159 (0.5058) [3.3236]	−0.0626 (0.7358) [2.8716]	−0.0186 (0.4912) [18.5736]	0.9070 (0.5863) [18.2216]	−0.6510 (0.6794) [19.1484]	−0.1192 (1.0823) [17.8854]
Duncan socioecon. index	−0.3499 (0.6185) [4.3239]	−0.2522 (0.8407) [4.5981]	−0.3388 (0.7316) [4.2919]	−1.0809 (1.0012) [3.3925]	−0.4529 (0.7931) [19.8944]	1.1373 (0.8798) [18.9747]	−1.5683 (1.1703) [21.0538]	−0.7018 (1.8652) [19.1638]
Lives on a farm	−0.0379 (0.0362) [0.5601]	−0.0166 (0.0469) [0.5409]	−0.0625 (0.0431) [0.5715]	0.0148 (0.0807) [0.5923]	−0.0249 (0.0397) [0.5662]	−0.0756 (0.0478) [0.5357]	0.0250 (0.0547) [0.5708]	−0.0344 (0.0694) [0.6473]
Works in agriculture	−0.0360 (0.0342) [0.1844]	−0.0206 (0.0417) [0.1830]	−0.0460 (0.0401) [0.1866]	−0.0318 (0.0590) [0.1820]	−0.0416 (0.0382) [0.6043]	−0.0769 (0.0489) [0.5783]	−0.0002 (0.0492) [0.6027]	−0.1030 (0.0665) [0.6909]
Works as craftsman or operative	−0.0022 (0.0092) [0.0217]	−0.0013 (0.0147) [0.0243]	−0.0037 (0.0117) [0.0216]	−0.0055 (0.0164) [0.0126]	0.0033 (0.0265) [0.1335]	0.0508 (0.0377) [0.1404]	−0.0425 (0.0339) [0.1389]	−0.0138 (0.0424) [0.0950]
Born in a different state	0.0029 (0.0237) [0.1620]	−0.0321 (0.0298) [0.1440]	0.0308 (0.0352) [0.1648]	0.0312 (0.0672) [0.2204]	0.0268 (0.0267) [0.1924]	0.0228 (0.0302) [0.1679]	0.0266 (0.0374) [0.2071]	0.0629 (0.0574) [0.2236]

Notes: Each cell reports the results from a separate regression of the indicated variable on pre-treatment hookworm × post. The dependent variables are indicated in each Panel heading, and are derived from reported occupational and birthplace information. Robust standard errors in parenthesis (clustering on SEA). Mean of dependent variable in square brackets. Single asterisk denotes statistical significance at the 90% level of confidence, double 95%, triple 99%. Sample consists of all whites and blacks in the IPUMS for the indicated ages in the RSC-surveyed geographic units in 1910-20. All specifications include dummies for SEA and for age × black × Census region × year.

This provides further evidence that hookworm eradication presents an empirical test of forward-looking models of the fertility transition; that is, of models that emphasize the effect of change in childrens’ welfare on parental fertility decisions against the alternative that the fertility transition is caused by a change in variables (e.g. female wages) affecting adults directly.

5. The Quantitative Importance of the Q-Q model

In this section, we compare the trend variation in fertility and schooling observed during this period in the American South with the variation in fertility and schooling induced by the eradication of hookworm. This comparison can inform us about the quantitative ability of the Q-Q model to explain the fertility transition.

In the spirit of the Q-Q model we express both fertility n and human capital investments h as functions of the prices of the quantity and quality of children (p_n; p_h) :

$$\begin{array}{cc}\hfill n_t& =n(p_n,p_h)\hfill \\ \hfill h_t& =h(p_n,p_h)\hfill \end{array}$$

Human-capital investments are understood broadly — they might include educational expenditures, health investments, or even expenditures on child quality of life. Empirically, we use school enrollment as a proxy for human-capital investments overall.

We interpret the eradication of hookworm as a change in the price of investing in children. The response to this shock is both an increase in the quality of children and a decrease in fertility. The post-period interactions reported in Table II then identify the response in fertility and human-capital investments to variation in the price of human-capital investments induced by variation in hookworm. In the notation above, these parameters measure

$$A\equiv \frac{\partial n}{\partial p_h}\frac{\partial p_h}{\partial \text{infection}};B\equiv \frac{\partial h}{\partial p_h}\frac{\partial p_h}{\partial \text{infection}}$$

While we do not observe $\frac{\partial p_h}{\partial \text{infection}}$ directly, the ratio $\frac{A}{B}$ allows us to measure the relative responsiveness of fertility and human capital investments with respect to variation in costs of human capital investments:

$$\frac{A}{B}=\frac{\partial n}{\partial p_h}/\frac{\partial h}{\partial p_h}$$

This relative responsiveness can be compared to the trend changes in the fertility (ΔN) and human capital investment measures (ΔH) we observe in the historical data. The question we want to consider is whether A/B is of the same order of magnitude as $\frac{\Delta N}{\Delta H}$.

It is important to understand that this comparision with historical data does not inform us about the contribution of hookworm eradication itself to the overall decline in fertility during the transition. Instead we consider the question of whether it is possible that the historically observed comovements of quantity and quality during the transition are consistent with the relative variation in quantity and quality caused by the eradication of the hookworm disease?

Our answer is yes. The regression results in Table II show the estimated fertility and human-capital response to hookworm eradication. Their ratio yields the change in fertility relative to the change in human-capital investments that is associated with eradication. This number is approximately −1.24.¹⁴ Thus, an increase in school enrollment by 1 percentage point due to hookworm eradication is associated with a decline in the generalized fertility rate of about 0.0124. The corresponding aggregate changes in school enrollment and fertility for 1910–1920 (presented in Table I) were, respectively, 0.089 and −0.060. Taking the ratio we observe a fertility decline of −0.67 percentage points per percentage point increase in enrollment.

These results imply that the co-variation in fertility and schooling caused by hookworm are of approximately equal relative size to the secular co-movements in fertility and schooling observed during this time. This provides support for a large role of the Q-Q interaction in explaining the fertility transition. Of course, it is not clear that this generalizes to other time periods or societies. To be able to generalize with confidence will require observing similar findings in many different countries and time periods.

6. Conclusion

This study contains evidence on the importance of competing models of the fertility transition observed during the development of societies to high income societies. The episode analyzed is the eradication of hookworm disease in the American South (c. 1910). In previous work, it was shown that the eradication of hookworm disease led to a significant increase in school attendance and literacy. The present study shows that this increase in human capital was accompanied by a fertility decrease that was both economically and statistically significant. A decline in the hookworm infection rate from 40% to 20% is associated with a decline in fertility that amounts to 40% of the entire fertility decline observed in the American South between 1910 and 1920.

These results can be used to test theoretical models on the interaction of fertility and human capital investments in growth. It provides broad support for models of the fertility transition that link parental fertility decisions to the educational investment decisions parents face with respect to their children. It strengthens the empirical support for the literature linking human-capital investment and fertility in models of economic growth and demographic transitions. These models argue that increases in returns to education cause the simultaneous observed increases in human capital investments and declines in fertility rates.

The relative change in fertility and schooling caused by hookworm eradication are approximately equal to aggregate co-movements during the period considered. This correspondence suggests an important role for the interaction of fertility and human capital investments in growth.

Data Appendix

A. Sources and Definitions for the Micro Data

The micro data consist of samples drawn from the Censuses of 1900, 1910, 1920, 1930, 1940, and 1950, accessed through the IPUMS project (Ruggles and Sobek (1997)). (The 1910 data include the black and hispanic oversamples. Results are not sensitive to their exclusion.) The sample consists of native-born whites and blacks in the age range [8,16] in the case of children, and in the age range [15,55] in the case of adults. The age criteria for children serves to select children of school age who are likely not yet old enough to have migrated on their own. The outcome variables are defined as follows:

• School enrollment

This is an indicator variable for whether the child has attended school at any time during a specified interval preceding the day of the Census. The length of this interval varies across the Censuses as follows: 1900, within the past year; 1910 and 1920, since September 1; 1940, since March 1; 1950, since February 1.

• Regular school attendance

This is an indicator variable that is switched on if the child is attending and not working. We consider a child to be working if the census recorded an occupation for him/her, which corresponds to an IPUMS occ1950 code that is not missing and less than or equal to 970.

• Literacy

This variable is an indicator for the ability to read and/or write. Census questions contained categories for being able to read but not write, vice versa, both or neither. We coded the first three as literate. (The first two responses were relatively rare.) These data were collected only for the 1900–20 samples. The literacy question was only asked for individuals 10 years and older.

• Fertility

The census data provide the following information on own children living in the household: total number, total number of those under age five, and the age of youngest child. These variables are used to define the following dependent variables:

• – The number of children less than 5.

• – An indicator variable for whether the woman has a child less than 5 years old.

• – An indicator variable for whether the woman has a child less than 1 year old.

• – The total number of children.

• – An indicator variable for whether the woman has any children.

• Labor-force participation

This ibinary variable indicate whether the individual is working. Prior to 1940, this variable is based on whether the individual's reported occupation was classified as a “gainful” one.

• Occupational income score

The occupational income score is an indicator of income by disaggregated occupational categories. It was calibrated using data from the 1950 Census, and is the average by occupation of all reported labor earnings. See Ruggles and Sobek (1997) for further details.

• Duncan socio-economic index

This measure is a weighted average of earnings and education among males within each occupation. The weights are based on analysis by Duncan (1961), who regressed a measure of perceived prestige of several occupations on its average income and education. This measure serves to proxy for both the income and skill requirements in each occupation. It was also calibrated using data from the 1950 Census.

• Works in agriculture

Defined as the IPUMS variable “occ1950” being equal to 100, 123, or anything in the 800s.

• Works as Craftsman or Operative

Defined as the IPUMS variable “occ1950” being between 500 and 699 (inclusive).

B. Sources and Definitions for the Aggregate Data

There are two units of observation for the area-level data: county and state economic area (SEA). Because county boundaries change over time and because county of residence is not available in the later Censuses, we use the SEA as the aggregate unit for the sequential-cross-section analysis. The SEAs are aggregations of counties, with an average number of 8.5 counties per SEA. SEA boundaries tend to be more stable, in part because they were often defined by a state boundary or significant natural feature (river or mountain range, e.g.).

The area-level data come from a variety of sources, but principally from the RSC annual reports and the ICPSR's study #3, the latter of which is a collection of historical Census tabulations. The following is a list of the aggregate variables with information on sources, definitions and method of aggregation. The source is indicated in parentheses at the end of each item's text.

• Hookworm infection rate

The source data are at the county level and from the period 1911–1915. The infection numbers in most cases are from surveys conducted by the Rockefeller Sanitary Commission (RSC) as prelude to (or simultaneously with) dispensing treatments. In a few instances, the RSC dispensaries had already visited the county before making the survey. For this latter case, we use the examinations conducted by the dispensaries to construct the hookworm infection rate, rather than using data that comes after the administration of the RSC treatments. (The hookworm-infection rates constructed from survey and examination have a correlation coefficient greater than 0.95 for those cases in which the survey was done first.) The infection data were aggregated to the SEA level using a population-weighted average. (RSC annual reports.)

• Individuals treated by the RSC, per capita

The source data are at the county level and from the period 1911–1915. The RSC dispensaries tracked how many individuals received de-worming treatments. We sum these numbers to the SEA level and divide by total population. (RSC annual reports.)

• Sanitary Index

The RSC conducted independent surveys of the condition of sanitation infrastructure, including whether buildings had proper latrines, clean water sources, etc. Several measures of sanitation were combined by the RSC to form an index. The coverage of this indicator is incomplete. Because SEAs were reasonably homogeneous, we construct a simple average of these indices, ignoring the missing data within SEA. (RSC annual reports.)

• Examined by RSC per capita

The source data are at the county level and from the period 1911–1915. The RSC dispensaries tracked how many individuals were examined by the dispensary's medical staff. We sum these numbers to the SEA and state levels and divide by total population. (RSC annual reports.)

• County spending

Data were input at the county level on county-government spending on education and health/sanitation for the years 1902 and 1932. (The 1922 publication in the series did not include these categories of spending, and the 1913 publication did not include earmarked transfers from the state government.) The health spending is normalized by total population, while the education expenditure is normalized by school-age population. We construct a population-weighted average for the SEAs. (County level: U.S. Bureau of the Census, 1915b and 1935. State level: annual reports of the federal Commissioner of Education.)

• Full-time health officer

These data were compiled at the county level, and include information on the first year each county employed a full time health officer. We coded this variable as one if such an office was created between 1910 and 1920 (inclusive). Only one county (Jefferson county in Kentucky) had created such a post before 1910, and the results above are not sensitive to its reclassification. To aggregate to the SEA level, we create a population-weighted average of the constituent counties. (Ferrell et al. 1932.)

• WWI Cantonment size per capita

We collected data on the troop numbers that were mustered and trained at the major Army cantonments of mobilization/embarkation for the World War I. Of the 32 cantonments, there were 19 camps in the South. These were “camps and cantonments that were used for mobilizing and training combat divisions,” but this excludes “miscellaneous groups” which comprised the “special camps, usually of semipermanent construction that were intended for mobilizing and training special troops, such as the Quartermaster Department Camp, Camp Joseph E. Johnston, Jacksonville, Florida.” We input the highest value given for the number of soldiers within a camp during 1918-20, aggregated to SEA level, and then normalized by total 1910 population. (Bowen, 1928.)

• Malaria mortality

These data were compiled at the county level and refer to the period 1919–1921. To construct SEA rates, We create a population-weighted average of the constituent counties. (Maxcy, 1923.) The state-level data are the fraction of total mortality in 1890. (Census, 1894.)

• Fertility Rate, 1910, and Change in fertility, 1900–10

The fertility rate for 1910 is measured from Census tabulations under the fraction of the population under six years of age, defined as 1 – (v41 + v53)/(v20 + v21) using the ICPSR variable names. For 1900, the tabulations permit calculating the fraction of the population under five for 1900, or 1 – (v22 + v37 + v39 + v41 + v43)/(v8 + v10). When computing the approximate difference, we up-weight the 1900 number by 5/4. To construct SEA rates, we sum the components over the constituent counties and apply the above formulae. State data is available through a separate tabulation, to which we apply the same formulae. (ICPSR Study #3.)

• Child Mortality, 1900–10

Defined from IPUMS samples using the methodology of Preston and Haines (1984), and aggregated to SEA level.

• Fraction black, 1910

These data come from the 1910 Census. Defined as the fraction of the areas males who are black, out of the total population of blacks and whites. Specifically this is defined as (v24 + v25)/(v24 + v25 + v22 + v23), using the variable codes of the ICPSR study. To construct SEA rates, we sum the components over the constituent counties and apply the above formulae. (ICPSR Study #3.)

• Rosenwald schools per capita

This measures the number of classrooms per capita built by the Julius Rosenwald Fund as of 1930. The denominator normalizes the number of classrooms by the population of blacks aged 5–19 in 1930. To construct SEA rates, we create a black-population-weighted average of the constituent counties. (Johnson et al., 1941.)

• Lynchings per capita, 1900–30

The base data is the number of lynchings per 100,000 population by county in the years 1900-30. The denominator is the county population in 1930. To construct SEA rates, we create a population-weighted average of the constituent counties. (Johnson et al., 1941.)

• Population urban

From Census tabulations measuring the population residing in metro areas. For 1910, the urban population is contained in variable v9 in the ICPSR data, which we scale by the total population as defined above. The 1900 fraction urban is also defined in the 1910 data as v13/(v13 + v14). We construct the change in urbanization using the difference between the two variables. To construct SEA rates, we sum the components over the constituent counties and apply the above formulae. State data is available through a separate tabulation, to which we apply the same formulae. (ICPSR Study #3.)

• Crop acreage per capita

The base data measures the total farmed acreage at the county level, regardless of tenancy. This is constructed with the formula (v155 + v164 + v175), using the ICPSR variable names, and scaled by total population. To construct SEA rates, we sum the components over the constituent counties and apply the above formula. (ICPSR Study #3.)

• Sharecropped areas per capita

The base data is a county-level measure of total acreage sharecropped (v164 using the ICPSR variable scheme). We scale this by total population. To construct SEA rates, we sum the components over the constituent counties and apply the above formula. (ICPSR Study #3.)

• Cotton acreage per capita

The base data is cotton acreage in 1910 by county. We normalize this number by the county population, as defined above. To construct SEA rates, We create a population-weighted average of the constituent counties. (Census, 1915.)

• Tobacco acreage per capita

The base data is tobacco acreage in 1910 by county. We normalize this number by the county population, as defined above. To construct SEA rates, we create a population-weighted average of the constituent counties. (Census, 1915.)

• Farm value per capita

The base data is a county-level measure of the value of farm land and buildings, regardless of tenancy. This is defined as (v177 + v166 + v157) using the ICPSR variable scheme). We scale this by total population, as defined above. To construct SEA rates, we sum the components over the constituent counties and apply the above formula. (ICPSR Study #3.)

• School Term Length

Average length of school term, in weeks. Kentucky county data are imputed from cross-tabulated data on number of schools by months. The imputation is calibrated using Alabama data, which contain a continuous measure and a cross-tabulation. (County level: Reports of state departments of education, various years, and author's calculations. State level: annual reports of the federal Commissioner of Education.)

• Average Monthly Salaries for Teachers

(County level: Reports of state departments of education, various years, and author's calculations. State level: annual reports of the federal Commissioner of Education.)

• School density

Number of schoolhouses operating in the county, divided by land area in square miles. (Reports of state departments of education, various years, and author's calculations.)

• Change in Number of Teachers per School

(Reports of state departments of education, various years, and author's calculations.)

• Pupil/Teacher Ratio

Average attendance divided by number of teachers. (County level: Reports of state departments of education, various years. State level: annual reports of the federal Commissioner of Education.)

• Value of School Plant and Equipment

(Reports of state departments of education, various years, and author's calculations.)

• Returns to Literacy for Adults

Measured from a regression of the occupational income score on literacy status, by SEA, for the 1910 and 1920 census samples of adults. (Authors’ calculations using the 1910 and 1920 IPUMS data.)

• Baptists

Defined as membership of Baptist Churches (1906) per total population (measured as the average of 1900 and 1910 total population). Baptist churchmembers are reported by variables 10 through 21. (ICPSR Study #2896.)

• Methodists

Defined as membership of Methodist Churches (1906) per total population (measured as the average of 1900 and 1910 total population). Methodists churches are described by variables 63 through 71 plus variable 89. (ICPSR Study #2896.)

• Catholic

Defined as membership of Catholic Churches (1906) per total population (measured as the average of 1900 and 1910 total population). (ICPSR Study #2896.)

• Non-Church Members

Defined as non-church-pertaining population (1906) as a fraction of total (measured as the average of 1900 and 1910 total population). (ICPSR Study #2896.)