A fast Monte Carlo EM algorithm for estimation in latent class model analysis with an application to assess diagnostic accuracy for cervical neoplasia in women with AGC

Abstract

In this article we use a latent class model (LCM) with prevalence modeled as a function of covariates to assess diagnostic test accuracy in situations where the true disease status is not observed, but observations on three or more conditionally independent diagnostic tests are available. A fast Monte Carlo EM (MCEM) algorithm with binary (disease) diagnostic data is implemented to estimate parameters of interest; namely, sensitivity, specificity, and prevalence of the disease as a function of covariates. To obtain standard errors for confidence interval construction of estimated parameters, the missing information principle is applied to adjust information matrix estimates. We compare the adjusted information matrix based standard error estimates with the bootstrap standard error estimates both obtained using the fast MCEM algorithm through an extensive Monte Carlo study. Simulation demonstrates that the adjusted information matrix approach estimates the standard error similarly with the bootstrap methods under certain scenarios. The bootstrap percentile intervals have satisfactory coverage probabilities. We then apply the LCM analysis to a real data set of 122 subjects from a Gynecologic Oncology Group (GOG) study of significant cervical lesion (S-CL) diagnosis in women with atypical glandular cells of undetermined significance (AGC) to compare the diagnostic accuracy of a histology-based evaluation, a CA-IX biomarker-based test and a human papillomavirus (HPV) DNA test.

1. Introduction

Standard measures of diagnostic accuracy include sensitivity (probability of positive diagnosis given disease), specificity (probability of negative diagnosis given no disease), positive predictive value (probability of disease given positive diagnosis), and negative predictive value (probability of no disease given negative diagnosis). A discussion of the relative merits of these diagnostic accuracy measures was presented in [30] and [31].

In medical literature the focus has been primarily on the estimation of sensitivity and specificity because these measures usually can be considered as characteristics of the diagnostic tests that are not influenced by varying prevalence or characteristics of the population. Positive predictive value (PPV) and negative predictive value (NPV), on the other hand, vary with the prevalence of disease in the population.

Note that sensitivity and specificity can be evaluated based on the premise that the true classification is known, i.e., a gold standard (GS) test that is regarded as definitive exists. In practice, it is often difficult, inappropriate, or impossible to have a true GS test because of prohibitive time and cost, risk to the living subjects or ethical concerns[45]. It has been found in about 1/3 of all medical articles, describing diagnostic test evaluations, that no well-defined GS was used [42]. In most such cases, naïve estimates of sensitivity and specificity were calculated by treating a reference method as if the reference was a “perfect” GS. Several authors [e.g., 14, 40] have pointed out that such naïve estimates are biased and, therefore, the misclassification in the reference test should not be ignored. Thus, the problem of assessing the accuracy of diagnostic tests when there is no perfect GS against which to compare is commonly faced by biostatisticians.

Latent class models (LCM) have been proposed as a statistical technique that allows such assessment [1, 37, 45]. An extensive treatment of LCM analysis was first presented in [20]. In traditional LCM applications, a dichotomous latent variable is used to indicate the true disease status of each patient. The test results are assumed conditionally independent (CI) given the latent disease class variable. A system of nonlinear moment estimating equations (MEEs) is constructed, setting the joint cell probabilities equal to functions of conditional probabilities of test results given disease status (sensitivities/specificities) and probability of disease status (prevalence). With a minimum of K = 3 observed tests, the MEEs can be uniquely solved because the number of parameters, 2K + 1, is equal to the available degrees of freedom, 2^K − 1.

Although applying MEEs to LCM analysis is straightforward, several difficulties arise. For instance, the numerical estimates for sensitivity, specificity and prevalence from MEEs may be out of interval [0, 1]. The prevalence in MEEs applied to traditional LCM is assumed to be constant, which might not be appropriate for some diseases, e.g., HPV prevalence in the United States, where risk of the disease may vary with age. Furthermore, this method does not handle the over-identified case well. When the number of MEEs to solve exceeds the number of parameters, the over-identification problem exists and is handled only in an ad hoc fashion. Lastly, the CI assumption may not always be valid. Estimators of diagnostic accuracy and disease prevalence can be problematic when the assumption of CI is violated [44]. Various extensions of traditional LCM have been proposed to relax this CI assumption [e.g., 43, 50, 51].

Alternatively, when three or more tests are applied simultaneously to the same individuals, the measures of test accuracy and true prevalence in the populations can be routinely estimated by maximum likelihood (ML) methods [e.g., 1, 2, 4, 16, 37]. The expectation-maximization (EM) algorithm can be used as an estimation tool in LCM analysis [6, 24, 47]. When the E-step in an EM algorithm is intractable because of difficulty in computing the expectation of the log-likelihood, Monte Carlo EM (MCEM) algorithm [3, 47] is suggested.

The EM/MCEM algorithm, however, does not produce standard errors of estimates directly. Louis [26] and Oakes [35] derived formulas for standard errors when using the EM algorithm, based on the missing information principle [36], by extracting the observed information matrix. McLachlan and Krishnan [29] recommended Louis’s method as the one best suited to be adapted for MCEM, although the performance of Louis’s adjusted information matrix for standard error estimates in MCEM is not yet clear.

In this article, we implement a fast MCEM algorithm to estimate parameters of interest and a Monte Carlo version of Louis’s formula for standard error estimates. Our study also compares the standard error estimates from Louis’s formula with the bootstrap standard error estimates [9, 10] in MCEM settings through an extensive Monte Carlo study. Simulation demonstrates that the Louis adjusted information matrix based approach usually overestimates standard error when the sample sizes are very large (n ≥ 500). When sample size is moderate (e.g., n = 122), Louis’s formula estimates standard errors that are similar to the bootstrap standard errors. Considering the coverage probabilities, the bootstrap percentile intervals are the most accurate.

The rest of our article is organized as follows. The motivating data example is described in Section 2. In Section 3, we first briefly summarize the proposed LCM technique and describe the fast MCEM algorithm for estimation in LCM analysis. We further study the performance of the proposed fast MCEM algorithm by discussing the rate of convergence for varying sizes of the observed and simulated samples as well as the levels of tolerance. We also present standard error estimation using Louis’s formula within MCEM framework. A simulation study follows in Section 4 comparing standard error estimates and confidence interval coverage probabilities between Louis adjusted information matrix based approach and bootstrap approaches. In Section 5, we focus on the application to the motivating data example. We close with Section 6 on a broader discussion on LCM for evaluating diagnostic tests in the absence of a perfect GS.

2. Motivating Example

As recently as the 1940s, invasive cervical cancer was a major cause of death among women of childbearing ages in the United States. However, with the introduction of the Papanicoloau (Pap) smear in the 1950s—a simple test that uses exfoliated cells to detect cervical cancer and its precursors—the incidence of invasive cervical cancer declined dramatically. Between 1955 and 1992, cervical cancer incidence in this country declined by 74% [32].

Many researchers [18, 21, 48] found that women with a cytological diagnosis of atypical glandular cells of undetermined significance (AGC) from Pap smear had a high rate of intraepithelial neoplasia or invasive carcinomas. Yet a notably high percentage of women with AGC [72% reported in 25] do not have a significant cervical lesion (SCL) and do not require the aggressive level of treatment that is often provided to those women. After a diagnosis of AGC, additional screening to distinguish between those women who have significant cervical precancerous or cancerous lesions and those who do not is needed to avoid an unnecessarily high referral rate and over treatment of healthy women.

Research conducted by the National Cancer Institute (NCI) and other investigators throughout the 1980s and 1990s demonstrated that in the United States virtually all cases of cervical neoplasia are caused by persistent infection with specific types of human papillomavirus (HPV), which can be transmitted by sexual contact. Dunne et al. [8] in their paper found a statistically significant trend for increasing HPV prevalence aged from 14 to 24 years among females (P < 0.001), followed by a gradual decline in prevalence through 59 years (P = 0.06). They indicated that the burden of prevalent HPV infection among females was greater than previous estimates and was highest among those aged 20 to 24 years.

Liao et al. [25] in their GOG-0171 study reported that in the United States additional screening for HPV status by the Digene® Hybrid Capture II (HC2) High-Risk HPV DNA test among women with AGC produced a 97% sensitivity, 87% specificity, and a 99% negative predictive value (NPV). In short, the HC2 method detects presence of any one or more of 13 high-risk type of HPV DNA including HPV types 16, 18, 31, 33, 35, 39, 45, 51, 52, 56, 58, 59 and 68 in a liquid-based cytology specimen. Thus, HC2 testing following a diagnosis of AGC fairly accurately identified those women with SCL. Their paper also assessed the accuracy of a carbonic anhydrase IX (CA-IX) biomarker of SCL and reported an overall sensitivity and specificity of 75% and 88%, respectively, and a NPV of 90%.

All of the accuracy statistics reported in [25] were based on an imperfect “Gold Standard” (“GS”) diagnosis determined from histological evaluation of the cervical transformation zone within 6 months of the initial cytologic diagnosis of AGC. This “GS”, however, produced observations that were contaminated to some degree by misclassifications. It is known that misclassified “GS” diagnosis caused a bias in the accuracy estimates when using the diagnosis as if they are the truth [14]. The estimates are generally biased toward zero, thus underestimating true accuracy, with the bias increasing with the percentage of misclassifications by the “GS”.

We want to assess the diagnostic accuracy of the HC2 test and the CA-IX tumor-associated biomarker as well as the histology-based “GS” without assuming true disease status is known. Either a positive (1) or negative (0) result is recorded for histological evaluation, CA-IX biomarker test, and HC2 test for each individual. Given the association described above of HPV prevalence with age [8] and hence, with cervical neoplasia, it is necessary to allow prevalence in the LCM to vary with age.

3. The Proposed Method

Let the latent binary variable X indicate the presence (X = 1) or absence (X = 0) of true disease. We observe the results of K (K ≥ 3) binary test variables, {Y₁, …, Y_K}, for each of i = 1, …, n patients. One of these variables may be the best available but yet imperfect reference test, and the others may be newly developed tests that would offer an advantage over the reference test, if accurate. A statistical model with vector parameter θ is assumed for the joint distribution of {Y₁, …, Y_K} given X, denoted by P_θ (Y₁, …, Y_K | X), and for the distribution of X, denoted by P_θ (X = x).

3.1 Conditional Independence Assumption

The simple yet popular model for P_θ (Y₁, …, Y_K|X) assumes conditional independence (CI), i.e., given the unobserved true disease status X, the test variables {Y₁, …, Y_K} are statistically independent. In this case the likelihood function is

$$ℒ(\mathit{\theta })=\prod _{i=1}^n\{\prod _{k=1}^K{P}_{\mathit{\theta }}(Y_{ik}|X_i)\}{P}_{\mathit{\theta }}(X_i=x_i).$$ (1)

Wasserman [46] argued this CI assumption intuitively means that once you know the true disease status X, the test result of Y₁ provides no extra information about any of Y₂, …, Y_K test results, which is reasonable in diagnostic settings for tests that have different bases, e.g., histology-based versus DNA test. The sensitivity and specificity of test k are P_θ (Y_ik = 1 | X_i = 1) and P_θ (Y_ik = 0 | X_i = 0), respectively. The prevalence of disease is P_θ (X_i = 1).

It is worth noting that even relaxing this CI assumption, the workflow to use our proposed algorithm in LCM analysis would stay the same. However, to focus more on the following estimation part, we assume CI holds at this stage.

3.2 Model Specification

In the current application, it is necessary to modify the traditional LCM to allow prevalence to vary as a function of covariates [e.g., 12, 15]. The prevalence P_θ (X_i = x_i) in Equation (1) is replaced by P_θ (X_i = x_i | Z_i), where Z_i is, potentially, a vector of covariates that are thought to affect the prevalence of disease. In our application, Z_i includes the variables age and age squared.

Since {Y₁, …, Y_K} and X are dichotomous variables, it is natural for us to model P_θ (Y_ik | X_i) and P_θ (X_i | Z_i) using logistic functions. The models are specified as

$$P_{\mathit{\theta }}(Y_{ik}=1|X_i)=\frac{\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)}{1+\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)},$$ (2)

$$P_{\mathit{\theta }}(X_i=1|Z_i)=\frac{\text{exp}({\gamma }_0+{\gamma }_1{Z}_i+{\gamma }_2{Z}_i^2)}{1+\text{exp}({\gamma }_0+{\gamma }_1{Z}_i+{\gamma }_2{Z}_i^2)}.$$ (3)

We use quadratic function to model the logit of P_θ (X_i = 1 | Z_i) because this pattern is indicated from raw data summary statistics as well as in [8]. In this setup, the vector parameter θ is being estimated rather than accuracy parameters themselves (sensitivity, specificity, and prevalence). This model specification guarantees that the diagnostic accuracy parameter estimates calculated from estimated θ are always bounded in [0, 1].

If the values of X were observed, by maximizing the complete data likelihood

$${ℒ}_c(\mathit{\theta };\mathbf{x},\mathbf{y},\mathbf{z})=\prod _{i=1}^n\left\{\prod _{k=1}^K{[P_{\mathit{\theta }}(Y_{ik}=1|X_i)]}^{I(Y_{ik}=1)}{[P_{\mathit{\theta }}(Y_{ik}=0|X_i)]}^{I(Y_{ik}=0)}\right\}\times {[P_{\mathit{\theta }}(X_i=1|Z_i)]}^{I(X_i=1)}{[P_{\mathit{\theta }}(X_i=0|Z_i)]}^{I(X_i=0)},$$

we would obtain the estimate for θ = [β₀₁, β₁₁, …, β_0K, β_1K, γ₀, γ₁, γ₂] and thus estimates for sensitivities, specificities and prevalence. Unfortunately, X’s were not available in LCM analysis. That is to say, we cannot directly apply ML method to ℒ_c (θ; x, y, z). Instead of dealing with complete data likelihood, the usually less tractable observed data likelihood, which integrates out the unobserved variable X, can be maximized,

$${ℒ}_{obs}(\mathit{\theta };\mathbf{y},\mathbf{z})=\prod _{i=1}^n{\int }_{\mathit{X}}\left\{\prod _{k=1}^K{[P_{\mathit{\theta }}(Y_{ik}=1|X_i)]}^{I(Y_{ik}=1)}{[P_{\mathit{\theta }}(Y_{ik}=0|X_i)]}^{I(Y_{ik}=0)}\right\}\times {[P_{\mathit{\theta }}(X_i=1|Z_i)]}^{I(X_i=1)}{[P_{\mathit{\theta }}(X_i=0|Z_i)]}^{I(X_i=0)}dF(\mathit{X}),$$

where F (·) is the distribution function for random variable X.

3.3 EM Algorithm

EM algorithm [6, 19] is an iterative method for ML parameter estimations when some of the random variables involved are not observed, and is very useful when maximizing ℒ_obs can be difficult but maximizing the conditional expectation of complete data log-likelihood given the observed data is relatively simple. Given a previous parameter estimate θ^(t−1), EM obtains an updated parameter estimate θ^(t) by maximizing the conditional expectation of complete data log-likelihood

$$Q(\mathit{\theta };{\mathit{\theta }}^{(t-1)})={\int }_{\mathit{X}}\text{log}{ℒ}_c(\mathit{\theta };\mathit{X},\mathbf{y},\mathbf{z})dF(\mathit{X}|\mathbf{y},\mathbf{z},{\mathit{\theta }}^{(t-1)})$$ (4)

with respect to θ. The conditional distribution of X_i for the i^th individual under our model specification and CI assumption is

$$P_{\mathit{\theta }}({\mathit{X}}_i|{\mathbf{y}}_i,z_i,{\mathit{\theta }}^{(t-1)})=\frac{\prod _{k=1}^K{P}_{\mathit{\theta }}\left(y_{ik}\right|X_i,\mathit{\theta }={\mathit{\theta }}^{(t-1)}\left)P_{\mathit{\theta }}\right(X_i|z_i,\mathit{\theta }={\mathit{\theta }}^{(t-1)})}{\sum _{X_i}\prod _{k=1}^K{P}_{\mathit{\theta }}(y_{ik}|X_i,\mathit{\theta }={\mathit{\theta }}^{(t-1)}\left)P_{\mathit{\theta }}\right(X_i|z_i,\mathit{\theta }={\mathit{\theta }}^{(t-1)})}.$$

Under regularity conditions [6, 46, 49], θ̂^(t) → θ̂ as t → ∞, where θ̂ is the ML estimate. It is shown that the observed data likelihood function evaluated at θ̂^(t) is nondescending with increasing t [49].

3.4 Monte Carlo EM Algorithm

We show above that the integral Q(θ; θ ^(t−1)) in Equation (4) can be calculated as weighted sum under our model specification. More often than not, however, it is analytically intractable or involves tedious evalution. Numerical quadrature integration is possible. Alternatively, the Monte Carlo EM (MCEM) as a modification of the EM algorithm was proposed [24, 47] where the conditional expectation step is computed numerically through Monte Carlo simulations. Let M Monte Carlo (MC) samples generated at t iteration for the i^th individual $X_{i1}^{(t)},\dots ,X_{iM}^{(t)}\stackrel{iid}{~}F(X_i|{\mathbf{y}}_i,z_i,{\mathit{\theta }}^{(t-1)})$, when M → ∞,

$$\mathrm{Q̃}(\mathit{\theta };{\mathit{\theta }}^{(t-1)})=\frac{1}{M}\sum _{j=1}^M\sum _{i=1}^n\text{log}{ℒ}_c(\mathit{\theta };X_{ij}^{(t)},{\mathbf{y}}_i,z_i)\stackrel{P}{\to }Q(\mathit{\theta };{\mathit{\theta }}^{(t-1)}).$$ (5)

MCEM maximizes Q̃ instead of Q to obtain ${\mathit{\theta ̃}}_M^{(t)}$, and ${\mathit{\theta ̃}}_M^{(t)}\to \mathit{\theta ̃}$ as t → ∞, M → ∞.

Levine and Casella [24] discussed Markov chain Monte Carlo routines such as the Gibbs and Metropolis-Hastings samplers [27, 28] as general approaches to obtaining MC samples in each iteration of an MCEM algorithm. However, in the following section, we would utilize the property of independent MC sampling and present a fast MCEM algorithm that is computationally efficient with binary data.

3.5 A Fast MCEM Algorithm for LCM Estimations

Recall that under the CI assumption, the i^th individual’s contribution to the complete data log-likelihood is

$$\text{log}{ℒ}_c(\mathit{\theta };{\mathit{X}}_i,{\mathbf{y}}_i,z_i)=\sum _{k=1}^K\{I(y_{ik}=1)\text{log}\frac{\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)}{1+\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)}+I(y_{ik}=0)\text{log}\frac{1}{1+\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)}\}+I(X_i=1)\text{log}\frac{\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)}{1+\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)}+I(X_i=0)\text{log}\frac{1}{1+\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)}.$$

We use capital X_i to emphasize that the latent variable is unobserved. Again from Bayes’ theorem,

$$P(X_i=1|{\mathbf{y}}_i,z_i,{\mathit{\theta }}^{(t-1)})=\frac{P({\mathbf{y}}_i|X_i=1,{\mathit{\theta }}^{(t-1)}\left)P\right(X_i=1|z_i,{\mathit{\theta }}^{(t-1)})}{{\sum }_{d=0}^{1}P({\mathbf{y}}_i|X_i=d,{\mathit{\theta }}^{(t-1)}\left)P\right(X_i=d|z_i,{\mathit{\theta }}^{(t-1)})}=\frac{\left\{\prod _{k=1}^{K}P\right(y_{ik}|X_i=1,{\mathit{\theta }}^{(t-1)})\left\}P\right(X_i=1|z_i,{\mathit{\theta }}^{(t-1)})}{\sum _{d=0}^1\left\{\prod _{k=1}^{K}P\right(y_{ik}|X_i=d,{\mathit{\theta }}^{(t-1)})\left\}P\right(X_i=d|z_i,{\mathit{\theta }}^{(t-1)})}$$

Note that modifications to the above equations are straightforward when we do not assume CI.

The usual data augmentation approach [47] to MCEM would involve generating $X_{ij}^{(t)}\stackrel{iid}{~}P(X_i|{\mathbf{y}}_i,z_i,{\mathit{\theta }}^{(t-1)})$, j = 1, 2, …, M observations and substituting into an augmented data (i.e., each observation in the original data set to be augmented and paired with generated X_ij’s at each iteration) log-likelihood to complete the E-step of the MCEM algorithm. Because the $X_{ij}^{(t)}$ in this study are Bernoulli observations [11], computational efficiency can be gained by working with the associated binomial distribution instead. The calculation of the i^th individual’s contribution to the expected log-likelihood can be written as follows:

$$E_{\mathit{\theta }}\text{log}{ℒ}_c(\mathit{\theta };X_i^{(t)},{\mathbf{y}}_i,z_i)=\frac{1}{M}\left(\sum _{j=1}^M{X}_{ij}^{(t)}\right)\left[\sum _{k=1}^K\right\{I(y_{ik}=1)\text{log}\frac{\text{exp}({\beta }_{0k}^{(t)}+{\beta }_{1k}^{(t)})}{1+\text{exp}({\beta }_{0k}^{(t)}+{\beta }_{1k}^{(t)})}+I(y_{ik}=0)\text{log}\frac{1}{1+\text{exp}({\beta }_{0k}^{(t)}+{\beta }_{1k}^{(t)})}\}+\text{log}\frac{\text{exp}({\gamma }_0^{(t)}+{\gamma }_1^{(t)}{z}_i+{\gamma }_2^{(t)}{z}_i^2)}{1+\text{exp}({\gamma }_0^{(t)}+{\gamma }_1^{(t)}{z}_i+{\gamma }_2^{(t)}{z}_i^2)}]+\frac{1}{M}(M-\sum _{j=1}^M{X}_{ij}^{(t)})\left[\sum _{k=1}^K\right\{I(y_{ik}=1)\text{log}\frac{\text{exp}\left({\beta }_{0k}^{(t)}\right)}{1+\text{exp}\left({\beta }_{0k}^{(t)}\right)}+I(y_{ik}=0)\text{log}\frac{1}{1+\text{exp}\left({\beta }_{0k}^{(t)}\right)}\}+\text{log}\frac{1}{1+\text{exp}({\gamma }_0^{(t)}+{\gamma }_1^{(t)}{z}_i+{\gamma }_2^{(t)}{z}_i^2)}]$$ (6)

This means rather than using the generated random samples in an augmented data log-likelihood function, we only need to count the number of generated 0’s and 1’s. This still requires heavy random sampling when M is large. Notice that here we utilize the property of independent MC sampling of M Bernoulli trials. Due to the fact that the sum of iid Bernoulli random variable follows binomial distribution, we could directly sample the number of 1’s out of M from the binomial distribution. This is to say, we will replace ${\sum }_{j=1}^M{X}_{ij}^{(t)}$ in Equation (6) with random count $C_i^{(t)}~\mathit{\text{Binomial}}(n,p)$ with n = M and p = P(X_i = 1|y_i, z_i, θ^(t)). It is worthwhile to point out that our implementation of the MCEM algorithm is not a new version from the Wei and Tanner [47] algorithm but rather a computationally faster version of it. Therefore, it is expected that statistical properties of the MCEM estimators studied in the current paper also hold for the estimators defined by the Wei and Tanner [47] algorithm. For the maximization step, commonly used optimization methods can be applied [e.g., see 7, 34]. When M is large, this technique would greatly reduce the computing time and cost.

3.6 Rate of Convergence for the Fast MCEM Algorithm

In this section, we study the rate of convergence of our proposed fast MCEM algorithm for varying sizes of the observed and MC simulated samples as well as the levels of tolerance. Because the computing time is dependent on machine capability, e.g., computer processor frequency and memory capacity, it is better to study the rate of convergence in terms of number of iterations till convergence.

It is known that number of iterations t for a convergent solution θ̂ depends on the size of both observed sample n and simulated MC sample M, as well as the tolerance criteria δ for stopping iterations. Here δ is defined as the stopping criteria for the fast MCEM algorithm, i.e., a convergent solution θ̂ is reached if $\Vert {\mathit{\theta ̂}}_M^{(t)}-{\mathit{\theta ̂}}_M^{(t-1)}\Vert <\delta$. Table 1 summarizes the rate of convergence of the algorithm. From the table, we could see that with the increase of simulated MC sample size M, the number of iterations needed for a convergent solution decreases. Also if the observed sample size n is larger, it is easier to reach convergence. However, if the tolerance criteria is more stringent, it takes more steps to reach a convergent solution, which is expected.

Table 1.

The number of iterations t for a convergent solution with varying sizes of observed and simulated MC sample

					M
			100	500	1000	5000	10000
δ = 10−4	n	100	28.12	23.06	17.78	13.34	11.25
		200	25.55	21.11	15.54	12.26	10.85
		300	22.49	18.22	14.31	11.88	10.10
		500	18.36	15.58	12.75	10.37	9.52
		1000	13.57	11.33	10.22	9.16	8.04
δ = 10−8	n	100	48.44	38.62	30.37	23.25	16.29
		200	39.27	32.09	25.54	19.45	15.87
		300	31.77	26.95	21.30	17.39	13.16
		500	25.76	21.53	17.69	15.08	12.35
		1000	17.05	15.74	13.90	12.61	10.95

Average iteration number based on 100 repetitions.

Under parameter config 1 as shown in Tables 3–5.

Several colleagues [e.g., 3, 17, 23, 24, 38] discussed automated rules for increasing the MC simulated sample size when the Monte Carlo error overwhelms the estimate at certain given iteration. From Table 1, a larger M corresponds to a smaller number of iterations needed for a convergent solution. Furthermore, with our fast MCEM algorithm, choosing a large M does not increase the computing cost significantly. Table 2 shows an illustrative example on computational efficiency. Therefore, it is always advised to consider a large (fixed) M across the iterations when using our fast MCEM algorithm.

Table 2.

Convergence times of MCEM estimation procedures for one Monte Carlo sample (n = 122, δ = 10⁻⁴)

M	Usual augmentation approach	The fast MCEM approach
100	60.51 sec(s)	0.89 sec(s)
1,000	≈ 16 min(s)	0.91 sec(s)
10,000	≈ 5 hour(s)	1.10 sec(s)

3.7 Standard Error Estimations in MCEM

After obtaining the MLE θ̃ using the proposed fast MCEM algorithm, it is necessary to estimate the covariance matrix for θ̃. The Fisher information [22] cannot be measured because of the unobserved/missing variable in the complete data likelihood function.

Louis [26] presented an adjustment technique for computing the observed information within the EM framework. Let 𝒮 (x, θ) be the gradient vector of log ℒ(θ; x, y, z) and ℋ(x, θ) be the associated second derivative matrix. We assume that the regularity conditions [41] hold. These guarantee that the Fisher information exists. The observed information is

$$I_{\mathbf{Y}}(\mathit{\theta })=E_{\mathit{\theta }}\{-\mathscr{H}(\mathbf{X},\mathit{\theta })\}-Va{r}_{\mathit{\theta }}\{𝒮(\mathbf{X},\mathit{\theta })\}.$$ (7)

For a detailed proof, please see the Appendix of [26]. Notice that all of these conditional expectations can be computed in the EM algorithm using only 𝒮 (x, θ) and ℋ(x, θ), the score vector and Hessian matrix [33] for the complete data problem. In the MCEM setting,

$$I_{\mathbf{Y}}(\mathit{\theta })\doteq \frac{1}{M}\sum _{j=1}^M\{-\sum _{i=1}^n\mathscr{H}(X_{ij}^{(t)},\mathit{\theta }\left)\right\}-\frac{1}{M}\sum _{j=1}^M\left\{\sum _{i=1}^n𝒮\right(X_{ij}^{(t)},\mathit{\theta })-\frac{1}{M}\sum _{j=1}^M\sum _{i=1}^n𝒮(X_{ij}^{(t)},\mathit{\theta }\left)\right\}{\left\{\sum _{i=1}^n𝒮\right(X_{ij}^{(t)},\mathit{\theta })-\frac{1}{M}\sum _{j=1}^M\sum _{i=1}^n𝒮(X_{ij}^{(t)},\mathit{\theta }\left)\right\}}^T$$ (8)

is an analogue observed information, which is an extension of Robert and Casella’s formula (see [39], pp. 186–187). We give computer code in the Appendix for calculating (i, j)^th element of I_Y (θ) in Equation (8).

Plugging in θ̃, I_Y(θ̃) could then be inverted to get the estimated covariance matrix of θ̃. The multivariate delta method could be applied to obtain standard errors of accuracy parameters (sensitivity, specificity, and prevalence) given the specifications in Equations (2) and (3).

Alternatively, the estimated standard errors of θ̃ could be computed through bootstrap resampling [9, 10]. The procedure is as follows. Resample the original data by row (subjects) with replacement and compute the estimated parameter θ̃_boot based on resampled data using the fast MCEM algorithm. Repeat this resampling step B = 1000 times and each time we get an estimated parameter θ̃_boot. Finally, due to the bootstrap plug-in principle we would get an estimate of the sampling distribution of parameters of interest. The results of Louis’s formula and the bootstrap for standard error estimates from the fast MCEM are to be compared.

4. Simulation Studies

We fix the ages, Z_i, in our first simulation study, to be those in the original GOG-0171 dataset (n = 122). In the second and third simulation study, Z_i’s ~ Uniform(2.0, 7.1) are generated with n = 500 and n = 1000, respectively. The simulated MC sample size M and the level of tolerance δ are fixed at 10000 and 10⁻⁴, respectively.

The unobserved truth, X_i, i = 1, 2, …, n, was generated from independent Bernoulli trials with $P(X_i=1|Z_i)={[1+\text{exp}{({\gamma }_0+{\gamma }_1{Z}_i+{\gamma }_2{Z}_i^2)}^{-1}]}^{-1}$, where γ₀ = −1.5093, γ₁ = 0.7245, γ₂ = −0.1271. This trend was indicated from the raw data as well as in [8]. The test results Y_ik given X_i, k = 1, 2, 3, were generated from independent Bernoulli trials with P (Y_ik = 1|X_i) = [1 + exp (β_0k + β_1kX_i)⁻¹]⁻¹, where β_0k, β_1k’s are preset according to true accuracy parameters (sensitivity and specificity). For instance, if β_0k = −1.7346, β_1k = 4.0482, this parameter setup would correspond to a sensitivity of 0.91 and specificity of 0.85 for test k. That is, we inversely solve for β_0k and β_1k based on Equation (2), 0.91 = exp(β_0k + β_1k)/ {1 + exp(β_0k + β_1k)}, 0.85 = 1/ {1 + exp(β_0k)}.

Each of the randomly generated datasets is to be analyzed by the fast MCEM to obtain parameter estimates. Following Section 3.7, standard error estimates for the parameters are derived from Louis’s formula in MCEM. The 95% confidence intervals based on normal approximation are computed for estimated accuracy parameters. The coverage probabilities as well as expected interval lengths are also investigated with 1000 Monte Carlo samples. For each of the 1000 Monte Carlo samples, bootstrap standard error estimates were derived by resampling B = 1000 times to obtain 1000 resampled datasets. An asymptotic 95% bootstrap confidence interval based on normal approximation as well as on bootstrap percentile were calculated for comparison.

The results of the simulation studies are summarized in Tables 3–5. The MCEM parameter estimates are nearly unbiased, very close to the true values on average. This suggests that with appropriately chosen initial values for MCEM iterations, the fast MCEM algorithm for the estimation of LCM parameters provides consistent and unbiased estimates for the chosen n.

Table 3.

Monte Carlo study results: mean parameter estimates, coverage probability, and mean length of 95% confidence intervals (n = 122, M = 10000, δ = 10⁻⁴)

					Coverage (Mean Length)
Config	Parameter	Test	True	MC Mean (SD)	Louis	Bootstrap 1†	Bootstrap 2‡
1	Sensitivity	1	0.85	0.8544 (0.0808)	0.918 (0.2895)	0.894 (0.2796)	0.946 (0.3003)
		2	0.68	0.6819 (0.0960)	0.942 (0.3677)	0.939 (0.3703)	0.948 (0.3759)
		3	0.91	0.9091 (0.0633)	0.887 (0.2204)	0.871 (0.2079)	0.904 (0.2272)
	Specificity	1	0.90	0.9025 (0.0397)	0.939 (0.1578)	0.918 (0.1522)	0.947 (0.1556)
		2	0.93	0.9334 (0.0318)	0.912 (0.1214)	0.893 (0.1166)	0.927 (0.1271)
		3	0.85	0.8488 (0.0491)	0.952 (0.1931)	0.936 (0.1910)	0.943 (0.1918)
2	Sensitivity	1	0.95	0.9492 (0.0381)	0.827 (0.1164)	0.822 (0.1169)	0.833 (0.1257)
		2	0.95	0.9478 (0.0398)	0.822 (0.1192)	0.824 (0.1203)	0.837 (0.1294)
		3	0.95	0.9519 (0.0393)	0.829 (0.1171)	0.830 (0.1168)	0.834 (0.1267)
	Specificity	1	0.95	0.9493 (0.0250)	0.916 (0.0920)	0.913 (0.0909)	0.928 (0.0935)
		2	0.95	0.9505 (0.0252)	0.913 (0.0922)	0.909 (0.0902)	0.925 (0.0937)
		3	0.95	0.9499 (0.0249)	0.915 (0.0915)	0.911 (0.0901)	0.926 (0.0931)
3	Sensitivity	1	0.85	0.8492 (0.0842)	0.921 (0.3088)	0.896 (0.2964)	0.946 (0.3142)
		2	0.90	0.8988 (0.0725)	0.888 (0.2456)	0.869 (0.2322)	0.924 (0.2534)
		3	0.75	0.7524 (0.1033)	0.937 (0.4072)	0.924 (0.3959)	0.955 (0.4040)
	Specificity	1	0.80	0.8043 (0.0584)	0.943 (0.2254)	0.932 (0.2203)	0.951 (0.2215)
		2	0.75	0.7466 (0.0611)	0.953 (0.2471)	0.943 (0.2457)	0.956 (0.2464)
		3	0.90	0.9021 (0.0421)	0.935 (0.1648)	0.921 (0.1547)	0.949 (0.1571)
4	Sensitivity	1	0.95	0.9444 (0.0547)	0.796 (0.1582)	0.781 (0.1470)	0.810 (0.1653)
		2	0.90	0.9032 (0.0698)	0.894 (0.2420)	0.882 (0.2287)	0.928 (0.2585)
		3	0.85	0.8446 (0.0809)	0.925 (0.3065)	0.902 (0.2942)	0.952 (0.3174)
	Specificity	1	0.75	0.7521 (0.0566)	0.949 (0.2322)	0.947 (0.2272)	0.951 (0.2267)
		2	0.80	0.7968 (0.0518)	0.940 (0.2107)	0.935 (0.2037)	0.949 (0.2133)
		3	0.85	0.8544 (0.0461)	0.935 (0.1864)	0.931 (0.1778)	0.950 (0.1822)
5	Sensitivity	1	0.95	0.9425 (0.0692)	0.815 (0.2078)	0.792 (0.1827)	0.823 (0.2181)
		2	0.85	0.8597 (0.0726)	0.918 (0.2842)	0.898 (0.2586)	0.942 (0.2787)
		3	0.75	0.7564 (0.0802)	0.929 (0.3142)	0.927 (0.3136)	0.945 (0.3253)
	Specificity	1	0.95	0.9488 (0.0348)	0.904 (0.1269)	0.882 (0.1122)	0.947 (0.1386)
		2	0.85	0.8585 (0.0456)	0.943 (0.1832)	0.934 (0.1738)	0.948 (0.1846)
		3	0.75	0.7536 (0.0498)	0.943 (0.2014)	0.941 (0.1981)	0.947 (0.2072)

^†Bootstrap Normal Confidence Interval

^‡Bootstrap Percentile Confidence Interval

Table 5.

Monte Carlo study results: mean parameter estimates, coverage probability, and mean length of 95% confidence intervals (n = 1000, M = 10000, δ = 10⁻⁴)

					Coverage (Mean Length)
Config	Parameter	Test	True	MC Mean (SD)	Louis	Bootstrap 1†	Bootstrap 2‡
1	Sensitivity	1	0.85	0.8499 (0.0219)	0.994 (0.1272)	0.944 (0.0851)	0.944 (0.0847)
		2	0.68	0.6803 (0.0285)	0.986 (0.1391)	0.942 (0.1114)	0.949 (0.1108)
		3	0.91	0.9098 (0.0169)	0.996 (0.1072)	0.947 (0.0682)	0.947 (0.0678)
	Specificity	1	0.90	0.9003 (0.0112)	0.984 (0.0553)	0.944 (0.0433)	0.943 (0.0431)
		2	0.93	0.9312 (0.0094)	0.980 (0.0448)	0.946 (0.0369)	0.948 (0.0367)
		3	0.85	0.8498 (0.0134)	0.981 (0.0648)	0.941 (0.0518)	0.942 (0.0515)
2	Sensitivity	1	0.95	0.9504 (0.0132)	0.962 (0.0582)	0.934 (0.0514)	0.941 (0.0510)
		2	0.95	0.9499 (0.0131)	0.964 (0.0584)	0.934 (0.0517)	0.943 (0.0513)
		3	0.95	0.9501 (0.0134)	0.964 (0.0583)	0.934 (0.0515)	0.946 (0.0512)
	Specificity	1	0.95	0.9501 (0.0082)	0.952 (0.0336)	0.935 (0.0315)	0.942 (0.0313)
		2	0.95	0.9498 (0.0083)	0.954 (0.0336)	0.941 (0.0316)	0.942 (0.0314)
		3	0.95	0.9501 (0.0078)	0.961 (0.0336)	0.948 (0.0315)	0.948 (0.0313)
3	Sensitivity	1	0.85	0.8509 (0.0212)	0.998 (0.1395)	0.944 (0.0848)	0.948 (0.0843)
		2	0.90	0.8998 (0.0182)	0.999 (0.1256)	0.946 (0.0713)	0.942 (0.0709)
		3	0.75	0.7493 (0.0271)	0.998 (0.1649)	0.945 (0.1033)	0.941 (0.1028)
	Specificity	1	0.80	0.7996 (0.0148)	0.992 (0.0766)	0.949 (0.0582)	0.946 (0.0577)
		2	0.75	0.7503 (0.0161)	0.986 (0.0816)	0.949 (0.0627)	0.946 (0.0624)
		3	0.90	0.8996 (0.0114)	0.991 (0.0613)	0.947 (0.0435)	0.941 (0.0433)
4	Sensitivity	1	0.95	0.9496 (0.0132)	0.998 (0.1012)	0.934 (0.0518)	0.937 (0.0514)
		2	0.90	0.8998 (0.0183)	0.997 (0.1226)	0.945 (0.0714)	0.944 (0.0712)
		3	0.85	0.8504 (0.0216)	0.996 (0.1375)	0.944 (0.0849)	0.948 (0.0845)
	Specificity	1	0.75	0.7501 (0.0157)	0.987 (0.0793)	0.957 (0.0628)	0.956 (0.0625)
		2	0.80	0.7997 (0.0148)	0.986 (0.0754)	0.943 (0.0582)	0.941 (0.0578)
		3	0.85	0.8501 (0.0136)	0.985 (0.0691)	0.938 (0.0517)	0.938 (0.0515)
5	Sensitivity	1	0.95	0.9491 (0.0132)	0.999 (0.1362)	0.945 (0.0521)	0.946 (0.0517)
		2	0.85	0.8509 (0.0217)	0.994 (0.1257)	0.942 (0.0849)	0.944 (0.0845)
		3	0.75	0.7495 (0.0269)	0.972 (0.1217)	0.938 (0.1033)	0.943 (0.1028)
	Specificity	1	0.95	0.9497 (0.0083)	0.996 (0.0554)	0.942 (0.0316)	0.945 (0.0314)
		2	0.85	0.8502 (0.0132)	0.988 (0.0719)	0.948 (0.0517)	0.946 (0.0515)
		3	0.75	0.7504 (0.0162)	0.972 (0.0734)	0.944 (0.0628)	0.944 (0.0625)

^†Bootstrap Normal Confidence Interval

^‡Bootstrap Percentile Confidence Interval

De Menezes [5] has shown that the standard error based on the asymptotic information matrix evaluated at the MLEs can be problematic when data are sparse. In our analysis with binary test outcome, compared to the bootstrap method, Louis’s formula for adjusting information matrix based estimates of standard errors performs reasonably well when n = 122. However, when sample sizes are getting large, e.g., n = 500 or n = 1000, Louis’s formula overestimates the standard errors resulting in much wider interval lengths for many simulation configurations.

When the true parameter is close to a boundary value of 1, the coverage probability is smaller than the nominal level of 95% for normal intervals from both Louis’s adjusted information matrix and the bootstrap method with sample size n = 122, while the bootstrap percentile interval has coverage closer to the nominal level. With sample size n = 500 and n = 1000, bootstrap confidence intervals generally have nominal coverage. We argue that it is probably due to greater asymmetry when the true parameter is close to boundary and thus large sample sizes are needed to hold the asymptotics. For this reason, the range-preserved bootstrap percentile method is preferred in constructing confidence intervals for sensitivities and specificities.

Nevertheless, Monte Carlo studies suggested that n = 122 is sufficiently large for the MLE asymptotics to hold approximately (Config 1). This indicates validity of our LCM analysis in the real data analysis with n = 122.

5. Analysis of GOG-0171 Data

The purpose of this study was to apply a LCM analysis to GOG-0171 data from the United States to assess the diagnostic accuracies of the HC2 test, CA-IX biomarker-based test, and the histological lesion evaluation, i.e., the imperfect “GS”. The dataset contains 122 patients with ages ranging from 2.0 to 7.1 (in decades). Of these, 38 were diagnosed positive by the imperfect “GS”; the CA-IX biomarker-based test detected 31 positive patients; and the HC2 test captured 48 positive cases.

Estimated sensitivities, specificities, bootstrap standard errors and corresponding 95% percentile-based confidence intervals (CIs) are presented in Table 6 for each of the tests. The estimates obtained by treating the histological lesion evaluation as the “GS” are also presented to illustrate the impact of its imperfection on accuracy estimates.

Table 6.

MCEM estimation of sensitivity/specificity of “GS”, CA-IX, and HC2 tests for cervical neoplasia in women with AGC

	“GS”	CA-IX	HC2
Sensitivity
Liao et al. est.	—	0.6579	0.9737
LCM est.	0.9958	0.6754	0.9985
Bootstrap SE	0.0173	0.0818	0.0005
95% CI	[0.9789, 0.9989]	[0.5107, 0.8331]	[0.9978, 0.9997]
Specificity
Liao et al. est.	—	0.9286	0.8690
LCM est.	0.9867	0.9289	0.8696
Bootstrap SE	0.0132	0.0279	0.0382
95% CI	[0.9566, 0.9997]	[0.8646, 0.9765]	[0.7904, 0.9413]

The logistic regression model with a quadratic predictor was fitted for the prevalence of SCL, p_i = P (X_i = 1|Z_i). The fitted curve in linear predictor form was:

$$\text{log}\left(\frac{{\mathrm{p̂}}_i}{1-{\mathrm{p̂}}_i}\right)=-1.5093+0.7245\times \mathit{\text{Age}}(\text{in decade})-0.1271\times {\mathit{\text{Age}}}^2$$ (9)

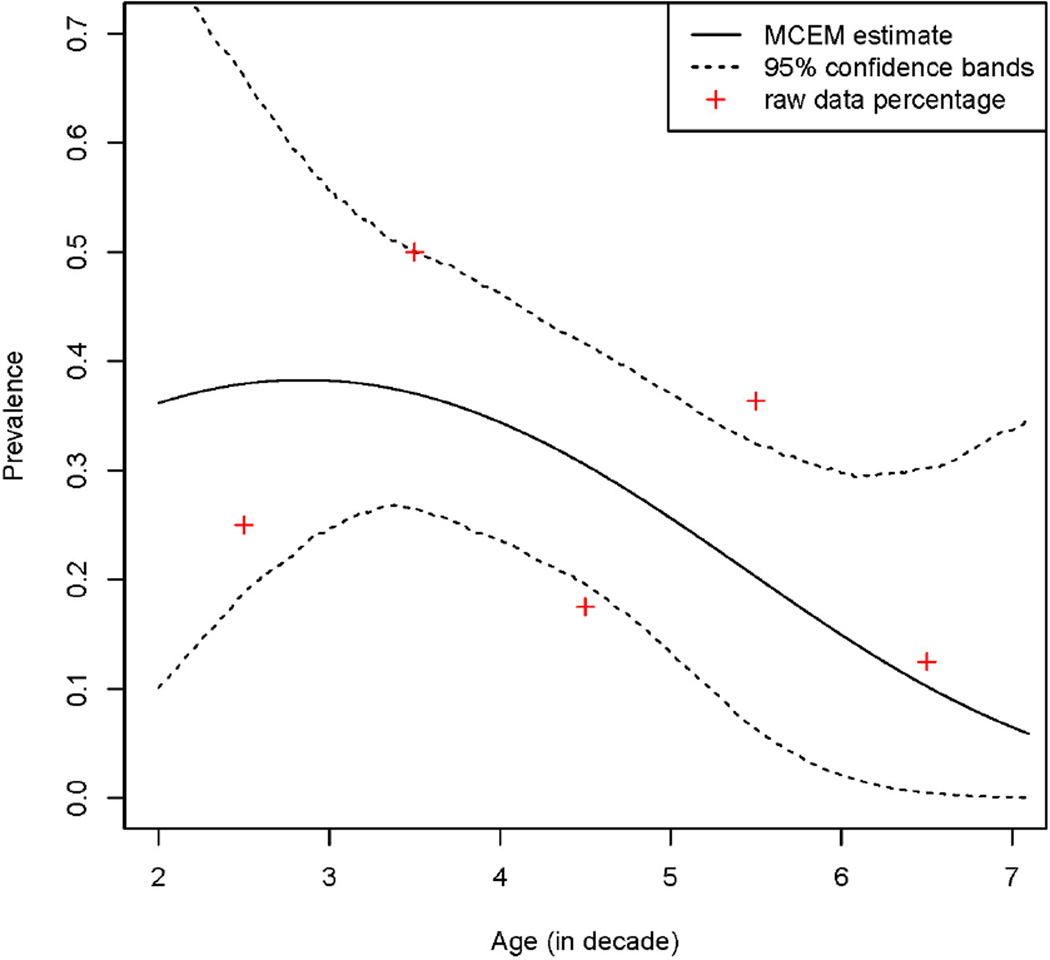
The estimated prevalence curve with 95% confidence bands superimposed is plotted in Figure 1. To see how well the model fits the data, we categorized the patients into 5 groups based on their ages in decade: ≤ 3; ≤ 4; ≤ 5; ≤ 6; > 6, and computed the positive rates for each category based on imperfect “GS”. The fitted curve follows the raw SCL prevalence trend, which is consistent with the trend observed in [8].

Figure 1.

Prevalence of SCL among women with AGC

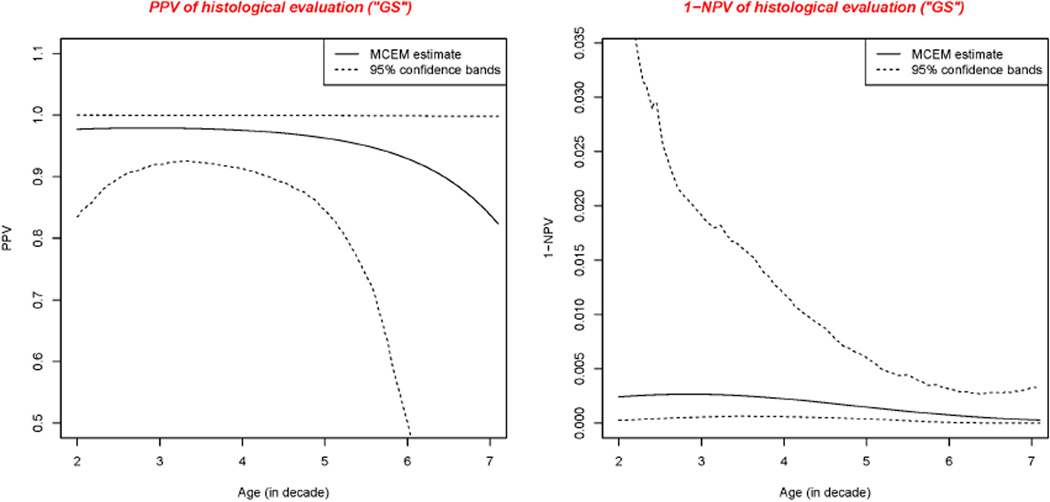
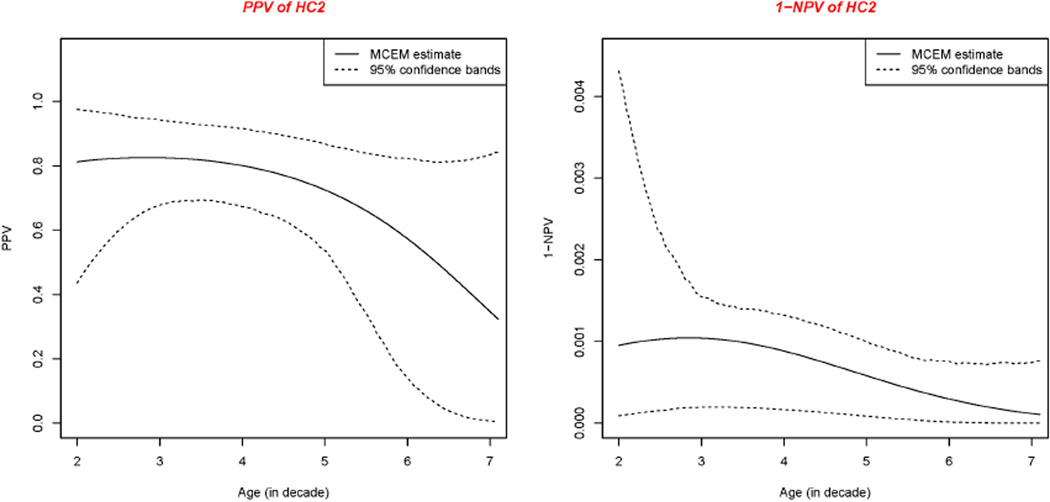
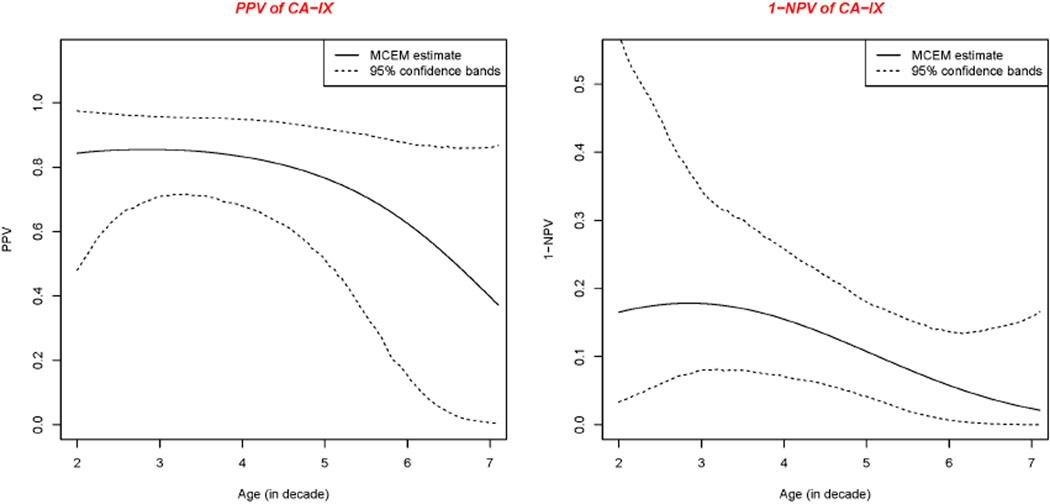
Positive predictive value (PPV) as well as the complement of negative predictive value (1−NPV) were calculated based on the estimated probability that women have a SCL given CA-IX, HC2 and “GS” test either positive or negative. Because the prevalence of the disease varies with the age of the woman, PPV and 1−NPV vary with age. We present the PPV and 1−NPV curves together with the corresponding confidence bands for each test in Figures 2–4, respectively.

Figure 2.

Positive predictive value and 1 minus negative predictive value of “GS”

Figure 4.

Positive predictive value and 1 minus negative predictive value of HC2

6. Discussion

From Table 6, we found “GS” was nearly perfect. This validated its use in the previous GOG-0171 study in which histological evaluation is considered as the GS.

CA-IX test had the lowest sensitivity to detect the cervical neoplasia. CA-IX is a transmembrane protein and the only tumor-associated carbonic anhydrase isoenzyme known. It is expressed in all clear-cell renal cell carcinomas, but is not detected in normal kidneys or most other normal tissues. It may or may not be involved in cell proliferation and transformation. Therefore, it is not odd that CA-IX test performs not so well. 1−NPV of the CA-IX test is unacceptably high for clinical use in determining whether a patient can safely forego an excisional procedure in favor of observational follow up.

The HC2 test, which detects high-risk HPV DNA types that are highly carcinogenic, has quite good performance considering the overall sensitivity and specificity. From the 1−NPV curve for HC2, a negative HC2 result is sufficient to safely rule out a SCL and forego the invasive treatment that is often provided to women from the United States with AGC. Such treatment is not safely indicated by a positive HC2 result alone, as at least 18% of women with a positive HC2 result did not have a SCL and underwent an invasive procedure that was not necessary. Further research to find additional biomarkers that will increase specificity and allow identification of HC2 test positive women who have a SCL is needed.

In this article, we replace the generation of M values from the Bernoulli distribution with a value generated from the Binomial in the MCEM algorithm to gain computational efficiency. It is shown that our fast MCEM algorithm for parameter estimation in LCM is accurate. We also address the problem of comparison between Louis’s formula and bootstrap standard error estimation in MCEM, which is the first time study of this kind to our knowledge. The adjusted information matrix based estimates of standard errors from Louis’s formula in MCEM can provide CIs with satisfactory coverage probabilities when the sample sizes are moderate, except when the true parameters are close to boundary values. When the sample sizes are getting large, say, n ≥ 500, Louis’s formula overestimates standard errors providing confidence intervals too conservative. We also need to point out that Louis’s formula in MCEM requires augmented data with generated 0’s and 1’s. See Equation (8). Of course, they need be evaluated only once on the last iteration of the MCEM procedure [26].

Bootstrap standard error estimation in MCEM is relatively computationally intensive, but with our fast MCEM algorithm, it is a straightforward approach. The proposed fast MCEM algorithm does not require heavy random generation of 0’s and 1’s but only the number of 1’s out of M trial at any iteration, which requires only a binomial sampling process. Simulation studies also indicate that bootstrap percentile interval has the best coverage properties.

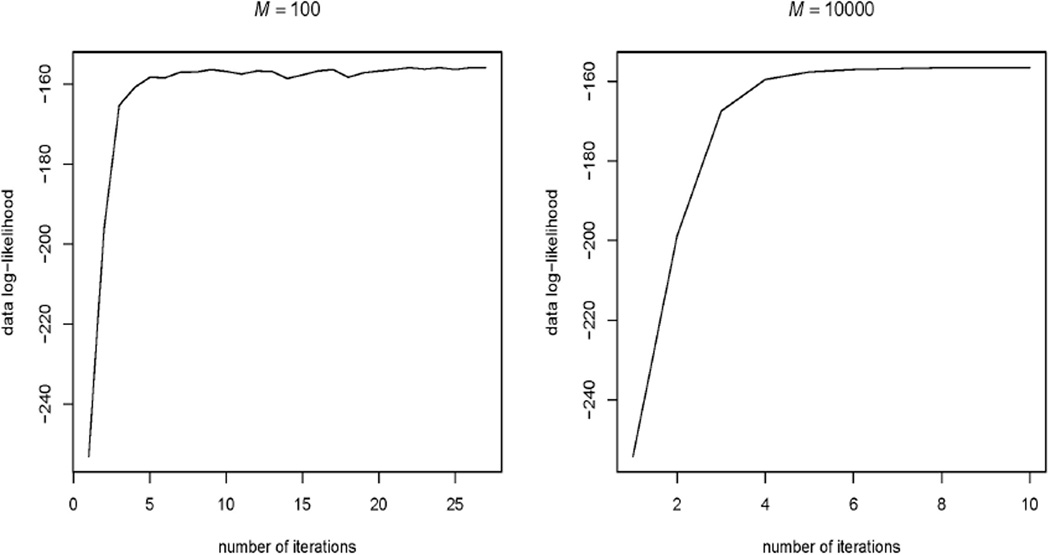
It is known that in MCEM estimation, a Monte Carlo error is introduced at the E-step and the monotonicity property of EM algorithm is lost. In our study, we also noticed this phenomenon. Our experience suggests using a large M, e.g., M = 10000, from the very beginning of MCEM iterations to decrease the Monte Carlo error when approximating the expected log-likelihood function. See Figure 5 with n = 122 and level of tolerance δ = 10⁻⁴. As we already pointed out, choosing a large M does not increase the computing cost significantly with our fast MCEM algorithm. Thus, it is advised to consider a large M when using our fast MCEM algorithm.

Figure 5.

Observed data log-likelihood versus number of iterations in MCEM with different M

Last but not least, there have been concerns about the conditional independence assumption in LCM analysis applied in diagnostic test settings [e.g., 13, 44]. It is important to realize the fact that different tests measure different biological processes does not always indicate that the different tests are conditionally independent given the truth. Failure to account for conditional dependence might lead to potential bias in diagnostic accuracy and prevalence estimation. In our study, our biological expertise provides reasonings that validate conditional independence assumption. On the other hand, it is not possible to model or test conditional dependence structure in LCM analysis for this study because there are only three diagnostic tests [20]. Future research incorporating conditional dependence is needed when additional diagnostic tests enter into the study.

In summary, our purpose in this article is two-fold: (1) to derive a fast MCEM algorithm for the general estimation problems in LCM analysis, and (2) to compare the standard error estimates from adjusted information matrix approach with the ones from bootstrap method in MCEM framework. The main advantages of implementing our fast MCEM algorithm are that deriving the E-step for any kind of likelihood function is numerically straightforward and bootstrap standard error or confidence interval estimation within MCEM framework becomes computationally accessible. We hope that the fast MCEM algorithm, our modification to LCM, demonstration of superior coverage of bootstrap confidence intervals relative to adjusted information based intervals, and their applications in this paper will promote the use of enhanced/improved LCM analysis in assessing diagnostic accuracy in the absence of true GS.

Figure 3.

Positive predictive value and 1 minus negative predictive value of CA-IX

Table 4.

Monte Carlo study results: mean parameter estimates, coverage probability, and mean length of 95% confidence intervals (n = 500, M = 10000, δ = 10⁻⁴)

					Coverage (Mean Length)
Config	Parameter	Test	True	MC Mean (SD)	Louis	Bootstrap 1†	Bootstrap 2‡
1	Sensitivity	1	0.85	0.8499 (0.0322)	0.992 (0.1807)	0.934 (0.1202)	0.940 (0.1195)
		2	0.68	0.6784 (0.0403)	0.986 (0.1972)	0.944 (0.1579)	0.945 (0.1571)
		3	0.91	0.9107 (0.0242)	0.991 (0.1495)	0.944 (0.0957)	0.951 (0.0951)
	Specificity	1	0.90	0.8998 (0.0156)	0.984 (0.0782)	0.942 (0.0614)	0.945 (0.0612)
		2	0.93	0.9307 (0.0134)	0.971 (0.0632)	0.938 (0.0518)	0.939 (0.0515)
		3	0.85	0.8505 (0.0179)	0.986 (0.0916)	0.954 (0.0729)	0.957 (0.0725)
2	Sensitivity	1	0.95	0.9498 (0.0185)	0.957 (0.0811)	0.924 (0.0729)	0.939 (0.0724)
		2	0.95	0.9502 (0.0188)	0.942 (0.0806)	0.906 (0.0723)	0.928 (0.0721)
		3	0.95	0.9504 (0.0195)	0.951 (0.0803)	0.908 (0.0722)	0.933 (0.0717)
	Specificity	1	0.95	0.9499 (0.0115)	0.948 (0.0474)	0.935 (0.0445)	0.936 (0.0443)
		2	0.95	0.9499 (0.0114)	0.954 (0.0474)	0.945 (0.0445)	0.948 (0.0443)
		3	0.95	0.9501 (0.0114)	0.952 (0.0474)	0.939 (0.0445)	0.946 (0.0442)
3	Sensitivity	1	0.85	0.8501 (0.0306)	0.996 (0.2002)	0.943 (0.1205)	0.944 (0.1197)
		2	0.90	0.8997 (0.0261)	0.996 (0.1762)	0.942 (0.1010)	0.949 (0.1003)
		3	0.75	0.7505 (0.0382)	0.996 (0.2374)	0.941 (0.1465)	0.941 (0.1457)
	Specificity	1	0.80	0.7998 (0.0207)	0.988 (0.1098)	0.947 (0.0818)	0.944 (0.0815)
		2	0.75	0.7498 (0.0226)	0.989 (0.1163)	0.948 (0.0886)	0.946 (0.0881)
		3	0.90	0.8998 (0.0156)	0.992 (0.0884)	0.948 (0.0614)	0.948 (0.0614)
4	Sensitivity	1	0.95	0.9491 (0.0186)	0.994 (0.1309)	0.927 (0.0729)	0.946 (0.0724)
		2	0.90	0.9001 (0.0262)	0.998 (0.1722)	0.938 (0.1008)	0.942 (0.1001)
		3	0.85	0.8507 (0.0314)	0.996 (0.1964)	0.942 (0.1201)	0.943 (0.1194)
	Specificity	1	0.75	0.7501 (0.0223)	0.985 (0.1135)	0.952 (0.0886)	0.952 (0.0882)
		2	0.80	0.8011 (0.0203)	0.991 (0.1086)	0.949 (0.0817)	0.951 (0.0813)
		3	0.85	0.8504 (0.0188)	0.986 (0.1010)	0.942 (0.0734)	0.942 (0.0726)
5	Sensitivity	1	0.95	0.9486 (0.0191)	0.992 (0.1710)	0.926 (0.0731)	0.939 (0.0726)
		2	0.85	0.8494 (0.0311)	0.987 (0.1792)	0.941 (0.1205)	0.942 (0.1198)
		3	0.75	0.7518 (0.0378)	0.968 (0.1729)	0.938 (0.1459)	0.943 (0.1452)
	Specificity	1	0.95	0.9509 (0.0115)	0.995 (0.0774)	0.944 (0.0444)	0.942 (0.0441)
		2	0.85	0.8508 (0.0187)	0.984 (0.1011)	0.940 (0.0732)	0.942 (0.0726)
		3	0.75	0.7502 (0.0236)	0.957 (0.1046)	0.934 (0.0886)	0.934 (0.0882)

^†Bootstrap Normal Confidence Interval

^‡Bootstrap Percentile Confidence Interval

Appendix A

Technical Detail

A.1 Mathematical Derivation

Louis’s formula requires the score vector and Hessian matrix of complete data log-likelihood function. For instance, given the specifications in Equations (2) and (3),

$$\frac{\partial }{\partial {\beta }_{0k}}\text{log}ℒ(\mathit{\theta };X_i,{\mathbf{y}}_i,z_i)=I(y_{ik}=1)\frac{1}{1+\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)}-I(y_{ik}=0)\frac{\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)}{1+\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)}=I(y_{ik}=1)-\frac{\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)}{1+\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)}$$

In a similar way, we could derive the following quantities,

$$\frac{\partial }{\partial {\beta }_{1k}}\text{log}ℒ=X_i\{I(y_{ik}=1)-\frac{\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)}{1+\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)}\},\frac{\partial }{\partial {\gamma }_0}\text{log}ℒ=I(X_i=1)-\frac{\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)}{1+\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)},\frac{\partial }{\partial {\gamma }_1}\text{log}ℒ=z_i\{I(X_i=1)-\frac{\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)}{1+\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)}\},\frac{\partial }{\partial {\gamma }_2}\text{log}ℒ=z_i^2\{I(X_i=1)-\frac{\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)}{1+\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)}\},-\frac{{\partial }^2}{\partial {\beta }_{0k}^2}\text{log}ℒ=\frac{\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)}{{[1+\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)]}^2},-\frac{{\partial }^2}{\partial {\beta }_{1k}^2}\text{log}ℒ=\frac{{\text{X}}_i^2\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)}{{[1+\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)]}^2},-\frac{{\partial }^2}{\partial {\beta }_{0k}\partial {\beta }_{1k}}\text{log}ℒ=\frac{X_i\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)}{{[1+\text{exp}({\beta }_{0k}+{\beta }_{1k}{X}_i)]}^2},-\frac{{\partial }^2}{\partial {\gamma }_0^2}\text{log}ℒ=\frac{\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)}{{[1+\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)]}^2},-\frac{{\partial }^2}{\partial {\gamma }_1^2}\text{log}ℒ=\frac{{\text{z}}_i^2\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)}{{[1+\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)]}^2},-\frac{{\partial }^2}{\partial {\gamma }_2^2}\text{log}ℒ=\frac{z_i^4\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)}{{[1+\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)]}^2},-\frac{{\partial }^2}{\partial {\gamma }_0\partial {\gamma }_1}\text{log}ℒ=\frac{z_i\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)}{{[1+\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)]}^2},-\frac{{\partial }^2}{\partial {\gamma }_0\partial {\gamma }_2}\text{log}ℒ=\frac{z_i^2\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)}{{[1+\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)]}^2},-\frac{{\partial }^2}{\partial {\gamma }_1\partial {\gamma }_2}\text{log}ℒ=\frac{z_i^3\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)}{{[1+\text{exp}({\gamma }_0+{\gamma }_1{z}_i+{\gamma }_2{z}_i^2)]}^2}.$$

The sensitivity and specificity are computed from estimated θ̂,

$$\mathit{\text{Sensitivity}}=P_{\mathit{\theta }}(Y_{ik}=1|X_i=1)=\frac{\text{exp}({\beta }_{0k}+{\beta }_{1k})}{1+\text{exp}({\beta }_{0k}+{\beta }_{1k})}\mathit{\text{Specificity}}=P_{\mathit{\theta }}(Y_{ik}=0|X_i=0)=\frac{1}{1+\exp ({\beta }_{0k})}$$

as well as estimated variances of sensitivity and specificity,

$$Var(\mathit{\text{Sensitivity}})={\left[\frac{\partial P_{\mathit{\theta }}(Y_{ik}=1|X_i=1)}{\partial \mathit{\theta }}\right]}^T{𝕍}_{[{\beta }_{0k},{\beta }_{1k}]}\left[\frac{\partial P_{\mathit{\theta }}(Y_{ik}=1|X_i=1)}{\partial \theta }\right]Var(\mathit{\text{Specificity}})={\left[\frac{\partial P_{\mathit{\theta }}(Y_{ik}=0|X_i=0)}{\partial \mathit{\theta }}\right]}^T{𝕍}_{[{\beta }_{0k}]}\left[\frac{\partial P_{\mathit{\theta }}(Y_{ik}=0|X_i=0)}{\partial \mathit{\theta }}\right],$$

where 𝕍 is the estimated variance-covariance matrix of θ̂.

A.2 R Code for Elements in Equation (8)

inv.logit <- function(x) p <- exp(x)/(1+exp(x))

####################################################
########## for calculating standard error ##########
####################################################

louis.func <- function(par.new,xxx) {
xx = as.vector(xxx)

########## first term in Louis paper begin ###########

Hx.generic <- function(par,x) {
px = inv.logit(par[1] + par[2]*x)
px*(1−px)
}

Hz.generic <- function(par,z) {
pz = inv.logit(par[1] + par[2]*z + par[3]*z^2)
pz*(1−pz)
}

H11=Hx.generic(par.new[1:2],xx)
H12=H22=xx*H11
H33=Hx.generic(par.new[3:4],xx)
H34=H44=xx*H33
H55=Hx.generic(par.new[5:6],xx)
H56=H66=xx*H55
H77=Hz.generic(par.new[7:9],mysimdata[,1])
H78=H77*mysimdata[,1]
H79=H77*mysimdata[,1]^2
H88=H77*mysimdata[,1]^2
H89=H77*mysimdata[,1]^3
H99=H77*mysimdata[,1]^4

################  compute B    ######################

B=matrix(0,9,9)

B[1,1]=sum( H11 )/N.mcsample
B[1,2]=sum( H12 )/N.mcsample;B[2,1]=B[1,2]
B[2,2]=sum( H22 )/N.mcsample

B[3,3]=sum( H33 )/N.mcsample
B[3,4]=sum( H34 )/N.mcsample;B[4,3]=B[3,4]
B[4,4]=sum( H44 )/N.mcsample

B[5,5]=sum( H55 )/N.mcsample
B[5,6]=sum( H56 )/N.mcsample;B[6,5]=B[5,6]
B[6,6]=sum( H66 )/N.mcsample

B[7,7]=sum( H77 )
B[7,8]=sum( H78 );B[8,7]=B[7,8]
B[7,9]=sum( H79 );B[9,7]=B[7,9]
B[8,8]=sum( H88 )
B[8,9]=sum( H89 );B[9,8]=B[8,9]
B[9,9]=sum( H99 )

########## first term in Louis paper end #################
########## second term in Louis paper start ##############

S1=function(par,x,y1)    y1−inv.logit(par[1] + par[2]*x)
S2=function(par,x,y1) x*(y1−inv.logit(par[1] + par[2]*x))
S3=function(par,x,y2)    y2−inv.logit(par[3] + par[4]*x)
S4=function(par,x,y2) x*(y2−inv.logit(par[3] + par[4]*x))
S5=function(par,x,y3)    y3−inv.logit(par[5] + par[6]*x)
S6=function(par,x,y3) x*(y3−inv.logit(par[5] + par[6]*x))
S7=function(par,x,z)      x−inv.logit(par[7] + par[8]*z + par[9]*z^2)
S8=function(par,x,z)   z*(x−inv.logit(par[7] + par[8]*z + par[9]*z^2))
S9=function(par,x,z) z^2*(x−inv.logit(par[7] + par[8]*z + par[9]*z^2))

Score1 = matrix(0,ncol=N.obs,nrow=N.mcsample)
Score9=Score8=Score7=Score6=Score5=Score4=Score3=Score2<-Score1

for (i in 1:N.obs) {
Score1[,i]=S1(par.new, xxx[,i], mysimdata[i,2])   ## S1, N.mcsample x N.obs
Score2[,i]=S2(par.new, xxx[,i], mysimdata[i,2])
Score3[,i]=S3(par.new, xxx[,i], mysimdata[i,3])
Score4[,i]=S4(par.new, xxx[,i], mysimdata[i,3])
Score5[,i]=S5(par.new, xxx[,i], mysimdata[i,4])
Score6[,i]=S6(par.new, xxx[,i], mysimdata[i,4])
Score7[,i]=S7(par.new, xxx[,i], mysimdata[i,1])
Score8[,i]=S8(par.new, xxx[,i], mysimdata[i,1])
Score9[,i]=S9(par.new, xxx[,i], mysimdata[i,1]) } ## S9, N.mcsample x N.obs

Savg.i=cbind(                                     ## S1,N.mcsample…S9,N.mcsample
rowSums(Score1),rowSums(Score2),rowSums(Score3),  ## N.mcsample x 9
rowSums(Score4),rowSums(Score5),rowSums(Score6),
rowSums(Score7),rowSums(Score8),rowSums(Score9) )

Savg=Savg.i-matrix(1,nrow=N.mcsample,ncol=1)%%*%%t(colMeans(Savg.i))

### Savg.sum1=matrix(0,9,9)
### for (j in 1:N.mcsample) {
### Savg.sum1=Savg.sum1+Savg[j,]%%*%%t(Savg[j,]) }
Savg.sum=t(Savg)%%*%%Savg ### vector computation
########## second term in Louis paper end ##############
info.mat = B − Savg.sum/N.mcsample
return(solve(info.mat))
}
########################################################
########### louis function end ########################
########################################################