Abstract
In protein-protein interaction (PPI) networks, functional similarity is often inferred based on the function of directly interacting proteins, or more generally, some notion of interaction network proximity among proteins in a local neighborhood. Prior methods typically measure proximity as the shortest-path distance in the network, but this has only a limited ability to capture fine-grained neighborhood distinctions, because most proteins are close to each other, and there are many ties in proximity. We introduce diffusion state distance (DSD), a new metric based on a graph diffusion property, designed to capture finer-grained distinctions in proximity for transfer of functional annotation in PPI networks. We present a tool that, when input a PPI network, will output the DSD distances between every pair of proteins. We show that replacing the shortest-path metric by DSD improves the performance of classical function prediction methods across the board.
Introduction
One of the best-studied classical problems on biological networks involves using proteins of known function, together with the structure of the network of known protein-protein interactions (PPI) to make predictions of functions of unlabeled protein nodes. This is an important problem because, even in the best-studied model organisms, such as S. cerevisiae, these networks contain many proteins whose function is still completely uncharacterized. There are many proposed methods for this problem, including versions of majority voting [1], neighborhood algorithms [2], [3], clustering algorithms [4]–[6], algorithms based on maximum flow [7], or multi-way cut [8], [9], and a number of others [10].
Modern approaches also seek to deal with data quality: generally, the known network is missing many valid interactions, and some interactions may be known with higher confidence than others [11], [12]. Other modern approaches integrate PPI network data with high-throughput biological interaction data, such as sequence information, genetic interactions, structural information, and expression data [8], [13]–[15]. However, nearly all methods that predict function using PPI network structure depend, entirely or at least partially, on the simple shortest-path distance metric applied to the PPI graph.
We start with the observation that there is an intrinsic drawback to relying on the ordinary shortest-path distance metric in PPI networks. PPI networks are known to be “small world” networks in the sense that they are small-diameter, and most nodes are close to all other nodes (though the exact details of the degree distribution and the resulting extent to which they are “scale free” is a subject of lively debate, see [13], [16]–[19]). Thus any method that infers similarity based on proximity will find that a large fraction of the network is proximate to any typical node. In fact, this issue has already been termed the “ties in proximity” problem in the computational biology literature [4].
Furthermore, the fact that two nodes are adjacent (i.e., have shortest-path distance 1) in a PPI network can signify something very different than the adjacency of two other nodes. For example, as we discuss below, in PPI networks two nodes with many low-degree neighbors in common should be thought of as “more similar” than nodes with few low-degree neighbors in common; and such nodes should also be thought of as “more similar” than two nodes whose common neighbors have high degree. Thus, characterizing node pairs based only on a shortest-path notion of distance fails to capture important knowledge encoded in the structure of the network.
What is needed instead is a finer-grained distance metric, capable of making more subtle distinctions of similarity than ordinary shortest-path distance would in a small-world network. To that end we introduce a new metric called Diffusion State Distance, or DSD. We show that DSD is much more effective than shortest-path distance for the problem of transferring functional labels across nodes in PPI networks.
We demonstrate the utility of the DSD metric by modifying a number of the most popular classical algorithms for function prediction to replace the ordinary notion of distance with DSD. For the problem of predicting functional labels in the S. cerevisiae network, this change improves all the algorithms we consider. We then show that similar improvements hold for the more sparsely annotated S. pombe network, implying that our advances should generalize to other biological networks.
Motivation for DSD
To start, we consider all known physical interactions in the S. cerevisiae PPI network – specifically, version 3.2.102 of BioGRID [20] on verified ORFs for S. cerevisiae, which contains 128,643 annotated physical interactions. After removing redundant edges and selecting the largest connected component, the resulting PPI network has 4990 nodes (where each ORF corresponds to a node) and 74,310 edges (where each edge corresponds to an annotated physical interaction).
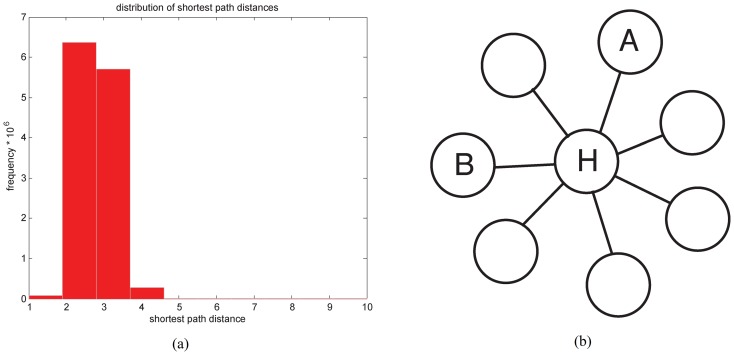
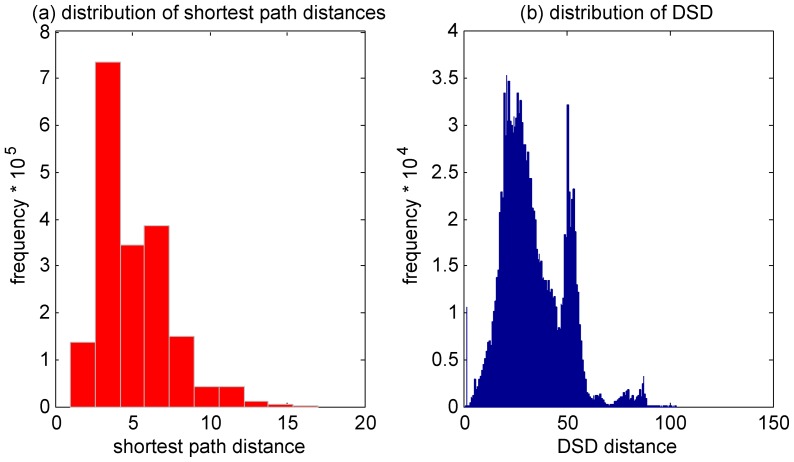
Figure 1(a) shows the histogram of shortest-path lengths from this network. The figure shows that almost all pairs of nodes (over 95%) are either 2 hops or 3 hops apart. Thus the “typical” distance between nodes under this metric is very small. Likewise, the overall network diameter is quite small as well.
Figure 1. Structure of shortest paths in the yeast PPI network.
(a) Distribution of shortest-path distances in the largest connected component of the yeast PPI network; (b) an example subgraph with a hub.
The fact that most node pairs are quite close together means that the concept of “neighborhood” using this metric is not very useful. For example, if one looks at the 2-hop neighborhood of a typical node, it probably includes around half of all nodes in the graph. Hence, shortest-path distance cannot be expected to give a good sense of locality or modularity in this network, and we observe that if one seeks to use graph structure to infer similarity of function in a PPI network, using shortest-paths to measure distance has serious drawbacks.
One of the reasons that paths are typically short in biological networks like the PPI network is due to the presence of hubs – very high degree nodes which represent proteins that have many physical interaction partners. In fact, in the case of PPI networks, hubs often represent proteins with different functional roles than their neighbors. For example, chaperone proteins (proteins that help other proteins fold correctly) are often hubs, and are not typically functionally related to their interaction partners. The same is true for proteins involved in translation. In our network, as an extreme example, the highest degree node is the protein NAB2, which has 2325 physical interactions in our PPI network. Its functional annotation terms: “3′-end processing”, “RNA binding” and “RNA transport” [21] suggest that this protein is involved in translation machinery and thus will bind with a highly diverse set of proteins with unrelated function. Hubs are also more likely to be proteins with multiple, distinct functions [22].
Hence, not all short paths provide equally strong evidence of similar function in PPI networks. Consider the network in Figure 1(b). Although nodes 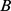 and
and 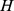 are only one hop apart, this does not suggest they are functionally related, since
are only one hop apart, this does not suggest they are functionally related, since 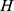 is a hub. Likewise,
is a hub. Likewise, 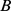 and
and 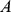 are not necessarily functionally related, since they are connected through a hub.
are not necessarily functionally related, since they are connected through a hub.
To capture the notion that 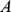 and
and 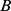 are not necessarily related, we note that a random walk starting at
are not necessarily related, we note that a random walk starting at 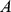 is not likely to reach
is not likely to reach 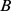 quickly. If we restrict attention to random walks of, say, 3 hops, then often one will not reach
quickly. If we restrict attention to random walks of, say, 3 hops, then often one will not reach 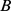 from
from 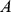 at all.
at all.
This motivates the first element of our new metric definition. Given some fixed 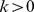 , we define
, we define 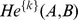 to be the expected number of times that a random walk starting at
to be the expected number of times that a random walk starting at 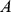 and proceeding for
and proceeding for 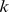 steps, will visit
steps, will visit 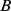 . Note that
. Note that 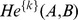 bears some resemblance to previous diffusion approaches suggested for PPI networks, see [23], [24], though we will next be building metric structure on top of
bears some resemblance to previous diffusion approaches suggested for PPI networks, see [23], [24], though we will next be building metric structure on top of 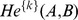 in a completely novel way. For now, note that
in a completely novel way. For now, note that 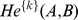 captures our intuition regarding similarity, because node pairs connected by many short paths of low-degree nodes will tend to have high
captures our intuition regarding similarity, because node pairs connected by many short paths of low-degree nodes will tend to have high 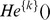 values. If node pairs with a large
values. If node pairs with a large 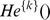 value are then somehow considered ‘similar’ in our metric, then clearly
value are then somehow considered ‘similar’ in our metric, then clearly 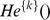 does a better job of capturing ‘similarity’ than does shortest-path distance. This is because
does a better job of capturing ‘similarity’ than does shortest-path distance. This is because 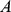 and
and 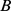 are relatively far under this metric; the influence of the hub
are relatively far under this metric; the influence of the hub 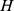 decreases the likelihood of a random walk from
decreases the likelihood of a random walk from 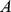 landing at
landing at 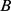 .
.
But a metric whose notion of similarity is based only on using 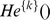 between the two given nodes directly does not solve all our problems. In particular, note that
between the two given nodes directly does not solve all our problems. In particular, note that 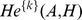 will indicate strong similarity, even though (as we have argued)
will indicate strong similarity, even though (as we have argued) 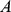 is not likely to be strongly functionally related to
is not likely to be strongly functionally related to 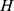 . Furthermore,
. Furthermore, 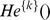 is still far from a metric; note it is not even symmetric. Also,
is still far from a metric; note it is not even symmetric. Also, 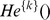 is only a pairwise, and not a global measure of node similarity. This observation leads us to use
is only a pairwise, and not a global measure of node similarity. This observation leads us to use 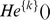 in a more subtle way, and in a different manner than previous diffusion approaches, resulting in the definition of DSD, which we describe next.
in a more subtle way, and in a different manner than previous diffusion approaches, resulting in the definition of DSD, which we describe next.
Definition of the New Distance Metric
Consider the undirected graph 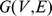 on the vertex set
on the vertex set 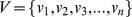 and
and 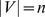 . Recall that
. Recall that 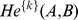 is defined as the expected number of times that a random walk starting at node
is defined as the expected number of times that a random walk starting at node 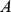 and proceeding for
and proceeding for 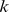 steps, will visit node
steps, will visit node 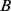 . In what follows, assume
. In what follows, assume 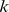 is fixed, and when there is no ambiguity, in the value of
is fixed, and when there is no ambiguity, in the value of 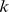 , we will denote
, we will denote 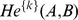 by
by 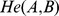 . We further define a
. We further define a  -dimensional vector
-dimensional vector 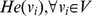 , where
, where
Then, the Diffusion State Distance (DSD) between two vertices  and
and 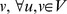 is defined as:
is defined as:
where 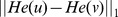 denotes the
denotes the 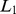 norm of the He vectors of u and v.
norm of the He vectors of u and v.
We will show for any fixed 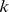 , that DSD is a metric, namely that it is symmetric, positive definite, and non-zero whenever
, that DSD is a metric, namely that it is symmetric, positive definite, and non-zero whenever 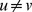 , and it obeys the triangle inequality. Thus, one can use DSD to reason about distances in a network in a sound manner. Further, we show that DSD converges as the
, and it obeys the triangle inequality. Thus, one can use DSD to reason about distances in a network in a sound manner. Further, we show that DSD converges as the 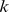 in
in 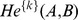 goes to infinity, allowing us to define DSD independent from the value
goes to infinity, allowing us to define DSD independent from the value 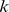 .
.
Characteristics of DSD
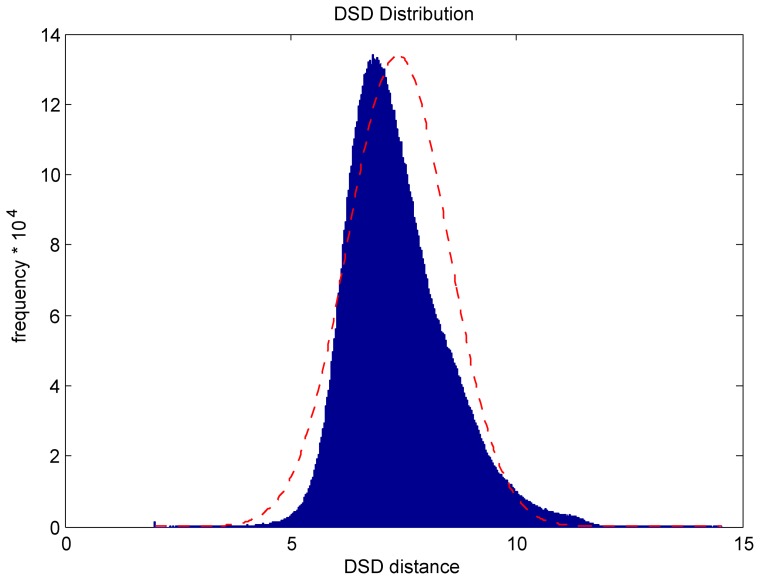
Figure 2 shows the distribution of DSD values in the PPI network of S. cerevisiae as downloaded in BioGRID [20]. The figure shows that DSD distances take on a smooth, continuous range of values. This is in sharp contrast to shortest-path distances, as shown in Figure 1(a), and shows that DSD is capable of making much finer-grained distinctions of similarity over pairs of nodes in the network.
Figure 2. Distribution of DSD in the largest connected component of the yeast PPI network; the red curve represents a fitted normal distribution for comparison.
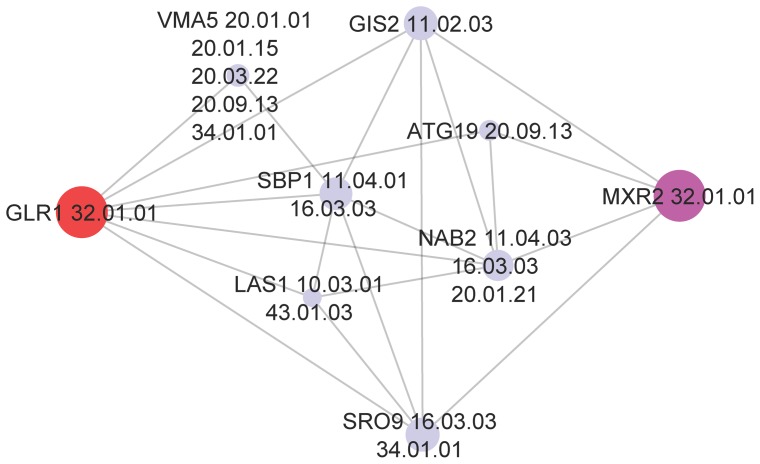
Figure 3 shows a typical example illustrating the nature of DSD. The Figure shows the gene GLR1 (in red at left) along with a subset of its local neighborhood. Node sizes have been made inversely proportional to their DSD distance from GLR1. None of GLR1's immediate neighbors contain its correct functional label at the third level of the MIPS hierarchy (32.01.01: oxidative stress response). However, the node closest in DSD is MXR2, which has exactly the same functional label. DSD recognizes that nodes having large common low-degree neighborhoods are highly similar and correctly identifies functionally similar node pairs, and does so in situations where shortest-path distance fails.
Figure 3. An example of functional annotation with DSD.
The correct functional annotation for GLR1, on the third level of the MIPS hierarchy, 32.01.01 (oxidative stress response) is found among none of its direct neighbors, but with the node that is closest in DSD, MXR2. MXR2 is closest in DSD because it has the most similar neighborhood to GLR1.
Methods
Functional Categories
We continue to work with the dataset described above, the largest connected component from an experimentally derived physical interaction PPI network from S. cerevisiae with 4990 nodes, and 74,310 edges. As in the papers introducing the classical function prediction methods we consider, we primarily use the MIPS (Munich Information Center For Protein Sequences) functional catalogue (FunCat) for our functional category labels [21]. We use the latest version of FunCat (version 2.1) and the first, second and third level functional categories, retaining those for which at least three proteins in our dataset are annotated with those labels. We present results for the first level (17 functional categories) second level (74 of the 80 functional categories that annotate at least one protein, annotate at least 3 proteins) and third level (154 of 181 functional categories that annotate at least one protein, annotate at least 3 proteins) MIPS annotations. MIPS is a shallow, leveled, hierarchical classification scheme for protein function, but we also present results for the popular Gene Ontology (GO) [25], where the variable depth hierarchy of the annotation labels makes the evaluation of labeling methods more complicated.
We assumed all published labels were correct and did not attempt for this study to weigh them by a level of confidence in each type of biological experiment. The following classical methods were tested in their original form (using shortest-path distance), against a DSD variant in cross validation.
Cross Validation Task
We considered 2-fold cross validation tasks. In each of the 2-fold cross validation tasks, we first randomly split the annotated proteins into 2 sets, and consider only the annotations on one partition in the training set, when trying to predict the annotations on proteins in the test set, and average the performance over the 2 folds of the cross validation. We conduct 10 runs of 2-fold cross-validation and report the mean and standard deviation of the following performance measures over these 10 runs.
Accuracy
This is the performance measurement suggested in [1]. Each protein is assigned its highest-scoring functional label. The label is considered correct if it appears among the labels that were assigned to the protein. We calculate the percentage of proteins that are assigned a correct label.
F1 score
This is the performance measurement suggested in [26]. For each protein, the possible functional labels the algorithm could assign are stored in a ranked list according to score. Each label is considered correct if it appears among the labels that were assigned to the protein, and incorrect otherwise. We calculate precision and recall by looking at the top  (in our case, we present results for
(in our case, we present results for 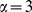 ) predicted annotations. Then the F1 score for each function can be calculated as:
) predicted annotations. Then the F1 score for each function can be calculated as:
We average F1 scores over the individual functions and obtain the overall F1 score for each algorithm.
Protein Function Prediction Methods
Neighborhood Majority Voting Algorithm
This is the simplest of all function prediction methods. Directly applying the concept of ‘guilt by association’, Schwikowski et al. [1] considered for each protein 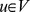 its neighboring proteins. Each neighbor votes for their own annotations, and the majority is used as the predicted functional label. To incorporate DSD, the neighborhood of
its neighboring proteins. Each neighbor votes for their own annotations, and the majority is used as the predicted functional label. To incorporate DSD, the neighborhood of  is defined simply as the
is defined simply as the  nearest neighbors of
nearest neighbors of  under the DSD metric. Furthermore, two schemes are considered: an unweighted scheme where all new neighbors vote equally, and a DSD weighted scheme where all new neighbors get a vote proportional to the reciprocal of their DSD distance.
under the DSD metric. Furthermore, two schemes are considered: an unweighted scheme where all new neighbors vote equally, and a DSD weighted scheme where all new neighbors get a vote proportional to the reciprocal of their DSD distance.
 Neighborhood Algorithm
Neighborhood Algorithm
In the original 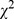 neighborhood algorithm [3], each annotation
neighborhood algorithm [3], each annotation  present in protein
present in protein  's neighborhood will be assigned a
's neighborhood will be assigned a 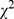 value based on the following formula:
value based on the following formula:
where 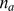 is the observed number of annotations
is the observed number of annotations  in the neighborhood, and
in the neighborhood, and 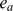 is the expected number of annotations
is the expected number of annotations  based on the whole protein-protein interaction network. Then protein
based on the whole protein-protein interaction network. Then protein  is assigned the functional label
is assigned the functional label  with the maximum
with the maximum 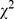 value. Again, it is straightforward to adapt this to use DSD: the neighborhood of
value. Again, it is straightforward to adapt this to use DSD: the neighborhood of  is simply defined as the
is simply defined as the  closest nodes to
closest nodes to  under the DSD metric.
under the DSD metric.
Multi-way cut Algorithm
We consider the minimal multi-way k-cut algorithm of Vazquez et al. [9] as implemented by [7]. The motivation is to minimize the number of times that annotations associated with neighboring proteins differ. In particular, the dual ILP (integer linear programming) is formulated, so we instead seek to maximize
subject to the constraints 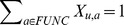 ,
, 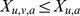 ,
, 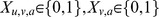 where the edge variables
where the edge variables 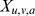 are defined for each function
are defined for each function  whenever there exists an edge between proteins
whenever there exists an edge between proteins  and
and  . It is set to 1, if protein
. It is set to 1, if protein  and
and  both are assigned function
both are assigned function  , and 0 otherwise. The node variables
, and 0 otherwise. The node variables 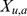 are set to 1 when
are set to 1 when  is labeled with function
is labeled with function  and 0 otherwise. The first constraint insures that each protein is only given one annotation. The second constraint makes sure only annotations that appear among the vertices can be assigned to the edges. While this problem is NP-hard, the ILP is tractable in practice; in our case we use the IBM CPLEX solver (version 12.4, dated 12/2011, http://www.ilog.com/products/cplex/). For the DSD version, we simply add additional edges between vertices whose DSD is below a threshold. We set a global threshold
and 0 otherwise. The first constraint insures that each protein is only given one annotation. The second constraint makes sure only annotations that appear among the vertices can be assigned to the edges. While this problem is NP-hard, the ILP is tractable in practice; in our case we use the IBM CPLEX solver (version 12.4, dated 12/2011, http://www.ilog.com/products/cplex/). For the DSD version, we simply add additional edges between vertices whose DSD is below a threshold. We set a global threshold 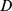 based on the average DSD of all pairs, specifically we set
based on the average DSD of all pairs, specifically we set 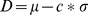 , where
, where 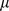 is the average, and
is the average, and  is the standard deviation of the global set of DSD values among all pairs of nodes in the graph. We experiment with
is the standard deviation of the global set of DSD values among all pairs of nodes in the graph. We experiment with  in the range
in the range 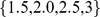 .
.
Functional Flow Algorithm
Nabieva at al. [7] use a network flow algorithm on the graph of protein interactions to label proteins. The idea is to consider each protein having a known function annotation as a ‘reservoir’ of that function, and to simulate flow of functional association through the network to make predictions. We adapt the approach to use DSD by creating an edge between each node pair, with a weight inversely proportional to DSD. For computational efficiency we do not create edges when the reciprocal of DSD is below a small value. As in the original functional flow, we calculate flow through this new network at each time step. We denote the size of the reservoir of function  at node
at node  and time step
and time step  , to be
, to be 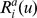 . For a given function (annotation)
. For a given function (annotation)  , we initialize the reservoir size at node
, we initialize the reservoir size at node  to be infinite if protein
to be infinite if protein  has been annotated with function
has been annotated with function  ; otherwise we set it to be 0. More formally:
; otherwise we set it to be 0. More formally:
We then update the reservoir over a sequence of timesteps (we use 6 timesteps, as in the original version):
where 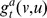 is the amount of flow
is the amount of flow  that moves from
that moves from  to
to  at time
at time  . We incorporate DSD into the edge weight as follows:
. We incorporate DSD into the edge weight as follows:
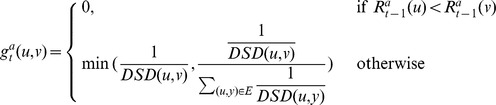 |
The final functional score for node  and function
and function  over 6 timesteps is computed as the total amount of incoming flow.
over 6 timesteps is computed as the total amount of incoming flow.
Formal Properties of DSD
We now present the formal proofs that DSD is a metric for any fixed 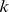 , that it converges as
, that it converges as 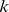 goes to infinity, and obtain the explicit form that allows the calculation of DSD values in the limit.
goes to infinity, and obtain the explicit form that allows the calculation of DSD values in the limit.
Lemma 1
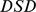 is a metric on
is a metric on  , where
, where 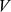 is the vertex set of a simple connected graph
is the vertex set of a simple connected graph 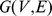 .
.
Proof
Clearly the DSD of a node to itself is 0, and DSD is non-negative and symmetric. It remains only to show that DSD satisfies the triangle inequality, and that 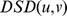 is strictly positive whenever
is strictly positive whenever 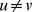 .
.
For all 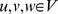 , we have by the
, we have by the  norm property:
norm property:
and therefore:
Thus, the triangle inequality follows easily:
Next we prove the identity of indiscernibles, namely, 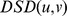 is non-zero for all
is non-zero for all 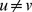 . We first need some notation. We define the one step transition probability matrix
. We first need some notation. We define the one step transition probability matrix 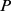 as the
as the  -dimensional square matrix, whose
-dimensional square matrix, whose 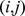 th entry is given by:
th entry is given by:
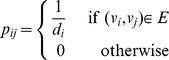 |
where 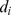 is the degree of node
is the degree of node 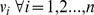 . Note that
. Note that 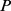 represents the probability to reach each neighbor in the random walk where all neighbors are reached with equal probability.
represents the probability to reach each neighbor in the random walk where all neighbors are reached with equal probability.
Then the definition of 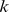 step transition probability matrix
step transition probability matrix 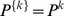 follows for all positive
follows for all positive 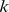 . We also define the 0 step transition matrix
. We also define the 0 step transition matrix 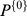 to be the identity matrix
to be the identity matrix 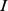 , because every random walk starts from the source vertex, and thus a zero-step random walk reaches its source vertex with probability 1 and all other vertices with probability 0. We denote by
, because every random walk starts from the source vertex, and thus a zero-step random walk reaches its source vertex with probability 1 and all other vertices with probability 0. We denote by 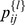 or
or 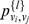 the
the 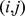 th entry in the
th entry in the 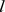 th transition probability matrix, where
th transition probability matrix, where 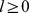 and
and 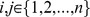 .
.
For each ordered pair of vertices 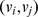 , recall that
, recall that 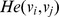 is defined as the expected number of times that a random walk with length
is defined as the expected number of times that a random walk with length 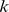 starting from
starting from 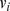 will visit
will visit 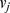 . In order to calculate
. In order to calculate 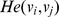 , we define an indicator variable
, we define an indicator variable 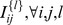 , where:
, where:
Therefore we have 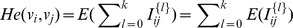 by linearity of expectation. Clearly,
by linearity of expectation. Clearly, 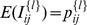 , and thus we have
, and thus we have 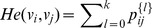 . Note that because we are adding the zero-step transition matrix, we will have that
. Note that because we are adding the zero-step transition matrix, we will have that 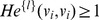 ,
, 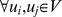 .
.
Now we are ready to show the identity of indiscernibles. Recall we are assuming the graph is connected. It is trivial when 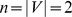 , so consider the case where
, so consider the case where 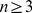 . We prove this next by contradition.
. We prove this next by contradition.
Assume there exists a pair of distinct vertices  and
and 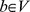 in the simple connected graph G, where
in the simple connected graph G, where 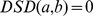 . Thus
. Thus 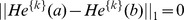 , and
, and 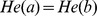 , which indicates that
, which indicates that 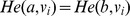 ,
, 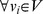 . We have
. We have  equations now:
equations now: 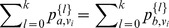 . Since the zero-step transition matrix
. Since the zero-step transition matrix 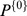 is an identity matrix, we know that
is an identity matrix, we know that 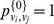 for
for 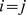 and 0, otherwise.
and 0, otherwise.
Thus we have
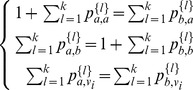 |
(1) |
where the third line represents a set of  equations: one for each
equations: one for each 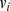 , distinct from
, distinct from  and
and 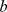 .
.
By multiplying a factor 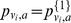 to both sides of all equations in the third line and summing over
to both sides of all equations in the third line and summing over  , we have:
, we have:
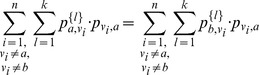 |
By completing the sum over  , we have:
, we have:
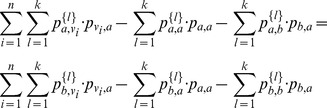 |
G doesn't contain self-loops; thus 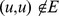 and
and 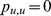 ,
, 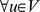 . For each
. For each 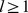 , we have
, we have
and
Therefore, we have
namely,
By applying to the equation above the first and the second equation in (1), where:
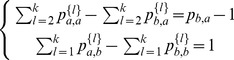 |
(2) |
we have:
namely,
Since 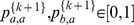 , we have
, we have 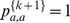 .
.
We next argue that it must be the case that 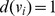 , for all
, for all 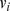 with
with 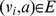 , namely, all of
, namely, all of  's neighbors must have degree 1.
's neighbors must have degree 1.
Starting from
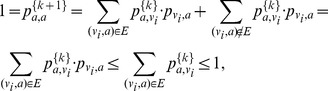 |
we must therefore have 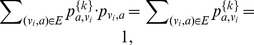 and
and 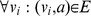 and
and 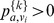 ,
, 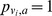 . Since we have
. Since we have 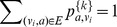 , there must exist at least one neighbor
, there must exist at least one neighbor  , s.t.
, s.t. 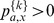 , and
, and 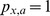 as well. Because
as well. Because 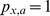 , we know that
, we know that  is the only neighbor to
is the only neighbor to  and
and 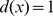 . Also due to the fact that
. Also due to the fact that 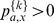 , there exists a path of length
, there exists a path of length 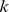 from
from  to
to  , which should consists of two parts, one path (denoted as
, which should consists of two parts, one path (denoted as 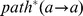 ) of length
) of length  from
from  to
to  and an edge from
and an edge from  to
to  as the last step in the path.
as the last step in the path.
Consider any neighbor 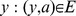 . By using the
. By using the 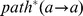 and the edge
and the edge 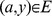 , we can construct a path of length
, we can construct a path of length 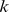 from
from  to
to 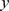 and therefore
and therefore 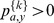 . Thus,
. Thus, 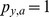 , and therefore
, and therefore 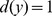 . Thus we have shown that it must be the case that
. Thus we have shown that it must be the case that 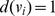 , for all
, for all 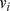 , with
, with 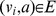 .
.
As a result, all of  's neighbors are only connected to
's neighbors are only connected to  .
.
If 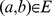 , then
, then  and
and 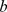 can't have any more neighbors because they must be the only neighbor of each other; thus for all
can't have any more neighbors because they must be the only neighbor of each other; thus for all 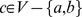 ,
,  is not connected to
is not connected to  or
or 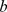 , which contradicts the fact that the graph G is connected. If
, which contradicts the fact that the graph G is connected. If 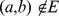 ,
,  and
and  are not connected because all of their neighbors are only adjacent to themselves respectively.
are not connected because all of their neighbors are only adjacent to themselves respectively.
Therefore, the existence of such pair 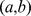 where
where 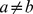 and
and 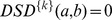 contradicts the fact that the graph is connected, and we can conclude that
contradicts the fact that the graph is connected, and we can conclude that 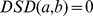 if and only if
if and only if 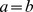 .
.
In the above we were reasoning about DSD for a fixed value of 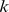 . Denote by
. Denote by 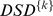 the value of DSD for a particular fixed
the value of DSD for a particular fixed 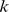 . Next we discuss how DSD values depend on
. Next we discuss how DSD values depend on 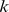 . We show that when the one-step transition matrix
. We show that when the one-step transition matrix 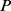 is diagonalizable then
is diagonalizable then 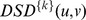 converges to a stationary value
converges to a stationary value 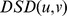 .
.
Lemma 2
Let 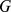 be a connected graph whose random walk one-step transition probability matrix
be a connected graph whose random walk one-step transition probability matrix  is diagonalizable and ergodic as a Markov chain, then for any
is diagonalizable and ergodic as a Markov chain, then for any  converges as
converges as 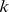 , the length of the random walk, approaches infinity.
, the length of the random walk, approaches infinity.
Proof
Since the one step transition probability matrix 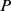 is diagonalizable, we have by diagonalization:
is diagonalizable, we have by diagonalization:
where the orthogonal matrix 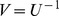 ; each column of
; each column of 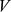 is the normalized right eigenvector of
is the normalized right eigenvector of 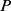 , each row of
, each row of 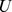 is the normalized left eigenvector of
is the normalized left eigenvector of 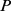 , and
, and 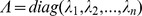 is the diagonal matrix of all eigenvalues where
is the diagonal matrix of all eigenvalues where 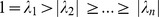 by ergodicity. Let
by ergodicity. Let 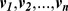 denote the normalized orthogonal column vectors in
denote the normalized orthogonal column vectors in 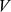 and
and 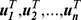 the normalized orthogonal row vectors in
the normalized orthogonal row vectors in 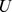 . We denote
. We denote 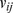 as the
as the 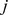 th entry in vector
th entry in vector 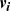 and
and 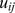 as the jth entry in vector
as the jth entry in vector 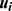 .
.
Thus it follows that 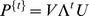 , namely
, namely 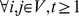 :
:
Next, for all 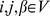 , we define an infinite sequence
, we define an infinite sequence 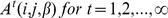 :
:
and 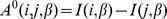 where
where 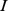 is the identity matrix.
is the identity matrix.
Therefore, by definition, we can rewrite 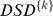 as the partial sum:
as the partial sum:
Claim 1
For all 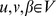 ,
, 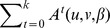 converges absolutely.
converges absolutely.
Before we prove the claim, we show that it produces what we need. If the claim is true, then the limit 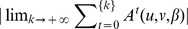 exists, and we can denote it as
exists, and we can denote it as 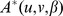 . Then it follows that:
. Then it follows that:
and we have proved convergence.
But Claim 1 is true from the Cauchy root test, namely,
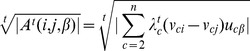 |
(3) |
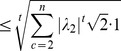 |
(4) |
| (5) |
where (3) & (5) hold by definition and (4) holds because 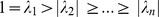 and
and 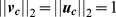 .
.
We now use this lemma to produce an explicit way to calculate in the limit. This frees DSD entirely from dependence on the parameter 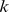 , and this is the version of DSD we use in our experiments. (We remark, that for our yeast PPI network, we found empirically that
, and this is the version of DSD we use in our experiments. (We remark, that for our yeast PPI network, we found empirically that 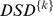 values were very close to the limit when
values were very close to the limit when 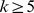 .)
.)
Lemma 3
Let 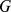 be a connected graph whose random walk one-step transition probability matrix
be a connected graph whose random walk one-step transition probability matrix 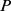 is diagonalizable and ergodic as a Markov chain, then for any
is diagonalizable and ergodic as a Markov chain, then for any 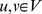 , we have
, we have 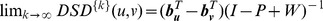 , where
, where 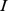 is the identity matrix,
is the identity matrix, 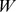 is the constant matrix in which each row is a copy of
is the constant matrix in which each row is a copy of 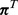 ,
, 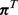 is the unique steady state distribution, and for any
is the unique steady state distribution, and for any 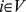 ,
, 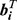 is the
is the 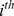 basis vector, i.e., the row vector of all zeros except for a 1 in the
basis vector, i.e., the row vector of all zeros except for a 1 in the 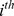 position.
position.
Proof
To start, we denote the matrix 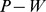 by
by 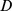 . By Lemma 2 where we have shown that
. By Lemma 2 where we have shown that 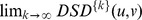 exists and is finite, we can denote the limit as simply
exists and is finite, we can denote the limit as simply 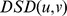 in the following context. It follows that for any
in the following context. It follows that for any 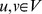 :
:
| (6) |
| (7) |
| (8) |
| (9) |
where (6) holds by definition, (7) holds because 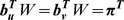 , (8) holds because
, (8) holds because 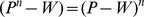 for all
for all 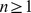 by Claim 2, and (9) holds by Claim 3, where we finish the proof of Lemma 3 by proving Claims 2 and 3 next.
by Claim 2, and (9) holds by Claim 3, where we finish the proof of Lemma 3 by proving Claims 2 and 3 next.
Claim 2
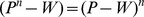 , for any non-zero positive integer n.
, for any non-zero positive integer n.
Proof
The proof is based on the following observations: 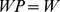 and
and 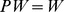 , so
, so 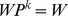 and
and 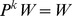 . Further,
. Further, 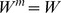 , so
, so 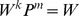 and
and 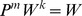 for any integers
for any integers 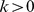 and
and 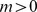 . Now, if you construct the binomial expansion of
. Now, if you construct the binomial expansion of 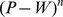 , each cross term of the type
, each cross term of the type 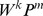 or
or 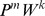 reduces to
reduces to 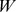 , and all of the
, and all of the 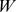 s cancel out except for one, leaving
s cancel out except for one, leaving 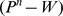 . Thus,
. Thus, 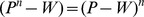 .
.
Claim 3
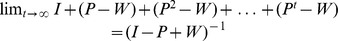 .
.
Proof
By Claim 2, 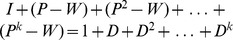
First we show that
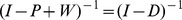 exists. We show that
exists. We show that 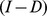 has full rank by showing that
has full rank by showing that  is the only vector in the left nullspace of
is the only vector in the left nullspace of 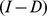 . That is, if
. That is, if 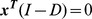 , then
, then 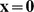 .
.
Now, we already know that 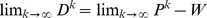 exists and is 0 by ergodicity. So we have
exists and is 0 by ergodicity. So we have
which is only satisfied by by 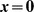 .
.
Since
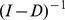 exists and
exists and 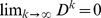 , we can calculate as follows:
, we can calculate as follows:
where  is defined as
is defined as 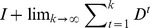 , which exists because
, which exists because 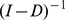 exists and
exists and 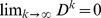 .
.
That finishes the proof for Lemma 3.
Results
MIPS Results
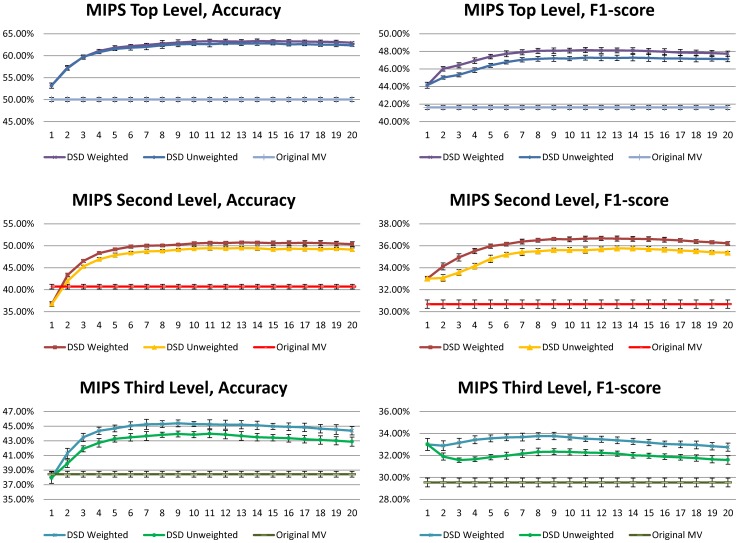
Both the DSD majority voting method and the 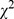 neighborhood method sort vertices in order of their smallest DSD to a given vertex, and set a threshold
neighborhood method sort vertices in order of their smallest DSD to a given vertex, and set a threshold  , where the first
, where the first  vertices participate in the functional vote. Table 1 gives the results in 2-fold cross validation for both these methods when we set
vertices participate in the functional vote. Table 1 gives the results in 2-fold cross validation for both these methods when we set 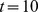 , whereas Figure 4 gives more details about the dependence on
, whereas Figure 4 gives more details about the dependence on  ; basically once enough neighbors were included (i.e.
; basically once enough neighbors were included (i.e. 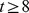 ) results of the DSD version of majority voting converged. Similar details about how the
) results of the DSD version of majority voting converged. Similar details about how the 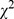 neighborhood method depends on
neighborhood method depends on  appears in (Figure S1). For the multi-way cut and functional flow results, we considered vertices to be in the DSD neighborhood of a node
appears in (Figure S1). For the multi-way cut and functional flow results, we considered vertices to be in the DSD neighborhood of a node  if their DSD from
if their DSD from  was less than
was less than  standard deviations below the mean DSD value across the entire dataset. Table 1 presents the 2-fold cross validation DSD multi-way cut results and DSD functional flow results with
standard deviations below the mean DSD value across the entire dataset. Table 1 presents the 2-fold cross validation DSD multi-way cut results and DSD functional flow results with 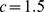 . In addition, Figure 5 gives more detail about the dependence of DSD functional flow on the parameter
. In addition, Figure 5 gives more detail about the dependence of DSD functional flow on the parameter  , where we tested
, where we tested 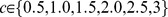 . Similar details about how the multiway cut method depends on
. Similar details about how the multiway cut method depends on  appear in (Figure S2).
appear in (Figure S2).
Table 1. Summary of DSD improvements of all four methods in 2-fold cross validation (mean and standard deviation in percentage) for the PPI network of S. cerevisiae.
| MIPS 1 | MIPS 2 | MIPS 3 | ||||
| Accuracy | F1 score | Accuracy | F1 score | Accuracy | F1 | |
| Majority Vote (MV) | 50.0±0.5 | 41.6±0.2 | 40.7±0.5 | 30.7±0.4 | 38.4±0.4 | 29.5±0.4 |
| MV with DSD | 63.7±0.4 | 47.2±0.2 | 49.3±0.5 | 35.6±0.2 | 43.8±0.4 | 32.3±0.3 |
| MV (weighted DSD) | 63.2±0.5 | 48.1±0.3 | 50.6±0.4 | 36.6±0.2 | 45.3±0.3 | 33.6±0.2 |
| Neighborhood (NH) | 43.3±0.3 | 34.5±0.2 | 32.4±0.6 | 26.1±0.3 | 31.3±0.5 | 24.8±0.3 |
| NH with DSD | 51.5±0.4 | 40.6±0.3 | 34.8±0.5 | 27.7±0.2 | 32.6±0.6 | 25.1±0.3 |
| Multi-cut | 55.2±0.4 | 42.1±0.2 | 42.0±0.6 | 28.1±0.2 | 36.6±0.4 | 24.8±0.3 |
| Multi-cut with DSD | 58.3±0.3 | 42.2±0.2 | 44.6±0.4 | 29.6±0.1 | 38.2±0.3 | 25.3±0.2 |
| Functional Flow (FF) | 50.5±0.6 | 37.0±0.3 | 32.1±0.4 | 22.6±0.3 | 25.4±0.6 | 18.3±0.3 |
| FF with DSD | 54.0±0.4 | 40.8±0.2 | 38.3±0.3 | 27.1±0.3 | 31.5±0.3 | 22.8±0.2 |
Figure 4. Improvement on Accuracy and F1 Score for at different neighborhood thresholds, for the majority voting algorithm in 10 runs of 2-fold cross validation for S. cerevisiae, with standard deviations.
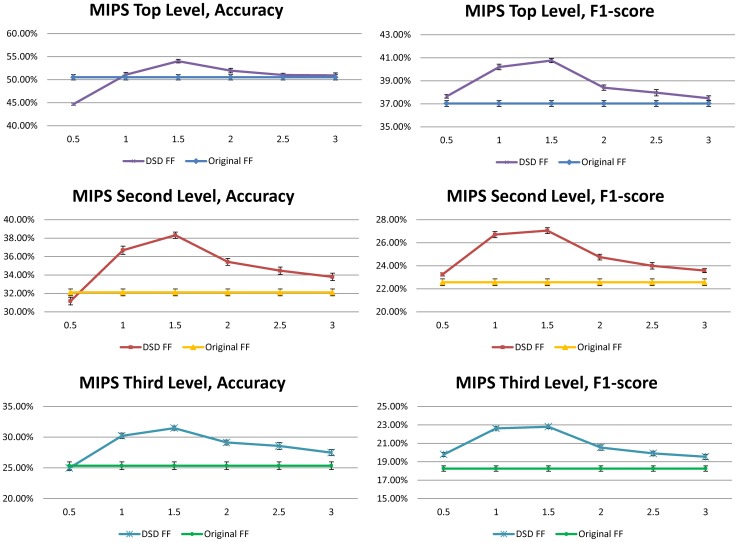
Figure 5. Improvement on Accuracy and F1 Score for DSD at different neighborhood thresholds, for the functional flow (FF) algorithm in 10 runs of 2-fold cross validation for S. cerevisiae, with standard deviations.
We notice from Table 1 that in every case, the DSD versions of all four methods perform better than the versions based on ordinary distance. It is particularly interesting that using DSD improves the functional flow algorithm, since functional flow already seeks to capture a notion of diffusion in the graph. In fact, the DSD versions of Majority Voting perform better than all four of the methods based on ordinary distance. The best performing algorithms among all the ordinary distance algorithms on the yeast MIPS annotations at all three levels of the MIPS hierarchy were the majority voting algorithms. The best performing algorithms overall are the DSD version of the majority voting algorithms, and they clearly achieve the best performance compared to all four ordinary distance and all three other DSD-based methods. In particular, they achieve 63.7% mean accuracy and 47.2% mean F1 score (unweighted) and 63.2% mean accuracy and 48.1% mean F1 score (weighted) on the first level of the MIPS hierarchy. This is compared to the original majority voting algorithm, which only obtains 50.0% mean accuracy and 41.6% mean F1 score. Hence DSD provides more than 13% improvement in accuracy and more than 5% improvement in F1 score for MIPS top level functional categories, and improves on ordinary DSD on the second and third levels of the MIPS hierarchy across the board.
GO Results
GO (Gene Ontology) [25] is a deeply hierarchical classification scheme, which makes defining and evaluating function prediction methods much more complicated. For this reason, most function prediction methods for yeast PPI networks use the “flatter” set of MIPS categories, but GO is the more widely used ontology. Thus we wished to measure performance for GO functional labels, despite the difficulties. For example, in GO, sometimes, nodes are labeled with child functions but not labeled with their parent functions, even though it is assumed that child functions are more specific and inherit the functions of their parent nodes. How much credit should be given to a node when we do not label it correctly at its most specific level, but succeed in labeling it with a less specific ancestor term? The exact match and functional path methods of Deng et al [27], [28] are designed to directly answer this question and evaluate methods that perform GO annotation. We tested the performance of ordinary distance versus DSD versions all four protein function prediction methods considered above also on the GO, and evaluated the results using the exact match method and functional path method of Deng et al. [27]. We find, again, that using the DSD-based algorithm improves performance.
We consider labels in the biological process category of the GO hierarchy (we used OBO v1.2 [29], data version 2013-07-18) along with annotations downloaded from the SGD database (data version 2013-07-13). We exclude GO terms that are annotated with evidence codes “IEA” “RCA” or “IPI”. For each protein that was labeled with a term in the GO hierarchy, we automatically also label it with all more general parent terms in the GO hierarchy as well. We then, define the informative nodes in the GO hierarchy to be functional annotation terms that 1) are at least three levels below the root and 2) are terms that annotate more than 50 proteins in our dataset, where the second condition on informative nodes, and the number 50 is suggested by the method of Deng et al. [27]. It is these GO functional terms, somehow capturing the middle levels in functional specificity, that we use instead of a level of the MIPS hierarchy for the functional labels. The result is 136 informative biological process GO terms among 4322 out of 4990 ORFs that will comprise our labeling set (the total number of annotations is 58,519); thus we have a label set that is close in size to the one from the third level of the MIPS hierarchy. The “exact match” method then simply counts the number of correct labels, just as we did for a fixed level of the MIPS hierarchy. We see similar improvements for GO annotation as we did for MIPS annotation; detailed results for accuracy and F1 score for all four methods appear in (Figure S3).
However, note that this exact match evaluation gives no credit when we label a protein with an incorrect child that still has many ancestor terms in common with the correct label. Thus, for a more fair evaluation of the predictions that takes into account hierarchical relations among the GO labels, we also use the functional path method of Deng et al. [27]. This presents a plausible way to give partial credit when a node is labeled partially correctly, in the sense that the lowest depth child label assigned to the node and the correct label of the node are different, but if we consider the path in the ontology from the root to these two labels, there are ancestor labels these two functional paths have in common. We use exactly the functional path method of [27] to calculate precision and recall values for each protein, and then overall precision and recall values are averaged over all the proteins. We calculated both alternative ways to count functional paths overlap presented in Deng et al. [27], one that simply counts the number of nodes that appear jointly in sets of known and predicted functional annotations (which we will call the overlap counting method) and the other which takes into account at what depth the functional paths from both sets diverge (which we will call the overlap depth method).
Setting  , the neighborhood threshold for DSD majority voting anywhere in the range starting from 2, the DSD version of majority voting improves precision and recall simultaneously, as compared to original majority voting, regardless of the method used for counting overlaps. For example at
, the neighborhood threshold for DSD majority voting anywhere in the range starting from 2, the DSD version of majority voting improves precision and recall simultaneously, as compared to original majority voting, regardless of the method used for counting overlaps. For example at 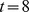 , we get precision = 67.3% ±0.3% and recall = 40.3% ±0.2% compared to precision = 59.6% ±0.4% and recall = 34.3% ±0.4% for the overlap counting method, and we get precision = 61.1% ±0.3% and recall = 27.3% ±0.1% compared to precision = 52.9% ±0.5% and recall = 20.5% ±0.4% for the overlap depth method, for 2-fold cross validation on the yeast PPI network. In fact, we find that all DSD versions of the four algorithms perform better than their ordinary distance versions, regardless of the methods used for keeping track of overlaps. Figure 6 shows the improvements in F1 scores (setting
, we get precision = 67.3% ±0.3% and recall = 40.3% ±0.2% compared to precision = 59.6% ±0.4% and recall = 34.3% ±0.4% for the overlap counting method, and we get precision = 61.1% ±0.3% and recall = 27.3% ±0.1% compared to precision = 52.9% ±0.5% and recall = 20.5% ±0.4% for the overlap depth method, for 2-fold cross validation on the yeast PPI network. In fact, we find that all DSD versions of the four algorithms perform better than their ordinary distance versions, regardless of the methods used for keeping track of overlaps. Figure 6 shows the improvements in F1 scores (setting 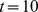 and
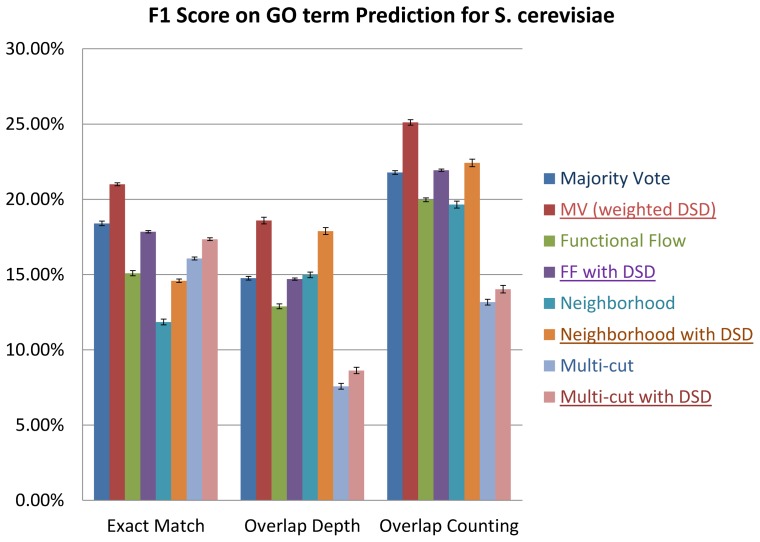
and 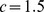 as before) over all three methods of counting the overlaps. Thus DSD is improving functional annotation also for GO annotation.
as before) over all three methods of counting the overlaps. Thus DSD is improving functional annotation also for GO annotation.
Figure 6. Improvement on F1 Score for DSD using three evaluation methods: exact match, overlap depth and overlap counting, on informative GO terms for the four algorithms for S. cerevisiae in 10 runs of 2-fold cross validation.
Discussion
Our function prediction results demonstrate the utility of defining and using a fine-grained distance measure that is specifically tailored to the subject application domain. For the PPI network, the observation that shortest-paths that go through hubs are less informative led to the particular design of the He () measure incorporated into the DSD definition. The He () measure has connections to other diffusion-based measures previously proposed [23]; however, using He () globally across all nodes, and comparing such vectors via L1 norm is entirely new and enables DSD to capture truly global properties of network topologies.
We have shown that substituting DSD for ordinary shortest path distance results in dramatic improvements when using network information to predict protein function for the S. cerevisiae PPI network. We expected that similar improvements would hold for the PPI-networks of other organisms as well, though the sparseness of current experimental known functional annotation and the number of PPI interactions currently known for other organisms means that we would not yet expect absolute levels of accuracy that are comparable to those achieved for S. cervesiae. We tested this intuition by also considering what is known of the PPI network of a different, less-well annotated yeast species, S. pombe. Based on the interactions in BIOGRID [20] version 3.2.102, the largest connected component has 1925 nodes and 4874 edges. Thus compared to the S. cerevisiae network, a much smaller and sparser subset of the PPI network is known. Figure 7 shows the shortest path and DSD distance distribution of this network. As expected, it is low-diameter but not yet as low-diameter as the S. cerevisiae network, and the DSD distribution is more spread out, but not yet as smooth as for the S. cerevisiae network. We would predict that the distribution would start looking more like S. cerevisiae as more of the network becomes known. We found no reliable MIPS annotation for S. pombe, so we instead used GO annotation, which we downloaded from the Pombase database, data version 2013-07-01 (http://www.pombase.org). We extract “biological process” GO terms only and remove GO terms annotated with evidence codes “IEA”, “IPI” and “RCA”, leaving 85 informative (see GO results section above, for definition) GO terms annotating 1722 out of 1925 proteins, with a total number of 5818 annotations. We did the “exact match” version of GO evaluation for 10 runs of cross-validation, and looked at the difference in performance for majority vote and functional flow methods using ordinary shortest path distance and DSD. We see similar improvements using DSD as with S. cervisiae; results appear in (Figure S4).
Figure 7. Shortest path distance and DSD distribution for S. pombe.
We present a simple to use, freely-available tool that given any PPI network will produce the DSD values between each pair of proteins, either as a webserver or for download from http://dsd.cs.tufts.edu/. This tool both allows the calculation of 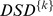 for some chosen
for some chosen 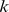 , and, as in the results presented in this paper, for DSD in the limit. In fact, we also tried
, and, as in the results presented in this paper, for DSD in the limit. In fact, we also tried 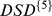 in place of DSD for all the methods in this paper and results were already quite similar to DSD in the limit. We suggest based on the dramatic improvements for the S. cerevisiae PPI network that DSD values be used in place of ordinary distance when using network information to predict protein function, either using the PPI network alone, or as part of a modern integrative function prediction method that includes data from a variety of sources beyond the PPI network, such as sequence information, genetic interaction, structural information or expression data [8], [13]–[15].
in place of DSD for all the methods in this paper and results were already quite similar to DSD in the limit. We suggest based on the dramatic improvements for the S. cerevisiae PPI network that DSD values be used in place of ordinary distance when using network information to predict protein function, either using the PPI network alone, or as part of a modern integrative function prediction method that includes data from a variety of sources beyond the PPI network, such as sequence information, genetic interaction, structural information or expression data [8], [13]–[15].
Acknowledgments
Crovella and Cowen thank the Institute for Mathematics and its Applications for inviting them to their “Network Links: Connecting Social, Communication, and Biological Network Analysis” workshop in March 2012, where we learned about each others' recent work and began the collaboration that resulted in this paper. We thank Andrew Gallant for helping review the DSD code.
Supporting Information
Improvement of mean Accuracy and F1 Score for DSD at different neighborhood thresholds for the
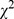 neighborhood algorithm in 10-runs of 2-fold cross validation (with standard deviation error bars).
neighborhood algorithm in 10-runs of 2-fold cross validation (with standard deviation error bars).
(TIF)
Improvement of mean Accuracy and F1 Score for DSD at different neighborhood thresholds for the multi-way cut algorithm in 10-runs of 2-fold cross validation (with standard deviation error bars).
(TIF)
Improvement of mean Accuracy and F1 Score for DSD at different neighborhood thresholds for all four methods in 10-runs of 2-fold cross validation (with standard deviation error bars) using the GO catagories (using the method that gives wcredit only for exact matches to each GO term).
(TIF)
Performance evalutaion for GO term prediction on the S. pombe network. (a) Comparison of mean F1 score of DSD and non-DSD majority vote (setting t = 10) and functional flow (setting c = 1.5) algorithms using all three methods of counting GO term matches; (b1,b2) Comparison of mean accuracy and F1 Score under the exact match method for different settings of the parameters t and c, over 10 runs of 2-fold cross validation (with standard deviation error bars).
(TIF)
Funding Statement
MC, HZ, NMD and LJC were supported in part by National Institutes of Health (NIH) R01 grant GM080330. JP was supported in part by NIH grant R01 HD058880. This material is based upon work supported by the National Science Foundation under grant numbers CNS-0905565, CNS-1018266, CNS-1012910, and CNS-1117039, and supported by the Army Research Office under grant W911NF-11-1-0227 (to MEC). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Schwikowski B, Uetz P, Fields S (2000) A network of protein-protein interactions in yeast. Nature Biotechnology 18: 1257–1261. [DOI] [PubMed] [Google Scholar]
- 2. Chua HN, Sung WK, Wong L (2006) Exploiting indirect neighbours and topological weight to predict protein function from protein–protein interactions. Bioinformatics 22: 1623–1630. [DOI] [PubMed] [Google Scholar]
- 3. Hishigaki H, Nakai K, Ono T, Tanigami A, Takagi T (2001) Assessment of prediction accuracy of protein function from protein-protein interaction data. Yeast 18: 523–531. [DOI] [PubMed] [Google Scholar]
- 4. Arnau V, Mars S, Marín I (2005) Iterative cluster analysis of protein interaction data. Bioinformatics 21: 364–378. [DOI] [PubMed] [Google Scholar]
- 5.Bader G, Hogue C (2003) An automated method for finding molecular complexes in large protein interaction networks. BMC Bioinformatics 4. [DOI] [PMC free article] [PubMed]
- 6. Song J, Singh M (2009) How and when should interactome-derived clusters be used to predict functional modules and protein function? Bioinformatics 25: 3143–3150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Nabieva E, Jim K, Agarwal A, Chazelle B, Singh M (2005) Whole-proteome prediction of protein function via graph-theoretic analysis of interaction maps. Bioinformatics 21: 302–310. [DOI] [PubMed] [Google Scholar]
- 8. Karaoz U, Murali T, Letovsky S, Zheng Y, Ding C, et al. (2003) Whole genome annotation by using evidence in functional-linkage networks. Proc Natl Acad Sci USA 101: 2888–2893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Vazquez A, Flammini A, Maritan A, Vespignani A (2003) Global protein function prediction from protein-protein interaction networks. Nature Biotechnology 21: 696–700. [DOI] [PubMed] [Google Scholar]
- 10. Sharan R, Ulitsky I, Shamir R (2007) Network-based prediction of protein function. Mol Syst Biol 3: 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Chiang T, Scholtens D, Sarkar D, Gentleman R, Huber W (2007) Coverage and error models of protein-protein interaction data by directed graph analysis. Genome Biology 8: R186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Huang H, Bader JS (2009) Precision and recall estimates for two-hybrid screens. Bioinformatics 25: 372–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lanckriet G, Deng M, Cristianini N, Jordan MI, Noble W (2004) Kernel-based data fusion and its application to protein function prediction in yeast. Pac Symp Biocomput: 300–311. [DOI] [PubMed]
- 14. Tanay A, Sharan R, Kupiec M, Shamir R (2004) Revealing modularity and organization in the yeast molecular network by integrated analysis of highly heterogeneous genomewide data. Proc Natl Acad Sci USA 101: 2981–2986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Wass MN, Barton G, Sternberg MJE (2012) Combfunc: predicting protein function using heterogeneous data sources. Nucleic Acids Res 40: W466–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Khanin R, Wit E (2006) How scale-free are biological networks? Journal of Computational Biology 13: 810–818. [DOI] [PubMed] [Google Scholar]
- 17. Friedel CC, Zimmer R (2006) Toward the complete interactome. Nature Biotechnology 24: 614–615. [DOI] [PubMed] [Google Scholar]
- 18. Han JDJ, Bertin N, Hao T, Goldberg DS, Berriz GF, et al. (2004) Evidence for dynamically organized modularity in the yeast protein-protein interaction network. Nature 430: 88–93. [DOI] [PubMed] [Google Scholar]
- 19. Przulj N, Corneil D, Jurisica I (2004) Modeling interactome: scale-free or geometric? Bioinformatics 20: 3508–3515. [DOI] [PubMed] [Google Scholar]
- 20. Stark C, Breitkreutz B, Reguly T, Boucher L, Breitkreutz A, et al. (2006) Biogrid: a general repository for interaction datasets. Nucleic Acids Res 34: D535–D539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Ruepp A, Zollner A, Maier D, Albermann K, Hani J, et al. (2004) The funcat, a functional annotation scheme for systematic classification of proteins from whole genomes. Nucleic acids research 32: 5539–5545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. He X, Zhang J (2006) Toward a molecular understanding of pleiotropy. Genetics 173: 1885–1891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Kohler S, Bauer S, Horn D, Robinson PN (2008) Walking the interactome for prioritization of candidate disease genes. Am J Hum Genet 82: 949–958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Erten S, Bebek G, Koyutürk M (2011) Vavien: an algorithm for prioritizing candidate disease genes based on topological similarity of proteins in interaction networks. Journal of computational biology: a journal of computational molecular cell biology 18: 1561–1574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, et al. (2000) Gene ontology: tool for the unification of biology. Nature genetics 25: 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Darnell SJ, Page D, Mitchell JC (2007) An automated decision-tree approach to predicting protein interaction hot spots. Proteins: Structure, Function, and Bioinformatics 68: 813–823. [DOI] [PubMed] [Google Scholar]
- 27. Deng M, Tu Z, Sun F, Chen T (2004) Mapping gene ontology to proteins based on protein–protein interaction data. Bioinformatics 20: 895–902. [DOI] [PubMed] [Google Scholar]
- 28.Deng M, Sun F, Chen T (2003) Assessment of the reliability of protein-protein interactions and protein function prediction. Pacific Symposium on Biocomputing: 140–151. [PubMed]
- 29. Day-Richter J, Harris MA, Haendel M, Lewis S, et al. (2007) Obo-editan ontology editor for biologists. Bioinformatics 23: 2198–2200. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Improvement of mean Accuracy and F1 Score for DSD at different neighborhood thresholds for the
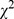 neighborhood algorithm in 10-runs of 2-fold cross validation (with standard deviation error bars).
neighborhood algorithm in 10-runs of 2-fold cross validation (with standard deviation error bars).
(TIF)
Improvement of mean Accuracy and F1 Score for DSD at different neighborhood thresholds for the multi-way cut algorithm in 10-runs of 2-fold cross validation (with standard deviation error bars).
(TIF)
Improvement of mean Accuracy and F1 Score for DSD at different neighborhood thresholds for all four methods in 10-runs of 2-fold cross validation (with standard deviation error bars) using the GO catagories (using the method that gives wcredit only for exact matches to each GO term).
(TIF)
Performance evalutaion for GO term prediction on the S. pombe network. (a) Comparison of mean F1 score of DSD and non-DSD majority vote (setting t = 10) and functional flow (setting c = 1.5) algorithms using all three methods of counting GO term matches; (b1,b2) Comparison of mean accuracy and F1 Score under the exact match method for different settings of the parameters t and c, over 10 runs of 2-fold cross validation (with standard deviation error bars).
(TIF)