Nonlinear Dynamics Support a Linear Population Code in a Retinal Target-Tracking Circuit

Abstract

A basic task faced by the visual system of many organisms is to accurately track the position of moving prey. The retina is the first stage in the processing of such stimuli; the nature of the transformation here, from photons to spike trains, constrains not only the ultimate fidelity of the tracking signal but also the ease with which it can be extracted by other brain regions. Here we demonstrate that a population of fast-OFF ganglion cells in the salamander retina, whose dynamics are governed by a nonlinear circuit, serve to compute the future position of the target over hundreds of milliseconds. The extrapolated position of the target is not found by stimulus reconstruction but is instead computed by a weighted sum of ganglion cell outputs, the population vector average (PVA). The magnitude of PVA extrapolation varies systematically with target size, speed, and acceleration, such that large targets are tracked most accurately at high speeds, and small targets at low speeds, just as is seen in the motion of real prey. Tracking precision reaches the resolution of single photoreceptors, and the PVA algorithm performs more robustly than several alternative algorithms. If the salamander brain uses the fast-OFF cell circuit for target extrapolation as we suggest, the circuit dynamics should leave a microstructure on the behavior that may be measured in future experiments. Our analysis highlights the utility of simple computations that, while not globally optimal, are efficiently implemented and have close to optimal performance over a limited but ethologically relevant range of stimuli.

Introduction

Target tracking is a ubiquitous problem for visual systems. As the image of a moving target crosses the retina, its trajectory is translated into a time varying pattern of neural activity distributed across hundreds of retinal ganglion cells (RGCs). However, the slow chemistry of phototransduction significantly delays ganglion cell responses—the neural image of a 2° target moving at 20°/s across a retina with a 100 ms latency would lag behind its true position by a full target diameter. Likewise, receptive fields often span visual angles that are substantially larger than the angular size of a target, making the spatial position of the target ambiguous to a single RGC (Sherry et al., 1998; Segev et al., 2006). Multiple sources of nonlinearities and adaptation further alter the target image in complex ways (Rieke, 2001; Hosoya et al., 2005; Schwartz et al., 2012). Thus, estimating the likely position of a moving target from RGC spike trains would seem to require significantly more computation than performing the same operations at the photoreceptor level.

The encoding complexities described above may necessitate that downstream visual areas first decode the ganglion cell signals using an internal model of the retina (Pillow et al., 2005, 2008). After reconstructing the input image from the RGC output, further computation would be needed to calculate the location of the target. Alternatively, it is conceivable that the RGC population has already computed the target location, and this is part of the reason the RGC responses already look so complex. If this were the case, the downstream circuits could estimate the location of the target via some simple transformation of the RGC output that is largely independent of the internal dynamics of the retina. Clearly, the brain could use either or both solutions. While much work has been done characterizing the sophisticated decoding approach to retinal signals, the plausibility of computations that refine the RGC output without reconstruction is less explored (Snippe, 1996), in particular for time-varying stimuli being processed by circuits with nonlinear dynamics.

If the retina indeed performs computations that allow simple downstream processing, what might they be? It has been shown that a fast-OFF ganglion cell circuit uses nonlinear feedback to extrapolate the future position of a long bar moving in one dimension (Berry et al., 1999). Such extrapolation could compensate for neural delays, provided it was robust to the other nonlinearities in the retinal circuitry. However, moving bars are quite different from the prey observed by a behaving organism, and it is unclear how accurately or robustly the fast-OFF cell network extrapolates the naturalistic motion patterns of small targets. Here we address both these points, and develop a simple and testable theory of how the fast-OFF cell network, combined with a linear position estimator, can be used to accurately track naturalistic two-dimensional target motion over a wide range of stimulus conditions in the presence of uncertainty in the encoding parameters. Our results suggest that a key role of neural circuit dynamics in the retina is to compute a small number of behaviorally relevant variables, in the process discarding most information, and to package them into a form that is easily used by downstream brain regions.

Materials and Methods

Electrophysiology and cell types.

Retinas of larval tiger salamanders (Ambystoma tigrinum) of either sex were isolated in darkness under infrared illumination, superfused with oxygenated Ringer's solution, removed from the pigment epithelium, and placed on a custom 61-channel multielectrode array for extracellular recording. Electrodes were spaced at 70 μm in an area 540 μm in diameter (10 μm electrode contacts). Recording sessions were typically 4–6 h in length. Spikes were detected by a threshold intensity crossing, and sorted into individual units using methods previously described (Meister et al., 1994). Spike trains were discretized into 5 ms bins and smoothed with a Hanning window (22.5 ms full-width at half-height) and averaged across trials to obtain a rate function, R(t). Note that this is a symmetric filter that adds no additional time delays to the system. For single-trial analyses, the firing rate for each trial at time t was represented by the inverse of the enclosed interspike interval surrounding t (Leonardo and Fee, 2005). Each trial was then smoothed as described above.

Neurons were classified into cell types based on their receptive field width and, most prominently, on the kinetics of their linear temporal response. We defined fast-OFF cells as those that responded to decrements in light intensity and whose latency (time from a pulse of light to peak ganglion cell response) was <100 ms. Typical fast-OFF latencies were 75–95 ms. ON cells were defined as those that responded to an increment in light intensity. These conventions are equivalent to those used elsewhere (Warland et al., 1997; Segev et al., 2006).

Ganglion cells with response properties similar to those of the fast-OFF cells studied in our larval salamanders have also been explored in a variety of other amphibians and mammals (Lettvin et al., 1959; Shapley and Victor, 1978; Berry et al., 1999; Petrusca et al., 2007), and are presumably found in both the larval and adult form of the tiger salamander. Indeed, contrast coding in the outer retina of larval tiger salamanders has been shown to be functionally equivalent to that in terrestrial adults (Burkhardt et al., 2006). For these reasons, we believe that the larval tiger salamander is both a representative and experimentally accessible system in which to begin studying the motion processing experienced by both aquatic and terrestrial amphibians.

Visual stimulation.

Stimuli were projected onto the retina from a 640 × 480 pixel video monitor (60 Hz frame rate). Mean intensity of the display on the retina was ∼10 mW/m². At the beginning of each experiment, receptive fields were mapped using a 30 min flickering binary checkerboard (∼56 × 56 μm checkers). This was followed by a long series (2–3 h) of motion stimuli (described below). At the conclusion of each experiment, a second receptive field mapping was frequently obtained to confirm that the basic response properties of each cell were stable.

Naturalistic motion consisted of a target moving in two dimensions at a fixed or linearly changing speed. The range of target sizes and speeds was based on those of a natural prey of the salamander—a 1.5 mm fruit fly, moving at 10 mm/s, over a distance of 5–40 mm. This yielded a canonical range of target angular sizes (2°, 4°, 8°), and speeds (10–60°/s). At any particular distance, prey of the metric size and speed given above would have a specific pairing of angular size and angular speed. For example, at a distance of 40 mm the fly would appear as a 2.1° target moving at 14.3°/s, at 20 mm as a 4.3° target moving at 28.1°/s, and at 10 mm as an 8.6° target moving at 53.1°/s. Motion stimuli were always circular black disks moving on a gray background.

Salamander rods and cones are ∼11 and ∼4.5 μm in diameter, respectively (Mariani, 1986; Sherry et al., 1998). Salamander eyes are ∼4–5 mm in diameter; if we assume a focal length of 2.5 mm, then rods and cones have an angular resolution of ∼0.25° and 0.10°. This gives a scale factor of ∼45 μm/° to convert from visual angle to distance on the salamander retina. To produce the target angular sizes and speeds described above, we generated stimuli of 90, 180, and 360 μm in size, and 271, 542, 813, 1084, 1356, 1629, 1890, 2175, and 2451 μm/s in speed. For comparison, the radius of a typical fast-OFF receptive field is ∼100 μm (half-width at 1σ point).

Receptive fields and cascade models.

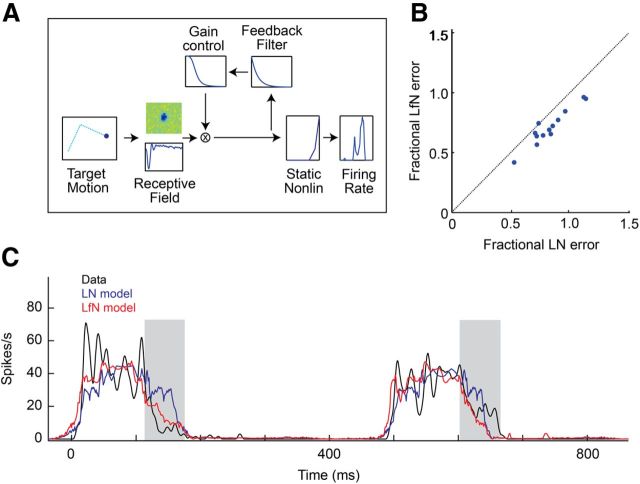
The relation between ganglion cell firing rate and visual stimulation was described by either a linear–nonlinear model (LN), or linear–nonlinear model with contrast gain control feedback (LfN). Both of these models are commonly used to describe the response of ganglion cells to stimuli such as flickering checkerboards and moving gratings. The multistage cascade model consisted of a receptive field, K(x, y, t), a linear spatiotemporal filter that projects the three-dimensional stimulus image into a one-dimensional generator potential u(t); a contrast gain control loop, G(v), that regulates the cell's sensitivity in response to image contrast; and a static nonlinearity, N(u), that maps generator potentials into firing rate outputs. K(x, y, t) was estimated using standard reverse correlation methods. In brief, a flickering checkerboard was presented to the retina, and the average stimulus pattern preceding a spike was calculated (Chichilnisky, 2001). The parameters {β, τ} of the gain control loop, G(v), and static nonlinearity, N(u), were estimated simultaneously using an iterative parameter search. N(u) was defined as the average spike rate produced at each binned generator potential. The full LfN cascade model and estimated firing rate, R̃(t), based on the image sequence S(x, y, t), was then defined as:

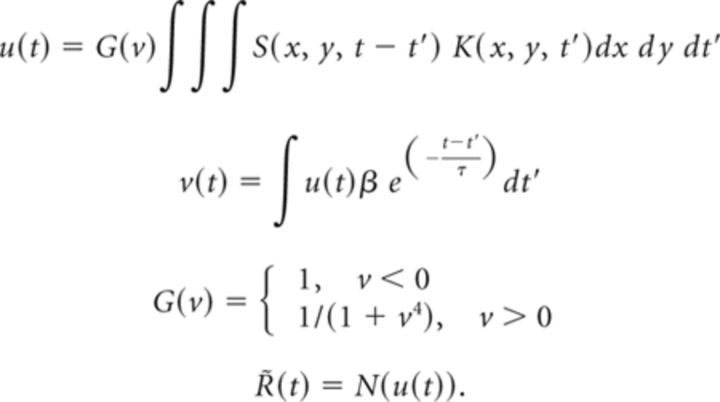The LN equations set G(v) = 1 (no feedback loop), but are otherwise the same. We evaluated the fit of the cascade model (LN or LfN) to the measured ganglion cell firing rate by examining the size of the model fitting error relative to the intrinsic single-trial variability of the cell. This “fractional RMS error,” was defined as follows:

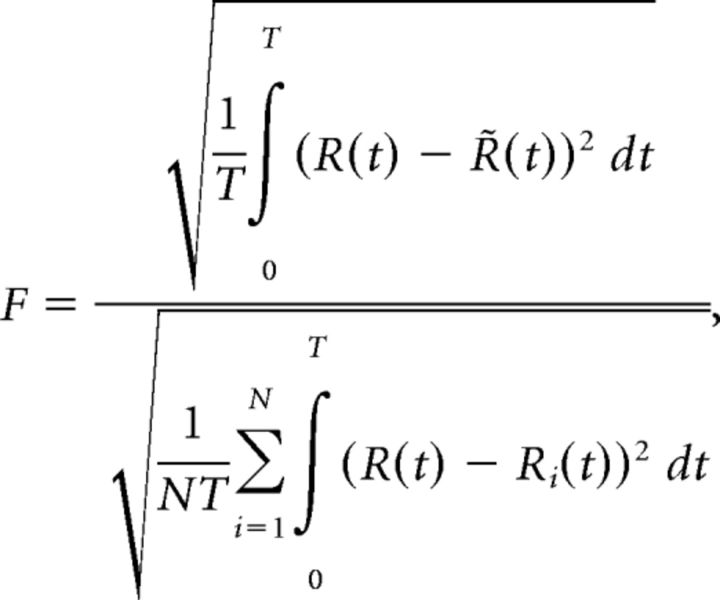where T is the duration of the recording, R_i(t) is the measured time varying firing rate of the neuron on trial i of N, R(t) is the average firing rate of the neuron, and R̃(t) is the estimated firing rate produced by the model.

Receptive field lattices and coverage factors.

Numerically simulated lattices of ganglion cells were based on the model described above, while experimentally reconstructed lattices were based only on the firing rates of neurons recorded on the electrode array. In both cases, the crucial components to define the lattice were the area of visual space it would span, and the density of receptive fields within it. We describe the calculations for both of these variables below. Cells in each lattice differed from each other only by a shift in their receptive field centers. The neurons were treated as independent units. Parameters for the LfN circuit were those measured experimentally in the previous section.

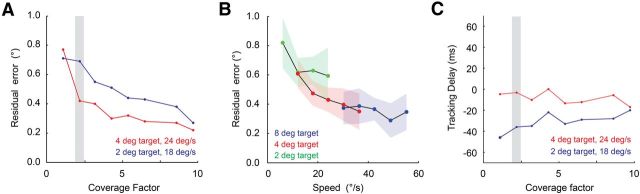
The coverage factor is defined as the product of the 1σ area of the average receptive field with the cell density in the lattice; it is effectively the number of cells that encode each point in space. There have been numerous estimates of ganglion cell receptive field coverage (Devries and Baylor, 1997; Segev et al., 2006; Gauthier et al., 2009). Experimentally observed coverage factors in salamander retina range from 2 to 20, but typical values for functionally identified cell types are on the order of ∼2.5 (Segev et al., 2006). Because we recorded from a large population of ganglion cells across several animals, we could pool neurons together and create a range of coverage factors. RGC lattices were reconstructed from a recorded population of 30 cells (fixed speed tracking experiments) or 9 cells (speed and size sweep experiments). Based on a typical fast-OFF 1σ receptive field radius of 100 μm, the experimentally reconstructed lattices had coverage factors from 1 to 10, for neural populations from 49 to 441 fast-OFF cells. For analysis in which we examined systematic biases in the population response (e.g., the tracking delay), we used a high coverage factor (∼5) to allow an accurate estimate of the average response. For analysis in which we examined trial-to-trial variability, we used a low coverage factor (∼2) to closely match the expected resolution seen in retina. Even in the most extreme conditions, the effects of varying the coverage factor were minimal (see Fig. 6).

Figure 6.

Sensitivity of tracking delay and residual error. A, Residual tracking error, after removing the tracking delay, as a function of the number of receptive fields covering each position in space. B, Residual tracking error as a function of target size and speed, for a coverage factor of ∼2. All plots are from trial-averaged experimental data. Colored shaded regions are the ±1 SD error contours from single-trial data. C, Tracking delay as a function of the number of receptive fields covering each position in space. Gray bars (A, C) show the coverage factor used for most analyses.

Prey tends to move continuously over large distances, with periodic turns (Robie et al., 2010). To simulate these motion patterns, a reasonably large amount of visual space is needed. In the case of our experiments, the motion patterns we examined traversed about 11° of visual angle (∼480 μm). The retina array we used was of a similar size (∼12° of visual angle, 540 μm diameter). Because the array did not sample every ganglion cell contained within its area, and because many of the ganglion cell receptive fields that were driven by our motion stimulus would lie outside the bounds of the array, we reconstructed RGC lattices larger than the microelectrode array by tiling the motion patterns. Each stimulus was presented to the retina multiple times, in which each successive presentation would shift the mean position of the motion by a receptive field radius (∼100 μm). In this manner, by presenting a tiling of 5 × 5 or 7 × 7 shifts of each motion pattern, we could reconstruct the effect the stimulus would have on cells far from the array center by observing how shifted versions of the stimulus drove the cells sampled by the array. These shifted motion patterns allowed us to reconstruct a virtual ganglion cell lattice of 29° × 23° (1300 × 1055 μm). The numerically simulated lattices spanned 40° × 44° (1788 × 2000 μm). Firing maps for simulated networks and experimental data (see Fig. 3) were produced from a two-dimensional interpolation across the spatially periodic (model) or aperiodic (data) lattices constructed from individual neurons.

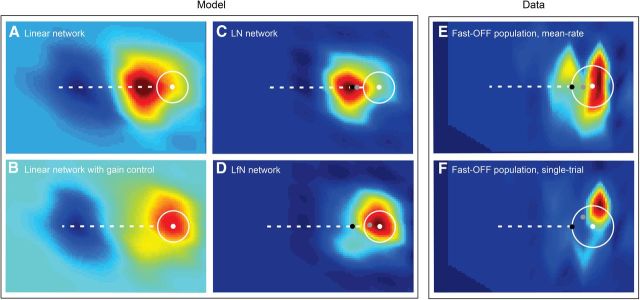
Figure 3.

Ganglion cell population activity patterns. A–F, Each panel represents the pattern of activity across an interpolated lattice of ganglion cells that was simulated numerically (A–D) or measured experimentally (E, F). Individual pixels represent the firing rate a ganglion cell would produce at each spatial position, with hot colors representing more positive activity and cool colors more negative activity. A, Response of a network of spatiotemporal linear filters (L) to target motion. B, Response of network in A passed through the gain control loop (Lf). C, Response of the L network in A passed through static nonlinearity (LN) to yield a firing rate map. D, Response of the Lf network in B, passed through static nonlinearity (LfN). E, Fast-OFF cell population activity reconstructed from experimentally measured mean rate data. F, Single-trial example of the data shown in E. In all panels, the white circle and dot show the area of the target and position of the target center at the time of the network activity pattern. The black dot is the position estimate that would be obtained from a linear network with a ∼60 ms delay but no other dynamics. C–F, Gray dots show the center of mass of the population firing rate maps. For networks lacking the gain control loop (C), the center of mass is closely approximated by the latency through the network and lags well behind the target area. For networks with gain control (D–F), the center of mass leads the network latency position and is contained within the target area.

Tracking algorithms.

The population vector average (PVA) estimates the position of the target, x⃗_est(t), as the sum of ganglion cell receptive field centers, c⃗_i, weighted by their firing rates, x_est(t) = ${\displaystyle {\sum }_i{f}_i\left(t\right){\overrightarrow{c}}_i/{\displaystyle {\sum }_i{f}_i\left(t\right)}}$. Receptive field center locations were calculated from the white noise analysis described above. The PVA was applied to firing rate data binned in 5 ms steps, as described above. For a sufficiently large population of uniformly distributed receptive fields, such as we have in the amphibian retina (Sherry et al., 1998), the PVA estimate of position should be unbiased (Georgopoulos et al., 1988), and, because it is a linear operator, the average of a series of PVA trials will be the same as the PVA operating on the trial-averaged firing rates. The PVA is well suited to the LfN cascade models discussed above, as they are generative models of average firing rates. The winner-take-all algorithm defined the tracking estimate at time t as the center of the receptive field with the highest firing rate in the population. The burst-time decoder (Gütig et al., 2013) used a restricted version of the PVA in which the spike train for each neuron was reduced to the first K spikes in each bursts. Bursts were defined as clusters of spikes whose interspike intervals were <100 ms.

Quantification of tracking error.

We define the following three quantities to evaluate the fidelity of a tracking algorithm: global tracking error, tracking delay, and residual tracking error. The tracking delay is the shift in time needed to minimize the error between the PVA tracking estimate and the true position of the target. The tracking delay is calculated by first fitting a line to the original time-varying motion pattern (slope m_traj in degrees per second; intercept b_traj in degrees), and to the PVA estimate (slope m_pva; intercept b_pva). The tracking delay is then defined as d = b_pva − b_traj)/m_traj. The residual tracking error is the root mean square (RMS) error remaining in the tracking estimate after compensating for this delay. If x⃗(t) is the original motion signal and x⃗_est(t) is the PVA estimate, then the residual tracking error is defined as $\sqrt{\frac{1}{T}{\displaystyle {\int }_0^T{\left(\overrightarrow{x}\left(t-d\right)-{\overrightarrow{x}}_{est}\left(t\right)\right)}^{2}dt}}$. The global tracking error is the error with d = 0 (i.e., the RMS error including that from the delay).

Robustness.

We quantified the robustness of different tracking algorithms by determining how tracking accuracy scaled as a function of uncertainty in the true values of the parameters needed by each tracking algorithm. Zero-mean Gaussian noise with variance σ² was added to the receptive field center and covariance of each fast-OFF ganglion cell in the population (each neuron received a different random draw from this distribution). The average RMS tracking error for this noise level was defined as the average over 10 independent runs of adding the same noise statistics to the single-trial data and tracking the same trajectory. By varying σ², we measured tracking robustness at many different noise levels.

Results

A foraging salamander is confronted with small targets moving erratically in two dimensions. When feeding, the salamander will first detect the motion of prey and make an orienting head movement toward it. The tongue is then launched ballistically, at extremely high acceleration, and reaches the position of the prey nearly instantaneously (Roth, 1987; Deban and Roth, 1997). The salamander retina contains no specialized high-acuity area like the fovea (Sherry et al., 1998), and consequently salamanders do not make eye saccades to track a moving target. Instead, target motion is directly translated into a neural image on the retina that moves with roughly the same statistics as the actual target, save for the occasional target-centering head movement. Furthermore, tongue projection is energetically expensive, and it takes time to initiate a subsequent projection after a miss (Deban et al., 2007). Given this cost, and the delays and nonlinearities in the retinal circuitry, how does the salamander know where to aim its tongue in a way that maximizes the chance of success?

To explore the effect of small target motion on retinal circuit dynamics, we developed a stimulus based on the naturalistic motion patterns of small moving prey (Branson et al., 2009; Robie et al., 2010). A small target was moved at a fixed bearing and speed, with periodic discrete changes in these parameters (Figs. 1, 4). The range of target sizes (2°, 4°, 8°) and speeds (6–60°/s) reflected the range of those seen in real prey at typical tongue projection distances (5–40 mm) (Roth, 1987). Although simpler than real prey, these stimuli are considerably more ethological than moving gratings and will actually elicit tongue projections from behaving amphibians (Roth, 1987). A 61-channel multielectrode array was used to record extracellularly from populations of ganglion cells in salamander retinal explants (Meister et al., 1994), while simultaneously presenting the retina with the motion patterns described above (Fig. 1A, inset). We measured the responses of a sufficiently large population of ganglion cells such that we could reconstruct a smooth lattice of receptive field coverage over an ∼30° region of space (Devries and Baylor, 1997; Gauthier et al., 2009). This was achieved, in part, by presenting the same motion stimulus at shifted positions on the retina (Jacobs and Werblin, 1998), allowing each recorded ganglion cell to act as a virtual cell at multiple positions (see Materials and Methods). These wide-field population measurements, and the two-dimensional movement patterns of naturalistic stimuli, distinguish our work from previous studies that have examined RGC encoding of the one-dimensional movement of drifting bars (Berry et al., 1999; Euler et al., 2002; Frechette et al., 2005).

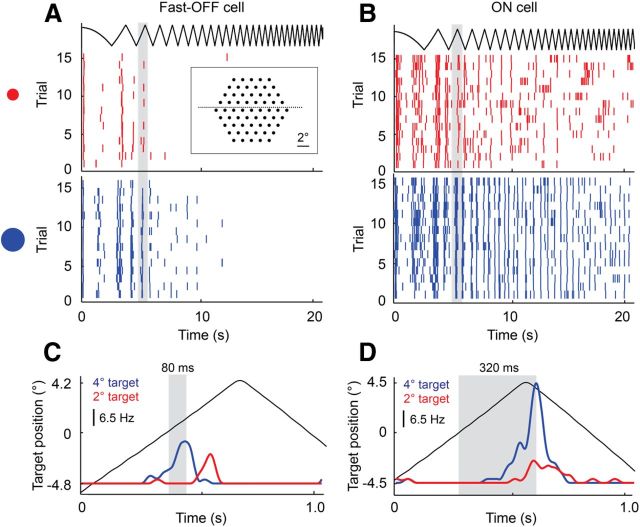
Figure 1.

Temporal response of single ganglion cells to target motion of different sizes and speeds. A target moved alternately left and right at linearly increasing speeds from 0 to 50 °/s. A, B, Spike rasters of a fast-OFF cell and an ON cell, respectively, for 15 repetitions of the trajectory for a small (red) and a large (blue) target moving across the electrode array (inset). C, Zoom of gray region in A, showing the average firing rate of the fast-OFF cell as the target passed through its receptive field. D, Zoom of gray region in B, showing the average firing rate of the ON cell as the target passed through its receptive field. Gray regions in C and D mark the latency from when the center of the target was aligned with the center of the receptive field to the peak of the subsequent fast-OFF and ON cell responses. For a 4° dark target moving at ∼10°/s, fast-OFF cells report the moment when the target crosses the receptive field center about four times faster than ON cells.

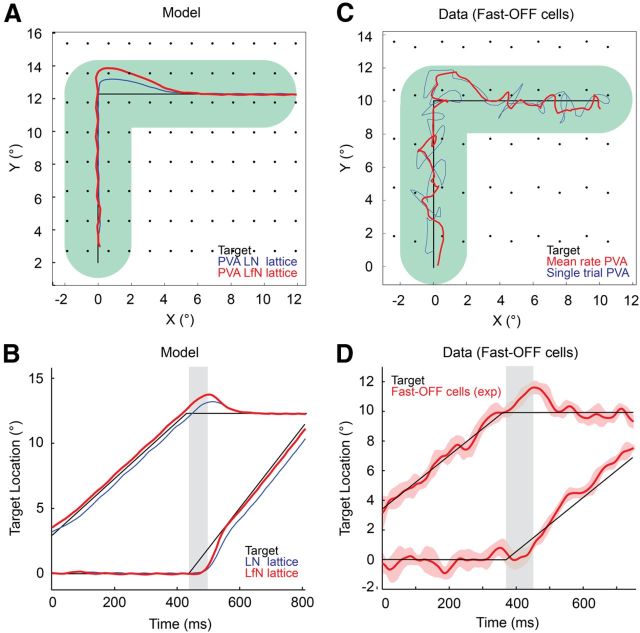
Figure 4.

PVA tracking estimates from fast-OFF cell populations. A, Two-dimensional target trajectory (black) and PVA tracking estimate for a network of LN (blue) and LfN (red) model neurons. Green track represents the width of the target. Black dots show the location of each receptive field center. B, Time series for the x and y components of motion for the data shown in A. The LfN network shows zero tracking delay, other than overshoots on turns. The LN network constantly lags behind the target position. Gray bars indicate the latency of the fast-OFF cells used in the network. C, Two-dimensional target trajectory (black) and PVA tracking estimate from mean rate data (red) or single-trial spike trains (blue) measured from a population of fast-OFF cells. Green track represents the width of the target. Black dots show the location of each receptive field center. D, Time series for the x and y components of the target motion and PVA estimate shown in C. The solid red line is the average position estimate across single trials, and the dashed red lines are the ±1 SD variability from single-trial data. Gray bars indicate the 80 ms latency of the fast-OFF cells.

Like all vertebrates, the salamander has several distinct types of RGCs that differ in morphology and visual response properties (Costa Lda and Velte, 1999; Segev et al., 2006). In this study, we focus in detail on the motion extrapolating fast-OFF type cells that have been found in salamanders and rabbits (Berry et al., 1999). Reports of RGCs with similar properties may be found for frogs (Barlow, 1953; Lettvin et al., 1959), cats (Shapley and Victor, 1978), primates (Petrusca et al., 2007), and other species. Ganglion cells with these properties thus reflect a common class of retinal neurons that exist in most or all vertebrate visual systems. Figure 1A shows the spike trains of a typical fast-OFF cell responding to a small dark moving target. The periodic response in the spike trains reflects the motion of the target as it repeatedly crossed through the cell's receptive field. Fast-OFF cells are driven by the leading edge of a dark target moving on a light background. The latency of the peak of the fast-OFF response relative to the time when the target crossed the receptive field center is dominated by phototransduction and synaptic delays of ∼80 ms (Fig. 1C). This basic sensitivity is modulated by the size and speed of the target. In contrast to OFF cells, ON cells were driven by the trailing edge of the target; this, combined with the intrinsic phototransduction delay, caused the ON cells to respond to target motion hundreds of milliseconds later than OFF cells (Fig. 1B,D) for a target of the same size and speed. ON cells are thus poorly suited as “bug detectors” of dark targets moving on light backgrounds, and we do not consider them further in this study.

Single-neuron and population models of fast-OFF cell dynamics

While it is well known that an LfN model accounts for the responses of fast-OFF cells to the one-dimensional motion of bars (Berry et al., 1999), it is unclear to what extent this model works for more complex, ethological stimuli. We extended the LfN model to two dimensions (Fig. 2A) and found that it more accurately described fast-OFF cell responses to the naturalistic motion patterns of small targets than did models lacking the gain control (Fig. 2B). The LfN model is composed of three stages of signal processing: a linear filter, a nonlinear feedback loop, and a static nonlinear firing rate function. The spatiotemporal linear filter represents the phototransduction delay and bandpass filter properties from photoreceptors to ganglion cells. The time to peak of this filter sets the response latency of the cell. The spatial component of this filter represents the restricted 5–10° region of visual space from which the cell gets input, and the temporal filter reflects the cell's latency and contrast sensitivity. The nonlinear feedback serves as a gain control; it monitors the output of the spatiotemporal filter and divisively reduces the gain of the neuron when this output is excessively large. Finally, the static nonlinearity maps the gain-controlled filter output into a firing rate, discarding signal components below a threshold and limiting the maximum output produced by the neuron. The spatiotemporal filter and static firing rate function comprise the classic LN model used to describe basic visual receptive fields (Chichilnisky, 2001). Fast-OFF cells follow these basic dynamics but are further modified by the gain control feedback. This feedback quenches the response even while the target is still in the receptive field, causing fast-OFF cells to respond asymmetrically to the motion of the target (Fig. 2C). Fast-OFF cell responses decay quickly after attaining their peak firing rate, whereas model neurons with only LN dynamics tend to have a symmetric firing rate profile before and after their peak response. This symmetry breaking alters the information provided by individual fast-OFF cells; for a moving target, the gain control increases the neuron's sensitivity at the perimeter of the receptive field and decreases sensitivity in the center of the receptive field.

Figure 2.

The LfN model accurately describes fast-OFF ganglion cell responses to small target motion. A, Three-stage LfN cascade model for fast-OFF ganglion cell responses to small target motion. Two-dimensional target motion is passed through a linear spatiotemporal filter (the receptive field) followed by a contrast gain control loop. A static nonlinearity converts this generator potential into spike rates. LN models contain the linear filter and static nonlinearly but lack the feedback loop. B, Comparison of LN and LfN descriptive power. The fractional RMS error is the ratio between the RMS error of the model prediction from mean rate data to the single-trial variability; it expresses the accuracy of the model fit relative to intrinsic cell variability. C, Mean firing rate time series (black) for a single fast-OFF ganglion cell to naturalistic motion is compared to predicted firing rates from an LN (blue) and LfN (red) model. While both the LN and LfN models captured the times when the cell's firing rate changes, the LfN model provided a more accurate description of the kinetics of each response, particularly the trailing component of each burst (gray bars).

Target tracking is a population-level computation, and while the gain control loop has only a subtle influence on the response of individual fast-OFF cells, it has a significant effect on the dynamics of the fast-OFF population as a whole. We numerically simulated the response of a lattice of fast-OFF neurons to the motion of a small moving target (see Materials and Methods). The model response was generated either with (LfN) or without (LN) the nonlinear feedback loop (Fig. 3). The comparison between these two model networks allows us to quantify what aspects of motion processing in the retina are due to simple receptive fields effects (LN) versus more nonlinear dynamics of the gain control circuit (LfN). We presented each network with a variety of trajectories of targets of different sizes, speeds, and motion types.

The structure of the network activity patterns elicited by small target motion stimuli was surprisingly simple, especially when considering the strong nonlinear elements that shaped the responses of the individual cells. The linear response of the network (Fig. 3A) was to produce a filtered image of the target across the spatial extent of the lattice. Cells in front of the target were strongly stimulated by the light–dark transitions as the leading edge of the target entered their receptive fields. Cells behind the target were strongly inhibited by the dark–light transitions as the target departed their receptive fields. This negative image of the trailing edge of the target was ultimately forced to zero by the output nonlinearity that approximates the spike generation mechanism of each cell. The gain control circuit of the LfN network primarily quenched the responses of cells that were behind the leading edge of the target (Fig. 3B). These small changes in the timing of individual LfN cell firing patterns thus collectively, across space, shifted the center of mass of the neural image forward along the direction of motion of the target. The center of the LN network image relative to the true target position was well approximated by the ganglion cell response latency, and lagged significantly behind the target center, often missing the target entirely (Fig. 3C). In contrast, the center of the LfN network image was significantly advanced relative to the LN network and would hit the target in many cases where the LN network would miss (Fig. 3C,D). For some target sizes and speeds, the LfN network activity center would lead the true center of the target (Fig. 4B). The reshaped LfN network image in essence represented a prediction of the future location of the target. Similar patterns of neural activity were observed in experimentally measured fast-OFF cell populations, both for mean rate and single-trial data (Fig. 3E,F).

Target tracking with fast-OFF cells

The network activity maps (Fig. 3) suggest that the center of the population activity pattern might be a good estimate of target location. The PVA is one convenient method of calculating such a center point (Georgopoulos et al., 1986) that is easily implemented with neural hardware (Lewis and Kristan, 1998). The PVA is a weighted vote in which each ganglion cell claims that the target is at its receptive field center with a confidence proportional to its firing rate. We used the PVA to estimate target position in stepped 5 ms windows, across the numerically simulated networks of LN and LfN fast-OFF cells (Fig. 4A; Materials and Methods). As before, we compare the LN and LfN networks to evaluate how the presence or absence of the gain control circuit influences subsequent estimates of target position from the retinal output.

The PVA estimate for the LN network lagged behind the true position of the target (Fig 4B); this is a consequence of the latency of the fast-OFF cell receptive field (Fig. 2A). In contrast, the simulated LfN network generated PVA estimates with nearly zero delay to the position of the target (Fig. 4B), exactly compensating for the latency of the ganglion cells. Purely LN fast-OFF networks lacking the gain control loop thus showed increased tracking error relative to that of the LfN networks (Figs. 3, 4B). At the moment of a turn, the LfN PVA estimate overshot on its original preturn bearing for ∼60 ms and then slowly rotated to the new bearing (Fig. 4A,B). This overshoot is the sine qua non of prediction: if the target turns, the fast-OFF cell network cannot know this for at least the latency of the ganglion cells, and any prediction must erroneously go forward on the original bearing (Schwartz et al., 2007b).

Numerical simulations suggest a significant extrapolation of target position occurs across the fast-OFF cell network. We verified these ideas by examining the tracking accuracy with both trial-averaged and single-trial data from 30 experimentally measured fast-OFF cells, tiled to a population of a few hundred cells, representing a visual region comparable to that of the numerical simulations (see Materials and Methods), using the same two-dimensional motion pattern described above. Trial-averaged data emphasize the systematic errors in the tracking estimates, whereas single-trial data emphasize variability in the tracking estimates from noise in the neural responses. As predicted by the model, there was nearly zero delay between the trial-averaged fast-OFF PVA estimate of the location and the true position of the target (Fig. 4C,D) when the target moved on a fixed bearing. PVA estimates calculated from single-trial fast-OFF cell data provided a noisier but qualitatively similar estimate of target position to that from mean firing rate data (Fig. 4C); the variability in the single-trial position estimate at 1 SD from the mean was ∼0.2° (Fig. 4D). After an abrupt 90° turn, the experimentally measured PVA estimate overshot on its preturn heading before decaying smoothly to the new bearing of the target; the duration of this overshoot was very close to the measured temporal latency of the fast-OFF cells (80 ms) and was consistent with model predictions (Fig. 4, compare B, D).

Prior work with long bars moving in one dimension observed a sharp synchronous peak in firing rates about 250 ms after a 180° reversal of motion (Schwartz et al., 2007b). We were unable to reproduce this reversal effect for two-dimensional small target motion patterns. One-dimensional reversals of motion (180° turns) were poorly tracked because in these cases the target would move directly into the region of inhibition created by the contrast gain control circuit, eliciting weak ganglion cell activity and producing a position estimate that was dominated by noise. The significance of these reversal-of-motion effects for behavior is unclear, as real prey rarely turn so sharply (Robie et al., 2010).

Accuracy and robustness of different target-tracking algorithms

To further quantify the accuracy and robustness of the target position estimates, we decomposed tracking errors into separable components to distinguish systematic biases, which should remain constant with neural population size, from noise, which should drop with increasing neural population density. We defined the tracking delay as the shift in time needed to minimize the error between the tracking estimate and the true position of the target; this is the systematic bias in the estimate. The residual tracking error is the RMS error in time after compensating for the tracking delay. The global error is the RMS difference between the tracking estimate and the true target position over time; it reflects the combined effects of the tracking delay and the residual error, summed in quadrature. We used the global error to compare the robustness of the PVA to other tracking algorithms, and the tracking delay and residual error to explore the bias and noise in the PVA itself.

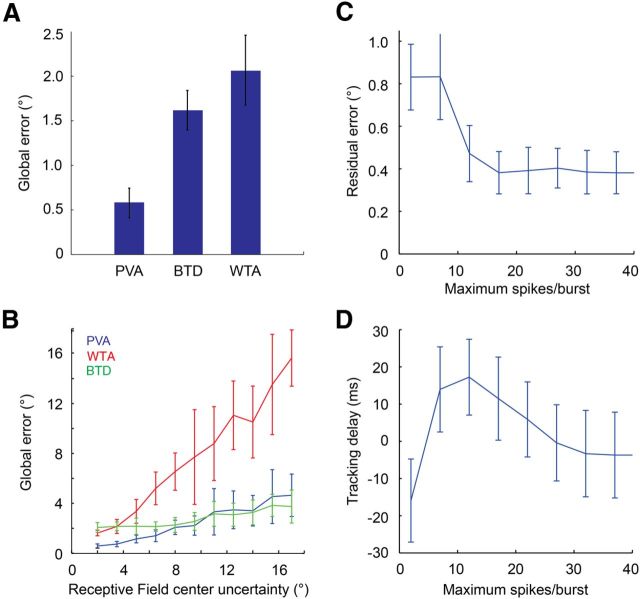
The PVA is one example of an algorithm that forms a position estimate simply by processing the neural image of the target from each snapshot without reference to the underlying generative dynamics. We considered two alternative readout methods: the first is known as the “winner-take-all”, or peak detection, method in which the receptive field of the neuron with the maximal firing rate is used as the position estimate (Berry et al., 1999; Schwartz et al., 2007a). The second is a burst-time decoder (Gütig et al., 2013), based on the observation that ganglion cells often respond with distinct bursts of firing (Berry et al., 1997) and that certain stimulus variables can be extracted already from the onset time of each burst (Gollisch and Meister, 2008). To test this notion, we identified bursts in the RGC spike trains and admitted only the first few spikes of each burst, followed by PVA analysis as before. A comparison of target tracking by each of these algorithms showed that global error rates for the PVA were considerably better than those of either alternative method (Fig. 5A). For the experimental dataset described above, global errors were ∼0.5° for the PVA and >1.5° for winner-take-all and burst-time decoding.

Figure 5.

Accuracy and robustness of different tracking algorithms. A, Global tracking error for the PVA, winner-take-all (WTA), burst-time decoding (BTD), for a 4° target moving at 24°/s. B, Global tracking error for the three tracking algorithms above, as a function of uncertainty in receptive field center positions. C, Residual tracking error for burst-time decoder, as a function of the number of spikes included per burst. D, Tracking delay for the burst-time decoder, as a function of the number of spikes included per burst. Positive delays indicate extrapolation.

The accuracy of any tracking algorithm will be affected by uncertainty in the parameters underlying its computations. For a downstream circuit to calculate a PVA from fast-OFF ganglion cells, it needs to know the location of the receptive field center of each neuron, encoded as a synaptic weight. These weights could be hard wired, but they also might be learned. In either case, noise would affect their precise values. To quantify how global tracking errors scaled as a function of parameter uncertainty, we added random Gaussian offsets (mean zero) to the values of the receptive field center locations of each neuron. As receptive field positional uncertainty increased, global tracking errors increased slowly for the PVA and rapidly for the winner-take-all algorithm (Fig. 5B). Interestingly, the burst-time decoder appears to offer increased robustness to receptive field center uncertainty (Fig. 5B), perhaps because it removes the noisiest spikes.

The superiority of the PVA compared to other static decoders arises largely from the extent to which it averages its response over a large population of cells. Small amounts of noise can shift the peak of the ganglion cell population response from one receptive field to another (∼5°), while changing the center of mass of the population only slightly (≪1°); this results in a considerably higher error for the winner-take-all method. Similar effects can be seen with burst-time decoding: if we vary the number of spikes allowed in each burst, residual tracking errors steadily decrease as spike count increases (Fig. 5C). For a strong burst-time code, in which only the initial spikes in each burst are used, there are many fewer active cells at each moment in time, resulting in a noisier estimate of position. A second property of the burst-time decoder estimate is that extrapolation increases as we reduce the spike count (Fig. 5D). However, this effect is small, with at most ∼20 ms of additional extrapolation for a 24°/s target (0.4° change in position estimate).

In addition to uncertainty in the position of receptive field centers, PVA accuracy will also be affected by trial-to-trial response variability of the fast-OFF cell population. The influence of both of these factors on residual tracking error should decrease as more receptive fields represent each point in space. How strong will these effects be for a realistic density of cells? Prior studies have shown that approximately two to three fast-OFF cells generally represent every point in space (Segev et al., 2006), but it is unclear whether these values are stable as a function of light level, contrast, and other visual scene statistics that can alter the shape and width of receptive fields. We varied the coverage factor over a 10-fold range, and found that for a fixed target size and speed, residual tracking error dropped with increases in coverage factor (Fig. 6A). For example, with typical coverage factors of 2.5, the residual error was ∼0.4° (approximately one rod photoreceptor) for the 2° target moving at 16°/s, and ∼0.6° for the 4° target moving at 24°/s. Lowering the coverage factor to 1, or raising it to 10, yielded residual RMS errors of ∼0.8° and ∼0.2°. As target size and speed decreased, there was an increase in the residual tracking error. However, these errors always remained at <1° for the full range of stimulus parameters we tested, even when computing the PVA with single-trial responses rather than trial-averaged responses (Fig. 6B).

In contrast with residual error, PVA tracking delays were relatively constant as a function of changes in coverage factor (Fig. 6C), consistent with these delays being systematic biases of the fast-OFF cell population response. For example, a 4° target moving at 24°/s lagged behind the true target position by ∼4 ms over a 10-fold range in coverage factors (Fig. 6C). Since the ganglion cells in this population had a latency of ∼80 ms, the fast-OFF cell circuitry was providing ∼76 ms of extrapolation for this target. In contrast, a 2° target moving at 16°/s had a delay of ∼30 ms—extrapolation was thus robust to coverage factor, but was a strong function of target size and speed.

Dependence of motion extrapolation on target size and speed

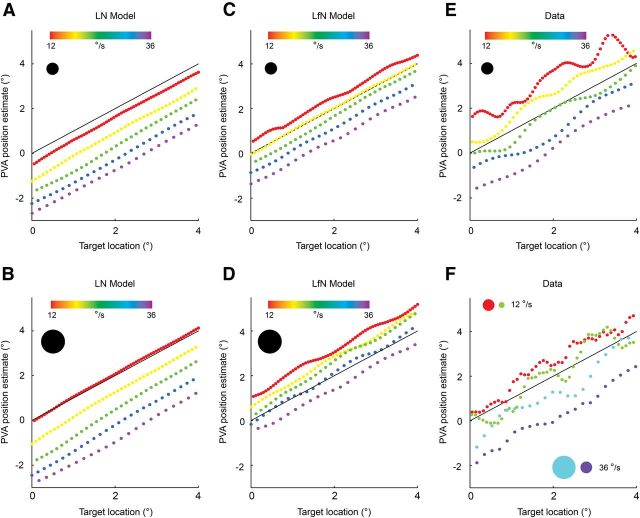
How does target size and speed affect tracking error? Motion extrapolation in the fast-OFF cell population depends on both the delay of the neural image of the target, the strength and speed of the gain control signal, and the size of the receptive field. The extent to which these elements are balanced to yield delay-free target tracking will be a function of many stimulus parameters. Because the tracking delays are systematic errors that vary with stimulus properties, they place fundamental limits on the fidelity of the tracking accuracy obtainable by the PVA. We characterized these errors in detail by examining the PVA position estimates for a wide variety of targets of different sizes, moving at different speeds, for both LN and LfN network simulations as well as experimental data (see Materials and Methods). For each target angular size and speed, we plotted the PVA estimate of the position of the target against the true position for the entire trajectory (Fig. 7). Regardless of the target size and speed, in the LN model the PVA estimate always lags behind the true target position (Fig. 7A,B). In contrast, for the LfN model, the nonlinear gain control loop adds progressively more extrapolation to the PVA estimate as target size and speed increase (Fig. 7C,D). Experimentally measured fast-OFF cell populations behave much the same as the simulated LfN populations (Fig. 7, compare E, C). In particular, if target size is held fixed, there is stronger extrapolation for slower targets, and if target speed is held fixed, there is stronger extrapolation for larger targets (Fig. 7F).

Figure 7.

PVA target tracking is a function of target size and speed. A, B, LN network tracking for small (A) and large (B) targets. Speed is shown in different colors. Black line is the zero error contour. Points above the black line overpredict target location, and points below the black line underpredict. C, D, LfN network, for the motion patterns show in A and B. E, Experimentally measured fast-OFF cell population shows the same size and speed tracking dynamics as simulated LfN networks (C). F, Fast-OFF cell PVA estimates from experimental data show that for a fixed speed, a larger target (red, cyan) is always tracked with more extrapolation than a smaller target (green, purple). Likewise, slower targets (red, green) are tracked with more extrapolation than faster targets (cyan, purple). The ripple seen at low speeds results from the slight inhomogeneity in receptive field coverage between the peaks of adjacent receptive fields. At higher speeds, the target crosses these areas quickly enough that the coverage irregularities are not noticed.

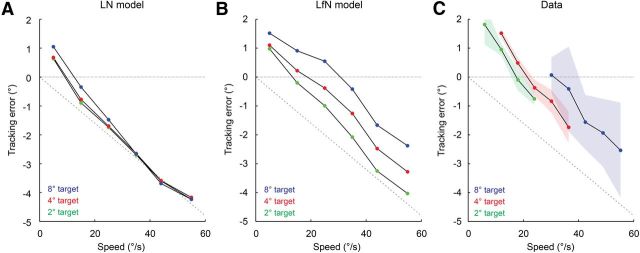
We distilled the relation between target size, speed, and tracking error for the LN model, the LfN model, and the fast-OFF cell data into a series of plots. For each pairing of target angular size and speed, there was a clear linear relation between the true and estimated target position. The y-intercept of the line fit to these points was used to quantify the spatial error (in degrees). This spatial error represents the expected tongue projection error a salamander would experience if using the fast-OFF cells and the PVA to guide tongue position; it is equivalent to the tracking delay described earlier, converted into spatial units appropriate for the speed of each target. At low speeds, LN networks showed weak extrapolation that was relatively independent of target size (Fig. 8A). This low speed target extrapolation arises from the leading-edge detection of the fast-OFF cell temporal kernel. However, once the target is moving at sufficient speed, the leading-edge effect is insufficient to compensate for the latency of the fast-OFF cells, and the PVA estimate follows the target with an error linearly related to the fast-OFF cell delay and essentially no other dynamics. LN networks thus track the target with zero delay only at extremely low speeds (Fig. 8A). In contrast, LfN networks vary their extrapolation as a function of both target size and speed (Fig. 8B). Slower targets are always tracked with more extrapolation than faster targets, and larger targets are tracked with more extrapolation than smaller targets. For LfN networks, zero delay tracking depends on target size and speed, and shifts to higher speeds as target size is increased (Fig. 8B).

Figure 8.

Errors in PVA estimates of target location as a function of network type, and target size and speed. A, Tracking for LN network shown in Figure 6, A and B. B, Tracking for LfN network shown in Figure 6, C and D. C, Tracking for fast-OFF cell population data shown in Figure 6E. Solid lines are derived from trial-averaged data, shaded regions show the ±1 SD contours from single trials, for each target size. A coverage factor of 2.5 was used. The latency of the cells used in the model and in the data was 80 ms. The gray dashed line shows the linear increase in tracking error that would occur for a network with a fixed 80 ms delay and no other dynamics.

Trial-averaged firing rate data from experimentally measured fast-OFF cell populations performed similarly to numerically simulated LfN networks, and quite differently from simulated LN networks. Extrapolation increased with decreasing target speed, and larger targets were tracked with more extrapolation than smaller targets (Fig. 8C). Note that this is exactly what happens in nature as the salamander gets increasingly close to a target of a fixed metric size and speed—the angular size and speed of the target increase with decreasing distance. This basic relation held even when accounting for the firing rate variability introduced from single-trial data (Fig. 8C). The tracking accuracy for the fast-OFF cell population data, read out using the PVA, is thus superior to that from purely linear networks of fast-OFF cells or other tracking algorithms such as winner-take-all and burst-time decoding. Furthermore, each of these different networks and algorithms produces a distinct signature, composed of stimulus-dependent tracking delays and error levels, which could in principle be measured in a behaving amphibian.

Discussion

There are four major results of our study. First, we found that single-neuron and population rate models of ganglion cells provide remarkably accurate descriptions of the retina's response to ethologically meaningful stimuli relevant for prey capture (Figs. 2, 3). Second, we have shown that downstream visual areas can read out this code using a simple PVA to track a moving target with nearly photoreceptor precision (Fig. 4). Third, the PVA target-tracking algorithm is superior to others, such as the winner-take-all and burst-time decoding methods, that have been considered in previous work (Fig. 5). Finally, we derived a series of quantitative predictions that can be tested behaviorally to confirm or falsify whether salamanders in fact use such a simple tracking algorithm for visually guided prey capture (Fig. 8). Together, these results support the view that nonlinear processing in the retina serves to format select visual information for easy access by downstream brain areas.

The remarkable efficacy of retinal circuit models and the population vector average

The utility of the LfN model can be seen in the fidelity with which it predicts both single-cell and population responses. At the single-cell level, the fast-OFF LfN model provides a good description of ganglion cell circuit dynamics; theory differs from experiment to less than the trial-to-trial variability of a single cell (Fig. 2B). Furthermore, the population dynamics we have measured experimentally in groups of neurons are in close agreement with predictions derived from a lattice of single-neuron models. These predictions include subtle effects such as the characteristic overshoots that occur when the target changes direction, and the dependencies of tracking accuracy on target size and speed (Figs. 4, 8). Thus, although the LfN model is not perfect (Fig. 2C), we believe it captures the essential retinal circuit dynamics underlying the processing of two-dimensional motion patterns of small moving targets.

It is worth noting how subtle aspects of the dynamics of a circuit can exert significant effects on its computational power. The addition of the nonlinear feedback loop to the basic LN model has no influence on when the neuron activates, it only modulates the time course of firing when the fast-OFF cells are already active (Fig. 2C). However, these changes in kinetics, pooled across many cells, lead to large-scale changes in population dynamics and underlie the collective computation used to predict target position. While the LfN model only provides a ∼10% better description of fast-OFF cell responses than the LN model (Fig. 2B), at the population level target-tracking accuracy is improved by a factor of nearly 2 (RMS) under appropriate motion conditions—a substantial difference. The LfN circuit thus significantly expands the range of prey the salamander might catch reliably (Fig. 8).

Our proposal for how salamanders might track a moving target is based on the dynamics of a circuit known to exist in the retina, and a downstream computation easily implemented with neural hardware (Lewis and Kristan, 1998). The PVA is robust in that it requires no knowledge of retinal circuit dynamics to compute target position and has only weak sensitivity to uncertainty in its knowledge of receptive field centers. In this regard, it is superior to other algorithms that process the neural image instantaneously, such as winner-take-all and burst-time decoding. Indeed, under mild assumptions (Snippe, 1996), the PVA is the best linear decoder. However, it is not difficult to find conditions under which the PVA will fail. If a target reverses direction and moves 180° backward, it will enter the region of inhibition created by the gain control feedback, and the ganglion cell population will be silent. The PVA will produce only noise under such conditions, whereas a time-dependent decoder would infer that the only direction the target could move to shut down ganglion cell activity was directly backward. The PVA thus does not yield optimal tracking for arbitrary stimuli, but it does something more significant—it provides tracking accuracy smaller than the size of a target over a wide range of speeds that concern a salamander (Figs. 6B, 8C), and it does so quickly and reliably. In this sense, the PVA is, “good enough,” and it is unclear whether the animal would benefit from further improvements. We view these ideas as an instantiation of the simplest algorithm a salamander might use to satisfy its target-tracking needs.

Behavioral predictions

There is little published work at present on the tongue projection accuracy of amphibians. It has been shown that at extremely dim light levels, amphibians seem to correct for the slowness of vision arising from long photoreceptor latencies (Aho et al., 1993). The circuit described in this article may shed light on such observations. If the fast-OFF cell network is used by a PVA to track moving targets, it cannot work well for all targets, and this should manifest itself in the accuracy of tongue projection for different types of stimuli. Two general predictions can be tested directly in behaving amphibians, and allow one to discriminate target tracking based largely on a PVA with fast-OFF cells from other cell types and algorithms. (1) Tongue projection accuracy should be a function of prey size and speed, in a manner corresponding to Figure 8. The most crucial property of the plot is the relation between the curves rather than the precise values of spatial errors (which will be affected by delays elsewhere in the brain). Tracking with other algorithms, such as purely linear networks, or other cell types (such as ON cells), will produce different error curves. (2) If the prey turns after the amphibian has committed to a strike, the tongue should overshoot the true target position (Fig. 4). The duration of this integration window should be closely related to the bandwidth of the underlying ganglion cell temporal kernels. Sudden trajectory changes will be difficult for all tracking algorithms, but the time to recovery will be characteristic of the fast-OFF cell and PVA dynamics.

Real prey motion will include looming as well as background motion, whereas the stimuli used in this study, and the behavioral predictions above, are specific to constant velocity trajectories with turns. However, amphibians will actively strike at these simplified but ethological motion patterns (Roth, 1987). Along these lines, it is interesting to note that the scaling of target angular size and speed with distance for real prey is reproduced in the fast-OFF cell PVA tracking dynamics: small targets are tracked most accurately at slow speeds, and large targets are tracked most accurately at faster speeds (Fig. 8).

Decoding versus computation

A common method of data analysis in system neuroscience is that of optimal decoding, the study of how information may be converted from one form to another (Bialek et al., 1991). A statistical model of the dynamics of a neural circuit can be used to allow the accurate reconstruction of the stimulus that drove a particular spike pattern from the circuit. Because they incorporate the full dynamics of the generating circuit, these types of estimators work extremely well and have been successfully applied to a variety of neural systems (Brown et al., 1998; Pillow et al., 2005). These studies can be viewed conceptually as an effort to find an inversion that projects the measured neural population activity back into the stimulus space, and are a useful tool in determining what information a population of neurons carries.

However, the use of decoding as a method of analyzing spike trains should not be confused with what the brain does with those spike trains. It is rather unlikely that the brain processes optic nerve signals by first estimating what the veridical light intensity was at each photoreceptor. This would entail some serious practical problems. For example, given the response delays of ganglion cells, the optimal decoder would require a delay of the same magnitude for a complete stimulus estimation. Furthermore, the dynamics and spatial receptive fields of ganglion cells vary considerably with light intensity and other stimulus (Shapley and Enroth-Cugell, 1984; Purpura et al., 1990; Baccus and Meister, 2002; Hosoya et al., 2005), necessitating that the circuits in the brain keep track of these input statistics to update the decoder accordingly. The resources required to implement this might well exceed what a salamander can afford in terms of both latency and complexity. At a more conceptual level, the very idea of reconstructing the stimulus from neural responses is reminiscent of the homunculus theory of brain processing (Descartes, 1664): presumably, a second visual system would then be needed to act on the reconstructed image.

Here we have taken a different approach: rather than attempting to invert the work of the retinal circuitry, we have asked what downstream computations it enables in a particularly effective way (Gollisch and Meister, 2010). We have found that while individual fast-OFF ganglion cells have strongly delayed and nonlinear input–output characteristics, the fast-OFF cell population has a nearly delay-free linear transfer function for a specific stimulus feature—position. In computing position with the PVA, the bulk of the information in the retinal signal is discarded, and there is no explicit stimulus reconstruction. Such a fast, simple, and robust output code would allow downstream neurons to compute target position trivially, freeing resources for additional computational problems critical to successful prey capture, such as depth estimation, or coordinating the tongue and neck muscles. The existence and fidelity of the extrapolation across the fast-OFF cell population is only observable in the correct stimulus regime, emphasizing the importance of studies that place neural circuits in a behavioral context. Our results suggest a simplifying principle of neural information processing—complexity may be localized within circuits, and neural outputs may be interpreted by downstream circuits in a manner largely decoupled from the dynamics that generated them. Such a mechanism would be highly convenient from an evolutionary perspective: if the fidelity of computation in one circuit improved without changing the output code, its downstream partner would instantly benefit from this with no changes on its own. This property is perhaps one of the defining features of computation—the results can be used without knowledge of their construction.