Finite detector based projection model for high spatial resolution

Abstract

For finite detector and focal spot sizes, here we propose a projection model for high spatial resolution. First, for a given x-ray source point, a projection datum is modeled as an area integral over a narrow fan-beam connecting the detector elemental borders and the x-ray source point. Then, the final projection value is expressed as the integral obtained in the first step over the whole focal spot support. An ordered-subset simultaneous algebraic reconstruction technique (OS-SART) is developed using the proposed projection model. In the numerical simulation, our method produces improved spatial resolution and suppresses high-frequency artifacts.

1. Introduction

In fan-beam or cone-beam CT geometry, the forward and back projection operations used for traditional iterative reconstruction usually assume that a projection datum is a linear integral along a path from the detector elemental center to the source focal center. The measured data is naturally viewed as a sample of the projection in the continuous domain on the detector center. Particularly, let f(x) be a 2D compactly supported function. The x-ray projection is normally modeled by

$$P(\mathbf{a},\beta )=\underset{0}{\overset{\infty }{\int }}f(\mathbf{a}+t\beta )dt,$$ (1)

where a ∈ ℝ² represents an x-ray source position and β ∈ 𝕊 denotes a 2D unit vector. Equation (1) can be refer to as line integral model (LIM). However, the real image geometry of a practical imaging system is more complicated than Eq. (1). Because the conventional analytic reconstruction methods (such as filtered back projection) treat projections as samples on the space ℝ² × 𝕊. As a result, the spatial resolution of a reconstructed image is severally limited by blurring effects due to finite detector elemental and source focal sizes [1–3]. On the other hand, iterative reconstruction methods were developed in the cases in which analytic reconstruction formulas are not available or sub-optimal [4], such as with a truncated dataset, limited angle setting, exterior problem [5], etc. When both the analytic and iteration methods are numerically implemented, both the forward and back projection operations play a primary role in the overall computational process.

To our best knowledge, the current forward and back projection techniques can be divided into three categories [6]. The first is the pixel-driven technique, which is used for back projection. It makes a line from the focal spot through the pixel center, and determines an intersection on a detector array. A value is obtained via interpolation from data in the detector array, and the result is accumulated on the pixel. The second is the ray-driven technique, which is used for forward projection and back projection. It casts rays through an image and discretes the line integral Eq. (1). A value is obtained via interpolation from the image pixel values, and the result is accumulated on corresponding detector elements. The third is called the distance-driven technique, which combines the advantages of the pixel-driven and ray-driven techniques to suppress high-frequency artifacts [6]. The key is to define an overlapping length between each image pixel and each detector element, which is the state-of-the art method. These techniques were extensively studied for fast implementation and quality optimization [7–10]. Given the finite detector elemental and source focal sizes, more precise models were studied to allow higher spatial resolution [11] or generate more realistic projections [12]. The idea is to discrete both of the detector element and the focal spot into finer components, and each pair of focal and detector components is modeled by the linear integral Eq. (1), and the final projection datum is a weighted sum of various results from Eq. (1).

When all the aforementioned techniques are implemented for iterative CT reconstructions, interpolation is unavoidable, and the spatial resolution is limited by the linear integral model Eq. (1). Here we report a new area integral model (AIM) for x-ray projections to replace Eq. (1), which does not require any interpolation in the forward and back projection steps for image reconstruction, and has a significant potential for improved CT resolution.

2. Methodology

2.1. Analytic projection model

Let Ω_s ⊂ ℝ² be a compact support of a focal spot. As shown in Fig. 1, the connection of two detector elemental border points to a ∈ Ω_s forms a narrow fan-beam, whose angle can be expressed as γa. A unit vector from a and to the detector element can be expressed as β(θ, a) with θ ∈ [0, γa]. Assume that the photon intensity along any direction from a point inside the x-ray focal spot a ∈ Ω_s is I₀, according to Beer’s law the number of photons detected by the detector element can be expressed as:

$$I(\mathbf{a},\theta )=I_0{e}^{-{\int }_0^{\infty }f(\mathbf{a}+t\beta (\theta ,\mathbf{a}))dt},$$ (2)

which is equivalent to Eq. (1) after a logarithm operation ln (I₀/I(a, θ)). Considering the finite detector and source sizes, the total number of received photons become

$$I=\underset{{\mathrm{\Omega }}_s}{\int }\underset{0}{\overset{\gamma \mathbf{a}}{\int }}I(\mathbf{a},\theta )d\theta d\mathbf{a}=I_0\underset{{\mathrm{\Omega }}_s}{\int }\underset{0}{\overset{\gamma \mathbf{a}}{\int }}{e}^{-{\int }_0^{\infty }f(\mathbf{a}+t\beta (\theta ,\mathbf{a}))dt}d\theta d\mathbf{a},$$ (3)

where da represents an area differential of the focal spot support. To make the model Eq. (3) consistent to Eq. (2), it can be normalized as:

$$\mathrm{I̅}=\frac{I_0\underset{{\mathrm{\Omega }}_s}{\int }\underset{0}{\overset{\gamma \mathbf{a}}{\int }}{e}^{-{\int }_0^{\infty }f(\mathbf{a}+t\beta (\theta ,\mathbf{a}))dt}d\theta d\mathbf{a}}{\underset{{\mathrm{\Omega }}_s}{\int }\underset{0}{\overset{\gamma \mathbf{a}}{\int }}d\theta d\mathbf{a}}=\frac{I_0\underset{{\mathrm{\Omega }}_s}{\int }\underset{0}{\overset{\gamma \mathbf{a}}{\int }}{e}^{-{\int }_0^{\infty }f(\mathbf{a}+t\beta (\theta ,\mathbf{a}))dt}d\theta d\mathbf{a}}{\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}d\mathbf{a}}.$$ (4)

It should be pointed out that the photon intensity may vary along the directions from a point inside the x-ray focal spot. For this case, a flatfield projection can be acquired without any imaging object in practical applications. Because a pixel value in the flatfield projection is proportional to the photon intensity, we can normalize the flatfield projection and obtain a photon intensity distribution. In otherwords, I₀ will depend on the x-ray source position and the detector cell location. Denote $p(\mathbf{a},\theta )={\int }_0^{\infty }f(\mathbf{a}+t\beta (\theta ,\mathbf{a}))dt$ and $\mathrm{p̄}(\mathbf{a})=\frac{1}{\gamma \mathbf{a}}\underset{0}{\overset{\gamma \mathbf{a}}{\int }}p(\mathbf{a},\theta )d\theta$. Equation (4) can be re-expressed as

$$\mathrm{I̅}=\frac{I_0\underset{{\mathrm{\Omega }}_s}{\int }{e}^{-\mathrm{p̄}(\mathbf{a})}\underset{0}{\overset{\gamma \mathbf{a}}{\int }}{e}^{\mathrm{p̄}(\mathbf{a})-p(\mathbf{a},\theta )}d\theta d\mathbf{a}}{\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}d\mathbf{a}}.$$ (5)

Because for a detector element, the x-ray beam is very narrow (e.g., γa is very small) and p(a, θ) is very smooth, p̄ (a)−p (a, θ) should be very small and smooth. Hence, by the first-order Taylor approximation, we have

$$\mathrm{I̅}\cong \frac{I_0\underset{{\mathrm{\Omega }}_s}{\int }{e}^{-\mathrm{p̄}(\mathbf{a})}\underset{0}{\overset{\gamma \mathbf{a}}{\int }}(1+\mathrm{p̄}(\mathbf{a})-p(\mathbf{a},\theta ))d\theta d\mathbf{a}}{\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}d\mathbf{a}}=\frac{I_0\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}{e}^{-\mathrm{p̄}(\mathbf{a})}d\mathbf{a}}{\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}d\mathbf{a}}.$$ (6)

Again, due to the focal spot size is very small, we define $\mathrm{p̿}=\frac{\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}\mathrm{p̄}(\mathbf{a})d\mathbf{a}}{\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}d\mathbf{a}}$ and obtain

$$\mathrm{I̅}\cong \frac{I_0\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}{e}^{-\mathrm{p̿}}{e}^{\mathrm{p̿}-\mathrm{p̄}(\mathbf{a})}d\mathbf{a}}{\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}d\mathbf{a}}\cong \frac{I_0{e}^{-\mathrm{p̿}}\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}(1+\mathrm{p̿}-\mathrm{p̄}(\mathbf{a}))d\mathbf{a}}{\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}d\mathbf{a}}=I_0{e}^{-\mathrm{p̿}}(\frac{(1+\mathrm{p̿})\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}d\mathbf{a}}{\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}d\mathbf{a}}-\frac{\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}\mathrm{p̄}(\mathbf{a})d\mathbf{a}}{\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}d\mathbf{a}})=I_0{e}^{-\mathrm{p̿}}\left(\right(1+\mathrm{p̿})-\mathrm{p̿})=I_0{e}^{-\mathrm{p̿}}$$ (7)

Equation (7) shows that we can obtain an approximate linearized projection p̿ associated with a given detector element and an x-ray focal spot, and p̿ can be computed as:

$$\mathrm{p̿}=\frac{\underset{{\mathrm{\Omega }}_s}{\int }\underset{0}{\overset{\gamma \mathbf{a}}{\int }}{\int }_0^{\infty }f(\mathbf{a}+t\beta (\theta ,\mathbf{a}))dtd\theta d\mathbf{a}}{\underset{{\mathrm{\Omega }}_s}{\int }\gamma \mathbf{a}d\mathbf{a}}\cong \frac{\underset{{\mathrm{\Omega }}_s}{\int }\frac{1}{\gamma \mathbf{a}}\underset{0}{\overset{\gamma \mathbf{a}}{\int }}{\int }_0^{\infty }f(\mathbf{a}+t\beta (\theta ,\mathbf{a}))dtd\theta d\mathbf{a}}{\underset{{\mathrm{\Omega }}_s}{\int }d\mathbf{a}},$$ (8)

where we have used the fact that γa is almost a constant.

Fig. 1.

Finite detector based projection model with a finite focal sport size in fan-beam geometry.

The integral $\underset{0}{\overset{\gamma \mathbf{a}}{\int }}{\int }_0^{\infty }f(\mathbf{a}+t\beta (\theta ,\mathbf{a}))dtd\theta$ in Eq. (8) is actually over the fan-beam defined by the two detector elemental borders and the x-ray source point. Therefore, Eq. (8) can be re-expressed as:

$$\mathrm{p̿}=\frac{\underset{{\mathrm{\Omega }}_s}{\int }\frac{1}{\gamma \mathbf{a}}\underset{{\mathrm{\Omega }}_b}{\int }f(\mathbf{x})\frac{d\mathbf{x}}{\Vert \mathbf{x}-\mathbf{a}\Vert }d\mathbf{a}}{\underset{{\mathrm{\Omega }}_s}{\int }d\mathbf{a}}=\frac{\underset{{\mathrm{\Omega }}_s}{\int }\underset{{\mathrm{\Omega }}_b}{\int }f(\mathbf{x})\frac{d\mathbf{x}}{\gamma \mathbf{a}\Vert \mathbf{x}-\mathbf{a}\Vert }d\mathbf{a}}{\underset{{\mathbf{\Omega }}_s}{\int }d\mathbf{a}},$$ (9)

where Ω_b denotes the narrow fan-beam region, and dx is the corresponding differential. The area integral model (AIM) Eq. (9) is the major contribution of this paper. When an ideal point source is considered, Eq. (9) can be reduced to $\mathrm{p̿}=\underset{{\mathrm{\Omega }}_b}{\int }f(\mathbf{x})\frac{d\mathbf{x}}{\gamma \mathbf{a}\Vert \mathbf{x}-\mathbf{a}\Vert }$.

2.2. Discrete projection model

In the forward and back projection steps in iterative reconstruction algorithms, a 2D function f(x) can be discretized as a 2D digital image f = (f_i,j) ∈ R^N_I × R^N_J , where the indices 1 ≤ i ≤ N_I and 1 ≤ j ≤ N_J are integers. Define

$$f_n=f_{i,j},n=(i-1)\times N_J+j,$$ (10)

with 1 ≤ n ≤ N and N = N_I × N_J, we can re-arrange the image into a vector f = [f₁, f₂,…, f_N]^T ∈ R^N. We may use either f_i,j or f_n to denote the image. Assume that the finite focal spot Ω_s can be discretized as a_q with 1 ≤ q ≤ Q. Let ${\mathbf{p}}^q={[p_1^q,p_2^q,\dots ,p_M^q]}^T\in R^M$ is measured data associated with the x-ray source a_q and all the detector elements, where M is the product of the number of projections and the number of detector elements. By Eq. (9), we have the following discrete linear system

$$\mathbf{p}=\frac{1}{Q}\sum _{q=1}^Q{\mathbf{p}}^q=\frac{1}{Q}\sum _{q=1}^Q{\mathbf{B}}^q\mathbf{f}=\left(\frac{1}{Q}\sum _{q=1}^Q{\mathbf{B}}^q\right)\mathbf{f}=\mathbf{B}\mathbf{f},$$ (11)

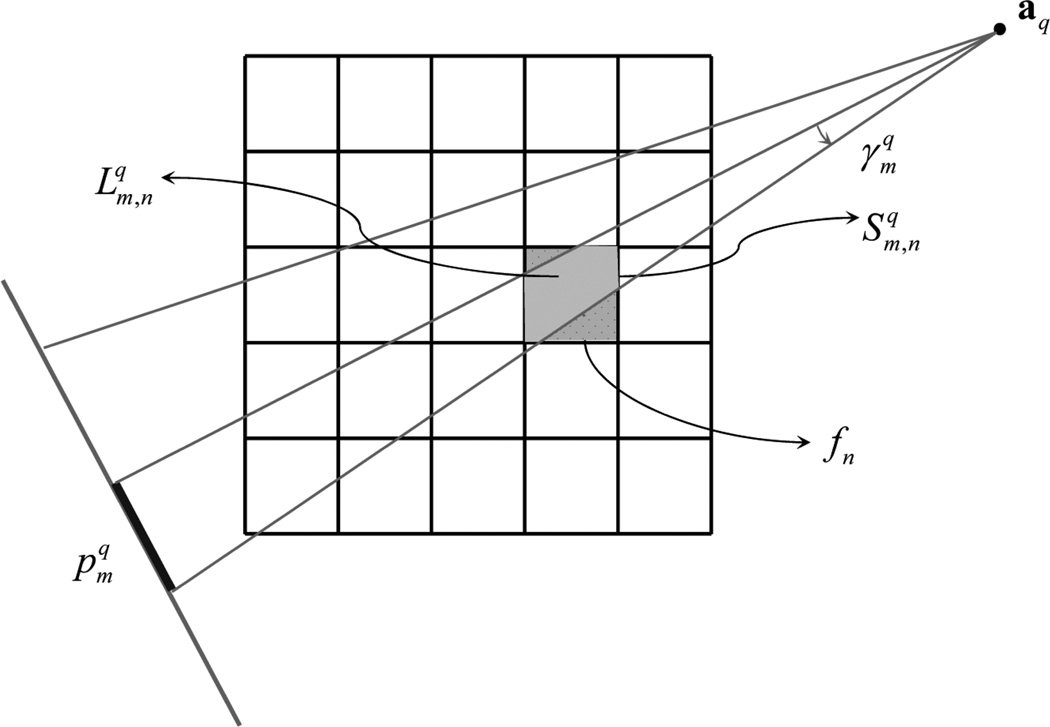
where ${\mathbf{B}}^q=(B_{m,n}^q)\in R^M\times R^N$ is the linear measurement matrix for the x-ray source a_q. As shown in Fig. 2, in fan-beam geometry the n^th pixel can be viewed as a rectangular region with a constant value f_n, the m^th measured datum $p_m^q$ can be viewed as an integral of those areas of pixels that are partially covered by a narrow beam from the x-ray source a_q to a detector element and weighted by the corresponding x-ray linear attenuation coefficients and fan-arc lengths, respectively. Thus, the component $B_{m,n}^q$ in Eq. (11) (or the discrete version of $\frac{d\mathbf{x}}{\gamma \mathbf{a}\Vert \mathbf{x}-\mathbf{a}\Vert }$ in Eq.(9)) can be expressed as

$$B_{m,n}^q=\frac{S_{m,n}^q}{L_{m,n}^q},$$ (12)

where $S_{m,n}^q$ is the discrete version of dx and denotes the interaction area between the n^th pixel and the m^th fan-beam path, and $L_{m,n}^q$ is the discrete version of γa ‖x − a‖ and can be approximately computed as the product of the narrow fan-beam angle ${\gamma }_m^q$ and the distance from the n^th pixel center to the x-ray source a_q, which can be viewed as fan-arc length of the narrow fan-beam through the n^th pixel center.

Fig. 2.

Discrete projection model assuming a discrete 2D image in fan-beam geometry.

Eq. (11) is a typical linear system and the solution can be written as

$${\mathbf{f}}^{*}=\text{arg}\underset{\mathbf{f}}{\text{min}}{\Vert \mathbf{p}-\mathbf{B}\mathbf{f}\Vert }^2.$$ (13)

The final image can be reconstructed in the OS-SART framework [13], whose convergence was proved under quite general conditions [14, 15].

3. Results

3.1. Numerical simulation

In the OS-SART framework [13], we developed and implemented an algorithm to reconstruct an image based on the proposed area integral model and the imaging system Eq. (11) in equi-angular fan-beam geometry. An fast iterative shrinkage/soft-thresholding algorithm (FISTA) [16] was employed to accelerate the convergence. Particularly, we simulated an imaging geometry of a Siemens SOMATOM Sensation 64 scanner, whose middle plane was in equi-angular fan-beam geometry. For a full scan along a circular trajectory, the fan-beam sinogram had 1160 projections, and each projection had 672 detector elements. The diameter of the field of view (FOV) was 501 mm and the maximum fan angle is 26.1°.

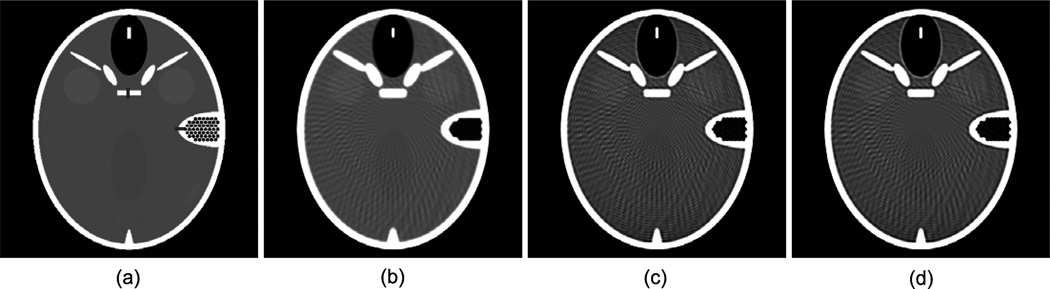
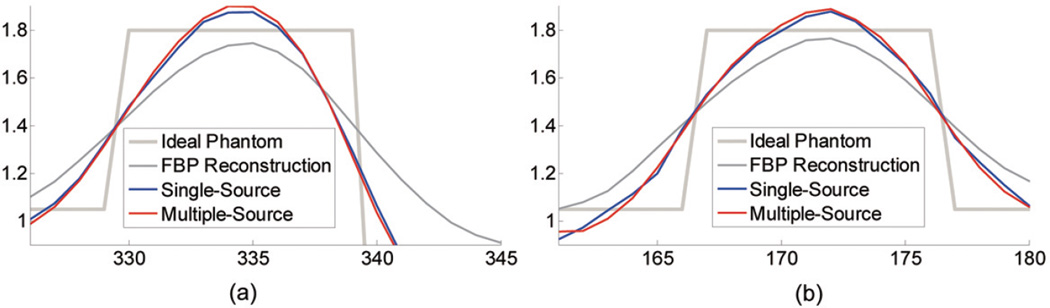
In a 70 × 70 mm region centered at the system origin, which equivalent to a maximum fan angle of 3.5°, we placed a FORBILD head phantom, which was uniformly sampled in a 2000 × 2000 matrix with the pixel size being 35 × 35 µm. Because the focal spot size along the direction parallel to the x-ray path is insensitive to the spatial resolution of the reconstructed image, we assumed a focal spot size of 0.9 mm along the direction perpendicular to the x-ray path passing through the origin and discretized it as 9 points. We generated the realistic simulated projections of the head phantom according to a discrete version of Eq. (4) plus a logarithm operation and the high-resolution discrete image. In a 75.3 × 75.3 mm region, we reconstructed the phantom in a 512 × 512 matrix with the pixel size being 147 × 147 µm. The stop criterion for all the reconstruction is that the data discrepancy is smaller than a given constant threshold. The results were shown in Fig. 3, where (a) is the ideal phantom image, (b) that was reconstructed using the conventional FBP algorithm, (c) and (d) that were reconstructed using the OS-SART method with the proposed projection model. While only one source point was assumed for (c), 3 source points were used for (d). Figure 3 clearly demonstrates the improved spatial resolution performance of the proposed finite detector based projection area integral model. This potential can be further seen in the magnifications of the right ear region shown in Fig. 4. It is well known that the higher the spatial resolution, the sharper the reconstructed edge image. The profiles along horizontal and vertical sharp edges as shown in Fig. 5 demonstrate that the reconstructed images using multi-source model has a better spatial resolution than that of single-source model.

Fig. 3.

Ideal and reconstructed images of FORBILD head phantom in a display window [0.8 1.2]. (a) is the ideal phantom image, (b) that was reconstructed using the conventional FBP algorithm, (c) and (d) that were reconstructed using the OS-SART method with the proposed projection model when the source was decomposed into 1 and 3 points respectively.

Fig. 4.

Magnifications of the right ear in Fig. 3 in a display window [0.87, 1.07]. (a)–(d) correspond to Fig. 3(a)–(d) respectively.

Fig. 5.

Profiles along the horizontal edge (a) and vertical edge (b) indicated in Fig. 3 (a).

3.2. Phantom experiment

A phantom experiment was performed on a GE Discovery CT750 HD scanner at Wake Forest University Health Sciences with a circular scanning trajectory. After appropriate pre-processing, we obtained a sinogram of the central slice in typical equi-angular fan-beam geometry. The radius of the scanning trajectory was 538.5 mm. Over a 360° range, 984 projections were uniformly acquired. For each projection, 888 detector elements were equi-angularly distributed, which defines a FOV of a 249.2 mm radius and an iso-center spatial resolution of 584 µm. As a comparison, we also implemented the aforementioned OS-SART algorithm with the aforementioned line integral model, where the system matrix $B_{m,n}^q$ in Eq. (11) is the length of the line-segment of the interaction between the x-ray path and pixel square.

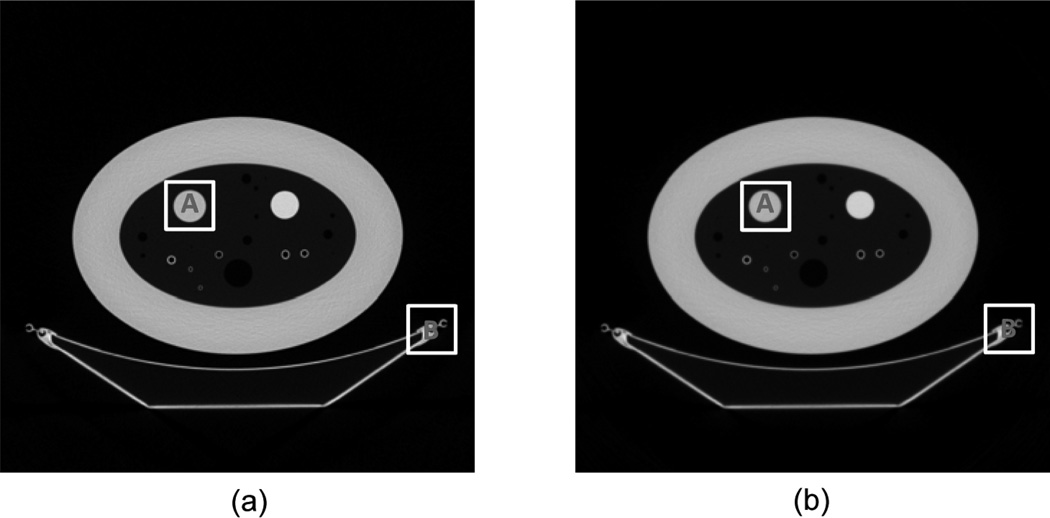
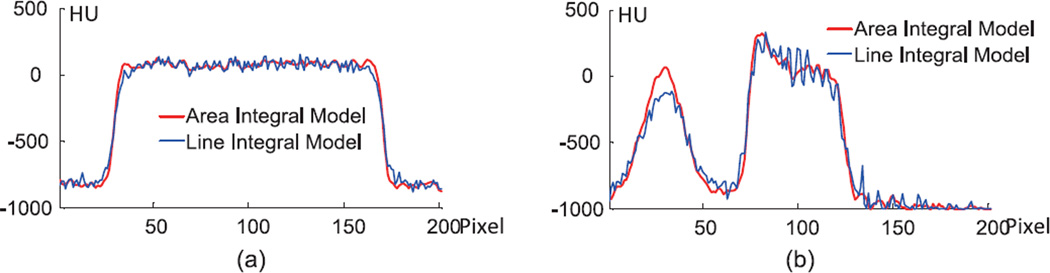
Assuming a point source and using the same parameters for the OS-SART algorithms with different projection models, we reconstructed an image matrix of 2048 × 2048 to cover the whole FOV, and each pixel covered an area of 243 × 243 µm. The results were shown in Fig. 6 and two subregions were magnified as in Fig. 7. The typical profiles along the central horizontal line for the magnified subregions in Fig. 7 were plotted in Fig. 8, which qualitatively confirmed the improved spatial resolution of the proposed area integral model. To quantitatively analyze the improvement of the proposed area integral model, we examined key image quality indexes of the magnified subregion “A” in Fig. 7 (a) & (b). The results are summarized in Table 1. The spatial resolution was statistically estimated orthogonally across the borders of the white disk and its background region as the full-width-of-half-maximum (FWHM) of the line response function fitted into the Gaussian function [17]. The noise was computed as the standard deviation of a flat region, which was a disk centered at the subregion “A” with a radius of 50 pixels. Clearly, the area integral model performed much better than the conventional line integral model. It should be pointed out that it is an under-determined problem to reconstruct an image of 2048 × 2048 pixels from a data set of 984 × 888. However, the OS-SART algorithm with both linear and area integral models can reconstruct high quality images very well without any additional constraint. This is because the back projection step in the iterative OS-SART method implies a smoothness constraint for the reconstructed image.

Fig. 6.

Reconstructed phantom images from a sinogram collected on a GE Discovery CT750 HD scanner with a display window [−1000 400] HU. While (a) was reconstructed using the proposed area integral model, (b) was reconstructed using the conventional line integral model.

Fig. 7.

Local magnifications of the reconstructed phantom images. While (a) and (b) are respectively the subregions indicated by “A” in Fig. 5 (a) and (b), (c) and (d) are respectively the subregions indicated by “B”.

Fig. 8.

Profiles along the central horizontal lines in the subregion “A” (a) and “B” (b) in the reconstructed phantom images.

Table 1.

Performance comparison between the area and line integral model in terms of image resolution and noise

	Resolution (mm)	Noise (HU)
Area Integral Model	1.67	20.8
Line Integral Model	2.41	29.0

4. Discussions and conclusion

It is our understanding that the proposed AIM can be simplified to the LIM-based distance-driven method under some approximation. Actually, the factor ‖x − a‖ in Eq. (9) is the distance between the pixel center to the x-ray source. Compared to the traditional LIM-based image reconstruction methods, the AIM-based method is more accurate but on the other hand more time-consuming due to the high computing cost of the system matrix B. Based on our experiments, the computational cost for the AIM-based system matrix is 5~10 times greater than that for the LIM-based system matrix. At this moment, we are working to perform quantitative comparison and analysis between the proposed AIM-based and distance-driven based OS-SART methods combining the fast iterative shrinkage/soft-thresholding algorithm (FISTA) [16, 18] in the compressed sampling framework. The details results will be reported in the near future.

In conclusion, we have proposed a finite detector based projection model, which is based on an accurate area integral in fan-beam geometry. With this model, the interpolation operation is avoided in the forward and back projection steps in iterative reconstruction algorithms. Consequently, our model can suppress interpolation artifacts and enable high spatial resolution. In the same spirit of our 2D model, cone-beam geometry can be similarly handled, where the interaction volume between a voxel and an elemental cone beam delimited by a detector cell aperture can be analytically computed [19].