Effects of the Number of Genome Segments on Primary and Systemic Infections with a Multipartite Plant RNA Virus

Abstract

Multipartite plant viruses were discovered because of discrepancies between the observed dose response and predictions of the independent-action hypothesis (IAH) model. Theory suggests that the number of genome segments predicts the shape of the dose-response curve, but a rigorous test of this hypothesis has not been reported. Here, Alfalfa mosaic virus (AMV), a tripartite Alfamovirus, and transgenic Nicotianatabacum plants expressing no (wild type), one (P2), or two (P12) viral genome segments were used to test whether the number of genome segments necessary for infection predicts the dose response. The dose-response curve of wild-type plants was steep and congruent with the predicted kinetics of a multipartite virus, confirming previous results. Moreover, for P12 plants, the data support the IAH model, showing that the expression of virus genome segments by the host plant can modulate the infection kinetics of a tripartite virus to those of a monopartite virus. However, the different types of virus particles occurred at different frequencies, with a ratio of 116:45:1 (RNA1 to RNA2 to RNA3), which will affect infection kinetics and required analysis with a more comprehensive infection model. This analysis showed that each type of virus particle has a different probability of invading the host plant, at both the primary- and systemic-infection levels. While the number of genome segments affects the dose response, taking into consideration differences in the infection kinetics of the three types of AMV particles results in a better understanding of the infection process.

INTRODUCTION

There is great variation in the architecture of the genome between viruses; the nucleic acid used, its polarity in the case of RNA viruses, replication and transcription strategies, and genome size all vary between viruses. Moreover, this variation has important implications for virus biology and evolution, imposing limitations and providing opportunities. Another characteristic that varies between viral genomes is the number of genome segments, which are essentially analogous to chromosomes, as they are the highest level of physical organization of the genome. Whereas many viral genomes are composed of only a single segment, some viruses have evolved genomes with multiple segments. For example, the members of the family Orthomyxoviridae have evolved six to eight genome segments, and reassortment of these segments during mixed-genotype infections is a key feature of their epidemiology and evolution (1, 2). Whereas all genome segments are packaged into a single virus particle in the family Orthomyxoviridae, some plant viruses are multipartite; each segment is packaged individually into a virus particle (3). The number of genome segments for multipartite plant RNA viruses ranges from two (i.e., Bymovirus) to four (i.e., Hordeivirus), whereas Nanovirus has a single-stranded DNA genome composed of six to eight single-stranded DNA genome segments (4).

The existence of multipartite viruses was first suggested by observations that were at odds with predictions of the independent-action hypothesis (IAH) model (5). The IAH model assumes that each virus particle has a nonzero probability of infection and that particles do not affect each other during the infection process (6–8). Many IAH model predictions have been confirmed experimentally for monopartite plant viruses (6, 7, 9–11). Given that different types of virus particles obligatorily need to complement each other for multipartite viruses, one would not expect the IAH model to hold for a multipartite virus. Multipartite viruses were indeed discovered because of the effects of multipartition on the relationship between the dose and the local-lesion number. Price and Spencer (12) first reported that the relationship between the dose and the number of local lesions for Alfalfa mosaic virus (AMV), Tobacco necrosis virus, and Tobacco ringspot virus on local-lesion hosts was steeper than predicted by the IAH model. It was quickly recognized that these steep dose–local-lesion relationships could be explained if there were complementation between different types of virus particles (13, 14). The groundbreaking work of Fulton (5) finally put this hypothesis on firm ground. Through a series of elegant experiments with Sour cherry necrotic ringspot virus (renamed Prunus necrotic ringspot virus) and Prune dwarf virus, Fulton demonstrated that the dose–local-lesion relationship was steeper than IAH predictions and that the infectivity of the virus sometimes could be influenced by inactivated virus, depending on whether the inactivation method degraded the viral RNA. The conclusion that at least two particles are needed to cause infection was then confirmed by the discovery that preparations of some plant viruses are composed of two or more virus particles (3). Moreover, preparations of a single type of particle had low infectivity, which was restored in mixtures of the different types of particles.

Although there is strong experimental evidence that multipartition of the genome affects infection kinetics (3, 5), numerous key issues related to the infection process of multipartite viruses have not been addressed. First, all work on infection kinetics concerns local lesions, meaning that the results cannot necessarily be extrapolated to infection of permissive hosts. Moreover, the effects of multipartition on systemic infection have not been considered. As it is precisely productive systemic infections that will result in transmission between hosts, this omission is biologically relevant. Will the kinetics of primary and systemic infections in a permissive host conform to the predictions for a multipartite virus? Second, if the different particle types are not present at the same frequency, this may have a profound effect on the dose response. Consider the hypothetical example of a bipartite virus one segment of which is 100 times as abundant as the other, while both segments have the same probability of entering host cells. In this case, the dose response will be limited and shaped by the low-frequency variant, because any site invaded by the low-frequency variant has probably already been invaded by the high-frequency variant. Therefore, it needs to be considered if different particle types are present at the same frequency and, if they are not, what the ramifications are for infection kinetics. Finally, there are methodological limitations in the original pioneering study of Fulton (5); the comparison between data and models is not rigorous, and the testing of hypotheses is purely qualitative. Although Fulton's work is seminal from a historical perspective, these shortcomings have not been addressed in subsequent studies to date.

Here the kinetics of multipartite virus infection was re-examined by using tripartite AMV and Nicotiana tabacum plants as a model system. A study design that allows a rigorous quantitative analysis of whether the genome segment number predicts the multipartite virus dose response and accounts for deviations from IAH model predictions was used. Three plants were used for dose-response experiments, Nicotiana tabacum L. cv. Samsun (referred to here as wild-type plants), a transgenic plant derived from N. tabacum cv. Samsun that expresses AMV genomic segment RNA2 under the control of the Cauliflower mosaic virus 35S promoter (P2 plants), and a transgenic plant expressing AMV genomic segments RNA1 and RNA2 (P12 plants) (15). Note that uncoated AMV RNA segments can achieve cell-to-cell movement (16–18), whereas for systemic movement, the formation of virus particles, each again encapsidating a single RNA segment, is required (17). It has already been shown that the P2 and P12 transgenic plants can support full-blown AMV systemic infection in the absence of the expressed segment in the inoculum (15), and it was anticipated that the expressed RNA segments could therefore complement virus particles to generate primary or systemic infection. Here, we attempted to alter the infection kinetics of AMV from those of a tripartite virus to those of a bipartite or monopartite virus by inoculating AMV into transgenic plants expressing one or two viral genome segments. These results show that the underlying mechanisms are more complex than previously thought and suggest reasons why multipartition has evolved.

MATERIALS AND METHODS

Preparation of viral stocks.

Virus was purified from infected Nicotiana benthamiana plants inoculated with transcripts of RNA1, RNA2, and RNA3 obtained from an infectious clone of AMV strain 425 Leiden. Virus particles were isolated 4 days postinoculation (dpi) as previously described (19). The purified particles were resuspended in PE buffer (10 mM NaH₂PO₄, 1 mM EDTA, pH 7.0), aliquoted in stocks of 50 μl, and stored at −80°C until use.

Dose-response experiments.

Plants were kept in a growth chamber at 24°C with 16 h of light a day for 1 week until transplantation from agar plates to soil. Thereafter, they were kept in a greenhouse at 24°C with 16 h of light a day. We opted for a large, single-block experiment, given that any block level experimental variation would tend to lead to smoother dose-response curves (20, 21). Fifteen 5-week-old plants were inoculated with each of eight virus doses obtained from a 5-fold dilution series in PE buffer and as mock-infected controls. Each plant was rub inoculated with 5 μl of serially diluted viral stock or only buffer, and Carborundum was used as an abrasive. Plants were monitored for symptoms of AMV infection daily until 14 dpi.

Detection of AMV infection.

The presence of AMV in inoculated and upper leaves was performed by tissue printing analysis using a transversal section of the corresponding petiole, as described previously (22). The inoculated leaves were also analyzed by grinding full leaves with 10 volumes of cold extraction buffer (50 mM sodium citrate, 5 mM EDTA, pH 8.5), which was then directly applied to the membrane as described previously (23). RNA was fixed to the membrane with a UV cross-linker (700 × 100 μJ/cm²). Hybridization and detection were conducted as previously described (24), with a digoxigenin (DIG)-riboprobe (Roche Diagnostic GmbH) complementary to nucleotides [nt] 1 to 964 (GenBank accession no. L00162.1) of AMV RNA4.

Quantification of viral stocks.

Total RNA was extracted from purified virus particles with TRI REAGENT (Sigma-Aldrich, Inc.) in accordance with the manufacturer's recommendations. Purified RNA was serially diluted (5-fold) in TE buffer, and 1 μl of each dilution was directly applied to a nylon membrane together with serial dilutions of known amounts of in vitro-transcribed RNA1, RNA2, and RNA3 of AMV. Quantification of the transcribed AMV RNAs was performed with an ND-1000 spectrophotometer (Nanodrop) and with agarose gel with an RNA ladder (RiboRuler High Range RNA Ladder 200 to 6000; Thermo Scientific). Replicas of the same membrane were hybridized with specific DIG-riboprobes for AMV RNA1 (complementary to nt 350 to 861; GenBank accession no. L00163.1), RNA2 (complementary to nt 162 to 680; GenBank accession no. X01572.1), RNA3 (complementary to nt 369 to 1248; GenBank accession no. K03542.1), and RNA4 (complementary to nt 1 to 964; GenBank accession no. L00162.1). Hybridization and detection were conducted as previously described (24), with a chemiluminescent substrate and the LAS-3000 digital imaging system (Fujifilm). As AMV RNA4 is a subgenomic RNA of RNA3, the concentration of RNA4 was estimated by subtracting the estimated RNA3 concentration.

To estimate the number of genome equivalents present and their frequencies, all data for the standard curve (input and readout values of known dilutions) were first log₁₀ transformed to ascertain the range over which the response was linear. The dynamic range was limited to 1 dilution before the response appeared to saturate. Linear regression of the log₁₀-transformed data was then performed, rendering high values for the coefficient of determination (mean r² ± standard deviation [SD] = 0.994 ± 0.006). For those samples that fell within the dynamic range, the estimated linear regression parameters were used to estimate the unknown concentrations in the virus samples. Finally, the number of genome equivalents was calculated on the basis of the length of the genome segment.

Estimation of the area of primary infection foci in different plant types.

N. tabacum wild-type, P1, P2, or P12 plants were inoculated with a mixture of capped transcripts corresponding to AMV RNA1 and RNA2, a modified RNA3 that expresses the green fluorescent protein (GFP) (25), and a few micrograms of purified AMV coat protein as described in reference 26. The fluorescence derived from chimeric AMV RNA3 encoding GFP was monitored with a Leica stereoscopic microscope. The area of infection foci was measured at 2 and 3 dpi with ImageJ software (27).

A generalized linear model (GLM) was used to statistically analyze the data (SPSS 20.0), with the Akaike information criterion (AIC) used to establish the best-supported model, by using a gamma distribution and log link. Pairwise comparisons were made by using the estimated marginal means with a Holm-Bonferroni correction. To test if there was an effect of the type of plant on the proportion of systemically infected leaves, the lowest dose at which the majority of the plants of each genotype was infected (1/625 dilution for wild-type plants, 1/3,125 dilution for P2 plants, and 1/78,125 dilution for P12 plants) was considered. The highest infected leaf was considered the limit of systemic infection, and the number of systemic leaves below the highest infected leaf positive for AMV infection was determined. A test of equal proportions was then performed (R 2.14), grouping the data by plant type. Pooled data for each plant type were used to perform pairwise comparisons, with a Holm-Bonferroni correction for multiple comparisons.

Modeling of the dose response: classic framework with equal frequencies of all types of virus particles.

A simple framework for considering the dose response of a multipartite virus which assumes that the different types of virus particles are present at the same frequency is described first. This model is equivalent to the description given by Fulton (5), although little detail is given in that publication. However, here the model is geared to describing the frequencies of primary and systemic infections, rather than the number of local lesions.

It is assumed that each virus particle type acts independently in the infection process up to the point at which it has successfully breached an epidermal cell and can then begin to support replication in the presence of the other necessary particle types, a part of the infection process that is referred to here as “invading” the host plant. The different particle types will behave differently in this process (e.g., in the presence of RNA1 and RNA2, there will be replication of these segments [28]), but the complete cellular infection cycle cannot be completed unless all three particles have invaded a cell (15). The assumption of independence is warranted if the virus is only passively carried until it enters the cell and if particles do not aggregate. The mean number of particles invading each cell is α_jd_j, where α_j is the probability of particle type j invading a cell and d_j is the dose of that particle type. Note that α, being a probability that reflects the ability of a segment to support virus replication, needs to be carefully interpreted here. The assumption is then made that the number of particles of type j per cell, v_j, follows a Poisson distribution, such that $Pr\left(v_j\right)={\left({\alpha }_j{d}_j\right)}^{v_j}{e}^{-{\alpha }_j{d}_j}/v_j!$, where j can take the values 1, 2 … k (k = 3 for AMV). Therefore, the frequency at which a cell is infected by at least one particle of type j, C_j, will then be $C_j=1-\mathrm{Pr}(v_j=0)=1-e^{-{\alpha }_j{d}_j}$. However, the virus can only replicate if all of the necessary k particle types have invaded the cell. If the frequency of the particles in the inoculum is the same, then for each dose (a dilution of the inoculum), the dose of each particle type (d) in the inoculum will also be the same. If it is also assumed that the probability of infection of each particle type is the same (e.g., α α₁ = α₂ = … = α_k) and that the successful infection of one cell will eventually lead to observable infection of the inoculated leaf, then the frequency of infection in the inoculated leaf (I) will be

$$I={\prod }_{j=1}^k{C}_j={(1-e^{-\alpha d})}^k$$ 1

For systemic infection of a plant, there is an additional infection step that each particle type surmounts with a probability β_j. Moreover, it is assumed that there is heterogeneity in host plants in their susceptibility to systemic infection by the virus. This assumption is made because even at high doses not all plants are always infected. These cases would be extremely unlikely under a maximum-likelihood framework that did not include heterogeneity in host susceptibility and hence would strongly affect model parameter estimates. Although heterogeneity in susceptibility could be modeled in detail (21), a simpler but in this case equally effective manner in which to take differences in susceptibility into account is to assume that only a fraction ψ of host plants can be systemically infected. If it is again assumed that systemic infection probabilities are the same for all particle types (β β₁ = β₂ = … = β_k), the frequency of systemic infection in plants (I_s) will be

$$I_s=\psi {(1-e^{-\alpha \beta d})}^k$$ 2

For both equations 1 and 2, when k = 1, the model collapses to an IAH model that assumes that each particle and particle type act independently. Therefore, when k = 1, this model is referred to as the IAH model. When k > 1, the infection presented above is referred to as the dependent-action (DA) model. Note that k can take values of less than 1, but this outcome is not expected here given previous results (5, 12). Note that for fitting of the classic infection model, the combined dose (d) of all three particle types was used.

Modeling of the dose response: a general framework.

A limitation of the classic framework for analysis of the dose responses of multipartite viruses is that it does not take into account the possibility that the frequency of different particle types varies in the inoculum. Moreover, the probabilities of primary and systemic infections in the inoculated and systemic leaves may also not be the same for each particle type. A simple model taking these three aspects into account is therefore introduced. For primary and systemic infections, the probabilities that a plant will be infected are, respectively,

$$I={\prod }_{j=1}^k{(1-e^{-{\alpha }_j{d}_j})}^{\omega }$$ 3

$$I_s=\psi {\prod }_{j=1}^k{(1-e^{-{\alpha }_j{\beta }_j{d}_j})}^{\omega }$$ 4

where ω is introduced so that the interactions between particles of one type can be nonadditive. When ω < 1, there are antagonistic interactions between particles of one type, whereas when ω > 1, there are synergistic interactions. When ω ≠ 1, the general model predictions are equivalent to those resulting from the classic model having an estimated k different from the actual number of genome segments. For the dose response in transgenic plants expressing one or two viral RNA segments, the term for infection of these segments becomes 1 (i.e., all plants have undergone the equivalent of being invaded by expressing the RNA segments) and it is dropped from the model. I.e., for primary infection of P2 plants, which express AMV RNA2, the frequency of primary infection is $I={(1-e^{-{\alpha }_1{d}_1})}^{\omega }{(1-e^{-{\alpha }_3{d}_3})}^{\omega }$ whereas for P12 plants it is $I={\left({1-e}^{-{\alpha }_3{d}_3}\right)}^{\omega }$.

To test whether the data support the inclusion of model parameters, model selection was performed over a series of models based on equations 3 and 4. Model 1 assumes additive interactions between particle types (ω = 1) and equal probabilities of primary and systemic infections between particle types (α α₁ = α₂ = α₃ and β β₁ = β₂ = β₃). Note that this model is equivalent to the classic model only if the frequencies of different particle types are equal. Three parameters must therefore be estimated, α, β, and ψ. Model 2 assumes no additive interactions between particles but allows probabilities of infection for the different particle types to vary. The frequencies of the different particle types were measured empirically, meaning that seven parameters must therefore be estimated, i.e., α₁, α₂, α₃, β₁, β₂, β₃, and ψ. Model 3 allows for nonadditive interactions between particles but assumes that probabilities of infection are equal. Four parameters must therefore be estimated, i.e., α, β, ψ, and ω. Model 4 allows for nonadditive interactions and allows probabilities of infection to vary for the different particle types. Eight parameters must therefore be estimated, α₁, α₂, α₃, β₁, β₂, β₃, ψ, and ω. Finally, model 5 allows the probabilities of primary infection for the first and third particle types (α₁ and α₃) to be host plant dependent and allows for nonadditive interactions. (The second particle type is needed only for infection of the wild-type plant, and only a single estimate of α₂ is therefore needed.) Model 5 is therefore the least restricted model. Although it is probably overparameterized, this model serves to test whether model fit can be further improved. Eleven parameters must be estimated, α_1,WT, α_1,P2, α₂, α_3,WT, α_3,P2, α_3,P12, β₁, β₂, β₃, ψ, and ω.

Model fitting and selection.

To fit the model to the data, a maximum-likelihood approach was used. Given that each plant represents an independent observation, the likelihood of a model prediction for I_i is $L(I_i\mid X,Y)=\left(\begin{array}{c}X\\ Y\end{array}\right){I_i}^y{(1-I_i)}^{X-Y}$, where X is the total number of plants inoculated and Y is the number of plants infected in the inoculated leaf, and likewise for systemic infection. From a biological perspective, a plant can become systemically infected only after successful primary infection has occurred. However, since primary and systemic infections were determined independently, the likelihood of systemic infection is also calculated over all of the data and not just over the fraction of plants found to have primary infections. The model was fitted to the data for each plant type by first performing grid searches over large parameter spaces to ensure that a global solution was found. Next, stochastic hill climbing was performed to determine exact parameter estimates. These searches were also performed on 1,000 bootstraps of the data to estimate the 95% confidence intervals (CIs) of the parameter estimates. AIC was then used to perform model selection.

The data used for modeling of the dose response have been deposited at Dryad (doi:10.5061/dryad.fj5m5).

RESULTS

Predictions of a simple infection model.

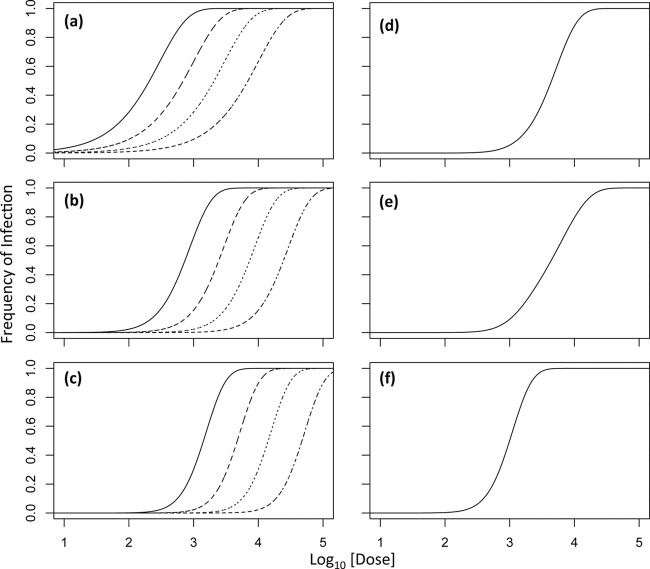
The IAH model (equation 1) predicts a dose-response curve with a singular shape (19), which can shift position, depending on the infection probability (Fig. 1a). The same model can be extended to a multipartite virus, when it is assumed (i) that particles of each type act independently in invading the host (entering host cells; see Materials and Methods) and (ii) that particles of k types are necessary for infection, which corresponds to the actual number of different segments. This infection model predicts a steeper dose-response curve for multipartite viruses if the frequencies of particles and their probabilities of invading the host are the same (Fig. 1b and c). In this case, the number of genome segments determines the shape of the dose-response curve, but it can again shift positions, depending on the infection probabilities of the different particle types (Fig. 1b and c). However, if the frequencies of different particle types are not the same or their infection probabilities are different, the dose-response curve will tend to be shallower (Fig. 1d), approaching the IAH response when, for example, one of the genome segments is very rare (Fig. 1e). On the other hand, a steep dose-response curve equivalent to simple model predictions for a tripartite virus can be achieved when the frequencies of particles are not equal (Fig. 1f), but the product of dose and infection probability (α_jd_j) is approximately the same for all particle types.

Fig 1.

Infection model predictions. In all of the panels, the log₁₀-transformed dose is on the abscissa (where the dose is the sum of the doses of each type of virus particle) and the infection frequency is on the ordinate. In panel a, predictions of the infection model for a virus with one genome segment (k = 1; IAH) are shown, with infection probabilities decreasing from 3.3 × 10⁻³ to 1 × 10⁻³ to 3.3 × 10⁻⁴ to 1 × 10⁻⁴ for the curves from left to right (the grain of the dotted line becomes finer as the infection probability decreases). Note that changing the infection probability shifts the curve but does not alter its shape. Panels b and c show model predictions for viruses with two (k = 2) and three (k = 3) genome segments at equal frequencies for different particle types, respectively, and the same infection probabilities. Note that while the genome segment number alters the shape of the curve, changing the infection probability only changes its shape. Panel d shows model predictions for a tripartite virus in which each segment has an infection probability of 3.3 × 10⁻³ but one segment has a 10-fold higher frequency than the other two. The shape of the dose-response curve is then similar to that of a bipartite virus. Panel e shows model predictions for a tripartite virus in which each segment has an infection probability of 3.3 × 10⁻³ but one segment has a 10-fold lower frequency than the other two. The dose response is then similar to that of a monopartite virus. In panel f, the frequencies of the different particle types are the same but the probability of infection for the rare segment is 3.3 × 10⁻². The dose-response curve is then as steep as possible for a tripartite virus in the absence of nonadditive interactions (k is equal to the actual number of genome segments or ω = 1), even though the particle frequencies are different.

One can therefore expect a steep dose-response curve for a multipartite virus corresponding to simple model predictions only under specific conditions. When these conditions are not met, the dose-response curve will tend to be smoother. Moreover, any experimental error (e.g., variation in virus dose or inoculum size) will also tend to make the dose-response curve smoother (20, 21). Therefore, the observation of steep dose-response curves for plant multipartite viruses seems to be somewhat unlikely from the outset, and its apparent commonality is therefore striking (5, 12).

Rejection of the IAH model of AMV infection of wild-type and P2 plants.

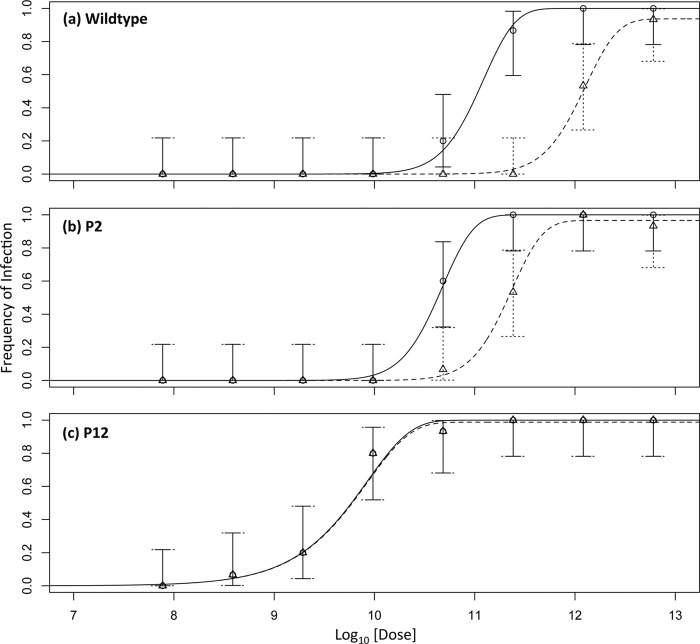
Recent work on the IAH for Tobacco etch virus, a monopartite Potyvirus, confirmed various IAH model predictions (7, 10, 11). On the other hand, the relationship between the AMV dose and the number of local lesions has been reported to be steeper than IAH predictions (12). Therefore, we first set out to confirm that the data for the infection of wild-type and P2 plants do not support the IAH model, whereas data for the P12 plants were expected a priori to support the IAH model. This analysis with the classic infection model was performed to test whether these experimental results and analysis are compatible with historical results. Equations 1 and 2 were fitted to the data, with a separate analysis for wild-type, P2, and P12 plants (see Materials and Methods). For wild-type plants, it was indeed found that the DA model was better supported than the IAH model (Table 1), as the dose-response curve was steeper than IAH model predictions (Fig. 2a). For P2 plants the DA model was also better supported than the IAH model (Table 1), as the dose-response curve for P2 plants was also steeper than IAH predictions (Fig. 2b). The steep dose-response curve for both wild-type and P2 plants is also shown by k values significantly greater than 1 (Table 1). On the other hand, for P12 plants, IAH was the best-supported model (Table 1) and the dose-response curve was very similar to model predictions, being shallower than for P2 or wild-type plants (Fig. 2c).

Table 1.

Model fitting and selection results for testing of the IAH and DA models^a

Plant and model	NLLb	AIC	ΔAICc	AWd	Parameter estimate (CI)
					α	β	k	ψ
Wild type
IAH	9.273	24.545	4.557	0.093	6.46 (4.17–10.23) × 10−12	7.08 (4.07–16.22) × 10−2		1 (0.830–1)
DA	5.994	19.989		0.907	1.35 (0.89–2.57) × 10−12	9.54 (4.90–16.98) × 10−2	2.635 (1.912–3.426)	0.937 (0.806–1)
P2
IAH	10.407	26.814	5.609	0.057	1.55 (1.07–2.45) × 10−11	0.204 (0.079–0.372)		0.965 (0.893–1)
DA	6.603	21.206	—	0.943	3.55 (2.40–5.62) × 10−11	0.204 (0.060–0.363)	2.801 (2.067–3.630)	0.996 (0.895–1)
P12
IAH	14.226	34.452	—	0.600	1.20 (0.25–2.04) × 10−10	1e		0.987 (0.922–1)
DA	13.633	35.265	0.814	0.400	7.59 (1.91–25.70) × 10−11	1 (0.977–1)	0.731 (0.521–1.380)	1 (0.926–1)

^aData for each plant type were analyzed separately to determine whether the IAH or DA model is best supported by the data. For wild-type and P2 plants, we expected to reject this model, as three and two particles types, respectively, are required for infection. For the P12 plant, we expected the hypothesis to be supported because only one particle type is required for infection, as the other two are supplied in trans by the plant. Note that each comparison of models is for the same plant type.

^bNLL, negative log likelihood, a measure of model fit.

^cΔAIC, difference between a given model and the best-fitting model.

^dAW, Akaike weight, a measure of the relative support for the model.

^eThe lower and upper 95% CI limits coincide with the estimated parameter value.

Fig 2.

Data and model predictions for different plant types. In all of the panels, the log₁₀-transformed total dose of particles is on the abscissa and the frequency of infection is on the ordinate. The dose is the sum of the doses of all three particle types. Solid lines represent the predicted dose-response curves for infection of the inoculated host obtained by the best-supported model, i.e., DA for wild-type and P2 plants and IAH for P12 plants. The dotted lines represent the model prediction of the dose-response curves for systemic infection. Circles represent the data for infection of the inoculated leaf, and triangles represent the systemic infection data. Error bars indicate the 95% CIs. Note the steeper dose-response curves for wild-type and P2 plants and the decrease between the dose-response curves for the inoculated leaf and systemic tissue, from wild-type to P2 to P12 plants, at which point the two curves practically coincide. For parameter estimates, see Table 1.

Frequencies of AMV particle types.

The frequencies of the three different AMV particle types were then considered, because these frequencies should be equal in order for an analysis with the classical model to be pertinent. However, it was found that particle types were present at different frequencies in the virus stock. The observed ratios (±SD) of RNA1 to RNA2 to RNA3 to RNA4 were 116.4 ± 17.5 to 44.8 ± 8.0 to 1.0 ± 0.3 to 123.6 ± 23.7, meaning that RNA3 is relatively scarce. Note that RNA4 was included in this analysis but is not required for infection (15).

The general infection model suggests a particle-dependent probability of host invasion.

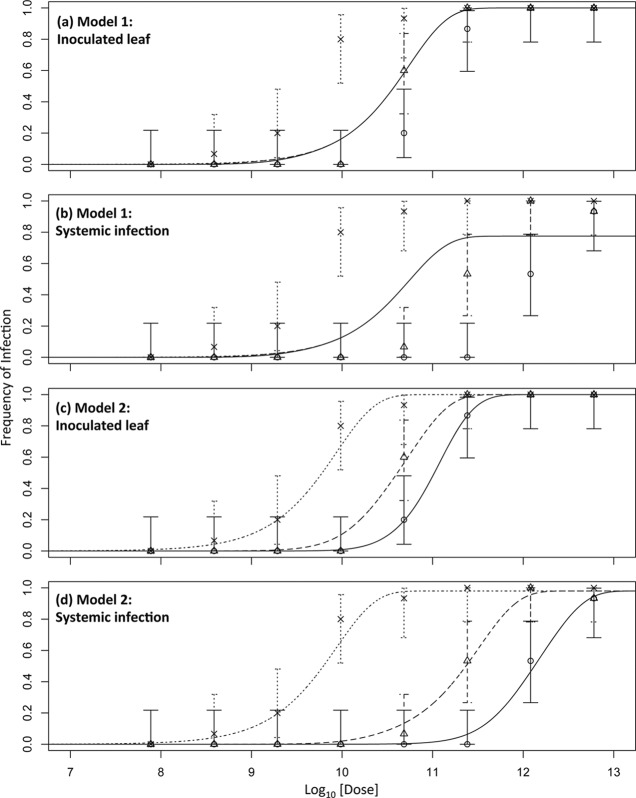
Initial analysis of the data by the classic infection model suggests that the DA model is supported for AMV infection of wild-type and P2 plants, whereas the IAH model is supported for infection of P12 plants. However, given that there are differences in the frequencies of the different particle types, the data were analyzed with a general infection model (see Materials and Methods). This second analysis was performed with the data of all three plants types at once. Moreover, this approach has the added benefit that it allows testing not only of whether the different particle types have different invasion probabilities but also of whether these invasion probabilities are independent of the presence of other particle types (i.e., host plant dependent in this setup). Models 1 to 5 were therefore fitted to the data, and model selection was performed. Model 2 was the best-supported model (Table 2 and Fig. 3). Although the fit (i.e., negative log likelihood) of models 4 and 5 is slightly better, model selection with AIC shows that the data provide less support for these models; the minor improvement in model fit does not compensate for the addition of extra parameters to the model (Table 2). Model 2 allows each particle type to have its own probabilities of invasion (α) and systemic infection (β) but does not include host plant-dependent infection probabilities or nonadditive interactions between particles during infection.

Table 2.

Model fitting and selection results for models 1 to 5^a

Model	NLLb	AIC	ΔAICc	AWd	Parameter estimate (CI)
					α	β	ψ	α1	α2	α3	β1	β2	β3	ω	α1,WT	α1,P2	α3,WT	α3,P2	α3,P12
1	152.742	311.483	237.805	0	2.95 (2.19–4.17) × 10−9	1 (0.209–1)	0.775 (0.775–0.948)
2	29.839	73.678		0.667			0.981 (0.901–0.998)	2.34 (0.11–8.51) × 10−11	3.24 (0.11–8.91) × 10−11	1.86 (0.10–9.77) × 10−8	0.182 (0.032–0.295)	6.17 (3.16–100) × 10−2	1 (0.324–1)
3	150.903	309.806	236.128	0	2.82 (2.29–28.84) × 10−9	0.525 (0.209–0.776)	0.845 (0.777–0.953)
4	29.768	75.768	1.858	0.264			0.980 (0.902–0.998)	2.45 (1.07–8.91) × 10−11	3.24 (1.07–9.55) × 10−11	2.00 (1.12–9.12) × 10−8	0.182 (0.34–0.302)	6.46 (3.47–100) × 10−2	1 (0.123–1)	0.949 (0.949–1.047)
5	28.105	78.210	4.532	0.069			0.980 (0.943–1)		1.51 (0.19–2.88) × 10−10		0.102 (0.043–0.234)	1.45 (0.81–16.60) × 10−2	1 (0.295–1)	0.976 (0.952–1.048)	2.51 (0.81–11.48) × 10−11	4.57 (2.23–16.57) × 10−11	1.41 (0.79–14.79) × 10−9	3.72 (0.45–6.31) × 10−9	1.78 (0.36–3.63) × 10−8

^aData for all three plant types were analyzed jointly to determine whether the general infection model, incorporating differences in the frequencies of different types, could adequately explain the dose-response data.

^bNLL, negative log likelihood, a measure of model fit.

^cΔAIC, difference between a given model and the best-fitting model.

^dAW, Akaike weight, a measure of the relative support for the model.

Fig 3.

Effects of genome segment number on dose response. In all of the panels, the log₁₀-transformed dose is on the abscissa and the frequency of infection is on the ordinate. The dose is the sum of the doses of all of the particle types. Solid lines represent the predicted dose-response curves for wild-type plants, coarse dotted lines represent the predicted dose-response curves for P2 plants, and fine dotted lines represent the predicted dose-response curves for P12 plants. Circles are the data for wild-type plants, triangles are the data for P2 plants, and crosses are the data for P12 plants, with errors bars indicating the 95% CIs. Panel a shows the results for model 1 fitted to the inoculated leaf data, panel b shows the results of model 1 for systemic infection, panel c shows the results of model 2 for the inoculated leaf, and panel d shows the results of model 2 for systemic infection. Both models include the empirically determined frequencies of different particle types. Model 1 fits the data poorly, because the invasion probabilities of all of the particle types are the same. The most abundant particle type (RNA1) then, in fact, determines the infection kinetics, resulting in a response that is independent of the plant type. Model 2 allows each particle type to have a different infection probability, even thought these infection probabilities do not depend on the plant type (i.e., model 5), and fits the data much better. Model 3 (not shown) fits the data poorly. Models 4 and 5 (not shown) fit the data slightly better than model 2, but model selection indicates that the improvements in fit do not justify the additional free parameters added.

Effects of the expression of genome segments on secondary infection.

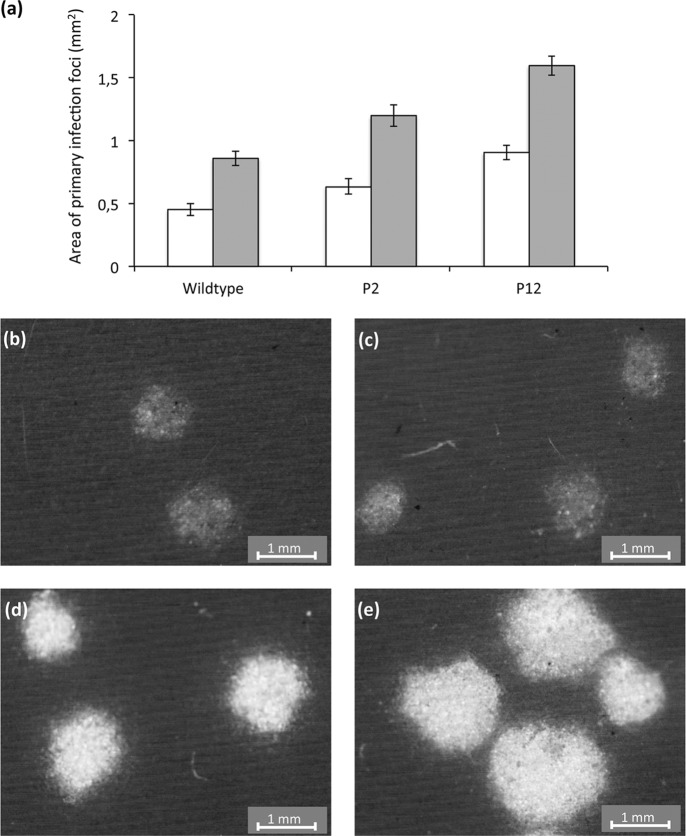
Given the large differences in systemic infection probabilities predicted by both models (Tables 1 and 2), we expected to observe qualitative differences in infection dynamics between the different plant types. To study infection dynamics, the area of primary infection foci was measured at two time points (Fig. 4a). If primary infection foci expand rapidly, then the probability of systemic infection may be larger; the virus may then reach vascular tissue before host responses limit its expansion (11, 22). There was a significant effect of the plant type on the area of primary infection foci (GLM, P = 0.001), and there were significant differences in area among all of the plant types (P < 0.001 for all pairwise comparisons). Moreover, there also appeared to be differences in the intensity of fluorescence, with lower fluorescence in wild-type than in P2 and P12 plants (Fig. 4b to d). In all cases, the differences are in line with expectations based on estimated probabilities of primary infection, i.e., P12 > P2 > wild type for focus area and fluorescence intensity.

Fig 4.

Effects of plant type on virus expansion in primary infection foci. Panel a gives the areas (mm²) of primary infection foci at 2 (white bars) and 3 (gray bars) dpi for the three plant types used. The error bars represent the 95% CIs. Primary infection foci at 3 dpi are shown for the wild-type (b and c), P2 (d), and P12 (e) plants. Besides the differences in size, the foci of the P2 and P12 plants have a higher intensity of fluorescence, suggesting that there are higher levels of infection.

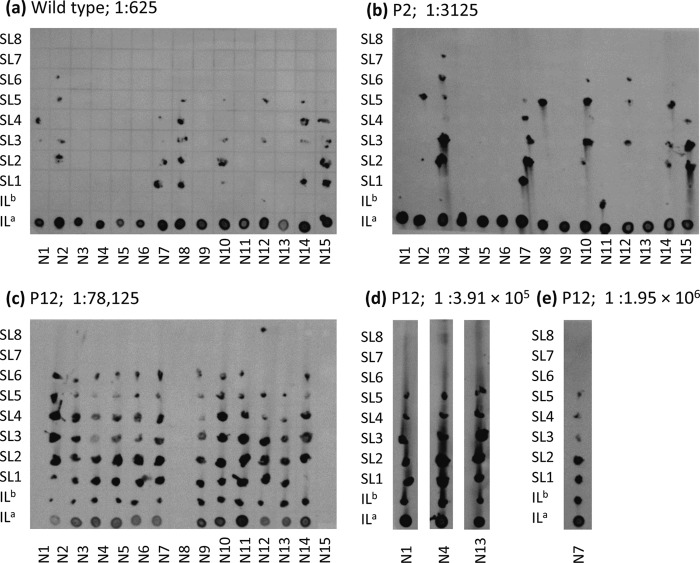
Whether there was evidence of qualitative differences in systemic AMV infection in the three different plant types used was also considered. There appeared to be fewer systemically infected leaves in systemically infected P2 and wild-type plants than in P12 plants (Fig. 5). To test if this effect was significant, the data from systemically infected plants at all doses were pooled and then a χ² test for trend in proportions was performed. A highly significant effect of the plant type was found (χ² = 13.476, 1 df, P < 0.001) overall. Pairwise comparisons showed that there were no significant differences between wild-type and P2 plants (P = 0.377), whereas there were significantly more infected leaves of P12 plants than of wild-type or P2 plants (P < 0.001 for both comparisons).

Fig 5.

Effects of plant type on systemic infection. All leaves from inoculated tobacco plants were sampled, and tissue-printing analysis was performed. To compare the effects of the plant type on systemic infection, the lowest dose with which the majority of inoculated plants were infected was considered, even though this dose was smaller for P12 than that for P2 plants and that for P2 plants was smaller than that for wild-type plants. The blot for each plant type is shown, and the dilution is shown to the right of the plant type. N numbers below the columns indicate the plant replicates, and the designations to the left of the rows indicate the leaves. IL^a is the inoculated leaf (ground whole leaf), IL^b is the inoculated leaf stem, and SL numbers represent the stems of systemic leaves, with SL1 being the leaf above the inoculated leaf. For P12 plants, the data for even higher dilutions are also presented to show that all of the leaves remained infected at all of the doses used (d and e).

DISCUSSION

The infection kinetics of AMV, a tripartite virus, was studied in wild-type tobacco plants and transgenic plants expressing one (P2) or two (P12) AMV genome segments (15). A steep dose-response curve was found in wild-type plants, concordant with previous results for multipartite viruses (5, 12). A rigorous analysis of the data with the classic infection model, which assumes that the three types of virus particles occur at the same frequency in the inoculum, was therefore highly congruent with these historical results. For P2 plants, similar results were obtained, confirming that IAH model predictions are not supported for tripartite viruses, even when the host plant expresses one genomic segment. On the other hand, for P12 plants, the dose-response curve was shallower and IAH model predictions were supported. These observations show that the expression of two viral RNA segments in the host plant could modify the infection kinetics of a tripartite virus to those of a monopartite virus.

Analysis of the dose response with the classical infection model assumes that all three types of virus particles occur at the same frequency. However, it was found that the different particle types were not present at the same frequency. Specifically, the virus particle containing RNA3 was present at a relatively low frequency. We have not encountered a discussion of the frequencies of different particle types in the literature on multipartite viruses. Nevertheless, published primary data on AMV support the particle frequencies observed here. The ultracentrifugation patterns (i.e., Schlieren peaks) obtained for two AMV preparations show a lower peak for the middle component than for the bottom component, while the top component is almost as abundant as the bottom component (see Fig. 1 on pg. 521 of reference 29). The frequency of RNA3 is so low that the “top component” in ultracentrifugation studies probably corresponds mainly to particles encapsulating RNA4. Electrophoresis of RNA purified from AMV particles clearly shows (i) that RNA1 and RNA4 are the most abundant, (ii) that levels of RNA2 are intermediate, and (iii) that RNA3 is scarce (see Fig. 7 on page 97 of reference 3). This congruence of observed patterns suggests that the frequency of particles estimated here might be a general pattern for AMV.

The different frequencies at which different virus particle types occur have implications for the shape and position of the dose-response curve. Given the scarcity of RNA3, the dose response for wild-type plants would be predicted to be similar to that predicted by the IAH model (Fig. 1e). The empirical dose-response curve is, however, significantly steeper than IAH model predictions (Fig. 2a). Data were therefore analyzed with a general infection model, and model selection identified model 2 as the best-supported model. This model incorporates the empirically measured frequencies of particle types and allows each particle type to have its own probability of invasion and systemic infection. Parameter estimates for model 2 suggest that the probability of invasion is more than 2 orders of magnitude higher for AMV particles encapsidating RNA3, whereas probabilities of invasion are more or less similar for the other two particle types (Table 2). Note that this result does not depend solely on analysis of infection in P2 and P12 plants alone; it also follows logically from observing both a steep dose-response curve in wild-type plants and different frequencies of the different particle types. Moreover, what makes this modeling result compelling is that the probabilities of invasion and systemic infection for different particle types also account for the positions of the dose-response curves of the different plant types. Figure 1 shows that the shape and position of the dose-response curve are both dependent on the invasion probability, and these results show that model 2 can also account for both. It would not have been surprising if the expression of genome segments by the host plant had affected the probability of invasion of another viral segment, but the model selection results suggest that no such effect occurs (i.e., model 2 has more support than model 5). Therefore, from the perspective of the theoretical framework developed here, the experimental system used (i.e., transgenic plants expressing viral RNA segments) responds exactly as expected. This rigorous and complete analysis therefore confirms results from the preliminary analysis with the classical model. However, it also shows that, in reality, infection kinetics are more complicated, as the inclusion of differences in particle frequencies illustrates that there are differences in the invasion probabilities of different particle types.

What mechanisms might account for these differences in invasion probability? Effective “invasion” of cells in the inoculated leaf may require fewer molecules of RNA3 than molecules of RNA1 and RNA2. We are not hereby suggesting a threshold, as such a model would behave differently than the infection models presented here. Rather, the invasion process can be seen as two steps, (i) physically breaching the cell and then (ii) being capable of supporting the infection process. In this framework, particles of each type have an independent probability of being successful at either step. This suggests two mechanistic explanations of the model. First, RNA3 is the shortest genome segment, and as a consequence, particles encapsidating RNA3 may be considerably more stable than those containing RNA1 and RNA2, or they may enter cells in the inoculated leaf more easily. In both cases, the probability of breaching a cell would be higher. Second, it may be that the probability that an RNA3 molecule that has breached the cell can support replication is higher than that RNA1 or RNA2 can do so. In this case, RNA1 and RNA2 might be degraded more quickly intracellularly. The fact that RNA1 and RNA2 contain all of the genes required for replication (15) suggests that these segments must prime the cell for replication but that once a cell is primed, the probability that an RNA3 molecule can successfully start a productive infection is considerably higher. One might therefore expect qualitative differences between the infection dynamics of different host plants. Indeed, primary infection foci expanded more rapidly in P2 and P12 plants, whereas systemic movement appeared to be enhanced only in P12 plants. These observations again suggest that little RNA3 is required during infection.

Key questions that remain are why multipartite genomes have evolved and what adaptive advantages multipartition confers. Four possible adaptive advantages conferred by genome segmentation alone—as opposed to multipartition—have been suggested. These advantages of segmentation alone may be relevant to this discussion because multipartition itself might be a pleiotropic effect of segmentation. I.e., given that most plant viruses are nonenveloped, segmentation of the genome might inevitably lead to the formation of multiple virus particles. First, at the usually high genomic mutation rate of RNA viruses (30), a small segment would have a greater chance of being replicated without errors than a larger one (31). Second, reassortment could allow rapid recombination, reducing the effects of clonal interference between beneficial mutations occurring on different genome segments while also bolstering purifying selection against deleterious mutations (32), although in one case, reassortment appears to be scarce in the field for a multipartite virus (33). Third, segmentation could allow regulation of expression, because each segment can have its own regulatory sequence, a hypothesis that has good experimental support (34). Fourth, segmentation can, in principle, allow faster replication of the viral genome through the accommodation of additional transcriptional units (35). In addition to the advantages conferred by genome segmentation alone, dividing the genome over multiple virus particles could confer the following three advantages. First, recent work suggests that the stability of particles will be improved by having shorter genome segments and smaller particles with a lower packaging density (36, 37), lending credence to the view that encapsidation imposes limits on the size of genome fragments. Second, it has been suggested that vectors may transmit smaller particles more efficiently (38), although this hypothesis has, to our knowledge, not been tested. Nonetheless, an increased chance of complementation would, theoretically, favor the evolution of a multipartite genome (39). Third, recent work suggests that the frequencies of different genome segments evolve to distinct levels, suggesting that virus particle frequencies might have a regulatory role in gene expression (40).

On the other hand, irrespective of the advantages it might confer, the packaging of different genome segments in multiple types of particles will also have a cost. This cost arises because infection requires the entry of all genome segments into the same cell during primary and systemic infections of the plant. If the total number of genomes that enter a cell during both processes is not large and if there are no mechanisms that physically link the different particle types during transmission between hosts and between cells, there will be an appreciable probability that not all types of genome segments will be represented. Assuming the same probability of cellular infection per genome segment of the complete (monopartite virus) or partial (multipartite virus) genome, the same number of encapsidated copies of the complete virus genome will, in principle, lead to lower levels of host infection with a multipartite virus than with a monopartite virus (39). The results presented here, however, strongly suggest that the infection probabilities of the different virus particles can be highly divergent. We speculate on a further reason why multipartite viruses have evolved and a mechanism that mitigates the cost of multipartition. If the probability that RNA3 can support infection (i.e., invade a cell) is higher than that for RNA1 and RNA2, then the virus could efficiently infect even if there are fewer copies of this segment present. Evolution could then favor the downregulation of RNA3 sequences by means of multipartition. Downregulation of RNA3 would then allow reallocation of cell resources to produce more particles encapsidating RNA1 and RNA2, the limiting factors at the start of infection. This higher production could then, in principle, boost overall levels of infection and therefore be adaptive. More evidence is needed to show that this hypothesis has merit, although it is compatible with other hypotheses of why multipartite viruses have evolved.