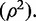Calculating statistical power in Mendelian randomization studies

Abstract

In Mendelian randomization (MR) studies, where genetic variants are used as proxy measures for an exposure trait of interest, obtaining adequate statistical power is frequently a concern due to the small amount of variation in a phenotypic trait that is typically explained by genetic variants. A range of power estimates based on simulations and specific parameters for two-stage least squares (2SLS) MR analyses based on continuous variables has previously been published. However there are presently no specific equations or software tools one can implement for calculating power of a given MR study. Using asymptotic theory, we show that in the case of continuous variables and a single instrument, for example a single-nucleotide polymorphism (SNP) or multiple SNP predictor, statistical power for a fixed sample size is a function of two parameters: the proportion of variation in the exposure variable explained by the genetic predictor and the true causal association between the exposure and outcome variable. We demonstrate that power for 2SLS MR can be derived using the non-centrality parameter (NCP) of the statistical test that is employed to test whether the 2SLS regression coefficient is zero. We show that the previously published power estimates from simulations can be represented theoretically using this NCP-based approach, with similar estimates observed when the simulation-based estimates are compared with our NCP-based approach. General equations for calculating statistical power for 2SLS MR using the NCP are provided in this note, and we implement the calculations in a web-based application.

Introduction

Mendelian randomization (MR) is the utilization of genetic variants as instrumental variables (IVs) to estimate causal effects of modifiable phenotypes of interest on disease-related outcomes.¹ Because of the very small amount of variation in phenotype that is predicted by most genetic variants, statistical power is considered to be one of the main challenges for MR,² with large sample sizes normally required.³ Ideally, as with all studies, power calculations should be performed before MR is carried out. In a previous paper published in this journal, Pierce and colleagues³ presented a range of specific power estimates for a given set of parameters in two-stage least squares (2SLS) MR analyses based on simulated data. However there are presently no specific equations for calculating power that researchers can apply to their particular MR study.

Typically in 2SLS MR, investigators simply evaluate the F-statistic and the R² from the first-stage regression of the exposure phenotype on the genetic variant. The F-statistic from this regression reflects the ‘strength’ of the genetic IV,⁴ and is an indicator of the extent (size and probability) of the relative bias that is likely to occur in estimating a causal association using the IV.⁵ The R² from this first-stage regression (i.e. the proportion of variability in the exposure phenotype that is explained by the genetic variant) is a strong determinant of statistical power to detect a causal effect.³ When using a genetic instrument, there is generally good prior knowledge of the variance in an exposure variable explained by genetic markers, and therefore the strength of the IV and power can be determined before commencing the study.

In this note, we show that the previous power estimates based on simulations by Pierce and colleagues³ for 2SLS MR using continuous variables can be derived using the asymptotic mean and variance of the IV estimator. We provide general equations for statistical power of 2SLS MR using continuous variables that researchers can apply to calculate statistical power and we have created an online web tool that performs the calculations.

Theory

We calculate statistical power to detect a putative causal relationship from an instrumental variable analysis using asymptotic theory. We use the simple example of a single-regressor single-instrument model for quantitative traits. We start by expressing power as a function of the non-centrality parameter (NCP) of the test statistic that is used to test whether the 2SLS IV regression coefficient is zero. NCP is a function of the asymptotic mean and variance of the IV estimator. Throughout we assume that the experimental sample size (n) is large enough so that the test statistic to test the IV regression coefficient is distributed as a standard normal under the null hypothesis and its square as a central χ² distribution with 1 degree of freedom. We assume that we have a valid instrument but that there may be confounding between the outcome and exposure variable.

Power is calculated as:

(1)

where β is the type-II error rate, 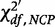is a random variable from a non-central χ² distribution with df degrees of freedom (df = 1 in our case) and 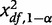is the threshold of a central χ² distribution for a type-I error rate of α.

The general form of the NCP is

(2)

Where b_2SLS is the (unknown) true parameter value of the 2SLS IV estimator. To calculate power for a potential MR, the NCP may be derived using a number of different parameterizations (see the Supplementary Appendix, available as Supplementary data at IJE online). One such expression (Equation A8) that may be used to estimate power is

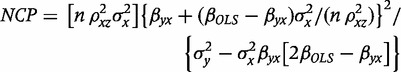(3)

with β_yx the causal effect of X on Y (i.e. the parameter of interest) and β_OLS the asymptotic value of the ordinary least squares (OLS) estimator of the effect of X and Y. In the presence of XY confounding, these two population parameters are not the same; n is the experimental sample size, 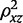the population value for the proportion of variance in the exposure variable explained by the genetic predictor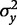, and and 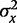the variances of Y and X, respectively.

In the absence of XY confounding (i.e. β_OLS=β_yx), the main determinants of the NCP and therefore of statistical power are the sample size and the proportion of variance in the exposure variable explained by the genetic instrument. At present and for most MR applications, it is the correlation between the single-nucleotide polymorphism (SNP) or allele score and the relevant exposure variable that appears most limiting, and this will need to be compensated for by large sample size. This is because single or multi-SNP predictors for common complex traits typically explain a small proportion of the variance in the exposure variable of interest (i.e. <10% for many traits and diseases, even when all genome-wide significant SNPs are considered together).⁶

Comparison with published simulations

We compared our approach for calculating power based on the NCP with the power estimates based on simulated data for MR studies using one genetic variant by Pierce et al. (‘Data simulation 1’ in their paper).³ The authors generated power estimates using 10 000 simulated data sets containing one or more biallelic loci (Z, in our terminology) in Hardy–Weinberg equilibrium, a continuous exposure (X) affected by Z and a continuous outcome (Y) affected positively by X. Each power estimate was obtained by applying 2SLS to all 10 000 simulated data sets and determining the percentage of data sets in which a positive effect of the fitted X on Y was observed using a two-sided significance test (α=0.05). Pierce et al.³ express the association between X and Y as a regression coefficient β_XY, for two scenarios: with XY confounding and no XY confounding (modelled as a correlation of the residuals of X and Y). They used a two-sided significance test but demanded the estimate of the regression coefficient to be positive, thus essentially applying a one-sided test with a type-I error rate of 0.025. In the Supplementary Appendix (available as Supplementary data at IJE online) we provide the parameters used in Pierce et al. for situations both with and without XY confounding and show how they can be transformed to parameters used in Equation (3).

Using our analytical framework, we calculated the NCP and statistical power for each simulated β_xy presented by Pierce et al. and compare the results in Tables 1 and 2. As can be seen, the power estimates generated using our NCP-based approach are very similar to those obtained by their simulations, across varying sample sizes, ρ² values and beta-coefficients, and in the absence or presence of XY confounding. The values from the analytical approach are slightly larger than those from simulations, which may be due to our use of the asymptotic sampling variance of the IV estimator.⁸ However, the differences in power are very small (the mean difference between the power calculated from theory and from simulation is 0.011, average for Tables 1 and 2) and not of practical importance.

Table 1.

Power estimates using alternative z-normal distribution for NCP-based calculations and simulation-based estimates; no XY confounding

Estimations of power
		Simulation-based estimatesa				Theoretical
		Power				power
		β yx				β yx
Sample Size	R2 b	0.0	0.1	0.3	0.5	0.0	0.1	0.3	0.5
n = 500
	0.005	0.00	0.00	0.03	0.09	0.025	0.04	0.07	0.12
	0.01	0.00	0.01	0.06	0.18	0.025	0.04	0.10	0.20
	0.05	0.01	0.07	0.35	0.70	0.025	0.07	0.34	0.73
	0.10	0.02	0.11	0.60	0.94	0.025	0.11	0.61	0.96
n = 1000
	0.005	0.00	0.01	0.06	0.18	0.025	0.04	0.10	0.20
	0.01	0.01	0.03	0.14	0.35	0.025	0.05	0.16	0.36
	0.05	0.02	0.11	0.58	0.92	0.025	0.11	0.59	0.95
	0.10	0.02	0.18	0.87	1.00	0.025	0.18	0.89	1.00
n = 5000
	0.005	0.02	0.07	0.32	0.68	0.025	0.07	0.32	0.71
	0.01	0.02	0.10	0.58	0.92	0.025	0.11	0.57	0.94
	0.05	0.02	0.36	1.00	1.00	0.025	0.37	1.00	1.00
	0.10	0.03	0.65	1.00	1.00	0.025	0.65	1.00	1.00
n = 10 000
	0.005	0.02	0.10	0.56	0.92	0.025	0.11	0.57	0.94
	0.01	0.02	0.17	0.84	1.00	0.025	0.17	0.85	1.00
	0.05	0.02	0.63	1.00	1.00	0.025	0.63	1.00	1.00
	0.10	0.03	0.92	1.00	1.00	0.025	0.92	1.00	1.00

^aPierce et al. (2011)³ simulations for no XY confounding (n. = 10 000 simulations), based on a single instrument.

^bAsymptotic R² [also interpreted as the adjusted R² for the regression of the exposure (X) on the genetic variant (Z)], which in our terminology is the population value .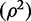

Table 2.

Power estimates using alternative z-normal distribution for NCP-based calculations and simulation-based estimates; with XY confounding

Estimations of Power
		Simulation-based estimatesa				Theoretical
		power				power
		β xy				β xy
Sample Size	R2 b	0.0	0.1	0.3	0.5	0.0	0.1	0.3	0.5
n = 500
	0.005	0.01	0.02	0.06	0.14	0.03	0.05	0.09	0.16
	0.01	0.01	0.03	0.11	0.23	0.03	0.05	0.12	0.23
	0.05	0.03	0.08	0.35	0.68	0.03	0.08	0.36	0.74
	0.10	0.03	0.12	0.59	0.92	0.03	0.12	0.62	0.96
n = 1000
	0.005	0.01	0.03	0.11	0.23	0.03	0.05	0.12	0.23
	0.01	0.02	0.05	0.18	0.37	0.03	0.06	0.18	0.39
	0.05	0.03	0.12	0.58	0.90	0.03	0.12	0.60	0.96
	0.10	0.03	0.19	0.86	1.00	0.03	0.19	0.90	1.00
n = 5000
	0.005	0.03	0.08	0.34	0.67	0.03	0.08	0.34	0.72
	0.01	0.03	0.12	0.57	0.90	0.03	0.11	0.58	0.94
	0.05	0.03	0.37	1.00	1.00	0.03	0.37	1.00	1.00
	0.10	0.03	0.65	1.00	1.00	0.03	0.66	1.00	1.00
n = 10 000
	0.005	0.03	0.11	0.56	0.90	0.03	0.11	0.58	0.95
	0.01	0.03	0.18	0.83	1.00	0.03	0.18	0.86	1.00
	0.05	0.03	0.62	1.00	1.00	0.03	0.64	1.00	1.00
	0.10	0.02	0.91	1.00	1.00	0.03	0.92	1.00	1.00

^aPierce et al. (2011)³ simulations for estimates with XY confounding (n = 10 000 simulations), based on a single instrument.

^bAsymptotic R² [also interpreted as the adjusted R²for the regression of the exposure (X) on the genetic variant (Z)], which in our terminology is the population value

Applying power calculations

Given the equations presented in this note, researchers may therefore compute the NCP for a planned MR study and subsequently calculate statistical power (i.e. using Equations 1 and 3 or the alternative expressions given in the Supplementary Appendix. Researchers will either know the sample size of their experiment or wish to calculate what sample size should be for a given probability of detection (power). Researchers will typically know before the experiment how much of the variation in the exposure variable is explained by SNPs because the genetic predictor is likely to come from prior information, for example large meta-analyses of genome-wide association studies. Researchers are also likely to have prior information on what effect of X on Y to expect, e.g. from a previous observational study, and the causal effect size of X and Y they want to test in the MR experiment. Therefore, one tangible outcome of performing a power calculation as presented here is not to pursue with the experiment at all because of insufficient power.

Once the NCP has been computed, calculating statistical power may be carried out in standard statistical software or using our online web tool (http://glimmer.rstudio.com/kn3in/mRnd/). Given a number of parameters specified by the user, our web tool computes the statistical power or, conversely, required sample size, for a 2SLS MR study for continuous variables. As it is often of interest to assess the causal association of X on Y based on the ZY association alone, we also include in the online web tool the option of calculating power based on the NCP for a ZY association [derivations are provided in the Supplementary Appendix (available as Supplementary data at IJE online), equations A17 and A18].

Conclusion

In summary, we have presented equations for calculating statistical power for 2SLS MR studies in the case of a single IV and continuous variables, using the non-centrality parameter (NCP). We show that NCP-based estimates were similar to previously published power estimates for 2SLS MR analyses that were generated using simulated data. We have also created a web-based tool that researchers may use to calculate statistical power for their particular MR study, using the NCP-based approach that we have described. In principle, extensions to non-continuous outcome variables or multiple IVs could also be pursued using the same asymptotic theory but these would be more complex and are outside the scope of this short note.

Supplementary Data

Supplementary data are available at IJE online.

Funding

M.J.B. was funded by the Wellcome Trust (WT085515) and the Leducq Foundation (12CDA02). P.M.V. acknowledges funding from the Australian National Health and Medical Research Council (613601 and 1048853). The research leading to this work has received funding from the EU 7th Framework Programme under grant agreement number 247642, GEoCoDE. P.M.V. will act as guarantor for the content of this manuscript.

Conflict of interest: None declared

KEY MESSAGES.

• Given the experimental sample size and population parameters that summarize variance explained in the exposure trait by the instrument and the causal and observational associations between the exposure and outcome, simple power calculations for a 2SLS MR can be generated.

• We provide general equations for calculating statistical power for 2SLS MR based on asymptotic theory and we implement the equations in a web-based application.