Accurate Prediction of the Bound Form of the Akt Pleckstrin Homology Domain using Normal Mode Analysis to Explore Structural Flexibility

Abstract

Molecular docking is often performed with rigid receptors. This can be a serious limitation, since the receptor often differs between bound and unbound forms, or between bound forms with different ligands. We recently developed a normal-mode based docking method and showed that it is possible to obtain reasonable estimates of the complexed form of the pleckstrin homology (PH) domain of Akt, starting with the free form of the receptor. With in-ositol (1,3,4,5)-tetrakisphosphate (IP4) as the ligand the docked results agree with the known high-resolution X-ray crystal structure of the IP4-Akt PH domain complex. We also tested our methods with PH4, SC66, and PIT-1, several recently designed PH domain inhibitors. The results are shown to be consistent with available experimental data and previous modeling studies. The method we described can be used for molecular docking analysis even when only an approximation of the experimental structure or model is known.

Introduction

Computational modeling plays an important role in drug discovery. One such recent example is the development of Akt pleckstrin homology (PH) domain inhibitors,^1–4 currently in preclinical trial, via virtual screening, followed by experimental evaluations.

The PH domains are membrane-targeting domains containing ~100 residues, and are found in a variety of proteins (such as spectrin, dynamin, and phospholipase C-δ1). They are structurally similar, but have a low sequence homology (< 30%).⁵ It is generally accepted that PH domains regulate cellular signaling and membrane trafficking by interacting with specific phosphoinositides on cell membranes.⁶ This serves to recruit various proteins to the membrane. In addition, there is evidence that binding of the PH domain to phospholipids modulates function via conformational changes. Examples include the PH domain associated with Dbl homology domains⁷ and the PH domain of protein kinase B/Akt.⁸

The structure of the PH domain of protein kinase B/Akt, bound to a mimic of a phospholipid headgroup, inositol-(1,3,4,5)-tetrakisphosphate (IP4), has been determined⁸ and deposited in the Protein Data Bank (PDB ID 1UNQ) along with the unbound form (PDB ID 1UNR). Comparison of the bound and unbound forms reveals a significant conformational change of the PH domain,⁸ including movement of the protein backbone (Figure 1, Figure 2). This flexibility must be taken into account in successful modeling/docking simulations.

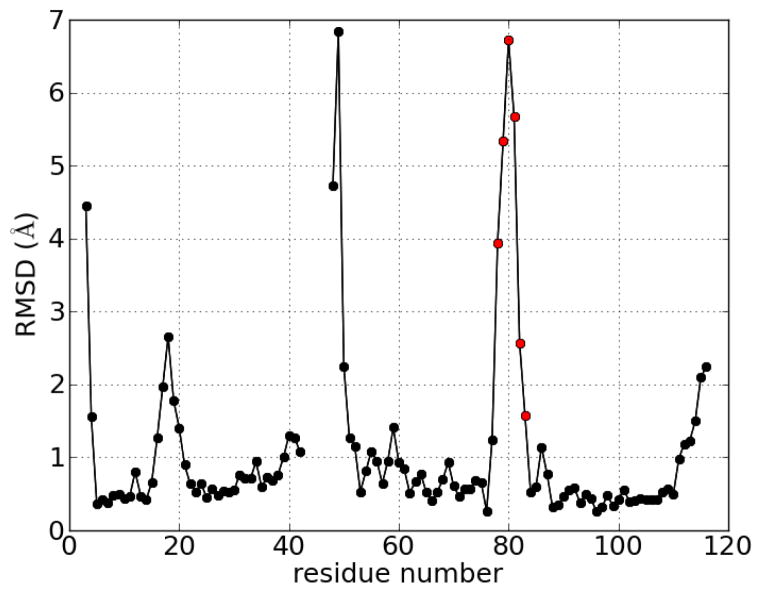
Figure 1.

RMSD deviation of C_α atoms from the unbound to the bound form of the PH domain of protein kinase B/Akt with IP4. Residues 43–47 were not located in the unbound crystal structure.⁸ Red dots denote the turn which is shaded red in Figure 2.

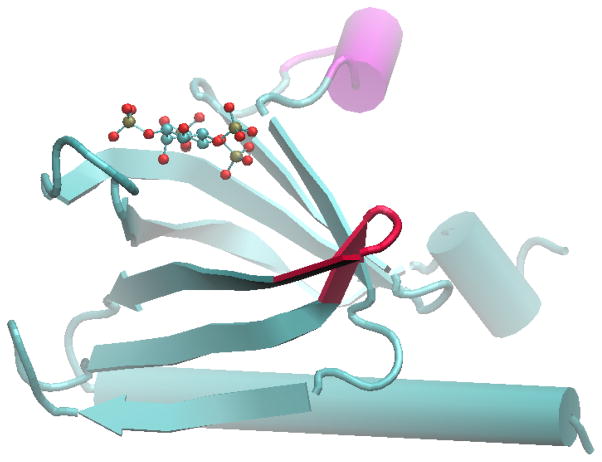
Figure 2.

Crystal structure of PH domain in complex with IP4.⁸ The red-colored turn corresponds to the red dots in Figure 1. The magenta region denotes residues which were not found in the unbound crystal structure.

Current molecular docking methods routinely handle flexible ligands, but including receptor flexibility still remains challenging. Finding the correct receptor conformation is difficult due to the large number of degrees of freedom of typical protein-sized receptors. In addition, the correct receptor conformation is likely different for different ligands. Current flexible-receptor docking methods capture this ligand-dependent effect in different ways. Broadly speaking, the effect of the ligand may be used during the selection of candidate receptor conformations, or afterwards. In the latter case, the generation of receptor conformations does not depend on the particular ligand one is interested in. This may seem a fine distinction, but it parallels two important theories of ligand-receptor interaction: the induced fit model, and the Monod-Wyman-Changeux (MWC) inspired models.

The induced fit model is the traditional model for ligand-receptor interaction, in which the presence of a ligand induces a conformational change in the receptor which causes it to be suitable for binding. Flexible-receptor docking methods emulating this mode of ligand interaction allow both the ligand and the receptor (or at least a portion of the receptor at the binding interface) to be flexible while simultaneously optimizing the mutual interaction between the ligand and receptor.

In contrast, in the MWC model, originally proposed as a theory of allosteric action,^9,10 the binding conformation is already adopted by the receptor even in the absence of the ligand, but this conformation is in constant equilibrium with an ensemble of other structures, and may be only transiently sampled. The action of the ligand is to select this preexisting conformation, and bind to it.

Despite being used as early as 1968¹¹ to explain certain biochemical experiments on aspartate transcarbamylase, the MWC model has only recently been generally accepted. The main evidence which initiated this change in perspective was the discovery of a wide range of receptors which retain constitutive activity even in the absence of their ligands/substrates.^12–14 The binding of ligand results in full activation, but is not required for a basal level of activity. Moreover, many oncogenic mutations in GPCR’s have been found to change the level of constitutive activity.¹⁴ The particular type of receptor flexibility relevant for ligand binding often involves global, concerted motions of large segments of proteins.^15–17

In previous modeling studies^1,4 a known crystal structure of the receptor (Akt PH domain) in complexed form was used to develop inhibitors of the PH domain. However, accurate experimental structures of complexes (or even of the unbound form) are not always available, and may be unreliable for binding predictions with different ligands. We will develop a method for sampling these global modes of receptor flexibility for use in docking. We describe a docking procedure which is able to use a known free, unbound form of the receptor to predict the bound form. This can be further generalized to employ any model or near-native structure for lead identification and optimization processes.

Incorporating flexibility into molecular docking

Prior strategies used to incorporate structural flexibility into molecular docking include the implementation of sidechain flexibility,¹⁸ or the use of an ensemble of receptor conformations.^19–23 In the ensemble method a finite set of structures representing the possible receptor conformations is generated. The ligand is then docked onto each member of the ensemble. There are various methods for generating receptor conformations.

Molecular dynamics as a method to pre-generate structures

Molecular dynamics (MD) simulations model the motions of proteins over time, and so initially appear to be an attractive means of incorporating flexibility into the docking process. MD simulations represent the atomic structure of molecules, and propagate their positions using Newton’s equations of motion and an empirically determined “force field” which represents different types of atomic interactions. One example is the use of MD by McCammon and coworkers, who have shown that incorporating a short molecular dynamics refinement step into an iterative docking method gives improved results and can find alternative docking poses which otherwise would be missed.¹⁹ MD has also been used to generate ensembles of RNA structures for docking.²³ However, MD simulations can be computationally expensive, especially if large numbers of diverse conformations are desired. The amount of computational time required for MD simulations limits its usefulness to short time scales and small motions, or for in-depth analysis of a small number of systems.

Sampling of global motions using normal mode analysis

There has recently been a large increase of interest in studying the collective motion of biomolecules using methods based on principal component analysis (PCA),²⁴ such as normal mode analysis (NMA) or essential dynamics. These methods are particularly useful in analyzing the low frequency modes of motion. These are the modes which encode long wavelength, cooperative global motions involving the entire protein. From a computational perspective, PCA-based methods are complementary to traditional molecular dynamics (MD)-based methods. Normal mode analysis approximates the global motions of proteins. This approximation allows the method to be computationally inexpensive.

In normal mode analysis^25–27 the global motion of a protein around equilibrium is treated with a harmonic approximation. Displacements of a protein’s configuration around its equilibrium conformation are decomposed into a set of normal modes, or basis vectors, each with 3N degrees of freedom.^28,29 Any conformation of the protein can be expressed in terms of a linear combination of normal modes. The low frequency modes represent large global movements, and the high frequency modes represent local fluctuations. Since normal mode analysis assumes a single equilibrium conformation, it should not apply to proteins which have multiple stable states. However, it has been found in practice that using a small number of the lowest normal modes is surprisingly successful at representing various types of protein motions^30–33 and the use of a small number of selected normal modes can give accurate docking results.³⁴ Alternatively, instead of selecting low-frequency normal modes, Mashiach and coworkers select relevant normal modes by comparing the normal mode displacements to the chemical forces (e.g. van der Waals forces) on each atom.³⁵ Use of these selected normal modes for backbone refinement leads to significantly improved docking scores, as compared with rigid-backbone docking.³⁵

Normal mode analysis has been successfully used to determine the difference between the bound and unbound conformations of several systems for which crystal structures are available,³⁶ to perform protein-protein docking,³² and to refine docked structures.³³ We will use normal mode analysis to generate an ensemble of conformations of the Akt PH domain representing the possible conformational fluctuations of its backbone. Sidechain flexibility will be incorporated by using flexible-sidechain docking.

Methods

Preparation of coordinate files

The unbound (apo) form of the protein kinase B/Akt PH domain contains a disordered loop which is not present in the crystal structure (PDB ID 1UNR). These missing residues (Q43-Q47) were built using loop modeling as implemented in the Modeller package.³⁷ Alterations in this area should not affect docking results, since the loop is relatively short (5 residues), and located away from the binding region. Therefore, we have selected the top model output by Modeller for use. Several N-terminal or C-terminal residues were missing or incomplete in either the apo form (PDB ID 1UNR) or holo form (PDB ID 1UNQ), and these residues were disregarded in our analysis, leaving us with 114 residues.

Elastic network model of protein structure

Given the current level of computational power, modeling domain flexibility and other large scale collective motions efficiently requires the use of simplified models. One such model is the elastic network model (ENM), first proposed by Tirion.³⁸ In ENM’s, each residue is replaced by a single particle located at its C_α atom, and the interactions between residues are represented by elastic springs. The topology and equilibrium structure are defined to correspond to the native state, usually obtained from a crystal structure. Thus ENM’s are models of fluctuations about the native state, and so are similar to Go-like models.^39,40

Given a set of native C_α coordinates, the ENM applies a harmonic potential with force constant k between all C_α atom pairs whose separation is within a certain cutoff distance r_c. The energy is then

$$U_{\mathit{ENM}}=\frac{1}{2}k\sum _{r_{ij}^0<r_c}{(\mid {\mathbf{r}}_i-{\mathbf{r}}_j\mid -r_{ij}^0)}^2$$ (1)

where r_i and r_j are the positions of the C_α atoms and $r_{ij}^0$ is the distance between i and j in the native structure. In our work, we will use r_c = 8 Angstroms.

The low frequency modes of ENM’s have been found to be a good approximation to global motions in proteins.⁴¹ That such a simplified model can describe protein dynamics may be surprising, since knowledge of the amino acid sequence (the sidechains) is not explicitly included. However, the effects of the sidechains are implicitly included since the sidechains determine the equilibrium structure of the protein, and it is the equilibrium structure which is used as input for the ENM.

Generation of normal mode structures

Starting from the crystal structure of the PH domain of protein kinase B⁸ (PDB ID 1UNR), missing residues were rebuilt using Modeller.³⁷ Then, an elastic network model of the protein³⁸ was built using the C_α coordinates of the protein, as described previously.

Computation of normal modes requires the construction of a matrix of second derivatives of the energy, the hessian, which was computed analytically⁴² and diagonalized to determine the normal modes and their associated frequencies. The routines for this computation were written using the NumPy library.⁴³ Conformations were generated by displacing the crystal structure conformation using each of the 20 normal modes with the lowest frequencies, such that the maximum C_α displacements were 1, 2, 3, 4, or 5 Angstroms. The displacements can be positive or negative, resulting in 10 conformations for each normal mode. To generate all-atom structures from the C_α-only normal modes, all atoms within a residue were initially displaced by the same amount which the C_α of that residue was displaced. This results in some distortion the structure, so a short minimization was done using the GROMACS software,⁴⁴ with 2000 steps of the steepest descent method. The resulting ensemble of structures was used for subsequent docking with Autodock 4.¹⁸

The procedure described above was repeated to generate normal mode structures starting with the known form of the PH domain complexed with IP4 (PDB ID 1UNQ).⁸

Molecular docking with Autodock

Autdock 4¹⁸ was used to perform molecular docking for several ligands (Figure 3). The lig-and (IP4) is highly charged, and it can be expected that its binding will strongly perturb charged residues in the binding pocket. The current version of Autodock allows limited sidechain flexibility during docking, and we set select charged residues in the binding pocket which appear to shift during binding¹⁸ to be flexible. The residues selected are: Lys14, Glu17, Arg23, Arg25, and Arg86. This procedure has the disadvantage of requiring knowledge of the binding site beforehand, but the particular method for docking of individual conformations does not affect our overall procedure. Any other docking program may be substituted, depending on individual preferences or requirements. During the development of our implementation, we also used GOLD⁴⁷ for evaluation, and similar results were observed as for Autodock.

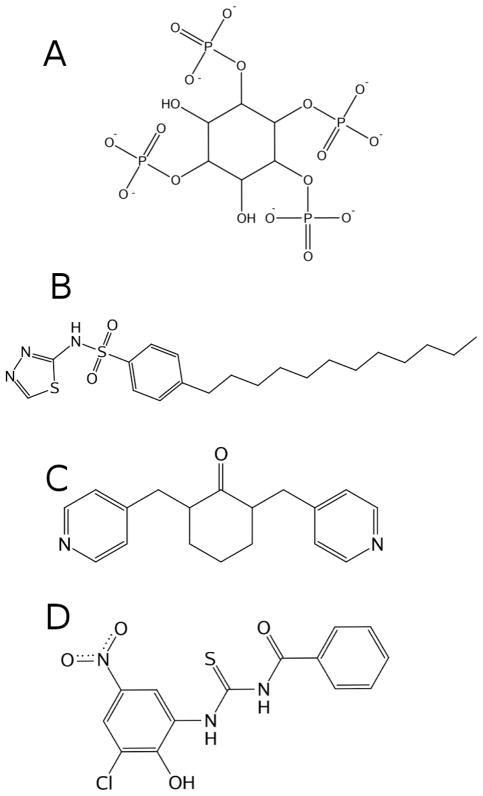
Figure 3.

Ligands used in docking. A: structure of inositol (1,3,4,5)-tetrakisphosphate. B: structure of PH4, a novel PH domain inhibitor designed by Du-Cuny et al.¹ C and D: small molecules targeting the PH domain, SC66⁴⁵ (C) and PIT-1⁴⁶ (D). Non-polar hydrogens are omitted for clarity.

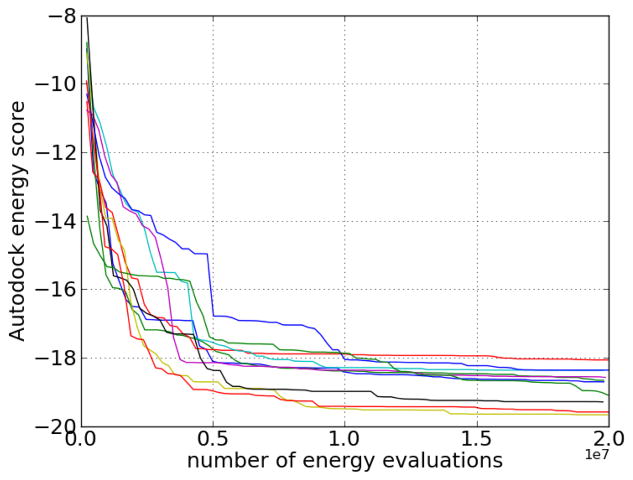
The binding site was defined to be centered at the centroid of the location of IP4 from the crystal structure of the PH domain/IP4 complex. For a cubic box with length 30 Angstroms at this location, Autodock grids were generated using the default grid spacing (0.375 Angstroms). Since the total number of torsions is large (IP4 was assigned 10 torsions, and the number of torsions for the flexible side chains of Lys14, Glu17, Arg23, Arg25, and Arg86 were 5, 3, 4, 4, and 4, respectively), several long test runs were performed to determine an appropriate number of energy evaluations during docking. The AutoDock energy convergence data is shown in Figure 4. Most of the decrease in energy occurs within 1.0 × 10⁷ evaluations, so the number of energy evaluations per run was chosen to be 1.5 × 10⁷, as a balance between speed and convergence. Since different runs may converge to slightly different energies, 50 runs per receptor structure were performed.

Figure 4.

Lowest Autodock energy score found as a function of the number of energy evaluations for 10 flexible docking runs for the binding of IP4 to the PH domain of Akt. (Energy scores are before conversion to binding free energies.)

Results

Milburn et al. have determined the structures of the unbound (apo) and bound (holo, with IP4) forms of the PH domain of protein kinase B/Akt,⁸ and have discovered significant changes upon ligand binding. There are significant changes in the sidechains in the binding site, but there also changes in the backbone structure as well, as revealed by measuring the RMSD difference between the receptor structures (Figure 1, Figure 2). Since this suggests that both “local” (sidechain) and “global” (backbone) conformational changes are important to binding, both should be accounted for during molecular docking.

Normal mode calculation

A total of 342 normal modes and their frequencies were calculated for both apo and holo forms of the PH domain. There are 6 normal modes with zero frequency corresponding to rigid body translations and rotations which were excluded from our analysis. It is useful to analyze the displacements of backbone C_α from the apo to the holo form in terms of the normal modes. Consider the normal modes generated using the apo structure as the starting point. Each normal mode Δr_nm,i is a vector representing the simultaneous displacements of all C_α atoms. Similarly, let Δr_apo→holo represent the C_α displacements from the apo to the holo crystal structures. Then, since the normal modes form a complete set, we can write:

$$\mathrm{\Delta }{\mathbf{r}}_{\mathit{apo}\to \mathit{holo}}=\sum _{i=1}^{N_{nm}}{A}_{nm,i}\mathrm{\Delta }{\mathbf{r}}_{nm,i}$$ (2)

The coefficients A_nm,i can be calculated as follows:

$$\mathrm{\Delta }{\mathbf{r}}_{\mathit{apo}\to \mathit{holo}}=\sum _{i=1}^{N_{nm}}(\mathrm{\Delta }{\mathbf{r}}_{nm,i}·\mathrm{\Delta }{\mathbf{r}}_{\mathit{apo}\to \mathit{holo}})\mathrm{\Delta }{\mathbf{r}}_{nm,i}$$ (3)

where N_nm is the total number of normal modes. To see that this is the case, note that the normal modes Δr_nm,i are the eigenvectors resulting from the diagonalization of H, the Hessian matrix, which contains the second derivatives of the potential energy,^38,48 the elements of which are:

$$\begin{array}{l}{H}_{ij}=\frac{{\partial }^{2}U}{\partial x_i\partial x_j}\\ =\frac{{\partial }^{2}U}{\partial x_j\partial x_i}\\ =H_{ji}\end{array}$$ (4)

where U is the potential energy, and x_i are Cartesian coordinates. Due to the symmetry of H, its eigenvectors (the normal modes) are orthogonal.⁴⁹ Also, we have chosen to normalize the eigenvectors to be of unit length. Thus, the normal modes are orthonormal:

$$\mathrm{\Delta }{\mathbf{r}}_{nm,i}·\mathrm{\Delta }{\mathbf{r}}_{nm,j}={\delta }_{ij}$$ (5)

We can use this to calculate the coefficients A_nm,i in (2) using the following relations:

$$\begin{array}{l}\sum _{i=1}^{N_{nm}}(\mathrm{\Delta }{\mathbf{r}}_{nm,i}·\mathrm{\Delta }{\mathbf{r}}_{\mathit{apo}\to \mathit{holo}})\mathrm{\Delta }{\mathbf{r}}_{nm,i}=\sum _{i=1}^{N_{nm}}\left(\mathrm{\Delta }{\mathbf{r}}_{nm,i}·\left(\sum _{i=1}^{N_{nm}}{A}_{nm,j}\mathrm{\Delta }{\mathbf{r}}_{nm,j}\right)\right)\mathrm{\Delta }{\mathbf{r}}_{nm,i}\\ =\sum _{i=1}^{N_{nm}}(A_{nm,i})\mathrm{\Delta }{\mathbf{r}}_{nm,i}\\ =\mathrm{\Delta }{\mathbf{r}}_{\mathit{apo}\to \mathit{holo}}\end{array}$$ (6)

where (5) was used on the second line, leading to a formula for the coefficeints:

$$A_{nm,i}=\mathrm{\Delta }{\mathbf{r}}_{nm,i}·\mathrm{\Delta }{\mathbf{r}}_{\mathit{apo}\to \mathit{holo}}$$ (7)

Surprisingly, it has often been found that a small number of the lowest frequency normal modes provides a good approximation to backbone movements.^30,31 Turning to the PH domain system, suppose we order the normal modes according to frequency, with normal mode i = 1 having the lowest frequency. Then, taking the M lowest normal modes, we can approximate Δr_apo→holo by truncating the sum in (6):

$$\mathrm{\Delta }{\mathbf{r}}_{\mathit{apo}\to \mathit{holo},\mathit{approx}(M)}=\sum _{i=1}^{M<N_{nm}}(\mathrm{\Delta }{\mathbf{r}}_{nm,i}·\mathrm{\Delta }{\mathbf{r}}_{\mathit{apo}\to \mathit{holo}})\mathrm{\Delta }{\mathbf{r}}_{nm,i}$$ (8)

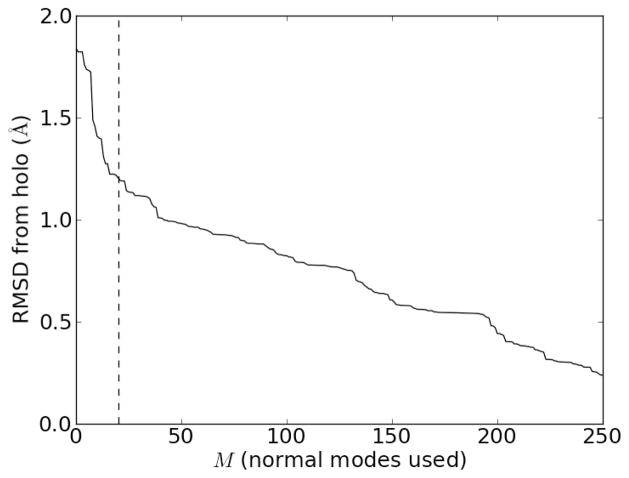
We can quantify the error of using only M normal modes, which we call Error(M) by examining the RMSD difference between Δr_{apo→holo,approx(M)} and Δr_apo→holo. Note that M = 0 represents the original (apo) form, so Error(M = 0) is just the RMSD between the apo and holo form. Figure 5 shows that as the number of normal modes used in the approximation, M, increases, the RMSD error decreases. The sharpest reduction in error occurs for small M (low frequencies), and the reduction in RMSD obtained by adding additional normal modes beyond approximately the first 20 or so becomes diminished.

Figure 5.

Error of using only the M lowest frequency normal modes of the apo form of the PH domain to calculate the holo form, using the approximation in (8). The dashed vertical line is drawn at M = 20 normal modes.

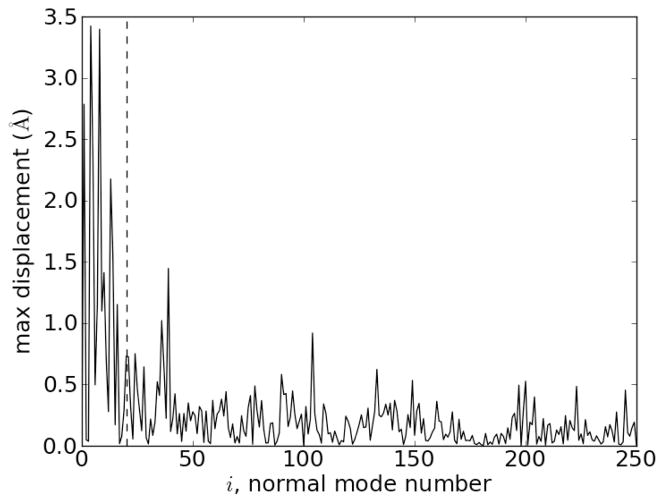
Another way to see this is to look at the contribution of each normal mode to the displacement from the apo to the holo form. This is shown in Figure 6, which shows the maximum C_α displacement induced by each normal mode i in the sum in (2). We see that the largest displacements are from the low frequency normal modes.

Figure 6.

Maximum C_α displacement induced by each normal mode i in the decomposition in (2). The dashed vertical line is drawn at M = 20. The normal modes are ordered with the lowest frequencies first (M = 1 has the lowest frequency).

Generation of receptor structures using normal modes

We choose to use the 20 lowest frequency normal modes to generate receptor (PH domain) conformations for docking. For each normal mode, the magnitude of the displacements was chosen such that the maximum C_α displacement was 1, 2, 3, 4, or 5 Angstroms. This covers a typical range of displacements, similar to that seen in Figure 6. The displacements can be positive or negative, and this gives us 200 normal mode receptor structures for both the apo and holo form of the PH domain. These were used for subsequent docking.

Docking results: using normal mode ensembles improves docked energies

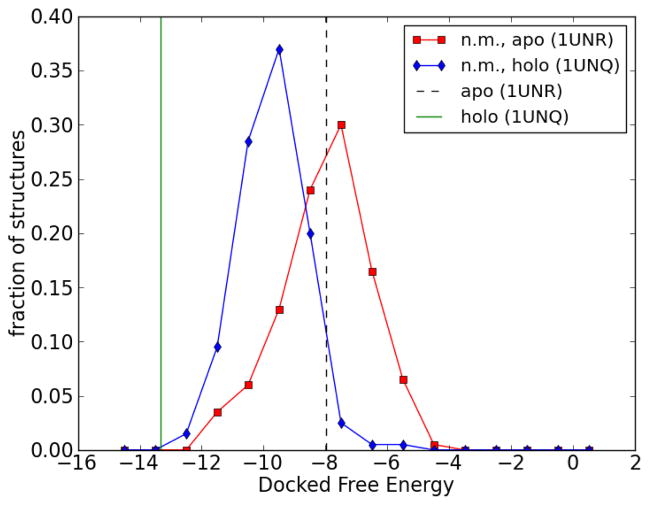
Autdock 4 was used to dock IP4 with each structure in the apo and holo normal mode ensembles. The histograms of binding (docked) free energies for each ensemble are shown in Figure 7. For reference, the original (from crystal structure) apo and holo PH domain structures were also docked with IP4 (using the same docking protocol used for each structure from the normal mode ensembles), and these binding energies are also shown in Figure 7. The binding energy of a receptor to a certain ligand can be thought of as an indicator of their mutual compatibility. However, this depends on the reliability of the receptor structure used. In many cases, no structure or only the unbound (apo) form of the receptor is known, which can lead to inaccurate docking results.

Figure 7.

Histogram of docked binding energies for the binding of IP4 to normal mode structures generated from the apo (squares) and holo (diamonds) forms of PH domain. (The fraction is normalized so the area under the curve is unity.) For reference, the docked binding energies of IP4 to the original (crystal structure) apo and holo forms of the PH domain are indicated by dashed and solid vertical lines, respectively. The apo and holo forms were obtained from Protein Data Bank structures 1UNR and 1UNQ, respectively.

Figure 7 shows that many of the normal mode structures generated from the apo form have binding energies less than the binding energy of the original apo structure. This means that an ensemble of normal mode structures generated from the apo structure can create conformations which are “more compatible” with ligand binding than the original apo structure. For comparison, Figure 7 also shows the binding energies of normal mode structures generated using the holo structure. In this case, the original (holo) structure is already in a conformation suitable for binding, as seen by its favorable docked binding energy, and the docking results from the (holo) normal mode ensemble do not improve upon this binding energy.

Thus, we are able to obtain conformations which are “more suitable” for binding, using docked free energy values as an indicator of suitability. We can also examine the docked structures to determine the accuracy of the docked conformations.

Docking results: structure

Ideally, the calculated binding free energies will correlate perfectly with actual binding affinities, so that the pose with the lowest predicted binding free energy will correspond to the experimentally determined structure. However, this “rank-ordering” of compounds by activity remains elusive, since the calculation of free energies of binding involves many complex, interrelated contributions from conformational changes of ligand, receptor, and solvent, so it is no surprise that modern docking software generally cannot accurately predict binding free energies and rankings.^50,51 As a result, it is likely that the lowest energy structure predicted by docking will not be the closest to the experimentally determined structure. As such, binding free energies obtained from docking are generally used to identify a promising set of structures for further development, not for the selection of a single, best structure. Despite these caveats, it is still useful to evaluate the similarity of docked structures from our analysis to the known complex.

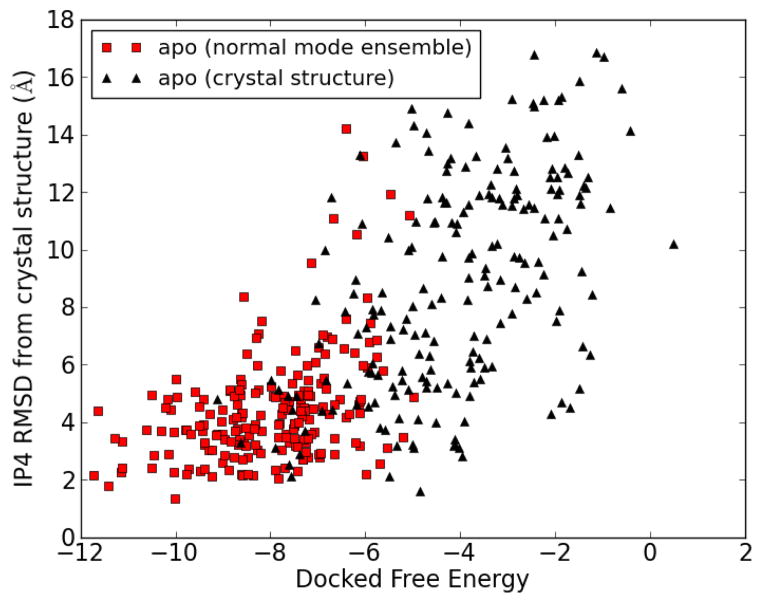
Each docked complex was fit to the crystal structure complex, by minimizing the RMSD of the receptor (PH domain) C_α atoms, after which the RMSD between the ligand (IP4) atom positions was measured to estimate the similarity of each docked complex to the crystal structure complex. Figure 8 shows a comparison of results of docking to the apo form of the PH domain, with and without normal mode analysis. The docking results from the 200-member normal mode ensemble are compared with results from 200 independent docking runs using the apo crystal structure. There is a general trend for low energy structures to have low RMSD, although the correlation is not perfect. There is a marked improvement in the overall docked free energies by using the normal mode ensemble. The lowest docked free energy found using the apo crystal structure was −9.1 kcal/mol, compared with −11.7 kcal/mol for the best result using the normal mode ensemble.

Figure 8.

Red squares: docking of IP4 onto the 200 structures of a normal mode ensemble generated from the apo crystal structure of the PH domain. Black triangles: 200 independent docking runs for the docking of IP4 to the apo crystal structure of the PH domain.

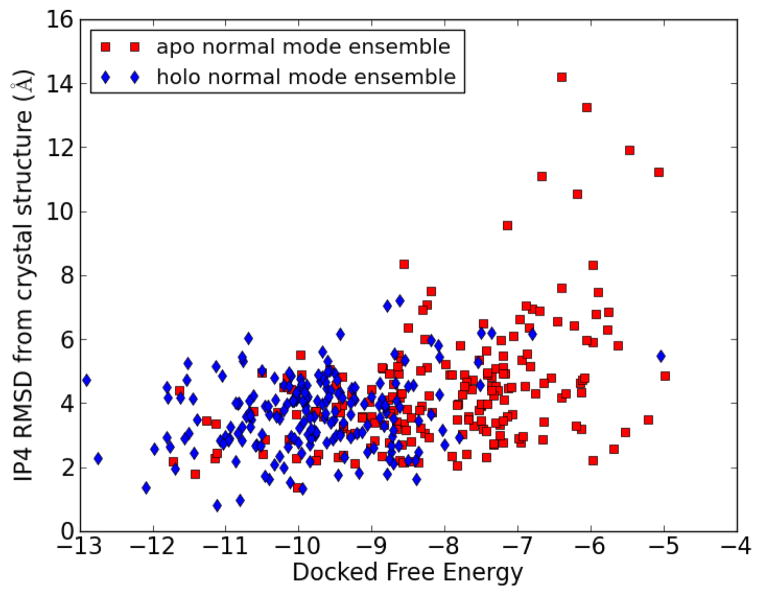
The IP4 RMSD vs the docked free energy of each docked complex is shown in Figure 9 for both apo and holo normal mode ensembles. There is a general trend for lower free energies to have lower RMSD, but this correlation is not perfect, as discussed above. This means that the correct docked pose will be one of those with low binding free energy, but not necessarily the one with the lowest. For further refinement, we would select a set of the best-scoring poses, e.g. the top 10–20 structures. We also note the significant overlap between results obtained from the apo vs. the holo normal mode ensemble in the low free energy/low RMSD region. This is promising, since this means that using either the apo or holo structure as a starting point for generating a normal mode ensemble will allow the sampling of similar good-scoring conformations. This bodes well for cases where the holo structure is not known, or even when no experimental structures (either apo or holo) are available. In the latter case, an approximate structure may be obtained by modeling (e.g. homology modeling) which can be used as input for normal mode analysis.

Figure 9.

RMSD of IP4 from docked structure to crystal structure vs. binding free energy for docking to normal mode structures. Each point represents a docking run of IP4 to a single normal mode conformation.

Selection of normal mode conformations by docking

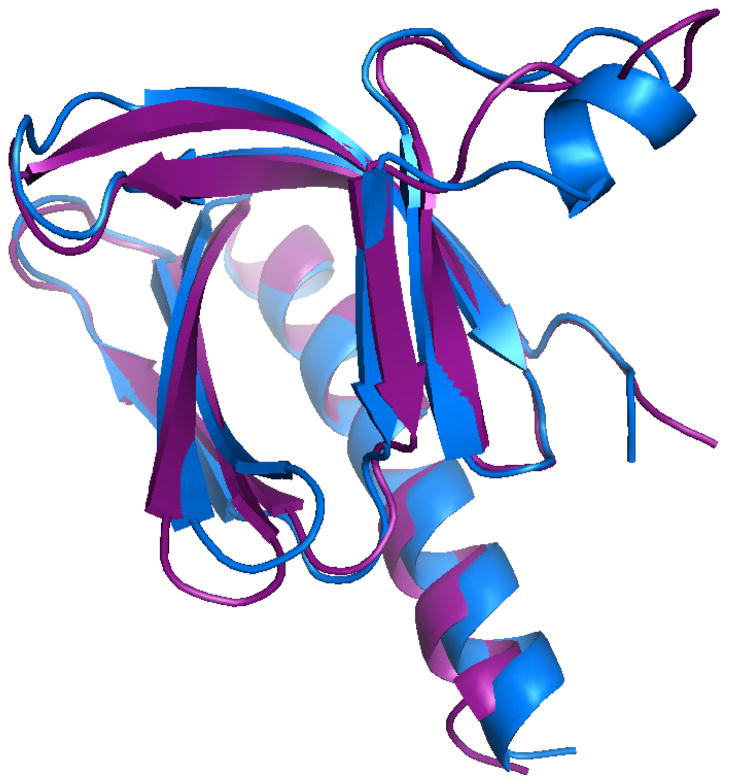
If the conformational selection mechanism of ligand binding is correct, the normal mode receptor conformations which give the best docking results should be similar to the (known) complexed receptor structure. Figure 10 shows the structure of the receptor from the best scoring complex from the apo normal mode ensemble, along with the receptor structure from the crystal structure of the complex. The best scoring apo normal mode receptor has a structure similar to that of the crystal structure of the receptor. This indicates a partial success in selecting the bound receptor conformation from an ensemble generated from the unbound conformation.

Figure 10.

Purple: structure of receptor from best scoring apo normal mode complex. Blue: crystal structure of bound form of PH domain (with IP4 as ligand).

Analysis of inhibitors of the PH domain

PH4

In recent studies, computational modeling lead to the identification of potent Akt PH domain inhibitors, whose activity was verified in both in vitro and in vivo binding assays.^1–4 The modeling component made use of the available structure of the PH domain in its bound form (with IP4). We apply our methods to this system to determine whether this type of computational lead identifica-tion be performed using the unbound form of Akt PH domain, to simulate a case where only the unbound form of a receptor is known.

The most promising compound identified by Du-Cuny et al.¹ is a sulfonamide with an attached long aliphatic chain, which was called PH4.^1,2 In these previous studies, docking and prediction of binding modes with the GOLD program⁴⁷ were performed using the structure of the PH domain from the complexed crystal structure.¹ We have docked PH4 to the ensemble of structures we have previously generated from the unbound PH domain structure, and also to the original unbound structure, using the exact procedure described previously, replacing IP4 with PH4 as the ligand.

Docking of PH4 to the unbound crystal structure gives a binding free energy of −4.7 kcal/mol (K_d = 340 μM at 25°C), whereas the best scoring complex from the normal mode ensemble gives a binding free energy of −6.2 kcal/mol (K_d = 28 μM). Not only does the normal mode ensemble method give a significantly improved binding free energy, but the magnitude of binding affinity more closely matches the experimentally determined value of K_d = 40.8 μM (Table 3 of Du-Cuny et al.¹).

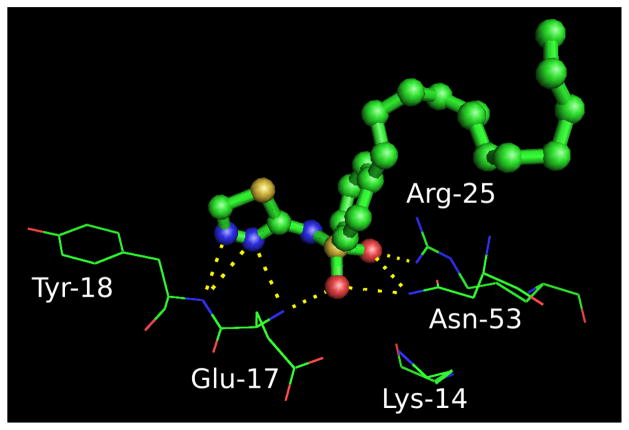
The predicted hydrogen bonding interactions of PH4 with the PH domain is shown in Figure 11. These interactions are consistent with those predicted by Du-Cuny et al.,¹ namely, that PH4 binds to the PH domain in a manner similar to IP4.

Figure 11.

Binding pose of PH4 with the PH domain, determined using a normal mode ensemble docking using the unbound PH domain structure. PH4 is shown in ball and stick, along with residues within the binding pocket. Hydrogen bonding interactions are shown as dashed lines.

SC66 and PIT-1

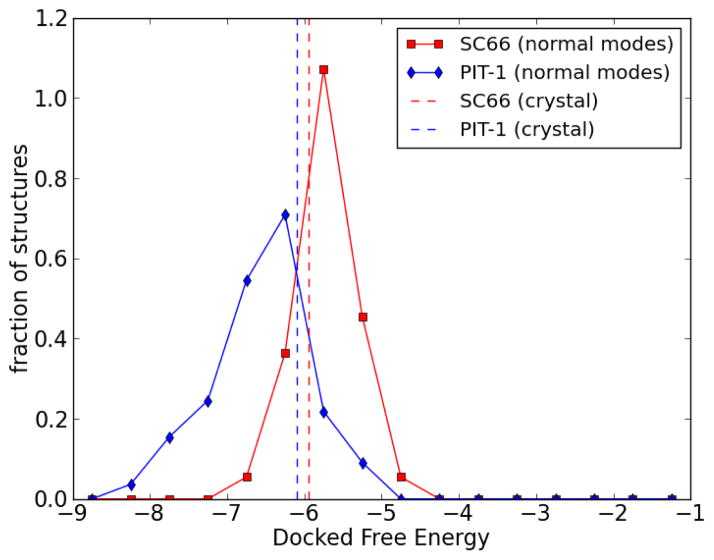
SC66⁴⁵ and PIT-1⁴⁶ are small molecules targeting the Akt PH domain which have been recently reported. Docking of these two molecules to the unbound form of the PH domain gives binding energies of −5.94 kcal/mol for SC66 and −6.10 kcal/mol for PIT-1. To see whether our method can improve these results, SC66 and PIT-1 were docked to the previously generated normal mode ensemble of the PH domain (generated from the apo crystal structure). The results (Figure 12) show that some normal mode structures indeed could give better docked results. The best docked free energy found for SC66 was −6.88 kcal/mol, and that for PIT-1 was −8.33 kcal/mol. This demonstrates that using normal mode analysis can improve predictions over that obtained by static-backbone docking.

Figure 12.

Solid lines: Histogram of docked free energies for docking of SC66 (red squares) and PIT-1 (blue diamonds) to the normal mode ensemble of the PH domain (unbound form). The area under the histograms are normalized to unity. Dashed lines: docked free energy of SC66 and PIT-1 to the crystal structure of the PH domain (unbound form).

Discussion

We have performed molecular docking of IP4 and PH4 to the PH domain of Akt starting with the receptor structure of the unbound (apo) form of the PH domain. Protein backbone flexibility was introduced using normal mode analysis to create an ensemble of candidate conformations for ligand docking. The success of docking a ligand to individual members of the ensemble depends on the receptor conformation, so this docking will select the conformation most suited to binding, similar to the conformational selection model for ligand binding proposed in the MWC theory.

The introduction of alternate conformations via normal mode analysis for docking to the unbound (apo) form of the PH domain results in the identification of many poses with better docking scores than the original unbound structure. RMSD calculations also demonstrated that these poses are close to the native (X-ray) structure of the PH domain-ligand complex.

Applicability of this approach

The method in this study can be used to explore one or more normal modes, and small or large displacements of the initial structure, depending on the available expert knowledge of the modeled system as well as the computing time that is acceptable. In particular, expert knowledge of the system should be always considered to improve predictions.^19,34,35,52 In cases where we know little about the bound state, this method can be applied to derive some essential knowledge such as regional flexibility and movement of the receptor. It can also be combined with homology modeling^53,54 which builds an approximation of the bound structure using known templates. Once this approximate structure is generated, our approach may be used to explore the structural space around this model. An alternate method involves using more expensive molecular dynamics simulations^55,56 to probe the transition between the bound and unbound forms.

High quality receptor structures are a necessary starting point for successful molecular docking, since exhaustive sampling or refinement of receptor conformations during docking is computationally intractable. Normal mode analysis, in conjunction with other modeling techniques, is a fast method to produce high quality receptor conformations, even when no experimental structures (NMR or crystal) are available. To produce an ensemble of 200 conformations, including the minimization of each conformation, takes < 1 hour on a modern desktop computer with an Intel E8400 3.0 GHz processor. Moreover, once generated, this ensemble may be used repeatedly for the docking of different ligands. As an example, we have docked the PH domain inhibitor PH4¹ using the apo normal mode ensemble we generated. The results are consistent with known experimental measurements, and with previous modeling results. The previous computational design of PH4 utilized a known bound complex of IP4/PH domain, but our results show that the normal mode ensemble method may be used when there is no available complex structure. Due to the nature of this method, it can be applied to the case where there is no experimental structures but homology models or ab initio models can be obtained.

In conclusion, we have shown that it is possible to predict bound conformations using normal mode analysis to generate an ensemble of structures for molecular docking. The time for the ensemble generation is negligible, since it is only performed once to generate input structures, and the same ensemble may be used for docking of different ligands. The main increase in computational expense is due to the ensemble size. For example, a 200 member ensemble increases computational time by 200-fold, since 200 docking runs must be performed in the place of a single run. Thus, this approach is particularly suited for lead optimization, but with sufficient computational resources, it can also be applied to the early stages of lead identification via virtual screening.