Across-muscle coherence is modulated as a function of wrist posture during two-digit grasping

Abstract

The purpose of this study was to investigate the extent to which correlated neural inputs, quantified as EMG-EMG coherence across intrinsic and extrinsic hand muscles, varied as a function of wrist angle during a constant force precision grip task. Eight adults (5 males; mean age 29 years) participated in the experiment. Subjects held an object using a two-digit precision grip at a constant force at a flexed, neutral, and extended wrist posture, while the EMG activity from intrinsic and extrinsic hand muscles was recorded through intramuscular fine-wire electrodes. The integral of z-transformed coherence computed across muscles pairs was greatest in the flexed wrist posture and significantly greater than EMG-EMG coherence measured in the neutral and extended wrist posture (P< 0.01 and 0.05, respectively). Furthermore, EMG-EMG coherence did not differ statistically between the extrinsic and intrinsic muscle pairs, even though it tended to be greater for the extrinsic muscle pair (P ≥ 0.063). These findings lend support to the notion of a functional role of correlated neural inputs to hand muscles for the task-dependent coordination of hand muscle activity that is likely mediated by somatosensory feedback.

Introduction

Dexterous manipulation requires coordinated activity of multiple hand muscles to produce fingertip forces. As several muscles insert into each digit, a given fingertip force vector can be produced through a large number of feasible muscle coordination patterns [17]. Besides the issue of muscle redundancy [2,14], our understanding of neuromuscular control of the hand is further challenged by the fact that a given fingertip force vector is the result of the combined action of extrinsic and intrinsic hand muscles, where only the former cross the wrist joint. Thus, changes in wrist joint angle change the length, and therefore force-generating capabilities, of the extrinsic but not the intrinsic muscles [1,10].

Previous evidence has suggested that the central nervous system (CNS) might simplify the control of redundant systems such as the hand by constraining the modulation of multiple hand muscles to act as a unit [6,15–17]. A study by Johnston et al. [6] indicated that extrinsic and intrinsic hand muscles were coordinated in a synergistic fashion when subjects were asked to exert a constant force during a precision grip task (thumb and index finger) at different wrist joint angles. Specifically, these authors found that electromyographic (EMG) amplitude of intrinsic and extrinsic muscles scaled uniformly with changes in wrist posture. Such a finding is not obligatory as neural activation of intrinsic muscles does not have to be modulated their length does not change with wrist posture as it should for extrinsic muscles. Based on these findings, Johnston et al. [6] suggested that neural inputs to hand muscles are shared across the two hand muscle groups, rather than being selectively targeted to each of the two muscle groups studied.

A complementary means through which task- or posture-dependent modulation of neural drive to hand muscles can be assessed is across-muscle coherence [3, 7, 8, 15]. Across-muscle coherence between EMG signals (EMG-EMG coherence) recorded from two muscles denotes the correlation of periodic neural inputs to that muscle pair. As such, the information provided by across-muscle coherence can complement, and is non-redundant with, that provided by analysis of EMG amplitude covariation [6]. Therefore, the purpose of this study was to determine the extent to which correlated neural inputs to intrinsic and extrinsic muscles, quantified by EMG-EMG coherence, varied as a function of wrist joint angle during a constant force precision grip task.

Poston et al. [15] observed that EMG amplitude from intrinsic and extrinsic hand muscles increased with higher forces exerted through a precision grip, whereas EMG-EMG coherence did not change. However, to our knowledge there are no studies that have examined whether EMG-EMG coherence changes as a function of muscle length. Therefore, two alternative outcomes can be envisioned: (1) EMG-EMG coherence is invariant with respect to changes in EMG magnitude that accompany changes in wrist joint postures [6], or (2) EMG-EMG coherence significantly changes as a function of EMG amplitude modulation associated with changes in wrist joint angle. The results of Poston et al. [15] would suggest that changes in EMG magnitude would not be accompanied by changes in EMG-EMG coherence when fingertip forces are modulated at the same hand posture. However, it is conceivable that the neural drive necessary to maintain a given force at different muscle lengths might require a modulation of the strength of the coupling with which the same or newly recruited motor units are coordinated.

Material and methods

Eight adults (5 males; mean age 29 years, range 22–45 years) participated in the experimental procedures. Subjects were without neurological and orthopedic disorders and gave written informed consent before participating in the study. The experimental procedures were approved by the Institutional Review Board at Arizona State University and were performed in accordance with the Declaration of Helsinki.

The experimental procedures have been described in detail in Johnston et al. [6]. Briefly, subjects held a grip device using the thumb and index finger tips. The device was held at three different wrist joint angles: neutral, flexed, and extended. The neutral wrist angle was set at 180° and then adjusted by ~5° to an angle that was comfortable and natural for subject. The flexed and extended wrist angles were defined as 50% of the angle between neutral and the maximum flexed and extended wrist angles that subjects were capable of producing, respectively. Participants were required to maintain the same digit posture at all wrist angles to ensure constant intrinsic muscle lengths.

Three six-dimensional position/orientation (P/O) sensors (Polhemus Fastrak, Colchester, VT) were used to determine invariance of digit posture across wrist joint posture, as well as to measure wrist joint angle (Fig. 1). One P/O sensor was placed on the back of the hand between the first and second metacarpals. Two other P/O sensors (S2, S3) were placed at the base of the grip device below the thumb and the index finger, respectively. S1, S2, and S3 define the vertices of a triangle denoting the digit configuration and the object orientation (see Fig. 1D in Johnston et al. 2010 for more details). We rendered S1, S2, and S3 as 3-D dots on a computer monitor as feedback to subjects to help them in maintaining the same grip posture at all wrist joint angles. The target wrist joint angles and the position of the sensors at each angle were calculated as a rotation angle relative to the neutral wrist joint angle that was derived from the angular deviations of S1 in the transverse plane. Subjects were required to maintain a wrist angle within ± 2° from the target wrist angle in the transverse plane (Fig. 1). Trials were repeated if subjects failed to maintain the target postures within the tolerance level throughout the recording period.

Figure 1. Experimental setup.

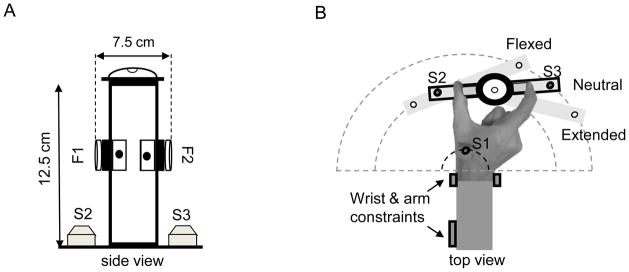
A: Side view of two digit precision grip device. F1 and F2 indicate the 3-D force/torque transducers. B: Top view of experimental setup. Subjects grasped the device in a flexed, neutral and extended wrist posture. Position orientation sensors S1 – S3 are located on the device and hand to measure wrist joint angle, and ensure the invariance of digit postures across wrist joint angles (see Methods for details).

Each experiment began with the assessment of subject’s two-digit maximal voluntary grip force (MVF). Subjects were asked to increase isometric grip force from rest to maximal over a period of 3 s and maintained the maximal force for 5 s. Subjects performed two MVF trials separated by approximately 60 s of rest. The total force from each maximal contraction was defined as the sum of thumb and index finger normal force and the greatest force of the two trials was defined as the MVF for normalization purposes. The experimental session consisted of five 5-s trials per wrist angle, in which the subjects held the grip device while producing a total grip force of 10% of MVF. Digit normal forces and normal to tangential force ratios were not significantly different across wrist joint angles (see Johnston et al. [6] for details on digit force analyses).

Multi-unit EMG activity was recorded from three extrinsic and two intrinsic hand muscles using intramuscular thin wire bipolar electrodes. The extrinsic muscles we recorded EMG from were the Flexor Pollicis Longus (FPL), and the index finger compartments of the Flexor Digitorum Profundus (FDP2) and Extensor Digitorum Communis (ED2). The intrinsic muscles we recorded EMG from were the First Dorsal Interosseous (FDI) and First Palmar Interosseous (FPI). EMG was sampled at 2 kHz and digit forces were sampled at 1 kHz. The EMG signals were amplified (1000×) and band-pass filtered (1–1000Hz; Grass Instruments). Position data were recorded at approximately 25 Hz.

We first assessed stationarity (see below) in pairs of EMG signals to determine which signals were useable across subjects. Lack of stationarity for some muscles prevented the comparison of all muscle pairs across all wrist postures. Therefore, pooled EMG-EMG coherence was computed across the following six muscle pairs from 5 of the 8 subjects and for each wrist posture: FPL-FDP2, FPL-ED2, FPL-PI, FDP2-ED2, FDP2-FPI and ED2-FPI. To address the question of whether coherence differs between intrinsic and extrinsic muscle pairs, we compared coherence in the 0–55 Hz frequency range at each wrist posture from the same 5 subjects between two muscle pairs (FDI-FPI and FPL-FDP2) as these were the muscle pairs characterized by the greatest number of trials with useable signals. Coherence was computed using the procedures described in Poston et al. [15]. EMG data was conditioned prior to coherence estimation in order to increase the reliability of the coherence estimation [11] as follows. EMG data from 5 trials per wrist posture were concatenated into one 20-s trial. Movement and noise artifacts were removed after visual inspection of each concatenated data set and the EMG signal was linearly de-trended using a sliding window of 16.7 ms to remove signal drift above 55 Hz and low-pass filtered at 500 Hz. A weak stationarity test was also performed using the procedures described by Halliday and colleagues [5] and non-stationary EMG traces were excluded from coherence calculations. The test compares EMG values from periodograms versus values expected for an exponentially distributed variate. Stationarity was defined by spread of values that are not significantly different from those obtained through an exponential distribution. For statistical purposes, the coherence estimates were transformed with a Fisher-z transformation.

We used nonparametric statistical analysis [13] to determine the effect of wrist angle on the integral of z-transformed EMG EMG coherence estimates (see [15] for details). Briefly, the null hypothesis was that EMG-EMG coherence does not vary across any of the pairwise comparison of wrist postures, i.e., flexed versus neutral, flexed versus extended, and neutral versus extended. The integral of the z-transformed coherence from subjects (n=5) was randomly assigned across the two wrist postures of interest and the test statistic was computed for each new random assignment, i.e., permutation. Note that for each permutation, the total number of observations for each wrist posture was the same (e.g. 5 for the flexed and neutral postures) and the mean difference between the integrals of z-transformed coherence from each posture was calculated. This procedure was repeated for all 32 possible permutations of the 5 pairs (2⁵) to generate a distribution of all mean differences. The proportion of mean coherence differences obtained from all permutations that was larger than the absolute value of the experimentally observed mean coherence difference was used to calculate the Monte Carlo P-value [11]. The null hypothesis was refuted if the P value was less than or equal to 0.05.

Results

Johnston et al. [6] reported that changes in wrist joint angle resulted in a uniform modulation of EMG amplitude across intrinsic and extrinsic hand muscles despite the fact that changes in wrist joint posture changes the force generating capabilities of the extrinsic but not intrinsic muscles. Here we extend these observations by showing that changes in wrist joint posture affected the magnitude of the integral of the z-transformed coherence values.

Figure 2 shows an example of EMG-EMG coherence pooled across all muscle pairs for one representative subject (S2) measured at the flexed, neutral, and extended wrist joint posture. For this subject, EMG-EMG coherence was largest in the flexed wrist posture and least in the extended wrist posture. This pattern was found across all subjects as shown by the integral of the z-transformed coherence measured at each wrist joint posture. The two-sided and one-sided statistical analyses revealed that z-transformed coherence was greater in the flexed compared to neutral wrist posture (two sided and one sided: P< 0.001; Fig. 3). Similarly, pooled coherence was greater in flexed compared to extended wrist posture (two-sided: P = 0.063; one-sided: P= 0.031; Fig. 3). Pooled coherence was not different between the neutral and extended wrist postures (two-sided: P = 0.188; one-sided: P = 0.094).

Figure 2. Across-muscle coherence as a function of wrist joint angle.

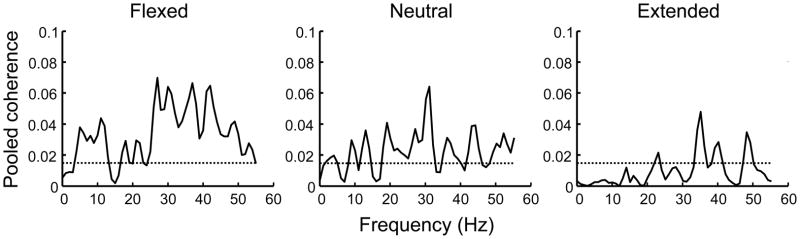
Coherence pooled across extrinsic and intrinsic muscle pairs (three and two muscle pairs, respectively) is shown as a function of wrist angle. Data is from one representative subject (S2). Horizontal dashed lines denote statistical significance threshold (P< 0.05).

Figure 3. Integral of z-transformed pooled coherence as a function of wrist joint angle.

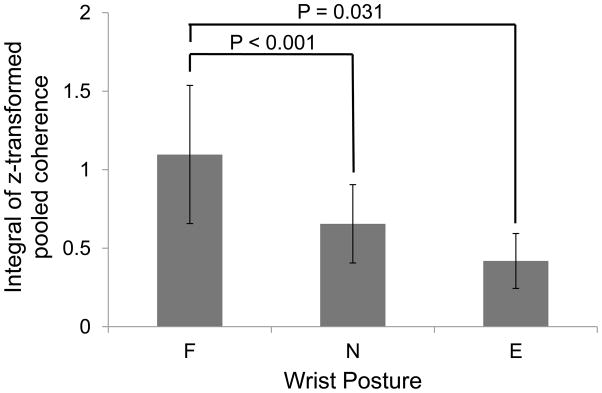
The integral of z-transformed coherence pooled across a subset of extrinsic and intrinsic hand muscles and subjects (see Methods), is shown as a function of wrist angle (F, N, and E denote wrist flexion, neutral posture, and extension, respectively).

We were also interested in assessing whether changes in wrist joint angle would affect intrinsic and extrinsic muscles in a similar fashion. Comparison of the integral of z-transformed coherence between FPL-FDP2 versus FDI-FPI revealed that coherence did not statistically differ at any posture (P≥ 0.063), but tended to be greater in FPL-FDP2 for the flexed wrist posture (P = 0.063).

Discussion

Poston et al. [15] observed that EMG amplitude of intrinsic and extrinsic hand muscles scaled uniformly with grip force, whereas the integral of z-transformed pooled coherence remained invariant. In contrast, the present findings indicate that the integral of the z-transformed coherence pooled across extrinsic and intrinsic hand muscles did vary with changes in wrist angle. In the same task, Johnston et al. [6] reported a uniform scaling of EMG amplitude with changes in wrist joint angle.

Closer examination of the present task and the task used by Poston et al. [15], however, points to differences that can provide insights into the association between EMG-EMG coherence, force production, and changes in muscle length. Specifically, uniform scaling of EMG amplitude across multiple muscles occurred in tasks in which subjects increased grip force at the same wrist/hand posture as well as when subjects maintained the same force exerted at different wrist joint angles. In both of these cases, EMG amplitude modulation can be accounted for by widely distributed and shared inputs to motor nuclei of extrinsic and intrinsic hand muscles. At the same time, uniform scaling of EMG amplitude is not necessarily associated with modulation of EMG-EMG coherence, as shown by the study by Poston et al. [15]. Therefore, we conclude that the mechanisms underlying the modulation of correlated neural inputs to hand muscles for fingertip force modulation differ from those involved in maintaining a constant force output in response to changes in muscle length. The mechanisms involved with modulating EMG-EMG coherence as a function of wrist posture might include changes in somatosensory feedback that accompany changes in muscle length and force-generating capabilities. This proposition is compatible with observations of reduced EMG-EMG coherence in deafferented subjects [9] and subjects who were given a digital nerve block [4] compared to healthy controls.

Although the integral of the z-transformed coherence was greatest for the extrinsic muscle pair compared to the intrinsic muscle pair in previous studies [15,3], the current findings did not reveal a statistical difference. However, the tendency was for coherence value of the extrinsic muscle pair to be greater than the intrinsic muscle pair. Greater coherence for extrinsic compared to intrinsic muscle pairs is consistent with literature on correlated neural input in the time domain, i.e., common input (e.g., [12,18]). However, the lack of difference in coherence between extrinsic versus intrinsic muscle pairs in the present study is likely due to the lower number of useable trials characterized by stationary EMG signals. Further work is needed to address the extent to which previously described differences in correlated neural input to extrinsic versus intrinsic hand muscles are found as a function of muscle length induced by changes in joint angle.

Conclusions

We found that EMG-EMG coherence varied as a function of wrist posture, the greatest coherence occurring at a flexed wrist posture. Similar to previous studies, EMG-EMG coherence tended to be greater for extrinsic muscle pairs. These findings suggest that the strength of correlated neural inputs to hand muscles can be altered by changes in muscle length resulting from changes in wrist posture. We speculate that somatosensory feedback arising from changes in joint angles and/or muscle length might be involved in the posture-dependent modulation of EMG-EMG coherence. Furthermore, these present findings underscore the task-dependency of across-muscle correlated neural input and therefore lend further support to the hypothesis that correlated neural input might have a functional role for the coordination of hand muscle activity.

Highlights.

• EMG-EMG coherence of hand muscles is modulated as a function of wrist posture

• EMG-EMG coherence tends to be larger in extrinsic than intrinsic muscle pairs

• The present results suggest task-dependency of across-muscle coherence