Supercapacitance from Cellulose and Carbon Nanotube Nanocomposite Fibers

Abstract

Multiwalled carbon nanotube (MWNT)/cellulose composite nanofibers have been prepared by electrospinning a MWNT/cellulose acetate blend solution followed by deacetylation. These composite nanofibers were then used as precursors for carbon nanofibers (CNFs). The effect of nanotubes on the stabilization of the precursor and microstructure of the resultant CNFs were investigated using thermogravimetric analysis, transmission electron microscopy and Raman spectroscopy. It is demonstrated that the incorporated MWNTs reduce the activation energy of the oxidative stabilization of cellulose nanofibers from ∼230 to ∼180 kJ mol^–1. They also increase the crystallite size, structural order, and electrical conductivity of the activated CNFs (ACNFs). The surface area of the ACNFs increased upon addition of nanotubes which protrude from the fiber leading to a rougher surface. The ACNFs were used as the electrodes of a supercapacitor. The electrochemical capacitance of the ACNF derived from pure cellulose nanofibers is demonstrated to be 105 F g^–1 at a current density of 10 A g^–1, which increases to 145 F g^–1 upon the addition of 6% of MWNTs.

1. Introduction

Supercapacitors, which work on the basis of electrochemical double-layer capacitance and/or redox reactions, are an excellent energy storage system because of their high power-density, rapid charging/discharging capacity, and long life-cycle stability.¹ Porous carbon materials such as activated carbons, aerogels, carbon nanotubes (CNTs) and graphene are ideal electrode materials for supercapacitors because of their large surface areas, which are accessible to the electrolyte, and their high electrical conductivity.^2,3

Activated carbons derived from biomass are promising electrode materials for supercapacitors and have been receiving great interest recently. This interest is because of the abundance and low cost of the precursors and their porous structures that ensures large surface areas for the resultant carbons. High electrochemical capacitances have been achieved with carbons derived from a variety of biomass such as plant leaves,^4,5 hemp fibers,⁶ watermelon,⁷ coconut and peanut shells,⁸⁻¹⁰ pollens¹¹ and seaweeds.¹² However, these biomass sources were all investigated in the form of mixtures which are typically composed of cellulose, hemicellulose and lignin; the dependence of electrochemical performance upon the composition of the biomass is unclear. To select a suitable biomass material for supercapacitors and to optimize the production process, it is important to better understand the carbonization process and the electrochemical performance of each individual component, particularly cellulose, which is the major component of plant cells.

Our previous studies have shown highly crystalline cellulose fibers are an excellent precursor for production of carbon fibers.^13,14 Moreover, nanoscale precursors showed advantages over the micrometer-sized cellulose fibers in terms of the ease of graphitization and the structural homogeneity along the fiber’s radial direction.¹³ In the present study, cellulose nanofibers were produced by electrospinning a cellulose acetate (CA) solution followed by deacetylation to regenerate into cellulose. Multi-walled carbon nanotubes (MWNTs) were also incorporated into the polymer solution to prepare MWNT/cellulose composite nanofibers. The electrospun nanofibers were then carbonized and the effects of MWNTs on the stabilization and carbonization of cellulose nanofibers were investigated systematically using thermogravimetric analysis (TGA), transmission electron microscopy (TEM) and Raman spectroscopy. The CNFs were activated in a steam/argon atmosphere and their application in a supercapacitor was explored. This is the first time a carbonized cellulosic precursor, combining MWNTs, has been reported as a potential material for a supercapacitor.

2. Experimental Section

2.1. Materials

Cellulose acetate (CA, M_n = 100 000), polyvinylidene fluoride (PVDF, M_n = 71 000), acetone, N,N-dimethylacetamide (DMAc), and N-methyl-2-pyrrolidone (NMP) were purchased from Sigma-Aldrich. Ethanol, NaOH and potassium hydroxide (KOH) were purchased from Fisher Scientific. MWNTs were purchased from Nanocyl (Belgium) Ltd. The average diameter was 5 nm and the purity was 95% according to the supplier. The conductive carbon black Super P was purchased from TIMCAL Graphite & Carbon. All chemicals were used as-received without further purification.

2.2. Preparation of the Solutions

To prepare the blend solution, MWNTs were firstly dispersed in a mixed solution of acetone and DMAc and ultrasonicated for 12 h using a sonication bath. CA was then added into the nanotube suspension and stirred for 6 h to ensure full dissolution of the polymer. The blend solution was then sonicated for 2 h again. The content of CA polymer was 15% and the loadings of MWNTs relative to the polymer were 0.5, 1, and 1.5%. The ratio between acetone and DMAc was 5:6 (w:w) for the blend solution with a MWNT loading of 1.5% and 1:1 (w:w) for all other solutions. All loadings were calculated on a weight basis.

2.3. Electrospinning

Electrospinning was carried out with the CA and MWNT/CA solutions in which the content of CA polymer was 15%. The spinning conditions were a voltage of 16 kV, a flow rate of 0.02 mL min^–1 and a needle tip-to-collector distance of 16 cm. The fibers were collected as a mat using a stationary earthed plate.

2.4. Deacetylation of the CA Nanofibers

Electrospun MWNT/CA and CA fibrous mats were deacetylated in a 0.05 M NaOH solution in ethanol for 48 h to regenerate into cellulose. The fibrous mats were then rinsed with water until neutral and kept over an ion-exchange resin (Rexyn I-300 H–OH from Fisher Scientific, Inc.) for 7 days to remove residual metal ions. The samples were thoroughly washed using water, and then dried under vacuum.

2.5. Carbonization and Activation of the Nanofibers

Heat treatments of the fibers were carried out using a Carbolite CTF16/75 furnace. The deacetylated nanofibers were initially stabilized by heating to 240 °C in air at a rate of 3 °C min^–1, followed by a 60-minute isotherm at the final maximum temperature. The stabilized fibers were then carbonized by heating at a rate of 10 °C min^–1, followed by a 150 min isotherm at 1000 °C in an argon atmosphere. The CNF mats were activated at 800 °C in a steam/argon (30 vol %) atmosphere with a flow rate of 400 mL min^–1 for 60 min to impart porous structures to the fibers. The weight loss during the thermal treatment was 80% for the neat cellulose and 20% for the MWNTs (see Figure S1 in the Supporting Information for TG curves). Therefore, the initial loadings of MWNT in the CA, 0.5, 1, and 1.5%, correspond to loadings of 2, 4, and 6%, respectively, for the MWNTs in CNFs. The loadings of MWNTs in the CNFs were assumed to be unaffected by the activation process. Herein, the final activated CNF is denoted as ACNF. ACNFs containing MWNTs are denoted as 2% MWNT/ACNF, 4% MWNT/ACNF, and 6% MWNT/ACNF.

2.6. Characterisation of Fibers

Raman spectra were obtained using a Renishaw system 1000 spectrometer coupled to a 633 nm laser. The laser spot size was ∼1–2 μm, and the power was ∼1 mW when the laser was focused on the sample using an Olympus BH-1 microscope. The crystal structure of the fibers was examined using a Philips X’PERT APD powder X-ray diffractometer (λ = 1.54 Å, CuKα radiation). The samples were rotated within the X-ray diffractometer chamber to mitigate problems of preferred orientation. The crystallinity was calculated as a ratio of crystalline peak area (A_c) to the background area (A_a) plus the crystalline peak area as given by the equation:

1

The morphology of the nanofibers was investigated after gold coating using a Philips XL30 FEG SEM, operated at an accelerating voltage of 5 kV. ACNF bundles were sonicated in ethanol for 10 min and deposited onto TEM grids and examined using a Philips CM20 TEM to investigate the microstructures in the nanofibers.

TGA of the cellulose and MWNT/cellulose nanofibers was carried out using a Jupiter Netzsch STA 449 C instrument. The fibers were placed into an alumina crucible and heated to 673 K at heating rates of 3, 5, and 10 K min^–1. The loading was kept at ∼3 mg for all samples. All thermal analysis was carried out in air. The surface area of the ACNFs was measured using the Brunauer-Emmett-Teller (BET) nitrogen adsorption method with a Coulter SA3100 instrument. The fibers were degassed under vacuum at 120 °C for 4 h before the BET measurement. The DC electrical conductivity of the ACNFs was measured using a Jandel four point probe system. The electrical conductivity σ was determined using the equation

2

where R is the electrical resistance, A is the cross-sectional area, and L is the distance between the electrodes, which is 6 × 10^–3 m in the Jandel instrument.

2.7. Preparation of Electrodes and Electrochemical Characterization

The ACNFs were ground and mixed with 10% of carbon black (CB) and 10% of PVDF binder. A small amount of NMP was added into the mixture to produce a paste. The paste was then cast onto nickel foam, dried under vacuum at 50 °C for 24 h and pressed under a pressure of 7 MPa to make electrodes. Supercapacitor cells were built by assembling two pieces of 1.0 cm² electrode, with a Whatman filter paper as a separator, in a coin cell containing 6 M aqueous KOH as the electrolyte. The loading of ACNF in each electrode was 3 mg. Cyclic voltammetry (CV) and galvanostatic charge/discharge measurements of the as-built supercapacitor cells were carried out using an Iviumstat Electrochemical Interface. Electrochemical Impedance Spectroscopy (EIS) analysis was carried out using a Solartron 1287 Electrochemical Interface, in the frequency range from 0.1 Hz to 100 kHz at an open circuit potential with an AC amplitude of 10 mV.

3. Results and Discussion

3.1. Morphology of the Nanofibers

Electrospinning is a simple yet versatile technique to produce polymer nanofibers, which allows the porosity and 3D structure of the fibrous mat to be readily tuned. It has been demonstrated previously that electrospinning of a CA solution (in mixed solvents, acetone:DMAc = 2:1) can be carried out using a broad range of conditions.¹³ In the present study, the ratio of acetone to DMAc was changed from 2:1 to 5:6 to increase the content of DMAc. It was found the higher content of polar DMAc in the mixed solvents can facilitate the dispersion of the nanotubes. Smooth fibers were spun from the CA and MWNT/CA blend solutions with a loading below 1% (Figure 1a). Incorporating 1.5% of MWNTs resulted in rough surfaces and a curled morphology for the composite fibers (Figure 1b). Loading MWNTs higher than 1.5% in the CA solution leads to an unstable electrospinning process, due possibly to the high viscosity and electrical conductivity and low surface tension of the blend solution.

Figure 1.

SEM images of (a) the neat CA and (b) the 1.5% MWNT/CA nanofibers.

The electrospun CA fibers were regenerated to cellulose via deacetylation in an NaOH/ethanol solution. This process of regeneration of a cellulosic structure has been demonstrated in our previously published study.¹³ The retention of a crystalline structure to the cellulose precursor is crucial as many of the physical features pass on to the resulting carbon fibers through carbonization.¹⁵ XRD was used to investigate the effect of the MWNTs on the crystalline structure of the cellulose precursor. Figure 2 shows typical XRD patterns of the neat cellulose and composite nanofibers. The neat cellulose nanofiber shows three crystalline peaks at 12.3, 20.2, and 22.0°, corresponding to the (110), (11̅0), and (200) planes of the cellulose crystallites, respectively, which are consistent with those reported for cellulose regenerated from CA.¹⁶ The crystallinity was determined using eq 1 and was found to increase slightly with the addition of MWNTs, from 60% for the pure cellulose to 64% for the 1.5% MWNT/cellulose. This is consistent with the finding by Lu et al.,¹⁶ although the change in crystallinity is observed at a higher loading of nanotubes in our fibers. The crystallinities for all fibers are listed in Table 1.

Figure 2.

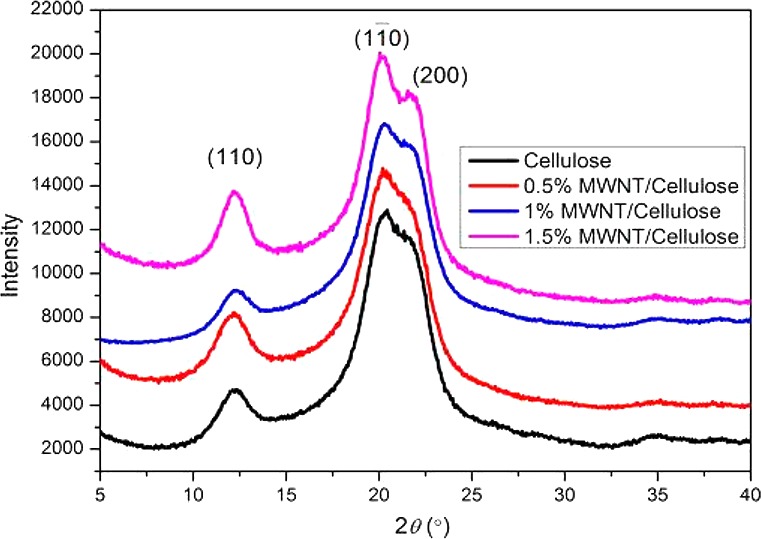
Typical XRD patterns of the regenerated cellulose and MWNT/cellulose nanofibers.

Table 1. Parameters for Stabilization, Structure and Properties of the Pristine ACNF and MWNT/ACNFs.

sample	crystallinitya (%)	activation energy (kJ mol–1)b	ID/IG	specific surface area (m2 g–1)	electrical conductivity (S m–1)	RS (Ω)	Rct (Ω)	specific capacitance (F g–1)c
ACNF	60	229 ± 20	1.21 ± 0.08	865 ± 20	1010 ± 95	0.38 ± 0.03	0.37 ± 0.03	105 ± 10
2% MWNT/ACNF	61	218 ± 20	1.25 ± 0.1	910 ± 23	1120 ± 104	0.35 ± 0.03	0.34 ± 0.03	121 ± 11
4% MWNT/ACNF	62	209 ± 18	1.28 ± 0.12	1050 ± 20	1185 ± 110	0.33 ± 0.03	0.32 ± 0.03	136 ± 12
6% MWNT/ACNF	64	182 ± 17	1.31 ± 0.08	1120 ± 25	1255 ± 100	0.30 ± 0.03	0.31 ±0 .03	145 ± 11

^aCrystallinity of the precursor fibers.

^bActivation energy for the stabilization reaction of the precursors.

^cSpecific capacitance measured at a current density of 10 A g^–1.

3.3. Stabilization of Nanofibers

Oxidative stabilization of the precursor is a crucial step during the production of carbon fibers. The stabilization process can be assessed by monitoring the weight loss as a function of temperature using a TGA instrument. Figure 3 shows the TG and differential thermogravimetric (DTG) curves of the nanofibers heated in air at a rate of 3 K min^–1. The exothermic peak at ∼573 K is due to the oxidative stabilization of the cellulose, which involves dehydration, thermal cleavage and thermal scission of C=O and C–O bonds.¹⁷ It can be seen the onset temperature of stabilization reaction decreases slightly with the addition of nanotubes. The activation energy, E_a, for the stabilization reaction can be determined from the TG curves using the equation developed by Broido¹⁸

3

where y is the fraction of the number of initial molecules not yet decomposed, R is the gas constant, T_m is the temperature (in Kelvin) of maximum reaction rate, R_H is the rate of heating, and Z is the frequency factor.

Figure 3.

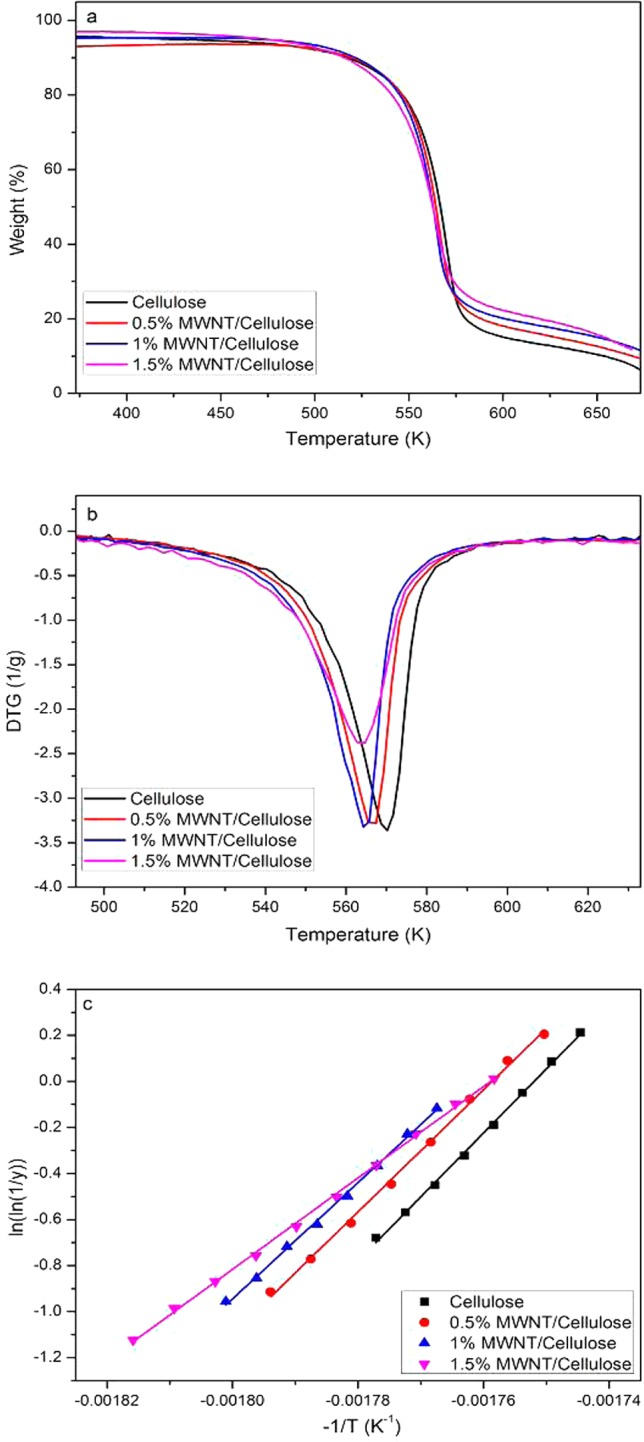
Typical (a) TG and (b) DTG curves of the regenerated cellulose and MWNT/cellulose nanofibers heated at a rate of 3 K min^–1; (c) Plots of ln(ln 1/y) vs −1/T and fitted using the Broido equation (eq 3).

The plots of ln(ln(1/y)) versus −1/T in the stabilization region (i.e., 553–593 K) for different precursors are shown in Figure 3c. The activation energy can be determined from the slopes of linear fits of eq 3 to these data which was found to be 229 kJ mol^–1 for the neat cellulose. TG measurements were also performed at different heating rates. It was found the onset temperature of stabilization reaction shifts to higher temperatures and the E_a decreases with the heating rates (see Figures S2 and S3 and Table S1 in the Supporting Information) because of the thermal lag effect. It is also noted that E_a decreases with the addition of MWNTs and the lowest value was 182 kJ mol^–1 for the composite fiber with a loading of 1.5% (values of E_a are listed in Table 1). It is known that stabilization occurs in the amorphous regions first and subsequently in the crystalline regions as the diffusion of oxygen is easier in the former regions than in the latter. Although the crystallinity increased slightly in the presence of nanotubes, the rougher surface and defects induced by nanotubes can also facilitate the diffusion of oxygen in the fiber and the overall effect is the activation energy of stabilization of the cellulose decreases progressively with an increasing loading of MWNTs.

3.4. Structure and Morphology of the ACNFs

Upon heat treatment at 1000 °C and steam activation, the nanofibers underwent an ∼80 % (estimated) volumetric shrinkage, but nevertheless retained their fiber morphology (Figure 4). Fibers deposited on a collector during electrospinning form a 3D network which is also retained after carbonization and activation processes, as can be seen from SEM images a and d in Figure 4 (images for CNFs without activation are shown in Figure S4 in the Supporting Information). The structural morphology of the ACNFs was investigated using TEM and the images for the pristine ACNF and 6% MWNT/ACNF are also shown in Figure 4. The pristine ACNFs exhibit straight and rigid features with defects on the surface (Figure 4b). Closer inspection reveals that the ACNFs consist of randomly oriented carbon layers (Figure 4c) with no obvious graphitic structure. In the composite fibers, the MWNTs are found to have been exfoliated and individualized with an average diameter of 5 nm. Nanotubes are observed to be mostly embedded in the matrix and aligned along the fiber axis (Figure 4e) as has also been observed with electrospun composite nanofibers in our previous studies.^19,20 Some nanotubes are however observed to protrude from the nanofiber surface (Figure 4f). The protrusion of nanotubes gives the fibers a rough surface, which results in an effective increase in the surface area of the ACNFs. BET nitrogen adsorption measurements show the specific surface area of the ACNFs increases with the loading of MWNTs, i.e., from 865 m² g^-1 for the pristine ACNF to 1120 m² g^–1 for the 6% MWNT/ACNF (values for the specific surface area are listed in Table 1).

Figure 4.

(a, d) SEM and (b, c, e, f) TEM images of (a–c) the pristine ACNF and (d–f) the 6% MWNT/ACNF. The black arrows indicate the presence of nanotubes.

Raman spectroscopy is a useful technique for the characterization of graphitic structures in carbonaceous materials. Figure 5 shows typical Raman spectra for the ACNF and MWNT/ACNF. There are two first-order Raman bands that are present in the region between 1100–1800 cm^–1; namely the D band centered at ∼1350 cm^–1 and the G band located at ∼1590 cm^–1. Tuinstra and Koenig have demonstrated that the intensity ratio between the D and G bands of sp² carbons, I_D/I_G, decreases with an increase in the crystallite size along the a-axis (L_a).²¹ The I_D/I_G ratio has been widely used for semi-quantitative determination of the crystallite size or structural order in various carbonaceous materials. However, it has been proposed by Ferrari and Robertson,^22,23 which has also been confirmed by our previous studies,^13,14 that the I_D/I_G ratio increases with the crystallite size for small crystallites (L_a < 2.5 nm). The I_D/I_G ratio increased from 1.21 for the pristine ACNF to 1.31 for the 6% MWNT/ACNF, which suggests the addition of nanotubes results in larger crystallites and a more ordered structure in the ACNFs. The crystalline structure was further characterized by XRD and the typical patterns are shown in Figure 6. The broad peaks in the region 20–25° for the ACNFs are indicative of less crystalline carbon. This peak becomes narrower with an increasing loading of MWNTs. The (101) reflection at 42° also narrows by adding MWNTs, which suggests the growth of crystallites in the lateral direction. This is thought to be due to the fact that MWNTs can serve as templates for the graphitization of precursors; this effect has been demonstrated by Papkov et al. with nanotube/polymer composites recently.²⁴ The improved crystalline structure was also reflected by an increase in electrical conductivity which was measured by a four-point probe method, from 1010 S m^–1 for the pristine ACNF to 1255 S m^–1 for the 6% MWNT/ACNF (values for the conductivity are listed in Table 1).

Figure 5.

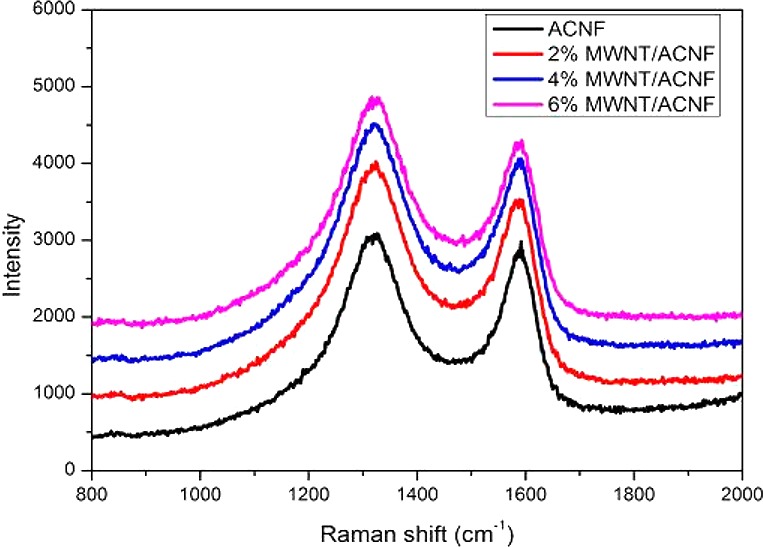
Typical Raman spectra for the pristine and composite ACNFs.

Figure 6.

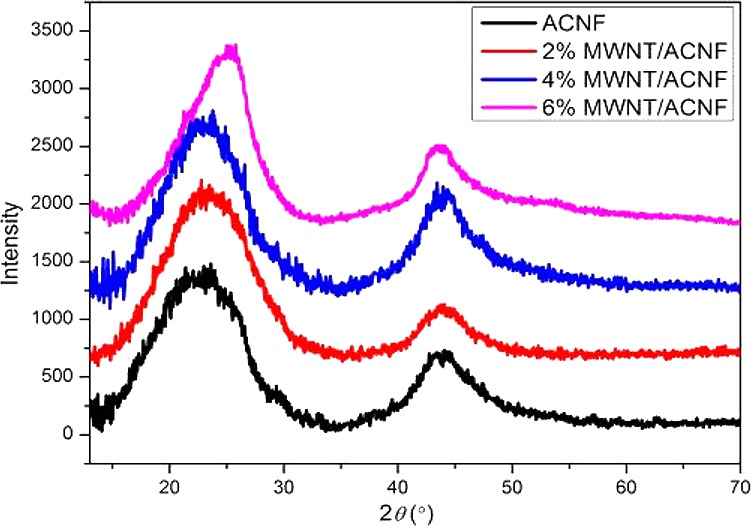
Typical XRD patterns for the pristine and composite ACNFs.

3.5. Capacitance of the ACNFs

The large surface areas and excellent conductivity of the ACNFs make them good candidates for electrode materials for supercapacitors. To investigate the effect of carbonization temperature on the electrochemical capacitance of the fibers, cellulose nanofibers were carbonized at 800, 1000, 1200, and 1500 °C and were all activated with steam at 800 °C. It was found that the specific surface area of the ACNFs decreased whereas the electrical conductivity increased monotonically with an increasing of carbonization temperature (values are listed in Table S2 in the Supporting Information). The pristine ACNFs treated at different temperatures were used as electrodes and the electrochemical performance of the electrodes was evaluated. Fibers carbonized at 1000 °C exhibited the highest specific capacitance according to our preliminary experiments (see Figure S5 in the Supporting Information) and thus all the fibers were carbonized at this temperature for application in supercapacitors.

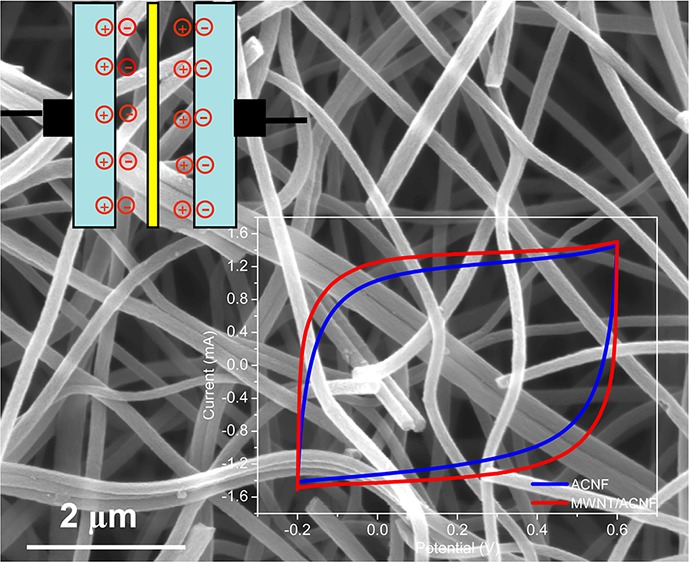
Typical CV curves obtained at a scan rate of 10 mV s^–1 for the ACNFs are shown in Figure 7a. Control electrodes containing only CB and PVDF binder (i.e., without the ACNFs) were also prepared and examined. All ACNFs were stable within the potential range used and the CV curves exhibited a rectangular shape, which is characteristic of an ideal double-layer capacitor. The CV curves for the MWNT/ACNF retained a rectangular shape without obvious distortion even at a scan rate up to 200 mV s^–1 (see Figure S6 in the Supporting Information), which indicates a small equivalent series resistance and fast diffusion of the electrolyte in this electrode. The large areas bound by the CV curves for ACNF electrodes suggest large electrochemical capacitances. It can be seen from the CV curve of the control electrode that the capacitance from the binder, CB, and current collector is negligible.

Figure 7.

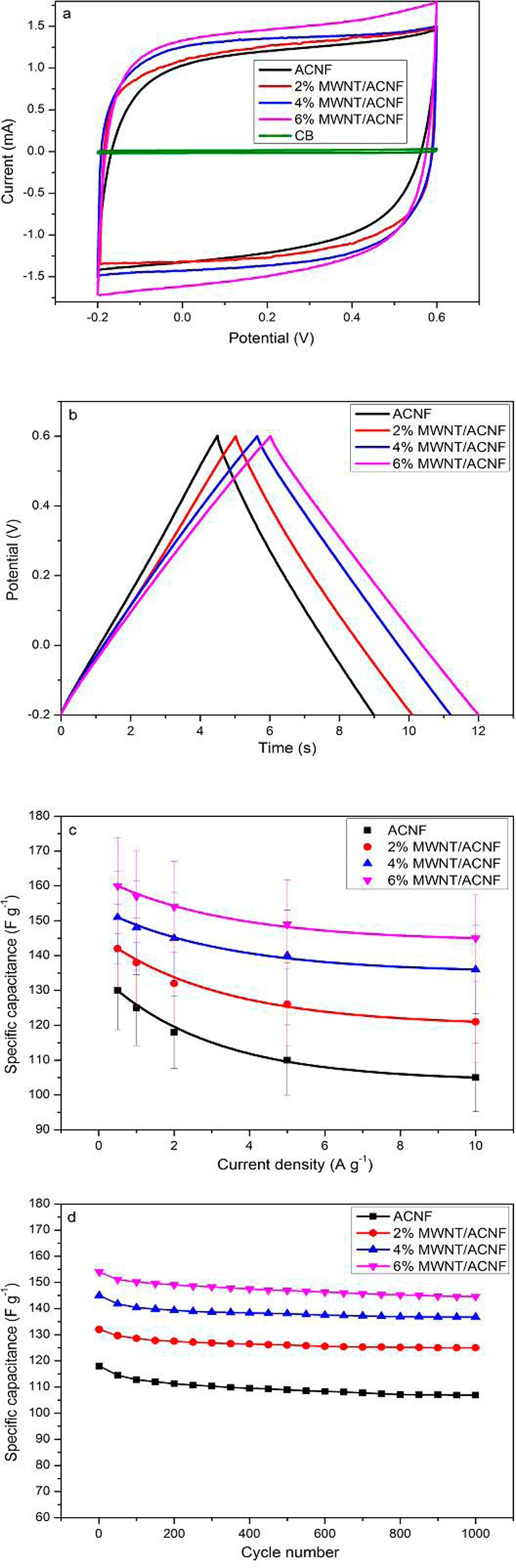
(a) Typical CV curves obtained at a scan rate of 10 mV s^–1 for the pristine ACNF, MWNT/ACNF and CB electrodes; (b) typical charge/discharge curves obtained at a current density of 10 A g^–1 for the ACNF electrodes; (c) specific capacitance of the electrodes as a function of current density; (d) cycling performance of the electrodes at a constant current density of 2 A g^–1.

Galvanostatic charge/discharge measurements were performed on the samples to obtain more detailed information on the electrochemical capacitance. Figure 7b shows typical charge/discharge curves at a current density of 10 A g^–1 for the ACNFs. All the charge/discharge curves were linear and symmetrical, and the voltage drop at the beginning of discharge curve is negligible for all the ACNFs, indicating small internal resistances for these electrodes, which has been further confirmed by EIS. The specific capacitance C_sp for each electrode can be determined using the equation²⁵

4

where I is the constant charge/discharge current, t is the discharge time, V is the potential during the discharge process, and m is the total mass of active materials in the two electrodes. The capacitance measured at a current density of 0.5 A g^–1 was 130 F g^–1 for the pristine ACNF, which increased to 160 F g^–1 for the 6% MWNT/ACNF. These values are significantly higher than that of carbons prepared from bacterial cellulose, which is due possibly to the higher specific areas of our ACNFs.²⁶

The charge/discharge measurements were also performed at different current densities to assess the rate performance which is of particular importance for practical applications. As can be seen from Figure 7c, the pristine ACNF retained 80%, whereas the 6% MWNT/ACNF retained 90% of their capacitances as the current density increased from 0.5 to 10 A g^–1. The good rate performance suggests rapid ion transport characteristics in all these devices, which is associated with the excellent electrical conductivity and porous structure in the ACNFs. It is also noted the improvement in capacitance by the MWNTs is even more pronounced at higher current density, i.e., from 105 F g^-1 for the pristine ACNF to 145 F g^–1 for the 6% MWNT/ACNF at 10 A g^–1.

Repetitive charge/discharge tests of the supercapacitors were performed at a current density of 2 A g^–1 for 1000 cycles to assess their cyclic performance. It can be seen from Figure 7d the pristine ACNF electrode retained 90% of its initial capacitance while the capacitance for all MWNT/ACNF electrodes decreased by only ∼6% after 1000 cycles, suggesting excellent stability and lifetime of the devices. This is attributed to the robust fibrous structure of the electrodes (see Figure S7 in the Supporting Information for the morphology of the electrodes), which prevent the exfoliation of the active materials in the electrode.

EIS analysis was carried out in the frequency range of 0.1 Hz–100 kHz to further investigate the behavior of the ACNF electrodes. The Nyquist plots in the high-frequency region for the ACNF and MWNT/ACNF electrodes are shown in Figure 8 (the full-range spectra are shown in the inset). The equivalent circuit model is also shown in the inset, where R_s is the solution resistance (which includes the electrode resistance, the bulk electrolyte resistance and the resistance at the electrolyte/electrode interface), C_d is the double layer capacitance, R_ct is the charge transfer resistance, W is the Warburg impedance, and C_F is the Faradic pseudocapacitance.²⁷R_s and R_ct can be determined by the intercept at the real axis (Z′) and the semicircle intercepts in the Nyquist plot, respectively. The R_s and R_ct were measured to be 0.38 and 0.37 Ω for the pristine ACNF system and 0.30 and 0.31 Ω for the 6% MWNT/ACNF system, respectively (values are listed in Table 1). The electrodes of the supercapacitors were also prepared by directly pressing the fiber mats into nickel foam without using any conductive additive or binder. The binder-free electrodes showed similar electrochemical behavior (see Figures S8 and S9 in the Supporting Information) with those containing CB and binder, but the R_s and R_ct values are slightly higher.

Figure 8.

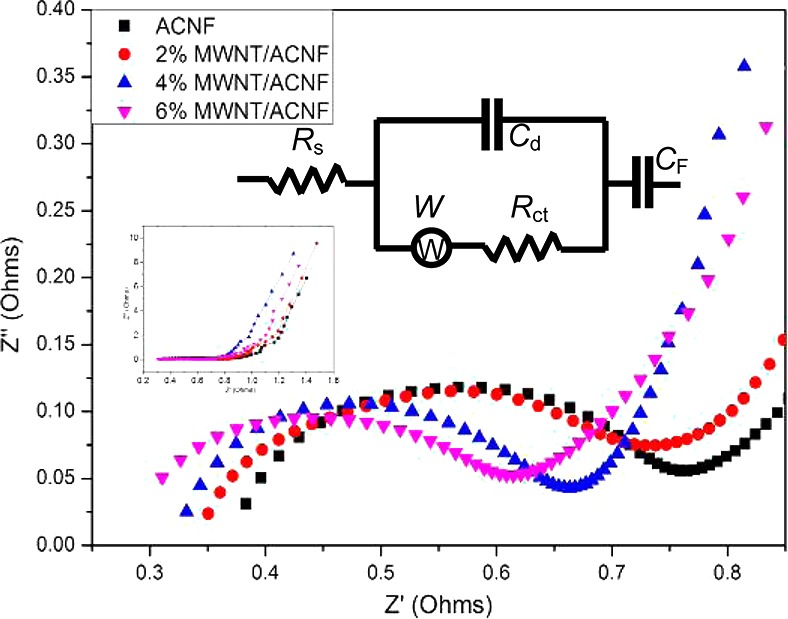
Impedance Nyquist plots in the high-frequency region of the electrodes. The insets show the equivalent circuit and the full-range spectra.

It is generally recognized that the electrochemical capacitance is dependent upon both the surface area and the electrical conductivity of the electrode material. However, to achieve a high electrical conductivity by creating a high degree of graphitic structure in CNFs usually leads to a reduction in micro- and mesopores and hence their surface areas.¹ It is a great challenge to increase both the specific surface area and electrical conductivity.¹⁰ As has been shown above, both the specific surface area and the electrical conductivity were increased by ∼25 % upon the incorporation of only 6 % of MWNTs into the ACNFs, which consequently resulted in a moderate increase in the capacitance of the ACNFs. The nucleating effect on graphitization at a low temperature, the excellent electrical conductivity and chemical stability make carbon nanotubes ideal additives for modulating the microstructure and improving the capacitance of electrode materials, as has been demonstrated by other groups,^12,28−31 but never before for cellulose precursors.

The specific capacitances of the ACNFs demonstrated in this study are comparable with those derived from poly(acrylonitrile), poly(benzimidazole), and polyimide nanofibers,³²⁻³⁴ and are the highest reported so far for pure cellulose-derived carbon to the best of our knowledge. The capacitances of our ACNFs are also comparable with those of cornstalk-carbon (carbonized at 1000 °C) where a catalyst K₄[Fe(CN)₆] was used to promote the graphitization of the precursor.³⁵ However, our values are still lower than those derived from other cellulosic biomass such as coconut shells.^8,9 This is partially due to the lower specific surface area of our ACNFs compared to the biomass carbons in which the inorganic components play an important role (e.g. intercalation of K⁺ in graphitic layers) in the activation of the biomass during thermal treatment. However, some types of bio-based supercapacitors suffer from poor cycle stability because of the poor mechanical properties of the electrode materials. Mi et al. reported an excellent capacitance for coconut-shell-derived carbon but the electrode retained only 71% of its initial capacitance after 1000 cycles.⁹ The fibrous structure of our ACNFs endows good mechanical stability to the electrodes which gives rise to better cycle life. Nevertheless, this work demonstrates the potential contribution of pure cellulose to the capacitance of the biomass carbons and it would be interesting to investigate the capacitance of other components such as hemicellulose and lignin in biomass.

4. Conclusions

MWNT/cellulose composite nanofibers have been prepared by electrospinning a MWNT/CA blend solution followed by deacetylation. The composite nanofibers were carbonized and the effect of nanotubes on carbonization of cellulose has been investigated. It has been found the incorporated MWNTs reduce the activation energy of the oxidative stabilization of cellulose from ∼230 to ∼180 kJ mol^–1. The nanotubes also increased the crystallite size, structural order and the electrical conductivity of the resultant ACNFs. The specific surface area of the ACNFs increased from ∼870 to ∼1120 m² g^–1 upon the addition of 6% of MWNTs due to a rougher surface. The ACNFs were activated in a steam/argon flow and used as the electrodes of a supercapacitor. The specific capacitance has been found to be ∼105 and ∼145 F g^–1 at a current density of 10 A g^–1 for the pristine ACNF and the 6% MWNT/ACNF, respectively. The improvement in capacitance of the MWNT/ACNF compared to the pristine ACNF is thought to be due to the increased surface area and electrical conductivity. Carbon nanotubes are excellent additives for the preparation of CNFs with improved microstructures and electrochemical capacitance. It is possible to achieve even higher loading of carbon nanomaterials such as graphene in biopolymer nanofibers and to improve the capacitance further using the method manifested in this study, which remains a topic for future work.

Supporting Information Available

S1, TG curves for the cellulose and MWNTs; S2, TG curves for the precursor fibers; S3, plots of ln(ln 1/y) vs −1/T and fitted using the Broido equation; S4, SEM images of (a) pristine CNF and (b) 6% MWNT/CNF; S5, (a) typical CV curves obtained at a scan rate of 10 mV s^–1 for pristine ACNFs carbonized at different temperatures; (b) typical charge/discharge curves obtained at a current density of 1 A g^–1 for the ACNFs; S6 CV curves for (a) the pristine ACNF and (b) the 4% MWNT/ACNF obtained at different scan rates, from inner to outer: 5, 10, 20, 50, 100, and 200 mV s^–1; S7, SEM micrographs of the ACNFs ground with CB: (a) pristine ACNF and (b) 4% MWNT/ACNF; S8, (a) typical CV curves obtained at a scan rate of 20 mV s^–1 for the pristine ACNF and 4% MWNT/ACNF electrodes; (b) typical charge/discharge curves obtained at a current density of 0.1 A g^–1 for the ACNF electrodes; S9, impedance Nyquist plots of the electrodes. The inset shows the plots at high frequencies; Table S1, activation energies of the electrospun fibers determined at different heating rates using the Broido equation; Table S2, properties of the pristine ACNFs carbonized at different temperatures, (PDF). This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

The manuscript was written through contributions of all authors.

The authors declare no competing financial interest.