Image analysis and empirical modeling of gene and protein expression

Abstract

Protein gradients and gene expression patterns are major determinants in the differentiation and fate map of the developing embryo. Here we discuss computational methods to quantitatively measure the positions of gene expression domains and the gradients of protein expression along the dorsal-ventral axis in the Drosophila embryo. Our methodology involves three layers of data. The first layer, or the primary data, consists of z-stack confocal images of embryos processed by in situ hybridization and/or antibody stainings. The secondary data are relationships between location, usually an x-axis coordinate, and fluorescent intensity of gene or protein detection. Tertiary data comprise the optimal parameters that arise from fits of the secondary data to empirical models. The tertiary data are useful to distill large datasets of imaged embryos down to a tractable number of conceptually useful parameters. This analysis allows us to detect subtle phenotypes and is adaptable to any set of genes or proteins with a canonical pattern. For example, we show how insights into the Dorsal transcription factor protein gradient and its target gene ventral-neuroblasts defective (vnd) were obtained using such quantitative approaches.

1 Introduction

In a developing animal, the distributions of signaling proteins, termed “morphogens”, dictate the patterning of gene expression within developing tissues in a concentration-dependent fashion [1]. High morphogen concentrations drive the expression of one set of genes, while low concentrations a different set. In this manner, a single protein, distributed in a spatial gradient, can be responsible for the gross patterning of an entire tissue. Therefore, to model cell-cell signaling and gene expression patterns in development, quantitative measurements of protein and RNA distribution within the embryo are necessary. Fluorescent experimental techniques, such as fluorescent antibody staining and fluorescent in situ hybridization, are sufficiently quantitative for such measurements [2–5]. Yet, to extract these measurements from the fluorescent image data, and in order to make meaningful comparisons across several embryos and sets of embryos, an image analysis protocol is needed [6–9].

Here we present a protocol to analyze image data consisting of three types of molecular species: (1) mRNA/non-nuclear proteins, (2) nuclear proteins, and (3) nascent transcripts (via intronic probes; sometimes called “nuclear dots”). The goal of this method is to distill fluorescent images down to a set of meaningful parameters that characterize the protein and mRNA distributions. To this end, we identify three levels of data: the fluorescent images are the primary data, secondary data are the relationships between position on the embryo and fluorescent intensity, and the tertiary data are parameters that arise from fitting our secondary data to empirical models of protein and mRNA localization.

The final, data-fitting step requires the development of accurate models of protein and gene expression, as well as numerical techniques for minimization of error. However, using the protocol of data fitting to empirical models has several advantages over more simplistic approaches. First, it involves the use of the entire secondary data set, rather than small sets of distinct points. Second, because it uses the entire data set, it is robust to noisy secondary data. Third, it allows for a systematic analysis of variance in the predicted parameters. Because of these advantages, we can be confident in our ability to detect very subtle phenotypes that otherwise are difficult to discern, either by eye or through comparison between sets of secondary data.

As a concrete example, we focus on the transcription factor Dorsal (dl), which acts as a morphogen in the early Drosophila embryo (rev. in [10]). dl nuclear localization is regulated spatially in the Drosophila embryo, in a gradient, such that high nuclear levels are present in ventral regions and very low nuclear levels are present in dorsal regions (Figure 1A). High levels of nuclear Dorsal support expression of genes such as snail (Figure 1B,C) and twist, and intermediate levels of nuclear Dorsal support expression of genes such as ventral neuroblast defective (vnd; Figure 1A,C) and short gastrulation (sog; Figure 1C). Dorsal can also function as a repressor of transcription and in this function limit the expression of some genes, such as decapentaplegic (dpp) and zerknüllt (zen), to dorsal regions (rev. in [11, 12]).

Figure 1. Examples of Drosophila embryo cross-sections analyzed with the methods presented in this paper.

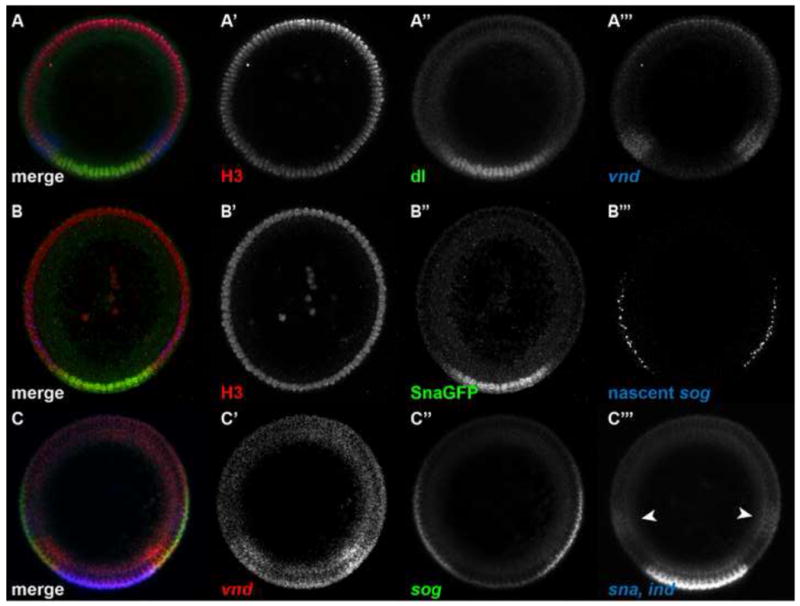
(A) Embryo stained with anti-histone H3 antibody (red; A′) and anti-dl antibody (green; A″), and hybridized with a vnd antisense RNA probe (blue; A‴). This embryo represents an example of a nuclear stain, a nuclear protein to be detected, and an mRNA expression pattern.

(B) Embryo stained with anti-histone H3 antibody (red; B′) and anti-GFP antibody (green; B″), and hybridized with a sog intronic probe (blue; B‴). This embryo represents an example of a nuclear stain, a nuclear protein to be detected, and a nascent transcript pattern.

(C) Embryo hybridized with antisense RNA probes against vnd (red; C′), sog (green, C″), and ind (blue; white arrowheads in C‴) and sna together (blue; C‴). This embryo represents an example of four mRNA expression patterns to be detected, including a single color channel that has two mRNA expression patterns simultaneously.

Each of these embryos is a manual cross section of a nc 14 wildtype embryo, with ventral side oriented down. The embryo in (A) is also present in Figures Figure 1 Figure 2–Figure 4 and Figure 6, Figure 7. The embryo in (B) is also present in Figure 5.

In this paper, we describe the steps in the image analysis protocol and give details of the calculations involved in the data fitting procedures. We demonstrate two cases in which our analysis protocol has allowed us to detect subtle, yet statistically significant, phenotypes in the dl patterning system. In the first case, we detect the slightly longer decay length in the nuclear gradient of a Venus-tagged version of dl, as compared to the nuclear gradient of wildtype dl [13]. The second case consists of measuring the subtle perturbation in placement of the vnd dorsal boundary in embryos that exhibit wider gradients. We also present an example of image analysis in a system other than a cross section of the Drosophila embryo.

2 Materials and Methods

Here we briefly present steps for experimental preparation of Drosophila embryo cross-sections and the mounting and imaging conditions required by our method. More details on the image analysis procedure can also be found in the supplementary material.

2.1 Collection, fixation and in situ hybridization of embryos

Fly stocks used in Figure 8 include dl-venus and dl-gfp constructs and are further described in Reeves et al. (2012) [13]. Embryos in Figure 9 come from the stock dl1/CyO; dl-gfp, H2A-rfp/TM3, and embryos in Figure 10 are F10 mutants [14]. Fluorescent in situ of vnd, ind, sna, and sog genes using antisense RNA probes, and antibody stainings of Dorsal (DSHB), histone H3 (Abcam), and GFP (Rockland) were performed using standard protocols. These steps proceeded according to published protocols [15]. When detecting protein distributions, the proteinase K treatment is skipped. After completion of the last wash, embryos are stored in 70% glycerol at −20°C in the dark.

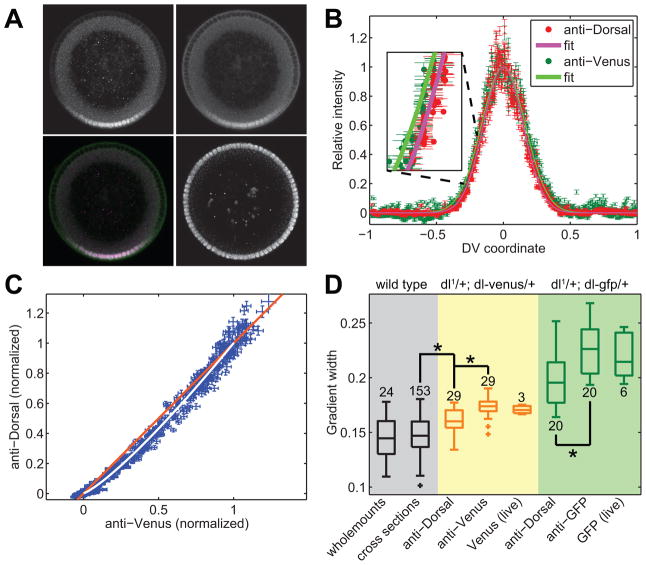
Figure 8. Expansion of the dl gradient in embryos carrying a copy of dl-Venus.

(A) A dl-venus embryo stained for anti-dl (upper left panel), anti-Venus (upper right), and anti-histone H3 (lower right). The lower left panel is a merge between anti-dl and anti-Venus images.

(B) Secondary data of the anti-dl (red dots) and anti-Venus (dark green dots) vs. DV axis location. The solid red and solid bright green curves are the fits to the empirical model of the dl gradient (Eqn 1). Inset: a higher magnification of the ventral-lateral portion of the two gradients. Errorbars denote one standard deviation.

(C) Direct plot of anti-dl vs anti-Venus for each nucleus in the embryo in (A). White curve: plot of the fit of anti-dl vs the fit of anti-Venus. Orange line: 45° line.

(D) Boxplot of gradient widths of several different cases. Gray: wildtype embryos. Yellow: dl-venus embryos. Green: dl-gfp embryos. The latter two genotypes have been measured with anti-dl, with anti-Venus, and live using the native fluorescence of the Venus or GFP tag. Stars indicate statistical significance. Plus signs indicate outliers. Numbers indicate sample size.

Wholemount data from [5]. All other data from [13]. This figure has been reproduced with permission from Developmental Cell, Elsevier Press [13].

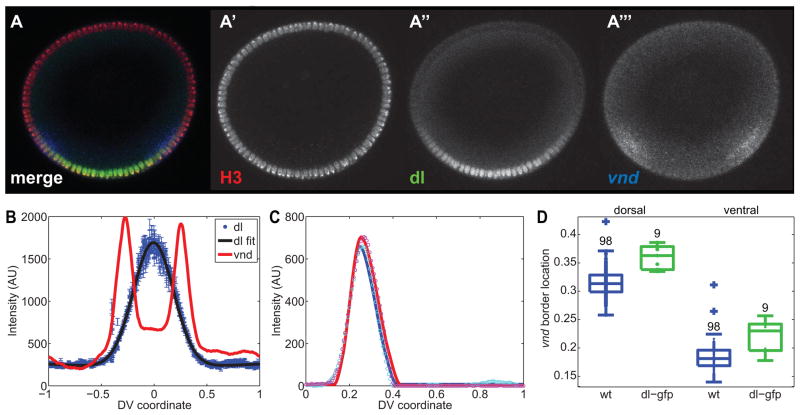
Figure 9. Expansion of the vnd dorsal border in embryos with expanded dl gradients.

(A) dl-gfp embryo stained with anti-histone H3 antibody (red; A′) and anti-dl antibody (green; A″), and hybridized with a vnd antisense RNA probe (blue; A‴).

(B) Plot of the secondary data from the dl-gfp embryo shown in (A).

(C) Fits of the vnd peaks for this embryo. Cyan and magenta circles are the right and left halves of (B), respectively. The blue and red solid curves are the fits of the canonical pattern to the measured right- and left-side patterns, respectively.

(D) Boxplot of vnd dorsal and ventral border locations in wildtype embryos (blue) and dl-gfp embryos (green). Each dot represents an embryo. Plus signs indicate outliers. Numbers indicate embryo sample size. For whether the dorsal border of vnd is the same between wt and dl-gfp, the p-val is 10^⁻⁴, and for the ventral borders being the same, p = 0.005.

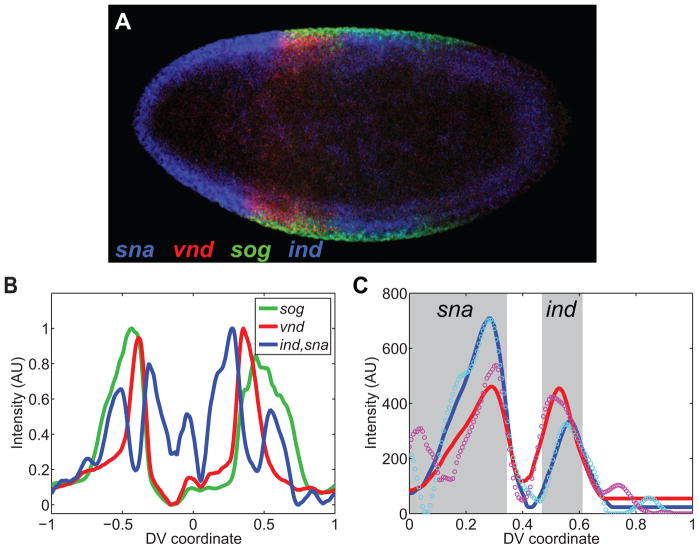
Figure 10. Quantification of gene expression profiles in a saggital section.

(A) Saggital section of F10 embryo hybridized with probes against sna (blue), vnd (red), sog (green), and ind (blue). Anterior is to the left, and posterior is to the right.

(B) Plot of the expression profiles of the genes from embryo in (A). Zero corresponds to the anterior pole (detected manually); one corresponds to the posterior pole.

(C) Fitting two canonical profiles in the same color channel. The canonical profiles of sna and ind used for this fit are specifically for F10 embryos. Cyan and magenta circles are the right and left halves of the sna/ind plot in (B), respectively. The blue and red solid curves are the fits of the canonical pattern to the measured right- and left-side patterns, respectively. The gray boxes signify the expression domains of sna and ind, separated in space.

2.2 Embryo manipulation

After the fluorescent in situ hybridization/antibody staining protocol is performed, embryos are transferred to a viewing dish with 70% glycerol. Using a brush, the appropriate stage is selected by morphology under a stereomicroscope and placed on a glass slide. Generally, ~10 embryos are sectioned at a time. This prevents over-drying and reduces exposure to light. A small amount of 70% glycerol may need to be added onto the slide to prevent embryos from desiccating. However, too much glycerol will cause difficulty in maneuvering the embryos. These embryos are then manually cross-sectioned with a 0.10 mm blade and mounted upright using a hair loop. Two pieces of double-sided tape are used to prevent pressure on and damage to the sections. A coverslip is placed on top, and 70% glycerol is pipetted between the slide and coverslip.

2.3 Confocal imaging

Cross-sectioned embryos were imaged with a 40x 1.3 NA oil objective; pinhole of 2.29 AU; pixel time of 3.20 μs. 15–20 slices with 1.3 μm-thickness containing the middle region of the embryo cylinder were acquired. For the success of the image analysis, it is crucial to have only the desired embryo in the image, and no other fluorescent materials, such as other embryos or dust. It is also imperative to have the entire embryo within the image for all z-slices; leave a comfortable padding of black space around the embryo. See Fig. 1A for an example.

2.4 Image analysis

There are five steps in the image analysis procedure, as outlined below. These procedures were developed and applied in recent studies [5, 13]. In those cases, we will provide references for additional background and a brief discussion.

2.4.1 Detecting the border of the embryo

This procedure was first introduced in [5] and utilized more recently in [13]. First, the geographical center of the image is assumed to reside inside the embryo. From this location, the image is divided into 60 slices in the azimuthal angle, (i.e., θ; see Figure 2A). The intensity of the image as a function of r (the distance from the center of the image) is found for each slice in θ (Figure 2B). The presumed location of the boundary of the embryo is where the intensity drops rapidly (red dot in Figure 2B). This point in (r, θ) coordinates is then transformed back into a pixel location (i.e., xy coordinates), resulting in a relatively tight border around the embryo (Figure 2C).

Figure 2. Finding the periphery.

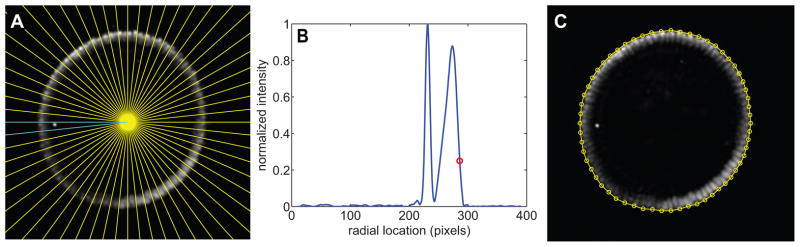
(A) The embryo image is divided into 60 domains radiating out from the image center (yellow lines). The two cyan lines represent the boundaries of the domain shown in (B).

(B) Intensity of the pixels in the domain shown in (A) as a function of radial distance from the center of the image. The red circle denotes the outermost point in which the image intensity rapidly drops from high to low, signifying the periphery of the embryo in this domain.

(C) For each domain shown in (A), the points where the boundary of the embryo is determined to be.

2.4.2 Calculation of average intensities

The next step is to detect average intensities around the periphery of the embryo, and is described briefly in [13], and in more detail here. The average intensities serve as measures of gene expression in color channels corresponding to mRNA probes or averaged values of other molecular species for which nuclear localization is not an important factor. This analysis proceeds in three steps. First, from the 60 points on the embryo periphery, a much denser outer ring of 300 points is interpolated (Figure 3A). For each point i on the outer ring, the outer ring points i, i+1 and two corresponding points, roughly 20 microns in from the periphery, form a quadrilateral (Figure 3B). Third, the average intensity inside this quadrilateral, t_i, is taken as the intensity value of this color channel at point s_i. The result of this analysis step is a vector of pseudo-arclength, s, and a corresponding array, t, which contains the intensities of each color channel as a function of s. For example, a plot of t vs. s will yield peaks of gene expression if the color channels in the image are fluorescent representations of mRNA probe hybridization (Figure 3C).

Figure 3. Measuring average intensity around the periphery of the embryo.

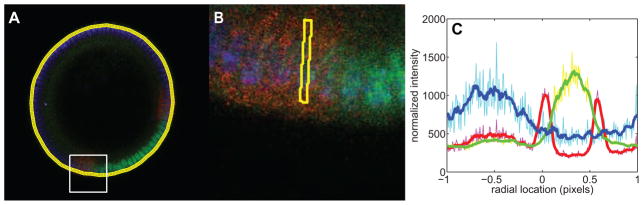
(A) RGB image of an embryo for which the boundary has been calculated. The yellow ring encircling the embryo is the dense mesh of 300 points. The white square denotes the portion of the image shown in (B).

(B) Higher magnification of the area shown in (A). The yellow quadrilateral denotes the domain for which a point of average intensity of each color channel is taken. 300 such quadrilaterals around the periphery of the embryo are used to generate the plot in (C).

(C) Average intensity in the quadrilaterals as you go around the periphery of the embryo (see (B) for an example). The colors correspond to the color channels in (A), (B). The lighter colors are the raw data, and the darker, thicker curves are the smoothed data. Before midline centering, 0 is taken to be the bottom-most point of the embryo in the image.

2.4.3 Locating nuclei

In the case of images with nuclear stains (such as antibodies against histone proteins, or other dyes like TOPRO or DAPI), the analysis program can locate the nuclei [13]. We briefly describe this analysis here, which proceeds in several steps. First, using the 60 points on the border of the embryo, as described in Sect. 2.4.1, the outer periphery of the embryo cross section (up to 20 microns deep) is “unrolled” into a long strip (Figure 4A), which we transform into a binary nuclear mask (Figure 4B). To accomplish this, the strip of nuclei is averaged in the radial (i.e., the apical-basal) direction to yield a one-dimensional representation of the nuclei (Figure 4C). Next, a watershed algorithm is used to determine the 1D locations of the cytoplasmic regions between nuclei. This allows us to put boundaries between the nuclei. These 1D locations are then mapped back onto the original unrolled strip to define rectangular regions, and inside of each rectangle, there is exactly one nucleus.

Figure 4. Locating nuclei.

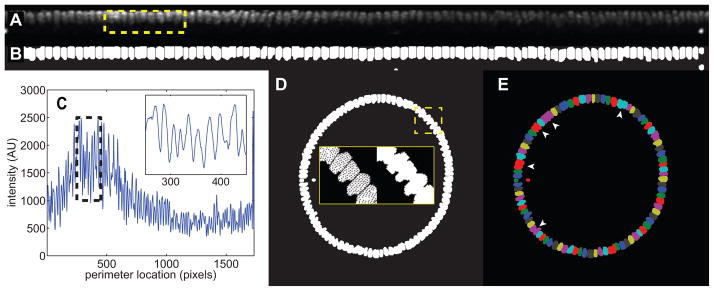
(A) Unrolled strip of nuclei. The yellow box represents the nuclei in the inset in (C).

(B) The nuclear mask of the unrolled strip, with nuclei in white.

(C) The image shown in (A), averaged in the vertical direction to reveal a 1D representation of the nuclei. Black dotted box: the area shown in the inset. The inset reveals that the individual nuclei can be resolved in this way.

(D) Nuclear mask shown in (B), re-mapped back onto the original 2D image. Yellow dashed box: area depicted in insets. Insets: zoomed-in view of re-mapped nuclei before (left) and after (right) filling in holes in the nuclei.

(E) Each nucleus, after being mapped back onto the original image, is identified by a separate color. That way, even if two nuclei overlap in the original image, they can be distinguished using the unrolling technique. Where the primary data provide poor contrast between nuclei, adjacent nuclei may be incorrectly lumped together (arrowheads).

Within each rectangle, the nucleus is segmented using a hard threshold, with the threshold level chosen using a best-fit protocol [16]. This local thresholding results in the ability to segment each individual nucleus from the surrounding cytoplasm (Figure 4B). Defining each rectangle is necessary to (1) differentiate between nuclei that are touching or almost touching, as each nucleus is given a distinct numerical label, and (2) avoid the problems associated with using a global threshold algorithm on the entire image.

Afterward, the pixels corresponding to each nucleus in the unrolled strip are mapped back to the original 2D image of the embryo (Figure 4D). As this is a non-linear transformation, and not a one-toone mapping, sometimes this results in solid nuclei with a handful of black pixels. These pixels are then “filled-in” with the numerical label corresponding to the nucleus they reside in (see insets in Figure 4D). This ensures the nuclear mask does not have missing pixels. Note this hole-filling step does not distort the data in any way; it is simply for complete labeling of individual nuclei.

The 2D image is then morphologically opened with a disk-shaped structuring element 5 microns in diameter. This removes the spurs and feathers from the nuclei, resulting in smooth nuclei (Figure 4D). At this point, the nuclear mask is complete, where the pixels in nucleus i have a value of i, so that even nuclei that touch after transforming back into the 2D image are distinguishable (Figure 4E). All other pixels are black.

In some cases, the quality of the primary data is not high enough to reliably distinguish nuclei from their neighbors, resulting in ill-defined boundaries between neighboring nuclei. In those cases, the program therefore lumps together multiple nuclei (arrowheads in Figure 4E).

The important parameters associated with each nucleus are the pixel list (so the location of the nucleus can be mapped into the other color channels), the centroid (which acts as single coordinate for the whole nucleus) and the nuclear intensity (which will act as a normalization factor for the other color channels; see Section 3.1).

It is important to point out that this method of detection of nuclei works very well in nuclear cycles (nc) 13 and 14 of Drosophila development, due to the relatively close-packing of the nuclei. Earlier nuclear cycles, such as nc 11 and 12, have a much lower density of nuclei, making it difficult to avoid false positives. We previously used manual nuclear detection to overcome this difficulty [13]; however, manual detection of nuclei is not discussed in this set of code.

2.4.4 Intensity of nuclear proteins

Once the nuclear mask is determined, if the given embryo has been immunostained for one or more nuclear-localized proteins, the fluorescent intensity of the channels corresponding to this (these) nuclear protein(s) is considered. For each nucleus identified in the nuclear mask, the corresponding pixels in the nuclear protein channels is found, and the average intensity of those pixels is counted to be the intensity of that nuclear protein for that nucleus. Standard errors of the mean for each of these measurements are also calculated. Coupled with the data for the centroid of each nucleus, these measurements give us a relationship between nuclear protein intensity and location on the periphery of the embryo.

2.4.5 Measuring nuclear dots

If the given embryo has been treated with anti-sense RNA probes made against intronic portions of genes (i.e., intronic probes), then nascent transcripts within nuclei (“nuclear dots”) can be measured. For each nucleus identified in the nuclear mask (Figure 5A), the highest intensity pixel in the color channel corresponding to the intronic probe is counted as the center of the nuclear dot (Figure 5B,C). Against the possibility this high intensity pixel is a random high intensity photon as measured by the photomultiplier tube, the median intensity in a 5-by-5 pixel neighborhood centered on the high intensity pixel (red box in Figure 5B inset) is chosen to be the strength of the nuclear dot. Coupled with the data for the centroid of each nucleus, these measurements give us a relationship between intronic dot intensity and location on the periphery of the embryo. This relationship reveals a “salt-and-pepper” pattern, in which a wide range of values occurs at any given location in the domain of gene expression (blue dots in Figure 5D). Furthermore, the same dot is likely represented as multiple datapoints, because it may be present in multiple slices of the z-stack.

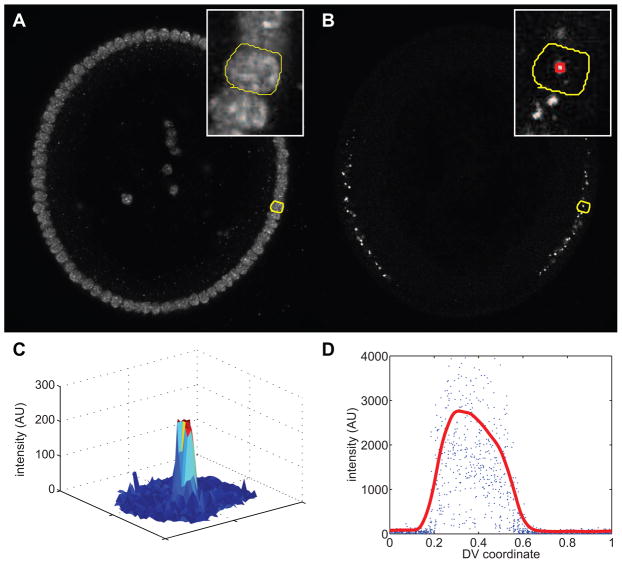
Figure 5. Measuring nuclear dots.

The embryo shown in this image has been immunostained with an anti-histone antibody to mark the nuclei and an intronic RNA probe against sog, which detects nascent transcripts of sog (nuclear dots). Cross-section view with ventral-side down.

(A) Nuclear channel. Yellow curve outlines a single nucleus. Inset: magnification of image near the highlighted nucleus (outlined in yellow).

(B) Intronic probe channel. The yellow curve outlines the same nucleus as in (A). Inset: magnification of image near the highlighted nucleus (outlined in yellow). Red box: the 5-by-5 neighborhood centered on the max intensity pixel.

(C) Surface plot representation of the intensity of the intronic probe channel for only the highlighted nucleus.

(D) Measurement of all intronic probe intensities as a function of DV location (blue dots). Data from each slice of a z-stack are plotted together; a single nascent transcript may be represented multiple times if identifiable in multiple slices. Red curve: smoothed version of the blue dots. The smoothed version identifies the trend.

In order to fit the pattern of nascent transcription to a smooth profile, we exchange the multi-valued relationship between nuclear dot intensity and location for a single-valued, smooth curve (red curve in Figure 5D). We do this in a similar manner to what was described previously [13]. First, the locations of the nuclei are binned into a mesh from minus one to one with 300 points. Next, for every bin that contains nuclei, the top 5 nuclear intensities are averaged together. This averaged value becomes the value of our raw curve at that location. For bins that have fewer than 5 nuclei, all nuclei are averaged together.

If bin i has zero nuclei, a value at location i must be chosen in order to maintain a smooth curve. The program searches bin i − 1 for a value. If no value is found, the program searches bin i − 2. This continues until a value is found to the left of bin i. Next, the program searches in a like manner to the right of bin i. After finding the closest values to the right and to the left of bin i, the value at bin i is the average between these two values.

Finally, the resulting curve is smoothed with a sliding window of five points, resulting in a curve similar to the red curve seen in Figure 5D.

3 Calculation

After the image analysis procedures, the primary data has been transformed into the secondary data, consisting of relationships between intensities of the fluorescent readouts of the molecular species probed and location on the periphery of the embryo. There are two aspects to further calculations that fit our secondary data to empirical models of protein and gene expression, resulting in the fitted parameters that comprise our tertiary data. The first is normalization with respect to nuclear intensity, and the second is data fitting. More details can also be found in the supplementary material.

3.1 Normalization with respect to nuclear intensity

Due to uneven illumination and loss of light collection with z-depth, we have found it useful to normalize the nuclear protein intensities with respect to intensities of the nuclear stain [5]. To ground this normalization in theory, we make the following assumptions. First, we assume the relationship between measured intensity, I_i, of a nuclear protein in nucleus i and the real nuclear concentration of the protein, c_i is as follows:

$$I_i=k_i({\mathrm{\Phi }}_1{c}_i+{\mathrm{\Phi }}_2)$$

Here, the factor k_i depends on the light path from the objective to nucleus i, and the constants Φ₁ and Φ₂ depend on experiment-wide factors, such as microscope settings, the concentration of antibody used, or the non-specific affinity of the antibody for embryonic tissue. In other words, when uneven illumination is taken into account, the fluorescent intensity is proportional to the protein concentration with an additive background constant.

In a similar vein, we assume the intensity, N_i, of the nuclear stain in nucleus i is related to the actual concentration, n_i, of the molecular species by:

$$N_i=k_i({\nu }_1{n}_i+{\nu }_2)$$

We also assume the concentration of the nuclear species is the same in each nucleus throughout the embryo, meaning the term v₁n_i + v₂ can be simply represented by a constant H. This implies

$$N_i=k_{i}H$$

Therefore, to eliminate the unknown dependence of I_i on the lightpath-dependent factor, k_i, we normalize I_i by N_i:

$$t_i=\frac{I_i}{N_i}=\frac{k_i({\mathrm{\Phi }}_1{c}_i+{\mathrm{\Phi }}_2)}{k_{i}H}={\phi }_1{c}_i+{\phi }_2,$$

where the new constants φ₁ and φ₂ are the old constants (Φ₁, Φ₂) divided by H. Thus, this normalized intensity, t_i, is simply proportional to the concentration, c_i, up to an additive background constant.

After normalizing each nuclear protein intensity with respect to the corresponding nuclear stain intensity, the value of t is typically close to one. To return t to a scale similar to its original intensity, we multiply by the mean intensity of all nuclei.

3.2 Data fitting

We next fit our secondary data to empirical curves. Doing so will result in a set of parameters that describe each of our secondary data relationships. We do this for mRNA, nascent transcripts, and nuclear-localized proteins.

3.2.1 mRNA

We fit our data of mRNA expression to “canonical” peaks of gene expression ([5, 13]; see also Figure 6A). In so doing, we can measure, in a systematic way, the dorsal and ventral boundaries of gene expression. Each canonical gene expression profile was obtained by manual alignment of 10 or more instances of gene expression. Once this profile is found, it can be manipulated by translation, stretching/shrinking, addition, and multiplication, in order to fit to a measured gene expression profile. We have found that virtually every measured profile of gene expression can be fit to the canonical profile this way.

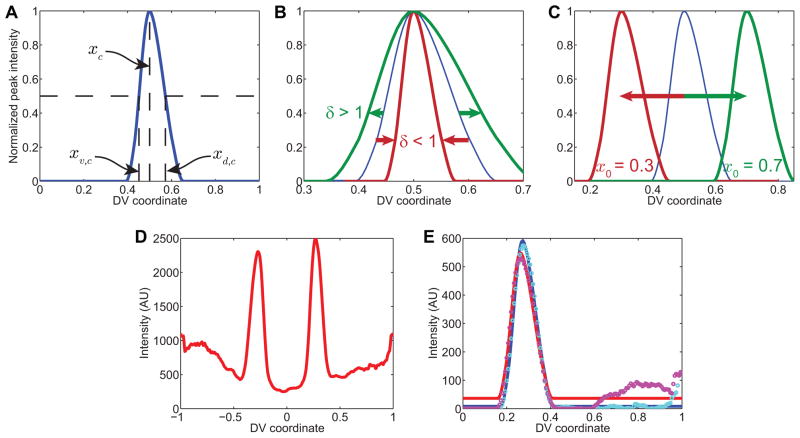
Figure 6. Peak fitting.

(A) Example of canonical gene expression pattern, using vnd. Horizontal dotted lines: half-maximal intensity. x_c is the location of the peak in intensity of the canonical pattern, x_v,c is the location of the ventral border of the canonical pattern, and x_d,c is the location of the dorsal border of the canonical pattern.

(B) Effect of changing the stretching factor, δ. When δ < 1, the pattern shrinks about its peak location (rust-colored curve), and when δ > 1, the pattern expands (green curve). The blue curve is the unstretched canonical pattern for vnd.

(C) Effect of changing the peak location, x₀. When x₀ is set to 0.3, the pattern shifts ventrally (rust-colored curve), while increasing x₀ causes the pattern to shift dorsally (green curve).

(D) Secondary data of vnd pattern from embryo in Figure 1A.

(E) Fits of the stretched and shifted canonical peak of vnd expression to the two peaks in vnd from part (D). Cyan and magenta circles are the right and left halves of (D), respectively. The blue and red solid curves are the fits of the canonical pattern to the measured right- and left-side patterns, respectively.

Consider a canonical gene expression profile, y_c(x), with a peak located at x_c, where x is the coordinate along the DV axis of the embryo (Figure 6A). Each measured gene expression profile, y(x), can be fit to y_c(x) in the following way:

$$y(x)\approx \alpha y_c\left(\frac{(x-x_c)-x_0}{\delta }\right)+\beta$$

In this equation, the two important parameters are the peak location, x₀, and the stretching factor, δ. These two parameters together dictate how the canonical gene expression profile is changed in space to accommodate the measured profile (Figure 6B,C). From these two parameters, we can calculate the dorsal and ventral borders of our measured gene expression profile.

As an example, consider the vnd profile of the embryo in Figure 1A (see Figure 6D). After background subtracting this profile, with the appropriately-sized structuring element [13], and plotting the two halves of the embryo on top of each other, we arrive at Figure 6E (circles; cyan corresponds to the right side of the embryo, and magenta to the left side). The fitted canonical profiles are plotted as solid curves, with blue corresponding to the cyan data points, and red to the magenta. These fits resulted in the parameters δ_R = 0.928, x_0,R = 0.272 and δ_L = 0.957, x_0,L = 0.263 (where R denotes the right side of the embryo, and L denotes the left).

The canonical gene expression profile, y_c(x), has a dorsal and ventral border associated with it, defined as the location in which the peak drops to half-maximal intensity (Figure 6A). If these two locations are denoted as x_d,c and x_v,c, respectively, then x_d and x_v (the dorsal and ventral borders of the measured gene expression profile) are given by:

$$\begin{array}{l}{x}_d=(x_{d,c}-x_c)\delta +x_0\\ x_v=(x_{v,c}-x_c)\delta +x_0\end{array}$$

Therefore, each gene expression profile for each embryo has the parameters δ, x₀, and from these, the dorsal and ventral borders of gene expression can be found quantitatively. Returning to our example of vnd, the canonical borders of gene expression for vnd are x_d,c = 0.572 and x_v,c = 0.451, with x_c = 0.5. Using these numbers in the example, x_d,R = 0.339 and x_d,L = 0.331; x_v,R = 0.227 and x_v,L = 0.216. However, we report the results of the dorsal and ventral borders of gene expression as the average of the borders calculated from both sides, meaning x_d = 0.335 and x_v = 0.221.

This approach has advantages over simply finding the location where the measured gene expression profile crosses half-maximal intensity for three reasons. First, if the measured gene expression profiles are noisy, then both the maximal intensity and the locations of half-maximal intensity cannot be found reliably. Second, finding the borders directly uses only a handful of data points from the measured gene expression profile, and thus may be inaccurate. Finally, using only a couple of data points does not allow the calculation of confidence intervals on the parameter estimates. Using the fitting procedure described here overcomes these problems.

The two parameters α and β refer to the max intensity of the peak and the background levels of image intensity, respectively. In general, neither of these fitted parameters informs us about the gene expression pattern, given that image intensity and background can be altered by microscope settings and slight differences in experimental procedure. However, if these factors are controlled for, then it is possible to perform a semi-quantitative analysis on the strength of gene expression, in which fluorescent intensities of either protein or gene expression can be compared embryo-to-embryo [13]. (See Discussion for more details.)

Our analysis package uses the Matlab function “fit” to find these parameters. Additionally, the function returns confidence estimates on the fitted parameters, α, β, δ, and x₀. We propagate these confidence intervals from δ and x₀ to x_d and x_v by the following formulae:

$$\begin{array}{l}{dx}_d=\sqrt{{(x_{d,c}-x_c)}^2{(d\delta )}^2+{({dx}_0)}^2}\\ {dx}_v=\sqrt{{(x_{v,c}-x_c)}^2{(d\delta )}^2+{({dx}_0)}^2}\end{array}$$

Here, the terms dδ, and dx₀ represent the radii of the 68% confidence intervals on these parameters, and can be thought of as the magnitude of one standard deviation. The interpretation of dx_d and dx_v are thus the magnitude of one standard deviation in these borders. These uncertainty measurements are typically on the order of one tenth of one percent of the DV axis, which is less than one nucleus wide. For our example embryo, dx_d = 0.0022 and dx_v = 0.0017.

Profiles of nascent transcripts and nuclear proteins can also be fit using this procedure. To fit profiles of nascent transcripts, the smoothed profile (red curve in Figure 5D) is treated as the measured gene expression profile, y(x). For nuclear proteins, see below (Section 3.2.2).

One thing to point out is this fitting procedure requires the ventral midline of the embryo to have previously been identified. This can be done either manually (see Example 3, Section S1.8.7 in the supplementary material), through the fitting of another molecular species that allows for unambiguous identification of the midline (e.g., the dl nuclear gradient; see Section 3.2.2), or through a rules-based procedure. Our current formulation employs the rules-based procedure, in which the program looks for certain kinds of peak maxima depending on which genes the user supplies. Once these peak maxima are found, the location of the midline is inferred. For example, if the gene is vnd, which is expressed in a symmetric, two-stripe, ventral-lateral pattern, the program locates the peak maxima and places the midline directly in between.

Another feature of this fitting procedure is that it can detect and resolve multiple gene expression profiles in the same color channel, as long as the two profiles are sufficiently separated in space. This is illustrated in Figure 1C and also in Figure 10. This feature can be extended to genes that have multiple domains of expression, such as rho and hb (see Section S.1.8.9 for an example).

3.2.2 Nuclear proteins

We originally developed this protocol to analyze the dl nuclear gradient. According to our previous analysis, the dl gradient can be empirically fit to a Gaussian-like function plus a slowly declining tail [5, 13]:

$$c_{dl}(x)\approx Aexp\left(-\frac{{(x-\mu )}^2}{2{\sigma }^2}\right)+B+M\mid x\mid$$ (1)

Using this empirical model, the amplitude of the peak in the dl gradient is A, the gradient “basal levels” (i.e., the value where the gradient ceases to decay according to x²) is B, the length scale of the Gaussian-like behavior is σ, the location of the ventral midline is μ, and the slope of the shallowly declining gradient tail is M.

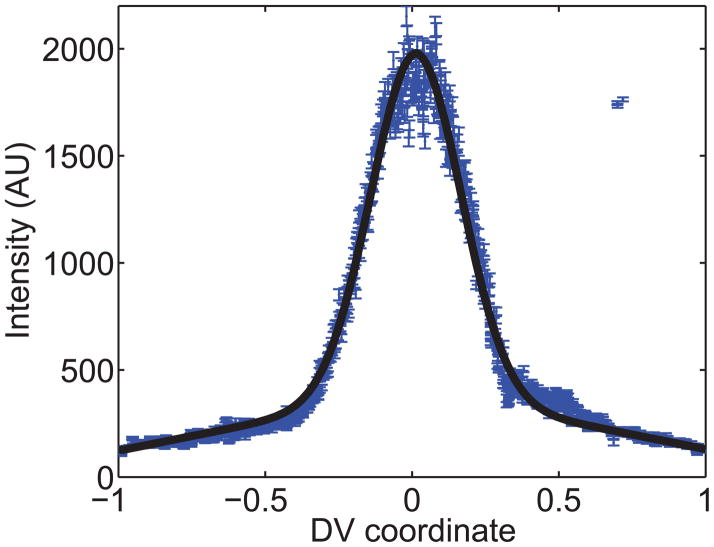
As an example, consider the dl nuclear gradient of the embryo in Figure 1A. After the image analysis step, we can plot the secondary data (the value of t for each nucleus) vs. nuclear location (blue dots with errorbars in Figure 7). Fitting these secondary data to Eqn 1 (see also black curve in Figure 7), we find the value of the Gaussian length parameter, σ, to be 0.15, and the normalized slope of the gradient tail, M/A, to be −0.17.

Figure 7. Gaussian fitting.

The dl nuclear gradient from the wildtype embryo in Figure 1A is plotted, with errorbars of one standard deviation, as secondary data. The black curve is the best-fit curve according to Eqn 1.

Despite the fact that Eqn 1 appears quite specific to dl, this can still be useful in other situations. For example, it is plausible that the pattern of pMad in the early embryo conforms well to Eqn 1. Even when the nuclear protein of interest does not conform to Eqn 1, as was the case with Sna-GFP [13], fitting the nuclear protein profile to Eqn 1 can often reliably find the midline, amplitude, and basal levels of the profile. The parameter σ will also be correlated to width of the profile, but a strict definition of σ will be lost.

However, nuclear proteins that do not conform to Eqn 1 can alternatively be fit to a canonical profile. As this is the more general case, we have written the workflow of our program to fit any nuclear protein not labeled ‘dl’ to a canonical profile (See S1.2).

As in fitting mRNA profiles, we use the Matlab function “fit” to find these parameters as well as their 68% confidence intervals.

4 Results

We use the dl morphogen system in nuclear cycle 14 (2–3 hour old) Drosophila embryos as a test case for our analysis and data-fitting program. Here we present two example scenarios that demonstrate our protocol can detect very subtle phenotypes not easily distinguished by eye. We also present a third example scenario that helps describe the generalizability of the program to alternative geometries.

4.1 Expanded dl nuclear gradient in embryos carrying a copy of Venus-tagged dl

The wildtype dl nuclear gradient conforms to a Gaussian-like decay with sloping tails (Eqn 1) [13, 5]. In previous work, we measured the spatial extent of the dl gradient, which is an important parameter in determining the ability of dl to pattern the DV axis. For wildtype embryos, we have found the width of the dl gradient to be roughly σ_wt = 0.14 ± 0.01 (Figure 8D; [5, 13]). Using our protocol, we can detect a subtle, systematic difference between the width of the wildtype dl nuclear gradient and width in embryos with perturbed dl gradients. Here, we present a case in which embryos from mothers with one null allele of endogenous dl and one copy of YFP venus-tagged dl (hereafter referred to as dl-venus embryos) have a statistically detectable increase in gradient width.

We detected the dl nuclear gradient in fixed dl-venus embryos both by using an antibody directed against dl (upper left panel in Figure 8A) and an antibody directed against GFP (which also recognizes Venus; upper right panel in Figure 8A). Judging from the similarity between the two images, we could make a case these two gradients are identical (for comparison, see merged image in the lower left panel in Figure 8A). However, the secondary data obtained from our image analysis protocol shows the gradient detected by anti-GFP, is wider than that detected by anti-dl (Figure 8B,C). Using our empirical model of the dl gradient, we measured the widths of these two gradients to be ${\sigma }_V^{dl}=0.16\pm 0.01$ for detection by anti-dl, and σ_V = 0.17 ± 0.01 for detection of Venus by anti-GFP (mean ± std dev; Figure 8D). This difference between these distributions in widths across the set of 29 embryos is statistically significant, using the t-test for correlated samples (p-value < 10⁻⁶; [13]).

We also found the gradient detected by anti-dl in dl-venus embryos is wider than the dl nuclear gradient in wildtype embryos. In summary, ${\sigma }_{wt}<{\sigma }_V^{dl}<{\sigma }_V$, implying the extent of the actual spatial gradient of dl-Venus in the dl-venus embryos is σ_V = 0.17, wider than the gradient of endogenous dl (σ_wt = 0.14) in these same embryos. Since the anti-dl antibody will recognize both endogenous dl and dl-Venus, the anti-dl measurement in these embryos ( ${\sigma }_V^{dl}=0.16$) is some intermediate value. Furthermore, the measurement of the dl-Venus gradient using anti-GFP is upheld by measurements of Venus fluorescence in live dl-venus embryos (Figure 8D).

This same trend is also seen in embryos from mothers with one null allele of endogenous dl and one copy of gfp-tagged dl (hereafter referred to as dl-gfp embryos; see Figure 9). The gradient width as detected by anti-dl ( ${\sigma }_G^{dl}=0.20\pm 0.02$) is not as wide as that detected by anti-GFP (σ_G = 0.23 ± 0.02), yet both are wider than the wildtype gradient. Live studies of these embryos also show the anti-GFP measurement to be accurate (Figure 8D).

4.2 Shifted vnd dorsal border in embryos with expanded dl gradients

We have also asked if the expanded width of the dl gradient in dl-gfp embryos has an effect on gene expression. We immunostained dl-gfp embryos with anti-dl and anti-histone H3 (to detect nuclei), and hybridized them with an antisense riboprobe against vnd (Figure 9A). It is clear from looking at the image that these embryos have expanded dl gradients (compare with Figure 1A). However, it is not obvious whether vnd expression domain is shifted as a result (see Figure 9B for a plot of the secondary data of this embryo). However, after fitting the vnd peaks to the vnd canonical gene expression profile (see Figure 9C for example), we find both the ventral and dorsal borders of vnd are shifted dorsally compared to wildtype (see boxplot in Figure 9D). For example, from our calculations, the dorsal border of vnd in dl-gfp embryos, x_d,G, is 0.36 ± 0.02, while in wildtype, x_d,wt = 0.32 ± 0.02. This difference of 4% DV axis length translates to a shift by roughly 2 nuclei.

4.3 Quantifying gene expression profiles in other geometries: saggital sections of Drosophila embryos

To demonstrate that our analysis is generalizable to geometries other than the circular cross-section of the Drosophila embryo, we present an example of quantification of gene expression profiles in a saggital section of the Drosophila embryo (Figure 10A). We chose embryos that express a dominant form of the Toll receptor (Toll10B) present in an anterior-posterior gradient (see Materials and Methods; [14]. The endogenous, ventral-to-dorsal nuclear gradient of Dorsal is missing in these embryos, replaced instead by an anterior-posterior nuclear gradient of Dorsal. We hybridized these embryos with riboprobes against sna, vnd, sog, and ind (Figure 10A) and quantified their gene expression profiles in sliding window around the embryo periphery (Figure 10B; compare to Figure 3). Aside from generating new canonical profiles for each gene, due to the different spacing as a result of changing the geometry, no alterations to the program is required. Note that both sna and ind occupy the same color channel; our peak-fitting procedure can differentiate between the two peaks (Figure 10C). This example demonstrates the program’s ability to quantify profiles in different geometries and to differentiate between two peaks of gene expression in the same color channel.

5 Discussion

In this paper, we have presented a protocol that analyzes primary fluorescent image data to produce relationships between fluorescent intensity and location on the periphery of an optical section within a single embryo. These relationships act as secondary data, which are further fit to empirical models of protein and/or gene expression, resulting in tertiary data: parameters physically meaningful to the researcher, such as boundaries of gene expression. Thus, this approach can distill fluorescent image data down to a handful of parameters, making it possible to compare important features of protein or gene expression across a large number of embryos, and/or across sets of embryos of different genotypes.

The method presented here is generalizable to other systems beyond cross-sections of early Drosophila embryos. In some cases, the Matlab files may work on other systems with no need for adjustment. One constraint is the pertinent information must be limited to the periphery of the embryo. However, the embryo need not be a perfect circle. Sagittal sections of Drosophila embryos work as well (see Section 4.3). Sea urchin embryos, which have more of a pear-like shape, may also work. The Matlab codes to support our protocol, along with a user’s manual, is available in the supplementary material.

There are several avenues for improvement. First, with the exception of the Gaussian-fit of the dl nuclear gradient, our empirical model of gene and protein expression is limited to domains that can vary in width and location, but not shape. For example, if one is interested in empirically modeling a gene that changes shape depending on the age of the embryo, such as for sog, or zen – the code must be adjusted to include stage-specific canonical profiles. In previous work, we took this difficulty into account manually, on a case-by-case basis, and did not incorporate it into the automated peak-fitting code [13]. Another example would be a gene expression pattern changing shape in genetically manipulated embryos. In sna mutants, sog, vnd, and other ventral-laterally expressed genes are derepressed ventrally, drastically changing the shape of their profiles. This problem can be overcome by creating a separate canonical profile for these alternative conditions.

Second, with careful attention to experimental detail and imaging conditions, it is possible to perform semi-quantitative analysis of fluorescent images (see also Section 3.2.1). In semi-quantitative analysis, not only are spatial patterns accurate, but background-subtracted fluorescent intensities are directly proportional to protein or transcript levels [2–5, 13]. This typically requires all experimental procedures to be performed in one set, all by the same user, and microscope settings to be constant. Changes in laser power are permissible, as they have a predictable effect on the fluorescent intensity of the image, but must be measured with each imaging session. Additionally, background levels must be measured, through imaging immunostained embryos that lack the protein of interest. The measurements of laser power and background levels must serve as additional inputs to the image analysis code. The automated protocol presented here currently does not support these inputs.

Finally, the procedure for nuclear detection can be improved. At low nuclear densities, such as in earlier timepoints of Drosophila development (nc 11 and 12), there is a very high incidence of false detection of nuclei. Manual nuclear identification resolves this issue [13], but is not a part of the code presented here. Furthermore, our detection of nuclei takes each slice in a z-stack individually. A more comprehensive, three-dimensional nuclear detection algorithm would expand on the accuracy of the code. For example, currently for identification of nascent transcripts, the strength of the nuclear dot present within each slice of a z-stack is plotted and a global trend in the data along the dorsal-ventral axis is inferred based on application of a smoothing function (see Fig. 5D). With three-dimensional nuclear detection, a single datapoint for each nascent transcript could be obtained (i.e. two datapoints for transcripts from autosomes; and 1 or 2 datapoints for transcripts from the X, depending on whether the embryo is male or female).

Because our approach also results in a rigorous statistical analysis of the uncertainty in the tertiary data, we can have confidence in our ability to detect subtle phenotypes. We have demonstrated this in two examples using the dl morphogen gradient in the early Drosophila embryo as a model system. These subtle phenotypes, not easily detected by eye, are nonetheless very significant, from a statistical standpoint. It is often the case that patterning is robust in developing embryos, making analysis of mutants challenging. Utilizing this method, we can be statistically confident in characterizing small changes in the system.

Another important advantage to the method of using empirical models of protein/gene expression is that we do not neglect the bulk of our secondary data. For instance, one approach to determining gene expression boundaries is to find where the peak of gene expression crosses the half-maximal intensity. In such a case, only two small regions of the secondary data are used: the region at the peak intensity (to determine the maximal value) and the region near the border (to determine the location). Furthermore, in this scenario, the ability to accurately measure the boundary location becomes quite weak when there is significant noise in the secondary data.

This is clearly not the first research to empirically model protein distributions or gene expression patterns. The Bicoid gradient, which is a protein gradient along the anterior-posterior axis in the early Drosophila embryo at the same time as the dl nuclear gradient, has often been empirically modeled by an exponential profile [17–19]. However, these choices of empirical models are very specific to the protein being studied. A more general approach, which we employ for gene expression, would be to use a canonical protein profile. Such an approach is mechanism-independent and can be used for any arbitrarily-shaped, but consistent, distribution.

The empirical modeling we present here, when related back to the canonical pattern, results in the definition of physically meaningful parameters, such as shifts in the locations of gene expression boundaries. This is not always the case in similar modeling studies, as another general approach that has been used to model gene expression patterns is fitting to Fourier series [20]. For this reason, when the mechanism is unknown, we argue for the utility of our approach based on empirical fitting. However, the future challenge is to use our quantitative measurements (i.e., the physically meaningful parameters) to help build mechanistic models of gene expression and infer biomolecular properties associated with the embryo. Ultimately, the overlying goal is to use such quantitative analyses to understand how gene expression in the embryo is controlled at the level of the gene regulatory network [21, 22].

Highlights.

• Morphogen gradients guide gene expression in the developing Drosophila embryo

• We develop computational methods to characterize domain boundaries

• This method yields parameters that can be compared in large datasets

• Canonical curve fitting produces high-confidence measurements resistant to noise

• Our quantitative analysis can detect subtle phenotypes in mutant embryos

Abbreviations

dl

Dorsal

nc

nuclear cycles

DV

dorsal-ventral

GFP

green fluorescent protein

YFP

yellow fluorescent protein

sog

short-gastrulation

zen

zerknüllt

vnd

ventral-neuroblasts defective