Theoretical study on high order interior tomography

Abstract

In this paper, we study a new type of high order interior problems characterized by high order differential phase shift measurement. This problem is encountered in local x-ray phase-contrast tomography. Here we extend our previous theoretical framework from interior CT to interior differential phase-contrast tomography, and establish the solution uniqueness in this context. We employ the analytic continuation method and high order total variation minimization which we developed in our previous work for interior CT, and prove that an image in a region of interest (ROI) can be uniquely reconstructed from truncated high order differential projection data if the image is known a priori in a sub-region of the ROI or the image is piecewise polynomial in the ROI. Preliminary numerical experiments support the theoretical finding.

1. Introduction

Since its invention in 1973, x-ray computed tomography (CT) has revolutionized medical imaging and become a cornerstone of modern radiology. Improving image resolution and reducing radiation dose are two critical issues in biomedical applications and remain the focuses of CT research. In conventional x-ray imaging, image contrast arises from attenuation discrepancy due to differences in composition, thickness and density within an object. Attenuation-based imaging shows excellent contrast only when highly attenuating structures are embedded in a weakly absorbing background [1]. However, biological soft tissues consist mainly of light elements, such as hydrogen, carbon, nitrogen and oxygen, and its elemental makeup is nearly uniform with little density variation. Hence, the attenuation contrast is insufficient to extract structural features of soft tissues [2]. Many normal and diseased tissues such as cancers display poor image contrast in current x-ray images as they have very similar attenuation characteristics, especially attenuation-based imaging is difficult to detect early-stage tumors [3].

While the attenuation characteristics requires tradeoffs between contrast resolution and radiation dose, x-ray phase-contrast imaging utilizes the diffraction properties of x-rays, and reveals significant differences indistinguishable with attenuation-based imaging. The propagation of x-rays in a medium is macroscopically characterized by the complex index of refraction. In the x-ray spectrum, the index of refraction for biological tissues is n = 1−δ+iβ, where n is approximately 1, δ and β quantify the phase distortion and magnitude attenuation respectively [4]. At x-ray energies of 20–100 keV, δ is about three orders of magnitude greater than β, depending on the x-ray wavelength and electron density [5]. Since the total phase shift is a line integral along an x-ray path, x-ray phase-contrast imaging generates projections of a refractive index distribution that can be inverted using x-ray CT techniques [6,7]. Moreover, because the x-ray phase shift varies more slowly than the attenuation counterpart at higher energies, x-ray phase-contrast imaging can be performed at an optimal energy level to minimize radiation damage to animals or humans.

The use of x-ray phase shifts as a new contrast mechanism has generated a considerable interest over the past decade [8–12]. In-line phase-contrast tomography is a computational imaging technique that reconstructs a 3D refractive index distribution from the intensity distributions of a coherent wave [13]. Mathematically, such an intensity distribution can be approximately related to the Laplacian of the parallel-beam projection of a refractive index distribution in an object. When an object is longitudinally homogeneous and the principal axis of the object is perpendicular to the direction of a coherent radiation beam, the Laplacian of the 2D parallel-beam projection is reduced to second derivative data of the 1D refractive index projection. Actually, even if an object is just locally homogeneous along one direction, the aforementioned second derivative data model can be still applied [13].

X-ray phase-contrast imaging can be also implemented using interferometry and diffractometry to extract differential phase shift data which correspond to the first derivatives of a refractive index projection. Because both interferometry and diffractometry require monochromatic x-rays and high precision crystals, they are necessarily associated with synchrotron radiation facilities [14]. Recently, Pfeiffer et al. [15,16] made a breakthrough to x-ray Talbot grating imaging so that x-ray phase-contrast signals can be generated using a regular x-ray tube. This grating-based approach suggests widespread applications such as biomedical imaging, industrial nondestructive testing, and security screening [15,17]. This approach defines small imaging apertures and produces individually coherent secondary sources with a source grating in front of a hospital-grade x-ray tube. Then, interference fringes are superimposed at a Talbot distance, and analyzed with phase-stepping interferometry based on the Talbot effect, a periodic self-imaging phenomenon, to extract the first derivative or differential data of a refractive index projection.

In this paper, we study high order interior tomography, which is to reconstruct an image in a region of interest (ROI) from the m-th order differential projection data associated with the ROI. In the context of x-ray differential phase-contrast imaging, we have m = 1 or m = 2 as the most common examples. High order interior tomography will allow us to use smaller and finer detectors and/or gratings for more imaging flexibility, better image quality and lower system cost. In the next section, we present our analytical results on the uniqueness of the solution to the high order interior problem. In the third section, we report our numerical simulation results. In the last section, we discuss relevant issues and conclude the paper.

2. High order interior problem and solution uniqueness

Without loss of generality, we assume the following conditions throughout this paper:

• Condition (1)

  An object image f₀(x) is compactly supported on a disc ${\Omega }_A=\{x=(x_1,x_2)\in {\mathbb{R}}^2:\mid x\mid <A\}$, where A is a positive constant. Furthermore, f₀ ∈ C^m(Ω_A), where m ≥ 1 is a constant integer;

• Condition (2)

  An internal ROI is a smaller disc ${\Omega }_a=\{x=(x_1,x_2)\in {\mathbb{R}}^2:\mid x\mid <a\}$, as shown in Fig. 1, where a is a positive constant and a < A;

• Condition (3)
  m is a positive integer, the m-th order differential projections of f₀ through the ROI

  $${\partial }_s^{m}R{f}_0(s,\theta ),-a<s<a,\theta \in S^1,$$ (1)

  are available, where

  $$R{f}_0(s,\theta )={\int }_{-\infty }^{\infty }{f}_0(s\theta +t{\theta }^{\perp })dt,$$

  $$\theta =(\cos \alpha ,\sin \alpha ),{\theta }^{\perp }=(-\sin \alpha ,\cos \alpha ),0\le \alpha <2\pi .$$

Fig. 1.

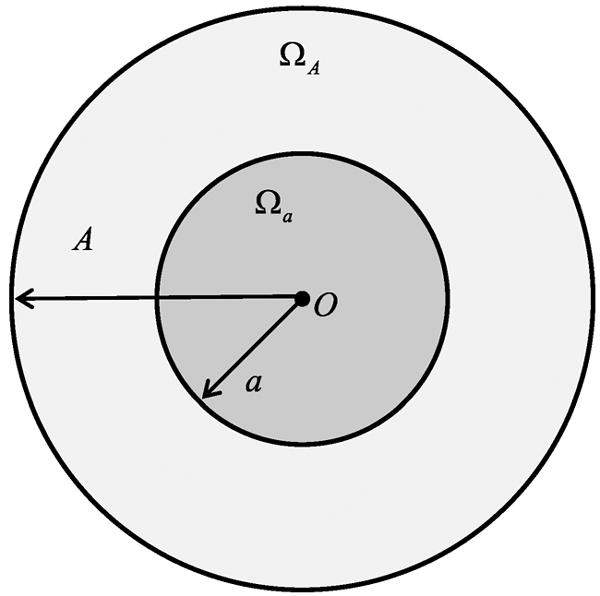
Object with a compact support and a region-of-interest (ROI) in the support.

The high order interior problem is to find an image f(x) from the truncated m-th order differential projection data such that

• Condition (4)

  f(x) is compactly supported on the disc Ω_A and f ∈ C^m(Ω_A);

• Condition (5)

  ${\partial }_s^{m}Rf(s,\theta )={\partial }_s^{m}R{f}_0(s,\theta ),-a<s<a,\theta \in S^1$ −a < s < a, θ ∈ S¹.

In the following, we will establish a theoretical framework similar to [18,19]. It is well known that under Conditions (4) and (5) the interior problem with truncated projection data (m = 0) does not have a unique solution in an unconstrained setting [20,21]. Evidently, the high order interior problem has no unique solution either in an unconstrained setting. The following theorem characterizes the structure of solutions to the high order interior problem.

Theorem 1. Any image f(x) satisfying Conditions (4) and (5) can be written as f(x) = f₀(x) + u(x) for $x\in {\mathbb{R}}^2$, where u(x) is an analytic function in the disc Ω_a, and

$${\partial }_s^{m}Ru(s,\theta )=0,-a<s<a,\theta \in S^1.$$

We call such an image f(x) a candidate image, and correspondingly u(x) an ambiguity image.

Proof: Let u(x) = f(x) − f₀(x). Clearly, u(x) is compactly supported on Ω_A, u ∈ C^m(Ω_A), and

$${\partial }_s^{m}Ru(s,\theta )=0,-a<s<a,\theta \in S^1.$$ (2)

By the Radon inversion formula, we have

$$u\left(x\right)=\frac{1}{4{\pi }^2}{\int }_0^{2\pi }{\int }_{-\infty }^{\infty }\frac{{\partial }_{s}Ru(s,\theta )}{x\cdot \theta -s}dsd\alpha =\frac{1}{4{\pi }^2}{\int }_0^{2\pi }{\int }_{\mid s\mid \ge a}\frac{{\partial }_{s}Ru(s,\theta )}{x\cdot \theta -s}dsd\alpha +\frac{1}{4{\pi }^2}{\int }_0^{2\pi }{\int }_{\mid s\mid \le a}\frac{{\partial }_{s}Ru(s,\theta )}{x\cdot \theta -s}dsd\alpha =u_1\left(x\right)+u_2\left(x\right)$$ (3)

where

$$\theta =(\cos \alpha ,\sin \alpha ),$$

$$u_1\left(x\right)=\frac{1}{4{\pi }^2}{\int }_0^{2\pi }{\int }_{\mid s\mid \ge a}\frac{{\partial }_{s}Ru(s,\theta )}{x\cdot \theta -s}dsd\alpha ,$$ (4)

$$u_2\left(x\right)=\frac{1}{4{\pi }^2}{\int }_0^{2\pi }{\int }_{\mid s\mid \le a}\frac{{\partial }_{s}Ru(s,\theta )}{x\cdot \theta -s}dsd\alpha ,$$ (5)

and u₁(x) is analytic in Ω_a [19]. To deal with u₂(x), we perform the Taylor expansion of ∂_sRu(s, θ) with variable s:

$$\begin{array}{cc}\hfill {\partial }_{s}Ru(s,\theta )& =\sum _{k=0}^{m-1}\frac{{\partial }_s^{k+1}Ru(0,\theta )}{k!}{s}^k=\sum _{k=0}^{m-1}\frac{{\partial }_s^{k+1}Ru(0,\theta )}{k!}\sum _{l=0}^k{C}_k^l{(x\cdot \theta )}^{k-1}{(s-x\cdot \theta )}^l\hfill \\ \hfill & =\sum _{l=0}^{m-1}\left(\sum _{k=l}^{m-1}\frac{C_k^l{\partial }_s^{k+1}Ru(0,\theta ){(x\cdot \theta )}^{k-1}}{k!}\right){(s-x\cdot \theta )}^l\hfill \\ \hfill & =\sum _{l=1}^{m-1}\left(\sum _{k=l}^{m-1}\frac{C_k^l{\partial }_s^{k+1}Ru(0,\theta ){(x\cdot \theta )}^{k-1}}{k!}\right){(s-x\cdot \theta )}^l+\sum _{k=0}^{m-1}\frac{{\partial }_s^{k+1}Ru(0,\theta ){(x\cdot \theta )}^k}{k!},s\in (-a,a).\hfill \end{array}$$ (6)

Inserting Eq. (6) into Eq. (5), we have

$$\begin{array}{cc}\hfill u_2\left(x\right)& =\frac{1}{4{\pi }^2}{\int }_0^{2\pi }{\int }_{\mid s\mid \le a}\frac{{\partial }_{s}Ru(s,\theta )}{x\cdot \theta -s}dsd\alpha \hfill \\ \hfill & =-\frac{1}{4{\pi }^2}\sum _{l=1}^{m-1}\sum _{k=l}^{m-1}{\int }_0^{2\pi }\left(\frac{C_k^l{\partial }_s^{k+1}Ru(0,\theta ){(x\cdot \theta )}^{k-l}}{k!}\right)\left({\int }_{\mid s\mid \le a}{(s-x\cdot \theta )}^{l-1}ds\right)d\alpha +\frac{1}{4{\pi }^2}\sum _{k=0}^{m-1}{\int }_0^{2\pi }\frac{{\partial }_s^{k+1}Ru(0,\theta ){(x\cdot \theta )}^k}{k!}\left(\text{p.v.}{\int }_{\mid s\mid \le a}\frac{ds}{x\cdot \theta -s}\right)d\alpha \hfill \\ \hfill & =-\frac{1}{4{\pi }^2}\sum _{l=1}^{m-1}\sum _{k=l}^{m-1}{\int }_0^{2\pi }\left(\frac{C_k^l{\partial }_s^{k+1}Ru(0,\theta ){(x\cdot \theta )}^{k-l}}{k!}\right)\left(\frac{{(a-x\cdot \theta )}^l-{(-a-x\cdot \theta )}^l}{l}\right)d\alpha +\frac{1}{4{\pi }^2}\sum _{k=0}^{m-1}{\int }_0^{2\pi }\frac{{\partial }_s^{k+1}Ru(0,\theta ){(x\cdot \theta )}^k}{k!}\text{ln}\left(\frac{a+x\cdot \theta }{a-x\cdot \theta }\right)d\alpha .\hfill \end{array}$$ (7)

The Taylor expansion of ln $\left(\frac{a+x\cdot \theta }{a-x\cdot \theta }\right)$ is

$$\begin{array}{cc}\hfill \text{ln}\left(\frac{a+x\cdot \theta }{a-x\cdot \theta }\right)& =\text{ln}\left(\frac{1+x\cdot \theta ∕a}{1-x\cdot \theta ∕a}\right)\hfill \\ \hfill & =\text{ln}(1+x\cdot \theta ∕a)-\text{ln}(1-x\cdot \theta ∕a)\hfill \\ \hfill & =\sum _{l=1}^{\infty }\frac{{(-1)}^{l-1}}{l}{\left(\frac{x\cdot \theta }{a}\right)}^l-\sum _{l=1}^{\infty }\frac{{(-1)}^{l-1}}{l}{\left(-\frac{x\cdot \theta }{a}\right)}^l\hfill \\ \hfill & =\sum _{l=0}^{\infty }\frac{2}{2l+1}{\left(\frac{x\cdot \theta }{a}\right)}^{2l+1}.\hfill \end{array}$$ (8)

Inserting Eq. (8) into Eq. (7), we have

$$u_2\left(x\right)=-\frac{1}{4{\pi }^2}\sum _{l=1}^{m-1}\sum _{k=l}^{m-1}{\int }_0^{2\pi }\left(\frac{C_k^l{\partial }_s^{k+1}Ru(0,\theta ){(x\cdot \theta )}^{k-l}}{k!}\right)\left(\frac{{(a-x\cdot \theta )}^l-{(-a-x\cdot x\cdot \theta )}^l}{l}\right)d\alpha +\frac{1}{2{\pi }^2}\sum _{l=0}^{\infty }\sum _{k=0}^{m-1}{\int }_0^{2\pi }\frac{{\partial }_s^{k+1}Ru(0,\theta ){(x\cdot \theta )}^{2l+k+1}}{k!(2l+1)a^{2l+1}}d\alpha .$$ (9)

Clearly, u₂(x) is analytic in Ω_a. Hence, u(x) is analytic in Ω_a.

Basing on Theorem 1, we can obtain the unique solution to the high order interior problem under some practical constrains.

First, if an image in a sub-region of the ROI is known a priori, then the image in the entire ROI can be uniquely determined.

Theorem 2. Let f(x) be a candidate image. If f(x) = f₀(x) in a sub-region Ω_small (as shown in Fig. 2) of an ROI Ω_a, then f(x) = f₀(x) in Ω_a.

Fig. 2.

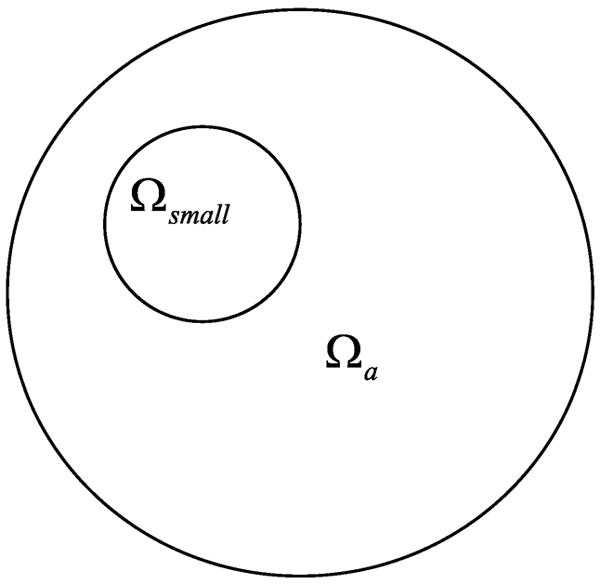
Known sub-region in the ROI.

Proof: From Theorem 1, we have f(x) = f₀(x) + u(x), where u(x) is analytic in Ω_a. Since f(x) = f₀(x) holds in Ωsmall, we have u(x) = 0 in Ω_small, which means u(x) = 0 in the entire Ω_a in light of the property of an analytic function, that is, f(x) = f₀(x) in Ω_a.

Next, let us prove that an ambiguity image cannot be polynomial in the ROI unless it is identically zero. Then, we prove that the ROI image can be uniquely reconstructed via high order total variation minimization under the assumption that the image is piecewise polynomial in some sub-regions within the ROI.

Lemma 1 [19]. Suppose that a is a positive constant. If

• (a)g(z) is analytic in $\mathbb{C}\backslash (-\infty ,-a]\cup [a,+\infty )$;
• (b)p(x) is a polynomial;
• (c)$g\left(x\right)=\frac{1}{\pi }\text{p.v}{\int }_{\mid t\mid <a}\frac{p\left(t\right)}{x-t}dt$, for x ∈ (−a, a),

then $\underset{y\to 0+}{\text{lim}}$, for x ∈ (−∞, −a) ∪ (a, +∞).

Lemma 2. Suppose that a and A are positive constants with a < A. If a function v(x) satisfies

• (d)v(x) is bounded with supp v ⊆ [−A, A];
• (e)v(x) = p(x) for x ∈ (−a, a), where p(x) is polynomial;
• (f)
  Hv(x = q(x), for x ∈ (−a, a), where Hv(x) is the Hilbert transform of v(x); that is,

  $$Hv\left(x\right)=\frac{1}{\pi }\text{p.v.}{\int }_{\mathbb{R}}\frac{v\left(t\right)}{x-t}dt,$$

  and q(x) is a polynomial,

then v(x) = 0 for x ∈ (−∞,∞).

Proof: The function (see Corollary 4.1.2 on page 40 in [22])

$$F\left(z\right)=\frac{1}{\pi }{\int }_{\mid t\mid \ge a}\frac{v\left(t\right)}{t-z}dt,$$ (10)

is analytic on $\mathbb{C}\backslash (-\infty ,-a]\cup [a,+\infty )$, and

$$\underset{y\to 0+}{\text{lim}}\text{Im}\left(F\right(x+iy\left)\right)=v\left(x\right),$$ (11)

for x ∈ (−∞, −a) ∪ (a, ∞) almost everywhere [19].

By Condition (f), we have

$$\begin{array}{cc}\hfill F\left(x\right)& =\frac{1}{\pi }\text{p.v.}{\int }_{\mathbb{R}}\frac{v\left(t\right)}{t-x}dt-\frac{1}{\pi }\text{p.v.}{\int }_{\mid t\mid <a}\frac{v\left(t\right)}{t-x}dt\hfill \\ \hfill & =Hv\left(x\right)+\frac{1}{\pi }\text{p.v.}{\int }_{\mid t\mid <a}\frac{p\left(t\right)}{x-t}dt\hfill \\ \hfill & =q\left(x\right)+\frac{1}{\pi }\text{p.v.}{\int }_{\mid t\mid ,a}\frac{p\left(t\right)}{x-t}dt,x\in (-a,a).\hfill \end{array}$$ (12)

Therefore, by analytic continuation, F (z) can be split into the following two terms

$$F\left(z\right)=q\left(z\right)+g\left(z\right),z\in \mathbb{C}\backslash (-\infty ,-a]\cup [a,+\infty ),$$ (13)

where

$$g\left(x\right)=\frac{1}{\pi }\text{p.v.}{\int }_{\mid t\mid <a}\frac{p\left(t\right)}{x-t}dt,\text{for}x\in (-a,a),$$

By Lemma 1, we obtain

$$\underset{y\to 0+}{\text{lim}}\text{Im}\left(g\right(x+iy\left)\right)=p\left(x\right),\text{for}x\in (-\infty ,-a)\cup (a,+\infty ).$$ (14)

Therefore,

$$\begin{array}{cc}\hfill \underset{y\to 0+}{\text{lim}}\text{Im}\left(F\right(x+iy\left)\right)& =\underset{y\to 0+}{\text{lim}}\text{Im}\left(q\right(x+iy\left)\right)+\underset{y\to 0+}{\text{lim}}\text{Im}\left(g\right(x+iy\left)\right)\hfill \\ \hfill & =\text{Im}\left(q\right(x\left)\right)+\underset{y\to 0+}{\text{lim}}\text{Im}\left(g\right(x+iy\left)\right)=\underset{y\to 0+}{\text{lim}}\text{Im}\left(g\right(x+iy\left)\right)=p\left(x\right).\hfill \end{array}$$ (15)

Combining Eqs (11), (14) and Condition (e), we have

$$v\left(x\right)=p\left(x\right),\text{for a.e.}x\in (-\infty ,\infty ).$$ (16)

Condition (d) and Eq. (16) imply p(x) ≡ 0. Hence, v(x) = 0 for a.e. x ∈ (−∞, ∞), which completes the proof.

Theorem 3. If an ambiguity image u(x) satisfies

• (g)u(x) = p(x) for x ∈ Ω_a, where p(x) is a 2-D polynomial function;
• (h)${\partial }_s^{m}Ru(s,\theta )=0$, for s ∈ (−a, a), θ ∈ S¹,

then u(x) = 0.

Proof: As illustrated in Fig. 3, for an arbitrary α₀ ∈ [0, π), let L_α0 denote the line through the origin and tilted by θ₀ = (cos α₀, sin α₀). When u(x) is restricted to the line L_α0, it can be expressed as

$$v_{{\alpha }_0}\left(t\right)=u\left(t\right(\cos {\alpha }_0,\sin {\alpha }_0\left)\right),t\in (-\infty ,\infty ).$$ (17)

By the relationship between the differentiated backprojection of projection data and the Hilbert transform of an image [23,24], we have

$$H{v}_{{\alpha }_0}\left(t\right)=-\frac{1}{2\pi }{\int }_{{\alpha }_0-\frac{\pi }{2}}^{{\alpha }_0+\frac{\pi }{2}}{\phantom{\mid }{\partial }_{s}Ru(s,\theta )\mid }_{s=x_{{\alpha }_0}^t\cdot \theta }d\alpha ,$$ (18)

where

$$x_{{\alpha }_0}^t=t(\cos {\alpha }_0,\sin {\alpha }_0),\theta =(\cos \alpha ,\sin \alpha ),x_{{\alpha }_0}^t\cdot \theta =t\cos (\alpha -{\alpha }_0).$$ (19)

Performing the Taylor expansion of ∂_sRu(s, θ) with respect to s, we have

$${\partial }_{s}Ru(s,\theta )=\sum _{k=0}^{m-1}\frac{{\partial }_s^{k+1}Ru(0,\theta )}{k!}{s}^k,s\in (-a,a).$$ (20)

Inserting Eq. (20) into Eq. (18), we have

$$H{v}_{{\alpha }_0}\left(t\right)=-\frac{1}{2\pi }{\int }_{{\alpha }_0-\frac{\pi }{2}}^{{\alpha }_0+\frac{\pi }{2}}\left(\sum _{k=0}^{m-1}\frac{{\partial }_s^{k+1}Ru(0,\theta )}{k!}{\left(t\cos \right(\alpha -{\alpha }_0\left)\right)}^k\right)d\alpha =\sum _{k=0}^{m-1}{b}_k{t}^k,\text{for}t\in (-a,a),$$ (21)

where

$$b_k=-\frac{1}{2\pi }{\int }_{{\alpha }_0-\frac{\pi }{2}}^{{\alpha }_0+\frac{\pi }{2}}\frac{{\partial }_s^{k+1}Ru(0,\theta )}{k!}{\left(\cos \right(\alpha -{\alpha }_0\left)\right)}^{k}d\alpha .$$ (22)

By Condition (g) and Eq. (17), we have

$$v_{{\alpha }_0}\left(t\right)=p\left(t\right(\cos {\alpha }_0,\sin {\alpha }_0\left)\right),\text{for}t\in (-a,a),$$ (23)

where p(t(cos α₀, sin α₀)) is a polynomial function with respect to t. Applying Lemma 2 to v_α0(t), we have

$$v_{{\alpha }_0}\left(t\right)=0,t\in (-\infty ,\infty ),{\alpha }_0\in [0,\pi ),$$ (24)

which implies that

$$u\left(x\right)=0,x\in {\mathbb{R}}^2.$$

Fig. 3.

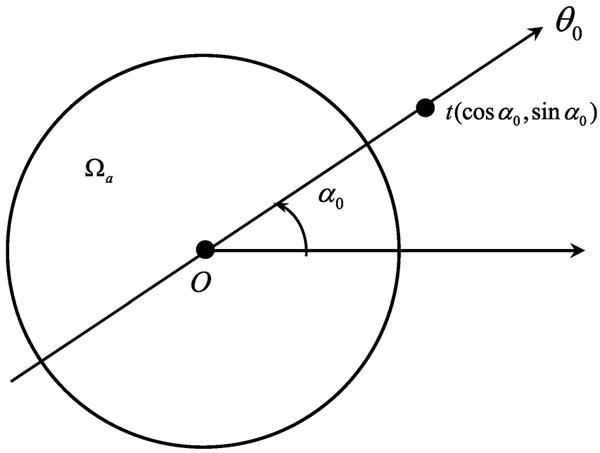
Radial line through the origin.

Now, let us analyze a candidate image under the assumption that f₀(x) is a piecewise polynomial function in Ω_a.

Theorem 4. Suppose that an object image f₀(x) is a piecewise polynomial in Ω_a. If some candidate image f(x) is also a piecewise polynomial in Ω_a, then f(x) = f₀(x).

Proof: By Theorem 1, we have that f(x) = f₀(x) + u(x), where u(x) is an analytic function in Ω_a. On the other hand, by the assumption of Theorem 4, u(x) = f(x) − f₀(x) is also a piecewise polynomial in Ω_a. Combining these two facts, u(x) must be a polynomial in Ωa. By Theorem 3, we have u(x) = 0.

Theorem 5. If there exist finitely many sub-regions Ω_i (as shown in Fig. 4) in an ROI Ω_a, 1 ≤ i ≤ L, such that Ω_i ∩ Ω_j = ∅ for 1 ≤ i < j ≤ L and

$$f_0\left(x\right)=p_i\left(x\right),\text{for}x\in {\Omega }_i,1\le i\le L,$$ (25)

where p_i(x) is a n-th polynomial function. For any candidate image f(x), let us define the n + 1-th high order total variation HOT_n+1(f) by

$${\text{HOT}}_{n+1}\left(f\right)=\sum _{i=1}^q{\int }_{{\Omega }_i}\sqrt{\sum _{r=0}^{n+1}{\left(\frac{{\partial }^{n+1}f}{\partial x_1^{n+1}\partial x_2^{n+1-r}}\right)}^2}dx.$$ (26)

If ${\text{HOT}}_{n+1}\left(h\right)=\underset{f=f_0+u}{\text{min}}{\text{HOT}}_{n+1}\left(f\right)$, then h(x) = f₀(x) for x ∈ Ω_a.

Fig. 4.

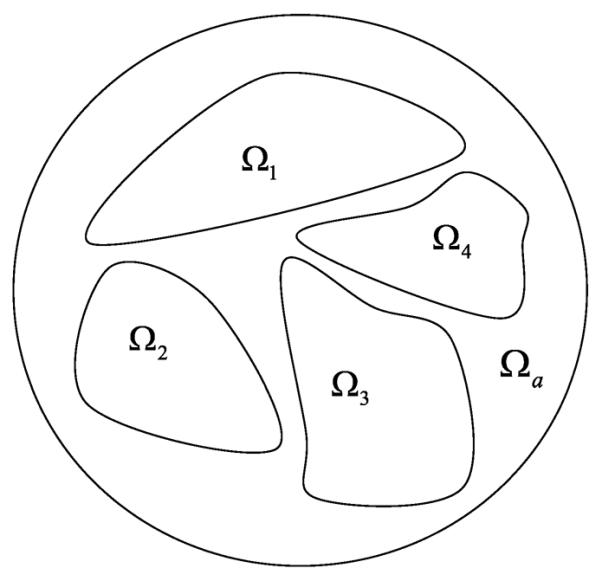
Sub-regions in the ROI.

Proof: Since

$${\text{HOT}}_{n+1}\left(f_0\right)=\sum _{i=1}^m{\int }_{{\Omega }_i}\sqrt{\sum _{r=0}^{n+1}{\left(\frac{{\partial }^{n+1}{p}_i}{\partial x_1^{n+1}\partial x_2^{n+1-r}}\right)}^2}dx=0,$$ (27)

the condition

$${\text{HOT}}_{n+1}\left(h\right)=\underset{f=f_0+u}{\min }{\text{HOT}}_{n+1}\left(f\right),$$

leads to HOT_n+1(h) = 0. Therefore, we have

$$\frac{{\partial }^{n+1}h\left(x\right)}{\partial x_1^{n+1}\partial x_2^{n+1-r}}=0,\text{for}x\in {\Omega }_i,1\le i\le L,0\le r\le n+1.$$ (28)

It means

$$h\left(x\right)=q_i\left(x\right),\text{for}x\in {\Omega }_i,1\le i\le L,$$ (29)

where q_i(x) is a n-th polynomial function. Combining Eqs (25) and (29), we have

$$u\left(x\right)=h\left(x\right)-f_0\left(x\right)=q_i\left(x\right)-p_i\left(x\right),\text{for}x\in {\Omega }_i,1\le i\le L,$$ (30)

On the other hand, by Theorem 1, u(x) is analytic in Ω_a. Hence, u(x) is a n-th polynomial function in Ω_a. By Theorem 3, u(x) = 0 for x ∈ Ω_a; that is, h(x) = f₀(x) for x ∈ Ω_a.

Remark: If we define HOT_n+1(f) by ${\text{HOT}}_{n+1}\left(f\right)={\sum }_{i=1}^m{\int }_{{\Omega }_i}{\sum }_{r=0}^{n+1}\mid \frac{{\partial }^{n+1}f}{\partial x_1^{n+1}\partial x_2^{n+1-r}}\mid dx$, Theorem 5 still holds.

3. Numerical simulation

3.1. Forbild numerical phantom

A numerical phantom was employed to evaluate the proposed interior tomography approach that deals with truncated second derivative data directly. The phantom consisted of 20 disks with different sizes in a background. Each disk was set to a constant refractive index in the range of [1.1×10⁻⁷, 1.6×10⁻⁷] to mimic biological tissues. An ROI was specified in the phantom, as shown in Fig. 5(a). We used a parallel-beam imaging geometry consistent to the x-ray phase-contrast imaging mode. The detector array had 368 elements to collect x-ray phase shift data through the ROI. Equi-angularly, 361 projections over an 180° range were used for interior reconstruction. The second-order differential phase shift data were computed using the numerical difference method from the projection data of the phantom, and corrupted by Gaussian noise to yield a signal-to-noise ratio of 40 dB.

Fig. 5.

Interior reconstruction of a numerical phantom. (a) The phantom with an ROI in a yellow circle, (b) the image reconstructed using our proposed interior tomography algorithm, and (c) the image reconstructed using the adapted FBP method.

The phase shift Φ(s, θ) can be expressed as a projection of the refractive indices along the x-ray direction. The refractive index distribution can be expressed as a linear system of equations in terms of measured two-order differential phase shift [25,26],

$$(-4{\pi }^2{\omega }^2\mathcal{F}({\mathbf{A}}_{\theta }\left)\right)\delta ={\mathbf{m}}_{\theta }$$ (31)

where m_θ is the discrete Fourier transform of the measured differential phase shifts ${\partial }_s^2\Phi (s,\theta )$, A_θ is a system matrix at a projection angle φ, which accounts for the imaging geometry, and δ is a discretized refractive index distribution to be reconstructed. Equation (31) can be solved using a classical iterative method, such as the algebraic reconstruction technique (ART). Furthermore, compressive sensing techniques can be applied for high quality image reconstruction from far less measurements than that required by the Nyquist criterion [27].

The ordered-subset simultaneous algebraic reconstruction technique (OSSART) coupled with total variation (TV) regularization was implemented to reconstruct the refractive index image. This iterative method consists of two key steps. In the first step, OSSART was used to reconstruct a refractive index image based on the truncated second-order differential projections. In the second step, the total variation was minimized using the standard steepest descent method. These two steps were iteratively performed in an alternating manner. We performed 50 iterations, and found that the reconstructed image in the ROI was in excellent agreement with the truth inside the ROI, as shown in Figs 5(a), (b), 6(a) and 6(b). Comparatively, we performed a locally adapted filtered backprojection (FBP) reconstruction from the truncated differential phase shift data. The adapted FBP formula for second-order differential phase shift data can be formulated as

$$\delta (x,y)=-{\int }_0^{\pi }{\int }_{-\infty }^{\infty }\frac{1}{4{\pi }^2\mid \omega \mid }\tilde{D}(\omega ,\theta )\text{exp}\left[i2\pi \omega \right(x\cos \theta +y\sin \theta \left)\right]d\omega d\theta$$ (32)

where $\tilde{D}(\omega ,\theta )$ is the Fourier transform of measured second-order differential projection data. Applying Eq. (32) to the truncated data, we obtained the refractive index image on ROI. It can be seen that the structure of the reconstructed refractive index image from FBP contained a bias and more noise, as shown in Fig. 5(c).

Fig. 6.

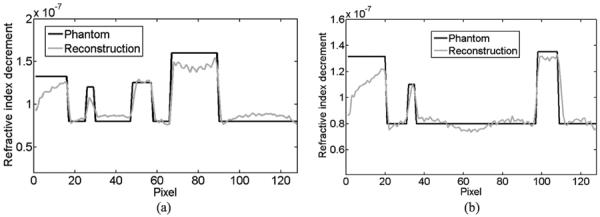
Profile comparison of the interior reconstructions. (a) and (b) The profiles along the horizontal and vertical middle lines respectively in the original phantom and the image reconstructed using our proposed interior tomography method.

3.2. Human chest numerical phantom

Because a commonly encountered function can be well approximated by a piecewise polynomial function, a refractive index distribution of biological tissues over an ROI can be considered as a piecewise polynomial function approximately. In this sense, although biological tissues are highly heterogeneous, the refractive index image of biological tissues can be well reconstructed using the proposed method. Here, we conducted a numerical experiment with a realistic phantom to demonstrate the feasibility of the proposed approach. The phantom was produced by a human chest CT slice image with 442×442 pixels, as shown in Fig. 7(a). The attenuation values of CT image were converted to a refractive index distribution. We used parallel-beam geometry to simulate the x-ray phase-contrast imaging mode, and equi-angularly acquired 361 projections over an 180° range. An ROI in the phantom was selected to contain 128×128 pixels, which occupies only 8% of the global area, as shown in Fig. 8(a). The truncated high-order differential phase shift data were computed and corrupted by Gaussian noise with a signal-to-noise ratio of 15 dB, as shown in Fig. 7(b). The OSSART with 2^nd total variation regularization was implemented to reconstruct the refractive index image from the truncated 2^nd differential phase shift data. The reconstructed image was in excellent agreement with the truth inside the ROI, and the detailed features in the ROI are quantitatively accurate, as shown in Fig. 8(b).

Fig. 7.

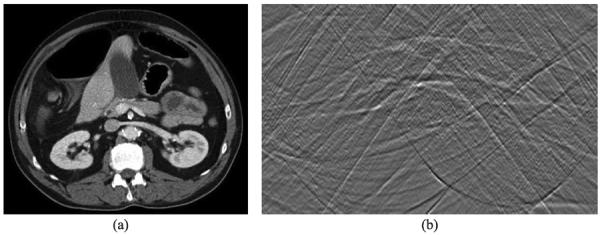
Human chest numerical phantom. (a) The original CT image, and (b) the sinogram of the 2^nd order differential phase projection data.

Fig. 8.

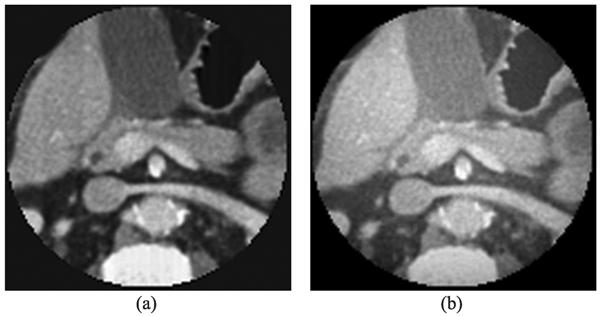
Interior reconstruction of a human chest numerical phantom. (a) The ROI in the original image, and (b) the image reconstructed using our proposed interior tomography algorithm.

4. Discussion and conclusion

As mentioned in the beginning, the availability of second derivative data is based on our assumption that a sample is longitudinally homogeneous. While this assumption gives us an initial mathematical model of practical significance and has led to good results, a general model should assume a heterogeneous sample. In that case, data measured using the in-line holographic imaging system would be the output of the Laplacian operator acted on a frame of projection data. Then, the high order interior problem becomes 3-D and more interesting. Our pilot data suggest that it seems feasible to obtain a good solution to this 3-D high order interior problem. We are actively working along this direction.

In conclusion, our newly-defined high order interior problem has a strong background of local x-ray differential phase-contrast tomography, and we have demonstrated that the high order interior problem has a unique solution within the class of piecewise polynomial functions. Furthermore, an accurate interior reconstruction can be achieved via high order TV minimization from truncated high order differential projection data through an ROI. We have developed an effective iterative algorithm dedicated to solve this problem, inspired by compressive sensing. Our proposed high order interior problem solving approach can be potentially applied to x-ray phase-contrast local imaging of biological soft tissues, and other similar applications.