Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2013 May 30;117(42):12759–12768. doi: 10.1021/jp401587e

Population Based Reweighting of Scaled Molecular Dynamics

William Sinko †,*, Yinglong Miao ‡, César Augusto F de Oliveira ‡, J Andrew McCammon †,‡
PMCID: PMC3808002  PMID: 23721224

Abstract

graphic file with name jp-2013-01587e_0007.jpg

Molecular dynamics simulation using enhanced sampling methods is one of the powerful computational tools used to explore protein conformations and free energy landscapes. Enhanced sampling methods often employ either an increase in temperature or a flattening of the potential energy surface to rapidly sample phase space, and a corresponding reweighting algorithm is used to recover the Boltzmann statistics. However, potential energies of complex biomolecules usually involve large fluctuations on a magnitude of hundreds of kcal/mol despite minimal structural changes during simulation. This leads to noisy reweighting statistics and complicates the obtainment of accurate final results. To overcome this common issue in enhanced conformational sampling, we propose a scaled molecular dynamics method, which modifies the biomolecular potential energy surface and employs a reweighting scheme based on configurational populations. Statistical mechanical theory is applied to derive the reweighting formula, and the canonical ensemble of simulated structures is recovered accordingly. Test simulations on alanine dipeptide and the fast folding polypeptide Chignolin exhibit sufficiently enhanced conformational sampling and accurate recovery of free energy surfaces and thermodynamic properties. The results are comparable to long conventional molecular dynamics simulations and exhibit better recovery of canonical statistics over methods which employ a potential energy term in reweighting.

Introduction

The simulation of biomolecules in an aqueous environment is an important tool in computational chemistry.1,2 Often conventional molecular dynamics (cMD) simulation is used to create a trajectory of biomolecular motion.1 If a simulation is run for an infinite amount of time, the ergodic hypothesis states that equilibrium properties may be extracted from the simulation. With modern computers, it is typically impossible to run simulations of complex biomolecules for a long enough period that the results converge to those of an infinite simulation or equilibrium. This problem is related to the observation that the time scales of interesting biomolecular motions are often milliseconds to seconds or even longer,3 but all-atom molecular dynamics simulations must be performed with a time step of femtoseconds. The difference in orders of maginitude between an individual time step and the time scales for many equilibrium properties of interest is usually too great for modern computers to perform the calculations. Therefore, equilibrium properties calculated from these simulations are subject to stochastic variations and starting structure bias in most cMD simulations of most biomolecular systems.

To combat this issue, many have proposed methods to enhance sampling,4−7 in addition to the ever increasing computational power which has pushed protein simulations toward longer time scales.8 The methodological advances in enhanced sampling often rely on two steps: (1) the modification to the potential energy surface (PES) to flatten it and speed transitions between the states, or increasing the simulation temperature, and (2) a reweighting scheme to recover the canonical ensemble at a given temperature.9

The potential energy functions in classical simulations of biomolecules usually contain a large number of individual terms, e.g., bonds, angles, dihedrals, electrostatics, and van der Waals. The fluctuations in each term are additive, which creates higher fluctuations in the total potential energy 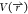Inline graphic for any given state. Reweighting of enhanced sampling simulations is often based on the value of the potential energy of each configuration of the trajectory which can exhibit large fluctuations in the potential energy of the system.7,10−12 This can create inaccuracies in the final ensemble generated in complex simulations. Although more conformations are sampled, the reweighted ensemble may be a poor representation of the canonical distribution.12 Rather, what is needed is a converged average of the potential energy for each microstate, Inline graphic. In most cases, obtaining an accurate estimate of the energy is extremely time-consuming and may also require the definition of collective variables a priori. It would be advantageous to avoid using individual calculations of Inline graphic or computationally expensive calculations of Inline graphic in the reweighting procedure. Ytreberg and Zuckerman pointed out that, as long as the important degrees of configurational freedom are accounted for, grouping similar configurations together can be accomplished in numerous ways during reweighting protocols.13

Here, we propose a scaled molecular dynamics (scaled MD) method that enhances biomolecular conformational sampling by scaling the PES and a reweighting protocol that is not biased by the fluctuations of energy but instead relies solely on the populations of conformations to reweight and recover the canonical ensemble. Scaled MD is based on earlier work of potential-scaled molecular dynamics and potential annealing,14,15 but the energy independent reweighting approach is novel to the best of our knowledge. Furthermore, we demonstrate the effectiveness of scaled MD in two well-studied systems, alanine dipeptide and a fast-folding protein chignolin.

Theory

In a classical system, the probability Inline graphic of any configuration is given by

graphic file with name jp-2013-01587e_m006.jpg 1

where β = (kBT)−1 with kB as the Boltzmann constant and T the temperature. The partition function, Inline graphic, can rarely be solved analytically or easily by computation, which presents a grand challenge in calculating the probability of any microstate Inline graphic. The non-normalized probability of microstates Inline graphic can be directly extracted from a cMD simulation of any length as

graphic file with name jp-2013-01587e_m010.jpg 2

To accurately estimate Z, the probability of different states must be similar to those that would occur in an infinite simulation to fulfill the ergodic hypothesis. For complex biomolecules of interest including proteins, DNA, and membranes, estimating Z generally requires computationally expensive calculations and it is less reliable because the ergodic hypothesis is rarely fulfilled. There are high energy transition states and local roughness along the energy landscape of biomolecules, and sampling all the possible configurations has proven difficult in most cases. 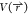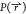Many modifications can be made to the potential energy Inline graphic to flatten and smooth the biomolecular PES for sampling a greater amount of conformational space in shorter simulations. However, the canonical distribution can only be recovered after a reweighting scheme is applied; i.e., a redistribution of the probability Inline graphic obtained from enhanced sampling simulations is required to calculate Inline graphic. Most enhanced sampling methods which modify the PES use a reweighting scheme based on the amount of energy change from Inline graphic at any given point. One could simply derive an enhanced sampling scheme from eq 2 such as eq 3 as Hamelberg et al. did in accelerated MD (aMD) simulations,7 where the modified probability is

graphic file with name jp-2013-01587e_m015.jpg 3

and Inline graphic is the change in energy from Inline graphic or boost potential applied to the system. With this, the reweighting scheme can be derived as

graphic file with name jp-2013-01587e_m018.jpg 4

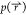In aMD simulations of complex biomolecules, Inline graphic usually undergoes large fluctuations and the reweighted probability Inline graphic can be greatly skewed toward a few microstates, leading to the “high energetic noise” problem. Additionally, the true exponential is rarely used in aMD.12,16 Although the true exponential is rarely used and the Boltzmann ensemble is rarely recovered, aMD has still been useful in conformational exploration; Wereszynski et al. provide a nice example of conformational exploration by employing aMD.17

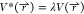To address this issue, we propose the use of a reweighting procedure that does not contain terms from the noisy energetic function but employs only the distribution of system configurations Inline graphic from the enhanced sampling simulation. Rather than adding a boost potential in aMD, we modify the biomolecular PES by scaling Inline graphic by a factor of λ that ranges from 0 to 1: Inline graphic. This generates the modified population distribution p*Inline graphic as

graphic file with name jp-2013-01587e_m025.jpg 5

With this, we can derive the corresponding reweighting equations to recover the canonical distribution of populations pInline graphic as

graphic file with name jp-2013-01587e_m027.jpg 6

We can also derive a more traditional method by which an energetic term is used as a weighting factor:

graphic file with name jp-2013-01587e_m028.jpg 7

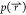When no configurational assumptions are made here and if all values of Inline graphic and Inline graphic are converged, these two equations yield equivalent results. However, as demonstrated in the following Results and Discussion section, population-based reweighting using eq 6 may be more accurate than energetic reweighting using eq 7 in practice. Often, it is of great interest to know the free energy difference between states, for example, the folded versus unfolded state of a protein. Both eqs 6 and 7 provide theoretically sound methods to recover the canonical distribution, from which the free energy difference of states can be calculated, but the reweighting in eq 6 is practically more accurate because it is independent of the potential energy term that is subject to large fluctuations. We can substitute Inline graphicfrom eq 6 into eq 1 and recover the canonical ensemble from a scaled MD simulation. Formally, the scaling factor can be applied to the temperature as well as the PES, and the reweighting eqs 6 and 7 may be applied in the same manner. There are practical considerations to using PES scaling rather than temperature though because the time steps may need to be shortened with high temperature runs, reducing efficiency. Others have used simulated annealing18 and temperature-based replica exchange19 to perform high temperature simulations. What is novel about this work is the reweighting method that depends only on populations and not energies.

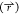To reweight using eq 6, we must bin the simulation-derived configurations Inline graphic and make a multidimensional histogram of all possible configurations. When binning data, there is an approximation made that all data within a bin is in the same microstate, while truly there may be different but conformationally related microstates contained within a bin. Equation 6 becomes exact as the bin size goes to zero, assuming a perfect description of microstates and infinite sampling. Our analysis of alanine dipeptide simulations did not show a significant change in the accuracy of the PMF from using bins of 1–12° (Figure S2, Supporting Information). Ytreberg and Zuckerman described a generalized black box weight that could be applied to any non-Boltzmann set of configurations. 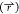However, their method relies on an accurate estimation of the energy term Inline graphic and thus was subject to the energetic noise problem already discussed.13 Since configurational space is often described by Cartesian coordinates of hundreds to millions of atoms or more, it is not feasible to describe the configurations without reducing the system dimensionality to the essential components that describe biomolecular motion. Principal component analysis (PCA) has proven useful for such dimensionality reduction. Additionally, it has been suggested that essential dynamics of proteins can be described by a few PCA modes with large eigenvalues.20 Many of the other modes are considered as fast fluctuations of the protein.21 By reducing the dimensionality of the system, it is easier to group similar configurations and understand the protein dynamics.22 Although we employ PCA and dihedral coordinates in this work, any method that reduces the dimensionality of configurational space while preserving the essential dynamics should suffice for the reweighting procedure. Methods like Markov state models have gained popularity in biomolecular simulation analysis23 and may be useful in the description of Inline graphic in future work with scaled MD. The accuracy of the reweighting procedure is dependent upon a good description of Inline graphic, reduction in dimensionality of Inline graphic, and complete sampling of Inline graphic. To the best of our knowledge, this is the first description of solely using populations of microstates to reweight an enhanced sampling simulation. This represents an entirely unexplored methodology that inherently bypasses a major challenge in enhanced sampling simulations, the need to calculate converged and accurate energy values to reweight.

Results and Discussion

The principle of scaled MD and its reweighting scheme is illustrated in Figure 1. The original biomolecular PES Inline graphic is modified by varying a scaling factor λ to produce flatter free energy surfaces, as shown in Figure 1A. These flatter energy surfaces should facilitate enhanced conformational sampling in any given amount of simulation steps (Figure 1A). When the enhanced sampling simulation is converged, we can calculate the corresponding modified population density Inline graphic and then Inline graphic of the canonical ensemble of Inline graphic using eq 6 (Figure 1B). In this one-dimensional case, the values of the energy function are accurately converged and the results of reweighting based on configuration populations (eq 6) and energy (eq 7) are equivalent.

Figure 1.

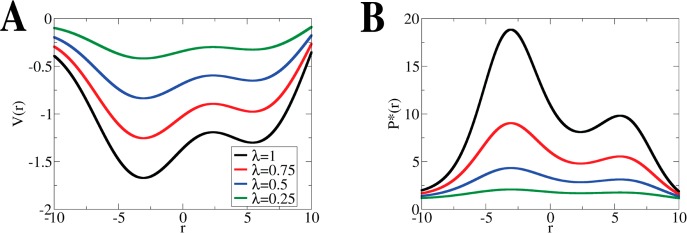
Figure 1

Open in a new tab

Schematic illustration of scaled MD: (A) Biomolecular PES 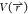Inline graphic can be scaled by a factor of λ to produce Inline graphic (black is the original PES or λ = 1, red λ = 0.75, blue λ = 0.5, green λ = 0.25, as shown in the legend). (B) The corresponding probability distribution functions. The probability functions for all values of λ obtained using either population-based (eq 6) or energetic (eq 7) reweighting are equivalent to populations derived from the original PES (λ = 1 or the black line).

Test System 1: Alanine Dipeptide

Alanine dipeptide is a common test system for molecular simulations24−30 because its energy surface can be well described by the Ramachandran plot31 and a long cMD simulation can give reasonable accuracy to search the phi (ϕ) and psi (ψ) angles. Therefore, we first tested scaled MD on alanine dipeptide in explicit solvent. The dipeptide conformations were described by phi–psi angles mapped on a free energy plot. Thus, we reduced the system dimensions to a 2D representation that is a histogram of phi and psi. We used a bin size of 12° in Figures 2 and S1 (Supporting Information) and 3° in Figures 3 and 4 for increased resolution of the free energy surface. As shown in Figure 2, conformational searching and mapping of the phi–psi free energy plot is enhanced by scaling the dipeptide PES during scaled MD simulations. The free energy plots generated by scaled MD were also compared with that of a 1000 ns cMD simulation (Figure 2A). In Figure 2B, 20 ns cMD simulation was not enough to reproduce the free energy surface of the long 1000 ns cMD simulation. This suggested that the free energy surface obtained from 20 ns cMD simulation was not converged and the dipeptide conformations were not sufficiently sampled with visible gaps in the sampling of phi–psi angles. In comparison, the free energy surface calculated from 20 ns scaled MD simulations with the scaling factor λ = 0.7, 0.5, and 0.3 is similar to that of the 1000 ns cMD simulation after applying population-based reweighting using eq 6 (Figure 2C–E). Scaled MD is capable of sampling a greater phi–psi conformational space than a cMD simulation of a similar length, and the canonical ensemble can be recovered remarkably accurately as compared with a much longer cMD simulation after reweighting.

Figure 2.

Figure 2

Open in a new tab

Comparison of scaled MD and cMD simulations on alanine dipeptide: Ramachandran plots of (A) 1000 ns cMD simulation, (B) 20 ns cMD simulation, (C) 20 ns reweighted scaled MD with λ = 0.7, (D) 20 ns reweighted scaled MD with λ = 0.5, and (E) 20 ns reweighted scaled MD with λ = 0.3.

Figure 3.

Figure 3

Open in a new tab

Comparison of population-based and energetic reweighting methods for scaled MD: Ramachandran plots of (A) 1000 ns cMD simulation, (B) scaled MD at λ = 0.7 reweighted using population-based eq 6, and (C) reweighted using energetic eq 7 frame by frame or (D) with an average Inline graphic per bin (bins with less than 10 frames were removed).

Figure 4.

Figure 4

Open in a new tab

Comparison of scaled MD and aMD simulations on alanine dipeptide: Ramachandran plots: (A) 1000 ns cMD simulation using 3 degree bins for phi and psi (the white dashed line indicates the free energy path shown in parts E and F), (B) 20 ns aMD simulation, and (C) 20 ns scaled MD simulation with λ = 0.7. (D) Time courses of phi of scaled MD with λ = 0.7 (top) and aMD (bottom) simulations show roughly equivalent sampling. Free energy profiles of phi obtained from (E) aMD and (F) scaled MD simulations with the black line representing the result from 1000 ns cMD simulation.

To quantitatively characterize the similarity of the free energy surfaces computed from the above 20 ns scaled MD simulations to that of the 1000 ns cMD simulation, we compared the difference between the computed free energy surfaces as plotted in Figure S1 (Supporting Information). As a reference, 20 ns cMD was not enough to sample the left-handed α-helix region (ϕ ∼ 50 and ψ ∼ 50), as shown in Figure S1A (Supporting Information). There was a major difference in the free energy plots associated with this lack of sampling at a maximum difference of 6 ± 0 kcal/mol and a mean average difference of 0.59 ±0.014 kcal/mol in all bins (error is reported as standard deviation). In contrast, the maximum and average differences were greatly reduced in 20 ns scaled MD simulations (see Figures S1B–D, Supporting Information). With a scaling factor of λ = 0.7, we obtained a maximum difference of 1.75 ± 0.34 kcal/mol and an average of 0.24 ±0.07 kcal/mol (Figure S1B, Supporting Information). The differences decreased as we flattened the energy surface more using λ = 0.5, where we obtained a maximum difference of 1.31 ± 0.58 kcal/mol and an average of 0.2 ± 0.04 kcal/mol (Figure S1C, Supporting Information). This reduction in the differences was associated with an increase in dipeptide conformational sampling due to the application of scaled MD. When we flattened the energy surface more using a scaling factor of λ = 0.3, we saw a modest increase in both the average difference to 0.29 ± 0.02 and a 1.71 ±0.18 kcal/mol maximum difference. Among the scaled MD simulations there is little difference in the error reported from λ = 0.3–0.7 despite the significant increases in sampling associated with low λ values. At λ = 0.3, omega angle rotations were observed, indicating greatly enhanced sampling of even very high energy states; however, the free energy plot could still be recovered remarkably well. Importantly, the difference between free energy plots generated via short scaled MD simulations (20 ns) and long cMD simulations (1000 ns) was greatly reduced using the scaled MD protocol in all cases as compared to short cMD (20 ns) simulations.

A Comparison of Population-Based vs Energetic Reweighting

To demonstrate the distinct advantage of reweighting using population statistics (eq 6) versus energetic terms (eq 7), we directly compared reweighting of scaled MD simulation at λ = 0.7 using eqs 6 and 7. At λ = 0.7, the simulation explores roughly the same conformational space as the 1000 ns cMD simulation as described above. As shown in Figure 3B, population reweighting of the scaled MD simulation using eq 6 recovers a good approximation of the 1000 ns cMD simulation. 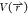However, eq 7 poorly reconstructs the Ramachandran plot due to large fluctuations in the Inline graphic (Figure 3C). Since the high fluctuations in Inline graphic were so problematic, we tried to bin all phi–psi angles and use a bin average of Inline graphic for reweighting. Bins that had less than 10 data points were removed to further reduce noise. The Ramachandran plot was improved, as shown in Figure 3D, but there was still a poor reproduction of the 1000 ns cMD simulation. Additionally, more than 95% of the reweighted statistics arose from only 0.001% snapshots of the scaled MD simulation using energetic reweighting of eq 7. In contrast, using population-based reweighting (eq 6), an excellent representation of the Ramachandran plot was recovered (Figure 3B) and 85% of the snapshots of the scaled MD simulation were incorporated into 95% of the reweighted configurations. This demonstrates the value of eliminating energetic noise from reweighting methods in practice.

To further demonstrate the advantage of using scaled MD and population-based reweighting, we compared scaled MD simulations of alanine dipeptide with aMD simulations that implement energetic reweighting using eq 4. To minimize the energetic noise, we applied boost potential to only the torsional terms in the aMD simulations (i.e., dihedral aMD). Nonetheless, the energetic noise was not eliminated effectively even in this small system. During reweighting of the aMD simulations to recover the canonical ensemble, we found that 95% of the reweighted configurations originate from only 5% of the snapshots from the original simulation. In comparison, 95% of the reweighted configurations from scaled MD originate from 85% of the original simulation at λ = 0.7 as described above. Even when λ is extremely aggressive at λ = 0.3, 55% of the scaled MD simulation snapshots contribute to 95% of the reweighted configurations, with much greater sampling enhancement as well. The lack of configurations contributing to the reweighting statistics of aMD is evident in the Ramachandran plot, especially when the bin size is small (3°). As shown in Figure 4A,B, the free energy wells computed from the 20 ns aMD simulation were not adequately populated to create a smooth energy surface and the free energy values were not accurately estimated either. With scaled MD at λ = 0.7, the energy wells were excellently reproduced with accurate energy values (Figure 4C). Note that the aMD simulation parameters were tuned to achieve roughly the same number of dihedral transitions in phi during 20 ns (across 0°) as the least-aggressive scaled MD simulation at λ = 0.7 (Figure 4D). Accelerated MD simulations have been used to reproduce the phi–psi free energy surface of long cMD simulations for alanine dipeptide, but these simulations tended to have more simulation steps with larger bins.7 It may be possible to achieve somewhat smoother energy surfaces with other parameter sets, as this was not tested exhaustively. Here we chose a difficult level of enhanced sampling to achieve and to build a PMF along a fine grid to test the limits of each method in the recovery of an accurate free energy surface.

Furthermore, we extracted a one-dimensional free energy profile with psi along the white dashed line shown in Figure 4A. The aMD simulations yielded a poor estimation of this free energy profile as compared to the long cMD simulation (Figure 4E). In contrast, the scaled MD simulation excellently reproduced the path with moderate fluctuations around the peak of the free energy barrier (Figure 4F). When comparing Figures 3C,D and 4B, we found that aMD outperformed scaled MD using energetic reweighting of eq 7. We hypothesize that scaled MD modified the entire PES, while this aMD simulation modified only the torsional term, reducing PES noise by only utilizing a subset of the PES terms. Additionally, using the Inline graphic term may reduce noise in the reweighting factor over the Inline graphic term used in eq 7. Nonetheless, the above results suggested that population-based reweighting using eq 6 of scaled MD simulations reproduces the PMF with less noise than energy based reweighting methods when achieving roughly equivalent levels of enhanced sampling.

Test System 2: Chignolin

To further demonstrate the capability of scaled MD on more complex systems, we simulated a fast-folding protein Chignolin with a sequence of 10 residues (GYDPETGTWG).32 This protein folds into a β-hairpin on an estimated sub-microsecond time scale, so it should not be uncommon that with 1 μs simulations using standard MD we may see at least one folding event.33 During 500 ns scaled MD simulation, we observed many folding and unfolding events, as shown in Figure 5A, where the RMSD of Cα atoms was calculated between the simulation snapshots and the NMR structure of the folded state (PDB ID: 1UAO).32 In comparison, we also performed three 1000 ns cMD simulations (Figure 5B–D) and chignolin was observed to fold into the NMR structure in two of the three simulations. In one of the three simulations, chignolin was caught in a partially folded state for the majority of the 1000 ns simulation time and never reached the fully folded state (Figure 5C). During the three cMD simulations, we did not witness any unfolding events.

Figure 5.

Figure 5

Open in a new tab

Comparison of scaled MD and MD simulations on Chignolin started from an extended form: RMSD between simulation snapshots and the folded NMR structure from (A) 500 ns scaled MD simulation with λ = 0.6 and (B–D) three 1000 ns MD simulations with different randomized atomic velocities.

Next, we performed PCA to use as an estimation of our various microstates Inline graphic. PCA allowed us to reduce the system dimensionality and characterize the conformational space sampled by Chignolin in the simulations. Using the first 6 PCs to reduce the dimensionality of the system, we describe, in the case of Chignolin, 71% of the molecular motion of the Cα atoms. As shown in Figure 6, three cMD simulations identified the NMR structure as the free energy minimum of Chignolin (Figure 6A). It was not certain if the partially folded intermediate state with PC1 ≈ 4 and PC2 ≈ −7 is accurately represented because no multiple folding and unfolding events were observed in the cMD simulation of Figure 5C. Using one 500 ns scaled MD simulation and population-based reweighting, we were able to accurately reproduce the free energy surface obtained from three cMD simulations of longer simulation times (1000 ns each), notably surrounding the free energy minimum region (Figure 6B and C). Moreover, scaled MD sampled the protein conformations rapidly between folded and unfolded states during only a 500 ns simulation length (Figure 5A). As shown in Figure 6C, the bulk of the free energy surface computed from scaled MD simulation was similar to that of 1000 ns cMD simulations. A ring of large difference (white regions in Figure 6C) was observed, largely due to the enhanced sampling at the edges of PC1 and PC2 by scaled MD that was absent in cMD simulations. It is important to note that the time scale for multiple folding events in Chignolin is likely more than 1000 ns, as no multiple folding events were observed in the three independent 1000 ns cMD simulations and one of the simulations failed to reach the fully folded state entirely (Figure 5B–D).

Figure 6.

Figure 6

Open in a new tab

Comparison of free energy profiles of Chignolin obtained from scaled MD and MD simulations: (A) three 1000 ns MD simulations combined, (B) one 500 ns scaled MD simulation with λ = 0.6, and (C) the difference between A and B. The white circles represent the NMR structures of Chignolin (PDB ID: 1UAO).

Conclusions

We have demonstrated that it is possible to apply scaled MD to achieve accurate reweighting results based on populations in simple to moderately complex systems in explicit solvent while substantially enhancing sampling, over cMD. By completely eliminating the noisy energetic term from reweighting, we can significantly improve the quality of the recovered canonical ensemble. Population-based reweighting is shown to be significantly advantageous when compared to methods cleverly designed to minimize the noise in the energetic term like aMD using only torsional terms. In addition, population-based reweighting is straightforward to use as a postprocessing step on a single scaled MD simulation that has had the potential energy scaled. We employ various postprocessing analyses, which describe the largest motions of the system as a critical step in the reweighting process. In the first example of alanine dipeptide, we employ simple analysis of the backbone dihedrals to reweight the simulation. When analyzing the simulations of a more complex system, the fast-folding polypeptide Chignolin, we applied PCA to describe the collective motions of the protein. We reduced the system’s dimensions to six principal components because this covered the majority of the protein motions. It is important to note that this reweighting method ignores the conformational changes of the explicit water in the reweighting method. However, in these systems, this assumption was not a large issue because the results we obtained matched the MD simulation results very well. The calculation of water structure is challenging to quantify, although it may be useful to incorporate this into the reweighting scheme, or simulate with implicit solvation in future work.

Additionally, we have discussed important issues for potential energy modification and enhanced sampling methods, which rely on reweighting schemes based on energetic values extracted from individual points of the simulations. Primarily, though, we have proposed a method by which potential energy modified MD simulations can be reweighted independently of the energetic function to recover the canonical distribution. We demonstrated the effectiveness of scaled MD on two test systems, alanine dipeptide and the fast-folding protein Chignolin. We have reproduced free energy plots with minimal error for both systems. We used widely varying scaling factors for alanine dipeptide to demonstrate that scaled MD may not be highly dependent on parametrization of the scaling factor λ, at least in these test systems. This method has so far proven robust, and the main limitations are the description of the microstates Inline graphic and limited sampling time (as with any MD simulation). PCA significantly reduces the dimensionality of the description of microstates Inline graphic and is widely used to describe complex simulations, and scaled MD can significantly speed phase space sampling and movement over energetic barriers which enhances conformational sampling. The reduction of dimensionality has long been used as a means to understand complex protein motions. Here, we have employed dimensionality reduction as a critical component of a reweighting scheme. We anticipate that scaled MD and the proposed population-based reweighting method may be applicable to a wide variety of biomolecular simulations to enhance conformational sampling and recover the canonical ensemble.

Computational Methods

All cMD, aMD, and scaled MD simulations were run using a modified version of AMBER 1134 on Nvidia GTX580 graphics processing units. Scaled MD will be released in the next release of AMBER (http://ambermd.org/). The simulated systems were built using the Xleap module of the AMBER package. All simulations used the AMBER99SB force field for solute molecules and the explicit TIP3P water model35 with a buffer region of 8–10 Å. The alanine dipeptide simulation contained 630 waters, and the chignolin simulation contained 2211 waters. A 2 fs time step was used in the simulations. The systems were initially minimized for 2000 steps using the conjugate gradient minimization algorithm, and then, the solvent was equilibrated for 50 ps in the isothermal–isobaric (NPT) ensemble with the solute atoms fixed. Another minimization was performed with all atoms free, and the systems were slowly heated to 300 K over 500 ps. Final system equilibration was achieved by a 200 ps isothermal–isovolumetric (NVT) and 400 ps isothermal–isobarometric (NPT) run to ensure that the simulation had reached the appropriate density. Then, production simulations were performed in the NVT ensemble.

Bonds containing hydrogen atoms were restrained with the SHAKE algorithm.36 Weak coupling to an external temperature and pressure bath was used to control both temperature and pressure.37 The electrostatic interactions were calculated using the PME (particle mesh Ewald summation), and the cutoff was 8.0 Å for long-range interactions. In scaled MD simulations, the forces on any atom were calculated and then scaled by λ at each time step, which is equivalent to scaling the PES, since force is equal to the derivative of potential with respect to position. For aMD simulations of alanine dipeptide, the Amber11 CUDA code38 was used and acceleration parameters for torsional angles were applied as α = 5 and E = 21.6 kcal/mol. The average dihedral energy calculated from cMD simulation of alanine dipeptide was 9.1 kcal/mol. These parameters roughly reproduced the same number of phi transitions, which was used as a metric for the level of enhanced sampling, as a scaled simulation with λ = 0.7. λ values were tested from the range 0.9–0.1 for alanine dipeptide. Optimal values when balancing enhanced sampling and minimal error in the Ramachandran plot compared to a long cMD simulation occurred between 0.5 and 0.7. Thus, a λ value of 0.6 was chosen for scaled MD simulations of Chignolin. It is not recommended to use λ close to 0, as this may explore very high energy states. Balance must be maintained between enhanced sampling and staying within a limited, physically relevant conformational ensemble, so we recommend using λ > 0.5 for typical biomolecular simulations.

Post-simulation analyses, including RMSD calculations and PCA, were performed using ptraj in the AMBER11 package, and then custom Matlab scripts and Python code were used to calculate free energy plots. Python code for general population based reweighting as well as an example scaled MD trajectory of alanine dipeptide with analysis scripts is available through the scaled MD Web site (http://scaledmd.ucsd.edu/) or by contacting the authors. PCA of scaled MD simulations was used to calculate the principal components (PCs), and the cMD simulations were projected upon the corresponding PC space. Structures of scaled MD simulations were aligned to the average structure by minimizing their RMSD, and then the covariance matrix was diagonalized to obtain the eigenvectors and eigenvalues. All PCA calculations were performed on the Cα atoms only. Using six principal components to describe Inline graphic in the six-dimensional histogram, we achieved a tractable number of possibilities in our histogram, and eliminated motions that do not provide insight into the essential dynamics of the simulation. We were able to calculate the reweighted free energy plot of these simulations in minutes on a desktop computer, a trivial computational cost in MD simulation and analysis. The PCA modes contained 38, 38, 19, 19, 16, and 14 bins per mode from PC1 to PC6, respectively, which allowed for approximately 117 million possible microstates Inline graphic. All bin sizes were uniform at 1 Å spacing. Plotting was performed with xmgrace, matlab, and python. The reference configuration for trajectory analysis of Chignolin was the NMR structure (PDB ID: 1UAO),32 although all simulations were started from a fully extended configuration built using xleap and the protein sequence.

Acknowledgments

The authors congratulate Professor Peter Wolynes for his many contributions on the occasion of his 60th birthday. This work was supported by the Molecular Biophysics Training Grant GM08326, ARCS (W.S.), the National Science Foundation Grant MCB-1020765, NBCR, CTBP, Howard Hughes Medical Institute, and National Institutes of Health Grant GM31749 (J.A.M.). We would like to thank Drs Yi Wang, Denis Bucher, Levi C. T. Pierce, Brock Luty, Hari S. Mudanna, Romelia Salomon-Ferrer, Ross C. Walker, and Michael K. Gilson for stimulating discussions.

Supporting Information Available

Additional figures of free energy profiles and PMFs using various reweighting parameters and comparisons with long MD simulations. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Notes

An example scaled MD simulation of alanine dipeptide as well as code for reweighting scaled MD simulations is available via the Web at http://scaledmd.ucsd.edu/ or by contacting the authors.

Funding Statement

National Institutes of Health, United States

Supplementary Material

jp401587e_si_001.pdf (435.5KB, pdf)

References

  1. Karplus M.; McCammon J. A. Molecular Dynamics Simulations of Biomolecules. Nat. Struct. Biol. 2002, 9, 646–652. [DOI] [PubMed] [Google Scholar]
  2. Wereszczynski J.; McCammon J. A. Statistical Mechanics and Molecular Dynamics in Evaluating Thermodynamic Properties of Biomolecular Recognition. Q. Rev. Biophys. 2012, 45, 1–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Frauenfelder H.; Sligar S. G.; Wolynes P. G. The Energy Landscapes and Motions of Proteins. Science 1991, 254, 1598–1603. [DOI] [PubMed] [Google Scholar]
  4. Sugita Y.; Okamoto Y. Replica-Exchange Molecular Dynamics Method for Protein Folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar]
  5. Torrie G. M.; Valleau J. P. Non-Physical Sampling Distributions in Monte-Carlo Free-Energy Estimation - Umbrella Sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar]
  6. Laio A.; Parrinello M. Escaping Free-Energy Minima. Proc. Natl. Acad. Sci. U.S.A. 2002, 99, 12562–12566. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Hamelberg D.; Mongan J.; McCammon J. A. Accelerated Molecular Dynamics: a Promising and Efficient Simulation Method for Biomolecules. J. Chem. Phys. 2004, 120, 11919–11929. [DOI] [PubMed] [Google Scholar]
  8. Shaw D. E.; Maragakis P.; Lindorff-Larsen K.; Piana S.; Dror R. O.; Eastwood M. P.; Bank J. A.; Jumper J. M.; Salmon J. K.; Shan Y.; Wriggers W. Atomic-Level Characterization of the Structural Dynamics of Proteins. Science 2010, 330, 341–346. [DOI] [PubMed] [Google Scholar]
  9. Hansmann U. H. E. Generalized-Ensemble Monte Carlo Method for Systems with Rough Energy Landscape. Phys. Rev. E 1997, 56, 2228–2233. [Google Scholar]
  10. Sugita Y.Replica-Exchange Molecular Dynamics Method for Protein Folding. Chem. Phys. Lett. 1999. [Google Scholar]
  11. Fajer M.; Hamelberg D.; McCammon J. A. Replica-Exchange Accelerated Molecular Dynamics (REXAMD) Applied to Thermodynamic Integration. J. Chem. Theory Comput. 2008, 4, 1565–1569. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Shen T.; Hamelberg D. A Statistical Analysis of the Precision of Reweighting-Based Simulations. J. Chem. Phys. 2008, 129, 034103. [DOI] [PubMed] [Google Scholar]
  13. Ytreberg F. M.; Zuckerman D. M. A Black-Box Re-Weighting Analysis Can Correct Flawed Simulation Data. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 7982–7987. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Mark A. E.; Van Gunsteren W. F.; Berendsen H. J. Calculation of Relative Free-Energy via Indirect Pathways. J. Chem. Phys. 1991, 94, 3808–3816. [Google Scholar]
  15. Tsujishita H.; Moriguchi I.; Hirono S. Potential-Scaled Molecular Dynamics and Potential Annealing: Effective Conformational Search Techniques for Biomolecules. J. Phys. Chem. 1993, 97, 4416–4420. [Google Scholar]
  16. Sinko W.; de Oliveira C. A. F.; Pierce L. C. T.; McCammon J. A. Protecting High Energy Barriers: A New Equation to Regulate Boost Energy in Accelerated Molecular Dynamics Simulations. J. Chem. Theory Comput. 2012, 8, 17–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Wereszczynski J.; McCammon J. A.. Nucleotide-Dependent Mechanism of Get3 as Elucidated from Free Energy Calculations. Proc. Natl. Acad. Sci. U.S.A. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kirkpatrick S.; Gelatt C. D.; Vecchi M. P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [DOI] [PubMed] [Google Scholar]
  19. Zuckerman D. M.Statistical Physics of Biomolecules: An Introduction; CRC Press: Boca Raton, FL, 2010. [Google Scholar]
  20. Amadei A.; Linssen A. B.; Berendsen H. J. Essential Dynamics of Proteins. Proteins 1993, 17, 412–425. [DOI] [PubMed] [Google Scholar]
  21. Zhuravlev P. I.; Materese C. K.; Papoian G. A. Deconstructing the Native State: Energy Landscapes, Function, and Dynamics of Globular Proteins. J. Phys. Chem. B 2009, 113, 8800–8812. [DOI] [PubMed] [Google Scholar]
  22. Teodoro M. L.; Phillips G. N.; Kavraki L. E. Understanding Protein Flexibility through Dimensionality Reduction. J. Comput. Biol. 2003, 10, 617–634. [DOI] [PubMed] [Google Scholar]
  23. Pande V. S.; Beauchamp K.; Bowman G. R. Everything You Wanted to Know about Markov State Models but Were Afraid to Ask. Methods 2010, 52, 99–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Yonezawa Y.; Fukuda I.; Kamiya N.; Shimoyama H.; Nakamura H. Free Energy Landscapes of Alanine Dipeptide in Explicit Water Reproduced by the Force-Switching Wolf Method. J. Chem. Theory Comput. 2011, 7, 1484–1493. [DOI] [PubMed] [Google Scholar]
  25. Ng K. M.; Solayappan M.; Poh K. L. Global Energy Minimization of Alanine Dipeptide via Barrier Function Methods. Comput. Biol. Chem. 2011, 35, 19–23. [DOI] [PubMed] [Google Scholar]
  26. Ferguson A. F. A. L.; Panagiotopoulos A. Z.; Debenedetti P. G.; Kevrekidis I. G. Integrating Diffusion Maps with Umbrella Sampling: Application to Alanine Dipeptide. J. Chem. Phys. 2011, 134. [DOI] [PubMed] [Google Scholar]
  27. Cruz V.; Ramos J.; Martinez-Salazar J. Water-Mediated Conformations of the Alanine Dipeptide as Revealed by Distributed Umbrella Sampling Simulations, Quantum Mechanics Based Calculations, and Experimental Data. J. Phys. Chem. B 2011, 115, 4880–4886. [DOI] [PubMed] [Google Scholar]
  28. Vondrasek J.; Vymetal J. Metadynamics as a Tool for Mapping the Conformational and Free-Energy Space of Peptides - The Alanine Dipeptide Case Study. J. Phys. Chem. B 2010, 114, 5632–5642. [DOI] [PubMed] [Google Scholar]
  29. Ishizuka R.; Huber G. A.; McCammon J. A. Solvation Effect on the Conformations of Alanine Dipeptide: Integral Equation Approach. J. Phys. Chem. Lett. 2010, 1, 2279–2283. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Adams J. P.; Smith D. A. Amber and Opls Studies of the Alanine Dipeptide Using the Gb Sa Solvation Method. Abstr. Pap. Am. Chem. Soc. 1993, 206, 42–COMP. [Google Scholar]
  31. Ramachandran G. N.; Ramakrishnan C.; Sasisekharan V. Stereochemistry of Polypeptide Chain Configurations. J. Mol. Biol. 1963, 7, 95–99. [DOI] [PubMed] [Google Scholar]
  32. Honda S.; Yamasaki K.; Sawada Y.; Morii H. 10 Residue Folded Peptide Designed by Segment Statistics. Structure 2004, 12, 1507–1518. [DOI] [PubMed] [Google Scholar]
  33. Suenaga A.; Narumi T.; Futatsugi N.; Yanai R.; Ohno Y.; Okimoto N.; Taiji M. Folding Dynamics of 10-Residue Beta-Hairpin Peptide Chignolin. Chem.—Asian J. 2007, 2, 591–598. [DOI] [PubMed] [Google Scholar]
  34. Case D. A.; Darden T. A.; Cheatham T. E. III; Simmerling C. L.; Wang J.; Duke R. E.; Luo R.; Walker R. C.; Zhang W.; Merz K. M.;. et al. AMBER 11; University of California: San Francisco, CA, 2010. [Google Scholar]
  35. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar]
  36. Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. C. Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of N-Alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar]
  37. Berendsen H. J. C.; Postma J. P. M.; Van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar]
  38. Pierce L. C. T.; Salomon-Ferrer R.; Augusto F de Oliveira C.; McCammon J. A.; Walker R. C. Routine Access to Millisecond Time Scale Events with Accelerated Molecular Dynamics. J. Chem. Theory Comput. 2012, 8, 2997–3002. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp401587e_si_001.pdf (435.5KB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES