How Well Does a Funneled Energy Landscape Capture the Folding Mechanism of Spectrin Domains?

Abstract

Three structurally similar domains from α-spectrin have been shown to fold very differently. Firstly, there is a contrast in the folding mechanism, as probed by Φ-value analysis, between the R15 domain and the R16 and R17 domains. Secondly, there are very different contributions from internal friction to folding: the folding rate of the R15 domain was found to be inversely proportional to solvent viscosity, showing no apparent frictional contribution from the protein, but in the other two domains a large internal friction component was evident. Non-native misdocking of helices has been suggested to be responsible for this phenomenon. Here, I study the folding of these three proteins with minimalist coarse-grained models based on a funneled energy landscape. Remarkably, I find that, despite the absence of non-native interactions, the differences in folding mechanism of the domains are well captured by the model, and the agreement of the Φ-values with experiment is fairly good. On the other hand, within the context of this model, there are no significant differences in diffusion coefficient along the chosen folding coordinate, and the model cannot explain the large differences in folding rates between the proteins found experimentally. These results are nonetheless consistent with the expectations from the energy landscape perspective of protein folding: namely, that the folding mechanism is primarily determined by the native-like interactions present in the Gō-like model, with missing non-native interactions being required to explain the differences in “internal friction” seen in experiment.

Introduction

One of the key features of the energy landscape theory of protein folding is that the folding mechanism is largely determined by the formation of native contacts, leading to a “funnel”-shaped energy landscape in which energy decreases with increasing formation of native structure.¹ An idealized funnel landscape may be realized for a given protein by constructing a Gōmodel, in which the only favorable pair interactions are those present in the native structure,² and such models have proved successful in predicting folding and binding mechanisms.^3,4 In many cases a single order parameter, such as the fraction of native contacts, is a good reaction coordinate for capturing the dynamics of folding. Specifically, folding may be modeled as diffusion on the one-dimensional free energy surface for this coordinate, which is usually barrier-limited due to the imperfect cancellation of changes in energy and chain entropy as the native state is approached^5–7 (to be precise the energy referred to here is the free energy as a function of the protein coordinates⁸). The diffusion coefficient should be determined by the local “roughness” of the energy landscape, that is, the heights of energy barriers between different protein configurations, for example due to torsion angle rotations or formation of contacts, as well as by contributions from the solvent viscosity.^9–11 In this picture, non-native contacts do not play any significant role in determining the mechanism of folding, but may modify the effective diffusion coefficient along the folding coordinate.^5,12 Here, mechanism refers to the order in which native structure is assembled on folding transition paths; non-native contacts can of course affect the free energy surface and folding rates.^13,14

Experimental measurements in which the solvent viscosity is varied therefore have the potential to tease apart the contributions to friction from solvent viscosity, and from internal friction due to the protein itself. Early efforts to identify a contribution from internal friction to the folding rate, by adding small molecule viscogenic agents, found it to be negligible for certain all-β and α/β proteins.^15–17 Internal friction was, however, detected for α-helical peptides¹⁸ and small, α-helical fast-folding proteins^19–21 and has also been inferred for fast-folding β-proteins.²² This discrepancy had been attributed to a greater sensitivity to internal friction contributions in the experiments on fast-folding proteins,²⁰ due to the greater relative importance of the prefactor in determining the folding rate.

The folding of the three spectrin domains from α-spectrin (R15, R16, R17) has several interesting connections with energy landscape theory. Despite their similar structure, extensive experimental folding studies,^23–29 have shown them to differ in two important respects. Firstly, there are differences in folding mechanism, which have been revealed by Φ-value analysis.^23–26 Secondly, despite folding on a millisecond time scale, evidence for internal friction has been obtained in two of the domains.²⁷ The viscosity of the solvent was varied by addition of a small-molecule viscogen, together with compensating amounts of chemical denaturant in order to offset the effect of the viscogen on protein stability thereby (assuming a linear free energy relation to hold) minimizing the effect on the free energy barrier to protein folding. This revealed that while the folding rate of one of the domains, R15, scaled inversely with the solvent viscosity (suggesting little contribution from internal friction to the folding rate), a strong indication of internal friction effects was obtained for the R16 and R17 domains. Given the close structural similarity of the domains (1), the exact origin of the differences in folding mechanism and internal friction effects remains unclear; molecular simulations may be able to shed some light on this question.

Here, I use structure-based (Gō) models in order to describe the folding of these three domains. The simulations predict the existence of sequential folding barriers in the energy landscape of R16 and a single barrier for R15, in qualitative agreement with experiment; a model with additional non-native interactions results in a broad barrier for both R16 and R17. Furthermore, Φ-values computed from the simulations are in fairly good agreement with experiment, considering the approximations involved. Thus, a smooth, “funneled” energy landscape appears to describe the qualitative features of the folding free energy landscape, and consequently, of the folding mechanism. However, there are no evident differences in the diffusion coefficient along the reaction coordinate between the three domains. Thus, the differences in internal friction between the domains are not captured by the model, suggesting that such effects are most likely due to non-native interactions, for example the mis-docking of helices which has been previously suggested.²⁷ Such a mis-docking mechanism is very plausible, considering the structure of the early transition states of R16 and R17 in the simulation (those in which internal friction has been identified experimentally²⁹).

Methods

Model and Simulation Methods

The Gō model for each protein was constructed from its native structure, taken from protein data bank entry 1U4Q³⁰ (R15: 1662-1773, R16: 1764-1879, R17: 1870-1979). In order to have all domains of the same length (116), residues which were present in the folding experiments but not in the crystal structure were added to the termini in a helical conformation: for R15, the N-terminal sequence KLKE was added, and for R17, the C-terminal sequence NSAFLQ was added. For each domain, a coarse grained Gō model was constructed using 1 bead per residue, according to the procedure described by Karanicolas and Brooks.³¹ The key features of the model are that the only favorable residue-residue contacts are those present in the native structure, pseudo-bond lengths and angles are taken from the experimental structure, and pseudo dihedral angles are given by a statistical potential based on their distribution in a subset of the protein data bank.³² The initial model was generated via the standard algorithm, following which all native contact energies were scaled by a factor of 1.25 in order to obtain folding temperatures of ∼ 350 K. The original version of the model includes only repulsive non-native interactions. A variant was also constructed in which non-native interactions were treated instead using a transferable protein-protein binding potential developed by Kim and Hummer;³³ the approach to combining this with the Gō model has been described previously.^11,34

All simulations were run with the CHARMM simulation code,³⁵ using a Langevin dynamics integrator³⁶ with a friction coefficient of 0.1 ps⁻¹. Pseudo bond lengths were fixed to their native values using the SHAKE algorithm³⁷ Free energy surfaces for each protein were constructed from a set of umbrella sampling simulations using the fraction of native contacts Q as a reaction coordinate. A restraint potential of the form V(Q) = k_Q(Q−Q₀)²/2 was used, with a force constant of k_Q = 600 kcal/mol and 16 windows with different target values Q₀ spanning the range 0–1; replica exchange moves were allowed between umbrella windows adjacent on Q. The weighted histogram method was used to combine the results from different temperatures and umbrella windows to compute thermodynamic quantities.³⁸

Diffusion coefficients on the reaction coordinate Q were calculated by discretizing Q and using a Bayesian procedure to determine local free energies G(Q_i) and diffusion coefficients D(Q_i) for each grid point Q_i from the propagators p(Q_j, t|Q_i, 0) estimated from the simulations, as described previously.^11,39–41 One important difference from previous work on fast-folding proteins was that, due to the slow folding rates of these domains, it was not possible to estimate diffusion coefficients from long equilibrium simulations. Instead, diffusion coefficients were estimated from simulations in which an inverse umbrella potential –F(Q) was added to the total system energy. The potential was represented as a cubic spline function. This approach has been shown to yield comparable results to equilibrium simulations, where Q is a good reaction coordinate.⁴¹

Results and Discussion

The approach taken here is to investigate to what extent “structure-based” or “Gō-like” models can capture the folding mechanism and unusual kinetics of the three spectrin domains considered. In these models, only native contacts are considered to be favorable energetically, and consequently the energy landscape is as close to a perfect “funnel” as possible, where increasing formation of native structure leads to lowering of the protein energy. The initial model considered is the generic Gō potential described by Karanicolas and Brooks,³¹ where the only element of the energy function not based on the native structure is the torsional potential, which is a statistical potential.

Free energy surfaces

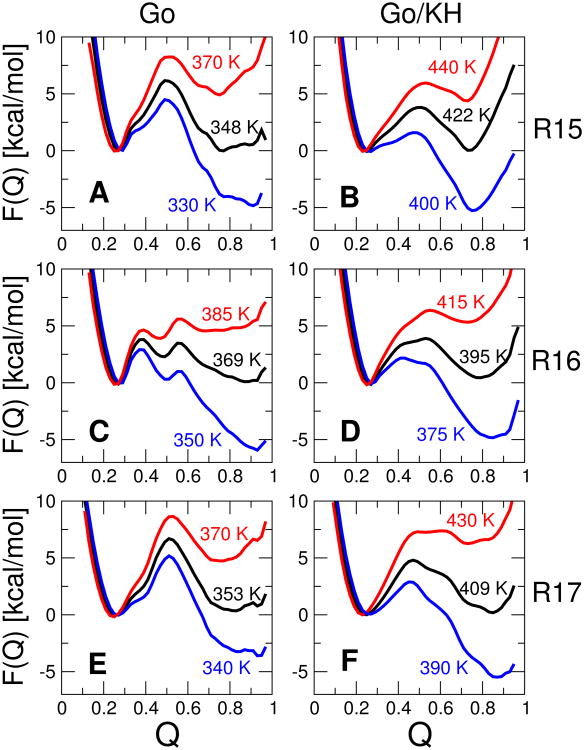
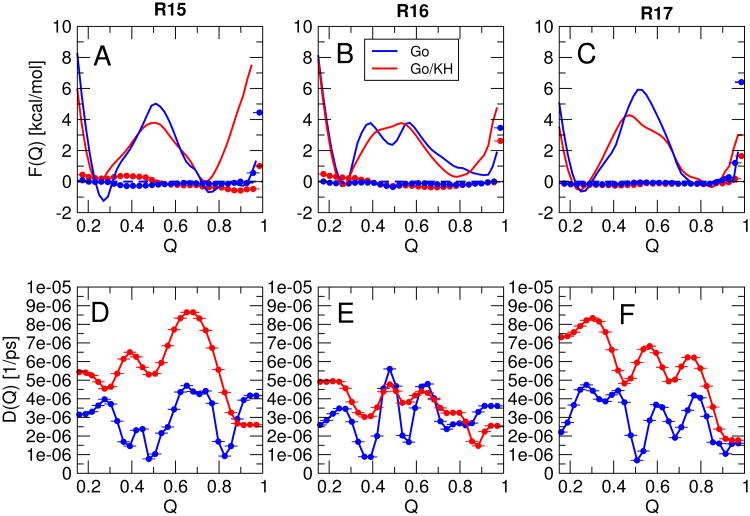
The free energy surfaces F(Q) for the fraction of native contacts Q are shown in 2A,C,E for each protein. As is evident, all the proteins are essentially “two-state”, i.e. there are only two states which are predominantly populated under any given equilibrium conditions.

A few features are immediately worth noting. At the midpoint, R15 and R17 each display a single energy barrier in F(Q), while two “sequential” barriers are evident for R16. This is consistent with the experimental evidence for either sequential barriers⁴² or a broad barrier⁴³ for R16, manifested in a downward curvature of the unfolding rate at high denaturant concentrations,^23,24 while there is no experimental evidence for sequential barriers in R15 and only certain mutants of R17 alter the slope of the unfolding arm of the chevron plot.²⁵ As in the experiments, the rate-limiting barrier is the early barrier under stabilizing conditions (low temperature in simulations, low denaturant in experiment), with the late barrier becoming prominent under destabilizing conditions (high temperature, high denaturant), consistent with the Hammond postulate, and earlier findings using lattice models.⁴⁴ There is also some evidence for heterogeneity in the native states of R15 and R17 (broad native minimum).

Gō-like models, as described above, can in fact exhibit “internal friction” effects, for example due to topological frustration.⁴⁵ However, since Gō models clearly exclude the possibility of internal friction effects due to attractive non-native interactions, I have also considered a model in which a “transferable” potential is used to describe non-native interactions. That is, instead of having only repulsive non-native interactions, as in the Gō model, the non-native interactions are described by a pair potential which depends only on the chemical identity of the participating residues. This is achieved by combining the standard Gō model as previously described¹¹ with a potential derived for protein-protein interactions due to Kim and Hummer;³³ this combination will be referred to as the Gō/KH potential. The idea of combining a non-native potential with a Gō model is not novel and has been pioneered by others.^8,46–50 It is important to note that residue pairs may be either mutually attractive or repulsive in this potential, depending on their types. The free energy surfaces for this modified model are shown in 2B,D,F. In general, the form of the free energy surfaces is still similar to that for the pure Gō model. R15 is still clearly two-state, with the barrier in much the same position (on Q) as before; the fully native state at high Q has become less stable, probably due to frustration arising from non-native interactions. The barrier is slightly lowered (seen also for the other two proteins) by non-native interactions, a finding which is consistent with predictions from theory and simulation,^51,52 although some simulation studies have found that non-native interactions may raise the folding barrier.⁴⁶ However, the sequential transition-states of R16 are less distinct, and appear as part of a single broad barrier. This may be because the non-native interactions destabilize the high energy intermediate, but it may also be due partly to the Q coordinate being slightly less suitable for describing free energy surfaces including non-native interactions. Another interesting difference from the pure Gō models, is that the surface for R17 also starts to show more of a “broad” barrier, which may be consistent with the ability of certain mutants to shift the slope of the unfolding arm of the chevron.²⁵ Notably, the addition of the non-native interactions shifts the major barrier at the midpoint temperature and below toward an earlier position on the reaction coordinate, similar to R16.

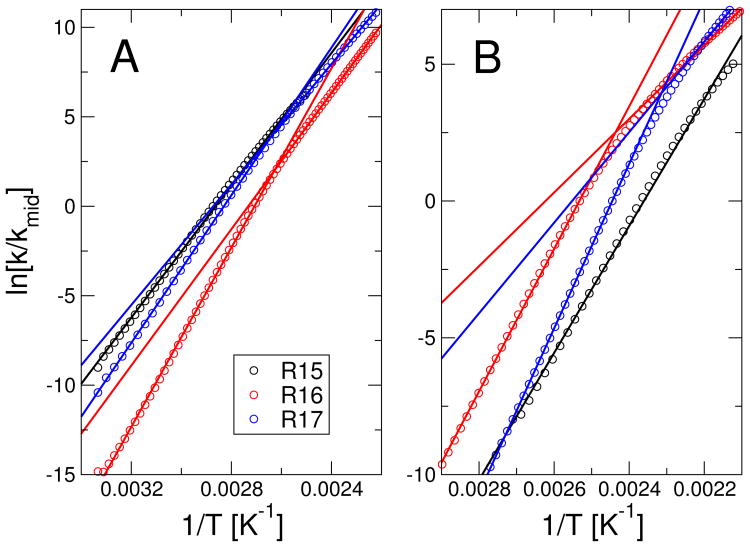
In order to confirm the relation between the observed sequential transition states or broad free energy barriers and the experimental observation of a non-linear dependence of unfolding rate on denaturant, I have determined the analogue of an experimental denaturant-dependent rate by varying the temperature in the simulations. Since carrying out explicit simulations at every temperature would be quite demanding given the height of the barrier for some of the proteins, we have instead used Kramers theory (described below) to approximate the rate at each temperature from the temperature-dependent free energy surface. Eyring plots of the unfolding rate in 3 show that I indeed obtain a slight inflection in the rate at the temperature at which the position of the transition state changes, for both R16 and R17 (the inflection is also slight in experiment). Such an inflection is missing for the Gō model of R15 and is much weaker for the Gō/KH model of that protein.

It should also be noted that sequential transition states or broad barriers, while sufficient to explain non-linear chevron plots, may not necessarily be the cause. For example, under conditions strongly favoring folding, strong rollover effects may have other causes, such as trapping in compact non-native configurations, or internal friction effects.^45,53 This type of effect may be the origin of the strong rollover seen in the folding of certain designed repeat proteins.⁵⁴ In the case of the spectrin domains, such an explanation is less likely, because there is no evidence in experiment for “rollover” in the folding rates, with the folding arm of the chevron being linear; only at relatively high denaturant concentration is there an inflection of the unfolding arm, which can be interpreted as a switch in barrier position.²⁵

Folding Mechanism

In order to compare the Gō model and Gō/KH models more quantitatively with the mechanism deduced from experiment, I have turned to folding Φ-values. The folding of each of the three spectrin domains has been extensively characterized via Φ-value analysis, including separate sets of Φ-values for the early and late transition states of R16. Experimentally, Φ-values are determined by considering the relative effect of a single-point mutation on the folding rate k_f and the equilibrium constant K_eq of a protein. That is, the Φ-value for a particular mutation is given by:

$$\Phi =\frac{ln[k_{\text{fold}}(\text{wt})/k_{\text{fold}}(\text{mut})]}{ln[K_{\text{eq}}(\text{wt})/K_{\text{eq}}(\text{mut})]}$$ (1)

The effect of any single point mutation on the energy function has been defined as a weakening of all native contact pairs involving the mutated residue; I have chosen to scale the pair contact energies by a factor of 1/2. I obtain the equilibrium constant directly from the umbrella sampling simulations used to generate the free energy surfaces, by integrating over F(Q)as

$$K_{\text{ep}}={\int }_{1/2}^{1}exp[-\beta F(Q)]\mathit{\text{dQ}}/{\int }_0^{1/2}exp[-\beta F(Q)]\mathit{\text{dQ}}$$ (2)

where β = 1/k_BT. A dividing surface of Q = 1/2 has been used in all cases, although the equilibrium constant is expected to be insensitive to this choice given the relatively high free energy barriers for these proteins. The free energy surfaces for the mutants were generated by perturbation using multidimensional WHAM³⁸ and equilibrium constants computed accordingly.

In principle, the rate coefficients could also be computed directly from simulations. Because of the relatively high barriers involved, it would be inefficient to do this via long equilibrium runs or first-passage time simulations, but it could be achieved via transition-path sampling.^55,56 However, because similar Φ values have been obtained by considering just the rates or only the contribution of the change in barrier height,⁵⁷ a thermodynamic approximation has been adopted here, where the diffusion coefficient along Q, D(Q), is assumed to be unaffected by the mutation; a similar approximation has been used successfully in previous simulation studies,^57,58 and I examine the validity of this approximation further below. To estimate the effect of barrier height on the rate, I use the overdamped Kramers result⁵⁹ that

$$k_{\text{fold}}^{-1}=D^{-1}{\int }_{1/2-\Delta }^{1/2+\Delta }exp[\beta F(Q)]\mathit{\text{dQ}}{\int }_0^{1/2}exp[-\beta F(Q)]\mathit{\text{dQ}}$$ (3)

and again computed the wild-type and mutant rates directly from their respective free energy surfaces, using a value of Δ = 0.15. In this expression, I am also making the assumption that D, the diffusion coefficient at the barrier top, is not affected by mutations (the actual value of D is not important for computing Φ-values). The results should be relatively insensitive to the choice of 1/2 as an approximate dividing surface, as long as [1/2−Δ, 1/2+Δ] includes the barrier region. Where possible, Φ-values were computed at the midpoint temperature (2). To compute separate Φ-values for the early and late transition states of R16, temperatures below and above the folding midpoint, respectively, were used. For the pure Gō model, these temperatures were 350 and 385 K, while for the Gō/KH model, temperatures of 375 and 415 K were used (see 2 for corresponding free-energy surfaces). Φ-values determined at the folding midpoint for R17 were very scattered – this likely reflects the very similar free energy of the early and late transition states for this protein, such that some mutations cause a shift in barrier near the midpoint. Therefore Φ-values were computed at a temperature below the midpoint, 390 K, as the experimental data refer to the early transition state.

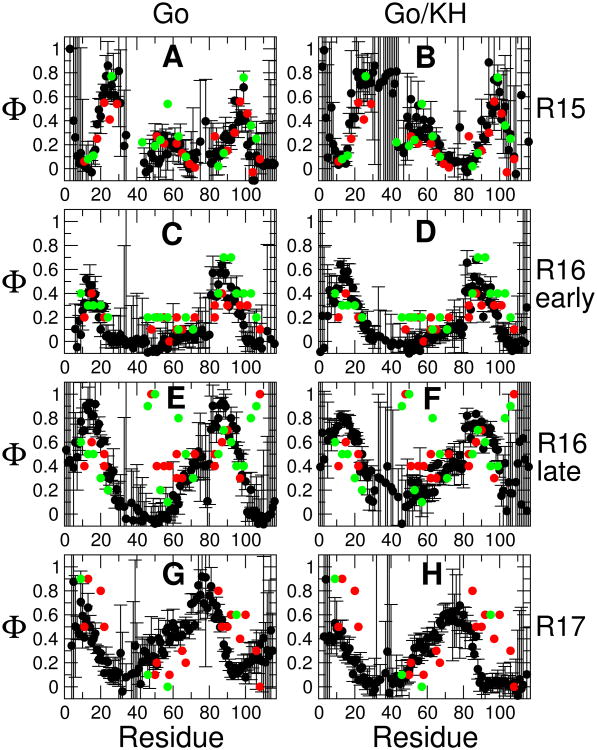
The resulting Φ-values are shown in 4, together with their experimental counterparts. For completeness, I have shown the calculated Φ-values for all residues, with the result that some of the errors are very large. This occurs for a similar reason to that causing large errors in experiment, namely that the change in stability for these residues upon mutation is comparable to the statistical error in the free energy estimate. This is because these residues tend to be forming few or only weak contacts and consequently would most likely be excluded from the experimental data set; the large errors should therefore not affect the comparison with experiment.

The agreement with experiment is generally good, particularly for R15 and R16. The addition of non-native contacts has a relatively small effect, slightly improving agreement with experiment for the late R16 transition state. This result is similar to what was obtained by Gin et al, who found that inclusion of non-native interactions affected the folding rates but not the mechanism.¹² There are several obvious outliers towards the center of the sequence and toward the end: these are the mutations H48A, A46G, A50G, A63G, A101G, A103G, A106G, L108A. All of these residues have very high Φ-values, with Φ ≥ 0.8. Nonetheless, the overall pattern of Φ-values through the sequence is reasonably well reproduced, including the increase of structure toward the N-terminus and center of the sequence in the late R16 transition state, relative to the early one. The match of the calculated Φ-values for R17 is less satisfactory. It appears that the experimental pattern of Φ-values is quite similar for R16 and R17, while the high Φ-value region of the R17 simulations has shifted toward the center of the sequence. Thus it is most likely that the relative interaction strengths stabilizing different regions of the structure are less well captured for R17 than for R16. Nonetheless, in comparing the results with R15, it is clear that the Gō and Gō/KH models do reflect the essential differences in mechanism between R15 and R16/R17. In the supporting information we provide corresponding scatter plots for the data, and a table of parameters describing the agreement with experiment. For the pure Gō model, the overall RMSD to experiment is 0.16, 0.19, 0.26 and 0.25 for R15, R16 early transition state, R16 late transition state (after excluding outliers) and R17 respectively, with the corresponding linear correlation coefficients being 0.76, 0.67, 0.68 and 0.25. A calculation of the mutual correlation between the different experimental and simulated Φ-values (Table S2) indicates that each experimental data set matches most closely the simulation of the corresponding protein, with the exception of the R17 data which matches the R16 simulatons more closely; however the Φ-values for R16 and R17 are quite similar. Because we model mutations using only contacts, one might expect the agreement to be worse for the helix-scanning Ala→Gly mutations on the surface, relative to the hydrophobic core mutations. Indeed a number of the very high “outlier” Φ values for the late R16 transition state are for Ala→Gly. However, the statistics in Table S2 do not indicate a systematic difference in accuracy between surface and core mutations, with the surface residues having lower RMSD than core residues in some cases, and higher RMSD than core residues in others. Thus it seems that the contact scaling model is no worse at capturing the effect of the Ala→Gly mutations than that of hydrophobic core mutations.

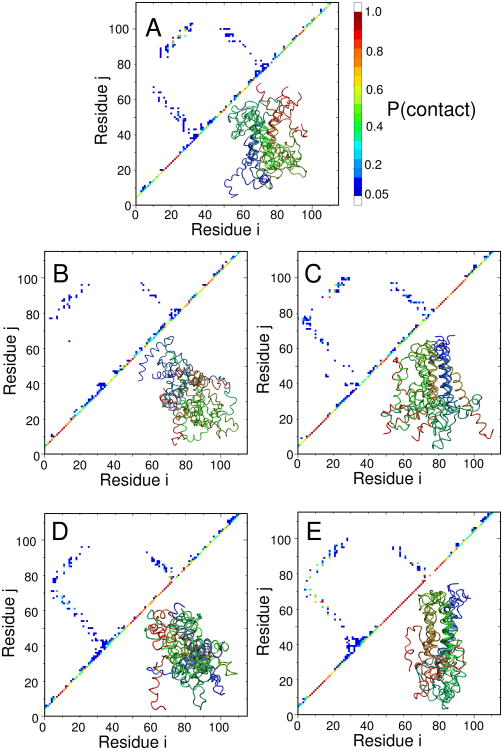
Having established consistency between the Φ-values from simulation and experiment, the simulations can be used to provide some structural insights into the folding mechanism. I do this by drawing structures from an equilibrium distribution at key values along the reaction coordinate Q, on the assumption that Q is a sufficiently good reaction coordinate – as it has been found to be for other proteins.^11,56,60 I have chosen to focus on the putative transition states for folding as being the key to establishing the folding mechanism. In order to simplify the analysis, we show only the results for the Gō/KH model in 5; results for the pure Gō model are very similar.

The transition state for R15 folding in 5 (A) shows the formation of ordered helical structure at the center of each of the three helices (diagonal), which are docked against each other, forming native contacts; the overall picture is very consistent with what would be deduced from a conventional interpretation of the Φ-values.⁶¹ The first transition states for R16 (5(B)) and R17 (5(D)) have some features in common, with native helix formation toward one end of the protein (N-terminus of helices 1 and 3 and C-terminus of helix 2), but relatively few contacts formed between the helices. In the corresponding late transition states, the native helix structure is even more extensive, with the three helices already docked in a native conformation at one end of the molecule; nascent contacts are being formed in the regions which are not yet helical.

What are the key differences between the different mechanisms, as deduced here? As has been concluded from a direct analysis of the experimental Φ-values, all of the transition states are somewhat similar, as reflected in the experimental Tanford β values, and the Q values which are all near 0.5 in the simulations. There is some overall similarity between all of the transition state contact maps. We focus on the comparison of the R15 and R16 transition states, as these are the ones best validated against the experimental Φ-values. In terms of tertiary structure, the R15 transition state is most similar to the R16 early transition state, with an RMSD for long range contacts (difference of residue indices greater than 5) between contact maps of 0.039, calculated over contacts that are formed in at least one of the transition states. This compares with an RMSD for long range contacts between the early and late transition states in R16 of 0.038. However, the differences in short range contacts (defined as not long range contacts) are larger, an RMSD of 0.23 between R15 and the early R16 transition state, but a difference of 0.11 between the early and late R16 transition states. This highlights the key difference between R15 and R16, namely the greater degree of secondary structure formation already in the early transition state of R16. The reason for the multi-state folding of R16/R17 appears to be a slight decoupling between the interactions in the two ends of the (rather elongated) spectrin domain, such that the end with the more stable interactions forms first. In R15, there does not appear to be such a decoupling and therefore native structure forms in a single step. So far, our results do not shed any light directly on the origin of the differences in internal friction observed for these domains. However, they are consistent: the large internal friction contribution is only observed for the early transition state for R16 and R17, which is absent from R15.²⁹ Secondly, the lack of ordered tertiary structure in the first transition state of R16/R17, in contrast to the relatively ordered secondary structure, would support a mechanism for internal friction involving misdocking of helices.

Although folding free energy barrier heights cannot be measured experimentally, it is nonetheless interesting to compare the relative midpoint barrier heights obtained in our model with the order of folding rates measured experimentally at the folding midpoint, i.e. R15 > R16 > R17. I find no correlation with barrier height for the pure Gō model, but the folding barriers of ∼ 3.5, ∼ 3.6, ∼ 4.5 kcal/mol for the Gō/KH model are consistent with the rank order of experimental folding rates. The improvement in agreement upon adding non-native interactions is most likely coincidental; however, it is noteworthy that a similar result was obtained by introducing electrostatic interactions into an Ising-like statistical mechanical model for these three proteins (i.e. the correct ranking was only obtained upon addition of electrostatics).⁶² However, in neither that work nor the present work was the difference in barrier height sufficient to explain the difference of over two orders of magnitude in folding rate between R15 and the other two domains.

Folding Dynamics

The unusual feature of the folding of this group of spectrin domains is the difference in internal friction, which may help to explain partially the large differences in folding rate. I therefore consider next the folding dynamics as represented by a one-dimensional diffusion model. In principle, differences in internal friction should manifest as differences in the diffusion coefficient along the folding coordinate, Q. I use a well established Bayesian method for determining free energies and diffusion coefficients for representing dynamics on a 1D reaction coordinate;^11,39,40 however, due to the high folding energy barriers, an additional trick was needed to sample diffusion coefficients in the high energy regions. Specifically, the free energy surface was “flattened” by adding the inverse potential −F(Q) to the total system energy. If Q is a good reaction coordinate and the dynamics can be represented by 1D diffusion along it, then diffusion coefficients obtained by this procedure should be identical to those for the original energy landscape, as we have previously shown.⁴¹

In 6 A-C I show the original free energy surfaces (lines), as well as the free energy surfaces resulting from sampling with the added inverse potential (symbols). As intended, the resulting free energy surfaces are flat, allowing sampling of diffusion at all values of Q. Diffusion coefficients for the Gō model and Gō/KH model are presented in 6 D-F.

As has previously been observed for other proteins, the variation in diffusion coefficients over the full range of Q is relatively small.¹¹ This occurs because even though diffusion is faster in Cartesian space for more unfolded states, the distance which must be travelled to form a contact is larger than it would be for more native-like state, and the two effects approximately compensate. In addition, there is very little difference between the diffusion coefficients for the different proteins when the Gō model only is considered. While that may not be unexpected, the diffusion coefficients obtained with the additional “non-native” interactions are also rather similar. Across all proteins and the two energy functions, the diffusion coefficients vary by only a factor of 2-3. Therefore, this model of non-native interactions does not explain the differences in folding rate between the different spectrin domains.

It must be noted, however, that the internal friction in the early transition states of R16 and R17 is highly localized, being undetectable in both the unfolded state and second transition state;²⁹ in fact the folding models I use here do correctly capture the similarity of the diffusion coefficients in the unfolded state, for example. Most likely, the internal friction in the first transition state is quite structurally specific in origin, and the specific model of non-native interactions employed here is simply not accurate enough to capture it.

To quantify how much of the variation in rates between the three proteins is captured by the diffusion model, I have determined the midpoint folding rates by constructing a 1D diffusion model in which I combine the unbiased free energy surfaces with the diffusion coefficients obtained with the flat free energy surface (1). The computed folding rates in 1 indicate that neither the Gō, nor the Gō/KH model captures the variation in folding rates seen in experiment. The Gō model suggests that R17 is the fastest folder, and while the Gō/KH model correctly indicates that R15 is fastest, the variation in folding rate between the three domains is much smaller than in experiment.

Combining unbiased free energy surfaces with diffusion coefficients obtained from the flat free energy surface assumes that 1D diffusion along Q is a good model for the folding dynamics. That assumption was previously shown to give reliable results for a model of protein G.⁴¹ However, I also find here that the rates from the diffusion model are in reasonable agreement with independent estimates for the same molecular simulation model. For example, computing the folding rate for R15 from the 1D diffusion model gives a rate of 3.2 ×10⁴ s⁻¹, whereas a separate estimate of the folding rate from transition-path sampling,⁵⁵ resulted in a rate of ∼ 6.4×10⁴ s⁻¹. Note that because of the low solvent friction and smooth energy landscapes used in the simulations, these rates are much faster than the experimental midpoint folding rate of ∼ 90 s⁻¹; this is a well-known deficiency of coarse-grained Gō models with two-body contact potentials.⁶³

The most likely reason for the failure of the Gō/KH model to capture the difference in folding rates between domains is that the model used for non-native interactions underestimates their strength relative to the native contacts. Although one cannot pinpoint the exact cause for this based on the results presented, one weakness of the current non-native model is the treatment of electrostatic interactions such that they may be too weak at short range. Thus, if the misdocking of helices were driven by misformation of non-native salt-bridges, their strength may be underestimated by the model. Given the involvement of charged residues in slowing the folding of R16 and R17,²⁸ this may be an significant deficiency in the model. Another respect in which the gap with experiment may be narrowed would be to adopt the same operational definition of internal friction in terms of the dependence of folding rate on solvent viscosity, as done in a recent simulation study.⁶⁴

Conclusions

The results presented here indicate that a purely “structure-based” model for folding based on only native-like interactions describes fairly well the folding mechanism of the set of three spectrin domains I have studied, as measured by folding Φ-values. The addition of a “transferable” non-native contact potential does improve the free energy surface in some cases (R17) to be more similar to that inferred experimentally. The accuracy of the prediction from a structure-based model is in general support of the energy landscape theory, in which native contacts play the dominant role in determining the folding mechanism,³ although there are exceptions in which non-native interactions do appear to play an important role in stabilizing folding intermediates.^65,66

The fact that a purely structure-based model does not distinguish the roughness of the different spectrin domains would suggest that such roughness must arise from non-native interactions – precisely the role these interactions play according to the energy landscape perspective. For example, the structure of the first transition-state for the Gō-based models would allow for non-native helix docking as suggested previously. A clear remaining challenge for future simulations and experiments is to resolve the remarkable differences in internal friction between these domains at a molecular level.

Figure 1.

Native structures of the three spectrin domains, overlaid. blue: R15, red: R16, grey: R17. Residues not present in the crystal structure 1U4Q³⁰ have been added in a helical conformation.

Figure 2.

Free energy surfaces F(Q) for the fraction of native contacts Q. A, C, E are surfaces for the pure Gō model for R15, R16 and R17 respectively and B, D, F are the corresponding surfaces for a Gō model with a transferable non-native potential. Black, blue and red curves are potentials of mean force at the midpoint (folding) temperature T_f, and at selected temperatures (displayed) below and above it respectively.

Figure 3.

Unfolding “limb” of chevron plots for (A) pure Gō model and (B) Gō model with non-native contacts added. Symbols represent the log-ratio of the unfolding rate relative to the midpoint unfolding rate, as estimated from the free energy surfaces using Eq. 3. Lines are linear fits to the full data range for R15 and separate fits to high and low temperature data for R16, R17.

Figure 4.

Φ-values. Φ-values estimated from simulation are shown by black symbols, with experimental Φ-values from “core” and Ala→Gly mutations indicated by red and green respectively. A, C, E, G are Φ-values estimated from a pure Gō model for R15, the early R16 transition state, late R16 transition state and R17; B, D, F, H are the corresponding results for a Gō model in which non-native interactions are treated by a transferable potential.

Figure 5.

Structures of putative transitions states: (A) R15 (Q = 0.5), (B) R16 early (Q = 0.39), (C) R16 late (Q = 0.55), (D) R17 early (Q = 0.46), (E) R17 late (Q = 0.63). All structures were drawn randomly from an equilbrium distribution at the specified Q-values for the Gō/KH model. For each transition state ensemble, an average contact map (upper left) and representative set of structures (lower right) are shown. Results for the pure Gō model are similar and are not shown for clarity (the R17 transition state in the Gō model is similar to the late R17 transition state in the Gō/KH model).

Figure 6.

Free energies and position-dependent diffusion coefficients for Q. Top: free energy surfaces for (A) R15, (B) R16, (C) R17; bottom: diffusion coefficients for (D) R15, (E) R16, (F) R17. Blue lines and symbols correspond to the original Gō model, while red lines and symbols correspond to the Gō/KH model. In (A)-(C), the lines represent the original potential of mean force F(Q) (see 2), while the symbols represent the free energy estimate from simulations in which an estimate of −F(Q) was added to the simulation energy as a cubic spline.

Table 1. Folding rates from 1D diffusion model, and from experiment, ²⁶ at the folding midpoint (Units of s⁻¹).

	R15	R16	R17
Gō	3.2×104	7.0×105	1.3×104
Gō/KH	4.7×106	1.1×106	2.0×106
Experiment	9.0×101	2.2×10−1	8.2×10−2